Foundations of Process Discovery

Abstract

Process discovery is probably the most interesting, but also most challenging, process mining task. The goal is to take an event log containing example behaviors and create a process model that adequately describes the underlying process. This chapter introduces the baseline approach used in most commercial process mining tools. A simplified event log is used to create a so-called Directly-Follows Graph (DFG). This baseline is used to explain the challenges one faces when trying to discover a process model. After introducing DFG discovery, we focus on techniques that are able to discover models allowing for concurrency (e.g., Petri nets, process trees, and BPMN models). The chapter distinguishes two types of approaches able to discover such models: (1) bottom-up process discovery and (2) top-down process discovery. The Alpha algorithm is presented as an example of a bottom-up technique. The approach has many limitations, but nicely introduces the idea of discovering local constraints. The basic inductive mining algorithm is presented as an example of a top-down technique. This approach, combined with frequency-based filtering, works well on most event logs. These example algorithms are used to illustrate the foundations of process discovery.

1 Introduction

Process discovery is typically the first step after extracting event data from source systems. Based on the selected event data, process discovery algorithms automatically construct a process model describing the observed behavior. This may be challenging because, in most cases, the event data cannot be assumed to be complete, i.e., we only witnessed example behaviors. There may also be conflicting requirements (e.g., recall, precision, generalization, and simplicity) [1, 3]. This makes process discovery both interesting and challenging.

Fig. 1.

This chapter focuses on process discovery. This is the first step after extracting event data from the source system(s). To set the scene, we consider only control-flow information, i.e., the ordering of activities.

Figure 1 positions this chapter. The input for process discovery is a collection of events and the output is a process model. Such a process model can be used to uncover unexpected deviations and bottlenecks. In the later stages of the process mining pipeline shown in Fig. 1, process models are used to check compliance, compare processes, detect concept drift, and predict performance and compliance problems.

Events may have many attributes and refer to multiple objects of different types [3]. However, in this chapter, we start from very basic event data. We assume that each event refers to a case, an activity, and has a timestamp. There may be many other attributes (e.g., resource), but we ignore these. Initially, we assume that timestamps are only used for the ordering of events corresponding to the same case. This implies that each case is represented by a sequence of activities. We call this a trace. For example, $\sigma = \langle a,b,c,e \rangle$ represents a case for which the activities a, b, c, and e occurred. Note that there may be many cases that have the same trace. Therefore, we represent an event log as a multiset of traces. For example, $L_1 = [\langle a,b,c,e \rangle ^{10},\langle a,c,b,e \rangle ^5, \langle a,d,e \rangle ]$ is an event log describing 16 cases and $10\times 4 + 5 \times 4 + 1 \times 3 = 63$ events. Note that trace $\sigma = \langle a,b,c,e \rangle$ appears 10 times. In [3], we use the term simplified event log. Here we drop the adjective “simplified” since the representation will be used throughout the chapter.

Definition 1 (Event Log)

 $\mathcal{U}_{ act }$ is the universe of activity names. A trace $\sigma = \langle a_1,a_2,\ldots ,a_n \rangle \in {\mathcal{U}_{ act }}^*$ is a sequence of activities. An event log $L \in \mathcal {B}({\mathcal{U}_{ act }}^*)$ is a multiset of traces.

Note that $L(\sigma )$ is the number of times trace $\sigma$ appears in event log L. For example, $L_1(\langle a,b,c,e \rangle )=10$, $L_1(\langle a,c,b,e \rangle )=5$, $L_1(\langle a,d,e \rangle )=1$, $L_1(\langle b,a \rangle )=0$, $L_1(\langle c \rangle )=0$, $L_1(\langle \,\rangle )=0$, etc.

Fig. 2.

Three process models learned from event log $L_1 = [\langle a,b,c,e \rangle ^{10},\langle a,c,b,e \rangle ^5, \langle a,d,e \rangle ]$.

Given an event log $L \in \mathcal {B}({\mathcal{U}_{ act }}^*)$, we would like to learn a process model adequately capturing the observed behavior. Figure 2 shows four process models discovered for $L_1 = [\langle a,b,c,e \rangle ^{10},\langle a,c,b,e \rangle ^5, \langle a,d,e \rangle ]$. The models also show frequencies.

Figure 2(b) shows a Directly-Follows Graph (DFG). The start, end, and five activities are the nodes of the graph. Activities a and e occurred 16 times, b and c occurred 15 times, and d only once. The arcs in Fig. 2(b) show how often an activity is directly followed by another activity. For example, a is 10 times directly followed by b, a is 5 times directly followed by c, and a is once directly followed by d. To indicate the start and end of cases, we use a start node $\blacktriangleright$ and an end node ${\scriptstyle {\blacksquare }}$. One can view $\blacktriangleright$ and ${\scriptstyle {\blacksquare }}$ as “dummy” activities or states. Although they do not present real activities, they are needed to describe the process adequately. Since all 16 cases start with a, the arc connecting $\blacktriangleright$ to a has a frequency of 16. Note that due to the cycles in the DFG, also traces such as $\langle a,b,c,b,c,b,c,b,e \rangle$ are possible according to the DFG (but did not appear in the event log).

Figure 2(c) shows a Petri net discovered using the same event log $L_1$. The transitions (i.e., squares) correspond to the five activities in the event log. The places (i.e., circles) constrain the behavior. The Petri net allows for the three traces in the event log and nothing more. Initially, only transition a is enabled. When a fires (i.e., occurs), a token is consumed from the input place and a token is produced for each of the two output places. As a result, transitions b, c, and d become enabled. If d fires, both tokens are removed and two tokens are produced for the input places of e. If b fires, only one token is consumed and one token is produced. After b fires, c is still enabled, and c will fire to enable e. Transition c can also occur before b, i.e., b and c are concurrent and can happen at the same time or in any order. There is a choice between d and the combination of b and c. The start of the process is modeled by the token in the source place. The end of the process is modeled by the double-bordered sink place.

Also, the process tree discovered for event log $L_1$ shown in Fig. 2(d) allows for the three traces in the event log and nothing more. The root node is a sequence ($\rightarrow$) with three “child nodes”: activity a, a choice, and activity e. These nodes are visited 16 times (once for each case). The choice node ($\times$) has two “child nodes”: a parallel node $\wedge$ and an activity node e. The parallel node ($\wedge$) has two “child nodes”: activity b and activity c. The whole process tree can be represented by the expression ${\rightarrow }(a,\times (\wedge (b,c),d),e)$. Note that the d node is visited only once. The $\wedge$, b, and c nodes are visited 15 times. In this example, each node has a unique label allowing us to refer easily. Often a tree has multiple nodes with the same label, e.g., ${\rightarrow }(a,\times ({\rightarrow }(a,a),a),a)$ where a appears five times and $\rightarrow$ two times.

In Fig. 2, we just show example results. In the remainder, we will see how such process models can be learned from event data. The goal of this chapter is not to give a complete survey (see also [10] for a recent survey). Instead, we would like to bring forward the essence of process discovery from event data, and introduce the main principles in an intuitive manner.

The remainder of this chapter is organized as follows. Section 2 presents a baseline approach that computes a Directly-Follows Graph (DFG). This approach is simple and highly scalable, but has many limitations (e.g., producing complex underfitting process models) [2]. In Sect. 3, we elaborate on the challenges of process discovery. Section 4 discusses higher-level representations such as Petri nets (Subsect. 4.1), process trees (Subsect. 4.2), and BPMN (Subsect. 4.3). Section 5 introduces “bottom-up” process discovery using the Alpha algorithm [1, 9] as an example. Section 6 introduces “top-down” process discovery using the basic inductive mining algorithm [22,23,24] as an example. Finally, Sect. 7 concludes the chapter with pointers to other discovery approaches (e.g., using state-based or language-based regions).

2 Directly-Follows Graphs: A Baseline Approach

In this chapter, we present a very simple discovery approach that is supported by most (if not all) process mining tools: Constructing a so-called Directly-Follows Graph (DFG) by simply counting how often one activity is followed by another activity (see Fig. 2(b)). We use this to also introduce filtering techniques to remove infrequent activities, infrequent variants, and infrequent arcs. The more advanced techniques presented later in this chapter build upon the simple notions introduced in this section.

Let us first try to describe the process discovery problem in abstract terms, independent of the selected process modeling notation. Therefore, we describe a model’s behavior as a set of traces.

Definition 2 (Process Model)

$\mathcal{U}_{ M }$ is the universe of process models. A process model $M \in \mathcal{U}_{ M }$ defines a set of traces $lang (M) \subseteq {\mathcal{U}_{ act }}^*$.

Examples of process models defined later are DFGs $\mathcal{U}_{ G }\subseteq \mathcal{U}_{ M }$ (Sect. 2.1), accepting Petri nets $\mathcal{U}_{ AN }\subseteq \mathcal{U}_{ M }$ (Sect. 4.1), process trees $\mathcal{U}_{ Q }\subseteq \mathcal{U}_{ M }$ (Sect. 4.2), and BPMN models $\mathcal{U}_{ BPMN }\subseteq \mathcal{U}_{ M }$ (Sect. 4.3). Consider, for example, the process models $M_1$ (DFG), $M_2$ (Petri net), and $M_3$ (process tree) in Fig. 2. $lang (M_2)= lang (M_3)= \{ \langle a,b,c,e \rangle ,\langle a,c,b,e \rangle , \langle a,d,e \rangle \}$. $lang (M_1) = \{\langle a,b,e \rangle , \langle a,c,e \rangle , \langle a,d,e \rangle ,\ldots ,\langle a,b,c,b,c,b,c,e \rangle ,\ldots \}$ contains infinitely many traces due to the cycle involving b and c.

The goal of a process discovery algorithm is to produce a model that explains the observed behavior.

Definition 3 (Process Discovery Algorithm)

A process discovery algorithm is a function $disc \in \mathcal {B}({\mathcal{U}_{ act }}^*) \rightarrow \mathcal{U}_{ M }$, i.e., based on a multiset of traces, a model is produced.

Given an event log L, a process discovery algorithm $disc$ returns a model allowing for the traces $lang ( disc (L))$. A discovery algorithm $disc$ guarantees perfect replay fitness if for any $L \in \mathcal {B}({\mathcal{U}_{ act }}^*)$: $\{\sigma \in L\} \subseteq lang ( disc (L))$. We write $\{\sigma \in L\}$ to turn a multiset of traces into a set of traces and make the model and the log comparable. All three models in Fig. 2 have perfect replay fitness (also called perfect recall).

2.1 Directly-Follows Graphs: Basic Concepts

We already informally introduced DFGs, but now we formalize the concepts needed to precisely describe the corresponding discovery algorithm.

Definition 4 (Directly-Follows Graph)

A Directly-Follows Graph (DFG) is a pair $G = (A,F)$ where $A \subseteq \mathcal{U}_{ act }$ is a set of activities and $F \in \mathcal {B}((A \times A) \cup (\{\blacktriangleright \} \times A) \cup (A \times \{{\scriptstyle {\blacksquare }}\}) \cup (\{\blacktriangleright \} \times \{{\scriptstyle {\blacksquare }}\}))$ is a multiset of arcs. $\blacktriangleright$ is the start node and ${\scriptstyle {\blacksquare }}$ is the end node ($\{\blacktriangleright ,{\scriptstyle {\blacksquare }}\} \cap \mathcal{U}_{ act }= \emptyset$). $\mathcal{U}_{ G }\subseteq \mathcal{U}_{ M }$ is the set of all DFGs.

$\blacktriangleright$ and ${\scriptstyle {\blacksquare }}$ can be viewed as artificially added activities to clearly indicate the start and end of the process. The nodes of a DFG are $\blacktriangleright$ to denote the beginning, ${\scriptstyle {\blacksquare }}$ to denote the end, and the activities in set A. Note that ${\blacktriangleright } \not \in A$ and ${{\scriptstyle {\blacksquare }}} \not \in A$ (this is also important in later sections). There are four types of arcs: $(\blacktriangleright ,a)$, $(a_1,a_2)$, $(a,{\scriptstyle {\blacksquare }})$, and $(\blacktriangleright ,{\scriptstyle {\blacksquare }})$ (with $a,a_1,a_2 \in A$). $F((\blacktriangleright ,a))$ indicates how many cases start with a, $F((a_1,a_2))$ indicates how often activity $a_1$ is directly followed by activity $a_2$, $F((a,{\scriptstyle {\blacksquare }}))$ indicates how many cases end with a, and $F((\blacktriangleright ,{\scriptstyle {\blacksquare }}))$ counts the number of empty cases. In the directly-follows graph, we only consider directly-follows within the same case. For example, $F((a,b)) = (10 \times 0) + (10 \times 0) + (10 \times 1) + (10 \times 2) + (10 \times 3)=60$ given some event log $[\langle a \rangle ^{10},\langle b \rangle ^{10}, \langle a,b \rangle ^{10}, \langle a,b,a,b \rangle ^{10},\langle a,b,a,b,a,b \rangle ^{10}]$.

The DFG in Fig. 2(b) can be described as follows: $M_1 = (A,F)$ with $A = \{a,b,c,d,e\}$ and $F = [ (\blacktriangleright ,a)^{16}, (a,b)^{10}, (a,c)^{5}, (a,d)^{1}, (b,c)^{10},(b,e)^{5},(c,b)^{5},(c,e)^{10},(d,e)^{1},(e,{\scriptstyle {\blacksquare }})^{16}]$.

Fig. 3.

Three process models learned from event log $L_2 = [ \langle a,b,c,e \rangle ^{50},\langle a,c,b,e \rangle ^{40},\langle a,b,c,d,b,c,e \rangle ^{30},\langle a,c,b,d,b,c,e \rangle ^{20},\langle a,b,c,d,c,b,e \rangle ^{10},\langle a,c,b,d,c,b,d,b,c,e \rangle ^{10} ]$.

Figure 3 shows process models discovered for another event log $L_2 = [ \langle a,b,c,e \rangle ^{50},\langle a,c,b,e \rangle ^{40},\langle a,b,c,d,b,c,e \rangle ^{30},\langle a,c,b,d,b,c,e \rangle ^{20},\langle a,b,c,d,c,b,e \rangle ^{10},\langle a,c,b,d,c,b,d,b,c,e \rangle ^{10} ]$. The fact that b, c, and d occur a variable number of times per case suggests that there is a loop. Figure 3(b) shows the corresponding DFG. This DFG can be described as follows: $M_4 = (A,F)$ with $A = \{a,b,c,d,e\}$ and $F = [ (\blacktriangleright ,a)^{160},$ $(a,b)^{90},$ $(a,c)^{70},$ $(b,c)^{150},$ $(b,d)^{40},$ $(b,e)^{50},$ $(c,b)^{90},$ $(c,d)^{40},$ $(c,e)^{110},$ $(d,b)^{60},$ $(d,c)^{20},$ $(e,{\scriptstyle {\blacksquare }})^{160}]$.

Definition 5 (Traces of a DFG)

Let $G = (A,F) \in \mathcal{U}_{ G }$ be a DFG. The set of possible traces described by G is $lang (G) = \{ \langle a_2, a_3, \ldots , a_{n-1} \rangle \mid a_1 = {\blacktriangleright } \ \wedge \ a_n = {\scriptstyle {\blacksquare }}\ \wedge \ \forall _{1 \le i < n}\ (a_i,a_{i+1}) \in F\}$.

Note that $\blacktriangleright$ and ${\scriptstyle {\blacksquare }}$ have been added to the DFG to have a clear start and end. However, these “dummy activities” are not part of the language of the DFG.

Consider the DFG $M_1$ shown in Fig. 2(b): $lang (M_1) = \{ \langle a,b,e \rangle ,\langle a,c,e \rangle ,\langle a,d,e \rangle ,\langle a,b,c,e \rangle ,\langle a,c,b,e \rangle ,\langle a,b,c,b,e \rangle ,\langle a,c,b,c,e \rangle ,\langle a,b,c,b,c,e \rangle ,\ldots \}$. Also the DFG $M_4$ in Fig. 3(b) has an infinite number of possible traces: $lang (M_4) = \{ \langle a,b,e \rangle ,\langle a,c,e \rangle ,\langle a,b,c,e \rangle ,\langle a,c,b,e \rangle ,\langle a,b,c,b,e \rangle ,\langle a,c,b,c,e \rangle ,\langle a,b,d,b,e \rangle ,\ldots \}$. Whenever the DFG has a cycle, then the number of possible traces is unbounded.

2.2 Baseline Discovery Algorithm

Since the event log only contains example traces, it is natural that the discovery algorithm aims to generalize the observed behavior to avoid over-fitting. Therefore, we start with a baseline discovery algorithm that ensures that all observed behavior is possible according to the discovered process model. The algorithm used to discover the DFGs in Fig. 2(b) and Fig. 3(b) is defined as follows.

Definition 6 (Baseline Discovery Algorithm)

Let $L \in \mathcal {B}({\mathcal{U}_{ act }}^*)$ be an event log. $disc _{{}_{ DFG }}(L) = (A,F)$ is the DFG based on L with:

• $A = \{a \in \sigma \mid \sigma \in L\}$ and

• $F = [ (\sigma _i,\sigma _{i+1}) \mid \sigma \in L' \ \wedge \ 1 \le i < \left| {\sigma }\right| ]$ with $L' = [ \langle \blacktriangleright \rangle \cdot \sigma \cdot \langle {\scriptstyle {\blacksquare }}\rangle \mid \sigma \in L]$.

Note that L, $L'$, and F in Definition 6 are multisets. Each trace in the event log L is extended with the artificially added activities. $L'$ adds $\blacktriangleright$ at the start and ${\scriptstyle {\blacksquare }}$ at the end of each trace in L. $M_1 = disc _{{}_{ DFG }}(L_1)$ is depicted in Fig. 2(b) and $M_4 = disc _{{}_{ DFG }}(L_2)$ is depicted in Fig. 3(b).

A DFG can be viewed as a first-order Markov model (i.e., the state is determined by the last activity executed). The baseline discovery algorithm (Definition 6) tends to lead to underfitting process models. Whenever two activities are not executed in a fixed order, a loop is introduced.

2.3 Footprints

A DFG can also be represented as a matrix, as shown in Table 1. This is simply a tabular representation of the graph and the arc frequencies, e.g., $F((\blacktriangleright ,\blacktriangleright ))=0$, ${F((\blacktriangleright ,a))}= 16$, and $F((c,e))= 10$. To capture the relations between activities, we can also create a so-called footprint matrix [1]. Table 2 shows the footprint matrix for the DFG in Fig. 2(b). Between two activities $a_1$ and $a_2$, precisely one of four possible relations holds:

• $a_1 \rightarrow a_2$ (i.e., $a_1$ is sometimes directly followed by $a_2$, but $a_2$ is never directly followed by $a_1$),

• $a_1 \leftarrow a_2$ (i.e., $a_2$ is sometimes directly followed by $a_1$, but $a_1$ is never directly followed by $a_2$),

• $a_1 {\Vert } a_2$ (i.e., $a_1$ is sometimes directly followed by $a_2$ and $a_2$ is sometimes directly followed by $a_1$), and

• $a_1 {\#} a_2$ (i.e., $a_1$ is never directly followed by $a_2$ and $a_2$ is never directly followed by $a_1$).

Table 1. Matrix representation of the DFG in Fig. 2(b).

Table 2. The footprint of the DFG in Fig. 2(b).

Table 2 (based on Fig. 2(b)) shows, for example, that $a \rightarrow b$, $b \leftarrow a$, $b \Vert c$, and $c \# d$. The creation of the footprint can be formalized as follows.

Definition 7 (Footprint)

Let $G=(A,F) \in \mathcal{U}_{ G }$ be a DFG. G defines a footprint $fp (G) \in (A' \times A') \rightarrow \{\rightarrow ,\leftarrow ,\Vert ,\#\}$ such that $A' = A \cup \{\blacktriangleright ,{\scriptstyle {\blacksquare }}\}$ and for any $(a_1,a_2) \in A' \times A'$:

• $fp (G)((a_1,a_2)) = {\rightarrow }$ if $(a_1,a_2)\in F$ and $(a_2,a_1)\not \in F$,

• $fp (G)((a_1,a_2)) = {\leftarrow }$ if $(a_1,a_2)\not \in F$ and $(a_2,a_1)\in F$,

• $fp (G)((a_1,a_2)) = {\Vert }$ if $(a_1,a_2)\in F$ and $(a_2,a_1)\in F$, and

• $fp (G)((a_1,a_2)) = {\#}$ if $(a_1,a_2)\not \in F$ and $(a_2,a_1)\not \in F$.

We write $a_1 \rightarrow _{{}_G} a_2$ if $fp (G)((a_1,a_2)) = {\rightarrow }$, $a_1 \#_{{}_G} a_2$ if $fp (G)((a_1,a_2)) = \#$, etc.

We can also create the footprint of an event log by first applying the baseline discovery algorithm: $fp (L) = fp ( disc _{{}_{ DFG }}(L))$. Hence, Table 2 also shows $fp (L_1) = fp ( disc _{{}_{ DFG }}(L_1)) = fp (M_1)$. This allows us to write $b {\rightarrow }_{L_1} e$, $b {\Vert }_{L_1} e$, $b {\#}_{L_1} d$, etc.

2.4 Filtering

Using the baseline discovery algorithm, an activity a appears in the discovered DFG when it occurs at least once and two activities $a_1$ and $a_2$ are connected by a directed arc if $a_1$ is directly followed by $a_2$ at least once in the log. Often, we do not want to see the process model that captures all behavior. Instead, we would like to see the dominant behavior. For example, we are interested in the most frequent activities and paths. Therefore, we would like to filter the event log and model. Here, we consider the three basic types of filtering:

• Activity-based filtering: project the event log on a subset of activities (e.g., remove the least frequent activities).

• Variant-based filtering: remove selected traces (e.g., only keep the most frequent variants).

• Arc-based filtering: remove selected arcs in the DFG (e.g., delete arcs with a frequency lower than a given threshold).

To describe the different types of filtering, we introduce some notations for traces and event logs.

Definition 8 (Frequency and Projection Functions)

Let $L \in \mathcal {B}({\mathcal{U}_{ act }}^*)$ be an event log.

• $act (L) = \{a \in \sigma \mid \sigma \in L\}$ are the activities in event log L,

• $var (L) = \{\sigma \in L\}$ are the trace variants in event log L,

• $\#^{ act }_{L}(a) = \sum _{\sigma \in L} \left| {\{i \in \{1, \ldots \left| {\sigma }\right| \} \mid \sigma _i = a \}}\right|$ is the frequency of activity $a \in act (L)$ in event log L,

• $\#^{ var }_{L}(\sigma ) = L(\sigma )$ is the frequency of variant $\sigma \in var (L)$ in event log L,

• for a subset of activities $A \subseteq act (L)$ and trace $\sigma \in L$, we define $\sigma {\uparrow } A$ such that $\langle \rangle {\uparrow } A = \langle \rangle$ and $(\sigma \cdot \langle a \rangle ) {\uparrow } A = \sigma {\uparrow } A \cdot \langle a \rangle$ if $a \in A$, and $(\sigma \cdot \langle a \rangle ) {\uparrow } A = \sigma {\uparrow } A$ if $a \not \in A$,

• $L {\uparrow } A = [\sigma {\uparrow } A \mid \sigma \in L]$ is the projection of L on a subset of activities $A \subseteq act (L)$,

• $L {\Uparrow } V = [\sigma \in L \mid \sigma \in V]$ is the projection of L on a subset of trace variants $V \subseteq var (L)$,

First, we define activity-based filtering using a threshold $\tau _{ act } \in \mathbb {N}= \{1,2,3, \ldots \}$. All activities with a frequency lower than $\tau _{ act }$ are removed from the event log, but all cases are retained.

Definition 9 (Activity-Based Filtering)

Let $L \in \mathcal {B}({\mathcal{U}_{ act }}^*)$ be an event log and $\tau _{ act } \in \mathbb {N}$. $filter ^{ act }(L,\tau _{ act }) = L {\uparrow } A$ with $A = \{ a \in act (L) \mid \#^{ act }_{L}(a) \ge \tau _{ act } \}$.

Again we use $L_1 = [\langle a,b,c,e \rangle ^{10},\langle a,c,b,e \rangle ^5,\langle a,d,e \rangle ]$ and $L_2 = [ \langle a,b,c,e \rangle ^{50},\langle a,c,b,e \rangle ^{40},\langle a,b,c,d,b,c,e \rangle ^{30},\langle a,c,b,d,b,c,e \rangle ^{20},\langle a,b,c,d,c,b,e \rangle ^{10},\langle a,c,b,d,c,b,d,b,c,e \rangle ^{10} ]$ to illustrate the definition. If $\tau _{ act } = 10$, then $filter ^{ act }(L_1,\tau _{ act }) = [\langle a,b,c,e \rangle ^{10},\langle a,c,b,e \rangle ^5,\langle a,e \rangle ]$ (only activity d is removed). If $\tau _{ act } = 16$, then $filter ^{ act }(L_1,\tau _{ act }) = [\langle a,e \rangle ^{16}]$ (only activities a and e remain). If $\tau _{ act } > 16$, then $filter ^{ act }(L_1,\tau _{ act }) = [\langle \rangle ^{16}]$. Note that the number of traces is not affected by activity-based filtering (even when all activities are removed). If $\tau _{ act } = 200$, then $filter ^{ act }(L_2,\tau _{ act }) = [ \langle b,c \rangle ^{50},\langle c,b \rangle ^{40},\langle b,c,b,c \rangle ^{30},\langle c,b,b,c \rangle ^{20},\langle b,c,c,b \rangle ^{10},\langle c,b,c,b,b,c \rangle ^{10} ]$ (only activities b and c remain).

Next, we define variant-based filtering using a threshold $\tau _{ var } \in \mathbb {N}$. All trace variants with a frequency lower than $\tau _{ var }$ are removed from the event log.

Definition 10 (Variant-Based Filtering)

Let $L \in \mathcal {B}({\mathcal{U}_{ act }}^*)$ be an event log and $\tau _{ var } \in \mathbb {N}$. $filter ^{ var }(L,\tau _{ var }) = L {\Uparrow } V$ with $V = \{ \sigma \in var (L) \mid \#^{ var }_{L}(\sigma ) \ge \tau _{ var } \}$.

If $\tau _{ var } = 5$, then $filter ^{ var }(L_1,\tau _{ var }) = [\langle a,b,c,e \rangle ^{10},\langle a,c,b,e \rangle ^5]$. If $\tau _{ var } = 10$, then $filter ^{ var }(L_1,\tau _{ var }) = [\langle a,b,c,e \rangle ^{10}]$. If $\tau _{ var } > 10$, then $filter ^{ var }(L_1,\tau _{ var }) = [~]$. Note that (unlike activity-based filtering) the number of traces may decrease.

Finally, we define arc-based filtering using a threshold $\tau _{ arc } \in \mathbb {N}$. Whereas activity-based filtering and variant-based filtering operate on event logs, arc-based filtering modifies the DFG and not the event log used to generate it. All arcs with a frequency lower than $\tau _{ arc }$ are removed from the graph.

Definition 11 (Arc-Based Filtering)

Let $G=(A,F) \in \mathcal{U}_{ G }$ be a DFG and $\tau _{ arc } \in \mathbb {N}$. $filter ^{ arc }(G,\tau _{ arc }) = (A,F')$ with $F' = [(x,y) \in F \mid F((x,y)) \ge \tau _{ arc }]$.

In its basic form $\tau _{ arc }$ retains all nodes even when they become fully disconnected from the rest. Consider the DFG $M_1 = (A,F)$ in Fig. 2(b) with $A = \{a,b,c,d,e\}$ and $F = [ (\blacktriangleright ,a)^{16},(a,b)^{10},(a,c)^{5},(a,d)^{1},(b,c)^{10},(b,e)^{5},(c,b)^{5},(c,e)^{10},(d,e)^{1},(e,{\scriptstyle {\blacksquare }})^{16}]$. If $\tau _{ var } = 10$, then $filter ^{ arc }(M_1,\tau _{ arc }) = (A,F')$ with $F' = [ (\blacktriangleright ,a)^{16},(a,b)^{10},(b,c)^{10},(c,e)^{10},(e,{\scriptstyle {\blacksquare }})^{16}]$. If $\tau _{ var } = 15$, then $filter ^{ arc }(M_1,\tau _{ arc }) = (A,F'')$ with $F'' = [ (\blacktriangleright ,a)^{16},(e,{\scriptstyle {\blacksquare }})^{16}]$. Note that the DFG is no longer connected.

The three types of filtering can be combined. Because arc-based filtering operates on the DFG, it should be done last. It is also better to conduct activity-based filtering before variant-based filtering. There are several reasons for this. The number of traces is affected by variant-based filtering. Moreover, activity-based filtering may lead to variants with a higher frequency. Consider $L_1$ with $\tau _{ act } = 16$ and $\tau _{ var } = 10$. If we first apply variant-based filtering, one variant remains after the first step and none of the activities is frequent enough to be retained in the second step: $filter ^{ act }( filter ^{ var }(L_1,\tau _{ var }),\tau _{ act }) = [\langle \rangle ^{10}]$. If we first apply activity-based filtering, then the two most frequent activities are retained and all 16 traces are considered in the second step: $filter ^{ var }( filter ^{ act }(L_1,\tau _{ act }),\tau _{ var }) = [ \langle a,e \rangle ^{16}]$. For $L_2$ with $\tau _{ act } = 200$ and $\tau _{ var } = 40$, we find that $filter ^{ act }( filter ^{ var }(L_2,\tau _{ var }),\tau _{ act }) = [\langle \rangle ^{90}]$ and $filter ^{ var }( filter ^{ act }(L_2,\tau _{ act }),\tau _{ var }) = [ \langle b,c \rangle ^{50},\langle c,b \rangle ^{40}]$.

These examples show that the order of filtering matters. We propose a refined baseline discovery algorithm using filtering. The algorithm first applies activity-based filtering followed by variant-based filtering. Then the original baseline algorithm is applied to the resulting event log to get a DFG (see Definition 6). Finally, arc-based filtering is used to prune the DFG.

Definition 12 (Baseline Discovery Algorithm Using Filtering)

Let $L \in \mathcal {B}({\mathcal{U}_{ act }}^*)$ be an event log. Given the thresholds $\tau _{ act } \in \mathbb {N}$, $\tau _{ var } \in \mathbb {N}$, and $\tau _{ arc } \in \mathbb {N}$:

$disc _{{}_{ DFG }}^{\tau _{ act },\tau _{ var },\tau _{ arc }}(L) = filter ^{ arc }( disc _{{}_{ DFG }}( filter ^{ var }( filter ^{ act }(L,\tau _{ act }),\tau _{ var })),\tau _{ arc })$.

$disc _{{}_{ DFG }}^{\tau _{ act },\tau _{ var },\tau _{ arc }}(L)$ returns a DFG using the three filtering steps. Only the last filtering step is specific for DFGs. Activity-based filtering and variant-based filtering can be used in conjunction with any discovery technique, because they produce filtered event logs. The footprint notion can also be extended to include these two types of filtering: $fp ^{\tau _{ act },\tau _{ var }}(L) = fp ( disc _{{}_{ DFG }}( filter ^{ var }( filter ^{ act }(L,\tau _{ act }),\tau _{ var })))$ is the footprint matrix considering only frequent activities and variants.

Fig. 4.

Three DFGs learned from event log $L_2 = [ \langle a,b,c,e \rangle ^{50},\langle a,c,b,e \rangle ^{40},\langle a,b,c,d,b,c,e \rangle ^{30},\langle a,c,b,d,b,c,e \rangle ^{20},\langle a,b,c,d,c,b,e \rangle ^{10},\langle a,c,b,d,c,b,d,b,c,e \rangle ^{10} ]$: (b) the original DFG considering all activities, (c) the problematic DFG obtained by simply removing activity d from the graph, and (d) the desired DFG obtained by removing activity d from the event log first.

Most process mining tools provide sliders to interactively set one or more thresholds. This makes it easy to seamlessly simplify the discovered DFG. However, it is vital that the user understands the different filtering approaches. Therefore, we highlight the following risks.

• The ordering of filters may greatly impact the result. As shown before: $filter ^{ var }( filter ^{ act }(L,\tau _{ act }),\tau _{ var }) \ne filter ^{ act }( filter ^{ var }(L,\tau _{ var }),\tau _{ act })$. If a tool provides multiple sliders, it is important to understand how these interact and what was left out.

• Applying projections to event logs is computationally expensive. Therefore, process mining tools may provide shortcuts that operate directly on the DFG without filtering the event log. Consider, for example, Fig. 4 showing (a) the event log and (b) the original DFG without filtering. Activity d has the lowest frequency. Simply removing node d from the graph leads to interpretation problems. Figure 4(c) shows the problem, e.g., b occurs 240 times but the frequencies of the input arcs add up to $90+90=180$ and the frequencies of output arcs add up to $50+150 = 200$. If we apply activity-based filtering using Definition 9, we obtain the DFG in Fig. 4(d). Now we see the loops involving b and c. Moreover, the frequencies of the input arcs of b add up to $90+120+30=240$ and the frequencies of output arcs also add up to $50+160+30 = 240$. Clearly, this is the DFG one would like to see after abstracting from d.

• Using activity-based filtering and variant-based filtering as defined in this section yields models where the frequency of a node matches the sum of the frequencies of the input arcs and the sum of the frequencies of the output arcs. As long as the resulting event log is not empty, the graph is connected and all activities are on a path from start to end. This leads to models that are easy to interpret. Arc-based filtering may lead to models that have disconnected parts and frequencies do not add up as expected (similar to the problems in Fig. 4(c)). Therefore, arc-based filtering should be applied with care.

• The above risks are not limited to control-flow (e.g., connectedness of the graph and incorrect frequencies). When adding timing information (e.g., the average time between two activities), the results are highly affected by filtering. Process mining tools using shortcuts that operate directly on the DFG without filtering the event log, quickly lead to misleading performance diagnostics [2].

2.5 A Larger Example

To further illustrate the concepts, we now consider a slightly larger event log $L_3 = [ \langle ie , cu , lt , xr , fe \rangle ^{285},$ $\langle ie , cu , lt , ct , fe \rangle ^{260},$ $\langle ie , cu , ct , lt , fe \rangle ^{139},$ $\langle ie , lt , cu , xr , fe \rangle ^{137},$ $\langle ie , lt , cu , ct , fe \rangle ^{124},$ $\langle ie , cu , xr , lt , fe \rangle ^{113},$ $\langle ie , xr , cu , lt , fe \rangle ^{72},$ $\langle ie , ct , cu , xr , fe \rangle ^{72},$

$\langle ie , cu , om , am , cu , lt , xr , fe \rangle ^{29},$ $\langle ie , cu , om , am , cu , lt , ct , fe \rangle ^{28},$ $\ldots ]$. We use the following abbreviations: $ie$ = initial examination, $xr$ = X-ray, $ct$ = CT scan, $cu$ = checkup, $om$ = order medicine, $am$ = administer medicine, $lt$ = lab tests, and $fe$ = final examination. The event log contains 11761 events corresponding to 1856 cases. Each case represents the treatment of a patient. There are 187 trace variants and 8 unique activities. For example, $\langle ie , cu , lt , xr , fe \rangle$ is the most frequent variant, i.e., 285 patients first get an initial examination ($ie$), followed by a checkup ($cu$), lab tests ($lt$), X-ray ($xr$), and a final examination ($fe$).

Fig. 5.

The discovered DFG $disc _{{}_{ DFG }}(L_3)$ generated by ProM.

Fig. 6.

The DFG $disc _{{}_{ DFG }}( filter ^{ act }(L_3,\tau _{ act }))$ generated by ProM using $\tau _{ act }=1000$.

Figure 5 shows the DFG for $L_3$ using the baseline discovery algorithm described in Definition 6. The DFG was produced by ProM’s “Mine with Directly Follows visual Miner”. Using a slider, it is possible to remove infrequent activities. Figure 6 shows the DFG $disc _{{}_{ DFG }}( filter ^{ act }(L_3,\tau _{ act }))$ with the activity threshold $\tau _{ act }$ set to 1000, i.e., all activities with a frequency of less than 1000 are removed from the event log using projection. In the resulting DFG, four of the eight activities remain.

Fig. 7.

The discovered DFG in Celonis before and after activity-based filtering, i.e., $disc _{{}_{ DFG }}(L_3)$ (left) and $disc _{{}_{ DFG }}( filter ^{ act }(L_3,\tau _{ act }))$ with $\tau _{ act }=1000$ (right).

The discovery of DFGs (as defined in this section) is supported by almost all process mining tools. Figure 7 shows the DFGs discovered using the Celonis EMS using the same settings as used in ProM. Although the layout is different, the Celonis-based DFG in Fig. 7 (left) is identical to the ProM-based DFG in Fig. 5. The DFG in Fig. 7 (right) is identical to the DFG in Fig. 6.

Fig. 8.

A discovered DFG in Celonis using variant-based filtering: $disc _{{}_{ DFG }}( filter ^{ var }(L_3,\tau _{ var }))$ with $\tau _{ var }=100$. There are six variants having a frequency above 100. These cover 57% of all cases, but only 3% of all variants.

Figure 8 shows variant-based filtering using the Celonis “Variant Explorer”. The six most frequent variants are selected. These are the variants that have a frequency above 100, i.e., the depicted DFG is $disc _{{}_{ DFG }}( filter ^{ var }(L_3,\tau _{ var }))$ with $\tau _{ var }=100$. There are 1856 cases distributed over 197 variants. The top six variants (i.e., 3% of all variants) cover 1058 cases (i.e., 57%). We also computed the DFG $disc _{{}_{ DFG }}( filter ^{ var }(L_3,\tau _{ var }))$ with $\tau _{ var }=10$. There are 22 variants meeting this lower threshold (i.e., 11% of all variants) covering 1483 cases (i.e., 80%). Most event logs follow such a Pareto distribution, i.e., a small fraction of variants explains most of the cases observed. This is also referred to as the “80/20 rule”, although the numbers 80 and 20 are arbitrary. For our example event log $L_3$, we could state that it satisfies the “80/11 rule” (but also the “57/3 rule”, “84/16 rule”, etc.).

If the distribution of cases over variants does not follow a Pareto distribution, then it is best to first apply activity-based filtering. If we project $L_3$ onto the top four most frequent activities, only 20 variants remain. The most frequent variant explains already 51% of all cases. The DFG $disc _{{}_{ DFG }}( filter ^{ var }( filter ^{ act }(L,\tau _{ act }),\tau _{ var }))$ with $\tau _{ act }=1000$ and $\tau _{ var }=100$ combines the activity-based filter used in Fig. 7 and the variant-based filter used in Fig. 8. The resulting DFG (not shown) explains 1672 of the 1856 cases (90%) and 7065 of 11761 events (60%) using only five variants.

The above examples show that, using filtering, it is possible to separate the normal (i.e., frequent) from the exceptional (i.e., infrequent) behavior. This is vital in the context of process discovery and can be combined with the later bottom-up and top-down discovery approaches.

3 Challenges

After introducing a baseline discovery algorithm and various filtering approaches, it is possible to better explain why process discovery is so challenging. In Definition 3, we stated that a process discovery algorithm is a function $disc \in \mathcal {B}({\mathcal{U}_{ act }}^*) \rightarrow \mathcal{U}_{ M }$, i.e., based on a multiset of traces L, a process model $M= disc (L)$ allowing for $lang (M) \subseteq {\mathcal{U}_{ act }}^*$ is produced.

The first challenge is that the discovered process model may serve different goals. Should the model summarize past behavior, or is the model used for predictions and recommendations? Also, should the process model be easy to read and understand by end-users? Answers to these questions are needed to address the trade-offs in process discovery. We already mentioned that most event logs follow a Pareto distribution. Hence, the process model can focus on the dominant behavior or also include exceptional behavior.

The second challenge is that different process model representations can be used. These may or may not be able to capture certain behaviors. This is the so-called representational bias of process discovery. Consider, for example, event log $L = [ \langle a,b,c,d \rangle ^{1000}, \langle a,c,b,d \rangle ^{1000}]$. There is no DFG that is able to adequately describe this behavior. The DFG will always need to introduce a loop involving b and c. Another example is $L = [ \langle a,b,c \rangle ^{1000}, \langle a,c \rangle ^{1000}]$. It is easy to create a DFG describing this behavior. However, when representing this as a Petri net or process tree, it is vital that one can use so-called silent activities (to skip b) or duplicate activities (to have a c activity following a and another c activity following b).

Another challenge is that the event log contains just example behavior. Most event logs have a Pareto distribution. Typically, a few trace variants are frequent and many trace variants are infrequent. Actually, there are often trace variants that are unique (i.e., occur only once). If one observes the process longer, new variants will appear. Conversely, if one observes the process in a different period, some variants may no longer appear. An event log is a sample and should be treated as such. Just like in statistics, the goal is to use the sample to say something about the whole population (here, the process). For example, when throwing a dice ten times, one may have the following sequence observations $\sigma = \langle 4,5,2,3,6,5,4,1,2,3 \rangle$. If we do not know that two subsequent throws are independent, the expected value is 3.5, the minimum is 1, the maximum is 6, and the probabilities of all six values are equal, then what can be concluded from the sample $\sigma$? We could conclude that even numbers are always followed by odd numbers. Real-life processes have many more behaviors, and the observed sample rarely covers all possibilities.

Although processes are stochastic, most process discovery techniques aim to discover process models that are “binary”, i.e., a trace is possible or not. This complicates analysis. Another challenge is that event logs do not contain negative examples. Process discovery can be seen as a classification problem: A trace $\sigma$ is possible ($\sigma \in lang (M)$) or not ($\sigma \not \in lang (M)$). In real applications, we never witness traces that are impossible. The event log only contains positive examples. If we also want to incorporate infrequent behavior in the discovered model, we may require $var (L) \subseteq lang (M)$. However, we cannot assume the reverse $lang (M) \subseteq var (L)$. For example, loops in models would be impossible, and for concurrent processes we would need a factorial number of cases.

Related to the above are the challenges imposed by concept drift. The behavior of the process that we are trying to discover may change over time in unforeseen ways. Certain traces may increase or decrease in likelihood. New trace variants may emerge while other variants no longer occur. Since process models already describe dynamic behavior, concept drift introduces second-order dynamics. Various techniques for concept-drift detection have been developed. However, this for sure complicates process discovery. If we cannot assume that the process itself is in steady-state, then what is the process we are trying to discover? Do we want to have a process model describing the past week or the past year?

Next to concept drift, there are the usual data quality problems [1]. Events may have been logged incorrectly and attributes may be missing or are imprecise. In some applications it may be difficult to correlate events and group them into cases. There may be different identifiers used for the same case and events may be shared by different cases. Since process discovery depends on the ordering of events in the event log, high-quality timestamps are important. However, the timestamp resolution may be too low (e.g., just a date) and different source systems may use different timestamp granularities or formats. Often the day and the month are swapped, e.g., 8/7/2022 is entered as 7/8/2022.

It is important to distinguish the evaluation of a process discovery algorithm $disc \in \mathcal {B}({\mathcal{U}_{ act }}^*) \rightarrow \mathcal{U}_{ M }$ from the evaluation of a specific process model M in the context of a specific event log L. To evaluate a process discovery algorithm $disc$, one can use cross-validation, i.e., split an event log into a training part and an evaluation part. The process model is trained using the training log and evaluated using the evaluation log. Ideally, the evaluation log has both positive and negative examples. This is unrealistic in real settings. However, it is possible to create synthetic event data with positive and negative cases using, for example, simulation. If we assume that the evaluation log is a multiset of positive traces $L^{+}_{ eval } \in \mathcal {B}({\mathcal{U}_{ act }}^*)$ and a multiset of negative traces $L^{-}_{ eval } \in \mathcal {B}({\mathcal{U}_{ act }}^*)$, then evaluation is simple. Let $M = disc (L^{+}_{ train })$ be the discovered process model using only positive training examples. Now, we can use standard notions such as $recall = \frac{\left| {[\sigma \in L^{+}_{ eval } \mid \sigma \in lang (M)]}\right| }{\left| {L^{+}_{ eval }}\right| }$ and $precision = \frac{\left| {[\sigma \in L^{-}_{ eval } \mid \sigma \not \in lang (M)]}\right| }{\left| {L^{-}_{ eval }}\right| }$ using the evaluation log. Recall is high when most of the positive traces in the evaluation log are indeed possible according to the process model. Precision is high when most of the negative traces in the evaluation log are indeed not possible according to the process model.

Unfortunately, the above view is very naïve considering process discovery in practical settings. We cannot assume negative examples when evaluating a specific model M in the context of a specific event log L observed in reality. Splitting L into a training log and an evaluation log does not make any sense since the model is given and we want to use the whole event log.

In spite of these problems, there is consensus in the process mining community that there are the following four quality dimensions to evaluate a process model M in the context of an event log L with observed behavior [1].

• Recall, also called (replay) fitness, aims to quantify the fraction of observed behavior that is allowed by the model.

• Precision aims to quantify the fraction of behavior allowed by the model that was actually observed (i.e., avoids “underfitting” the event data).

• Generalization aims to quantify the probability that new unseen cases will fit the model (i.e., avoids “overfitting” the event data).

• Simplicity refers to Occam’s Razor and can be made operational by quantifying the complexity of the model (number of nodes, number of arcs, understandability, etc.).

There exist various measures for recall. The simplest one computes the fraction of traces in event log L possible according to the process model M. It is also possible to define such a notion at the level of events. There are many simplicity notions. These do not depend on the behavior of the model, but measure its understandability and complexity. Most challenging are the notions of precision and generalization. Also, these notions can be quantified, but there is less consensus on what they should measure. The goal is to strike a balance between precision (avoiding “underfitting” the sample event data) and generalization (avoiding “overfitting” the sample event data). A detailed discussion is outside the scope of this chapter. Therefore, we refer to [1, 4, 15, 31] for further information.

4 Process Modeling Notations

We have formalized the notion of an event log and the behavior represented by a DFG. Now we focus on higher-level process models able to model sequences, choices, loops, and concurrency. We formalize Petri nets and process trees and provide an informal introduction to a relevant subset of BPMN.

4.1 Labeled Accepting Petri Nets

Figures 2(c) and 3(c) already showed example Petri nets. Since their inception in 1962 [28], Petri nets have been used in a wide variety of application domains. Petri nets were the first formalism to capture concurrency in a systematic manner. See [17, 18] for a more extensive introduction. Other notations such as Business Process Model and Notation (BPMN), Event-driven Process Chains (EPCs), and UML activity diagrams all build on Petri nets and have semantics involving “playing the token game”. For process mining, we need to use the so-called labeled accepting Petri nets. These are standard Petri nets where transitions are labeled to refer to activities in the event log and, next to an initial marking, these nets also have a final marking. The behavior described by such nets are all the “paths” leading from the initial state to the final state. We explain these concepts step-by-step.

Fig. 9.

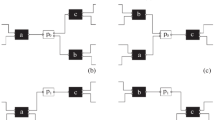
Four accepting Petri nets: (a) $AN _1 = (N_1,[ p1 ],[ p6 ])$, (b) $AN _2 = (N_2,[ p1 ],[ p6 ])$, (c) $AN _3 = (N_3,[ p1 , p2 ],[ p4 , p5 ])$, and (d) $AN _4 = (N_4,[ p1 ],[ p6 ])$. $AN _1$ was discovered for $L_1$ (see Fig. 2(c)) and $AN _2$ was discovered for $L_2$ (see Fig. 3(c)).

States in Petri nets are called markings that mark certain places (represented by circles) with tokens (represented by black dots). Transitions (represented by squares) are the active components able to move the Petri net from one marking to another marking. Transitions may have a label referring to the corresponding activity. There may be multiple transitions that refer to the same activity and there may be transitions without an activity label. The former is needed if the same activity can occur at multiple stages in the process. The latter is needed if activities can be skipped. Later we will give examples illustrating the importance of the labeling function in the context of process mining.

Definition 13 (Labeled Petri Net)

A labeled Petri net is a tuple $N=(P,T,F,l)$ with P the set of places, T the set of transitions, $P \cap T = \emptyset$, $F\subseteq (P \times T) \cup (T \times P)$ the flow relation, and $l \in T \not \rightarrow \mathcal{U}_{ act }$ a labeling function. We write $l(t) = \tau$ if $t \in T {\setminus } dom (l)$ (i.e., t is a silent transition that cannot be observed).

Figure 9 shows four accepting Petri nets. The first two were discovered for the event logs $L_1$ and $L_2$ used to introduce DFGs. Figure 9(a) shows the labeled Petri net $N_1 = (P_1,T_1,F_1,l_1)$ with $P_1 = \{ p1 , p2 , p3 , p4 , p5 , p6 \}$ (six places), $T_1 = \{ t1 , t2 , t3 , t4 , t5 \}$ (five transitions), $F_1 = \{( p1 , t1 ),( t1 , p2 ),( t1 , p3 ), \ldots , ( t5 , p6 )\}$ (fourteen arcs), and $l_1 = \{( t1 , a ),( t2 , b ),( t3 , c ),( t4 , d ),( t5 , e )\}$ (labeling function).

As mentioned, there may be multiple transitions with the same label and there may be transitions that have no label (called “silent transitions”). This is illustrated by $N_4 = (P_4,T_4,F_4,l_4)$ in Fig. 9(d) with $l_4 = \{( t1 , a ),( t2 , b ),( t3 , a )\}$. Note that $dom (l_4) = \{ t1 , t2 , t3 \}$ does not include $t4$ and $t5$ which are silent. This is denoted by the two black rectangles in Fig. 9(d). Also note that $l_4( t1 ) = l_4( t3 ) = a$, i.e., $t1$ and $t3$ refer to the same activity.

Since a place may have multiple tokens, markings are represented by multisets. Transitions may have input and output places. For example, t1 in Fig. 9(a) has one input place and two output places. A transition is called enabled if each of the input places has a token. An enabled transition may fire (i.e., occur), thereby consuming a token from each input place and producing a token for each output place.

An accepting Petri net has an initial marking $M_{ init } \in \mathcal {B}(P)$ and a final marking $M_{ final } \in \mathcal {B}(P)$. The accepting Petri nets $AN _1 = (N_1,[ p1 ],[ p6 ])$, $AN _2 = (N_2,[ p1 ],[ p6 ])$, and $AN _4 = (N_4,[ p1 ],[ p6 ])$ in Fig. 9 have the same initial and final marking. $AN _3 = (N_3,[ p1 , p2 ],[ p4 , p5 ])$ in Fig. 9(c) has an initial marking $M_{ init } = [ p1 , p2 ]$ (denoted by the black tokens) and a final marking $M_{ final } = [ p4 , p5 ]$ (denoted by the double-bordered places).

Definition 14 (Accepting Petri Net)

An accepting Petri net is a triplet $AN =(N,M_{ init },M_{ final })$ where $N=(P,T,F,l)$ is a labeled Petri net, $M_{ init } \in \mathcal {B}(P)$ is the initial marking, and $M_{ final } \in \mathcal {B}(P)$ is the final marking. $\mathcal{U}_{ AN }\subseteq \mathcal{U}_{ M }$ is the set of accepting Petri nets.

An accepting Petri net starts in the initial marking and may move from one marking to the next by firing enabled transitions. Consider, for example, $AN _3 = (N_3,[ p1 , p2 ],[ p4 , p5 ])$ in Fig. 9(c). Initially, three transitions are enabled in $[ p1 , p2 ]$: $t1$, $t2$, and $t3$. Firing $t1$ results in marking $[ p2 , p4 ]$, firing $t2$ results in marking $[ p1 , p3 ]$, and firing $t3$ results in marking $[ p3 , p4 ]$. If $t1$ fires (i.e., activity a occurs), then $t1$ and $t3$ are no longer enabled and only $t2$ remains enabled. If $t2$ fires in $[ p2 , p4 ]$, we reach the marking $[ p3 , p4 ]$. In this marking, only $t4$ is enabled. Firing $t4$ results in the marking $[ p4 , p5 ]$. This is also the final marking of $AN _3$. A firing sequence is a sequence of transition occurrences obtained by firing enabled transitions and moving from one marking to the next. A complete firing sequence starts in the initial marking and ends in the final marking. $AN _3$ has four possible complete firing sequences: $\langle t1 , t2 , t4 \rangle$, $\langle t2 , t1 , t4 \rangle$, $\langle t2 , t4 , t1 \rangle$, and $\langle t3 , t4 \rangle$.

Definition 15 (Complete Firing Sequences)

Let $AN =(N,M_{ init },M_{ final }) \in \mathcal{U}_{ AN }$ be an accepting Petri net with $N=(P,T,F,l)$. $cfs ( AN ) \subseteq T^*$ is the set of complete firing sequences of $AN$, i.e., all firing sequences starting in the initial marking $M_{ init }$ and ending in the final marking $M_{ final }$.

$cfs ( AN_1 ) = \{ \langle t1 , t2 , t3 , t5 \rangle ,\langle t1 , t3 , t2 , t5 \rangle ,\langle t1 , t4 , t5 \rangle \}$ and $cfs ( AN_3 ) = \{ \langle t1 , t2 , t4 \rangle ,\langle t2 , t1 , t4 \rangle ,\langle t2 , t4 , t1 \rangle ,\langle t3 , t4 \rangle \}$. Note that $cfs ( AN_2 )$ and $cfs ( AN_4 )$ contain an infinite number of complete firing sequences due to the loop involving $t4$.

As stated in Definition 2, a process model defines a set of traces. Earlier, we defined $lang (G) \subseteq {\mathcal{U}_{ act }}^*$ for a DFG $G = (A,F)$. Now we need to define $lang ( AN ) \subseteq {\mathcal{U}_{ act }}^*$ for an accepting Petri net $AN =(N,M_{ init },M_{ final })$. For this purpose, we need to be able to apply the labeling function l to firing sequences. Let $\sigma \in T^*$ be a firing sequence and $l \in T \not \rightarrow \mathcal{U}_{ act }$ a labeling function. Function l is generalized to sequences, i.e., transitions are replaced by their labels and are dropped if they do not have a label. Formally, $l(\langle \rangle ) = \langle \rangle$, $l(\sigma \cdot \langle t \rangle ) = l(\sigma ) \cdot \langle l(t) \rangle$ if $t \in dom (l)$, and $l(\sigma \cdot \langle t \rangle ) = l(\sigma )$ if $t \not \in dom (l)$. Consider, for example, the complete firing sequence $\sigma = \langle t1 , t2 , t3 , t4 , t3 , t2 , t5 \rangle \in cfs ( AN_4 )$ of the accepting Petri net in Fig. 9(d). $l(\sigma ) = \langle a,b,a,a,b \rangle$, i.e., $t1$, $t2$, and $t3$ are mapped to the corresponding labels, and $t4$ and $t5$ are dropped.

Definition 16 (Traces of an Accepting Petri Net)

Let $AN =(N,M_{ init },M_{ final }) \in \mathcal{U}_{ AN }$ be an accepting Petri net. $lang ( AN ) = \{ l(\sigma ) \mid \sigma \in cfs ( AN )\}$ are the traces possible according to $AN$.

Now we can reason about the traces of the four accepting in Fig. 9. $lang ( AN _1)= \{ \langle a,b,c,e \rangle , \langle a,c,b,e \rangle , \langle a,d,e \rangle \}$. $lang ( AN _2)= \{ \langle a,b,c,e \rangle , \langle a,c,b,e \rangle , \langle a,b,c,d,b,c,e \rangle , \langle a,c,b,d,b,c,e \rangle , \ldots , \langle a,c,b,d,b,c,d,c,b,d,c,b,e \rangle , \ldots \}$. $lang ( AN _3)= \{ \langle a,b,d \rangle , \langle b,a,d \rangle , \langle b,d,a \rangle , \langle c,d \rangle \}$. $lang ( AN _4)= \{ \langle a,b,a \rangle , \langle a,a,b \rangle , \langle a,b,a,b,a \rangle , \langle a,a,b,b,a \rangle , \ldots , \langle a,a,b,b,a,a,b,a,b \rangle , \ldots \}$.

It is important to note the consequences of restricting $lang ( AN )$ to the behavior of complete firing sequences. If $AN$ has livelocks of deadlocks, then these are not considered to be part of the language. If we remove the arc from p4 to t4 in $AN _2$, then $lang ( AN _2)= \{ \langle a,b,c,e \rangle , \langle a,c,b,e \rangle \}$, because there are no complete firing sequences involving t4.

In literature, Petri nets are normally not equipped with a labeling function and a final marking. However, both the labeling function l and a defined final marking $M_{ final }$ are vital in the context of process mining. The final marking allows us to reason about complete firing sequences, just like traces in an event log have a clear ending. If we would consider ordinary Petri nets rather than accepting Petri nets, the language would also include all prefixes. This would make it impossible to describe the behavior found in an event log such as $L = [\langle a,b,c\rangle ^{1000}]$, because the corresponding Petri net would also allow for traces $\langle a,b\rangle$, $\langle a\rangle$, and $\langle \rangle$.

The labeling function $l \in T \not \rightarrow \mathcal{U}_{ act }$ also greatly improves expressiveness. The alternative would be that transitions are uniquely identified by activities, i.e., $T \subseteq \mathcal{U}_{ act }$. However, this would make it impossible to describe many behaviors seen in event logs. Consider, for example, an event log such as $L = [\langle a,b,c\rangle ^{1000},\langle a,c\rangle ^{1000}]$ where b can be skipped. It is easy to model this behavior using a silent transition to skip b or by using two transitions with a c label. Although it is trivial to create a DFG G such that $lang (G) = \{ \langle a,b,c\rangle ,\langle a,c\rangle \}$ (simply apply the baseline algorithm described in Definition 6), it is impossible to create an accepting Petri net $AN$ with $lang ( AN ) = \{ \langle a,b,c\rangle ,\langle a,c\rangle \}$ without using a labeling function allowing for silent or duplicate transitions.

4.2 Process Trees

The two process trees discovered for event logs $L_1$ and $L_2$ (see Fig. 2(c) and Fig. 3(c)) are depicted as $Q_1 = \,{\rightarrow }(a,\times (\wedge (b,c),d),e)$ and $Q_2 = \,{\rightarrow }(a,{\circlearrowleft }(\wedge (b,c),d),e)$ in Fig. 10. Their language is the same as $AN _1$ and $AN _2$ in Fig. 9.

Process trees are not commonly used as a modeling language. However, state-of-the-art process discovery techniques use process trees as an internal representation. The behavior of process trees can be visualized using Petri nets, BPMN, UML activity diagrams, EPCs, etc. However, they also have their own graphical representation, as shown in Fig. 10.

The main reason for using process trees is that they have a hierarchical structure and are sound by construction. This does not hold for other notations such as Petri nets and BPMN. For example, if we remove the arc $( t4 , p2 )$ in $AN _2$ shown in Fig. 9(b), then the process may deadlock. The process gets stuck in marking $[ p5 ]$ making it impossible to reach the final marking. If we remove the arc $( p4 , t4 )$ in $AN _2$, then the process may livelock. It is possible to put an arbitrary number of tokens in $p2$ and $p4$, but after the occurrence of d it is impossible to reach the final marking. If both arcs are removed, the accepting Petri net is again sound (i.e., free of anomalies such as deadlocks and livelocks). When discovering process model constructs locally, these potential soundness problems are difficult to handle (see [6] for more details on analyzing soundness of process models). Therefore, a range of inductive mining techniques has been developed using process trees that are sound by construction [22,23,24].

Fig. 10.

Three process trees: (a) $Q_1 = \,{\rightarrow }(a,\times (\wedge (b,c),d),e)$, (b) $Q_2 = \,{\rightarrow }(a,{\circlearrowleft }(\wedge (b,c),d),e)$, and (c) $Q_3 = \,{\rightarrow }(a,{\circlearrowleft }(\wedge (b,a),\tau ))$.

A process tree is a tree-like structure with one root node. The leaf nodes correspond to activities (including the silent activity $\tau$, which is similar to a silent transition in Petri nets). Four types of operators can be used in a process tree: $\rightarrow$ (sequential composition), $\times$ (exclusive choice), $\wedge$ (parallel composition), and $\circlearrowleft$ (redo loop). This way it is possible to construct process trees such as the ones shown in Fig. 10.

Definition 17 (Process Tree)

Let $PTO = \{\rightarrow ,\times ,\wedge ,\circlearrowleft \}$ be the set of process tree operators and let $\tau \not \in \mathcal{U}_{ act }$ be the so-called silent activity. Process trees are defined as follows.

• if $a \in \mathcal{U}_{ act }\cup \{\tau \}$, then $Q = a$ is a process tree,

• if $n \ge 1$, $Q_1, Q_2, \ldots , Q_n$ are process trees, and $\oplus \in \{\rightarrow ,\times ,\wedge \}$, then $Q = \oplus (Q_1,Q_2, \ldots Q_n)$ is a process tree, and

• if $n \ge 2$ and $Q_1, Q_2, \ldots , Q_n$ are process trees, then $Q = \,{\circlearrowleft }(Q_1,Q_2, \ldots Q_n)$ is a process tree.

$\mathcal{U}_{ Q }\subseteq \mathcal{U}_{ M }$ is the set of all process trees.

Consider the process tree $Q_1 = \,{\rightarrow }(a,\times (\wedge (b,c),d),e)$ shown in Fig. 10(a). The leaf nodes correspond to the activities a, b, c, d, and e. The root node is a sequence operator ($\rightarrow$) having three children: a, $\times (\wedge (b,c),d)$, and e. The root node of the subtree $\times (\wedge (b,c),d)$ is a choice operator ($\times$) having two children: $\wedge (b,c)$ and d. The root node of the subtree $\wedge (b,c)$ is a parallel operator ($\wedge$) having two children: b and c.

Fig. 11.

The semantics of the four process tree operators, i.e., $\rightarrow$ (sequential composition), $\times$ (exclusive choice), $\wedge$ (parallel composition), and $\circlearrowleft$ (redo loop), expressed in terms of Petri nets.

Although it is fairly straightforward to define the semantics of process trees directly in terms of traces, we can also use the mapping onto accepting labeled Petri nets shown in Fig. 11. A silent activity, i.e., a leaf node labeled $\tau$, is mapped onto a silent transition. A normal activity a is mapped onto a transition t with label $l(t) = a$. Sequential composition ${\rightarrow }(a,b,c,\ldots , z)$ corresponds to the Petri net structure shown in Fig. 11, i.e., first a occurs and only if a has finished, b may start, after b completes, c can start, etc. The sequential composition ends when the last element completes. Note that $a,b,c,\ldots , z$ do not need to be atomic activities. These elements may correspond to large subprocesses, each represented by a subtree of arbitrary complexity. Exclusive choice $\times (a,b,c,\ldots , z)$ and parallel composition $\wedge (a,b,c,\ldots , z)$ can be mapped onto Petri nets as shown in Fig. 11. Also here the elements do not need to be atomic and may correspond to subtrees of arbitrary complexity. Figure 11 also shows the semantics of the redo loop operator $\circlearrowleft$. In ${\circlearrowleft }(a,b,c,\ldots , z)$, first a is executed. This is called the “do” part (again a may be a subprocess). Then there is the option to stop (fire the silent transition to go to the end place) or one of the “redo elements” is executed. For example, b is executed. After the completion of b, we again execute the “do” part a after which there is again the choice to stop or pick one of the “redo elements”, etc. Note that semantically ${\circlearrowleft }(a,b,c,\ldots , z)$ and ${\circlearrowleft }(a,\times (b,c,\ldots , z))$ are the same.

Definition 18 (Traces of a Process Tree)

Let $Q \in \mathcal{U}_{ Q }$ be a process tree and $AN _Q \in \mathcal{U}_{ AN }$ the corresponding accepting Petri net constructed by recursively applying the patterns depicted in Fig. 11. $lang (Q) = lang ( AN _Q)$ are the traces possible according to Q.

Using the above definition, we can compute the set of traces for the three process trees in Fig. 10: $Q_1 = \,{\rightarrow }(a,\times (\wedge (b,c),d),e)$, $Q_2 = \,{\rightarrow }(a,{\circlearrowleft }(\wedge (b,c),d),e)$, and $Q_3 = \,{\rightarrow }(a,{\circlearrowleft }(\wedge (b,a),\tau ))$. $lang (Q_1) = \{ \langle a,b,c,e \rangle , \langle a,c,b,e \rangle , \langle a,d,e \rangle \}$, $lang (Q_2) = \{ \langle a,b,c,e \rangle , \langle a,c,b,e \rangle , \langle a,b,c,d,b,c,e \rangle , \langle a,c,b,d,b,c,e \rangle , \ldots , \langle a,c,b,d,b,c,d,c,b,d,c,b,e \rangle , \ldots \}$, and $lang (Q_3) = \{ \langle a,b,a \rangle , \langle a,a,b \rangle , \langle a,b,a,b,a \rangle , \langle a,a,b,b,a \rangle , \ldots , \langle a,a,b,b,a,a,b,a,b \rangle , \ldots \}$.

Some additional examples to illustrate the expressiveness of process trees:

• $lang ({\rightarrow }(a,\times (b,\tau ),c)) = \{ \langle a,b,c \rangle ,\langle a,c \rangle \}$ (ability to skip b).

• $lang ({\rightarrow }(a,a)) = \{ \langle a,a\rangle \}$ (ability to specify that a should occur twice).

• $lang ({\circlearrowleft }(a,\tau )) = \{ \langle a \rangle ,\langle a,a \rangle , \langle a,a,a \rangle , \ldots \}$ (at least one a).

• $lang ({\circlearrowleft }(\tau ,b)) = \{ \langle \rangle ,\langle b \rangle , \langle b,b \rangle , \ldots \}$ (any number of b’s)

• $lang ({\circlearrowleft }(a,b)) = \{ \langle a \rangle ,\langle a,b,a \rangle , \langle a,b,a,b,a \rangle , \ldots \}$ (alternate a and b).

• $lang ({\circlearrowleft }(\tau ,a,b,c, \ldots , z)) = \{a,b,c, \ldots , z\}^*$ (all traces over given set of activities).

Fig. 12.

Two labeled accepting Petri nets with behaviors that are difficult to discover in terms of a process tree. The top model (a) corresponds to the process tree $Q=\wedge ({\rightarrow }(a,b,c),{\rightarrow }(d,e,f))$ with the additional requirement that b should be executed before e. The bottom model (b) corresponds to the process tree $Q=\,{\rightarrow }(\times (a,b),c,d,\times (e,f))$ with the additional requirement that a should be followed by e and b should be followed by f.

There are also behaviors that are difficult to express in terms of a process tree. For example, it is difficult to synchronize between subtrees. Consider, for example, the process tree $Q=\wedge ({\rightarrow }(a,b,c),\,{\rightarrow }(d,e,f))$ with the additional requirement that b should be executed before e. This can only be handled by duplicating activities, e.g., $Q= \times ( {\rightarrow }( \wedge ({\rightarrow }(a,b),d), \wedge (c,{\rightarrow }(e,f)) ), {\rightarrow }(a,b,c,d,e,f) )$. Trying to capture arbitrary synchronizations between subprocesses leads to incomprehensible process trees whose behavior is still easy to express in terms of a BPMN model or a labeled accepting Petri net. Figure 12(a) shows how this can be expressed in terms of a labeled accepting Petri net. Similarly, process trees cannot capture long-term dependencies (e.g., a choice at the beginning of the process influences a choice later in the process). Figure 12(b) shows an example where the first choice depends on the second choice. This simple example can be modeled using the process tree $Q = \times ({\rightarrow }(a,c,d,e),{\rightarrow }(b,c,d,f))$, which enumerates the two traces and duplicates activities c and d. In general, process-tree based discovery techniques are unable to create such models. Nevertheless, process trees provide a powerful representational bias that can be exploited by process discovery techniques.

4.3 Business Process Model and Notation (BPMN)

Business Process Model and Notation (BPMN) is the de facto representation for business process modeling in industry [19, 36]. The BPMN standard is maintained by the Object Management Group (OMG) [27], is supported by a wide range of vendors, and is used by numerous organizations. The OMG specification is 532 pages [27]. Given our focus on process discovery, the constructs for control-flow are most relevant. Moreover, most tools only support a small subset of the BPMN standard and an even smaller subset is actually used on a larger scale. When using the more advanced constructs like inclusive/complex gateways and multiple instance activities, the execution semantics are also not so clear (see Chapter 13 of [27]). Therefore, we only cover start and end events, activities, exclusive gateways, parallel gateways, and sequence flows. Constructs such as pools, lanes, data objects, messages, subprocesses, and inclusive gateways are relevant for more advanced forms of process mining, but outside the scope of this chapter.

Fig. 13.

Three BPMN models corresponding to the accepting Petri nets $AN _1$, $AN _2$, and $AN _4$, and the process trees $Q_1$, $Q_2$, and $Q_3$ used before.

Figure 13 shows three BPMN models ($B_1$, $B_2$, and $B_3$) and a limited set of BPMN notations. We (informally) refer to the class of BPMN models constructed using these building blocks as $\mathcal{U}_{ BPMN }$. The behavior represented by the BPMN model $B_1 \in \mathcal{U}_{ BPMN }$ is the same as the accepting Petri net $AN _1 = (N_1,[ p1 ],[ p6 ])$ in Fig. 9(a) and the process tree $Q_1 = \,{\rightarrow }(a,\times (\wedge (b,c),d),e)$ in Fig. 10(a). Hence, $lang (B_1) = \{ \langle a,b,c,e \rangle , \langle a,c,b,e \rangle , \langle a,d,e \rangle \}$. BPMN model $B_2 \in \mathcal{U}_{ BPMN }$ corresponds to $AN _2$ in Fig. 9(b) and the process tree $Q_2$ in Fig. 10(b). BPMN model $B_3 \in \mathcal{U}_{ BPMN }$ corresponds to $AN _4$ in Fig. 9(d) and the process tree $Q_3$ in Fig. 10(c). We do not provide formal semantics for these BPMN constructs. However, the examples should be self-explaining and demonstrate that a BPMN model $B \in \mathcal{U}_{ BPMN }$ defines indeed a set of traces $lang (B)$.

In this chapter, we have introduced four types of models: DFGs $\mathcal{U}_{ G }\subseteq \mathcal{U}_{ M }$, accepting Petri nets $\mathcal{U}_{ AN }\subseteq \mathcal{U}_{ M }$, process trees $\mathcal{U}_{ Q }\subseteq \mathcal{U}_{ M }$, and BPMN models $\mathcal{U}_{ BPMN }\subseteq \mathcal{U}_{ M }$. There exist discovery approaches for all of them. Since they all specify sets of possible complete traces, automated translations are often possible. For example, a discovery technique may use process trees internally, but use Petri nets or BPMN models to visualize the result.

5 Bottom-Up Process Discovery

In Sect. 2, we presented a baseline discovery approach to learn a DFG from an event log. As stated in Definition 3, a process discovery algorithm is a function $disc \in \mathcal {B}({\mathcal{U}_{ act }}^*) \rightarrow \mathcal{U}_{ M }$ that, given an event log L, produces a model $M = disc (L)$ that allows for the traces in $lang (M)$. The DFG-based baseline approach has many limitations. One of the main limitations is the inability to represent concurrency. The DFG produced tends to have an excessive number of cycles leading to Spaghetti-like underfitting models. Therefore, we introduced higher-level process model notations such as accepting Petri nets (Sect. 4.1), process trees (Sect. 4.2), and a subset of the BPMN notation (Sect. 4.3).

In this chapter, we group the more advanced approaches into two groups: “bottom-up” process discovery and “top-down” process discovery. The first group aims to uncover local patterns involving a few activities. The second group aims to find a global structure that can be used to decompose the discovery problem into smaller problems. In this section, we introduce “bottom-up” process discovery using the Alpha algorithm [1, 9] as an example. In Sect. 6, we introduce “top-down” process discovery using the basic inductive mining algorithm [22,23,24] as an example.

Both “bottom-up” and “top-down” process discovery can be combined with the filtering approaches presented in Sect. 2.4, in particular activity-based and variant-based filtering. Without filtering, the basic Alpha algorithm and basic inductive mining algorithm will not be very usable in real-life settings. Therefore, we assume that the event logs have been preprocessed before applying “bottom-up” or “top-down” discovery algorithms.

Definition 19 (Basic Log Preprocessing)

Let $L \in \mathcal {B}({\mathcal{U}_{ act }}^*)$ be an event log. Given the thresholds $\tau _{ act } \in \mathbb {N}$ and $\tau _{ var } \in \mathbb {N}$: $L^{\tau _{ act },\tau _{ var }} = filter ^{ var }( filter ^{ act }(L,\tau _{ act }),\tau _{ var })$.

In the remainder, we assume that the event log was preprocessed and that we want to discover a process model describing the filtered event log.

5.1 The Essence of Bottom-Up Process Discovery: Admissible Places

To explain “bottom-up” process discovery, we first introduce the notion of a “flower model” for an event log. This is the accepting Petri net without places. We use this as a basis and then add places one-by-one.

Definition 20 (Flower Model)

Let $L \in \mathcal {B}({\mathcal{U}_{ act }}^*)$ be an event log with activities $A = act (L)$. The flower model of L is the accepting Petri net $disc _{{}_{ flower }}(L) = (N,[~],[~])$ with $N=(\emptyset ,A,\emptyset ,\{(a,a)\mid a \in A\})$.

Note that $disc _{{}_{ flower }}(L)$ contains no places and one transition per activity. The flower model of $L_1$ is shown in Fig. 14(a). In a Petri net, a transition is enabled if all of its input places contain a token. Hence, a transition without an input place is always enabled. Moreover, the Petri net is always in the final marking [ ]. Therefore, $lang ( disc _{{}_{ flower }}(L)) = A^*$, i.e., all traces over activities seen in the event log. Such a flower model can also be represented as a process tree. If $A = \{a_1,a_2, \ldots , a_n\} = act (L)$, then $Q = \,{\circlearrowleft }(\tau ,a_1,a_2, \ldots , a_n)$ is the process tree that allows for any behavior over A, i.e., $lang (Q) = A^*$. Although it is easy to create such a process tree, it is not so clear how to add constraints to it. As mentioned earlier, it is impossible to synchronize activities in different subtrees. However, when looking at the flower Petri net $disc _{{}_{ flower }}(L)$, it is obvious that places can be added to constrain the behavior. Therefore, we use Petri nets to illustrate “bottom-up” process discovery.

Fig. 14.

Four accepting Petri nets: (a) a flower model, (b) $AN _{p_2}$ with just one place $p_2 = (\{a\},\{b,d\})$, (c) an accepting Petri net with three additional redundant places $p_7 = (\emptyset ,\{e\})$, $p_8 = (\{a\},\{e\})$, and $p_9 = (\{a\},\emptyset )$, and (d) the accepting Petri net $AN _{1}$ already shown in Fig. 9(a) (discovered by applying the original Alpha algorithm [1, 9] to event log $L_1$).

Next, we consider a Petri net having a single place constraining the behavior of the flower model. The place $p = (A_1,A_2)$ is characterized by a set of input activities $A_1$ and a set of output activities $A_2$. We would like to add places that allow for the behavior seen in the event log. Such a place is called an admissible place.

Definition 21 (Admissible Place)

Let $L \in \mathcal {B}({\mathcal{U}_{ act }}^*)$ be an event log with activities $A = act (L)$. $p = (A_1,A_2)$ is a candidate place if $A_1 \subseteq A$ and $A_2 \subseteq A$. The corresponding single place accepting Petri net is $AN _p=(N,M_{ init },M_{ final })$ with $N=(P,T,F,l)$, $P = \{p\}$, $T = A$, $F = \{(a,p) \mid a\in A_1\} \cup \{(p,a) \mid a\in A_2\}$, $l = \{(a,a)\mid a \in A\})$, $M_{ init } = [ p \mid A_1 = \emptyset ]$, and $M_{ final } = [ p \mid A_2 = \emptyset ]$. Candidate place $p = (A_1,A_2)$ is admissible if $var (L) \subseteq lang ( AN _p)$. $P^{{}^{ adm }}(L)$ is the set of all admissible places, given an event log L.

Given a candidate place $p = (A_1,A_2)$, $AN _p$ is the accepting Petri net consisting of one transition per activity and a single place p. The transitions in $A_1$ produce tokens for p and the transitions in $A_2$ consume tokens from p. If p is a source place (i.e., $A_1 = \emptyset$), then it has to be initially marked to be meaningful (otherwise, it would remain empty by definition). If p is a sink place (i.e., $A_2 = \emptyset$), then it has to be marked in the final marking to be meaningful (otherwise, it could never be marked on a path to the final marking). We also assume that all other places are empty both at the beginning and at the end. Hence, only source places are initially marked and only sink places are marked in the final marking. This explains the reason that $M_{ init } = [ p \mid A_1 = \emptyset ]$ (p is initially marked if it is a source place) and $M_{ final } = [ p \mid A_2 = \emptyset ]$ (p is marked in the final marking if it is a sink place).

A candidate place $p = (A_1,A_2)$ is admissible if the corresponding $AN _p$ allows for all the traces seen in the event log, i.e., event log L and single-place net $AN _p$ are perfectly fitting. Consider, for example, $L_1 = [\langle a,b,c,e \rangle ^{10},\langle a,c,b,e \rangle ^5, \langle a,d,e \rangle ]$. Examples of admissible candidate places are $p_1 = (\emptyset ,\{a\})$, $p_2 = (\{a\},\{b,d\})$, $p_3 = (\{a\},\{c,d\})$, $p_4 = (\{b,d\},\{e\})$, $p_5 = (\{c,d\},\{e\})$, $p_6 = (\{e\},\emptyset )$. These are the places shown earlier in Fig. 9(a) (for convenience the accepting Petri net $AN _1$ is again shown in Fig. 14(d)). However, we now consider an accepting Petri net per place, i.e., $AN _{p_1}, AN _{p_2}, AN _{p_3}, \ldots , AN _{p_6}$. Figure 14(b) shows $AN _{p_2}$ with $p_2 = (\{a\},\{b,d\})$. Other admissible places (not shown in Fig. 9(a)) are $p_7 = (\emptyset ,\{e\})$, $p_8 = (\{a\},\{e\})$, $p_9 = (\{a\},\emptyset )$. Examples of candidate places that are not admissible are $p_{10} = (\emptyset ,\{b\})$ (the initial token in $p_{10}$ is not consumed when replaying $\langle a,d,e \rangle$), $p_{11} = (\{a\},\{b\})$ (the token produced for $p_{11}$ by a is not consumed when replaying $\langle a,d,e \rangle$), $p_{12} = (\{b\},\{e\})$ (it is impossible to replay $\langle a,d,e \rangle$ because of a missing token in $p_{12}$), and $p_{13} = (\{b\},\emptyset )$ (the sink place is not marked when replaying $\langle a,d,e \rangle$).

Note that places correspond to constraints. Place $p_4 = (\{b,d\},\{e\})$ allows for all the traces in $L_1$ but does not allow for traces such as $\langle a,e \rangle$, $\langle a,b,d,e \rangle$, $\langle a,b,e,e \rangle$, etc.

Assuming that we want to ensure perfect replay fitness (i.e., 100% recall), we only add admissible places. This is a reasonable premise if filtered the event log (cf. Definition 19) before conducting discovery. This means that process discovery is reduced to finding a subset of $P^{{}^{ adm }}(L)$ (i.e., a selection of admissible places given event log L).

Why not simply add all places in $P^{{}^{ adm }}(L)$ to the discovered process model? There are two reasons not to do this: redundancy and overfitting. A place is redundant if its removal does not change the behavior. Consider, for example, Fig. 14(c) with two source places, two sink places, and an additional place connecting a and e. The places $p_7 = (\emptyset ,\{e\})$, $p_8 = (\{a\},\{e\})$, and $p_9 = (\{a\},\emptyset )$ are redundant, i.e., we can remove them without allowing for more behavior. Moreover, adding all possible places in $P^{{}^{ adm }}(L)$ may lead to overfitting. As explained in Sect. 3, the event log contains example behavior and it would be odd to assume that behaviors that have not been observed are not possible. Note that there are $2^n \times 2^n = 2^{2n}$ candidate places with $n = \left| { act (L)}\right|$. Hence, for a log with just ten activities there are over one million candidate places ($2^{2\times 10} = 1048576)$). Many of these will be admissible by accident. This problem is comparable to “multiple hypothesis testing” in statistics. If one tests enough hypotheses, then one will find seemingly significant results by accident (cf. Bonferroni correction).

There are many approaches to select a suitable subset of $P^{{}^{ adm }}(L)$. For example, it is easy to remove redundant places and only consider places with a limited number of input and output arcs [7, 26]. However, there is the additional problem that the above procedure requires evaluating each candidate place with respect to the whole event log. This means that a naïve approach quickly becomes intractable for larger event logs and processes.

5.2 The Alpha Algorithm

In the remainder of this section, we present the first process discovery technique able to discover concurrent models (e.g., Petri nets) from event logs: the Alpha algorithm [9]. The Alpha algorithm is completely based on the footprint of the (filtered) event log L. This implies that one pass through the event log is sufficient. Hence, the algorithm is linear in the size of the log (a naïve implementation is exponential in the number of unique activities, but this number is typically low). One can implement the Alpha algorithm efficiently by combining $\rightarrow$ relations that meet certain constraints. These constrains are monotonic, allowing for an apriori-style algorithm [1].

We have adapted the original presentation used in [9] to leverage the notations and insights already provided in this chapter. We use as input a DFG and as a result also add a dummy start ($\blacktriangleright$) and end (${\scriptstyle {\blacksquare }}$) activity. However, in essence, the algorithm did not change. We elaborate on the differences with [9] later. The Alpha algorithm discovers an accepting Petri net for any event log L.

Definition 22 (Alpha Algorithm)

The alpha algorithm $disc _{ alpha } \in \mathcal {B}({\mathcal{U}_{ act }}^*) \rightarrow \mathcal{U}_{ AN }$ returns an accepting Petri net $disc _{ alpha }(L)$ for any event log $L \in \mathcal {B}({\mathcal{U}_{ act }}^*)$. Let $A = act (L)$ and $fp (L) = fp ( disc _{{}_{ DFG }}(L))$ the footprint of event log L. This allows us to write $a_1 \rightarrow _L a_2$ if $fp (L)((a_1,a_2)) = {\rightarrow }$ and $a_1 {\#}_L a_2$ if $fp (L)((a_1,a_2)) = {\#}$ for any $a_1,a_2 \in A' = A \cup \{\blacktriangleright ,{\scriptstyle {\blacksquare }}\}$.

• 1. $Cnd = \{ (A_1,A_2)\mid A_1 \subseteq A' \ \wedge \ A_1 \ne \emptyset \ \wedge \ A_2 \subseteq A' \ \wedge \ A_2 \ne \emptyset \ \wedge \ \forall _{a_1\in A_1}\forall _{a_2\in A_2}\ a_1 \rightarrow _L a_2 \ \wedge \ \forall _{a_1,a_2\in A_1}\ a_1 {\#}_L a_2 \ \wedge \ \forall _{a_1,a_2\in A_2}\ a_1 {\#}_L a_2 \}$ are the candidate places,

• 2. $Sel = \{ (A_1,A_2) \in Cnd \mid \forall _{(A_1',A_2')\in Cnd }\ A_1 \subseteq A_1' \ \wedge A_2 \subseteq A_2' \Longrightarrow (A_1,A_2) = (A_1',A_2') \}$ are the selected maximal places,

• 3. $P = \{p_{(A_1,A_2)} \mid (A_1,A_2) \in Sel \} \cup \{p_{\blacktriangleright },p_{{}_{\scriptstyle {\blacksquare }}}\}$ is the set of all places,

• 4. $T = \{ t_a \mid a \in A'\}$ is the set of transitions,

• 5. $F = \{ (t_a,p_{(A_1,A_2)}) \mid (A_1,A_2) \in Sel \wedge \ a \in A_1 \} \ \cup \ \{ (p_{(A_1,A_2)},t_a) \mid (A_1,A_2) \in Sel \wedge \ a \in A_2 \} \ \cup \{ (p_{\blacktriangleright },t_{\blacktriangleright }),(t_{{}_{{\scriptstyle {\blacksquare }}}},p_{{}_{{\scriptstyle {\blacksquare }}}})\}$ is the set of arcs,

• 6. $l = \{(t_a,a) \mid a \in A\}$ is the labeling function,

• 7. $M_{ init } = [p_{\blacktriangleright }]$ is the initial marking, $M_{ final } = [p_{{}_{{\scriptstyle {\blacksquare }}}}]$ is the final marking, and

• 8. $disc _{ alpha }(L) = ((P,T,F,l),M_{ init },M_{ final })$ is the discovered accepting Petri net.

The complexity of the algorithm is in the first two steps building the sets $Cnd$ and $Sel$ that are used to create the places in Step 3. The rest builds on the ideas and notions introduced before. The Alpha algorithm creates a transition $t_a$ for each activity a in the event log and also adds a start transition $t_{\blacktriangleright }$ and an end transition $t_{{}_{{\scriptstyle {\blacksquare }}}}$ (Step 4). Transitions are labeled with the corresponding activity (Step 6). Transitions $t_{\blacktriangleright }$ and $t_{{}_{{\scriptstyle {\blacksquare }}}}$ are silent, $t_{\blacktriangleright }$ has a source place $p_{\blacktriangleright }$ as input and $t_{{}_{{\scriptstyle {\blacksquare }}}}$ has a sink place $p_{{}_{{\scriptstyle {\blacksquare }}}}$ as output. The initial marking only marks the source place $p_{\blacktriangleright }$ and the final marking only marks the sink place $p_{{}_{{\scriptstyle {\blacksquare }}}}$ (Step 7). Steps 3–8 can be seen as “bookkeeping”. The essence of the algorithm is in the first two steps.

Step 1 of the algorithm creates candidate places similar to the construction of candidate places used in Definition 21. $(A_1,A_2)$ corresponds to a candidate place p such that activities in $A_1$ produce tokens for p and activities in $A_2$ consume tokens from p. Note that technically $(A_1,A_2)$ is a pair of non-empty sets of activities (including start and end). The requirement $\forall _{a_1\in A_1}\forall _{a_2\in A_2}\ a_1 \rightarrow _L a_2$ states that any activity in $A_1$ can be directly followed by any activity in $A_2$, but no activity in $A_2$ can be directly followed by an activity in $A_1$. The requirements $\forall _{a_1,a_2\in A_1}\ a_1 {\#}_L a_2$ and $\forall _{a_1,a_2\in A_2}\ a_1 {\#}_L a_2$ state that activities in the sets $A_1$ and $A_2$ cannot directly follow any other member of the same activity set. As a consequence, an activity that can follow itself directly (i.e., $a {\Vert }_L a$) cannot be in $A_1$ or $A_2$. This also implies that $A_1$ and $A_2$ are disjoint. $Cnd$ is the set of all pairs of activity sets meeting these requirements. $Sel \subseteq Cnd$ retains the “maximal elements”. Candidate $(A_1,A_2) \in Cnd$ is maximal if there is no other $(A_1',A_2') \in Cnd$ that is strictly larger, i.e., it cannot be that $A_1 \subseteq A_1'$, $A_2 \subseteq A_2'$, and $(A_1',A_2') \ne (A_1,A_2)$. Each selected maximal element, i.e., $(A_1,A_2) \in Sel$, corresponds to a place $p_{(A_1,A_2)}$ connecting the transitions corresponding to $A_1$ (i.e., $\{t_a \mid a \in A_1\}$) to the transitions corresponding to $A_2$ (i.e., $\{t_a \mid a \in A_2\}$).

Fig. 15.

Four accepting Petri nets created using the Alpha algorithm from Definition 22. The place and transition names are as specified in Definition 22. The four event logs used are: $L_1 = [\langle a,b,c,e \rangle ^{10},\langle a,c,b,e \rangle ^5, \langle a,d,e \rangle ]$, $L_2 = [ \langle a,b,c,e \rangle ^{50},\langle a,c,b,e \rangle ^{40},\langle a,b,c,d,b,c,e \rangle ^{30},\langle a,c,b,d,b,c,e \rangle ^{20},\langle a,b,c,d,c,b,e \rangle ^{10},\langle a,c,b,d,c,b,d,b,c,e \rangle ^{10} ]$, $L_4 = [\langle a,b \rangle ^{35},\langle b,a \rangle ^{15}]$, and $L_5 = [\langle a \rangle ^{10}, \langle a,b \rangle ^{8}, \langle a,c,b \rangle ^6, \langle a,c,c,b \rangle ^3, \langle a,c,c,c,b \rangle ]$. Note that unlike in [9] invisible start and end transitions are added to be more general.

Figure 15 shows some examples where the Alpha algorithm is applied to a smaller event log. The place names reflect the elements of the set $Sel$ created in Step 2 of the algorithm. For $L_1 = [\langle a,b,c,e \rangle ^{10},\langle a,c,b,e \rangle ^5, \langle a,d,e \rangle ]$, $Sel = \{ (\{{\blacktriangleright }\},\{a\}), (\{a\},\{b,d\}), (\{a\},\{c,d\}), (\{b,d\},\{e\}), (\{c,d\},\{e\}), (\{e\},\{{{\scriptstyle {\blacksquare }}}\}) \}$. Note that $Cnd {\setminus } Sel = \{ (\{a\},\{b\}), (\{a\},\{c\}), (\{a\},\{d\}),$ $(\{b\},\{e\}), (\{c\},\{e\}), (\{d\},\{e\})\}$. These candidates were removed because they are not maximal. Figure 15(a) shows the resulting accepting Petri net $disc _{ alpha }(L_1)$. Figure 15(b) shows $disc _{ alpha }(L_2)$. Note that the Alpha algorithm is able to discover concurrency, choices, and loops. Comparing the process models for $L_1$ and $L_2$ with the accepting Petri nets in Fig. 2 (for $L_1$) and Fig. 3 (for $L_2$), we can see that $p_{\blacktriangleright }$, $t_{\blacktriangleright }$, $t_{{}_{{\scriptstyle {\blacksquare }}}}$, and $p_{{}_{{\scriptstyle {\blacksquare }}}}$ have been added. These can be removed if start and end activities happen only at the beginning or end. In $L_1$ and $L_2$, the only start activity is a and a can only happen in the first position. Also, the only end activity is e and e can only happen in the last position. If this is the case, we do not need to add an artificial start ${\blacktriangleright }$ or end ${{\scriptstyle {\blacksquare }}}$.

Figure 15(c) shows why it is sometimes necessary to add an artificial start or end. In $L_4 = [\langle a,b \rangle ^{35},\langle b,a \rangle ^{15}]$, a is a start activity in trace $\langle a,b \rangle$, but can also happen at the second position (cf. $\langle b,a \rangle$). The same holds for activity b. Therefore, we need to add an artificial start ${\blacktriangleright }$. a and b are also end activities, but do not appear just at the end, e.g., b may also happen in the first position. Therefore, we need to add an artificial end ${{\scriptstyle {\blacksquare }}}$. Note that Definition 22 is slightly different from the original algorithm in [9] due to the addition of the dummy start and end activities. For logs where the traditional algorithm already produces the correct result, one can simply remove $p_{\blacktriangleright }$, $t_{\blacktriangleright }$, $t_{{}_{{\scriptstyle {\blacksquare }}}}$, and $p_{{}_{{\scriptstyle {\blacksquare }}}}$. However, the algorithm in Definition 22 is able to handle start and end activities that can also appear in the middle of a trace. Hence, it is more general.

Figure 16 shows the model discovered for the larger event log $L_3 = [ \langle ie , cu , lt , xr , fe \rangle ^{285},$ $\langle ie , cu , lt , ct , fe \rangle ^{260},$ $\langle ie , cu , ct , lt , fe \rangle ^{139},$ $\langle ie , lt , cu , xr , fe \rangle ^{137},$ $\langle ie , lt , cu , ct , fe \rangle ^{124},$ $\langle ie , cu , xr , lt , fe \rangle ^{113},$ $\langle ie , xr , cu , lt , fe \rangle ^{72},$ $\langle ie , ct , cu , xr , fe \rangle ^{72},$ $\langle ie , cu , om , am , cu , lt , xr , fe \rangle ^{29},$ $\langle ie , cu , om , am , cu , lt , ct , fe \rangle ^{28},$ $\ldots ]$ using the full activity names, i.e., $ie$ = initial examination, $xr$ = X-ray, $ct$ = CT scan, $cu$ = checkup, $om$ = order medicine, $am$ = administer medicine, $lt$ = lab tests, and $fe$ = final examination. The model was generated using the Alpha algorithm implemented in ProM. Note that there was no need to add artificial start or end activities because $ie$ happens only at the beginning and $fe$ happens only at the end.

Fig. 16.

The accepting Petri net that was discovered by the Alpha algorithm implemented in ProM, based on the larger event log $L_3$ introduced in Sect. 2.5. Note that the artificial start and end activities have not been added, and the full activity names are used.

The Alpha algorithm should be seen as a baseline algorithm to discover concurrency. It has many limitations, as pointed out in the original paper presenting the algorithm [9]. Event log $L_5 = [\langle a \rangle ^{10}, \langle a,b \rangle ^{8}, \langle a,c,b \rangle ^6, \langle a,c,c,b \rangle ^3, \langle a,c,c,c,b \rangle ]$ is used to illustrate two of these problems: skipping and self-loops. Figure 15(d) shows the discovered process model $disc _{ alpha }(L_5)$. The selected maximal elements are $Sel = \{ (\{{\blacktriangleright }\},\{a\}), (\{a\},\{b\}), (\{a\},\{{{\scriptstyle {\blacksquare }}}\}), (\{b\},\{{{\scriptstyle {\blacksquare }}}\}) \}$. Note that $(\{a\},\{b,{{\scriptstyle {\blacksquare }}}\}) \not \in Sel$, because $b \rightarrow _{L_5} {{\scriptstyle {\blacksquare }}}$ and not $b \#_{L_5} {{\scriptstyle {\blacksquare }}}$. Because $c \Vert _{L_5} c$ (c can be directly followed by c) and not $c \#_{L_5} c$, activity c does not appear in $Sel$, implying that $t_c$ remains disconnected from the rest of the model. Activity b can be seen as a “skippable” activity and the Alpha algorithm cannot handle such activities, because these require silent transitions. The basic Alpha algorithm can also not discover the self-loop involving c. The Alpha algorithm has been extended to address these problems, and there exist variants to deal with self-loops, skipping, long-term dependencies, etc. See [1] for more information on the limitations of the basic algorithm and pointers to extensions addressing these problems.

6 Top-Down Process Discovery

The Alpha algorithm is an example of a bottom-up discovery approach that tries to add places to the Petri net to locally constrain behavior. Top-down discovery approaches try to recursively decompose the event log into smaller event logs until the problem gets trivial. The whole event log L is decomposed into smaller event logs $L_1, L_2, \ldots , L_n$ that have a clear relationship, e.g., $L_i$ may contain events that occur before $L_j$ if $i<j$, or $L_i$ and $L_j$ are fully disjoint for all $i \ne j$. Each event in L ends up in precisely one of the sublogs. However, cases may be distributed over multiple sublogs. Each of the smaller event logs is analyzed and (if needed) decomposed into smaller event logs, e.g., $L_i$ is in turn decomposed into $L_{i,1}, L_{i,2}, \ldots , L_{i,m}$, etc. Again the events in $L_i$ are partitioned over $L_{i,1}, L_{i,2}, \ldots , L_{i,m}$. This is repeated until we encounter a so-called base case, i.e., a sublog containing just one activity, e.g., $[\langle a \rangle ^{160}]$, $[\langle a \rangle ^{80},\langle \rangle ^{80}]$, or $[\langle a \rangle ^{80},\langle a,a \rangle ^{60},\langle a,a,a \rangle ^{20}]$.

Due to the recursive decomposition of logs into smaller event logs, we automatically get a tree-like structure where the root corresponds to the original event log and the leaves correspond to trivial event logs (the so-called base cases). This fits well with the process tree formalism introduced in Sect. 4.2.

Before introducing a particular approach, let’s use a few simple event logs to illustrate the idea of splitting an event log.

• Event log $L = [ \langle a, b, c \rangle ^{100}]$ is decomposed into base cases $L_1= [ \langle a \rangle ^{100}]$, $L_2= [ \langle b \rangle ^{100}]$, and $L_3= [ \langle c \rangle ^{100}]$ leading to the discovery of $Q=\,{\rightarrow }(a,b,c)$.

• Event log $L = [ \langle a \rangle ^{50}, \langle b \rangle ^{25}, \langle c \rangle ^{25}]$ is decomposed into base cases $L_1= [ \langle a \rangle ^{50}]$, $L_2= [ \langle b \rangle ^{25}]$, and $L_3= [ \langle c \rangle ^{25}]$ leading to the discovery of $Q=\times (a,b,c)$.

• Event log $L = [ \langle a,b,c \rangle ^{30}, \langle a,c,b \rangle ^{20}, \langle b,a,c \rangle ^{20}, \langle b,c,a \rangle ^{10}, \langle c,a,b \rangle ^{10}, \langle c,b,a \rangle ^{10} ]$ is decomposed into base cases $L_1= [ \langle a \rangle ^{100}]$, $L_2= [ \langle b \rangle ^{100}]$, and $L_3= [ \langle c \rangle ^{100}]$ leading to the discovery of $Q=\wedge (a,b,c)$.

• Event log $L = [ \langle a \rangle ^{50}, \langle a,b,a \rangle ^{25}, \langle a,b,a,b,a \rangle ^{25}]$ is decomposed into base cases $L_1= [ \langle a \rangle ^{175}]$ and $L_2= [ \langle b \rangle ^{75}]$ leading to the discovery of $Q=\,{\circlearrowleft }(a,b)$.

• Event log $L = [ \langle a, c \rangle ^{50}, \langle a, b, c \rangle ^{50}]$ is decomposed into base cases $L_1= [ \langle a \rangle ^{100}]$, $L_2= [ \langle \rangle ^{50}, \langle b \rangle ^{50}]$, and $L_3= [ \langle c \rangle ^{100}]$ leading to the discovery of $Q=\,{\rightarrow }(a,\times (b,\tau ),c)$.

• Event log $L = [ \langle a, c \rangle ^{50}, \langle a, b, c \rangle ^{20}, \langle a, b,b, c \rangle ^{20}, \langle a, b, b, b, c \rangle ^{10}]$ is decomposed into base cases $L_1= [ \langle a \rangle ^{100}]$, $L_2= [ \langle \rangle ^{50},\langle b \rangle ^{20},\langle b,b \rangle ^{20},\langle b,b,b \rangle ^{10}]$, and $L_3= [ \langle c \rangle ^{100}]$ leading to the discovery of $Q=\,{\rightarrow }(a,{\circlearrowleft }(\tau ,b),c)$.

In this section, we use the basic inductive mining algorithm to illustrate top-down discovery [22,23,24]. This algorithm uses DFGs to find so-called cuts partitioning the set of observed activities into subsets of activities. Set $A = act (L)$ is partitioned into pairwise disjoint sets of activities $A_1, A_2, \ldots , A_n$. These activity sets are used to distribute the events in L over $L_1, L_2, \ldots , L_n$ such that $A_1 = act (L_1)$, $A_2 = act (L_2)$, etc. There are cuts for all four process tree operators, i.e., $\rightarrow$ (sequential composition), $\times$ (exclusive choice), $\wedge$ (parallel composition), and $\circlearrowleft$ (redo loop).

Definition 23 (Sequence, Exclusive-Choice, Parallel, and Redo-Loop Cuts)

Let $L \in \mathcal {B}({\mathcal{U}_{ act }}^*)$ be an event log having a DFG $disc _{{}_{ DFG }}(L) = (A,F)$ based on L (note that $A= act (L)$) with start activities $A^{ start } = \{a \in A \mid ({\blacktriangleright },a) \in F\}$ and end activities $A^{ end } = \{a \in A \mid (a,{{\scriptstyle {\blacksquare }}}) \in F\}$. An n-ary $\oplus$-cut of L is a partition of A into $n \ge 2$ pairwise disjoint subsets $A_1, A_2, \ldots , A_n$ (i.e., $A= \bigcup _{i\in \{1,\ldots ,n\}} A_i$ and $A_i \cap A_j = \emptyset$ for $i\ne j$) with $\oplus \in \{\rightarrow ,\times ,\wedge ,\circlearrowleft \}$. Such a $\oplus$-cut is denoted $(\oplus ,A_1, A_2, \ldots A_n)$. For each type of operator $\oplus \in \{\rightarrow ,\times ,\wedge ,\circlearrowleft \}$ specific conditions apply:

• An exclusive-choice cut of L is a cut $(\times ,A_1, A_2, \ldots A_n)$ such that

  • $\forall _{i,j \in \{1, \ldots n\}} \forall _{a \in A_i} \forall _{b \in A_j} \ i \ne j \ \Rightarrow \ (a,b) \not \in F$.

• A sequence cut of L is a cut $({\rightarrow },A_1, A_2, \ldots A_n)$ such that

  • $\forall _{i,j \in \{1, \ldots n\}} \forall _{a \in A_i} \forall _{b \in A_j} \ i < j \ \Rightarrow \ ((a,b) \in F^+ \ \wedge \ (b,a) \not \in F^+)$. (Note that $F^+$ is the non-reflexive transitive closure of F, i.e., $(a,b) \in F^+$ means that there is a path from a to b in the DFG.)

• A parallel cut of L is a cut $(\wedge ,A_1, A_2, \ldots A_n)$ such that

  • $\forall _{i \in \{1, \ldots n\}} \ A_i \cap A^{ start } \ne \emptyset \ \wedge \ A_i \cap A^{ end } \ne \emptyset$ and

  • $\forall _{i,j \in \{1, \ldots n\}} \forall _{a \in A_i} \forall _{b \in A_j} \ i \ne j \ \Rightarrow (a,b) \in F$.

• A redo-loop cut of L is a cut $(\circlearrowleft ,A_1, A_2, \ldots A_n)$ such that

  • $A^{ start } \cup A^{ end } \subseteq A_1$,

  • $\forall _{i,j \in \{2, \ldots n\}} \forall _{a \in A_i} \forall _{b \in A_j} \ i \ne j \ \Rightarrow \ (a,b) \not \in F$,

  • $\{a \in A_1 \mid (a,b) \in F \ \wedge \ b \not \in A_1 \} = A^{ end }$,

  • $\{a \in A_1 \mid (b,a) \in F \ \wedge \ b \not \in A_1 \} = A^{ start }$,

  • $\forall _{(a,b) \in F}\ a \in A_1 \ \wedge \ b \not \in A_1 \ \Rightarrow \ \forall _{a' \in A^{ end }} \ (a',b) \in F$, and

  • $\forall _{(b,a) \in F}\ a \in A_1 \ \wedge \ b \not \in A_1 \ \Rightarrow \ \forall _{a' \in A^{ start }} \ (b,a') \in F$.

Fig. 17.

Four types of cuts: $(\oplus ,A_1, A_2, \ldots A_n)$ with $\oplus \in \{\times ,\rightarrow ,\wedge ,\circlearrowleft \}$ (based on [1]).

Figure 17 illustrates the four types of cuts. There is an exclusive-choice cut when the DFG can be split into disconnected parts after leaving out the artificial start ${\blacktriangleright }$ and end ${{\scriptstyle {\blacksquare }}}$. (Recall that ${\blacktriangleright } \not \in A$ and ${{\scriptstyle {\blacksquare }}} \not \in A$.) There is a sequence cut when the DFG can be split into sequential parts where only “forward connections” are possible. Note that we need to use the non-reflexive transitive closure of F. There is a parallel cut when the DFG can be split into concurrent parts where any activity in one part can be followed by any activity in another part. The redo-loop cut has the most complex definition. All start and end activities should be in $A_1$ (the “do part”) and none of the “redo parts” can have start or end activities. Moreover, the “redo parts” ($A_2, A_3, \ldots , A_n$) are only connected through the “do part” ($A_1$). $B^{ start } =\{b \mid (a,b) \in F \ \wedge \ a \in A_1 \ \wedge \ b \not \in A_1\}$ are the start activities of the “redo parts” connected to end activities in the “do part” and $B^{ end } =\{b \mid (b,a) \in F \ \wedge \ a \in A_1 \ \wedge \ b \not \in A_1\}$ are the end activities of the “redo parts” connected to start activities in the “do part”. The requirements in Definition 23 imply that $A^{ end } \times B^{ start } \subseteq F$ and $B^{ end } \times A^{ start } \subseteq F$. This implies that all end activities of the “do part” are connected to all start activities of the “redo parts” and all end activities of the “redo parts” are connected to all start activities of the “do part”. For more explanations, see [1].

How the event log L is decomposed into $L_1,L_2, \ldots , L_n$ based on $\oplus$-cut $(\oplus ,A_1, A_2,\ldots A_n)$ depends on the type of cut $\oplus \in \{\rightarrow ,\times ,\wedge ,\circlearrowleft \}$. In all log decompositions, each event ends up in precisely one event log, i.e., the number of events remains invariant through decomposition. We use the previously introduced event logs to illustrate this.

First, we consider $L_1 = [\langle a,b,c,e \rangle ^{10},\langle a,c,b,e \rangle ^5, \langle a,d,e \rangle ]$ and construct the corresponding DFG to find one of the four cuts. We check the presence of a cut using the order in Definition 23, i.e., (1) $\times$, (2) $\rightarrow$, (3) $\wedge$, (4) $\circlearrowleft$. There is no exclusive-choice cut for $L_1$, but there is a sequence cut $({\rightarrow },\{a\},\{b,c,d\},\{e\})$. Using this cut, $L_1$ is split into $L_{a} = [\langle a \rangle ^{16}]$, $L_{b,c,d} = [\langle b,c \rangle ^{10},\langle c,b \rangle ^5, \langle d \rangle ]$, and $L_{e} = [\langle e \rangle ^{16}]$. $L_{a}$ and $L_{e}$ correspond to base cases since there is just one activity left: $L_{a}$ is modeled by a single occurrence of activity a, and $L_{e}$ is modeled by a single occurrence of activity e. Hence, the process tree starts with ${\rightarrow }(a,?,e)$, where ? corresponds to the subtree describing $L_{b,c,d}$. Next, we create a DFG for $L_{b,c,d}$ and see that we can apply an exclusive-choice cut $(\times ,\{b,c\},\{d\})$. Using this cut, $L_{b,c,d}$ is split into $L_{b,c} = [\langle b,c \rangle ^{10},\langle c,b \rangle ^5]$ and $L_{d} = [\langle d \rangle ]$. $L_{d}$ corresponds to a base case since there is just one activity left. Hence, the subtree for $L_{b,c,d}$ has the following structure $\times (?,d)$, where ? corresponds to the subtree describing $L_{b,c}$. The overall tree created thus far is ${\rightarrow }(a,\times (?,d),e)$. Next, we create a DFG for $L_{b,c}$ and see that we can apply a parallel cut $(\wedge ,\{b\},\{c\})$. It is not possible to apply an exclusive-choice cut or a sequence cut. Using cut $(\wedge ,\{b\},\{c\})$ sublog $L_{b,c}$ is split into $L_{b} = [\langle b \rangle ^{15}]$ and $L_{c} = [\langle c \rangle ^{15}]$. Both correspond to base cases. Hence, the subtree for $L_{b,c}$ is $\wedge (b,c)$. The overall tree is ${\rightarrow }(a,\times (\wedge (b,c),d),e)$. This is process tree $Q_1$ in Fig. 10(a) shown before.

Next, we consider $L_2 = [ \langle a,b,c,e \rangle ^{50},\langle a,c,b,e \rangle ^{40},\langle a,b,c,d,b,c,e \rangle ^{30},\langle a,c,b,d,b,c,e \rangle ^{20},\langle a,b,c,d,c,b,e \rangle ^{10},\langle a,c,b,d,c,b,d,b,c,e \rangle ^{10} ]$. Again, we construct the corresponding DFG to find one of the four cuts. The first cut we find is a sequence cut $(\rightarrow ,\{a\},\{b,c,d\},\{e\})$. Using this cut, $L_2$ is split into $L_{a} = [\langle a \rangle ^{160}]$, $L_{b,c,d} = [ \langle b,c \rangle ^{50},\langle c,b \rangle ^{40},\langle b,c,d,b,c \rangle ^{30},\langle c,b,d,b,c \rangle ^{20},\langle b,c,d,c,b \rangle ^{10},\langle c,b,d,c,b,d,b,c \rangle ^{10} ]$, and $L_{e} = [\langle e \rangle ^{160}]$. $L_{a}$ and $L_{e}$ correspond to base cases suggesting that the process has the following structure ${\rightarrow }(a,?,e)$, with ? corresponding to the subtree describing $L_{b,c,d}$. Again we check the presence of a cut. The first cut we find is the redo loop cut $(\circlearrowleft ,\{b,c\},\{d\})$. Using this cut, $L_{b,c,d}$ is split into $L_{b,c} = [\langle b,c \rangle ^{150},\langle c,b \rangle ^{90}]$ and $L_{d} = [\langle d \rangle ^{80}]$. Note that $L_{b,c}$ has 240 cases because the “do part” happened $50+40+(2 \times 30)+(2 \times 20)+(2 \times 10)+(3 \times 10)=240$ times. The “redo part” happened $30+20+10+(2 \times 10)=80$ times. The redo part is trivial since d is always executed once. Hence, the subtree for $L_{b,c,d}$ has the following structure ${\circlearrowleft }(?,d)$, where ? corresponds to the subtree describing $L_{b,c}$. For $L_{b,c}$, we find the subtree $\wedge (b,c)$. The overall tree is, therefore, ${\rightarrow }(a,{\circlearrowleft }(\wedge (b,c),d),e)$. This is process tree $Q_2$ in Fig. 10(b) shown before.

To explain the Alpha algorithm, we also used $L_4$ and $L_5$ in Fig. 15. Applying the basic inductive mining algorithm to $L_4 = [\langle a,b \rangle ^{35},\langle b,a \rangle ^{15}]$ yields the process tree $\wedge (a,b)$. For $L_5 = [\langle a \rangle ^{10}, \langle a,b \rangle ^{8}, \langle a,c,b \rangle ^6, \langle a,c,c,b \rangle ^3, \langle a,c,c,c,b \rangle ]$, we find the process tree ${\rightarrow }(a,{\circlearrowleft }(\tau ,c),\times (b,\tau ))$. Note that the subtree ${\circlearrowleft }(\tau ,c)$ is created for the sublog involving just c, because c happens 0, 1, 2, or 3 times. The subtree $\times (b,\tau )$ is created for the sublog involving just b, because b happens at most once.

It is possible that none of the cuts in Definition 23 can be applied while the sublog still has multiple activities. In this case, one can always apply so-called fallthroughs, e.g., use ${\circlearrowleft }(\tau ,a_1,a_2, \ldots , a_n)$ that allows for any behavior. Note that such fallthroughs are not needed when the original process was expressible in terms of a process tree (for the exact conditions, see [1, 22]). Moreover, it is also possible to use smarter fallthroughs that separate the problematic activities or behavior from the rest. Suppose that there is a cut $(\oplus ,A_1, A_2, \ldots A_{k})$ possible considering only activities $A_{ good } = A_1 \cup A_2 \cup \ldots \cup A_{k}$ and leaving out $A_{ bad } = A {\setminus } A_{ good } = \{a_1,a_2, \ldots , a_n\}$. Then one can first apply the parallel cut $(\wedge ,A_{ good },A_{ bad })$ followed by cut $(\oplus ,A_1, A_2, \ldots A_{k})$ and cut ${\circlearrowleft }(\tau ,a_1,a_2, \ldots , a_n)$ applied to the two sublogs. There are many other fallthroughs, e.g., separating the empty traces from the rest.

Definition 24 (Inductive Mining Algorithm)

The basic inductive mining algorithm $disc _{ IM } \in \mathcal {B}({\mathcal{U}_{ act }}^*) \rightarrow \mathcal{U}_{ Q }$ returns a process tree $disc _{ IM }(L)$ for any event log $L \in \mathcal {B}({\mathcal{U}_{ act }}^*)$ using the four types of cuts, log decomposition, and fallthroughs described before.

Fig. 18.

Process tree $disc _{ IM }(L_3)= \,{\rightarrow }( ie , \wedge ( \times ( xr , ct ), {\circlearrowleft }( cu ,{\rightarrow }( om , am )), lt ), fe )$ discovered and visualized using ProM’s Inductive Visual Miner.

Earlier, we introduced event log $L_3$, containing 11761 events corresponding to 1856 cases. Using the following abbreviations $ie$ = initial examination, $xr$ = X-ray, $ct$ = CT scan, $cu$ = checkup, $om$ = order medicine, $am$ = administer medicine, $lt$ = lab tests, and $fe$ = final examination, we find $disc _{ IM }(L_3)=\, {\rightarrow }( ie , \wedge ( \times ( xr , ct ), {\circlearrowleft }( cu ,{\rightarrow }( om , am )), lt ), fe )$. Figure 18 shows a screenshot of ProM’s Inductive Visual Miner while analyzing $disc _{ IM }(L_3)$ using a BPMN-like notation. No fallthroughs were needed. Note that also the frequencies are shown. It is also possible to show timing information, e.g., average waiting times.

Fig. 19.

Process tree $disc _{ IM }(L_3)= \,{\rightarrow }( ie , \wedge ( \times ( xr , ct ), {\circlearrowleft }( cu ,{\rightarrow }( om , am )), lt ), fe )$ discovered and visualized as a BPMN model using the Celonis EMS.

Figure 19 shows $disc _{ IM }(L_3)$ discovered using Celonis. Celonis also uses a BPMN-like visualization of the process tree. The translation of process trees to BPMN or Petri nets is rather straightforward, and the resulting models are easier to interpret by most users.

In this section, we only introduced the basic inductive mining algorithm. We assume that the event log was filtered in advance to remove infrequent behavior. However, there are also extended versions of the inductive mining algorithm dealing with infrequent behavior [23]. The basic inductive mining algorithm may become intractable for huge event logs, because repeatedly sublogs need to be created. There are also more scalable variants that make a single pass through the event log and use a single overall DFG [24]. These provide fewer formal guarantees. The basic inductive mining algorithm has strong guarantees. For example, $disc _{ IM }(L)$ guarantees perfect replay fitness (i.e., 100% recall). Formally, $var (L) \subseteq lang ( disc _{ IM }(L))$. See [22,23,24] for additional formal guarantees provided by these top-down approaches.

Next two the process discovery techniques presented this chapter, there are dozens of other techniques. In [12] additional techniques are presented.

7 Conclusion

The goal of this chapter is to introduce the foundations of process discovery without aiming to provide a complete survey or details on specific algorithms (see also [10]). After reading this chapter, it should be clear that process discovery is a challenging topic with many competing requirements. We started by introducing a baseline approach that produces a Directly-Follows Graph (DFG) for an event log converted into a multiset of traces. For real-life event logs, the DFG may have an excessive number of arcs making the model incomprehensible. Therefore, we discussed three filtering approaches that can also be combined to create simpler DFGs. We also showed that the interpretation of such process models highly depends on the log preprocessing [2].

After presenting the baseline DFG discovery approach, we focused on process representations able to capture concurrency: Petri nets, process trees, and BPMN models. This is needed because, if activities do not occur in a fixed order due to concurrency, then the discovered DFGs are underfitting and contain many loops. This allowed us to introduce more advanced process discovery approaches. We characterized these as (1) bottom-up approaches and (2) top-down approaches. Bottom-up approaches try to find local process patterns constraining the process model to better fit the event log. Top-down approaches tackle the problem differently and try to partition larger event logs into smaller ones that can be analyzed more easily. Two representative approaches we described in more detail: the Alpha algorithm and the inductive mining algorithm. These should be seen as representative examples of both categories. However, there are dozens of process discovery techniques, and it is impossible to name them all.

For example, there exist many extensions of the Alpha algorithm, e.g., variants that can discover silent transitions (e.g., skipping) [34] and non-free choice constructs (e.g., long-term dependencies) [33]. The heuristic mining approach [32] can be seen as another bottom-up approach that incorporates frequency information. The approach can discover complex process structures, but often leads to models that are not sound. Region-based process-discovery approaches provide formal guarantees, but are often not very applicable (e.g., they may produce huge and overfitting process models or take too long to compute). There are two types of regions: state-based regions (which require the construction of a transition system) and language-based regions (that work on sets of traces). State-based regions were introduced by Ehrenfeucht and Rozenberg [20] in 1989 and generalized by Cortadella et al. [16]. In [8], it is shown how these state-based regions can be applied to process mining by first creating a log-based transition system using different abstractions. In [14, 30], refinements are proposed to tailor state-based regions towards process discovery. In parallel, several authors applied language-based regions to process mining [13, 35, 37]. There are also numerous bottom-up approaches combining different ideas. An example is the so-called split-miner [11] which aims to balance recall and precision. This approach also starts from a filtered DFG, but identifies combinations of splits that capture the concurrency, conflict and causal relations between neighbors in the DFG. As mentioned, there also exist different variants of the inductive mining approach presented in this chapter [22,23,24].

In this chapter, we only considered a simple event log $L \in \mathcal {B}({\mathcal{U}_{ act }}^*)$, ignoring additional event and case attributes (e.g., resources, data, transactional information). However, other logging formats may be considered. There are process discovery approaches that exploit timing information, data attributes, object references, partial order information (e.g., events happening on the same day), explicit uncertainty (e.g., imprecise timestamps or missing case identifiers), etc. We also only focused on mainstream representations such as DFGs, Petri nets, and BPMN. However, there are also discovery techniques that aim to discover stochastic process models [29], declarative process models (using Declare or DCR graphs) [25], or object/artifact-centric models (e.g., object-centric Petri nets) [5, 21].

The above illustrates that the topic of process discovery has many facets, providing interesting scientific challenges. Moreover, there are several open-source tools (e.g., ProM, bupaR, PM4Py, and RapidProM) and over 40 commercial process mining tools (e.g., Celonis, Disco/Fluxicon, Lana/Appian, Minit, Apromore, myInvenio/IBM, PAFnow, Signavio/SAP, Timeline/Abby and ProcessGold/UiPath) that already provide solid discovery approaches, and are sometimes applied to processes with billions of events. However, as applications of process mining become more demanding, new discovery approaches are needed that are better scalable and can deal with more complex processes and data structures. Therefore, process discovery is not just a great research topic, but also of great practical relevance.