Abstract
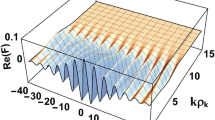
Within the framework of the quantum mechanics of a photon, constructed by the authors in previous works, using the Maple environment, a numerical modeling was carried out of two-photon interference arising in the scheme of Young’s experiment from two one-photon sources emitting simultaneously photons, the propagation of which is described by “spherical” diverging wave functions in the coordinate representation—the wave packets normalized to the total unit probability, which are a superpositions of six-component generalized eigenfunctions of the energy, momentum, and helicity operators, with a Gaussian isotropic distribution in photon momenta. In general, the curve graphically displaying the results obtained demonstrates a pronounced two-photon interference with characteristic maxima and minima and agrees well with an independently constructed curve modeled in a “quasi-classical” approach in terms of classical electrodynamics. It is concluded that the results obtained allow, in the future, using more powerful means of numerical analysis and calculations, to set the tasks of describing one- and two-photon phenomena observed in modern experiments, such as quantum cryptography and quantum computing, within the framework of the concept of photons as localized carriers of quantum information, using the wave function of a photon or a system of photons, including in an entangled state.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Berestetskii VB, Lifshitz EM, Pitaevskii LP (1982) Quantum electrodynamics, 2nd edn. Pergamon, NY
Bialynicki-Birula I (1996) The photon wave function. In: Eberly JH, Mandel L, Wolf E (eds) Coherence and quantum optics VII. Plenum Press, NY, pp 313–323
Bialynicki-Birula I (1996) Photon wave function. In: Wolf E (ed) Progress in optics, vol. XXXVI, pp 248–294. Elsevier, Amsterdam
Bohm D (1954) Quantum theory. Constable, London
Chiao RY, Kwiat PG, Steinberg AM (1995) Quantum non-locality in two-photon experiments at Berkeley. Quantum Semiclassical Optics J Eur Optical Soc Part B 7(3):259–278
Cugnon J (2011) The photon wave function. Open J Microphysics 1(3):41–52. https://doi.org/10.4236/ojm.2011.13008
Davydov AP, Zlydneva TP (2019) One-photon light interference in terms of the photon wave function in coordinate representation. Actual Probl Mod Sci Technol Educ 10(1):156–162
Davydov AP, Zlydneva TP (2019) On the wave-particle duality within the framework of modeling single-photon interference. J Phys Conf Ser 1399:02219. https://doi.org/10.1088/1742-6596/1399/2/022019.
Grangier P, Roger G, Aspect A (1986) Experimental evidence for a photon anti-correlation effect on a beamsplitter. Europhys Lett 1(4):173–179
Hawton M (1999) Photon wave functions in a localized coordinate space basis. Phys Rev A 59(5):3223–3227
Jacques V, Wu E, Grosshans F, Treussart F, Grangier P, Aspect A, Roch J-F (2007) Experimental realization of Wheeler’s delayed choice experiment. Science 315:966–968. https://doi.org/10.1126/science.1136303
Kramers HA (1958) Quantum mechanics (original ed. 1937). North-Holland, Amsterdam
Landau L, Peierls R (1930) Quantenelectrodynamik im Konfigurationsraum. Zeit F Phys 62:188–198
Mandel M, Wolf E (1995) Optical coherence and quantum optics. Cambridge University Press, Cambridge
Newton TD, Wigner EP (1949) Localized states for elementary particles. Rev Mod Phys 21:400–406
Peruzzo A, Shadbolt P, Brunner N, Popescu S, O’Brien JL (2012) A quantum delayed choice experiment. Science 338(6107):634–637. https://doi.org/10.1126/science.1226719
Power EA (1964) Introductory quantum electrodynamics. Longmans Press Ltd., London
Saari P (2012) Photon localization revisited. In: Lyagushyn S (ed) Quantum optics and laser experiments, pp 49–66. InTech – Open Access Publisher, Croatia
Scully MO, Zubairy MS (1997) Quantum optics. Cambridge University Press, Cambridge
Sipe JE (1995) Photon wave functions. Phys Rev A 52:1875–1883
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Davydov, A., Zlydneva, T. (2022). On Numerical Modeling of the Young’s Experiment with Two Sources of Single-Photon Spherical Coordinate Wave Functions. In: Tchernykh, A., Alikhanov, A., Babenko, M., Samoylenko, I. (eds) Mathematics and its Applications in New Computer Systems. MANCS 2021. Lecture Notes in Networks and Systems, vol 424. Springer, Cham. https://doi.org/10.1007/978-3-030-97020-8_30
Download citation
DOI: https://doi.org/10.1007/978-3-030-97020-8_30
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-97019-2
Online ISBN: 978-3-030-97020-8
eBook Packages: Intelligent Technologies and RoboticsIntelligent Technologies and Robotics (R0)