Surrogate Model-Based Uncertainty Quantification for a Helical Gear Pair

Abstract

Competitive industrial transmission systems must perform most efficiently with reference to complex requirements and conflicting key performance indicators. This design challenge translates into a high-dimensional multi-objective optimization problem that requires complex algorithms and evaluation of computationally expensive simulations to predict physical system behavior and design robustness. Crucial for the design decision-making process is the characterization, ranking, and quantification of relevant sources of uncertainties. However, due to the strict time limits of product development loops, the overall computational burden of uncertainty quantification (UQ) may even drive state-of-the-art parallel computing resources to their limits. Efficient machine learning (ML) tools and techniques emphasizing high-fidelity simulation data-driven training will play a fundamental role in enabling UQ in the early-stage development phase.

This investigation surveys UQ methods with a focus on noise, vibration, and harshness (NVH) characteristics of transmission systems. Quasi-static 3D contact dynamic simulations are performed to evaluate the static transmission error (TE) of meshing gear pairs under different loading and boundary conditions. TE indicates NVH excitation and is typically used as an objective function in the early-stage design process. The limited system size allows large-scale design of experiments (DoE) and enables numerical studies of various UQ sampling and modeling techniques where the design parameters are treated as random variables associated with tolerances from manufacturing and assembly processes. The model accuracy of generalized polynomial chaos expansion (gPC) and Gaussian process regression (GPR) is evaluated and compared. The results of the methods are discussed to conclude efficient and scalable solution procedures for robust design optimization.

1 Introduction

The design of industrial transmission systems is characterized by conflicting key performance indicators (KPIs), which need to be optimized simultaneously. This multi-objective optimization problem of the main objectives efficiency, NVH, and weight is constrained by the requirement of minimum tooth flank and tooth root load carrying capacity [18]. The challenge is, moreover, the expansive evaluation of the KPIs and the impact of uncertainty due to manufacturing tolerances. The definition of tolerances [1] and gear accuracy grade [3] is especially crucial in this design process. On the one hand, an upgrade in the gear accuracy grade drives the cost up to $+$80% [21]; on the other, it has a significant influence on the design objectives. However, the influences of manufacturing tolerances often rely on experience or are not fully considered [5].

The influence of tolerances on objective functions has been investigated in previous works, ranging from engineering tolerances to a prior assumptions on approximation model form and its parametrization. The impact of geometrical deviation on the objective unloaded kinematic transmission error is analyzed in [6]. The tooth contact analysis algorithm determines the kinematic relationships of each tooth meshing, neglecting elastic deformations under load. Due to the simplicity of the underlying model, a Monte-Carlo simulation is used for statistical analysis. In [5], Brecher considers multiple design objectives, which are evaluated by a finite element-based simulation. The uncertain parameters are discretized, and a full factorial approach is pursued to calculate the mean and the variance of the objectives.

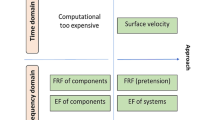
In this study, the application of surrogate models for uncertainty quantification in transmission design is proposed. A surrogate or meta model approximates the expansive objective function. To enable robust optimization of real transmission systems in an early design stage, it is essential to reduce the number of expansive objective function evaluations to a minimum. Therefore, the focus of this study is the data-efficiency of surrogates, i.e. a high model accuracy based on small data sets of high-fidelity simulations. Gaussian process regression (GPR) and generalized polynomial chaos expansion (gPC) have received much attention in the field of uncertainty quantification [9] and are analyzed in combination with different sampling methods employing two exemplary applications (see Fig. 1). The surrogates are used for global sensitivity analysis and forward uncertainty propagation. Global sensitivity analysis helps to determine the importance of each model input in predicting the response. It can help to reduce the complexity of surrogates by considering only key inputs. In forward uncertainty propagation, the effect of the uncertain inputs on the response is evaluated. In the exemplary analyzed applications, the inherently variable tolerances are aleatoric uncertainties of the model’s inputs with a probability distribution defined by the production process. For reasons of clarity, the study is limited to a single KPI, the NVH indicator transmission error of a helical gear pair. The peak-to-peak transmission error calculation via loaded tooth contact analysis (LTCA) is described in Sect. 2.

Section 3 introduces numerical methods for uncertainty quantification covering the above mentioned surrogate models GPR (Sect. 3.1) and gPC (Sect. 3.2), sampling methods (Sect. 3.3) and Sobol indices for global sensitivity analysis (Sect. 3.4). In Sect. 4 these methods are applied and evaluated regarding data-efficiency in example applications with two (Sect. 4.1) and five (Sect. 4.2) uncertain input parameters followed by the conclusion in Sect. 5.

Fig. 1.

Selected surrogate models and sampling methods for numerical forward uncertainty quantification and global sensitivity analysis

2 Evaluation of NVH Performance

The static transmission error is a measure of gear excitation. It is a typical objective function for the NVH performance of a gear pair in an early design stage. The TE is defined as the gear pairs load-dependent deviation of the ideal kinematic angular displacement. The deviations are mainly caused by elastic deformation, flank modifications, tooth manufacturing variances, misalignment of the gears, and pitch deviations. Typically the angular transmission error is projected onto the line of action by multiplying it with the base radius $r_{b0}$ (1):

$$\begin{aligned} TE = (\theta _0 -\theta _1 \frac{z_1}{z_0}) r_{b0} \end{aligned}$$

(1)

in which the subscripts 0 and 1 respectively refer to the pinion and wheel gear, $\theta$ is the angular displacement, and z represents the number of teeth. The absolute transmission error value depends on the respective position during a gearing cycle. Relevant for the excitation of a transmission system is the varying part. Therefore, either the truncated spectral representation of the cycle or the difference between maximum and minimum, the peak-to-peak transmission error, are commonly used as NVH indicators (see Fig. 2) [11].

To derive the TE, the relative angular position of pinion and wheel is evaluated under load for a discrete number of positions $\theta _0$ during a gearing cycle. The exact tooth contact and the deformation are computed via loaded tooth contact analysis. This calculation is not standardized and a variety of methods of different fidelities exists.

Essentially a full FE approach can be taken. Well-established commercial FE solvers are equipped with universal contact algorithms. The contact zone requires a high-resolution FE mesh to model the interaction between meshing gears precisely. Flank and profile modifications are implemented onto the surface mesh. Even though computationally expansive, this approach automatically incorporates the effects of extended contact zones due to deformation, the impact of rim geometry, and the interaction of neighboring teeth.

Fig. 2.

NVH indicator transmission error: evaluation of a gearing cycle

In transmission design, the utilization of tailored methods for specific gear types is state of the art. In the first step, the contact lines are discretized. An explicit description of the ideal helical gear pairs contact line is available exploiting the kinematic equations. The contact point’s stiffnesses can be analytically approximated. The stiffness components are composed of tooth bending, gear body deformation, and Hertzian deformation. The gear flank is separated into slices in this approach. Empirical constants characterize the interconnection of these slices and the gear body deformation. Hence, the analytical approximation of the stiffness has limited validity.

Higher fidelity methods use FE models to calculate the stiffness [8]. In a preprocessing step, a unit force is applied to every point of the FE mesh involute surface respectively to obtain influence coefficients. The stiffness matrix of the discrete contact points can be deduced from these influence coefficients. Therefore, a linear system of equations is given. The relative displacements of the contact points are corrected according to the flank modifications. The influence coefficients of a macro geometry design can be reused for different gear mesh positions and the evaluation of flank modifications. This system must be solved iteratively to find the loaded points of contact.

In this study, the multibody simulation (MBS) solver Adams with the plug-in GearAT is used, an LTCA implementation based on FE influence coefficients. Contact simulations are performed under quasi-static loading conditions. The choice of an MBS solver enables the evaluation of dynamic KPIs in further investigations.

3 Numerical Methods for Uncertainty Quantification

Numerical methods for uncertainty quantification determine the impact of uncertain input variables on the objective function. A primary result of forward uncertainty propagation is determining the output distribution’s central moments, such as the statistical measures mean and standard deviation. Generally, this problem cannot be solved in closed form, particularly when the objective function’s explicit representation is unknown. Yet, the dominant approach is to treat the inputs as random variables and thus convert the original deterministic system into a stochastic system [27]. This work aims to survey suitable UQ approaches for transmission systems. This class of high-dimensional engineering problems requires computationally expensive simulations to predict physical system behavior with high-fidelity models. In the present work, GPR and gPC as surrogate models for uncertainty quantification are investigated. This approach is classified as a non-intrusive method since the objective function is treated as a black box model [23].

3.1 Gaussian Process Regression

Gaussian Process regression (GPR) or Kriging is a non-parametric model that is not committed to a specific functional form. It was first introduced in [15]. A Gaussian Process (GP) is a distribution over functions, sharing a joint Gaussian distribution defined by a mean and covariance function (2) [19].

$$\begin{aligned} f(x) \sim \mathcal {GP}(m(x), k(x,x')) \end{aligned}$$

(2)

A common assumption is a zero mean and squared exponential (SE) covariance function. The covariance function defines the entries of the covariance matrix K. For the d-dimensional variables $x_p$ and $x_q$ the anisotropic squared exponential function (3) has a separate length scale $l_i$ in each input dimension i. Adjacent points have a covariance close to unity and are therefore strongly correlated. In Fig. 3a four realizations of a GP are displayed. The grey shaded area represents the $95\%$ confidence interval of the function values.

$$\begin{aligned} \text {cov}(f(\mathbf {x_p}),f(\mathbf {x_q})) = k(\mathbf {x_p},\mathbf {x_q}) = \exp \left( {-\sum _{i=1}^{d}\frac{1}{2 l_i}} |x_{p,i}-x_{q,i}|^{2}\right) \end{aligned}$$

(3)

Fig. 3.

Gaussian Process

A given training data set is represented by X sample points with $\mathbf {y} = \mathbf {f}(X) + \mathcal {N}(0, \sigma _n^2)$ being the observations of the underlying function with additional Gaussian noise. The hyperparameters of the GP are determined by maximizing the marginal log likelihood function (4). In this case, the observations are computer simulations. Therefore, the noise $\sigma _n$ in (4) can be set to zero [20]. For the anisotropic SE kernel, the hyperparameters are the length scales $l_i$. The inverse of the length scales can be interpreted as activity parameter with lager $l_i$ relating to less relevant input parameters [7].

$$\begin{aligned} \log p( \mathbf {y} |X)= -\tfrac{1}{2} \mathbf {y}^T (K+\sigma _n^2 I)^{-1}\mathbf {y}-\tfrac{1}{2} \log |K+ \sigma _n^2 I| - \tfrac{n}{2}\log 2\pi \end{aligned}$$

(4)

The prediction $\mathbf {f_*}$ of the underlying function at $X_*$ requires the extension of the joint distribution, see (5).

$$\begin{aligned} \begin{aligned} \left[ \begin{array}{c}\mathbf {y}\\ \mathbf {f_*}\end{array}\right] \sim \mathcal {N} \left( \mathbf {0}, \left[ \begin{array}{cc}K(X,X)+\sigma _n^2 I \ \ &{}K(X,X_*)\\ K(X_*,X) \ \ &{}K(X_*,X_*)\end{array}\right] \right) \end{aligned} \end{aligned}$$

(5)

The conditional distribution $\mathbf {f_*}$ given the data $\mathbf {y}, X$, and the sample points $X_*$ in case of noiseless observations is:

$$\begin{aligned} \begin{aligned} \mathbf {f_*}|X_*,X,\mathbf {f} \sim \mathcal {N}(&K(X_*,X)K(X,X)^{-1} \mathbf {f}, \\&K(X_*,X_*)-K(X_*,X)K(X,X)^{-1}K(X,X_*)) \end{aligned} \end{aligned}$$

(6)

The mean of this distribution are the predicted values $\mathbf {f_*}$. A strength of a GPR is the capability of additionally supplying a measure of uncertainty about the predictions. In Fig. 3b, the expected function values are represented by the solid line. The $95\%$ confidence interval is again shaded in grey. The uncertainty in the prediction increases with the distance to the three given noise-free data samples.

3.2 Generalized Polynomial Chaos Expansion

In contrast to GPR, a generalized polynomial chaos expansion (gPC) model is a parametric surrogate. Given a model with random independent input parameters $\mathbf {X}=\{X_1,X_2,...X_d\}$ with the probability density function $f_\mathbf {X}(\mathbf {x})$, the output $Y=F(\mathbf {X})$ is also a random variable. Assuming a finite variance of Y, the function can be expressed by an infinite series of polynomials (7). To make this problem computationally tractable, the function is approximated by a truncated series.

$$\begin{aligned} F(\mathbf {X}) = \sum _{j \in \mathbb {N}}^{\infty } y_j \mathbf {\Psi _j}(\mathbf {X}) \approx \tilde{M}(\mathbf {X}) =\sum _{\boldsymbol{\mathbf {\alpha }} \in \mathbb {N}^d}^{P} y_{\boldsymbol{\mathbf {\alpha }}} \boldsymbol{\mathbf {\Psi _\alpha }}(\mathbf {X}) \end{aligned}$$

(7)

The multivariate polynomials $\boldsymbol{\mathbf {\Psi _\alpha }}(\mathbf {X})$ are defined by the tensor product of univariate polynomials $\psi _{\alpha _i}^{(i)}(x_i)$ of the Askey scheme (8). In the initial PC formulation Ghanem [10] used Hermite polynomials as an orthogonal basis. Xui extended this approach to gPC by using polynomials from the Askey scheme, depending on the underlying probability distribution (see Table 1) in order to achieve optimal convergence [28].

$$\begin{aligned} \boldsymbol{\mathbf {\Psi _\alpha (x)}} = \prod _{i=1}^{d} \psi _{\alpha _i}^{(i)}(x_i) \end{aligned}$$

(8)

Table 1. Types of gPC and their underlying random variables [27]

The orthogonality is transmitted from the univariate polynomials to the multivariate polynomials:

$$\begin{aligned} \mathbb {E}[\boldsymbol{\mathbf {\Psi _\alpha }}(\boldsymbol{\mathbf {X}}) \boldsymbol{\mathbf {\Psi _\beta }}(\boldsymbol{\mathbf {X}})] = \int _{\mathcal {D}_{\mathbf {X}}}\boldsymbol{\mathbf {\Psi _\alpha }}(\boldsymbol{\mathbf {x}})\boldsymbol{\mathbf {\Psi _\beta }}(\boldsymbol{\mathbf {x}})f_{\boldsymbol{\mathbf {X}}} (\boldsymbol{\mathbf {x}})d\boldsymbol{\mathbf {x}} =\delta _{\boldsymbol{\mathbf {\alpha \beta }}} \ \ \ \ \forall \boldsymbol{\mathbf {\alpha , \beta }} \in \mathbb {N}^d \end{aligned}$$

(9)

in which $\delta _{\boldsymbol{\mathbf {\alpha \beta }}}$ represents the Kronecker delta.

The total number of $y_{\boldsymbol{\mathbf {\alpha }}}$-coefficients is determined by input dimension d and the maximum polynomial degree p of the truncated series:

$$\begin{aligned} P = \frac{(D+p)!}{D!p!}-1 \end{aligned}$$

(10)

The computation of these coefficients can be carried out by ordinary least-squares analysis. As a rule of thumb, the number of samples should be about $n \approx 2-3 * P$ to avoid overfitting [16]. These models will be referred to as PCR. The coefficients can also be computed by the spectral projection making use of the orthogonality of the polynomials. The integral in Eq. (11) can be approximated via a sparse grid quadrature using the Smolyak algorithm [26]. An increased level of sparse grid integration leads to a higher number of simulation model evaluations. Models based on this approach will be referred to as pseudo-spectral projection (PSP). In contrast, adaptive pseudo-spectral projections models (APSP) use an anisotropic sparse grid in which the importance of each input dimensionality will be evaluated before expanding the sparse grid with further samples per epoch.

$$\begin{aligned} \boldsymbol{\mathbf {y_\alpha }} = \mathbb {E}[Y(\boldsymbol{\mathbf {X}}), \boldsymbol{\mathbf {\Psi _\alpha }}(\boldsymbol{\mathbf {X}})] = \int _{\mathcal {D}_{\boldsymbol{\mathbf {X}}}} Y(\boldsymbol{\mathbf {X}})\boldsymbol{\mathbf {\Psi _\alpha }}(\boldsymbol{\mathbf {X}}) f_{\boldsymbol{\mathbf {X}}}(\boldsymbol{\mathbf {x}})d\boldsymbol{\mathbf {x}} \end{aligned}$$

(11)

Once a gPC model is trained, it can be used as a computationally efficient surrogate to propagate the uncertainty via Monte-Carlo simulation. The mean, variance and Sobol indices can be directly computed from the coefficients $\boldsymbol{\mathbf {y_\alpha }}$ [16].

3.3 Sampling Methods

In numerical sampling the n input sample points $\mathbf {x_i} = [x_i^{(1)}, x_i^{(2)}, ... x_i^{(d)}]$ for a d-dimensional design of experiment $\mathbf {X}=[\mathbf {x_1, x_2, ... x_n }]^T$ are set. There are several sampling methods to set up computer experiments [24]. Two of the most common ones are compared in this study: Monte-Carlo sampling (MCS) and Latin hypercube sampling (LHC).

In MCS, the samples are randomly drawn according to their probability distribution. A pseudo-random number generator outputs a number in the interval [0, 1], projected into the physical domain by the input variables underlying cumulative distribution function. The samples are independent, potentially leading to clustering of sample points, whereas part of the design space is poorly sampled. LHC, in contrast, is a stratified random sampling strategy that was introduced by McKay [17], yielding samples that are better distributed in the design space. Each input variable is partitioned into n intervals of equal probability. A random sample is drawn from every interval before shuffling the samples separately in each dimension.

3.4 Sensitivity Analysis

As an initial step to any UQ study or optimization task, sensitivity analysis helps determine how important each model input is in predicting the response and may reduce the number of uncertain parameters. In this study, Sobol indices as a global variance-based method are used [22]. The first order indices describe the share of variance of Y due to a given input parameter $X_\text {d}$.

$$\begin{aligned} S_d = \frac{\text {Var}(\mathbb {E}(Y|X_\text {d}))}{\text {Var}(Y)} \end{aligned}$$

(12)

Higher-order indices quantify the amount of total variance associated with the interaction of parameters. The calculation of Sobol indices is based on surrogates in this study (cf. [16]). The Sobol indices of a PC model can be computed analytically from the coefficients $\boldsymbol{\mathbf {y_\alpha }}$. For GP models, in contrast, a Monto-Carlo integration approach is applied using the open-source python library ASLib [12].

4 Application of UQ Methods in Transmission Design

This investigation’s main objective is to develop a data-efficient surrogate model to determine the impact of tolerances on the NVH indicator TE. A data-efficient surrogate provides a high model accuracy based on a small data set. The tolerances are treated as a random input variable. The TE is calculated via LTCA.

This investigation includes the analysis of a helical gear pair of transmission ration $i=3.2$. The input torque is applied to the smaller pinion gear. The output speed defines the angular displacement of the wheel. The peak-to-peak TE is calculated during a single gear mesh cycle (see Fig. 2a). The bearing system for pinion and wheel is modeled as a rotation joint with only one degree of freedom. Therefore, the possible tolerances reduce to the relative position of the axis and deviations of the gear flank geometry. The simplicity of this system enables large-scale DoEs.

The considered parameter ranges may be applicable for transmission systems of traction eAxles. Recommendations for admissible values for shaft deviations can be found in [1]. A distinction is made for in-plane deviation $f_{\varSigma \delta }$ and out-of-plane deviations $f_{\varSigma \beta }$ (see Fig. 4a). Assuming gear quality grade, $Q=6$ leads to $f_{\varSigma \delta }={29.47}\,\upmu \text {m}$ and $f_{\varSigma \beta }={14.74}\,\upmu \text {m}$. For practical applications of real transmission systems, the assumptions for axis parallelism would rather be determined by a statistical tolerance analysis. The flank deviations are modeled as variation in the gears microgeometry in terms of profile barreling $C_\alpha$ (see Fig. 4b) and lead crowning $C_\beta$ (see Fig. 4c).

In the following, two example applications are presented comparing the different surrogates.

4.1 Analysis with Two Uncertain Parameters

In this analysis, the influence of axis parallelism variations on the TE is evaluated. The position of the bearing seats induces axis parallelism. Tolerances of injection molded parts tend to be uniformly distributed due to the wear of the tool over time [13]. Therefore, both uncertain parameters are assumed to be uniformly distributed within the tolerances $f_{\varSigma \delta }$ and $f_{\varSigma \beta }$. The input torque is set to 100 Nm. Further fixed parameters are listed in Table 2 - 4.1.

Fig. 4.

Considered uncertain parameters according to ISO definition [1, 2]. a) $f_{\varSigma \delta }$, $f_{\varSigma \beta }$ and $A_{ae}/A_{ai}$, b) $C_\alpha$ c) $C_\beta$

Table 2. Uncertain parameters in unit $\upmu \text {m}$. All varying parameters are assumed to be uniformly distributed.

Training and Validation of a Reference Model. PCR and GPR are based on a randomized sampled data set (see Sect. 3.3). It is thus not sufficient to compare the models based on a single random training set. It is desired to train models several times with an identical sample size to evaluate the consistency of the method. The computation of the high number of required LTCA simulations is very time-consuming. To avoid this computational burden, a precise reference model based on a large DoE is developed to substitute the actual LTAC simulation. A PCR and a GPR model are trained with a training set size of $n_\text {tr}=5000$ and validated by a test set consisting of $n_\text {te}=500$ samples. The training and the test data sets are sampled independently via LHC. The model’s accuracy is commonly assessed by the coefficient of determination $r^2$, with (13) [4].

$$\begin{aligned} r^2=1-\frac{RMSE}{\sigma _\text {te}} \end{aligned}$$

(13)

The root mean square error (RMSE) between surrogate prediction and test data is set into relation with test data objective functions standard deviation $\sigma _\text {te}$. Therefore, the coefficient of determination is independent of the output scale and converges towards one with increased model accuracy. Additionally, the distribution of the relative error $\epsilon _\text {te}$ (see (14)) is displayed in form of a histogram, in which $Y_\text {te}$ represents the actual TE of the test data and $Y_\text {m}$ the surrogate model’s predictions.

$$\begin{aligned} \epsilon _{te} = 1-\frac{Y_\text {m}}{Y_\text {te}} \end{aligned}$$

(14)

Fig. 5.

Properties of reference surrogate models based on 5000 training and 500 test data samples. The top row shows results of the polynomial chaos regression model, the bottom row of the Gaussian process regression model.

The Q-Q plot in Fig. 5a indicates a good correlation of test data and surrogate model prediction. The GPR model is slightly more accurate than the PCR at $r^2=0.99935$. The relative error is smaller than $3\%$ for every test sample and for the GPR less than $2\%$ in $99.6\%$ of the test cases (see Fig. 5b). Mean and standard deviation are in accordance within $1\times {10}^{-4}\,\upmu \text {m}$. These values and the probability distribution, which is approximated by a histogram, serve as a reference solution for the surrogate models based on smaller sample sizes (see Fig. 5c). The GPR is sufficiently accurate and will substitute LTCA. Hereafter, it is referred to as the reference model.

Data-Efficiency Analysis of the Surrogate Models. First, PCR and GPR models are compared based on Monte-Carlo sampling. The sample size ranges from 15 to 100. For each sample size, the DoE generation and model training is repeated 100 times. The coefficient of determination $r^2$ is calculated with regards to the test set consisting of $n_\text {te}=500$ samples. The results are presented in box plots, see Fig. 6. With an increasing number of training samples, both models increase in accuracy, whereas the spread between models of the same sample size decreases. Overall, GPR is superior to PCR. Neglecting outliers GPR models require a sample size of at least $n_\text {tr}=70$ to achieve $r^2 > 0.95$, PCR models require $n_\text {tr}=90$.

Fig. 6.

Accuracy of surrogate model based on Monte-Carlo sampling considering two uncertain parameters. a) Gaussian process regression b) polynomial chaos regression

Next, the DoEs are generated via Latin hypercube sampling. The observed trends are analogous to MSC-based surrogate models (see Fig. 7). In general, accuracy is improved through LHC sampling. Assuming that the complexity of the underlying functions does not differ significantly between different gear designs, these plots help to choose the correct number of samples to achieve the desired accuracy. For PSP and APSP models, the training sets are predefined. Hence, only a single result per sample size can be evaluated, see Fig. 7c. For this problem with two uncertain parameters, spectral projection methods turn out to be very data-efficient. With a training sample size of $n_\text {tr}=31$, APSP has a coefficient of determination of $r^2=0.969$, predicting $\mu ={7.50}\times 10^{-2}\,\upmu \text {m}$ and $\sigma =1.73\times 10^{-1}\,\upmu \text {m}$.

4.2 Analysis with Five Uncertain Parameters

The analysis is extended by the uncertain parameters center distance allowance $A_{ae}/A_{ei}$, profile barreling $C_{\alpha }$ and lead crowning $C_{\beta }$. The identical microgeometry is applied to both pinion and wheel gear. The assumptions for tolerance width and parameter distribution are summarized in Table 2 - 4.2a. For clarity, all parameters are assumed to be uniformly distributed. Therefore Legendre polynomials are used as a basis for the PC surrogates, see Table 1. If information about the actual input parameters distribution is available, this assumption needs to be adapted, affecting the output distribution. The resulting flank topologies are in compliance within the tolerance definition of gear accuracy grade $Q=6$, see [3]. The simulation model setup is identical to Sect. 4.1, the input torque is set to 100 Nm.

Fig. 7.

Accuracy of surrogate model based on Latin hypercube sampling in a) and b) considering two uncertain parameters. a) Gaussian process regression b) polynomial chaos regression c) generalized polynomial chaos expansion based on pseudo-spectral projection and adaptive pseudo-spectral projection

Training and Validation of a Reference Model. Analogous to the previous section, a reference surrogate model is created. A GPR is trained with a Latin hypercube DoE composed of $n_\text {tr}=5000$, resulting in a coefficient of determination of $r^2=0.9998$. Even though the absolute error ($RMSE={1.49}\times 10^{-3}\,\upmu \text {m}$) of this model is higher compared to the case with two uncertain parameters (cf. Sect. 4.1), $r^2$ is closer to one since the error is set into relation with the standard deviation of the data, which is also increased due to the additional parameter, see (13).

Data-Efficiency Analysis of the Surrogate Models. Figure 8 shows comparisons of the surrogate types regarding model accuracy. For each sample size, the regression models are trained again with data sets from 100 different Latin hypercube DoEs. In this case, accuracy converges in significantly fewer iterations. Additionally, the range of achieved model accuracy with identical sample size is remarkably narrower. A possible reason for this unexpected result could be the dominant effect of the additional uncertain parameters on the objective function. The coefficient of determination $r^2$ is higher if the regression models fit the effect well, while the standard deviation $\sigma _\text {te}$ is increased, even though more uncertain parameters are considered, see (13).

However and regarding data-efficiency, the model ranking is equivalent to the case of two uncertain parameters. Since the sample grid points for the PSP model are extended uniformly in every uncertain parameter dimension, the step size between models of higher accuracy is reasonably large. With five uncertain parameter dimensions, a level $k=1$ of sparse grid integration results in a grid consisting of 11 sample points, a level $k=2$ in 71, and level $k=3$ in 341 sample points.

Fig. 8.

Accuracy of surrogate model based on Latin hypercube sampling in a) and b) considering five uncertain parameters. a) Gaussian process regression b) polynomial chaos regression c) generalized polynomial chaos expansion based on pseudo-spectral projection and adaptive pseudo-spectral projection

The APSP model with a training set size of $n_\text {tr}=23$ is compared to the reference model. Figure 9a shows a comparison of the first-order Sobol indices (see Sect. 3.4) of the uncertain parameters. For the APSP model, the Sobol indices can be directly derived by the polynomial coefficients, whereas for the reference model first, a DoE needs to be set up as described in Sect. 3.4. A good concordance between the reference model and the data-efficient APSP is achieved despite the small number of training samples of the APSP model. Given the assumptions made in Table 2 - 4.2a, the influence of the parameters defining the flank topology is dominant. If the tolerance range of $C_{\alpha }$ and $C_{\beta }$ is reduced to ${0.5}\,\upmu \text {m}$ (see Table 2 - 4.2b), the axis parallelism, defined by $f_{\varSigma \delta }$ and $f_{\varSigma \beta }$, has a similar influence on the peak-to-peak TE, see Fig. 9b. As expected, the center distance allowance has the most negligible impact since an involute gear still fulfills the law of gearing as the center distance is changed.

Fig. 9.

First order Sobol indices: reference model vs. data-efficient surrogate model

Next, a Latin hypercube DoE with 100.000 samples is used to propagate the uncertainty of input parameters through the models. Figure 10 shows the approximated peak-to-peak TE distribution of the reference model and the data-efficient APSP via a histogram. The APSP model predicts the mean value and the standard deviation very precisely. In case tolerances are neglected, the nominal peak-to-peak TE value of ${2.157}\times 10^{-1}\,\upmu \text {m}$ is close to the mean value because the distribution is only slightly skewed.

Fig. 10.

TE distribution: reference model vs. data-efficient APSP surrogate model with $n_\text {tr}=23$

5 Conclusion

In this study, the potential of high-fidelity data-efficient surrogate modeling for uncertainty quantification in transmission design is investigated. Selected surrogate types are developed for a simple helical gear transmission system to enable forward uncertainty propagation and global sensitivity analysis for the NVH indicator peak-to-peak transmission error. Based on identical training sample set sizes, Gaussian process regression is advantageous compared to polynomial chaos regression regarding model accuracy for the presumed manufacturing tolerances. Our evaluation of sampling methods indicates that Latin hypercube sampling is particularly beneficial compared to Monte-Carlo sampling for smaller sample sizes. Notably, it was found that polynomial chaos models based on adaptive pseudo-spectral projection generally show faster convergence rates of model accuracy than the investigated regression models GPR and PCR in both example applications. Additionally, mean, variance, and Sobol indices can be determined efficiently due to the polynomial formulation of this model. Therefore, it is recommended to pursue this surrogate type for future design robustness analysis and explore its scalability for additional uncertain parameters and further KPIs. The use of surrogate models significantly reduces the required number of high-fidelity simulations for forward uncertainty quantification enabling robustness evaluation of KPIs in an early design state for optimization.