Abstract
We construct the currently most efficient signature schemes with tight multi-user security against adaptive corruptions. It is the first generic construction of such schemes, based on lossy identification schemes (Abdalla et al.; JoC 2016), and the first to achieve strong existential unforgeability. It also has significantly more compact signatures than the previously most efficient construction by Gjøsteen and Jager (CRYPTO 2018). When instantiated based on the decisional Diffie–Hellman assumption, a signature consists of only three exponents.
We propose a new variant of the generic construction of signatures from sequential OR-proofs by Abe, Ohkubo, and Suzuki (ASIACRYPT 2002) and Fischlin, Harasser, and Janson (EUROCRYPT 2020). In comparison to Fischlin et al., who focus on constructing signatures in the non-programmable random oracle model (NPROM), we aim to achieve tight security against adaptive corruptions, maximize efficiency, and to directly achieve strong existential unforgeability (also in the NPROM). This yields a slightly different construction and we use slightly different and additional properties of the lossy identification scheme.
Signatures with tight multi-user security against adaptive corruptions are a commonly-used standard building block for tightly-secure authenticated key exchange protocols. We also show how our construction improves the efficiency of all existing tightly-secure AKE protocols.
Supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme, grant agreement 802823.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The commonly accepted standard security goal for digital signatures is existential unforgeability under adaptive chosen message attacks (
 ). This security model considers a single-user setting, in the sense that the adversary has access to a single public key and its goal is to forge a signature with respect to this key. A stronger security notion is
). This security model considers a single-user setting, in the sense that the adversary has access to a single public key and its goal is to forge a signature with respect to this key. A stronger security notion is
 -security in the multi-user setting with adaptive corruptions (\(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\)). In this security model, the adversary has access to multiple public keys, and it is allowed to adaptively corrupt certain users, and thus obtain their secret keys. The goal of the adversary is to forge a signature with respect to the public key of an uncorrupted user. A straightforward argument, which essentially guesses the user for which the adversary creates a forgery at the beginning of the security experiment, shows that
-security in the multi-user setting with adaptive corruptions (\(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\)). In this security model, the adversary has access to multiple public keys, and it is allowed to adaptively corrupt certain users, and thus obtain their secret keys. The goal of the adversary is to forge a signature with respect to the public key of an uncorrupted user. A straightforward argument, which essentially guesses the user for which the adversary creates a forgery at the beginning of the security experiment, shows that
 security implies \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) security. However, this guessing incurs a linear security loss in the number of users, and thus cannot achieve tight \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) security.
security implies \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) security. However, this guessing incurs a linear security loss in the number of users, and thus cannot achieve tight \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) security.
The question how tightly \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\)-secure signatures can be constructed, and how efficient these constructions can be, is interesting for different reasons. Most importantly, \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) security seems to reflect the security requirements of many applications that use digital signatures as building blocks more directly than
 security. This holds in particular for many constructions of authenticated key exchange protocols (AKE) that use signing keys as long-term keys to authenticate protocol messages. Standard AKE security models, such as the well-known Bellare–Rogaway [8] or the Canetti–Krawczyk [10] model and their countless variants and refinements, allow for adaptive corruption of users, which then translates to adaptive corruptions of secret keys. Therefore Bader et al. [5] introduced the notion of \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) as a building block to construct the first tightly-secure AKE protocol. This security model was subsequently used to construct more efficient tightly-secure AKE protocols [23, 28, 34], or to prove tight security of real-world protocols [14, 15]. Note that tight security is particularly interesting for AKE, due to the pervasive and large-scale use of such protocols in practice (e.g., the TLS Handshake is an AKE protocol). Furthermore, we consider the goal of understanding if, how, and how efficiently strong security notions for digital signatures such as \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) can be achieved with tight security proofs also as a general and foundational research question in cryptography.
security. This holds in particular for many constructions of authenticated key exchange protocols (AKE) that use signing keys as long-term keys to authenticate protocol messages. Standard AKE security models, such as the well-known Bellare–Rogaway [8] or the Canetti–Krawczyk [10] model and their countless variants and refinements, allow for adaptive corruption of users, which then translates to adaptive corruptions of secret keys. Therefore Bader et al. [5] introduced the notion of \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) as a building block to construct the first tightly-secure AKE protocol. This security model was subsequently used to construct more efficient tightly-secure AKE protocols [23, 28, 34], or to prove tight security of real-world protocols [14, 15]. Note that tight security is particularly interesting for AKE, due to the pervasive and large-scale use of such protocols in practice (e.g., the TLS Handshake is an AKE protocol). Furthermore, we consider the goal of understanding if, how, and how efficiently strong security notions for digital signatures such as \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) can be achieved with tight security proofs also as a general and foundational research question in cryptography.
The Difficulty of Constructing Tightly \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) -Secure Signatures. The already mentioned straightforward reduction showing that
 security implies \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) security guesses the user for which the adversary creates a forgery. Note that this user must not be corrupted by a successful adversary. Hence, the reduction can define this user’s public key as the public key obtained from the
security implies \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) security guesses the user for which the adversary creates a forgery. Note that this user must not be corrupted by a successful adversary. Hence, the reduction can define this user’s public key as the public key obtained from the
 experiment. The keys of all users are generated by the reduction itself, such that it knows all corresponding secret keys. On the one hand, this enables the reduction to respond to all corruption queries made by the adversary, provided that it has guessed correctly. On the other hand, this makes the reduction lossy, since it may fail if the reduction did not guess correctly.
experiment. The keys of all users are generated by the reduction itself, such that it knows all corresponding secret keys. On the one hand, this enables the reduction to respond to all corruption queries made by the adversary, provided that it has guessed correctly. On the other hand, this makes the reduction lossy, since it may fail if the reduction did not guess correctly.
A reduction proving \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) security tightly (under some complexity assumption) has to avoid such a guessing argument. However, note that this implies that the reduction must satisfy the following two properties simultaneously:
-
1.
It has to know the secret keys of all users, in order to be able to respond to a corruption query for any user, without the need to guess uncorrupted users.
-
2.
At the same time, the reduction has to be able to extract a solution to the underlying assumed-to-be-hard computational problem, while knowing the secret key of the corresponding instance of the signature scheme.
Since these two properties seem to contradict each other, one might think that tight \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) security is impossible to achieve. Indeed, one can even prove formally that \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) security is not tightly achievable [6] (under non-interactive assumptionsFootnote 1), however, this impossibility result holds only for signature schemes satisfying certain properties. While most schemes indeed satisfy these properties, and thus seem not able to achieve tight \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) security, there are some constructions that circumvent this impossibility result.
Known Constructions of Tightly \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) -Secure Signatures. To our best knowledge, there are only a few schemes with tight \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) security under non-interactive hardness assumptions (cf. Table 1). Bader et al. (BHJKL) [5] describe a scheme with constant security loss (“fully-tight”), but it uses the tree-based scheme from [27] as a building block and therefore has rather large signatures. The scheme is proven secure in the standard model, using pairings. Bader et al. also describe a second scheme with constant-size signatures, which is also based on pairings and in the standard model, but which has a linear security loss in the security parameter (“almost-tight”) and has linear-sized public keys. The currently most efficient tightly \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\)-secure scheme is due to Gjøsteen and Jager (GJ) [23]. It has constant-size signatures and keys, as well as a constant security loss, in the random oracle model. The security proof requires “programming” of the random oracle in the sense of [19].
Strong Existential Unforgeability. Currently there exists no signature scheme with tight multi-user security under adaptive corruptions that achieves strong existential unforgeability. Here “strong” unforgeability refers to a security model where the adversary is considered to successfully break the security of a signature scheme, even if it outputs a new signature for a message for which it has already received a signature in the security experiment. Hence, strong unforgeability essentially guarantees that signatures additionally are “non-malleable”, in the sense that an adversary is not able to efficiently derive a new valid signature \(\sigma ^{*}\) for a message m when it is already given another valid signature \(\sigma \) for m, where \(\sigma \ne \sigma ^{*}\).
Strong unforgeability is particularly useful for the construction of authenticated key exchange protocols where partnering is defined over “matching conversations”, as introduced by Bellare and Rogaway [8]. Intuitively, matching conversations formalize “authentication” for AKE protocols, by requiring that a communicating party must “accept” a protocol session (and thus derive a key for use in a higher-layer application protocol) only if there exists a unique partner oracle to which it has a matching conversation, that is, which has sent and received exactly the same sequence of messages that the accepting oracle has received and sent.
Consider for instance the “signed Diffie–Hellman” AKE protocol. Standard existential unforgeability of the signature scheme is not sufficient to achieve security in the sense of matching conversations, because this security notion does not guarantee that signatures are non-malleable. Hence, an adversary might, for instance, be able to efficiently re-randomize probabilistic signatures, and thus always be able to break matching conversations efficiently. This is a commonly overlooked mistake in many security proofs for AKE protocols [33]. Therefore Bader et al. [5] need to construct a more complex protocol that additionally requires strongly-unforgeable one-time signatures to achieve security in the sense of matching conversations. Gjøsteen and Jager [23] had to rely on the weaker partnering notion defined by Li and Schäge [33] in order to deal with potential malleability of signatures.
Hence, strongly-unforgeable digital signatures are particularly desirable in the context of AKE protocols, in order to achieve the strong notion of “matching conversation” security from [8].
Our Contributions. We construct strongly \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\)-secure digital signature schemes, based on lossy identification schemes as defined by Abdalla et al. [2, 3] and sequential OR-proofs as considered by Abe et al. [4] and Fischlin et al. [18]. This construction provides the following properties:
-
It is the first generic construction of \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\)-secure digital signatures, which can be instantiated from any concrete hardness assumption that gives rise to suitable lossy identification schemes. This includes instantiations from the decisional Diffie–Hellman (DDH) assumption, and the \(\phi \)-Hiding assumption.
-
It is the first construction of \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\)-secure digital signatures that achieves strong existential unforgeability. Here we use “uniqueness” of the lossy identification scheme in the sense of [2, 3].
-
When instantiated under the DDH assumption, a signature consists of only three elements of \(\mathbb {Z} _q\), where q is the order of the underlying algebraic group. For comparison, Schnorr signatures [36] and ECDSA [16], for instance, have signatures consisting of two elements of \(\mathbb {Z} _q\), but do not enjoy tight security proofs (not even in the single-user setting) [17, 20,21,22, 35, 37]. In case of Schnorr signatures [36], security can be based on the weaker discrete logarithm assumption, though. Katz-Wang signatures [29] also consist of two \(\mathbb {Z} _{q}\)-elements and have tight security in the single-user setting, but not in the multi-user setting with adaptive corruptions.
-
Similar to the work by Fischlin et al. [18], the proof does not rely on programming a random oracle, but holds in the non-programmable random oracle model [19]. This yields the first efficient and tightly multi-user secure signature scheme that does not require a programmable random oracle.
Our construction is almost identical to the construction based on sequential OR-proofs (as opposed to “parallel” OR-proofs in the sense of [13]), which was originally described by Abe et al. [4]. Fischlin, Harasser, and Janson [18] formally analyzed this construction and showed that it implies
 -secure digital signatures based on lossy identification schemes. Their main focus is to achieve security in the non-programmable random oracle model [19], since the classical construction of signatures from lossy identification schemes [2, 3] requires a programmable random oracle.
-secure digital signatures based on lossy identification schemes. Their main focus is to achieve security in the non-programmable random oracle model [19], since the classical construction of signatures from lossy identification schemes [2, 3] requires a programmable random oracle.
We observe that this approach also gives rise to tightly-secure signatures in a multi-user model with adaptive corruptions, by slightly modifying the construction. Due to the fact that the reduction is always in possession of a correctly distributed secret key for all users, it can both (i) respond to singing-queries and (ii) respond to corruption-queries without the need to guess in the \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) security experiment.
Also, our security proof is based on slightly different and additional properties of the lossy identification scheme. We use that a sequential OR-proof is perfectly witness indistinguishable when both instances of the lossy identification scheme are in non-lossy mode. This enables us to argue that the adversary receives no information about the random bit b chosen by the key generation algorithm of one user, such that the probability that the adversary creates a forgery with respect to \( sk _{1-b}\) is 1/2. This enables us then to construct a distinguisher for the lossy identification scheme with only constant security loss.
Another difference to the proof by Fischlin et al. [18] is that we directly achieve strong unforgeability by leveraging uniqueness of lossy identification schemes, as defined by Abdalla et al. [2, 3]. Also, their construction does not yet leverage “commitment-recoverability” of a lossy identification scheme, such that their DDH-based instantiation consists of four elements of \(\mathbb {Z} _{q}\).
In particular, Table 2 shows that our scheme does not only improve the overall performance of all the presented protocols, but it also enables the protocols by GJ and LLGW to catch up to the communication complexity of JKRS. This means that when instantiated with our signature scheme, the constructions by GJ, LLGW, and JKRS achieve the same communication complexity. This observation suggests that especially constructions that exchange two or more signatures will benefit from an instantiation with our new signature scheme.
Applications to Tightly-Secure AKE Protocols. Since tightly \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}} \)-secure signatures are commonly used to construct tightly-secure AKE protocols, let us consider the impact of our scheme on the performance of known protocols. Since the performance gain obtained by the signature scheme has already been discussed, we focus here only on the communication complexity of the considered protocols, that is, the number of bits exchanged when running the protocol. Table 2 shows the impact of our signature schemes on known AKE protocols with tight security proofs. We compare instantiations with the signature scheme by Gjøsteen and Jager [23] to instantiations with our signature scheme. Note that the Gjøsteen–Jager scheme is also based on the DDH assumption, and so are the considered protocols (except for TLS 1.3 and Sigma, which are based on the strong Diffie–Hellman assumption).
We omit the protocol by Bader et al. [5], since it is more of a standard-model feasibility result, which does not aim for maximal efficiency. Their protocol has a communication complexity of \(O(\lambda )\) group elements when instantiated with constant security loss, and 14 group elements plus 4 exponents when instantiated with their “almost-tight” signature scheme with a security loss of \(O(\lambda )\). Cohn-Gordon et al. [12] construct a protocol which entirely avoids signatures and aims to achieve tightness, however, they achieve only a linear security loss and also show that this is optimal for the class of protocols they consider.
Outline. The remainder of this work is organized as follows. In the next section, we introduce standard definitions for signatures and their security. In Sect. 3, we recall lossy identification schemes and their security properties. The generic construction of our signature scheme from any lossy identification scheme alongside a security proof is presented in Sect. 4. We conclude our work with a detailed discussion on possible instantiations of our scheme in Sect. 5.
2 Preliminaries
For strings a and b, we denote the concatenation of these strings by \(a \mathbin \Vert b\). For an integer \(n \in \mathbb {N} \), we denote the set of integers ranging from 1 to n by  . For a set \(X = \{x_1, x_2, \dotsc \}\), we use \((v_{i})_{i \in X}\) as a shorthand for the tuple \((v_{x_1}, v_{x_2}, \dotsc )\). We denote the operation of assigning a value y to a variable x by
. For a set \(X = \{x_1, x_2, \dotsc \}\), we use \((v_{i})_{i \in X}\) as a shorthand for the tuple \((v_{x_1}, v_{x_2}, \dotsc )\). We denote the operation of assigning a value y to a variable x by  . If S is a finite set, we denote by
. If S is a finite set, we denote by  the operation of sampling a value uniformly at random from set S and assigning it to variable x.
the operation of sampling a value uniformly at random from set S and assigning it to variable x.
2.1 Digital Signatures
We recall the standard definition of a digital signature scheme by Goldwasser, Micali, and Rivest [24] and its standard security notion.
Definition 1
A digital signature scheme is a triple of algorithms \(\mathsf {Sig} = (\mathsf {Gen},\mathsf {Sign},\mathsf {Vrfy})\) such that
-
1.
\(\mathsf {Gen} \) is the randomized key generation algorithm generating a public (verification) key \( pk \) and a secret (signing) key \( sk \).
-
2.
\(\mathsf {Sign} ( sk , m)\) is the randomized signing algorithm outputting a signature \(\sigma \) on input of a message \(m \in M\) and a signing key \( sk \).
-
3.
\(\mathsf {Vrfy} ( pk , m, \sigma )\) is the deterministic verification algorithm outputting either 0 or 1.
We say that a digital signature scheme \(\mathsf {Sig} \) is \(\rho \)-correct if for  , and any \(m \in M\), it holds that
, and any \(m \in M\), it holds that
And we say \(\mathsf {Sig} \) is perfectly correct if it is 1-correct.
Definition 2
Let \(\mathsf {Sig} = (\mathsf {Gen},\mathsf {Sign},\mathsf {Vrfy})\) be a signature scheme and let \(N \in \mathbb {N} \) be the number of users. Consider the following experiment \(\mathsf {Exp}_{\mathsf {Sig}, N}^{\mathsf {MU\text {-}} \mathsf {sEUF\text {-}CMA} ^{\mathsf {corr}}} (\mathcal A)\) played between a challenger and an adversary \(\mathcal A\):
-
1.
The challenger generates a key pair
 for each user \(i \in [N]\), initializes the set of corrupted users
for each user \(i \in [N]\), initializes the set of corrupted users  , and N sets of chosen-message queries
, and N sets of chosen-message queries  issued by the adversary. Subsequently, it hands \(( pk ^{(i)})_{i \in [N]}\) to \(\mathcal A\) as input.
issued by the adversary. Subsequently, it hands \(( pk ^{(i)})_{i \in [N]}\) to \(\mathcal A\) as input. -
2.
The adversary may adaptively issue signature queries \((i,m) \in [N] \times M\) to the challenger. The challenger replies to each query with a signature
 and adds \((m,\sigma )\) to \(\mathcal Q^{(i)}\). Moreover, the adversary may adaptively issue corrupt queries \(\mathsf {Corrupt} (i)\) for some \(i \in [N]\). In this case, the challenger adds i to \(\mathcal Q^\mathsf {corr} \) and forwards \( sk ^{(i)}\) to the adversary. We call each user \(i \in \mathcal Q^\mathsf {corr} \) corrupted.
and adds \((m,\sigma )\) to \(\mathcal Q^{(i)}\). Moreover, the adversary may adaptively issue corrupt queries \(\mathsf {Corrupt} (i)\) for some \(i \in [N]\). In this case, the challenger adds i to \(\mathcal Q^\mathsf {corr} \) and forwards \( sk ^{(i)}\) to the adversary. We call each user \(i \in \mathcal Q^\mathsf {corr} \) corrupted. -
3.
Finally, the adversary outputs a tuple \((i^*, m^*, \sigma ^*)\). The challenger checks whether \(\mathsf {Vrfy} (pk^{(i^*)}, m^*, \sigma ^*) = 1\), \(i^*\not \in \mathcal Q^\mathsf {corr} \) and \((m^*, \sigma ^*) \not \in \mathcal Q^{(i^*)}\). If all of these conditions hold, the experiment outputs 1 and 0 otherwise.
We denote the advantage of an adversary \(\mathcal A\) in breaking the strong existential unforgeability under an adaptive chosen-message attack in the multi-user setting with adaptive corruptions (\(\mathsf {MU\text {-}} \mathsf {sEUF\text {-}CMA} ^{\mathsf {corr}}\)) for \(\mathsf {Sig} \) by

where \(\mathsf {Exp}_{\mathsf {Sig}, N}^{\mathsf {MU\text {-}} \mathsf {sEUF\text {-}CMA} ^{\mathsf {corr}}} (\mathcal A)\) is as defined as above.
3 Lossy Identification Schemes
We adapt the definitions of a lossy identification scheme [2, 3, 30].
Definition 3
A lossy identification scheme is a five-tuple \(\mathsf {LID} = (\mathsf {LID}.\mathsf {Gen},\mathsf {LID}.\mathsf {LossyGen},\mathsf {LID}.\mathsf {Prove},\mathsf {LID}.\mathsf {Vrfy},\mathsf {LID}.\mathsf {Sim})\) of probabilistic polynomial-time algorithms with the following properties.
-
\(\mathsf {LID}.\mathsf {Gen} \) is the normal key generation algorithm. It outputs a public verification key \( pk \) and a secret key \( sk \).
-
\(\mathsf {LID}.\mathsf {LossyGen} \) is a lossy key generation algorithm that takes the security parameter and outputs a lossy verification key \( pk \).
-
\(\mathsf {LID}.\mathsf {Prove}\) is the prover algorithm that is split into two algorithms:
-
 is a probabilistic algorithm that takes as input the secret key and returns a commitment \(\mathsf {cmt}\) and a state \(\mathsf {st}\).
is a probabilistic algorithm that takes as input the secret key and returns a commitment \(\mathsf {cmt}\) and a state \(\mathsf {st}\). -
\(\mathsf {resp} \leftarrow \mathsf {LID}.\mathsf {Prove} _2( sk , \mathsf {cmt}, \mathsf {ch}, \mathsf {st})\) is a deterministic algorithmFootnote 2 that takes as input a secret key \( sk \), a commitment \(\mathsf {cmt}\), a challenge \(\mathsf {ch}\), a state \(\mathsf {st}\), and returns a response \(\mathsf {resp}\).
-
-
\(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch}, \mathsf {resp})\) is a deterministic verification algorithm that takes a public key, and a conversation transcript (i.e., a commitment, a challenge, and a response) as input and outputs a bit, where 1 indicates that the proof is “accepted” and 0 that it is “rejected”.
-
\(\mathsf {cmt} \leftarrow \mathsf {LID}.\mathsf {Sim} (pk, \mathsf {ch}, \mathsf {resp})\) is a deterministic algorithm that takes a public key \( pk \), a challenge \(\mathsf {ch}\), and a response \(\mathsf {resp}\) as inputs and outputs a commitment \(\mathsf {cmt}\).
We assume that a public key \( pk \) implicitly defines two sets, the set of challenges \(\mathsf {CSet} \) and the set of responses \(\mathsf {RSet} \).
Definition 4
Let \(\mathsf {LID} = (\mathsf {LID}.\mathsf {Gen}, \mathsf {LID}.\mathsf {LossyGen}, \mathsf {LID}.\mathsf {Prove}, \mathsf {LID}.\mathsf {Vrfy}, \mathsf {LID.Sim})\) be defined as above. We call \(\mathsf {LID}\) lossy when the following properties hold:
-
Completeness of normal keys. We call \(\mathsf {LID}\) \(\rho \)-complete, if

We call \(\mathsf {LID}\) perfectly-complete, if it is 1-complete.
-
Simulatability of transcripts. We call \(\mathsf {LID}\) \(\varepsilon _s\)-simulatable if for
 ,
,  , the distribution of the transcript \((\mathsf {cmt}, \mathsf {ch},\mathsf {resp})\) where \(\mathsf {cmt} \leftarrow \mathsf {LID}.\mathsf {Sim} (pk, \mathsf {ch}, \mathsf {resp})\) is statistically indistinguishable from honestly generated transcript (with a statistical distance up to \(\varepsilon _s\)) and we have that \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch}, \mathsf {resp})=1\). If \(\varepsilon _s = 0\), we call \(\mathsf {LID}\) perfectly simulatable.
, the distribution of the transcript \((\mathsf {cmt}, \mathsf {ch},\mathsf {resp})\) where \(\mathsf {cmt} \leftarrow \mathsf {LID}.\mathsf {Sim} (pk, \mathsf {ch}, \mathsf {resp})\) is statistically indistinguishable from honestly generated transcript (with a statistical distance up to \(\varepsilon _s\)) and we have that \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch}, \mathsf {resp})=1\). If \(\varepsilon _s = 0\), we call \(\mathsf {LID}\) perfectly simulatable.Note that this simulatability property is different from the original definition in [2] where the simulator simulates the whole transcript.
-
Indistinguishability of keys. This definition is a generalization of the standard key indistinguishability definition of a lossy identification scheme extended to N instances. For any integer \(N>0\), we define the advantage of an adversary \(\mathcal {A}\) breaking the N-key-indistinguishability of \(\mathsf {LID}\) as
 $$\begin{aligned} \left| \Pr \left[ \mathcal {A} ( pk ^{(1)},\cdots , pk ^{(N)}) = 1 \right] - \Pr \left[ \mathcal {A} ( pk '^{(1)},\cdots , pk '^{(N)}) = 1 \right] \right| , \end{aligned}$$
$$\begin{aligned} \left| \Pr \left[ \mathcal {A} ( pk ^{(1)},\cdots , pk ^{(N)}) = 1 \right] - \Pr \left[ \mathcal {A} ( pk '^{(1)},\cdots , pk '^{(N)}) = 1 \right] \right| , \end{aligned}$$where
 and
and  for all \(i\in [N]\).
for all \(i\in [N]\). -
Lossiness. Consider the following security experiment
 described below, played between a challenger and an adversary \(\mathcal {A}\):
described below, played between a challenger and an adversary \(\mathcal {A}\): -
1.
The challenger generates a lossy verification key
 and sends it to the adversary \(\mathcal {A}\).
and sends it to the adversary \(\mathcal {A}\). -
2.
The adversary \(\mathcal {A}\) may now compute a commitment \(\mathsf {cmt}\) and send it to the challenger. The challenger responds with a random challenge
 .
. -
3.
Eventually, the adversary \(\mathcal {A}\) outputs a response \(\mathsf {resp}\). The challenger outputs \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch}, \mathsf {resp})\).
We call \(\mathsf {LID}\) \(\varepsilon _{\ell }\)-lossy if no computationally unrestricted adversary \(\mathcal {A}\) wins the above security game with probability

-
1.
Below are two more properties for lossy identification schemes defined in [2, 3].
Definition 5
Let  be a lossy public key and let \((\mathsf {cmt}, \mathsf {ch}, \mathsf {resp})\) be any transcript which makes \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch}, \mathsf {resp})=1\). We say \(\mathsf {LID}\) is \(\varepsilon _u\)-unique with respect to lossy keys if the probability that there exists \(\mathsf {resp} '\ne \mathsf {resp} \) such that \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch}, \mathsf {resp} ')=1\) is at most \(\varepsilon _u\), and perfectly unique with respect to lossy keys if \(\varepsilon _u=0\).
be a lossy public key and let \((\mathsf {cmt}, \mathsf {ch}, \mathsf {resp})\) be any transcript which makes \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch}, \mathsf {resp})=1\). We say \(\mathsf {LID}\) is \(\varepsilon _u\)-unique with respect to lossy keys if the probability that there exists \(\mathsf {resp} '\ne \mathsf {resp} \) such that \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch}, \mathsf {resp} ')=1\) is at most \(\varepsilon _u\), and perfectly unique with respect to lossy keys if \(\varepsilon _u=0\).
Definition 6
Let  be any honestly generated key pair and
be any honestly generated key pair and  be the set of commitments associated to \( sk \). We define the min-entropy with respect to \(\mathsf {LID}\) as
be the set of commitments associated to \( sk \). We define the min-entropy with respect to \(\mathsf {LID}\) as

Below is another property for lossy identification schemes defined in [30].
Definition 7
A lossy identification scheme \(\mathsf {LID}\) is commitment-recoverable if the algorithm \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch}, \mathsf {resp})\) first recomputes a commitment \(\mathsf {cmt} ' = \mathsf {LID.Sim}( pk , \mathsf {ch}, \mathsf {resp})\) and then outputs 1 if and only if \(\mathsf {cmt} ' = \mathsf {cmt} \).
Below, we define a new property for lossy identification schemes which requires that the \(\mathsf {LID}.\mathsf {Sim}\) algorithm is injective with respect to the input challenge.
Definition 8
A lossy identification scheme \(\mathsf {LID}\) has an injective simulator if for any  , any response \(\mathsf {resp} \in \mathsf {RSet} \), any \(\mathsf {ch} \ne \mathsf {ch} '\), it holds that \(\mathsf {LID}.\mathsf {Sim} (pk,\mathsf {ch},\mathsf {resp})\ne \mathsf {LID}.\mathsf {Sim} (pk,\mathsf {ch} ',\mathsf {resp})\).
, any response \(\mathsf {resp} \in \mathsf {RSet} \), any \(\mathsf {ch} \ne \mathsf {ch} '\), it holds that \(\mathsf {LID}.\mathsf {Sim} (pk,\mathsf {ch},\mathsf {resp})\ne \mathsf {LID}.\mathsf {Sim} (pk,\mathsf {ch} ',\mathsf {resp})\).
In Sect. 5 we give a detailed discussion which of the existing lossy identification schemes [1,2,3, 26, 29] satisfy which of the above properties.
4 Construction and Security of Our Signature Scheme
Let \(\mathsf {LID} = (\mathsf {LID}.\mathsf {Gen}, \mathsf {LID}.\mathsf {LossyGen}, \mathsf {LID}.\mathsf {Prove}, \mathsf {LID}.\mathsf {Vrfy}, \mathsf {LID}.\mathsf {Sim})\) be a lossy identification scheme and let \(\mathsf {H} :\{0,1\} ^* \rightarrow \mathsf {CSet} \) be a hash function mapping finite-length bitstrings to the set of challenges \(\mathsf {CSet}\). Consider the following digital signature scheme \(\mathsf {Sig} = (\mathsf {Gen}, \mathsf {Sign}, \mathsf {Vrfy})\).
-
Key generation. The key generation algorithm \(\mathsf {Gen}\) samples a bit
 and two independent key pairs
and two independent key pairs  and
and  . Then it sets
. Then it sets 
Note that the secret key consists only of \( sk _{b}\) and the other key \( sk _{1-b}\) is discarded.
-
Signing. The signing algorithm \(\mathsf {Sign}\) takes as input \(sk = (b, sk _{b})\) and a message \(m \in \{0,1\} ^{*}\). Then it proceeds as follows.
-
1.
It first computes
 and sets
and sets 
Note that the \(\mathsf {ch} _{1-b}\) is derived from \(\mathsf {cmt} _b\) and m.
-
2.
It generates the simulated transcript by choosing
 and
and 
using the simulator.
-
3.
Finally, it computes

and outputs the signature
 . Note that \(\mathsf {ch} _{1}\) is not included in the signature.
. Note that \(\mathsf {ch} _{1}\) is not included in the signature.
-
1.
-
Verification. The verification algorithm \(\mathsf {Vrfy}\) takes as input a public key \(pk = ( pk _0, pk _1)\), a message \(m \in \{0,1\} ^{*}\), and a signature \(\sigma = (\mathsf {ch} _{0}, \mathsf {resp} _{0}, \mathsf {resp} _{1})\). It first recovers

From \(\mathsf {cmt} _0\) it can then compute

and then recover

Finally, the reduction outputs 1 if and only if \(\mathsf {ch} _{0} = \mathsf {H} (m, \mathsf {cmt} _1)\).
One can easily verify that the above construction \(\mathsf {Sig}\) is perfectly correct if \(\mathsf {LID}\) is commitment-recoverable and perfectly complete. Also, note that, even though algorithm \(\mathsf {LID}.\mathsf {Vrfy} \) is not used in algorithm \(\mathsf {Vrfy} \), we have that \(\mathsf {Vrfy} ( pk ,m,\sigma )=1\) implies that \(\mathsf {LID}.\mathsf {Vrfy} ( pk _j, \mathsf {cmt} _j, \mathsf {ch} _j, \mathsf {resp} _j)=1\) for both \(j\in \{0,1\}\). This is directly implied by our definition of the lossy identification scheme’s simulatability of transcripts.
Theorem 9
If \(\mathsf {H}\) is modeled as a random oracle and \(\mathsf {LID}\) is commitment-recoverable, perfectly simulatable, \(\varepsilon _{\ell }\)-lossy, \(\varepsilon _u\)-unique, has \(\alpha \)-bit min-entropy and has an injective simulator, then for each adversary \(\mathcal {A}\) with running time \(t_\mathcal {A} \) breaking the \(\mathsf {MU\text {-}} \mathsf {sEUF\text {-}CMA} ^{\mathsf {corr}}\) security of the above signature scheme \(\mathsf {Sig}\), we can construct an adversary \(\mathcal {B}\) with running time \(t_\mathcal {B} \approx t_\mathcal {A} \) such that

where \(q_\mathsf {S}\) is the number of signing queries and \(q_\mathsf {H} \) is the number of hash queries.
Proof
We prove Theorem 9 through a sequence of games. See Table 3 for an intuitive overview of our proof. In the sequel, let \(X_{i}\) denote the event that the experiment outputs 1 in Game i.
Game 0. This is the original security experiment \(\mathsf {Exp}_{\mathsf {Sig}, N}^{\mathsf {MU\text {-}} \mathsf {sEUF\text {-}CMA} ^{\mathsf {corr}}} (\mathcal A)\). In this experiment, adversary \(\mathcal {A}\) is provided with oracles \(\mathsf {Sign} \) and \(\mathsf {Corrupt} \) from the security experiment, as well as a hash oracle \(\mathsf {H} \) since we are working in the random oracle model. In the following, it will be useful to specify the implementation of this game explicitly:
-
The game initializes the chosen-message sets
 , the set of corrupted users
, the set of corrupted users  and an implementation of the random oracle
and an implementation of the random oracle  . It then runs the signature key generation algorithm \(\mathsf {Gen} \) N times to get the key pair \((pk ^{(i)},sk ^{(i)})\) for each \(i \in [N]\). More precisely, the game samples a bit
. It then runs the signature key generation algorithm \(\mathsf {Gen} \) N times to get the key pair \((pk ^{(i)},sk ^{(i)})\) for each \(i \in [N]\). More precisely, the game samples a bit  and two independent key pairs
and two independent key pairs  and
and  . Then it sets
. Then it sets  and stores \((pk ^{(i)}, b^{(i)}, sk^{(i)}_0, sk^{(i)}_1)\). Finally, it runs adversary \(\mathcal {A}\) with input \((pk ^{(i)})_{i \in [N]}\). In the following proof, to simplify the notation, we will use \( pk ^{(i)}_b, pk ^{(i)}_{1-b}, sk ^{(i)}_b, sk ^{(i)}_{1-b}\) to denote \( pk ^{(i)}_{b^{(i)}}, pk ^{(i)}_{1-b^{(i)}}, sk ^{(i)}_{b^{(i)}}, sk ^{(i)}_{1-b^{(i)}}\) respectively.
and stores \((pk ^{(i)}, b^{(i)}, sk^{(i)}_0, sk^{(i)}_1)\). Finally, it runs adversary \(\mathcal {A}\) with input \((pk ^{(i)})_{i \in [N]}\). In the following proof, to simplify the notation, we will use \( pk ^{(i)}_b, pk ^{(i)}_{1-b}, sk ^{(i)}_b, sk ^{(i)}_{1-b}\) to denote \( pk ^{(i)}_{b^{(i)}}, pk ^{(i)}_{1-b^{(i)}}, sk ^{(i)}_{b^{(i)}}, sk ^{(i)}_{1-b^{(i)}}\) respectively. -
\(\mathsf {H} (x)\). When the adversary or the simulation of the experiment make a hash oracle query for some \(x\in \{0,1\} ^*\), the game checks whether \((x,y)\in \mathcal {L} \) for some \(y\in \mathsf {CSet} \). If it does, the game returns y. Otherwise the game selects
 , logs (x, y) into set \(\mathcal {L} \) and returns y.
, logs (x, y) into set \(\mathcal {L} \) and returns y. -
\(\mathsf {Sign} (i,m)\). When the adversary queries the signing oracle with user i and message m, the game first sets
 , then computes
, then computes 
and sets
 by making a hash query. Then, the game chooses
by making a hash query. Then, the game chooses  and uses the simulator to compute
and uses the simulator to compute  . Finally, the game queries hash oracle to get
. Finally, the game queries hash oracle to get  and then uses \(\mathsf {LID}.\mathsf {Prove} _2\) to compute
and then uses \(\mathsf {LID}.\mathsf {Prove} _2\) to compute 
The game outputs signature
 to \(\mathcal {A}\) and logs the pair \((m,\sigma )\) in set \(\mathcal {Q} ^{(i)}\).
to \(\mathcal {A}\) and logs the pair \((m,\sigma )\) in set \(\mathcal {Q} ^{(i)}\). -
\(\mathsf {Corrupt} (i)\). When the adversary \(\mathcal {A} \) queries the \(\mathsf {Corrupt} \) oracle for the secret key of user i, the game returns
 to the adversary and logs i in the set \(\mathcal {Q} ^\mathsf {corr} \).
to the adversary and logs i in the set \(\mathcal {Q} ^\mathsf {corr} \). -
Finally, when adversary \(\mathcal {A} \) outputs a forgery attempt \((i^*, m^*, \sigma ^*)\), the game outputs 1 if and only if \(\mathsf {Vrfy} (pk^{(i^*)},m^*,\sigma ^*)=1\), \(i^*\not \in \mathcal {Q} ^\mathsf {corr} \), and \((m^*,\sigma ^*)\notin \mathcal {Q} ^{(i^*)}\) hold. More precisely, for \(\sigma ^* = (\mathsf {ch} _{0}^*, \mathsf {resp} _{0}^*, \mathsf {resp} _{1}^*)\), the game recovers
 and queries the hash oracle to get
and queries the hash oracle to get  . Then it recovers
. Then it recovers  and queries the hash oracle to get
and queries the hash oracle to get  . Finally, the game outputs 1 if and only if \(\mathsf {ch} _{0}^* = \mathsf {ch} ^*\), \(i^*\not \in \mathcal {Q} ^\mathsf {corr} \) and \((m^*,\sigma ^*)\notin \mathcal {Q} ^{(i^*)}\).
. Finally, the game outputs 1 if and only if \(\mathsf {ch} _{0}^* = \mathsf {ch} ^*\), \(i^*\not \in \mathcal {Q} ^\mathsf {corr} \) and \((m^*,\sigma ^*)\notin \mathcal {Q} ^{(i^*)}\).
It is clear that \(\Pr [X_0]=\mathsf {Adv}_{\mathsf {Sig}, N}^{\mathsf {MU\text {-}} \mathsf {sEUF\text {-}CMA} ^{\mathsf {corr}}} (\mathcal A)\).
Game 1. Game 1 is the same with Game 0 except with one change. Denote with \(\mathsf {cmtColl} \) the event that there exists a signing query \(\mathsf {Sign} (i,m)\) such that at least one of the two hash queries \(\mathsf {H} (m,\mathsf {cmt} _{b^{(i)}})\) and \(\mathsf {H} (m,\mathsf {cmt} _{1-b^{(i)}})\) made in this signing query has been made before.
Game 1 outputs 0 when \(\mathsf {cmtColl} \) happens. In other words, \(X_1\) happens if and only if \(X_0\wedge \lnot \mathsf {cmtColl} \) happens. We can prove the following lemma.
Lemma 10
where \(q_{\mathsf {S}}\) is the number of signing queries made by \(\mathcal {A}\) and \(q_\mathsf {H} \) is the number of hash queries made in Game 0.
Proof
To prove Lemma 10, we divide the event \(\mathsf {cmtColl} \) into two subevents.
-
There exists a signing query \(\mathsf {Sign} (i,m)\) such that \(\mathsf {H} (m,\mathsf {cmt} _{b^{(i)}})\) has been made before. If this happens, then \(\mathsf {cmt} _{b^{(i)}}\) is the output of \(\mathsf {LID}.\mathsf {Prove} _1( sk ^{(i)})\) for any signing query. Since \(\mathsf {LID}\) has \(\alpha \)-bit min-entropy (cf. Definition 6), the probability that this happens is at most \(q_{\mathsf {S}}q_\mathsf {H}/2^\alpha \) by a union bound.
-
There exists a signing query \(\mathsf {Sign} (i,m)\) such that \(\mathsf {H} (m,\mathsf {cmt} _{1-b^{(i)}})\) has been made before. Note that \(\mathsf {cmt} _{1-b^{(i)}}\) is the output of
$$ \mathsf {LID}.\mathsf {Sim} (pk^{(i)}_{1-b},\mathsf {ch} _{1-b^{(i)}},\mathsf {resp} _{1-b^{(i)}}) $$where \(\mathsf {ch} _{1-b^{(i)}}=\mathsf {H} (m,\mathsf {cmt} _{b^{(i)}})\). Since \(\mathsf {LID}.\mathsf {Sim}\) is deterministic, we know that \(\mathsf {cmt} _{1-b^{(i)}}\) is determined by \(pk^{(i)}_{1-b},m,\mathsf {cmt} _{b^{(i)}}\) and \(\mathsf {resp} _{1-b^{(i)}}\). Furthermore, since \(\mathsf {LID}.\mathsf {Sim}\) is injective with respect to challenges (cf. Definition 8), we know that the entropy of \(\mathsf {cmt} _{1-b^{(i)}}\) in any fixed signing query is at least the entropy of \(\mathsf {cmt} _{b^{(i)}}\) in that query. Thus, we obtain that the probability that this subevent happens is at most \(q_{\mathsf {S}}q_\mathsf {H}/2^\alpha \).
Thus, we have that \(\Pr [\mathsf {cmtColl} ]\le 2q_{\mathsf {S}} q_{\mathsf {H}}/2^{\alpha }\) and Lemma 10 follows. \(\square \)
Remark 11
Note that, from Game 1 on, the hash queries \(\mathsf {H} (m,\mathsf {cmt} _{b^{(i)}})\) and \(\mathsf {H} (m,\mathsf {cmt} _{1-b^{(i)}})\) are not made before any signing query \(\mathsf {Sign} (i,m)\) if the game finally outputs 1. This implies that each signing query uses independent and uniformly random \(\mathsf {ch} _{1-b^{(i)}}\) and \(\mathsf {ch} _{b^{(i)}}\), and they are not known to the adversary at that time.
Game 2. Game 2 differs from Game 1 only in the way the game checks the winning condition. More precisely, Game 1 issues two hash queries \(\mathsf {H} (m^*,\mathsf {cmt} _0^*)\) and \(\mathsf {H} (m^*,\mathsf {cmt} _1^*)\) to check the validity of a forgery attempt \((i^*, m^*, \sigma ^*)\). In the following, we call the former \(\mathsf {H} (m^*, \mathsf {cmt} _0^*)\) a “0-query ” and the latter \(\mathsf {H} (m^*, \mathsf {cmt} _1^*)\) a “1-query ”. Let \(\mathsf {Both} \) denote the event that both a 0-query and a 1-query have been made by the signing oracle or by the adversary before submitting the forgery attempt \((i^*, m^*, \sigma ^*)\).
Game 2 outputs 0 if event \(\mathsf {Both} \) does not happen. In other words, \(X_2\) happens if and only if \(X_1\wedge \mathsf {Both} \) happens. We can prove the following lemma.
Lemma 12
\(\Pr [X_2]\ge \Pr [X_1]- 2/|\mathsf {CSet} |\).
Proof
We know that \(\Pr [X_1] = \Pr [X_1\wedge \lnot \mathsf {Both} ] + \Pr [X_2]\). We will prove that \(\Pr [X_1\wedge \lnot \mathsf {Both} ]\le 2/|\mathsf {CSet} |\) and the lemma follows. Note that
-
\(X_1\wedge 1\text {-}\textsf {query} \text { is never made}\): Event \(X_1\) implies that \(\mathsf {Vrfy} (pk^{(i^*)},m^*,\sigma ^*)=1\). This further implies that the value \(\mathsf {ch} _{0}^*\) (chosen by the adversary) equals the 1-query hash result \(\mathsf {ch} ^*=\mathsf {H} (m^*,\mathsf {cmt} _1^*)\), which is a random element in \(\mathsf {CSet} \). Since the 1-query is never made at this time, the adversary has no knowledge about this value, which yields
$$ \Pr [X_1\wedge 1\text {-}\mathsf {query}\text { is never made}]\le \frac{1}{|\mathsf {CSet} |}. $$ -
\(X_1\wedge 0\text {-}\textsf {query} \text { is never made}\): The 0-\(\mathsf {query}\) value \(\mathsf {ch} _{1}^*=\mathsf {H} (m^*,\mathsf {cmt} _0^*)\) is used to recover \(\mathsf {cmt} _1^* = \mathsf {LID}.\mathsf {Sim} ( pk _{1}^{(i^*)}, \mathsf {ch} _1^*, \mathsf {resp} _1^*)\). Since the 0-query is not made at that time, the adversary has no knowledge about \(\mathsf {ch} _{1}^*\) except that it is a random element in \(\mathsf {CSet} \). Together with the fact that algorithm \(\mathsf {LID}.\mathsf {Sim} \) is injective (cf. Definition 8), the adversary only knows that \(\mathsf {cmt} _1^*\) is uniformly distributed over a set of size \(|\mathsf {CSet} |\). To make the verification pass, the adversary would need to select \(\mathsf {ch} _0^*\) which equals to \(\mathsf {H} (m^*,\mathsf {cmt} _1^*)\). However, there are \(|\mathsf {CSet} |\) possible values for \(\mathsf {cmt} _1^*\) so that this can happen with probability at most \(1/|\mathsf {CSet} |\). Thus,
$$\begin{aligned} \Pr [X_1\wedge 0\text {-}\textsf {query} \text { is never made}]\le \frac{1}{|\mathsf {CSet} |}. \end{aligned}$$
Putting both together, we have \(\Pr [X_1\wedge \lnot \mathsf {Both} ]\le 2/|\mathsf {CSet} |\). \(\square \)
Game 3. Game 3 is exactly the same as Game 2, except for one change. We denote by \(\mathsf {ImplicitUsage} \) the event that the first 0-query and the first 1-query are made in a signing query \(\mathsf {Sign} (i^*,m^*)\), and the pair \((\mathsf {cmt} _0^*,\mathsf {cmt} _1^*)\) equals to the pair \((\mathsf {cmt} _0,\mathsf {cmt} _1)\), which is generated in this signing query. Game 3 outputs 0 if event \(\mathsf {ImplicitUsage} \) happens.
Hence, \(X_3\) happens if and only if \(X_2\wedge \lnot \mathsf {ImplicitUsage} \) happens. We prove the following lemma.
Lemma 13
We can construct an adversary \(\mathcal {B}\) with running time \(t_\mathcal {B} \approx t_\mathcal {A} \) such that

Remark 14
Note that this proof can be potentially simplified if we define the uniqueness property of LID with respect to normal public keys. However, this would introduce a non-standard LID property compared to the standard LID definition by Abdalla et al. [2, 3].
Proof
We know that \(\Pr [X_2] = \Pr [X_2\wedge \mathsf {ImplicitUsage} ] + \Pr [X_3]\). We will prove that  such that the above lemma follows.
such that the above lemma follows.
Note that \(\mathsf {ImplicitUsage} \) implies that
for \(j\in \{0,1\}\). Together with the fact that \((m^*,\sigma ^*)\notin \mathcal {Q}^{(i^*)}\), we must have that \((\mathsf {resp} _{0}^*,\mathsf {resp} _{1}^*)\ne (\mathsf {resp} _{0},\mathsf {resp} _{1})\). Then two subcases are possible.
-
\(X_2 \wedge \mathsf {ImplicitUsage} \wedge (\mathsf {resp} _{1-b^{(i^*)}}^*=\mathsf {resp} _{1-b^{(i^*)}})\wedge (\mathsf {resp} _{b^{(i^*)}}^*\ne \mathsf {resp} _{b^{(i^*)}})\). This subcase intuitively implies that the adversary successfully guesses the bit \(b^{(i^*)}\), since the adversary has to choose \(\mathsf {resp} _{0}^*,\mathsf {resp} _{1}^*\) such that \(\mathsf {resp} _{1-b^{(i^*)}}^*\) is equal and \(\mathsf {resp} _{b^{(i^*)}}^*\) is unequal. However, in Game 2, the secret bit \(b^{(i^*)}\) is perfectly hidden to the adversary due to the following facts.
-
The public key \( pk ^{(i^*)}\) is independent of \(b^{(i^*)}\).
-
User \(i^*\) is not corrupted (or otherwise the forgery is invalid, anyway), so the bit \(b^{(i^*)}\) is not leaked through corruptions.
-
The signature \(\sigma \) returned by oracle \(\mathsf {Sign} (i^*, m)\) is independent of bit \(b^{(i^*)}\). The reason is that \(X_2\) implies that \(\mathsf {cmtColl} \) does not happen. As shown in Remark 11, each \(\mathsf {Sign} (i^*, m)\) query will use uniformly random \(\mathsf {ch} _{1-b^{(i^*)}}\) and \(\mathsf {ch} _{b^{(i^*)}}\). Thus, the signature essentially contains the two transcripts
$$ (\mathsf {cmt} _{b^{(i^*)}},\mathsf {ch} _{b^{(i^*)}},\mathsf {resp} _{b^{(i^*)}}) \quad \text {and}\quad (\mathsf {cmt} _{1-b^{(i^*)}},\mathsf {ch} _{1-b^{(i^*)}},\mathsf {resp} _{1-b^{(i^*)}}) $$Note that the \(b^{(i^*)}\) transcript is an “honestly generated” transcript and the \((1-b^{(i^*)})\) transcript is a “simulated” transcript with uniformly random \(\mathsf {ch} _{1-b^{(i^*)}}\) and \(\mathsf {resp} _{1-b^{(i^*)}}\). Due to the perfect simulatability of \(\mathsf {LID}\), we know that these two transcripts are perfectly identically distributed. Thus, \(\mathcal {A}\) gains no information about \(b^{(i^*)}\) through signatures.
In summary, we conclude that this subcase happens with probability
$$\frac{1}{2}\Pr [X_2 \wedge \mathsf {ImplicitUsage} ].$$ -
-
\(X_2 \wedge \mathsf {ImplicitUsage} \wedge (\mathsf {resp} _{1-b^{(i^*)}}^*\ne \mathsf {resp} _{1-b^{(i^*)}})\). For this subcase, we can prove the following claim.
Claim
We can construct an adversary \(\mathcal {B}\) with running time \(t_\mathcal {B} \approx t_\mathcal {A} \) such that

Proof
To prove this claim, we define a new intermediate game Game \(2'\), which is exactly the same as Game 2, except that we choose a lossy public key  for every user \(i \in [N]\) in Game \(2'\). We can build an adversary \(\mathcal {B}\) with running time \(t_{\mathcal {B}}\approx t_\mathcal {A} \) such that
for every user \(i \in [N]\) in Game \(2'\). We can build an adversary \(\mathcal {B}\) with running time \(t_{\mathcal {B}}\approx t_\mathcal {A} \) such that

The construction of \(\mathcal {B} \) using \(\mathcal {A} \) is straightforward. It receives \(( pk '_i)_{i \in [N]}\), which is either generated by algorithm \(\mathsf {LID}.\mathsf {Gen} \) or by \(\mathsf {LID}.\mathsf {LossyGen} \). Then, it simulates Game 2 for the adversary \(\mathcal {A} \) and sets  for all \(i \in [N]\). Note that, in Game 2, the secret key \( sk _{1-b}^{(i)}\) is not used for any user i. So \(\mathcal {B}\) is able to simulate the game perfectly. Finally, \(\mathcal {B} \) outputs 1 if and only if \(\mathcal {A} \) wins and \(\mathsf {ImplicitUsage} \wedge (\mathsf {resp} _{1-b^{(i^*)}}^*\ne \mathsf {resp} _{1-b^{(i^*)}})\) happens. It is clear that \(\mathcal {B}\) perfectly simulates Game 2 if it receives normal public keys and \(\mathcal {B}\) perfectly simulates Game \(2'\) if it receives lossy public keys. Thus, Eq. (1) follows.
for all \(i \in [N]\). Note that, in Game 2, the secret key \( sk _{1-b}^{(i)}\) is not used for any user i. So \(\mathcal {B}\) is able to simulate the game perfectly. Finally, \(\mathcal {B} \) outputs 1 if and only if \(\mathcal {A} \) wins and \(\mathsf {ImplicitUsage} \wedge (\mathsf {resp} _{1-b^{(i^*)}}^*\ne \mathsf {resp} _{1-b^{(i^*)}})\) happens. It is clear that \(\mathcal {B}\) perfectly simulates Game 2 if it receives normal public keys and \(\mathcal {B}\) perfectly simulates Game \(2'\) if it receives lossy public keys. Thus, Eq. (1) follows.
Now in Game \(2'\), the key \( pk _{1-b}^{(i^*)}\) is lossy. Since \(X_{2'}\) implies that \(\sigma ^*\) is a valid signature with respect to \(m^*\), we know that
Since the signing oracle \(\mathsf {Sign} (i^*, m^*)\) also outputs valid signature \(\sigma \) for \(m^*\), we have that
In this subcase, we have \((\mathsf {cmt} _{1-b^{(i^*)}}, \mathsf {ch} _{1-b^{(i^*)}})=(\mathsf {cmt} _{1-b^{(i^*)}}^*, \mathsf {ch} _{1-b^{(i^*)}}^*)\) and \(\mathsf {resp} _{1-b^{(i^*)}}\ne \mathsf {resp} _{1-b^{(i^*)}}^*\). Due to the uniqueness property of \(\mathsf {LID}\) with respect to lossy public keys, we must have
Applying Eq. (1) to the obtained bounds, the claim follows. \(\square \)
Putting both subcases together, we obtain that

which implies that  . \(\square \)
. \(\square \)
Game 4. Game 4 further modifies the winning condition. We denote \(\mathsf {Before} \) as the event that \(\mathsf {Both} \) happens and the first \((1-b^{(i^*)})\mathsf {\text {-}query} \) is made before the first \(b^{(i^*)}\mathsf {\text {-}query} \) is made. Game 4 outputs 0 if event \(\mathsf {Before} \) does not happen.
Hence, \(X_4\) happens if and only if \(X_{3}\wedge \mathsf {Before} \) happens. We can prove the following lemma.
Lemma 15
\(\Pr [X_4] \ge 1/2 \cdot \Pr [X_3]\).
Proof
Since we know that event \(\mathsf {Both} \) happens, we can divide \(X_3\) into three subcases.
-
Both the first 0-query and the first 1-query are made in one and the same signing query \(\mathsf {Sign} (i^*,m^*)\).
In this subcase, we have that two hash queries \(\{\mathsf {H} (m^*,\mathsf {cmt} _0^*),\mathsf {H} (m^{*}, \mathsf {cmt} _1^*)\}\) made by the final verification algorithm have the same input as the two hash queries \(\{\mathsf {H} (m^*, \mathsf {cmt} _0),\mathsf {H} (m^*, \mathsf {cmt} _1)\}\) made by the signing oracle. We know that \(X_3\) implies that \(\mathsf {ImplicitUsage} \) does not happen, so we must have that \((\mathsf {cmt} _0^*,\mathsf {cmt} _1^*)=(\mathsf {cmt} _1,\mathsf {cmt} _0)\). Since the signing algorithm always makes a \(\mathsf {H} (m^*,\mathsf {cmt} _{b^{(i^*)}})\) query before \(\mathsf {H} (m,\mathsf {cmt} _{1-b^{(i^*)}})\), we have that event \(\mathsf {Before} \) always happens in this subcase.
-
Both the first 0-query and the first 1-query are made in one signing query \(\mathsf {Sign} (i',m^*)\) for some \(i'\ne i^*\).
In this subcase, the \(b^{(i')}\textsf {-query}\) is made first and \(\mathsf {Before} \) happens if and only if \(b^{(i')}=1-b^{(i^*)}\).
-
The first 0-query and the first 1-query are not made in exactly one signing query. In other words, they lie in different signing queries or at least one of them is made by the adversary.
In this subcase, the adversary \(\mathcal {A}\) actually has full control which one is queried first. Suppose the \(\beta \textsf {-query}\) is made first for some implicit bit \(\beta \in \{0,1\}\) chosen by the adversary. Then, event \(\mathsf {Before} \) happens if and only if \(\beta = b^{(i^*)}\).
Similar to the proof of Lemma 13, we can show that the bit \(b^{(i^*)}\) is perfectly hidden to the adversary. So if the second or the third subcase happens, the probability that \(\mathsf {Before} \) happens is 1/2. Together with the fact that \(\mathsf {Before} \) always happen in the first subcase, Lemma 15 follows. \(\square \)
Game 5. In this game, we change the generation of the key \( pk _{1-b}^{(i)}\). Namely, the key generation in Game 5 is exactly as in Game 4 except that we choose lossy public keys  for every user \(i \in [N]\) in Game 5.
for every user \(i \in [N]\) in Game 5.
Lemma 16
We can construct an adversary \(\mathcal {B}\) with running time \(t_\mathcal {B} \approx t_\mathcal {A} \) such that

Proof
The proof of the lemma is straightforward. We can construct \(\mathcal {B} \) using \(\mathcal {A} \) as a subroutine. \(\mathcal {B} \) receives as input \(( pk '_i)_{i \in [N]}\), which is either generated by algorithm \(\mathsf {LID}.\mathsf {Gen} \) or by \(\mathsf {LID}.\mathsf {LossyGen} \). Then, it simulates Game 5 for the adversary \(\mathcal {A} \) and set  for all \(i \in [N]\).
for all \(i \in [N]\).
\(\square \)
Finally, we can prove the following lemma.
Lemma 17
where \(q_\mathsf {H} \) is the number of hash queries made in Game 5.
Note that the lossiness of \(\mathsf {LID}\) guarantees that \(\varepsilon _{\ell }\) is statistically negligible (even for computationally unbounded adversaries). Hence, the multiplicative term \(N\cdot q_\mathsf {H} ^2\) does not break the tightness of our signature scheme. It will convenient to prove this claim by reduction.
Proof
To prove this lemma, we build an adversary \(\mathcal {B}\) against the lossiness of \(\mathsf {LID}\). On getting a lossy public key  , \(\mathcal {B}\) uniformly selects
, \(\mathcal {B}\) uniformly selects  and
and  . Then \(\mathcal {B}\) generates all the public keys for \(\mathcal {A}\) according to Game 5 except that it sets
. Then \(\mathcal {B}\) generates all the public keys for \(\mathcal {A}\) according to Game 5 except that it sets  . Then \(\mathcal {B}\) invokes \(\mathcal {A}\) and answers all the queries according to Game 5 with the following exceptions.
. Then \(\mathcal {B}\) invokes \(\mathcal {A}\) and answers all the queries according to Game 5 with the following exceptions.
-
In the \(j_1\)-th hash query \(\mathsf {H} (m,\mathsf {cmt})\), \(\mathcal {B}\) submits \(\mathsf {cmt}\) to its own challenger and get back
 .
. -
In the \(j_2\)-th hash query \(\mathsf {H} (m,\mathsf {cmt} ')\), \(\mathcal {B}\) returns \(\mathsf {ch}\) as response and logs \(((m,\mathsf {cmt} '),\mathsf {ch})\) into the hash list \(\mathcal {L}\).
After \(\mathcal {A}\) submits the forgery attempt \((i^*, m^*, \sigma ^*=(\mathsf {ch} _{0}^*, \mathsf {resp} _{0}^*, \mathsf {resp} _{1}^*))\), \(\mathcal {B}\) checks whether all the following events happen:
-
\(X_5\) happens,
-
\(i'=i^*\),
-
the first \((1-b^{(i^*)})\mathsf {\text {-}query} \) is exactly the \(j_1\)-th hash query,
-
the first \(b^{(i^*)}\mathsf {\text {-}query} \) is exactly the \(j_2\)-th hash query.
If all of these events happen, \(\mathcal {B}\) outputs \(\mathsf {resp} _{1-b^{(i^*)}}^*\) to its own challenger. Otherwise, \(\mathcal {B}\) halts and outputs nothing.
The probability that \(\mathcal {B}\) does not halt is at least \(\Pr [X_5]/(N\cdot q_\mathsf {H} ^2)\). We will show that in this case
and hence \(\mathcal {B}\) wins the lossiness game. This is implied by the following facts.
-
\(i'=i^*\) indicates that \( pk = pk _{1-b}^{(i^*)}\).
-
The \(j_1\)-th hash query is the first \((1-b^{(i^*)})\mathsf {\text {-}query} \) indicates that \(\mathsf {cmt} =\mathsf {cmt} _{1-b^{(i^*)}}^*\).
-
The \(j_2\)-th hash query is the first \(b^{(i^*)}\mathsf {\text {-}query} \) indicates that \(\mathsf {ch} =\mathsf {ch} _{1-b^{(i^*)}}^*\).
-
\(X_3\) happens indicates that \(\mathsf {Vrfy} ( pk ^{(i^*)}, m^*, \sigma ^*)=1\), which further indicates that
$$ \mathsf {LID}.\mathsf {Vrfy} ( pk _{1-b}^{(i^*)}, \mathsf {cmt} _{1-b^{(i^*)}}^*, \mathsf {ch} _{1-b^{(i^*)}}^*, \mathsf {resp} _{1-b^{(i^*)}}^*)=1. $$
Thus, we have that \(\Pr [X_5]/(N\cdot q_\mathsf {H} ^2)\le \Pr [\mathcal {B} \text { wins}]\le \varepsilon _{\ell }\) and Lemma 17 follows.
\(\square \)
Theorem 9 now follows. \(\square \)
5 Instantiations of Our Scheme
In the previous section we identified the necessary properties of the underlying lossy identification scheme. We now continue to discuss how suitable schemes can be instantiated based on concrete hardness assumptions. The constructions described in this section are derived from [1,2,3, 29] and are well-known. The purpose of this section is to argue and justify that these constructions indeed satisfy all properties required for our signature scheme.
5.1 Instantiation Based on Decisional Diffie–Hellman
The well-known DDH-based lossy identification scheme uses the standard Sigma protocol to prove equality of discrete logarithms by Chaum et al. [11] (cf. Fig. 1) as foundation, which was used by Katz and Wang [29] to build tightly-secure signatures (in the single-user setting without corruptions).
The DDH-based identification scheme [11].
The DDH Problem. Let \((\mathbb {G},g,q)\) be a cyclic group of prime order q and generator g. Further, let \(h \in \mathbb {G} \). We denote the set of DDH tuples in \(\mathbb {G} \) with respect to g and h as

and the set of “non-DDH tuples” as

Definition 18
Let \((\mathbb {G},g,q)\) be a cyclic group of prime order q and generator g. Further, let  . We define the advantage of an algorithm \(\mathcal {B}\) in solving the DDH problem in \(\mathbb {G} \) with respect to (g, h) as
. We define the advantage of an algorithm \(\mathcal {B}\) in solving the DDH problem in \(\mathbb {G} \) with respect to (g, h) as

where  and
and  are chosen uniformly random.
are chosen uniformly random.
A DDH-Based LID Scheme. Let \((\mathbb {G},g,q)\) be a cyclic group of prime order q and generator g and let \(h \in \mathbb {G} \). We define the lossy identification scheme \(\mathsf {LID} = (\mathsf {LID}.\mathsf {Gen}, \mathsf {LID}.\mathsf {LossyGen}, \mathsf {LID}.\mathsf {Prove}, \mathsf {LID}.\mathsf {Vrfy}, \mathsf {LID}.\mathsf {Sim})\) based on the protocol presented above as follows:
-
Key generation. The algorithm \(\mathsf {LID}.\mathsf {Gen} \) chooses a value
 uniformly at random. It sets
uniformly at random. It sets  and
and  , and outputs \(( pk , sk )\).
, and outputs \(( pk , sk )\). -
Lossy key generation. The algorithm \(\mathsf {LID}.\mathsf {LossyGen} \) chooses two group elements
 uniformly and independently at random. It outputs
uniformly and independently at random. It outputs 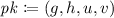 .
. -
Proving. The algorithm \(\mathsf {LID}.\mathsf {Prove} \) is split up into the following two algorithms:
-
1.
The algorithm \(\mathsf {LID}.\mathsf {Prove} _1\) takes as input a secret key \( sk = x\), chooses a random value
 , and computes a commitment
, and computes a commitment  , where g, h are the value of the \( pk \) corresponding to \( sk \). It outputs \((\mathsf {cmt}, \mathsf {st})\) with
, where g, h are the value of the \( pk \) corresponding to \( sk \). It outputs \((\mathsf {cmt}, \mathsf {st})\) with  .
. -
2.
The algorithm \(\mathsf {LID}.\mathsf {Prove} _2\) takes as input a secret key \( sk = x\), a commitment \(\mathsf {cmt} = (e,f)\), a challenge \(\mathsf {ch} \in \mathbb {Z} _q\), a state \(\mathsf {st} = r\), and outputs a response
 .
.
-
1.
-
Verification. The verification algorithm \(\mathsf {LID}.\mathsf {Vrfy} \) takes as input a public key \( pk = (g,h,u,v)\), a commitment \(\mathsf {cmt} = (e,f)\), a challenge \(\mathsf {ch} \in \mathbb {Z} _q\), and a response \(\mathsf {resp} \in \mathbb {Z} _q\). It outputs 1 if and only if \(e = g^\mathsf {resp} \cdot u^\mathsf {ch} \) and \(f = h^\mathsf {resp} \cdot v^\mathsf {ch} \).
-
Simulation. The simulation algorithm \(\mathsf {LID}.\mathsf {Sim} \) takes as input a public key \( pk = (g,h,u,v)\), a challenge \(\mathsf {ch} \in \mathbb {Z} _q\), and a response \(\mathsf {resp} \in \mathbb {Z} _q\). It outputs a commitment \(\mathsf {cmt} = (e, f) = ( g^\mathsf {resp} \cdot u^\mathsf {ch}, h^\mathsf {resp} \cdot v^\mathsf {ch})\).
Remark 19
Note that an honest public key generated with \(\mathsf {LID}.\mathsf {Gen} \) is of the form \( pk = (g,h,u,v)\) such that \((u,v) \in \mathsf {DDH}(\mathbb {G}, g, h) \), whereas a lossy public key generated with \(\mathsf {LID}.\mathsf {LossyGen} \) is of the form \( pk = (g,h,u,v)\) such that \((u,v) \not \in \mathsf {DDH}(\mathbb {G}, g, h) \) with high probability.
Theorem 20
The scheme \(\mathsf {LID} \) defined above is lossy with
and from any efficient adversary \(\mathcal {A} \) we can construct an efficient adversary \(\mathcal {B} \) such that

Furthermore, \(\mathsf {LID}\) is perfectly unique with respect to lossy keys (i.e., \(\varepsilon _u = 0\)), \(\mathsf {LID}\) has \(\alpha \)-bit min-entropy with \(\alpha = \log _2(q)\), \(\mathsf {LID}\) is commitment-recoverable, and \(\mathsf {LID}\) has an injective simulator.
The proof of this theorem is rather standard and implicitly contained in the aforementioned prior works. For completeness, we provide a sketch in Appendix A.
Concrete Instantiation. We can now use the DDH-based lossy identification scheme to describe an explicit instantiation of our signature scheme based on the DDH assumption, in order to assess its concrete performance. Let \(\mathbb {G} \) be a group of prime order p with generator g, let  be a random generator and let \(\mathsf {H} :\{0,1\}^* \rightarrow \mathbb {Z} _{p}\) be a hash function. We construct a digital signature scheme \(\mathsf {Sig} = (\mathsf {Gen}, \mathsf {Sign}, \mathsf {Vrfy})\) as follows.
be a random generator and let \(\mathsf {H} :\{0,1\}^* \rightarrow \mathbb {Z} _{p}\) be a hash function. We construct a digital signature scheme \(\mathsf {Sig} = (\mathsf {Gen}, \mathsf {Sign}, \mathsf {Vrfy})\) as follows.
-
Key generation. The key generation \(\mathsf {Gen}\) algorithm samples
 ,
,  . Then it sets
. Then it sets 
-
Signing. The signing algorithm \(\mathsf {Sign}\) takes as input \(sk = (b, x_{b})\) and a message \(m \in \{0,1\} ^{*}\). Then it proceeds as follows.
-
1.
It first chooses a random value
 , and sets
, and sets  and
and 
-
2.
Then it samples a value
 and computes $$ e_{1-b} = g^{\mathsf {resp} _{1-b}} u_{1-b}^{\mathsf {ch} _{1-b}} \qquad \text {and}\qquad f_{1-b} = h^{\mathsf {resp} _{1-b}} v_{1-b}^{\mathsf {ch} _{1-b}}. $$
and computes $$ e_{1-b} = g^{\mathsf {resp} _{1-b}} u_{1-b}^{\mathsf {ch} _{1-b}} \qquad \text {and}\qquad f_{1-b} = h^{\mathsf {resp} _{1-b}} v_{1-b}^{\mathsf {ch} _{1-b}}. $$ -
3.
Finally, it computes

and outputs the signature
 .
.
-
1.
-
Verification. The verification algorithm takes as input a public key
 , a message \(m \in \{0,1\} ^{*}\), and a signature \(\sigma = (\mathsf {ch} _{0}, \mathsf {resp} _{0}, \mathsf {resp} _{1})\). If first computes $$ e_{0} = g^{\mathsf {resp} _{0}} u_{0}^{\mathsf {ch} _{0}} \qquad \text {and}\qquad f_{0} = h^{\mathsf {resp} _{0}} v_{0}^{\mathsf {ch} _{0}}. $$
, a message \(m \in \{0,1\} ^{*}\), and a signature \(\sigma = (\mathsf {ch} _{0}, \mathsf {resp} _{0}, \mathsf {resp} _{1})\). If first computes $$ e_{0} = g^{\mathsf {resp} _{0}} u_{0}^{\mathsf {ch} _{0}} \qquad \text {and}\qquad f_{0} = h^{\mathsf {resp} _{0}} v_{0}^{\mathsf {ch} _{0}}. $$From \((e_{0}, f_{0})\) it is then able to compute

and then
$$ e_{1} = g^{\mathsf {resp} _{1}} \cdot u_{1}^{\mathsf {ch} _{1}} \qquad \text {and}\qquad f_{1} = h^{\mathsf {resp} _{1}} \cdot v_{1}^{\mathsf {ch} _{1}}. $$Finally, the algorithm outputs 1 if and only if
$$ \mathsf {ch} _{0} = \mathsf {H} (m, e_{1}, f_{1}). $$
Note that public keys are \(pk \in \mathbb {G} ^4\), secret keys are \(sk \in \{0,1\} \times \mathbb {Z} _p\), and signatures are \(\sigma \in \mathbb {Z} _p^3\).
5.2 Instantiation from the \(\phi \)-Hiding Assumption
Another possible instantiation is based on the Guillou–Quisquater (GQ) identification scheme [25], which proves that an element \(U = S^e \bmod N\) is an e-th residue (cf. Fig. 2). Abdalla et al. [1] describe a lossy version of the GQ scheme, based on the \(\phi \)-hiding assumption. We observe that we can build a lossy identification scheme on a weaker assumption, which is implied by \(\phi \)-hiding.
In order to achieve tightness in a multi-user setting, we will need a common setup, which is shared across all users. This setup consists of a public tuple (N, e) where \(N = p \cdot q\) is the product of two large random primes and e a uniformly random prime of length \(\ell _e\le \lambda /4\) that divides \(p-1\). The factors p and q need to remain secret, so we assume that (N, e) either was generated by a trusted party, or by running a secure multi-party computation protocol with multiple parties.
The Guillou–Quisquater LID Scheme. We define the lossy identification scheme \(\mathsf {LID} = (\mathsf {LID}.\mathsf {Gen}, \mathsf {LID}.\mathsf {LossyGen}, \mathsf {LID}.\mathsf {Prove}, \mathsf {LID}.\mathsf {Vrfy}, \mathsf {LID}.\mathsf {Sim})\) based on the protocol presented above as follows:
-
Common setup. The common system parameters are a tuple (N, e) where \(N = p \cdot q\) is the product of two distinct primes p, q of length \(\lambda /2\) and e is random prime of length \(\ell _e\le \lambda /4\) such that e divides \(p-1\). Note that the parameters (N, e) are always in “lossy mode”, and not switched from an “injective” pair (N, e) where e is coprime to \(\phi (N) = (p-1)(q-1)\) to “lossy” in the security proof, as common in other works.
-
Key generation. The algorithm \(\mathsf {LID}.\mathsf {Gen}\) samples
 and computes \(U = S^e\). It sets \( pk = (N, e, U)\) and \( sk = (N, e, S)\), where (N, e) are from the common parameters.
and computes \(U = S^e\). It sets \( pk = (N, e, U)\) and \( sk = (N, e, S)\), where (N, e) are from the common parameters. -
Lossy key generation. The lossy key generation algorithm \(\mathsf {LID}.\mathsf {LossyGen} \) samples U uniformly at random from the e-th non-residues modulo N.Footnote 3
-
Proving. The algorithm \(\mathsf {LID}.\mathsf {Prove} \) is split up into the following two algorithms:
-
1.
The algorithm \(\mathsf {LID}.\mathsf {Prove} _1\) takes as input a secret key \( sk = (N, e, S)\), chooses a random value
 , and computes a commitment
, and computes a commitment  . It outputs
. It outputs  with
with  .
. -
2.
The algorithm \(\mathsf {LID}.\mathsf {Prove} _2\) takes as input a secret key \( sk = (N, e, S)\), a commitment \(\mathsf {cmt} \), a challenge \(\mathsf {ch} \in \{0, \ldots , 2^{\ell _e} - 1\}\), a state \(\mathsf {st} = r\), and outputs a response
 .
.
-
1.
-
Verification. The verification algorithm \(\mathsf {LID}.\mathsf {Vrfy} \) takes as input a public key \( pk = (N, e, U)\), a commitment \(\mathsf {cmt} \), a challenge \(\mathsf {ch} \), and a response \(\mathsf {resp} \). It outputs 1 if and only if \(\mathsf {resp} \ne 0 \bmod N\) and \(\mathsf {resp} ^e = \mathsf {cmt} \cdot U^\mathsf {ch} \).
-
Simulation. The simulation algorithm \(\mathsf {LID}.\mathsf {Sim} \) takes as input a public key \( pk = (N, e, U)\), a challenge \(\mathsf {ch} \), and a response \(\mathsf {resp} \). It outputs a commitment \(\mathsf {cmt} = \mathsf {resp} ^e / U^\mathsf {ch} \).
The Guillou–Quisquater identification scheme [25].
Theorem 21
The scheme \(\mathsf {LID} \) defined above is lossy with
and from any efficient adversary \(\mathcal {A} \) we can construct an efficient adversary \(\mathcal {B} \) such that

Furthermore, \(\mathsf {LID}\) is perfectly unique with respect to lossy keys (i.e., \(\varepsilon _u = 0\)), \(\mathsf {LID}\) has \(\alpha \)-bit min-entropy with \(\alpha \ge \lambda - 2\), \(\mathsf {LID}\) is commitment-recoverable, and \(\mathsf {LID}\) has an injective simulator.
The above theorem has been proven in [1] for most of its statements. What is left is a proof for n-key-indistinguishability, which we provide in Appendix B.
5.3 On Instantiations of Lossy ID Schemes from Other Assumptions
There also exist lossy identification schemes based on the decisional short discrete logarithm problem, the ring LWE problem, and the subset sum problem (all due to Abdalla et al. [2, 3]). However, they do not directly translate to a tight multi-user signature scheme that is existentially unforgeable with adaptive corruptions.
Our security proof requires tight multi-instance security of the underlying hardness assumption. While, for example, the DDH-based scheme satisfies this via its self-reducibility property, it is not obvious how schemes based on, for example, lattices or subset sum achieve this notion in a tight manner.
Notes
- 1.
One can always prove tight \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) security under the interactive assumption that the scheme is \(\mathsf {MU\text {-}} \mathsf {EUF\text {-}CMA} ^{\mathsf {corr}}\) secure.
- 2.
All known instantiations of lossy identification schemes have a deterministic \(\mathsf {LID}.\mathsf {Prove} _2\) algorithm. However, if a new instantiation requires randomness, then it can be “forwarded” from \(\mathsf {LID}.\mathsf {Prove} _1\) in the state variable \(\mathsf {st}\). Therefore the requirement that \(\mathsf {LID}.\mathsf {Prove} _{2}\) is deterministic is without loss of generality, and only made to simplify our security analysis.
- 3.
This is indeed efficiently possible as
 is a not an e-th residue with probability \(1 - 1/e\) and we can efficiently check whether a given U is an e-th residue when the factorization of N is known [1].
is a not an e-th residue with probability \(1 - 1/e\) and we can efficiently check whether a given U is an e-th residue when the factorization of N is known [1].
References
Abdalla, M., Ben Hamouda, F., Pointcheval, D.: Tighter reductions for forward-secure signature schemes. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 292–311. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36362-7_19
Abdalla, M., Fouque, P.-A., Lyubashevsky, V., Tibouchi, M.: Tightly-secure signatures from lossy identification schemes. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 572–590. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_34
Abdalla, M., Fouque, P.-A., Lyubashevsky, V., Tibouchi, M.: Tightly secure signatures from lossy identification schemes. J. Cryptol. 29(3), 597–631 (2016)
Abe, M., Ohkubo, M., Suzuki, K.: 1-out-of-n signatures from a variety of keys. In: Zheng, Y. (ed.) ASIACRYPT 2002. LNCS, vol. 2501, pp. 415–432. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-36178-2_26
Bader, C., Hofheinz, D., Jager, T., Kiltz, E., Li, Y.: Tightly-secure authenticated key exchange. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 629–658. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_26
Bader, C., Jager, T., Li, Y., Schäge, S.: On the impossibility of tight cryptographic reductions. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 273–304. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_10
Bellare, M., Boldyreva, A., Micali, S.: Public-key encryption in a multi-user setting: security proofs and improvements. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 259–274. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_18
Bellare, M., Rogaway, P.: Entity authentication and key distribution. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 232–249. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_21
Cachin, C., Micali, S., Stadler, M.: Computationally private information retrieval with polylogarithmic communication. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 402–414. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48910-X_28
Canetti, R., Krawczyk, H.: Analysis of key-exchange protocols and their use for building secure channels. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 453–474. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_28
Chaum, D., Evertse, J.-H., van de Graaf, J.: An improved protocol for demonstrating possession of discrete logarithms and some generalizations. In: Chaum, D., Price, W.L. (eds.) EUROCRYPT 1987. LNCS, vol. 304, pp. 127–141. Springer, Heidelberg (1988). https://doi.org/10.1007/3-540-39118-5_13
Cohn-Gordon, K., Cremers, C., Gjøsteen, K., Jacobsen, H., Jager, T.: Highly efficient key exchange protocols with optimal tightness. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part II. LNCS, vol. 11694, pp. 767–797. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_25
Cramer, R., Damgård, I., Schoenmakers, B.: Proofs of partial knowledge and simplified design of witness hiding protocols. In: Desmedt, Y.G. (ed.) CRYPTO 1994. LNCS, vol. 839, pp. 174–187. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48658-5_19
Davis, H., Günther, F.: Tighter proofs for the sigma and TLS 1.3 key exchange protocols. Cryptology ePrint Archive, Report 2020/1029 (2020). https://eprint.iacr.org/2020/1029
Diemert, D., Jager, T.: On the tight security of TLS 1.3: theoretically-sound cryptographic parameters for real-world deployments. Cryptology ePrint Archive, Report 2020/726; to appear in the Journal of Cryptology (2020). https://eprint.iacr.org/2020/726
Digital Signature Standard (DSS). National Institute of Standards and Technology (NIST), FIPS PUB 186-3, U.S. Department of Commerce (2009). http://csrc.nist.gov/publications/fips/fips186-3/fips_186-3.pdf
Fersch, M., Kiltz, E., Poettering, B.: On the provable security of (EC)DSA signatures. In: Weippl, E.R., Katzenbeisser, S., Kruegel, C., Myers, A.C., Halevi, S (eds.) ACM CCS 2016, pp. 1651–1662. ACM Press, October 2016
Fischlin, M., Harasser, P., Janson, C.: Signatures from sequential-OR proofs. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020, Part III. LNCS, vol. 12107, pp. 212–244. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45727-3_8
Fischlin, M., Lehmann, A., Ristenpart, T., Shrimpton, T., Stam, M., Tessaro, S.: Random oracles with(out) programmability. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 303–320. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_18
Fleischhacker, N., Jager, T., Schröder, D.: On tight security proofs for Schnorr signatures. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014, Part I. LNCS, vol. 8873, pp. 512–531. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45611-8_27
Fleischhacker, N., Jager, T., Schröder, D.: On tight security proofs for Schnorr signatures. J. Cryptol. 32(2), 566–599 (2019)
Garg, S., Bhaskar, R., Lokam, S.V.: Improved bounds on security reductions for discrete log based signatures. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 93–107. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_6
Gjøsteen, K., Jager, T.: Practical and tightly-secure digital signatures and authenticated key exchange. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part II. LNCS, vol. 10992, pp. 95–125. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_4
Goldwasser, S., Micali, S., Rivest, R.L.: A digital signature scheme secure against adaptive chosen-message attacks. SIAM J. Comput. 17(2), 281–308 (1988)
Guillou, L.C., Quisquater, J.-J.: A “paradoxical” indentity-based signature scheme resulting from zero-knowledge. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 216–231. Springer, New York (1990). https://doi.org/10.1007/0-387-34799-2_16
Hasegawa, S., Isobe, S.: Lossy identification schemes from decisional RSA. In: International Symposium on Information Theory and its Applications, ISITA 2014, Melbourne, Australia, 26–29 October 2014, pp. 143–147. IEEE (2014)
Hofheinz, D., Jager, T.: Tightly secure signatures and public-key encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 590–607. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_35
Jager, T., Kiltz, E., Riepel, D., Schäge, S.: Tightly-secure authenticated key exchange, revisited. Cryptology ePrint Archive, Report 2020/1279 (2020). https://eprint.iacr.org/2020/1279
Katz, J., Wang, N.: Efficiency improvements for signature schemes with tight security reductions. In: Jajodia, S., Atluri, V., Jaeger, T. (eds.) ACM CCS 2003, pp. 155–164. ACM Press, October 2003
Kiltz, E., Masny, D., Pan, J.: Optimal security proofs for signatures from identification schemes. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part II. LNCS, vol. 9815, pp. 33–61. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_2
Kiltz, E., O’Neill, A., Smith, A.: Instantiability of RSA-OAEP under chosen-plaintext attack. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 295–313. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_16
Krawczyk, H.: SIGMA: the “SIGn-and-MAc” approach to authenticated Diffie-Hellman and its use in the IKE protocols. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 400–425. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_24
Li, Y., Schäge, S.: No-match attacks and robust partnering definitions: defining trivial attacks for security protocols is not trivial. In: Thuraisingham, B.M., Evans, D., Malkin, T., Xu, D. (eds.) ACM CCS 2017, pp. 1343–1360. ACM Press, October/November 2017
Liu, X., Liu, S., Gu, D., Weng, J.: Two-pass authenticated key exchange with explicit authentication and tight security. In: Moriai, S., Wang, H. (eds.) ASIACRYPT 2020, Part II. LNCS, vol. 12492, pp. 785–814. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64834-3_27
Paillier, P., Vergnaud, D.: Discrete-log-based signatures may not be equivalent to discrete log. In: Roy, B. (ed.) ASIACRYPT 2005. LNCS, vol. 3788, pp. 1–20. Springer, Heidelberg (2005). https://doi.org/10.1007/11593447_1
Schnorr, C.P.: Efficient identification and signatures for smart cards. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 239–252. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_22
Seurin, Y.: On the exact security of Schnorr-type signatures in the random oracle model. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 554–571. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_33
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Proof of Theorem 20
Random Self-reducibility of DDH. It is well-known that the DDH problem is random self-reducible, which we summarize in the following lemma. See [7, Lemma 5.2] for a proof.
Lemma 22
There exists an efficient algorithm \(\mathsf {ReRand} \) that takes as input (g, h) and a DDH instance \((u,v) \in \mathbb {G} ^{2}\) and an integer \(N \), and outputs \(N \) new DDH instances \((u^{(i)},v^{(i)})\) such that
for all \(i \in [N ]\). The running time of this algorithm mainly consists of \(\mathcal O(N)\) exponentiations in \(\mathbb {G} \).
Proof. To show that \(\mathsf {LID} \) is lossy, we need to show that it satisfies all properties presented in Definition 4.
-
Completeness of normal keys. We claim that the above scheme is perfectly-complete. To prove this, we show that for any honest transcript it holds that \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch}, \mathsf {resp}) = 1\). Let
 be an (honest) key pair and let \((\mathsf {cmt}, \mathsf {ch}, \mathsf {resp})\) be an honest transcript, that is,
be an (honest) key pair and let \((\mathsf {cmt}, \mathsf {ch}, \mathsf {resp})\) be an honest transcript, that is,  ,
,  and
and 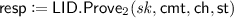 . By definition of the scheme, we have \( pk = (g,h,u,v)\) with \((u,v) \in \mathsf {DDH}(\mathbb {G}, g, h) \) and \( sk = x\) and \(\mathsf {cmt} = (e,f) = (g^r, h^r)\) and \(\mathsf {resp} = r - \mathsf {ch} \cdot x\). Further, \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch}, \mathsf {resp}) = 1\) if and only if \(e = g^\mathsf {resp} \cdot u^\mathsf {ch} \) and \(f = h^\mathsf {resp} \cdot v^\mathsf {ch} \). Observe that $$ g^\mathsf {resp} \cdot u^\mathsf {ch} = g^{r - \mathsf {ch} \cdot x} \cdot g^{\mathsf {ch} \cdot x} = g^r = e. $$
. By definition of the scheme, we have \( pk = (g,h,u,v)\) with \((u,v) \in \mathsf {DDH}(\mathbb {G}, g, h) \) and \( sk = x\) and \(\mathsf {cmt} = (e,f) = (g^r, h^r)\) and \(\mathsf {resp} = r - \mathsf {ch} \cdot x\). Further, \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch}, \mathsf {resp}) = 1\) if and only if \(e = g^\mathsf {resp} \cdot u^\mathsf {ch} \) and \(f = h^\mathsf {resp} \cdot v^\mathsf {ch} \). Observe that $$ g^\mathsf {resp} \cdot u^\mathsf {ch} = g^{r - \mathsf {ch} \cdot x} \cdot g^{\mathsf {ch} \cdot x} = g^r = e. $$An analogous equation holds for f if g is replaced by h. Hence, \(\mathsf {LID}.\mathsf {Vrfy} \) outputs 1 for every honest transcript.
-
Simulatability of transcripts. We claim that the above scheme is perfectly simulatable. To show this, we need to argue that the two distributions

and

are identical. Recall that we have \( pk = (g,h,u,v)\) with \((u,v) \in \mathsf {DDH}(\mathbb {G}, g, h) \), \( sk = x\), \(\mathsf {cmt} = (e,f) = (g^r, h^r)\) with
 , and \(\mathsf {resp} = r - \mathsf {ch} \cdot x\) for an honest transcript (i.e., in the former distribution). Thus, we have that \(\mathsf {cmt} = (e,f)\) is uniformly distributed over \(\mathbb {G} ^2\). Consequently, since
, and \(\mathsf {resp} = r - \mathsf {ch} \cdot x\) for an honest transcript (i.e., in the former distribution). Thus, we have that \(\mathsf {cmt} = (e,f)\) is uniformly distributed over \(\mathbb {G} ^2\). Consequently, since  and
and  , we also have that the response \(\mathsf {resp} \) is distributed uniformly and independently (of \(\mathsf {cmt} \) and \(\mathsf {ch} \)) over \(\mathbb {Z} _q\).
, we also have that the response \(\mathsf {resp} \) is distributed uniformly and independently (of \(\mathsf {cmt} \) and \(\mathsf {ch} \)) over \(\mathbb {Z} _q\).We will now take a look at the later distribution. Note that \(\mathsf {ch}\) and \(\mathsf {resp}\) are both uniformly random elements over \(\mathbb {Z} _p\). It remains to show that \(\mathsf {cmt} \) in the simulated transcript is distributed uniformly over \(\mathbb {G} ^2\).
Recall that
 is defined as
is defined as  . Observe that \(\log _g(e) = \mathsf {resp} + \mathsf {ch} \cdot x\) and \(\log _g(f) = \log _g(h) \cdot \left( \mathsf {resp} + \mathsf {ch} \cdot x \right) \). Since
. Observe that \(\log _g(e) = \mathsf {resp} + \mathsf {ch} \cdot x\) and \(\log _g(f) = \log _g(h) \cdot \left( \mathsf {resp} + \mathsf {ch} \cdot x \right) \). Since  and
and  , we have that both \(\log _g(e)\) and \(\log _g(f)\) are distributed uniformly and independently (of \(\mathsf {ch} \) and \(\mathsf {resp} \)) over \(\mathbb {Z} _q\) and thus (e, f) is distributed uniformly over \(\mathbb {G} ^2\). Note that e, f are not distributed independently of each other (as it is the case in the honest transcript).
, we have that both \(\log _g(e)\) and \(\log _g(f)\) are distributed uniformly and independently (of \(\mathsf {ch} \) and \(\mathsf {resp} \)) over \(\mathbb {Z} _q\) and thus (e, f) is distributed uniformly over \(\mathbb {G} ^2\). Note that e, f are not distributed independently of each other (as it is the case in the honest transcript). -
Indistinguishability of keys. As already remarked above, honest keys contain a DDH tuple, whereas lossy keys contain a non-DDH tuple. Therefore, we claim that for every adversary \(\mathcal {A} \) trying to distinguish honest from lossy keys of \(\mathsf {LID} \), we can construct an adversary \(\mathcal {B} \) such that

To prove this claim, we give a construction of \(\mathcal {B} \) running \(\mathcal {A} \) as a subroutine. The adversary \(\mathcal {B} \) receives a tuple (g, h, u, v) such that (u, v) either is a DDH tuple (i.e., \((u,v) \in \mathsf {DDH}(\mathbb {G}, g, h) \)) or not. Then, it uses the algorithm of Lemma 22 to re-randomize (u, v) into N tuples
 such that $$ (u,v) \in \mathsf {DDH}(\mathbb {G}, g, h) \iff \forall i \in [N] : (u^{(i)}, v^{(i)}) \in \mathsf {DDH}(\mathbb {G}, g, h) $$
such that $$ (u,v) \in \mathsf {DDH}(\mathbb {G}, g, h) \iff \forall i \in [N] : (u^{(i)}, v^{(i)}) \in \mathsf {DDH}(\mathbb {G}, g, h) $$and hands \(( pk _i = (g,h,u^{(i)}, v^{(i)}))_{i \in [N]}\) to \(\mathcal {A} \) as input. When \(\mathcal {A} \) halts and outputs a bit b, \(\mathcal {B} \) halts and outputs b as well. Observe that by Lemma 22, we have
$$ \Pr [ \mathcal {B} (g,h,u,v) = 1 ] \ge \Pr [ \mathcal {A} ( pk ^{(1)}, \dotsc , pk ^{(N)}) ] $$with
 ,
,  , and
, and  . Further, we have $$ \Pr [ \mathcal {B} (g,h,\bar{u},\bar{v}) = 1 ] \ge \Pr [ \mathcal {A} ( pk '^{(1)}, \dotsc , pk '^{(N)}) ] $$
. Further, we have $$ \Pr [ \mathcal {B} (g,h,\bar{u},\bar{v}) = 1 ] \ge \Pr [ \mathcal {A} ( pk '^{(1)}, \dotsc , pk '^{(N)}) ] $$with
 ,
,  for every \(i \in [N]\), and
for every \(i \in [N]\), and  . In conclusion, we have
. In conclusion, we have 
-
Lossiness. We claim that the above scheme \(\mathsf {LID} \) is 1/q-lossy. To show this, we first recall a classical result showing the soundness of the protocol to “prove DDH tuples” by Chaum et al. presented above. Namely, we claim that if \(\log _g(u) \ne \log _h(v)\) holds for the public key \( pk = (g,h,u,v)\) (i.e., \( pk \) is a lossy key and \((u,v) \not \in \mathsf {DDH}(\mathbb {G}, g, h) \)), for any commitment \(\mathsf {cmt} \) there can only be at most one challenge \(\mathsf {ch} \) such that the transcript is valid. We prove this statement by contradiction.
Let \(\mathcal {A} \) be an unbounded adversary that on input of a lossy public key
 , outputs commitment \(\mathsf {cmt} = (e,f)\). We now show that \(\mathcal {A} \) can only output a correct \(\mathsf {resp} \) for one \(\mathsf {ch} \) such that \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch}, \mathsf {resp}) = 1\). Suppose that \(\mathcal {A} \) was able to come up with two responses \(\mathsf {resp} _1\) and \(\mathsf {resp} _2\) for two different challenge \(\mathsf {ch} _1 \ne \mathsf {ch} _2\) such that \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch} _1, \mathsf {resp} _1) = 1\) and \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch} _2, \mathsf {resp} _2) = 1\) holds. This implies by the definition of \(\mathsf {LID}.\mathsf {Vrfy} \) that $$ e = g^{\mathsf {resp} _1} u^{\mathsf {ch} _1} = g^{\mathsf {resp} _2} u^{\mathsf {ch} _2} \qquad \text{ and } \qquad f = h^{\mathsf {resp} _1} v^{\mathsf {ch} _1} = h^{\mathsf {resp} _2} v^{\mathsf {ch} _2}. $$
, outputs commitment \(\mathsf {cmt} = (e,f)\). We now show that \(\mathcal {A} \) can only output a correct \(\mathsf {resp} \) for one \(\mathsf {ch} \) such that \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch}, \mathsf {resp}) = 1\). Suppose that \(\mathcal {A} \) was able to come up with two responses \(\mathsf {resp} _1\) and \(\mathsf {resp} _2\) for two different challenge \(\mathsf {ch} _1 \ne \mathsf {ch} _2\) such that \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch} _1, \mathsf {resp} _1) = 1\) and \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch} _2, \mathsf {resp} _2) = 1\) holds. This implies by the definition of \(\mathsf {LID}.\mathsf {Vrfy} \) that $$ e = g^{\mathsf {resp} _1} u^{\mathsf {ch} _1} = g^{\mathsf {resp} _2} u^{\mathsf {ch} _2} \qquad \text{ and } \qquad f = h^{\mathsf {resp} _1} v^{\mathsf {ch} _1} = h^{\mathsf {resp} _2} v^{\mathsf {ch} _2}. $$Equivalently, we get by using the assumption that \(\mathsf {ch} _1 \ne \mathsf {ch} _2\):
$$ \log _g(u) = \frac{(\mathsf {resp} _1 - \mathsf {resp} _2)}{\mathsf {ch} _2 - \mathsf {ch} _1} \qquad \text{ and } \qquad \log _h(v) = \frac{(\mathsf {resp} _1 - \mathsf {resp} _2)}{\mathsf {ch} _2 - \mathsf {ch} _1}. $$However, this is a contraction to the assumption that \(\log _g(u) \ne \log _h(v)\). Thus, \( pk \) must be a lossy key.
Using this, we have that for every commitment \(\mathcal {A} \) outputs, there can only be at most one challenge \(\mathsf {ch} \) such that the adversary generated a valid transcript. Note that we have an unbounded adversary and based on \(\mathsf {cmt} \) and \(\mathsf {ch} \) it can compute a response. As there is only one challenge for \(\mathsf {cmt} \) output by \(\mathcal {A} \) and the challenge is chosen uniformly at random, the adversary can only win with a probability of at most 1/q.
-
Uniqueness with respect to lossy keys. Let \( pk = (g,h,u,v)\) with \((u,v) \not \in \mathsf {DDH}(\mathbb {G}, g, h) \) and \((\mathsf {cmt}, \mathsf {ch}, \mathsf {resp})\) with \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch}, \mathsf {resp}) = 1\). Suppose that there is a \(\mathsf {resp} ' \ne \mathsf {resp} \) such that \(\mathsf {LID}.\mathsf {Vrfy} ( pk , \mathsf {cmt}, \mathsf {ch}, \mathsf {resp} ') = 1\). In this case, we have for \(\mathsf {cmt} = (e,f)\) that
$$ e = g^\mathsf {resp} u^\mathsf {ch} = g^{\mathsf {resp} '} u^\mathsf {ch} \qquad \text{ and } \qquad f = h^\mathsf {resp} v^\mathsf {ch} = h^{\mathsf {resp} '} v^\mathsf {ch}. $$However, this implies that
$$ g^\mathsf {resp} = g^{\mathsf {resp} '} \qquad \text{ and } \qquad h^\mathsf {resp} = h^{\mathsf {resp} '}, $$which implies that \(\mathsf {resp} = \mathsf {resp} '\), contradicting the initial assumption.
-
Min-entropy. For any secret key \( sk \), the commitment
 equals \((g^r,h^r)\) for
equals \((g^r,h^r)\) for  , which is independent of \( sk \). So the min-entropy of \(\mathsf {cmt} \) is \(\alpha =\log _2(q)\).
, which is independent of \( sk \). So the min-entropy of \(\mathsf {cmt} \) is \(\alpha =\log _2(q)\). -
Commitment-recoverable. The verification algorithm of \(\mathsf {LID} \) first recovers a commitment using the simulator and then compares the result with the commitment in the transcript. So \(\mathsf {LID}\) is commitment-recoverable.
-
Injective simulator. For any normal public key \( pk =(g,h,u,v)\), any response \(\mathsf {resp}\) and any challenge \(\mathsf {ch} \ne \mathsf {ch} '\), we have that
$$\begin{aligned} \begin{aligned} \mathsf {LID}.\mathsf {Sim} ( pk , \mathsf {ch}, \mathsf {resp})&= (g^{\mathsf {resp}} u^{\mathsf {ch}}, h^{\mathsf {resp}} v^{\mathsf {ch}}),\\ \mathsf {LID}.\mathsf {Sim} ( pk , \mathsf {ch} ', \mathsf {resp})&= (g^{\mathsf {resp}} u^{\mathsf {ch} '}, h^{\mathsf {resp}} v^{\mathsf {ch} '}). \end{aligned} \end{aligned}$$Thus, if the above two pairs are equal, we must have that \((u^{\mathsf {ch}}, v^{\mathsf {ch}}) = (u^{\mathsf {ch} '}, v^{\mathsf {ch} '})\). That implies \(\mathsf {ch} = \mathsf {ch} '\).
\(\square \)
B Proof of Theorem 21
The following definition is from [1].
Definition 23
(RSA modulus generation algorithm). Let \(\ell _N\) be a positive integer and let \(\mathsf {RSA}_{\ell _N}\) be the set of all tuples \((N,p_1,p_2)\) such that \(N=p_1p_2\) is a \(\ell _N\)-bit number and \(p_1,p_2\) are two distinct primes in the set of \(\ell _N/2\)-bit primes \(\mathbb {P}_{\ell _N/2}\). Let R be any relation on \(p_1\) and \(p_2\), define \(\mathsf {RSA}_{\ell _N}[R]:=\{(N,p_1,p_2)\in \mathsf {RSA}_{\ell _N} \mid R(p_1,p_2)=1\}\).
We can use it to define the n-fold higher residuosity assumption as well as the \(\phi \)-hiding assumption [1, 9, 31].
Definition 24
(n-fold higher residuosity assumption). Let e be a random prime of length \(\ell _e\le \ell _N/4\) and

and let \(\mathsf {HR}_{N}[e]:=\{g^e\bmod N \mid g\in \mathbb {Z} _N^*\}\) be the set of e-th residues modulo N. We define the advantage of any \(\mathcal {A}\) in solving the higher residuosity problem as
where  and
and  . The e-residuosity problem is \((t,\varepsilon )\)-hard if for any \(\mathcal {A}\) with running time at most t, \(\mathsf {Adv}_{}^{n\text {-}\mathsf {HR}} (\mathcal {A})\) is at most \(\varepsilon \).
. The e-residuosity problem is \((t,\varepsilon )\)-hard if for any \(\mathcal {A}\) with running time at most t, \(\mathsf {Adv}_{}^{n\text {-}\mathsf {HR}} (\mathcal {A})\) is at most \(\varepsilon \).
We prove the following lemma.
Lemma 25
For any adversary \(\mathcal {A}\) with running time \(t_\mathcal {A} \) against the n-key-indistinguishability of \(\mathsf {LID}\) in Fig. 2, we can construct an adversary \(\mathcal {B} \) with running time \(t_{\mathcal {B}}\approx t_\mathcal {A} \) such that

Proof
The proof is a straightforward reduction. \(\mathcal {B} \) receives \((N,e,y_{1}, \ldots , y_{n})\) as input and defines the common parameters as (N, e) and
Note that this defines real keys if the \(y_{i}\) are e-th residues, and lossy keys if the \(y_{i}\) are e-th non-residues. \(\square \)
Finally, we can show that the n-fold higher residuosity assumption is tightly implied by the \(\phi \)-hiding assumption, for any polynomially-bounded n.
Definition 26
(\(\phi \)-hiding assumption [1, 9, 31]). Let \(c\le 1/4\) be a constant. For any adversary \(\mathcal {A}\), define the advantage of \(\mathcal {A}\) in solving the \(\phi \)-hiding problem to be
where  ,
,  and
and  . The \(\phi \)-hiding problem is \((t,\varepsilon )\)-hard if for any \(\mathcal {A}\) with running time at most t, \(\mathsf {Adv}_{}^{\phi \text {H}} (\mathcal {A})\) is at most \(\varepsilon \).
. The \(\phi \)-hiding problem is \((t,\varepsilon )\)-hard if for any \(\mathcal {A}\) with running time at most t, \(\mathsf {Adv}_{}^{\phi \text {H}} (\mathcal {A})\) is at most \(\varepsilon \).
Lemma 27
For any adversary \(\mathcal {A}\) with running time \(t_\mathcal {A} \) we can construct an adversary \(\mathcal {B} \) with running time \(t_{\mathcal {B}}\approx t_\mathcal {A} \) such that
Proof
First, we have that
where  and
and  . We can prove the following claim.
. We can prove the following claim.
Claim
\(\left| \Pr [\mathcal {A} (N,e,y_{1}, \ldots , y_{n})=1] - \Pr [\mathcal {A} (N',e,y'_{1}, \ldots , y'_{n})=1] \right| \le \mathsf {Adv}_{}^{\phi \text {H}} (\mathcal {B})\).
The proof is again a very straightforward reduction. \(\mathcal {B} \) receives as input (N, e). It samples  uniformly random and then defines \(y_{i} := x_{i}^{e} \bmod N\) for \(i \in \{1, \ldots , n\}\). Then it runs \(\mathcal {A} \) on input \((N,e,y_{1}, \ldots , y_{n})\) and returns whatever \(\mathcal {A} \) returns.
uniformly random and then defines \(y_{i} := x_{i}^{e} \bmod N\) for \(i \in \{1, \ldots , n\}\). Then it runs \(\mathcal {A} \) on input \((N,e,y_{1}, \ldots , y_{n})\) and returns whatever \(\mathcal {A} \) returns.
Note that if (N, e) is a “lossy” key, so that \(e \mid \phi (N)\), then the \(y_{i}\) are random e-th residues. However, if \(\gcd (e, \phi (N))=1\), then all \(y_{i}\) are random e-th non-residues, since the map \(x \mapsto x^{e} \bmod N\) is a permutation.
Using a similar idea, we can prove that
Claim
\(\left| \Pr [\mathcal {A} (N',e,y'_{1}, \ldots , y'_{n})=1] - \Pr [\mathcal {A} (N,e,y'_{1}, \ldots , y'_{n})=1] \right| \le \mathsf {Adv}_{}^{\phi \text {H}} (\mathcal {B})\).
Putting the two claims together, we have that \(\mathsf {Adv}_{}^{n\text {-}\mathsf {HR}} (\mathcal {A}) \le 2\mathsf {Adv}_{}^{\phi \text {H}} (\mathcal {B})\) and Lemma 27 follows. \(\square \)
Rights and permissions
Copyright information
© 2021 International Association for Cryptologic Research
About this paper
Cite this paper
Diemert, D., Gellert, K., Jager, T., Lyu, L. (2021). More Efficient Digital Signatures with Tight Multi-user Security. In: Garay, J.A. (eds) Public-Key Cryptography – PKC 2021. PKC 2021. Lecture Notes in Computer Science(), vol 12711. Springer, Cham. https://doi.org/10.1007/978-3-030-75248-4_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-75248-4_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-75247-7
Online ISBN: 978-3-030-75248-4
eBook Packages: Computer ScienceComputer Science (R0)





 for each user
for each user  , and N sets of chosen-message queries
, and N sets of chosen-message queries  issued by the adversary. Subsequently, it hands
issued by the adversary. Subsequently, it hands  and adds
and adds  is a probabilistic algorithm that takes as input the secret key and returns a commitment
is a probabilistic algorithm that takes as input the secret key and returns a commitment 
 ,
,  , the distribution of the transcript
, the distribution of the transcript 
 and
and  for all
for all  described below, played between a challenger and an adversary
described below, played between a challenger and an adversary  and sends it to the adversary
and sends it to the adversary  .
.
 and two independent key pairs
and two independent key pairs  and
and  . Then it sets
. Then it sets 
 and sets
and sets 
 and
and 

 . Note that
. Note that 


 , the set of corrupted users
, the set of corrupted users  and an implementation of the random oracle
and an implementation of the random oracle  . It then runs the signature key generation algorithm
. It then runs the signature key generation algorithm  and two independent key pairs
and two independent key pairs  and
and  . Then it sets
. Then it sets  and stores
and stores  , logs (x, y) into set
, logs (x, y) into set  , then computes
, then computes 
 by making a hash query. Then, the game chooses
by making a hash query. Then, the game chooses  and uses the simulator to compute
and uses the simulator to compute  . Finally, the game queries hash oracle to get
. Finally, the game queries hash oracle to get  and then uses
and then uses 
 to
to  to the adversary and logs i in the set
to the adversary and logs i in the set  and queries the hash oracle to get
and queries the hash oracle to get  . Then it recovers
. Then it recovers  and queries the hash oracle to get
and queries the hash oracle to get  . Finally, the game outputs 1 if and only if
. Finally, the game outputs 1 if and only if  .
.
 uniformly at random. It sets
uniformly at random. It sets  and
and  , and outputs
, and outputs  uniformly and independently at random. It outputs
uniformly and independently at random. It outputs 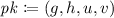 .
. , and computes a commitment
, and computes a commitment  , where g, h are the value of the
, where g, h are the value of the  .
. .
. ,
,  . Then it sets
. Then it sets 
 , and sets
, and sets  and
and 
 and computes
and computes 
 .
. , a message
, a message 
 and computes
and computes  , and computes a commitment
, and computes a commitment  . It outputs
. It outputs  with
with  .
. .
.
 is a not an e-th residue with probability
is a not an e-th residue with probability  be an (honest) key pair and let
be an (honest) key pair and let  ,
,  and
and 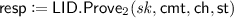 . By definition of the scheme, we have
. By definition of the scheme, we have 

 , and
, and  and
and  , we also have that the response
, we also have that the response  is defined as
is defined as  . Observe that
. Observe that  and
and  , we have that both
, we have that both 
 such that
such that  ,
,  , and
, and  . Further, we have
. Further, we have  ,
,  for every
for every  . In conclusion, we have
. In conclusion, we have 
 , outputs commitment
, outputs commitment  equals
equals  , which is independent of
, which is independent of 