Abstract
We give a taxonomy of computational assumptions in the algebraic group model (AGM). We first analyze Boyen’s Uber assumption family for bilinear groups and then extend it in several ways to cover assumptions as diverse as Gap Diffie-Hellman and LRSW. We show that in the AGM every member of these families is implied by the q-discrete logarithm (DL) assumption, for some q that depends on the degrees of the polynomials defining the Uber assumption.
Using the meta-reduction technique, we then separate \((q+1)\)-DL from q-DL, which yields a classification of all members of the extended Uber-assumption families. We finally show that there are strong assumptions, such as one-more DL, that provably fall outside our classification, by proving that they cannot be reduced from q-DL even in the AGM.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
A central paradigm for assessing the security of a cryptographic scheme or hardness assumption is to analyze it within an idealized model of computation. A line of work initiated by the seminal work of Nechaev [Nec94] introduced the generic group model (GGM) [Sho97, Mau05], in which all algorithms and adversaries are treated as generic algorithms, i.e., algorithms that do not exploit any particular structure of a group and hence can be run in any group. Because for many groups used in cryptography (in particular, groups defined over some elliptic curves), the best known algorithms are in fact generic, the GGM has for many years served as the canonical tool to establish confidence in new cryptographic hardness assumptions. Moreover, when cryptographic schemes have been too difficult to analyze in the standard model, they have also directly been proven secure in the GGM (for example LRSW signatures [LRSW99, CL04]).
Following the approach first used in [ABM15], a more recent work by Fuchsbauer, Kiltz, and Loss [FKL18] introduces the algebraic group model, in which all algorithms are assumed to be algebraic [PV05]. An algebraic algorithm generalizes the notion of a generic algorithm in that all of its output group elements must still be computed by generic operations; however, the algorithm can freely access the structure of the group and obtain more information than what would be possible by purely generic means. This places the AGM between the GGM and the standard model. In contrast to the GGM, one cannot give information-theoretic lower bounds in the AGM; instead, one analyzes the security of a scheme by giving security reductions from computational hardness assumptions.
Because of its generality and because it provides a powerful framework that simplifies the security analyses of complex systems, the AGM has readily been adopted, in particular in the context of SNARK systems [FKL18, MBKM19, Lip19, GWC19]. It has also recently been used to analyze blind (Schnorr) signatures [FPS20], which are notoriously difficult to prove secure in the standard or random oracle model. Another recent work by Agrikola, Hofheinz and Kastner [AHK20] furthermore shows that the AGM constitutes a plausible model, which is instantiable under falsifiable assumptions in the standard model.
Since its inception, many proofs in the AGM have followed a similar structure, which often consists of a series of tedious case distinctions. A natural question is whether it is possible to unify a large body of relevant hardness assumptions under a general ‘Uber’ assumption. This would avoid having to prove a reduction to a more well-studied hardness assumption for each of them in the AGM separately. In this work, we present a very rich framework of such Uber assumptions, which contain, as special cases, reductions between hardness assumptions in the AGM from prior work [FKL18, Los19]. We also show that there exists a natural hierarchy among Uber assumptions of different strengths. Together, our results give an almost complete classification in the AGM of common hardness assumptions over (bilinear) groups of prime order.
1.1 Boyen’s Uber Assumption Framework
The starting point of our generalizations is the Uber assumption framework by Boyen
[Boy08], which serves as an umbrella assumption in the bilinear GGM. Consider a bilinear group \(\mathcal {G}= (\mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, e, p)\), where \(\mathbb {G}_i\) is a group of prime order p and \(e:\mathbb {G}_1\times \mathbb {G}_2\rightarrow \mathbb {G}_T\) is a (non-degenerate) bilinear map, and let \(g_1\), \(g_2\) and \(g_T\) be generators of \(\mathbb {G}_1\), \(\mathbb {G}_2\) and \(\mathbb {G}_T\), respectively. Boyen’s framework captures assumptions that are parametrized by polynomials \(R_1,\ldots ,R_r,S_1,\ldots ,S_s, T_1,\ldots ,T_t\) and F in a set of formal variables \(X_1,\ldots ,X_m\) as follows. The challenger picks a vector of randomly chosen points  and gives the adversary a list of group elements
and gives the adversary a list of group elements
The adversary is considered successful it is able to compute \(g_T^{F(\vec {x})}\). Note that for this not to be trivially computable, F must be independent from \(\vec {R},\vec {S}\) and \(\vec {T}\). That is, it must not be a linear combination of elements from \(\vec {T}\) and (pairwise products of) elements of \(\vec {R}\) and \(\vec {S}\); otherwise, \(g_T^{F(x)}\) could be computed from the given group elements via group operations and the bilinear map.
Boyen gives lower bounds for this family of assumptions following the common proof paradigm within the GGM. He also extends the idea of this first Uber assumption [BBG05] with a fixed target polynomial F to an adaptive version called flexible Uber Assumption, in which the adversary can choose the target polynomial F itself (as long as it satisfies the same notion of independence from \(\vec R\), \(\vec S\) and \(\vec T\) that makes computing \(g_T^{F(\vec x)}\) non-trivial). Finally, Boyen proposes an extension of his bounds to assumptions in which the elements of \((\vec R, \vec S, \vec T)\) and F may be rational fractions, that is, fractions of polynomials. We start with considering a straightforward generalization of Boyen’s framework where the solution the adversary must find can also be in one of the source groups, that is, of the form \(g_1^{F_1(\vec x)}\) or \(g_2^{F_2(\vec x)}\), as long as they satisfy some non-triviality conditions (Definition 5). We next discuss the details of our adaptation of (our generalization of) Boyen’s framework to the AGM.
1.2 An Uber-Assumption Framework for the AGM
The main challenge in analyzing Boyen’s framework in the AGM setting is that we can no longer prove lower bounds as in the GGM. The next best thing would be to reduce the Uber assumption to a well-established assumption such as the discrete logarithm (DLog) assumption. Due to the general nature of the Uber assumption, this turns out to be impossible; in particular, our negative result (see below) establishes that algebraic reductions in the AGM can only reduce DLog to Uber assumptions that are defined by linear polynomials.
Indeed, as for Boyen’s [Boy08] proofs in the GGM, the degrees of the involved polynomials are expected to appear in our reductions. In our first theorem in Sect. 3 we show that in the AGM any Uber assumption is implied by a parametrized variant of the discrete logarithm problem: in the q-DLog problem the adversary, on top of the instance \(g^z\), is also given \(g^{z^2},\ldots ,g^{z^q}\) and must compute z. We prove that if the maximum total degree of the challenge polynomials in \((\vec R, \vec S, \vec T)\) of an Uber assumption is at most q, then it is implied by the hardness of the q-DLog problem. This establishes that under q-DLog, anything that is not trivially computable from a given instance (represented by \((\vec R, \vec S, \vec T)\)) is infeasible to compute. We prove this by generalizing a technique first used by Fuchsbauer et al. [FKL18] to prove soundness of Groth’s SNARK [Gro16] under the q-DLog assumption in the AGM.
Proof idea. To convey our main idea, consider a simple instance of the Uber assumption parametrized by polynomials \(R_1,\ldots ,R_r,F_1\) and let \(\vec S=\vec T=\emptyset \). That is, the adversary is given group elements \(\mathbf {U}_1=g_1^{R_1(\vec x)},\dots ,\mathbf {U}_r = g_1^{R_r(\vec x)}\) for a random \(\vec x\) and must compute \(\mathbf {U}'=g_1^{F_1(\vec x)}\). For this problem to be non-trivial, \(F_1\) must be linearly independent of \(R_1,\dots ,R_r\), that is, for all  we have \(R'(\vec X)\ne \sum _i a_i R_i(\vec X)\).
we have \(R'(\vec X)\ne \sum _i a_i R_i(\vec X)\).
Since the adversary is assumed to be algebraic (see Definition 2), it computes its output \(\mathbf {U}'\) from its inputs \(\mathbf {U}_1,\dots ,\mathbf {U}_r\) by generic group operations, that is, for some vector \(\vec \mu \) we have \(\mathbf {U}' = \prod _i \mathbf {U}_i^{\mu _i}\). In the AGM, the adversary is assumed to output this vector \(\vec \mu \). Taking the logarithm of the previous equation yields
Since \(R'\) is independent from \(\vec R\), the polynomial \(P(\vec X):= R'(\vec X) - \sum _i \mu _i R_i(\vec X)\) is non-zero. On the other hand, (1) yields \(P(\vec x) = 0\) for a successful adversary.
The adversary has thus (implicitly) found a non-zero polynomial P, which has the secret \(\vec x\) among its roots. Now, in order to use this to solve a q-DLog instance \((g_1,g_1^z,\dots ,g_1^{z^q})\), we embed a randomized version of z into every coordinate of \(\vec x\). In particular, for random vectors \(\vec y\) and \(\vec v\), we implicitly let \(x_i:=y_iz+v_i\bmod p\). By leveraging linearity, the reduction can compute the group elements \(\mathbf {U}_i=g_1^{R_i(\vec x)}\), etc, from its DLog instance.
If \(P(\vec X)\) is non-zero then \(Q(Z):=P(y_1Z+v_1,\ldots ,y_mZ+v_m)\) is non-zero with overwhelming probability: the values \(v_i\) guarantee that the values \(y_i\) are perfectly hidden from the adversary and, as we show (Lemma 1), the leading coefficient of Q is a non-zero polynomial evaluated at \(y_1,\ldots ,y_m\), values that are independent of the adversary’s behavior. Schwartz-Zippel thus bounds the probability that the leading coefficient of Q is zero, and thus, that \(Q\equiv 0\). Since \(Q(z)=P(\vec x)=0\), we can factor the univariate polynomial Q and find the DLog solution z, which is among its roots.
Extensions. We next extend our approach to a flexible (i.e., adaptive) version of the static Uber assumption, where the adversary can adaptively choose the polynomials (Sect. 4) as well as a generalization from polynomials to rational fractions (Sect. 5). We combine the flexible framework with the rational fraction framework in Sect. 6. After these generalizations, our framework covers assumptions such as strong Diffie-Hellman [BB08], where the adversary must compute a rational fraction of its own choice in the exponent.
In a next step (Sect. 7), we extend our framework to also cover gap-type assumptions such as Gap Diffie-Hellman (GDH) [OP01], which was recently proven equivalent to the DLog assumption in the AGM by Loss [Los19]. GDH states that the CDH assumption remains true even when the DDH assumption no longer holds. Informally, the idea of the proof given in [Los19] (first presented in [FKL18] for a restricted version of GDH) is to argue that the DDH oracle given to an algebraic adversary is useless, unless the adversary succeeds in breaking CDH during an oracle query. The reduction simulates the DDH oracle by always returning false. We generalize this to a broader class of assumptions, using a different simulation strategy, which avoids a security loss.
We also present (Sect. 8) an extension of our (adaptive) framework that allows to capture assumptions as strong as the LRSW assumption [LRSW99], which forms the basis of the Camenisch-Lysyanskaya signature scheme [CL04]. The LRSW assumption falls outside (even the adaptive version of) Boyen’s Uber framework, since the adversary need not output the polynomial it is computing in the exponent.
The LRSW and GDH assumptions were previously studied in the AGM in the works of [FKL18, Los19], who gave very technical proofs spanning multiple pages of case distinctions. By comparison, our Uber Framework offers a more general and much simpler proof for both of these assumptions. Finally, we are able to prove all these results using tight reductions. This, in particular, improves upon the non-tight reduction of DLog to LRSW in [FKL18].
1.3 Classifying Assumptions in Our Framework
Finally, we prove two separation results that show the following:
Separating \(\varvec{(q+1)}\)-DLog from \(\textit{\textbf{q}}\)-DLog. This shows that with respect to currently known (i.e., algebraic) reduction techniques, the Uber assumption, for increasing degrees of the polynomials, defines a natural hierarchy of assumptions in the AGM. More concretely, the q-lowest class within the established hierarchy consists of all assumptions that are covered by a specific instantiation of the Uber assumption which can be reduced from the q-DLog problem. Our separation result (Theorem 7) shows that there is no algebraic reduction from the q-DLog problem to the \((q+1)\)-DLog problem in the AGM. This implies that assumptions within different classes are separated with respect to algebraic reductions. Interestingly, we are even able to show our separation for reductions that can rewind and choose the random coins of the solver for the \((q+1)\)-DLog problem freely.
Separating OMDL from \(\textit{\textbf{q}}\)-DLog. Our second result (Theorem 8) shows a separation result between the one-more-DLog problem (OMDL) (where the adversary has to solve q DLog instances and is given an oracle that computes discrete logarithms, which it can access \(q-1\) times) and the q-DLog problem (for any q) in the AGM. Our result strengthens a previous result by Bresson, Monnerat, and Vergnaud [BMV08], who showed a separation between the discrete logarithm problem (i.e, where \(q=1\)) and the 2-one-more-DLog problem with respect to black-box reductions. By comparison, our result holds even in the AGM, where reductions are inherently non-black-box, as the AGM implicitly assumes an efficient extractor algorithm that extracts algebraic coefficients from the algebraic adversary. As the extractor is non-black-box (since it depends on the algebraic adversary), neither is any reduction that non-trivially leverages the AGM.
Our result clearly establishes the limits of our framework, as it excludes the OMDL family of assumptions. Unlike our first separation, this one comes with the caveat that it only applies to reductions that are “black-box in the AGM”, meaning that they simply obtain the algebraic coefficients via the extractor, but cannot rewind the adversary or choose its random coins.
1.4 Related Work
A long line of research has considered frameworks to capture general classes of assumptions. We give an overview of the most closely related works. The first Uber assumptions were introduced by Boyen et al. [BBG05, Boy08]. Others later gave alternative concepts to classify assumptions within cyclic groups. The works of Chase et al. [CM14, CMM16] study assumptions in bilinear groups of composite order, which are not considered in the original Uber framework. They show that several q-type assumptions are implied by (static) “subgroup-hiding” assumptions. This gives evidence that this type of assumption, which is specific to composite-order groups, is particularly strong.
More recently, Ghadafi and Groth [GG17] studied a broader class of assumptions in which the adversary must compute a group element from \(\mathbb {G}_T\). Like our work, their framework applies to prime-order groups and extends to the case where the exponents can be described by rational fractions, and they also separate classes of assumptions from each other. However, their framework only deals with non-interactive assumptions, which do not cover the adaptive type of assumptions we study in our flexible variants (in fact, the authors mention extending their work to interactive assumptions as an open problem [GG17]). Their work does not cover assumptions such as GDH or LRSW, which we view as particularly interesting (and challenging) to classify. Indeed, our framework appears to be the first in this line of work that offers a classification comprising this type of assumptions.
A key difference is that Ghadafi and Groth’s results are in the standard model whereas we work in the AGM. While this yields stronger results for reductions, their separations are weaker (in addition to separating less broad types of Uber assumptions), as they are with respect to generic reductions, whereas ours hold against algebraic reductions that can assume that the adversary is algebraic. Furthermore, their work considers black-box reductions that treat the underlying solver as an (imperfect) oracle, while we show the non-existence of reductions in the AGM, which are, by definition, non-black-box (see above). A final difference to the work of [GG17] lies in the tightness of all our reductions, whereas non of theirs are tight.
At CT-RSA’19 Mizuide, Takayasu, and Takagi [MTT19] studied static (i.e., non-flexible) variants and generalizations of the Diffie-Hellman problem in prime-order groups (also with extensions to the bilinear setting) by extending proofs from [FKL18] in the obvious manner. Most of their results are special cases of our Uber assumption framework. Concretely, when restricting the degrees of all input polynomials to 1 in our static Uber Assumption, our non-triviality condition implies all corresponding theorems in their paper (except the ones relating to Matrix assumptions, which are outside the scope of this work). By our separation of q-DLog for different q, our results for higher degrees do not follow from theirs by currently known techniques. Finally, they do not cover the flexible (adaptive) variants nor oracle-enhanced- and hidden-polynomial-type assumptions (such as GDH and LRSW).
A further distinction that sets our work apart from these prior works is our formulation of the aforementioned ‘hidden-type’ assumptions, where we allow the adversary to solve the problem with respect to a group generator of its own choice instead of the one provided by the game. A recent work [BMZ19] shows that even in the GGM, allowing randomly chosen generators results in unexpected complications when proving lower bounds. Similarly, giving the adversary this additional freedom makes proving (and formalizing) our results more challenging. We also give this freedom to the reductions that we study (and prove impossible) in our separation results.
2 Algebraic Algorithms and Preliminaries
Algorithms. We denote by  the uniform sampling of the variable s from the (finite) set S. All our algorithms are probabilistic (unless stated otherwise) and written in uppercase letters \(\mathsf {A},\mathsf {B}\). To indicate that algorithm \(\mathsf {A}\) runs on some inputs \(\left( x_1,\ldots ,x_n\right) \) and returns y, we write
the uniform sampling of the variable s from the (finite) set S. All our algorithms are probabilistic (unless stated otherwise) and written in uppercase letters \(\mathsf {A},\mathsf {B}\). To indicate that algorithm \(\mathsf {A}\) runs on some inputs \(\left( x_1,\ldots ,x_n\right) \) and returns y, we write  . If \(\mathsf {A}\) has access to an algorithm \(\mathsf {B}\) (via oracle access) during its execution, we write
. If \(\mathsf {A}\) has access to an algorithm \(\mathsf {B}\) (via oracle access) during its execution, we write  .
.
Polynomials and rational fractions. We denote polynomials by uppercase letters P, Q and specify them by a list of their coefficients. If m is an integer, we denote by  the set of m-variate polynomials with coefficients in
the set of m-variate polynomials with coefficients in  and by
and by  the set of rational fractions in m variables with coefficients in
the set of rational fractions in m variables with coefficients in  . We define the total degree of a polynomial
. We define the total degree of a polynomial  as \(\max \limits _{~~\vec i \in \mathbb {N}^m\,:\, \lambda _{i_1,\ldots ,i_m} \not \equiv _p 0} \big \{ \sum _{j=1}^m i_j\big \}\).
as \(\max \limits _{~~\vec i \in \mathbb {N}^m\,:\, \lambda _{i_1,\ldots ,i_m} \not \equiv _p 0} \big \{ \sum _{j=1}^m i_j\big \}\).
For the degree of rational fractions we will use the “French” definition
[AW98]: for  we define
we define
This definition has the following properties: The degree does not depend on the choice of the representative; it generalizes the definition for polynomials; and the following holds: \(\deg (F_1 \cdot F_2) = \deg F_1 + \deg F_2 \), and \(\deg (F_1 + F_2) \le \max \{\deg F_1, \deg F_2 \}\).
We state the following technical lemma, which we will use in our reductions and prove in the full version.
Lemma 1
Let P be a non-zero multivariate polynomial in  of total degree d. Define
of total degree d. Define  as \(Q(Z) := P(Y_1 Z + V_1,\dots , Y_m Z + V_m)\). Then the coefficient of maximal degree of Q is a polynomial in
as \(Q(Z) := P(Y_1 Z + V_1,\dots , Y_m Z + V_m)\). Then the coefficient of maximal degree of Q is a polynomial in  of degree d.
of degree d.
We will use the following version of the Schwartz-Zippel lemma [DL77]:
Lemma 2
Let  be a non-zero polynomial of total degree d. Let \(r_1,\ldots , r_m\) be selected at random independently and uniformly from
be a non-zero polynomial of total degree d. Let \(r_1,\ldots , r_m\) be selected at random independently and uniformly from  . Then \(\Pr \big [P(r_1,\ldots ,r_m)\equiv _p 0\big ]\le \textstyle \frac{d}{p-1}.\)
. Then \(\Pr \big [P(r_1,\ldots ,r_m)\equiv _p 0\big ]\le \textstyle \frac{d}{p-1}.\)
Bilinear Groups. We next state the definition of a bilinear group.
Definition 1
(Bilinear group). A bilinear group (description) is a tuple \(\mathcal {G}= (\mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, e, \phi , \psi ,p)\) such that
-
\(\mathbb {G}_i\) is a cyclic group of prime order p, for \(i\in \{1,2,T\}\);
-
e is a non-degenerate bilinear map \(e:\mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\), that is, for all
 and all generators \(g_1\) of \(\mathbb {G}_1\) and \(g_2\) of \(\mathbb {G}_2\) we have that \(g_T:=e(g_1,g_2)\) generates \(\mathbb {G}_T\) and \(e(g_1^a,g_2^b) = e(g_1,g_2)^{ab}=g_T^{ab}\);
and all generators \(g_1\) of \(\mathbb {G}_1\) and \(g_2\) of \(\mathbb {G}_2\) we have that \(g_T:=e(g_1,g_2)\) generates \(\mathbb {G}_T\) and \(e(g_1^a,g_2^b) = e(g_1,g_2)^{ab}=g_T^{ab}\); -
\(\phi \) is an isomorphism \(\phi :\mathbb {G}_1\rightarrow \mathbb {G}_2\), and \(\psi \) is an isomorphism \(\psi :\mathbb {G}_2 \rightarrow \mathbb {G}_1\).
All group operations and the bilinear map e must be efficiently computable. \(\mathcal {G}\) is of Type 1 if the maps \(\phi \) and \(\psi \) are efficiently computable; \(\mathcal {G}\) is of Type 2 if there is no efficiently computable map \(\phi \); and \(\mathcal {G}\) is of Type 3 if there are no efficiently computable maps \(\phi \) and \(\psi \). We require that there exist an efficient algorithm \(\mathsf {GenSamp}\) that returns generators \(g_1\) of \(\mathbb {G}_1\) and \(g_2\) of \(\mathbb {G}_2\), so that \(g_2\) is uniformly random, and (for Types 1 and 2) \(g_1=\psi (g_2)\) or (Type 3) \(g_1\) is also uniformly random. By \(\mathsf {GenSamp}_i\) we denote a restricted version that only returns \(g_i\).
In the following, we fix a bilinear group \(\mathcal {G}= (\mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, e, \phi , \psi ,p)\).
(Algebraic) Security games. We use a variant of (code-based) security games [BR04]. In game \(\mathbf {G}_{\mathcal {G}}\) (defined relative to \(\mathcal {G}\)), an adversary \(\mathsf {A}\) interacts with a challenger that answers oracle queries issued by \(\mathsf {A}\). The game has a main procedure and (possibly zero) oracle procedures which describe how oracle queries are answered. We denote the output of a game \(\mathbf {G}_{\mathcal {G}}\) between a challenger and an adversary \(\mathsf {A}\) by \(\mathbf {G}_{\mathcal {G}}^{\mathsf {A}}.\) \(\mathsf {A}\) is said to win if \(\mathbf {G}_{\mathcal {G}}^{\mathsf {A}}=1.\) We define the advantage of \(\mathsf {A}\) in \(\mathbf {G}_{\mathcal {G}}\) as \(\mathbf {Adv}^{\mathbf {G}}_{\mathcal {G},\mathsf {A}}:=\Pr \big [\mathbf {G}_{\mathcal {G}}^{\mathsf {A}}=1\big ]\) and the running time of \(\mathbf {G}_{\mathcal {G}}^{\mathsf {A}}\) as \(\mathbf {Time^{\mathbf {G}}_{\mathcal {G},\mathsf {A}}}\). In this work, we are primarily concerned with algebraic security games \(\mathbf {G}_{\mathcal {G}}^{}\), in which we syntactically distinguish between elements of groups \(\mathbb {G}_1,\mathbb {G}_2\) and \(\mathbb {G}_T\) (written in bold, uppercase letters, e.g., \(\mathbf {Z}\)) and all other elements, which must not depend on any group elements.
We next define algebraic algorithms. Intuitively, the only way for an algebraic algorithm to output a new group element \(\mathbf {Z}\) is to derive it via group operations from known group elements.
Definition 2
(Algebraic algorithm for bilinear groups). An algorithm \(\mathsf {A}_\mathsf {alg}\) executed in an algebraic game \(\mathbf {G}_{\mathcal {G}}^{}\) is called algebraic if for all group elements \(\mathbf {Z}\in \mathbb {G}\) (where \(\mathbb {G}\in \{\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T\}\)) that \(\mathsf {A}_\mathsf {alg}\) outputs, it additionally provides a representation in terms of received group elements in \(\mathbb {G}\) and those from groups from which there is an efficient mapping to \(\mathbb {G}\); in particular: if \(\mathbf {U}_0,\ldots ,\mathbf {U}_\ell \in \mathbb {G}_1\), \(\mathbf {V}_0,\ldots ,\mathbf {V}_m\in \mathbb {G}_2\) and \(\mathbf {W}_0,\ldots ,\mathbf {W}_t\in \mathbb {G}_T\) are the group elements received so far then \(\mathsf {A_{alg}}\) provides vectors \(\vec \mu ,\vec \nu ,\vec \zeta ,\vec \eta ,\vec \delta \) and matrices \(A=(\alpha _{i,j}),B=(\beta _{i,j}),\varGamma =(\gamma _{i,j})\) such that

We remark that oracle access to an algorithm \(\mathsf {B}\) in the AGM includes any (usually non-black-box) access to \(\mathsf {B}\) that is needed to extract the algebraic coefficients. Thus, our notion of black-box access in the AGM mainly rules out techniques such as rewinding \(\mathsf {B}\) or running it on non-uniform random coins.
2.1 Generic Security Games and Algorithms
Generic algorithms \(\mathsf {A}_\mathsf {gen}\) are only allowed to use generic properties of a group. Informally, an algorithm is generic if it works regardless of what group it is run in. This is usually modeled by giving an algorithm indirect access to group elements via abstract handles. It is straight-forward to translate all of our algebraic games into games that are syntactically compatible with generic algorithms accessing group elements only via abstract handles. We measure the running times of generic algorithms as queries to an oracle that implements the abstract group operation, i.e., every query accounts for one step of the algorithm. We highlight this difference by denoting the running time of a generic algorithm with the letter o rather than t. We say that winning algebraic game \(\mathbf {G}_{\mathcal {G}}^{}\) is \((\varepsilon ,o)\)-hard in the generic group model if for every generic algorithm \(\mathsf {A}_\mathsf {gen}\) it holds that
As all of our reductions run the adversary only once and without rewinding, the overhead in the running time of our reductions is additive only. We make the reasonable assumption that, compared to the running time of the adversary, this is typically small, and therefore ignore the losses in the running times for this work in order to keep notational overhead low.
We assume that a generic algorithm \(\mathsf {A}_\mathsf {gen}\) provides the representation of \(\mathbf {Z}\) relative to all previously received group elements, for all group elements \(\mathbf {Z}\) that it outputs. This assumption is w.l.o.g. since a generic algorithm can only obtain new group elements by querying two known group elements to the generic group oracle; hence a reduction can always extract a valid representation of a group element output by a generic algorithm. This way, every generic algorithm is also an algebraic algorithm.
Furthermore, if \(\mathsf {B}_\mathsf {gen}\) is a generic oracle algorithm and \(\mathsf {A}_\mathsf {alg}\) is an algebraic algorithm, then \(\mathsf {B}_\mathsf {alg}:=\mathsf {B}_\mathsf {gen}^{\mathsf {A}_\mathsf {alg}}\ \) is also an algebraic algorithm. We refer to [Mau05] for more on generic algorithms.
Security Reductions. All our security reductions are (bilinear) generic algorithms, which allows us to compose all of our reductions with hardness bounds in the (bilinear) generic group model (see next paragraph). Let \(\mathbf {G}_\mathcal {G},\mathbf {H}_\mathcal {G}\) be security games. We say that algorithm \(\mathsf {R_{gen}}\) is a generic \((\varDelta ^{(\cdot )}_{\varepsilon },\varDelta ^{(+)}_{\varepsilon },\varDelta ^{(\cdot )}_o,\varDelta ^{(+)}_{o})\)-reduction from \(\mathbf {H}_\mathcal {G}\) to \(\mathbf {G}_\mathcal {G}\) if \(\mathsf {R_{gen}}\) is generic and if for every algebraic algorithm \(\mathsf {A_{alg}}\), algorithm \(\mathsf {B_{alg}}\) defined as \(\mathsf {B_{alg}}:= \mathsf {R^\mathsf {A_{alg}}_{gen}}\) satisfies
Furthermore, for simplicity of notation, we will make the convention of referring to \(\big (1,\varDelta _{\varepsilon },1,\varDelta _o\big )\)-reductions as \((\varDelta _{\varepsilon },\varDelta _o)\)-reductions.
Composing information-theoretic lower bounds with reductions in the AGM. The following lemma from [Los19] explains how statements in the AGM compose with bounds from the GGM.
Lemma 3
Let \(\mathbf {G}_\mathcal {G}\) and \(\mathbf {H}_\mathcal {G}\) be algebraic security games and let \(\mathsf {R_{gen}}\) be a generic \(\big (\varDelta ^{(\cdot )}_{\varepsilon },\varDelta ^{(+)}_{\varepsilon },\varDelta ^{(\cdot )}_o,\varDelta ^{(+)}_{o}\big )\)-reduction from \(\mathbf {H}_\mathcal {G}\) to \(\mathbf {G}_\mathcal {G}\). If \(\mathbf {H}_\mathcal {G}\) is \((\varepsilon ,o)\)-secure in the GGM, then \(\mathbf {G}_\mathcal {G}\) is \((\varepsilon ',o')\)-secure in the GGM where
The q -discrete logarithm assumption and variants. For this work, we consider two generalizations of the DLog assumption, which are parametrized (i.e., “q-type”) variants of the DLog assumption. We describe them via the algebraic security games
 and
and
 in Fig. 1.
in Fig. 1.
The following Lemma, which follows similarly to the generic security of q-SDH in [BB08], is proved (asymptotically) in [Lip12]. For completeness, we give a concrete proof in the full version.
Lemma 4
Let \(o, q_1, q_2 \in \mathbb {N}\), let \(q:= \max \{q_1, q_2\}\). Then q-DLog and \((q_1, q_2)\)-DLog are \(\big (\frac{\left( o + q + 1\right) ^2q}{p-1}, o\big )\)-secure in the bilinear generic group model.
We remark that all though our composition results are stated in the bilinear GGM, it is straight forward to translate them to the standard GGM if the associated hardness assumption is stated over a pairing-free group. This is true, because in those cases, our reductions will also be pairing-free and hence are standard generic algorithms themselves.
3 The Uber-Assumption Family
Boyen [Boy08] extended the Uber-assumption framework he initially introduced with Boneh and Goh [BBG05]. We start with defining notions of independence for polynomials and rational fractions (of which polynomials are a special case):
Definition 3
Let  and
and  . We say that W is linearly dependent on \(\vec R\) if there exist coefficients
. We say that W is linearly dependent on \(\vec R\) if there exist coefficients  such that \( W = \sum _{i=1}^r a_{i}R_i. \) We say that W is (linearly) independent from \(\vec R\) if it is not linearly dependent on \(\vec R\).
such that \( W = \sum _{i=1}^r a_{i}R_i. \) We say that W is (linearly) independent from \(\vec R\) if it is not linearly dependent on \(\vec R\).
Definition 4
(
[Boy08]). Let \(\vec R\), \(\vec S\), \(\vec F\) and W be vectors of rational fractions from  of length r, s, f and 1, respectively. We say that W is (“bilinearly”) dependent on \((\vec R, \vec S, \vec F)\) if there exist coefficients \(\{a_{i,j}\}\), \(\{b_{i,j}\}\), \(\{c_{i,j}\}\) and \(\{d_k\}\) in
of length r, s, f and 1, respectively. We say that W is (“bilinearly”) dependent on \((\vec R, \vec S, \vec F)\) if there exist coefficients \(\{a_{i,j}\}\), \(\{b_{i,j}\}\), \(\{c_{i,j}\}\) and \(\{d_k\}\) in  such that
such that
We call the dependency of Type 2 if \(b_{i,j}=0\) for all i, j and of Type 3 if \(b_{i,j}=c_{i,j}=0\) for all i, j. Else, it is of Type 1. We say that W is (Type-\(\tau \)) independent from \((\vec R, \vec S, \vec F)\) if it is not (Type-\(\tau \)) dependent on \((\vec R, \vec S, \vec F)\). (Thus, W can be Type-3 independent but Type-2 dependent.)
Consider the Uber-assumption game in Fig. 2, which is parametrized by vectors of polynomials \(\vec R\), \(\vec S\) and \(\vec F\) and polynomials \(R'\), \(S'\) and \(F'\). For a random vector \(\vec x\), the adversary receives the evaluation of the (vectors of) polynomials in the exponents of the generators \(g_1\), \(g_2\) and \(g_T\); its goal is to find the evaluation of the polynomials \(R'\), \(S'\) and \(F'\) at \(\vec x\) in the exponents. Note that we do not explicitly give the generators to the adversary. This is without loss of generality because we can always set \(R_1 = S_1 = F_1 \equiv 1\).
It is easily seen that the game can be efficiently solved if one of the following conditions hold (where we distinguish the different types of bilinear groups and interpret all polynomials over \(\mathbb {Z}_p\)):
-
(Type 1) If \(R'\) is dependent on \(\vec R\) and \(\vec S\), and \(S'\) is dependent on \(\vec R\) and \(\vec S\), and \(F'\) is Type-1 dependent (Definition 4) on \((\vec R,\vec S,\vec F)\).
-
(Type 2) If \(R'\) is dependent on \(\vec R\) and \(\vec S\), \(S'\) is dependent on \(\vec S\), and \(F'\) is Type-2 dependent (Definition 4) on \((\vec R,\vec S,\vec F)\).
-
(Type 3) If \(R'\) is dependent on \(\vec R\), \(S'\) is dependent on \(\vec S\), and \(F'\) is Type-3 dependent (Definition 4) on \((\vec R,\vec S,\vec F)\).
For example, in Type-2 groups, if \(R'=\sum _i a'_i R_i + \sum _i b'_i S_i\) and \(S'=1\), and \(F'= \sum _i\sum _j a_{i,j}R_iS_i + \sum _i\sum _j c_{i,j}S_iS_j\), then from a challenge \((\vec {\mathbf {U}},\vec {\mathbf {V}},\vec {\mathbf {W}})\), one can easily compute a solution \(\mathbf {U}':=\prod _i \mathbf {U}_i^{a'_i}\cdot \psi (\prod _i\mathbf {V}_i^{b'_i})\), \(\mathbf {V}':=g_2\), \(\mathbf {W}':=\prod _i\prod _j e(\mathbf {U}_i,\mathbf {V}_j)^{a_{i,j}}\cdot \prod _i\prod _j e(\psi (\mathbf {V}_i),\mathbf {V}_j)^{b_{i,j}}\).
In our main theorem, we show that whenever the game in Fig. 2 cannot be trivially won, then for groups of Type \(\tau \in \{1,2\}\), it can be reduced from
 , and for Type-3 groups, it can be reduced from
, and for Type-3 groups, it can be reduced from
 (for appropriate values of \(q,q_1,q_2\)). To state the theorem for all types of groups, we first define the following non-triviality condition (which again we state for the more general case of rational fractions):
(for appropriate values of \(q,q_1,q_2\)). To state the theorem for all types of groups, we first define the following non-triviality condition (which again we state for the more general case of rational fractions):
Definition 5
(Non-triviality). Let  ,
,  ,
,  . We say that the tuple \((\vec R,\vec S,\vec F,R',S',F')\) is non-trivial for groups of type \(\tau \), for \(\tau \in \{1,2,3\}\), if:
. We say that the tuple \((\vec R,\vec S,\vec F,R',S',F')\) is non-trivial for groups of type \(\tau \), for \(\tau \in \{1,2,3\}\), if:

We have argued above that if the tuple \((\vec R,\vec S,\vec F,R',S',F')\) is trivial then the \((\vec R,\vec S,\vec F,R',S',F')\)-
 problem is trivial to solve, even with a generic algorithm. In Theorem 1 we now show that if the tuple is non-trivial then the corresponding Uber assumption holds for algebraic algorithms, as long as a type of q-DLog assumption holds (whose type depends on the type of bilinear group).
problem is trivial to solve, even with a generic algorithm. In Theorem 1 we now show that if the tuple is non-trivial then the corresponding Uber assumption holds for algebraic algorithms, as long as a type of q-DLog assumption holds (whose type depends on the type of bilinear group).
The (additive) security loss of the reduction depends on the degrees of the polynomials involved (as well as the group type and its order). E.g., in Type-3 groups, if \(R'\) is independent of \(\vec R\) then the probability that the reduction fails is the maximum degree of \(R'\) and the components of \(\vec R\), divided by the order of \(\mathcal {G}\). In Type-1 and Type-2 groups, due to the homomorphism \(\psi \), the loss depends on the maximum degree of \(R'\), \(\vec R\) and \(\vec S\). Similar bounds hold when \(S'\) is independent of \(\vec S\) (and \(\vec R\) for Type 1); and slightly more involved ones for the independence of \(F'\). If several of \(R',S'\) and \(F'\) are independent then the reduction chooses the strategy that minimizes the security loss.
Definition 6
(Degree of non-trivial tuple of polynomials). Let \((\vec R,\vec S,\vec F,R',S',F')\) be a non-trivial tuple of polynomials in  . Define \(d_{\vec R} := \max \{\deg R_i \}_{1 \le i \le r}\), \(d_{\vec S} := \max \{\deg S_i \}_{1 \le i \le s} \), \(d_{\vec F} := \max \{\deg F_i \}_{1 \le i \le f}\). We define the type-\(\tau \) degree \(d_\tau \) of \((\vec R,\vec S,\vec F,R',S',F')\) as follows:
. Define \(d_{\vec R} := \max \{\deg R_i \}_{1 \le i \le r}\), \(d_{\vec S} := \max \{\deg S_i \}_{1 \le i \le s} \), \(d_{\vec F} := \max \{\deg F_i \}_{1 \le i \le f}\). We define the type-\(\tau \) degree \(d_\tau \) of \((\vec R,\vec S,\vec F,R',S',F')\) as follows:

If \((\tau ,i)\) does not hold, we set \(d_{\tau ,i}:=\infty \) and define \(d_\tau :=\min \{d_{\tau .1},d_{\tau .2},d_{\tau .T}\}\). (By non-triviality, \(d_\tau <\infty \).)
Theorem 1 (DLog implies Uber in the AGM)
Let \(\mathcal {G}\) be of type \(\tau \in \{1,2,3\}\) and  be a tuple of polynomials that is non-trivial for type \(\tau \) and define \(d_{\vec R} := \max \{\deg R_i \}\), \(d_{\vec S} := \max \{\deg S_i \}\), \(d_{\vec F} := \max \{\deg F_i \}\). Let \(q,q_1,q_2\) be such that \(q \ge \max \{d_{\vec R}, d_{\vec S}, {d_{\vec F}}/{2}\}\) as well as \(q_1\ge d_{\vec R}\), \(q_2\ge d_{\vec S}\) and \(q_1+q_2\ge d_{\vec F}\). If
be a tuple of polynomials that is non-trivial for type \(\tau \) and define \(d_{\vec R} := \max \{\deg R_i \}\), \(d_{\vec S} := \max \{\deg S_i \}\), \(d_{\vec F} := \max \{\deg F_i \}\). Let \(q,q_1,q_2\) be such that \(q \ge \max \{d_{\vec R}, d_{\vec S}, {d_{\vec F}}/{2}\}\) as well as \(q_1\ge d_{\vec R}\), \(q_2\ge d_{\vec S}\) and \(q_1+q_2\ge d_{\vec F}\). If
-
(Type 1)
 or
or
 is \((\varepsilon ,t)\)-secure in the AGM,
is \((\varepsilon ,t)\)-secure in the AGM, -
(Type 2)
 is \((\varepsilon ,t)\)-secure in the AGM,
is \((\varepsilon ,t)\)-secure in the AGM, -
(Type 3)
 is \((\varepsilon ,t)\)-secure in the AGM,
is \((\varepsilon ,t)\)-secure in the AGM,
then
 is \((\varepsilon '\!,t')\)-secure in the AGM with
is \((\varepsilon '\!,t')\)-secure in the AGM with
where \(d_\tau \) is the maximal degree of \((\vec R,\vec S,\vec F,R',S',F')\), as defined in Definition 6, \(o_1 := o_0 + 2 + (2\lfloor \log _2(p) \rfloor ) ((d_{\vec R}+ 1)r + (d_{\vec S}+1)s + (d_{\vec F}+1)f + d_\tau ) + r d_{\vec R} + s d_{\vec S} + f d_{\vec F} \) with \(o_0 := d_{\vec {R}} + d_{\vec {F}} + 2\) for Types 1 and 2, and \(o_0 := d_{\vec {F}}+ 1\) for in Type 3.
Proof
We give a detailed proof for Type-2 bilinear groups and then explain how to adapt it to Types 1 and 3. For  and \(i\in \{1,2,T\}\) we let \([u]_i\) denote \(g_i^u\).
and \(i\in \{1,2,T\}\) we let \([u]_i\) denote \(g_i^u\).
Let \(\mathsf {A}_\mathsf {alg}\) be an algebraic algorithm against
 that wins with advantage \(\varepsilon \) in time t. We construct a generic reduction with oracle access to \(\mathsf {A}_\mathsf {alg}\), which yields an algebraic adversary \(\mathsf {B}_\mathsf {alg}\) against
that wins with advantage \(\varepsilon \) in time t. We construct a generic reduction with oracle access to \(\mathsf {A}_\mathsf {alg}\), which yields an algebraic adversary \(\mathsf {B}_\mathsf {alg}\) against
 . There are three (non-exclusive) reasons for \((\vec R,\vec S,\vec F,R',S',F')\) being non-trivial, which correspond to conditions (2.1), (2.2) and (2.T) in Definition 5. Each condition enables a different type of reduction, of which \(\mathsf {B_{alg}}\) runs the one that minimizes \(d_2\) from Definition 6.
. There are three (non-exclusive) reasons for \((\vec R,\vec S,\vec F,R',S',F')\) being non-trivial, which correspond to conditions (2.1), (2.2) and (2.T) in Definition 5. Each condition enables a different type of reduction, of which \(\mathsf {B_{alg}}\) runs the one that minimizes \(d_2\) from Definition 6.
We start with Case (2.1), that is, \(R'\) is linearly independent from \(\vec {R}\) and \(\vec S\).
-
Adversary \(\mathsf {B}_\mathsf {alg}(g_2,\mathbf {Z}_1,\dots ,\mathbf {Z}_q)\): On input a problem instance of game
 with \(\mathbf {Z}_i = [z^i]_2\), \(\mathsf {B}_\mathsf {alg}\) simulates
with \(\mathbf {Z}_i = [z^i]_2\), \(\mathsf {B}_\mathsf {alg}\) simulates
 for \(\mathsf {A}_\mathsf {alg}\). It defines \(g_1\leftarrow \psi (g_2)\) and \(g_T\leftarrow e(g_1,g_2)\). Then, it picks random values
for \(\mathsf {A}_\mathsf {alg}\). It defines \(g_1\leftarrow \psi (g_2)\) and \(g_T\leftarrow e(g_1,g_2)\). Then, it picks random values  and
and  , implicitly sets \(x_i:=y_iz + v_i \bmod p\) and computes \(\vec {\mathbf {U}} := [\vec {R}\left( x_1, \dots , x_m \right) ]_1\), \(\vec {\mathbf {V}} := [\vec {S}\left( x_1, \dots , x_m \right) ]_2\), \( \vec {\mathbf {W}} := [\vec {F}\left( x_1, \dots , x_m \right) ]_T\) from its q-DLog instance, the isomorphism \(\psi :\mathbb {G}_2 \rightarrow \mathbb {G}_1\) and the pairing \(e:\mathbb {G}_1\times \mathbb {G}_2\rightarrow \mathbb {G}_T\). It can do so efficiently since the total degrees of the polynomials in \(\vec R\), \(\vec S\) and \(\vec F\) are bounded by q, q and 2q respectively.Footnote 1 Next, \(\mathsf {B_{alg}}\) runs
, implicitly sets \(x_i:=y_iz + v_i \bmod p\) and computes \(\vec {\mathbf {U}} := [\vec {R}\left( x_1, \dots , x_m \right) ]_1\), \(\vec {\mathbf {V}} := [\vec {S}\left( x_1, \dots , x_m \right) ]_2\), \( \vec {\mathbf {W}} := [\vec {F}\left( x_1, \dots , x_m \right) ]_T\) from its q-DLog instance, the isomorphism \(\psi :\mathbb {G}_2 \rightarrow \mathbb {G}_1\) and the pairing \(e:\mathbb {G}_1\times \mathbb {G}_2\rightarrow \mathbb {G}_T\). It can do so efficiently since the total degrees of the polynomials in \(\vec R\), \(\vec S\) and \(\vec F\) are bounded by q, q and 2q respectively.Footnote 1 Next, \(\mathsf {B_{alg}}\) runs  . Since \(\mathsf {A_{alg}}\) is algebraic, it also returns vectors and matrices \(\vec \mu ,\vec \nu ,\vec \zeta ,\vec \delta ,A=(\alpha _{i,j})_{i,j}\), \(\varGamma =(\gamma _{i,j})_{i,j}\) such that $$\begin{aligned} \mathbf {U}'&= \textstyle \prod _i\mathbf {U}_i^{\mu _i} \cdot \prod _i\psi (\mathbf {V}_i)^{\nu _i} \end{aligned}$$(2a)$$\begin{aligned} \mathbf {V}'&= \textstyle \prod _i\mathbf {V}_i^{\eta _i} \end{aligned}$$(2b)$$\begin{aligned} \mathbf {W}'&= \textstyle \prod _i\prod _j e\big (\mathbf {U}_i,\mathbf {V}_j\big )^{\alpha _{i,j}} \cdot \prod _i\prod _j e\big (\psi (\mathbf {V}_i),\mathbf {V}_j\big )^{\gamma _{i,j}} \cdot \prod _i\mathbf {W}_i^{\delta _i}. \end{aligned}$$(2c)
. Since \(\mathsf {A_{alg}}\) is algebraic, it also returns vectors and matrices \(\vec \mu ,\vec \nu ,\vec \zeta ,\vec \delta ,A=(\alpha _{i,j})_{i,j}\), \(\varGamma =(\gamma _{i,j})_{i,j}\) such that $$\begin{aligned} \mathbf {U}'&= \textstyle \prod _i\mathbf {U}_i^{\mu _i} \cdot \prod _i\psi (\mathbf {V}_i)^{\nu _i} \end{aligned}$$(2a)$$\begin{aligned} \mathbf {V}'&= \textstyle \prod _i\mathbf {V}_i^{\eta _i} \end{aligned}$$(2b)$$\begin{aligned} \mathbf {W}'&= \textstyle \prod _i\prod _j e\big (\mathbf {U}_i,\mathbf {V}_j\big )^{\alpha _{i,j}} \cdot \prod _i\prod _j e\big (\psi (\mathbf {V}_i),\mathbf {V}_j\big )^{\gamma _{i,j}} \cdot \prod _i\mathbf {W}_i^{\delta _i}. \end{aligned}$$(2c)\(\mathsf {B}_\mathsf {alg}\) then computes the following multivariate polynomial, which corresponds to the exponents of (2a):
$$\begin{aligned} \textstyle P_1(\vec X) = R'(\vec X) - \sum _{i=1}^r \mu _i R_i(\vec X) - \sum _{i=1}^s \nu _i S_i(\vec X), \end{aligned}$$(3)which is non-zero because in Case (2.1) \(R'\) is independent from \(\vec R\) and \(\vec S\). From \(P_1\), it defines the univariate polynomial
$$\begin{aligned} Q_1(Z) := P_1(y_1Z + v_1,\dots ,y_mZ + v_m ). \end{aligned}$$(4)If \(Q_1\) is the zero polynomial then \(\mathsf {B_{alg}}\) aborts. \((*)\)
Else, it factors \(Q_1\) to obtain its roots \(z_1,\ldots \) (of which there are at most \(\max \{\deg R',d_{\vec R},d_{\vec S}\}\); we analyse the degree of \(Q_1\) below). If for one of them we have \(g_2^{z_i} = \mathbf {Z}\), then \(\mathsf {B_{alg}}\) returns \(z_i\).
We analyze \(\mathsf {B_{alg}}\)’s success probability. First note that \(\mathsf {B_{alg}}\) perfectly simulates game
 , as the values \(x_i\) are uniformly distributed in
, as the values \(x_i\) are uniformly distributed in  and \(\vec {\mathbf {U}}\), \(\vec {\mathbf {V}}\) and \(\vec {\mathbf {W}}\) are correctly computed.
and \(\vec {\mathbf {U}}\), \(\vec {\mathbf {V}}\) and \(\vec {\mathbf {W}}\) are correctly computed.
Moreover, if \(\mathsf {B_{alg}}\) does not abort in \((*)\) and \(\mathsf {A_{alg}}\) wins game
 , then \(\mathbf {U}' = [R'(\vec x)]_1\). On the other hand,
, then \(\mathbf {U}' = [R'(\vec x)]_1\). On the other hand,
Together, this means that \(P_1(\vec x)\equiv _p 0\) and since \(x_i \equiv _p y_iz+v_i\), moreover \(Q_1(z)\equiv _p 0\). By factoring \(Q_1\), reduction \(\mathsf {B_{alg}}\) finds thus the solution z.
It remains to bound the probability that \(\mathsf {B_{alg}}\) aborts in \((*)\), that is, the event that \(0\equiv Q_1(Z) = P_1 \left( y_1Z+ v_1,\dots ,y_mZ + v_m\right) \). Interpreting \(Q_1\) as an element from  , Lemma 1 yields that its maximal coefficient is a polynomial \(Q^\text {max}_1\) in \(Y_1,\ldots ,Y_m\) whose degree is the same as the maximal (total) degree d of \(P_1\). From \(P_1\not \equiv 0\) and \(P_1(\vec x)=0\), we have \(d>0\).
, Lemma 1 yields that its maximal coefficient is a polynomial \(Q^\text {max}_1\) in \(Y_1,\ldots ,Y_m\) whose degree is the same as the maximal (total) degree d of \(P_1\). From \(P_1\not \equiv 0\) and \(P_1(\vec x)=0\), we have \(d>0\).
We note that the values \(y_1z,\ldots ,y_mz\) are completely hidden from \(\mathsf {A_{alg}}\) because they are “one-time-padded” with \(v_1,\ldots ,v_m\), respectively. This means that the values \((\vec \mu ,\vec \nu )\) returned by \(\mathsf {A_{alg}}\) are independent from \(\vec {y}\). Since \(\vec {y}\) is moreover independent from \(R'\), \(\vec {R}\) and \(\vec S\), it is also independent from \(P_1, Q_1\) and \(Q^\text {max}_1\). The probability that \(Q_1\equiv 0\) is thus upper-bounded by the probability that its maximal coefficient \(Q^\text {max}_1(\vec y)\equiv _p 0\) when evaluated at the random point \(\vec y\). By the Schwartz-Zippel lemma, the probability that \(Q_1(Z)\equiv 0\) is thus upper-bounded by \(\frac{d}{p-1}\). The degree d of \(Q_1\) (and thus of \(Q^\text {max}_1\)) is upper-bounded by the total degrees of \(P_1\), which is \(\max \{d_R',d_{\vec R},d_{\vec S}\}=d_{2.1}\) in Definition 6. \(\mathsf {B_{alg}}\) thus aborts in line (*) with probability at most \(\frac{d_{2,1}}{p-1}\).
Case (2.2), that is, \(S'\) is linearly independent from \(\vec S\), follows completely analogously, but with \(d=d_{2.2}=\max \{d_{S'},d_{\vec S}\}\).
Case (2.T), when \(F'\) is type-2-independent of \(\vec R\), \(\vec S\) and \(\vec F\), is also analogous; we highlight the necessary changes: From \(\mathsf {A_{alg}}\)’s representation  for \(\mathbf {W}'\) (see (2c)), that is,
for \(\mathbf {W}'\) (see (2c)), that is,
Analogously to (3) we define
which is of degree at most \(d_{2.T}:= \max \{\deg F',d_{\vec R}+ d_{\vec S},2\cdot d_{\vec S},d_{\vec F}\}\). Polynomial \(P_T\) is non-zero by Type-2-independence of \(F'\) (Definition 4). The reduction also computes \(Q_T(Z) := P_T(y_1Z + v_1,\dots ,y_mZ + v_m )\).
If \(\mathsf {A_{alg}}\) wins then \(\mathbf {W}'=[F'(\vec x)]_T\), which together with (5) implies that \(P_T(\vec x) \equiv _p 0\) and thus \(Q_T(z) \equiv _p 0\). Reduction \(\mathsf {B_{alg}}\) can find z by factoring \(Q_T\); unless \(Q_T(Z)\equiv 0\), which by an analysis analogous to the one for case (2.1) happens with probability \(\frac{d_{2.T}}{p-1}\). (We detail the reduction for the case where \(\mathbf {W}'\) is independent in the proof of Theorem 3, which proves a more general statement.)
Theorem 1 for Type-2 groups now follows because
 and \(\mathsf {B_{alg}}\) follows the type of reduction that minimizes its abort probability to \(\min \big \{\frac{d_{2.1}}{p-1},\frac{d_{2.2}}{p-1},\frac{d_{2.T}}{p-1}\big \}=\frac{d_2}{p-1}\).
and \(\mathsf {B_{alg}}\) follows the type of reduction that minimizes its abort probability to \(\min \big \{\frac{d_{2.1}}{p-1},\frac{d_{2.2}}{p-1},\frac{d_{2.T}}{p-1}\big \}=\frac{d_2}{p-1}\).
Groups of Type 1 and 3. The reduction for bilinear groups of Type 1 to
 is almost the same proof. The only change is that for Case (1.T) the polynomial \(P_T\) in (6) has an extra term \(-\sum _{i=1}^r\sum _{j=1}^r \beta _{i,j} R_i(\vec X)R_j(\vec X)\), because of the representation of \(\mathbf {W}'\) in Type-1 groups (see Definition 2); the degree of \(P_T\) is then bounded by \(\max \{\deg F',2\, d_{\vec R},2\, d_{\vec S},d_{\vec F}\}\). Analogously for Case (1.2), \(S'\) can now depend on \(\vec S\) as well as \(\vec R\). The reduction for Type-1 groups to
is almost the same proof. The only change is that for Case (1.T) the polynomial \(P_T\) in (6) has an extra term \(-\sum _{i=1}^r\sum _{j=1}^r \beta _{i,j} R_i(\vec X)R_j(\vec X)\), because of the representation of \(\mathbf {W}'\) in Type-1 groups (see Definition 2); the degree of \(P_T\) is then bounded by \(\max \{\deg F',2\, d_{\vec R},2\, d_{\vec S},d_{\vec F}\}\). Analogously for Case (1.2), \(S'\) can now depend on \(\vec S\) as well as \(\vec R\). The reduction for Type-1 groups to
 is completely symmetric by swapping the roles of \(\mathbb {G}_1\) and \(\mathbb {G}_2\) and replacing \(\psi \) by \(\phi \).
is completely symmetric by swapping the roles of \(\mathbb {G}_1\) and \(\mathbb {G}_2\) and replacing \(\psi \) by \(\phi \).
The reduction for Type-3 groups relies on the
 assumption, as it requires \(\{[z_i]_1\}_{i=1}^{q_1}\) and \(\{[z_i]_2\}_{i=1}^{q_2}\) to simulate \(\{[R_i(\vec x)]_1\}_{i=1}^r\) and \(\{[S_i(\vec x)]_2\}_{i=1}^s\). without using any homomorphism \(\phi \) or \(\psi \). Apart from this, the proof is again analogous. (We treat the Type-3 case in detail in the proof of Theorem 3.) In the full version we detail the analysis of the running times of these reductions. \(\square \)
assumption, as it requires \(\{[z_i]_1\}_{i=1}^{q_1}\) and \(\{[z_i]_2\}_{i=1}^{q_2}\) to simulate \(\{[R_i(\vec x)]_1\}_{i=1}^r\) and \(\{[S_i(\vec x)]_2\}_{i=1}^s\). without using any homomorphism \(\phi \) or \(\psi \). Apart from this, the proof is again analogous. (We treat the Type-3 case in detail in the proof of Theorem 3.) In the full version we detail the analysis of the running times of these reductions. \(\square \)
Using Lemmas 3 and 4 we obtain the following corollary to Theorem 1:
Corollary 1
Let \(\mathcal {G}\) be of type \(\tau \) and \((\vec R,\vec S,\vec F,R',S',F')\) be non-trivial for \(\tau \) of maximal degree \(d_\tau \). Then
 is \(\big (\frac{(o + o_1 +1+q)^2q}{p-1} + \frac{d_\tau }{p-1},o \big )\)-secure in the generic bilinear group model.
is \(\big (\frac{(o + o_1 +1+q)^2q}{p-1} + \frac{d_\tau }{p-1},o \big )\)-secure in the generic bilinear group model.
Comparison to previous GGM results. Boneh, Boyen and Goh [BBG05, Theorem A.2] claim that the decisional Uber assumption for the particular case \(r=s\) and \(f=0\) is \(\big (\frac{(o + 2r + 2)^2q}{2p},o\big )\)-secure in the generic group model, and with the same reasoning, one can obtain the more general bound \(\big (\frac{(o + r + s + f+ 2)^2q}{2p},o\big )\). Note that the loss in their bound is only linear in the maximum degree while ours cubic. Our looser bound is a result of our reduction, whereas Boneh, Boyen and Goh prove their bound directly in the GGM.Footnote 2
4 The Flexible Uber Assumption
Boyen [Boy08] generalizes the Uber assumption framework to flexible assumptions, where the adversary can define the target polynomials (\(R',S'\) and \(F'\) in Fig. 2) itself, conditioned on the solution not being trivially computable from the instance, for non-triviality as in Definition 5. In Sect. 6 we consider this kind of flexible Uber assumption in our generalization to rational fractions and thereby cover assumptions like q-strong Diffie-Hellman [BB08].
For polynomials, we generalize this further by allowing the adversary to also (adaptively) choose the polynomials that constitute the challenge. The adversary is provided with an oracle that takes input a value \(i\in \{1,2,T\}\) and a polynomial \(P(\vec X)\) of the adversary’s choice, and returns \(g_i^{P(\vec x)}\), where \(\vec x\) is the secret value chosen during the game. The adversary then wins if it returns polynomials \((R^*,S^*,F^*)\), which are independent from its queries, and \(\big (g_1^{R^*(\vec x )}\!,g_2^{S^*(\vec x )}\!,g_T^{F^*(\vec x)}\big )\). The game for this flexible Uber assumption is specified in Fig. 3.
Theorem 2
Let \(m\ge 1\), let \(\mathcal {G}\) be a bilinear-group of type \(\tau \in \{1,2,3\}\) and consider an adversary \(\mathsf {A_{alg}}\) in game
 . Let \(d'_1,d'_2,d'_T, d^*_1, d^*_2, d^*_T\) be such that \(\mathsf {A_{alg}}\)’s queries \((i,P(\vec X))\) satisfy \(\deg P \le d'_i\) and its output values \(R^*,S^*,F^*\) satisfy \(\deg R^*\le d^*_1\), \(\deg S^*\le d^*_2\), \(\deg F^*\le d^*_T\). Let \(q,q_1,q_2\) be such that \(q \ge \max \{d'_1, d'_2, d'_T/{2}\}\) as well as \(q_1\ge d'_1\), \(q_2\ge d'_2\) and \(q_1+q_2\ge d'_T\). If
. Let \(d'_1,d'_2,d'_T, d^*_1, d^*_2, d^*_T\) be such that \(\mathsf {A_{alg}}\)’s queries \((i,P(\vec X))\) satisfy \(\deg P \le d'_i\) and its output values \(R^*,S^*,F^*\) satisfy \(\deg R^*\le d^*_1\), \(\deg S^*\le d^*_2\), \(\deg F^*\le d^*_T\). Let \(q,q_1,q_2\) be such that \(q \ge \max \{d'_1, d'_2, d'_T/{2}\}\) as well as \(q_1\ge d'_1\), \(q_2\ge d'_2\) and \(q_1+q_2\ge d'_T\). If
-
(Type 1)
 or
or
 is \((\varepsilon ,t)\)-secure in the AGM,
is \((\varepsilon ,t)\)-secure in the AGM, -
(Type 2)
 is \((\varepsilon ,t)\)-secure in the AGM,
is \((\varepsilon ,t)\)-secure in the AGM, -
(Type 3)
 is \((\varepsilon ,t)\)-secure in the AGM,
is \((\varepsilon ,t)\)-secure in the AGM,
then
 is \((\varepsilon '\!,t')\)-secure in the AGM with
is \((\varepsilon '\!,t')\)-secure in the AGM with
where \(d_\tau \) is as in Definition 6 after the following replacements: \(d_{\vec R}\leftarrow d'_1\), \(d_{\vec S}\leftarrow d'_2\), \(d_{\vec F}\leftarrow d'_F\), \(\deg R'\leftarrow d^*_1\), \(\deg S'\leftarrow d^*_2\) and \(\deg F'\leftarrow d^*_T\).
Proof (sketch)
Inspecting the proof of Theorem 1, note that the values \([R_i(\vec x)]_1\), \([S_i(\vec x)]_2\) and \([F_i(\vec x)]_T\) need not be known in advance and can be computed by the reduction at any point, as long as the degrees of \(R_i\) and \(S_i\) are bounded by q and those of \(F_i\) by 2q. The adversary could thus specify the polynomials via oracle calls and the reduction can compute \(\mathbf {U}_i\), \(\mathbf {V}_i\) and \(\mathbf {F}_i\) on the fly.
Likewise, the polynomials \(P_1\), \(P_2\) and \(P_T\) (and their univariate counterparts which the reduction factors) are only defined after \(\mathsf {A_{alg}}\) stops; therefore, \(R'\), \(S'\) and \(F'\), from which they are defined, need only be known then. The proof of Theorem 1 is thus adapted to prove Theorem 2 in a very straightforward way. \(\square \)
5 The Uber Assumption for Rational Fractions
Reconsider the Uber assumption in Fig. 2, but now let \(\vec R,\vec S,\vec F,R',S'\) and \(F'\) be rational fractions over  rather than polynomials. We will show that even this generalization of the Uber assumption is implied by q-DLog assumptions. We start with introducing some notation. We view a rational fraction as defined by two polynomials, its numerator and its denominator, and assume that the fraction is reduced. For a rational fraction
rather than polynomials. We will show that even this generalization of the Uber assumption is implied by q-DLog assumptions. We start with introducing some notation. We view a rational fraction as defined by two polynomials, its numerator and its denominator, and assume that the fraction is reduced. For a rational fraction  , we denote its numerator by \(\hat{R}\) and its denominator by \(\check{R}\). That is
, we denote its numerator by \(\hat{R}\) and its denominator by \(\check{R}\). That is  are such that \(R=\hat{R}/\check{R}\). As rational fractions are not defined everywhere, we modify the game from Fig. 2 so the adversary wins should the experiment choose an input \(\vec x\) for which one of the rational fractions is not defined. The rational-fraction uber game is given in Fig. 4.
are such that \(R=\hat{R}/\check{R}\). As rational fractions are not defined everywhere, we modify the game from Fig. 2 so the adversary wins should the experiment choose an input \(\vec x\) for which one of the rational fractions is not defined. The rational-fraction uber game is given in Fig. 4.
For a vector of rational fractions  , we define its common denominator
, we define its common denominator  as a least common multiple of the denominators of the components of \(\vec R\). In particular, fix an algorithm LCM that given a set of polynomials returns a least common multiple of them. Then we define:
as a least common multiple of the denominators of the components of \(\vec R\). In particular, fix an algorithm LCM that given a set of polynomials returns a least common multiple of them. Then we define:

We let \(\check{d}_{\vec R}\) denote the degree of  and \( d_{\vec R}\) denote the maximal degree of the elements of \(\vec R\), that is \( d_{\vec R}:=\max \{\deg ( R_1),\dots ,\deg ( R_r)\}\). Note that this integer could be negative and is lower bounded by \(-\check{d}_{\vec R}\). The security loss in Theorem 3 depends on the type of the bilinear group, the reason for the tuple \((\vec R,\vec S,\vec F,R',S',F')\) being non-trivial, as well as the degrees of the numerators and denominators of the involved rational fractions. We summarize this in the following technical definition.
and \( d_{\vec R}\) denote the maximal degree of the elements of \(\vec R\), that is \( d_{\vec R}:=\max \{\deg ( R_1),\dots ,\deg ( R_r)\}\). Note that this integer could be negative and is lower bounded by \(-\check{d}_{\vec R}\). The security loss in Theorem 3 depends on the type of the bilinear group, the reason for the tuple \((\vec R,\vec S,\vec F,R',S',F')\) being non-trivial, as well as the degrees of the numerators and denominators of the involved rational fractions. We summarize this in the following technical definition.
Definition 7
(Degree of non-trivial tuple of rational fractions). Let \((\vec R,\vec S,\vec F,R',S',F')\) be a non-trivial tuple whose elements are rational fractions in  . Let \(d_{\mathrm{den}}:= \check{d}_{\vec R\Vert \vec S\Vert \vec F\Vert R'\Vert S'\Vert F'}\). We define the type-\(\tau \) degree \(d_\tau \) of \((\vec R,\vec S,\vec F,R',S',F')\) as follows, distinguishing the kinds of non-triviality defined in Definition 5.
. Let \(d_{\mathrm{den}}:= \check{d}_{\vec R\Vert \vec S\Vert \vec F\Vert R'\Vert S'\Vert F'}\). We define the type-\(\tau \) degree \(d_\tau \) of \((\vec R,\vec S,\vec F,R',S',F')\) as follows, distinguishing the kinds of non-triviality defined in Definition 5.
-
(Type 1)
-
If (1.1) holds, let \(d_{1.1}:= d_{\mathrm{den}} + \check{d}_{R'} + \check{d}_{\vec R\Vert \vec S} + \max \{d_{R^\prime }, d_{\vec R}, d_{\vec S}\}\)
-
if (1.2) holds, let \(d_{1.2}:=d_{\mathrm{den}} + \check{d}_{S'} + \check{d}_{\vec R\Vert \vec S} + \max \{ d_{S^\prime }, d_{\vec R}, d_{\vec S}\}\)
-
if (1.T) holds, \(d_{1.T}:= d_{\mathrm{den}} + \check{d}_{F'} + \check{d}_{\vec R\Vert \vec S\Vert \vec F} + \check{d}_{\vec R\Vert \vec S} + \max \{ d_{F^\prime }, 2d_{\vec S}, 2d_{\vec R}, d_{\vec F}\}\)
-
-
(Type 2)
-
If (2.1) holds, let \(d_{2.1}:= d_{\mathrm{den}} + \check{d}_{R'} +\check{d}_{\vec R\Vert \vec S} + \max \{d_{R^\prime }, d_{\vec R}, d_{\vec S} \}\)
-
if (2.2) holds, let \(d_{2.2}:= d_{\mathrm{den}} + \check{d}_{S'} + \check{d}_{\vec S} + \max \{d_{S^\prime }, d_{\vec S} \}\)
-
if (2.T) holds, \(d_{2.T}:= d_{\mathrm{den}} + \check{d}_{F'} + \check{d}_{\vec R\Vert \vec S \Vert \vec F} + \check{d}_{\vec S} + \max \{ d_{F^\prime }, 2d_{\vec S}, d_{\vec R} + d_{\vec S}, d_{\vec F}\}\)
-
-
(Type 3)
-
If (3.1) holds, let \(d_{3.1}:= d_{\mathrm{den}} + \check{d}_{R'} + \check{d}_{\vec R} + \max \{d_{R^\prime }, d_{\vec R} \}\)
-
if (3.2) holds, let \(d_{3.2}:= d_{\mathrm{den}} + \check{d}_{S'} + \check{d}_{\vec S}+ \max \{d_{S^\prime }, d_{\vec S}\}\)
-
if (3.T) holds, \(d_{3.T}:=d_{\mathrm{den}} + \check{d}_{F'} + \check{d}_{\vec R \Vert \vec F} + \check{d}_{\vec S} + \max \{ d_{F^\prime }, d_{\vec R} + d_{\vec S}, d_{\vec F}\}\)
-
If \((\tau ,i)\) does not hold, set \(d_{\tau ,i}:=\infty \). Define \(d_\tau :=\min \{d_{\tau .1},d_{\tau .2},d_{\tau .T}\}\).
Theorem 3 (DLog implies Uber for rational fractions in the AGM)
Let \(\mathcal {G}\) be a bilinear group of type \(\tau \in \{1,2,3\}\) and let  be a tuple that is non-trivial for type \(\tau \) (Definition 5). Let \(q,q_1\) and \(q_2\) be such that \(q\ge \check{d}_{\vec R\Vert \vec S\Vert \vec F} + \max \{ d_{\vec R}, d_{\vec S}, d_{\vec F}/{2}\}\) and \(q_1\ge \check{d}_{\vec R\Vert \vec F} + d_{\vec R}\) and \(q_2\ge \check{d}_{\vec S} + d_{\vec S}\) and \(q_1+q_2\ge \check{d}_{\vec R\Vert \vec F} + \check{d}_{\vec S} + d_{\vec F}\). If
be a tuple that is non-trivial for type \(\tau \) (Definition 5). Let \(q,q_1\) and \(q_2\) be such that \(q\ge \check{d}_{\vec R\Vert \vec S\Vert \vec F} + \max \{ d_{\vec R}, d_{\vec S}, d_{\vec F}/{2}\}\) and \(q_1\ge \check{d}_{\vec R\Vert \vec F} + d_{\vec R}\) and \(q_2\ge \check{d}_{\vec S} + d_{\vec S}\) and \(q_1+q_2\ge \check{d}_{\vec R\Vert \vec F} + \check{d}_{\vec S} + d_{\vec F}\). If
-
(Type 1)
 or
or
 is \((\varepsilon ,t)\)-secure in the AGM,
is \((\varepsilon ,t)\)-secure in the AGM, -
(Type 2)
 is \((\varepsilon ,t)\)-secure in the AGM,
is \((\varepsilon ,t)\)-secure in the AGM, -
(Type 3)
 is \((\varepsilon ,t)\)-secure in the AGM,
is \((\varepsilon ,t)\)-secure in the AGM,
then
 , as defined in Fig. 4, is \((\varepsilon '\!,t')\)-secure in the AGM with
, as defined in Fig. 4, is \((\varepsilon '\!,t')\)-secure in the AGM with
where \(d_\tau \) is the maximal degree of \((\vec R,\vec S,\vec F,R',S',F')\), as defined in Definition 7.
The proof extends the ideas used to prove Theorem 1 by employing a technique from
[BB08]. Consider a group of Type 1 or 2. The reduction computes  , a least common multiple of the denominators of the instance. Given a q-DLog instance \(g_2, g_2^z, g_2^{z^2}, \ldots \), it first implicitly sets \(x_i:=y_iz+v_i \bmod p\), then it checks whether any denominator evaluates to zero at \(\vec x\) (this entails the additive loss \(d_{\mathrm{den}}\)). Then it computes a new random generator \(h_2:=g_2^{D(y_1z+v_1,\ldots ,y_mz+v_m)}\) and \(h_1:=\psi (h_2)\). For rational fractions \(S_i=\hat{S}_i/\check{S}_i\), it then uses \(h_1,h_2\) to compute the Uber challenge elements \(h_2^{S_i(\vec x)}\) as \(g_2^{\overline{S}(\vec x)}\) for the polynomial \(\overline{S}(\vec X):=(\hat{S}_i\cdot D/\check{S}_i)(\vec X)\), and likewise for \(R_i\) and \(F_i\). This explains the lower bound on q in the theorem statement. When the adversary returns a group element \(h_i^{R'(\vec x)}\) so that \(R'\) is non-trivial, then from the algebraic representations of this element we can define a polynomial (which with overwhelming probability is non-zero) that vanishes at z. The difference here is that we expand by the denominator of \(R'\) in order to obtain a polynomial. The degree of this polynomial is bounded by the values in Definition 7, which also bound the failure probability of the reduction. In Type-3 groups, the reduction can set
, a least common multiple of the denominators of the instance. Given a q-DLog instance \(g_2, g_2^z, g_2^{z^2}, \ldots \), it first implicitly sets \(x_i:=y_iz+v_i \bmod p\), then it checks whether any denominator evaluates to zero at \(\vec x\) (this entails the additive loss \(d_{\mathrm{den}}\)). Then it computes a new random generator \(h_2:=g_2^{D(y_1z+v_1,\ldots ,y_mz+v_m)}\) and \(h_1:=\psi (h_2)\). For rational fractions \(S_i=\hat{S}_i/\check{S}_i\), it then uses \(h_1,h_2\) to compute the Uber challenge elements \(h_2^{S_i(\vec x)}\) as \(g_2^{\overline{S}(\vec x)}\) for the polynomial \(\overline{S}(\vec X):=(\hat{S}_i\cdot D/\check{S}_i)(\vec X)\), and likewise for \(R_i\) and \(F_i\). This explains the lower bound on q in the theorem statement. When the adversary returns a group element \(h_i^{R'(\vec x)}\) so that \(R'\) is non-trivial, then from the algebraic representations of this element we can define a polynomial (which with overwhelming probability is non-zero) that vanishes at z. The difference here is that we expand by the denominator of \(R'\) in order to obtain a polynomial. The degree of this polynomial is bounded by the values in Definition 7, which also bound the failure probability of the reduction. In Type-3 groups, the reduction can set  and
and  , which leads to better bounds. We detail this case in our proof of Theorem 3, which can be found in the full version due to space constraints.
, which leads to better bounds. We detail this case in our proof of Theorem 3, which can be found in the full version due to space constraints.
6 The Uber Assumption for Rational Fractions and Flexible Targets
For rational fractions, we can also define a flexible generalization, where the adversary can choose the target polynomials \(R',S'\) and \(F'\) in Fig. 2 itself, conditioned on the tuple \((\vec R,\vec S,\vec F, R', S', F')\) being non-trivial. The game is specified in Fig. 5. This extension covers assumptions such as the q-strong DH assumption by Boneh and Boyen
[BB08], which they proved secure in the generic group model. A q-SDH adversary is given \((g_i,g_i^z,g_i^{z^2},\ldots ,g_i^{z^q})\) for \(i=1,2\) and must compute \((g_1^{(z+c)^{-1}},c)\) for any  of its choice. This is an instance of the flexible game in Fig. 5 when setting \(m=1\), \(r=s=q+1\), \(f=0\) and \(R_i(X)=S_i(X)=X^{i-1}\), and the adversary returns \(R^*(X)= 1/(X+c)\), \(S^*(X)=F^*(X)=0\).
of its choice. This is an instance of the flexible game in Fig. 5 when setting \(m=1\), \(r=s=q+1\), \(f=0\) and \(R_i(X)=S_i(X)=X^{i-1}\), and the adversary returns \(R^*(X)= 1/(X+c)\), \(S^*(X)=F^*(X)=0\).
Theorem 4 (DLog implies flexible-target Uber for rational fractions in the AGM)
Let \(\mathcal {G}\) be a bilinear group of type \(\tau \in \{1,2,3\}\) and let  be a tuple of rational fractions.
be a tuple of rational fractions.
Consider an adversary \(\mathsf {A_{alg}}\) in game
 (Fig. 5) and let \( d^*_1, d^*_2,d^*_T, \check{d}^*_1,\check{d}^*_2,\check{d}^*_T\) be such that \(\mathsf {A_{alg}}\)’s outputs \(R^*,S^*,F^*\) satisfy \(\deg R^*\le d^*_1\), \(\deg S^*\le d^*_2\), \(\deg F^*\le d^*_T\), \(\deg \check{R}^*\le \check{d}^*_1\), \(\deg \check{S}^*\le \check{d}^*_2\) and \(\deg \check{F}^*\le \check{d}^*_T\).
(Fig. 5) and let \( d^*_1, d^*_2,d^*_T, \check{d}^*_1,\check{d}^*_2,\check{d}^*_T\) be such that \(\mathsf {A_{alg}}\)’s outputs \(R^*,S^*,F^*\) satisfy \(\deg R^*\le d^*_1\), \(\deg S^*\le d^*_2\), \(\deg F^*\le d^*_T\), \(\deg \check{R}^*\le \check{d}^*_1\), \(\deg \check{S}^*\le \check{d}^*_2\) and \(\deg \check{F}^*\le \check{d}^*_T\).
Let \(q,q_1\) and \(q_2\) be such that \(q\ge \check{d}_{\vec R\Vert \vec S\Vert \vec F} + \max \{ d_{\vec R}, d_{\vec S}, d_{\vec F}/{2}\}\) and let \(q_1\ge \check{d}_{\vec R\Vert \vec F} + d_{\vec R}\) and \(q_2\ge \check{d}_{\vec S} + d_{\vec S}\) and \(q_1+q_2\ge \check{d}_{\vec R\Vert \vec F} + \check{d}_{\vec S} + d_{\vec F}\), where \(\check{d}_{\vec R} = \check{d}_{(\hat{R}_1/\check{R}_1,\ldots ,\hat{R}_r/\check{R}_r)} = \deg \mathrm{LCM}\{\check{R}_1,\ldots ,\check{R}_r\}\). If
-
(Type 1)
 or
or
 is \((\varepsilon ,t)\)-secure in the AGM,
is \((\varepsilon ,t)\)-secure in the AGM, -
(Type 2)
 is \((\varepsilon ,t)\)-secure in the AGM,
is \((\varepsilon ,t)\)-secure in the AGM, -
(Type 3)
 is \((\varepsilon ,t)\)-secure in the AGM,
is \((\varepsilon ,t)\)-secure in the AGM,
then
 is \((\varepsilon '\!,t')\)-secure in the AGM with
is \((\varepsilon '\!,t')\)-secure in the AGM with
where \(d_\tau \) is defined as in Definition 7, except for defining \(d_{\mathrm{den}}:=\check{d}_{\vec R \Vert \vec S\Vert \vec F}\) and replacing \((\check{d}_{R'}, \check{d}_{S'}, \check{d}_{F'}, d_{R'}, d_{S'}, d_{F'})\) by \((\check{d}^{*}_{1}, \check{d}^{*}_{2}, \check{d}^{*}_{T}, d^{*}_{1}, d^{*}_{2}, d^{*}_{T})\).
Proof (sketch)
Much in the way the proof of Theorem 1 is adapted to Theorem 2, Theorem 4 is proved similarly to Theorem 3. Since \(P_1, P_2\) and \(P_T\) are only defined once the adversary returns its rational fractions \(R^*,S^*,F^*\), they need not be known in advance. (Note that, unlike for polynomials (Theorem 2), the instance \((\vec R,\vec S,\vec F)\) does have to be fixed, as the reduction uses it to set up the generators \(h_1\) and \(h_2\).) A difference to Theorem 4 is the value \(d_{\mathrm{den}}\) in the security loss, which is now smaller since the experiment need not check the denominators of the target fractions. \(\square \)
7 Uber Assumptions with Decisional Oracles
In this section we show that we can provide the adversary, essentially for free, with an oracle that checks whether the logarithms of given group elements satisfy any polynomial relation. In more detail, the adversary is given access to an oracle that takes as input a polynomial  and group elements \(\mathbf {Y}_1,\ldots ,\mathbf {Y}_n\) (from any group \(\mathbb {G}_1,\mathbb {G}_2\) or \(\mathbb {G}_T\)) and checks whether \(P(\log \mathbf {Y}_1,\ldots ,\log \mathbf {Y}_n)\equiv _p 0\). Decisional oracles can be added to any type of Uber assumption; for concreteness, we extend the most general variant from the previous section. The game
and group elements \(\mathbf {Y}_1,\ldots ,\mathbf {Y}_n\) (from any group \(\mathbb {G}_1,\mathbb {G}_2\) or \(\mathbb {G}_T\)) and checks whether \(P(\log \mathbf {Y}_1,\ldots ,\log \mathbf {Y}_n)\equiv _p 0\). Decisional oracles can be added to any type of Uber assumption; for concreteness, we extend the most general variant from the previous section. The game
 (“d” for decisional oracles) is defined in Fig. 6. This extension covers assumptions such as Gap Diffie-Hellman (DH)
[OP01], where the adversary must solve a DH instance while being given an oracle that checks whether a triple \((\mathbf {Y}_1,\mathbf {Y}_2, \mathbf {Y}_3)\) is a DH tuple, i.e., \(\mathbf {Y}_1^{\log \mathbf {Y}_2} = \mathbf {Y}_3\). This oracle is a special case of the one in Fig. 6, when called with \(P(X_1,X_2,X_3):=X_1X_2-X_3\).
(“d” for decisional oracles) is defined in Fig. 6. This extension covers assumptions such as Gap Diffie-Hellman (DH)
[OP01], where the adversary must solve a DH instance while being given an oracle that checks whether a triple \((\mathbf {Y}_1,\mathbf {Y}_2, \mathbf {Y}_3)\) is a DH tuple, i.e., \(\mathbf {Y}_1^{\log \mathbf {Y}_2} = \mathbf {Y}_3\). This oracle is a special case of the one in Fig. 6, when called with \(P(X_1,X_2,X_3):=X_1X_2-X_3\).
Theorem 5 (DLog implies flexible-target Uber for rational fractions with decisional oracles in the AGM)
The statement of Theorem 4 holds when
 is replaced by
is replaced by
 .
.
Proof (sketch)
The reduction \(\mathsf {B_{alg}}\) from
 to q-DLog (or \((q_1,q_2)\)-DLog) works as for Theorem 4 (as detailed in the proof of Theorem 3), except that \(\mathsf {B_{alg}}\) must also answer \(\mathsf {A_{alg}}\)’s oracle queries, which we describe in the following for Type-3 groups.
to q-DLog (or \((q_1,q_2)\)-DLog) works as for Theorem 4 (as detailed in the proof of Theorem 3), except that \(\mathsf {B_{alg}}\) must also answer \(\mathsf {A_{alg}}\)’s oracle queries, which we describe in the following for Type-3 groups.
As for Theorem 4, \(\mathsf {B_{alg}}\), on input \((\vec {\mathbf {Y}},\vec {\mathbf {Z}})\) with \(\mathbf {Y}_i = [z^i]_1\) and \(\mathbf {Z}_i = [z^i]_2\), for \(0\le i\le q\), computes LCMs of denominators  ,
,  and
and  . It picks
. It picks  and
and  , implicitly sets \(x_i:=y_iz + v_i \bmod p\) and checks if \(D(\vec x)\equiv _p0\). If so, the reduction derives the corresponding univariate polynomial and finds z. Otherwise it computes \(h_1:=[D_1(\vec x)]_1\), \(h_2:=[D_2(\vec x)]_2\) (note that \(D_1(\vec x)\) and \(D_2(\vec x)\) are non-zero), \(\mathbf {U}_i = [(D_1\cdot R_i)(\vec x)]_1\), \(\mathbf {V}_i = [(D_2\cdot S_i(\vec x)]_2\) and \(\mathbf {W}_i = [(D_1\cdot D_2\cdot F_i)(\vec x)]_T\).
, implicitly sets \(x_i:=y_iz + v_i \bmod p\) and checks if \(D(\vec x)\equiv _p0\). If so, the reduction derives the corresponding univariate polynomial and finds z. Otherwise it computes \(h_1:=[D_1(\vec x)]_1\), \(h_2:=[D_2(\vec x)]_2\) (note that \(D_1(\vec x)\) and \(D_2(\vec x)\) are non-zero), \(\mathbf {U}_i = [(D_1\cdot R_i)(\vec x)]_1\), \(\mathbf {V}_i = [(D_2\cdot S_i(\vec x)]_2\) and \(\mathbf {W}_i = [(D_1\cdot D_2\cdot F_i)(\vec x)]_T\).
Consider a query \(\mathsf {O}_{}(P,(\mathbf {Y}_1,\ldots ,\mathbf {Y}_n))\) for some n and  , and \(\mathbf {Y}_i\in \mathbb {G}_{\iota _i}\) for \(\iota _i\in \{1,2,T\}\). Since \(\mathsf {A_{alg}}\) is algebraic, it provides representations of the group elements \(\mathbf {Y}_i\) with respect to its input \((\vec {\mathbf {U}}, \vec {\mathbf {V}}, \vec {\mathbf {W}})\); in particular, for each \(\mathbf {Y}_i\), depending on the group, it provides \(\vec \mu _i\) or \(\vec \eta _i\) or \((A_i,\vec \delta _i)\) such that:
, and \(\mathbf {Y}_i\in \mathbb {G}_{\iota _i}\) for \(\iota _i\in \{1,2,T\}\). Since \(\mathsf {A_{alg}}\) is algebraic, it provides representations of the group elements \(\mathbf {Y}_i\) with respect to its input \((\vec {\mathbf {U}}, \vec {\mathbf {V}}, \vec {\mathbf {W}})\); in particular, for each \(\mathbf {Y}_i\), depending on the group, it provides \(\vec \mu _i\) or \(\vec \eta _i\) or \((A_i,\vec \delta _i)\) such that:
-
(\(\mathbf {Y}_i\in \mathbb {G}_1\)) \(\,\mathbf {Y}_i = \prod _{j=1}^r\mathbf {U}_j^{\mu _{i,j}} = \big [\sum _{j=1}^r\mu _{i,j}(D_1\cdot R_j)(\vec x)\big ]_1 =: \big [Q_i(z)\big ]_1\)
-
(\(\mathbf {Y}_i\in \mathbb {G}_2\)) \(\,\mathbf {Y}_i = \prod _{j=1}^s\mathbf {V}_j^{\eta _{i,j}} = \big [\sum _{j=1}^s\eta _{i,j}(D_2\cdot S_j)(\vec x)\big ]_2 =: \big [Q_i(z)\big ]_2\)
-
(\(\mathbf {Y}_i\in \mathbb {G}_T\)) \(\mathbf {Y}_i = \prod _{j=1}^r\prod _{k=1}^s e(\mathbf {U}_j,\mathbf {V}_k)^{\alpha _{i,j,k}}\cdot \prod _{j=1}^f\mathbf {W}_j^{\delta _{i,j}}\) \( = \big [\sum _{j=1}^r\sum _{k=1}^s \alpha _{i,j,k}(D_1\cdot R_j)(\vec x)\,(D_2\cdot S_j)(\vec x) + \sum _{j=1}^f\delta _{i,j}(D_1\cdot D_2\cdot F_j)(\vec x)\big ]_T\) \( =: \big [Q_i(z)\big ]_T\),
where \(D_1\cdot R_j\), \(D_2\cdot S_j\) and \(D_1\cdot D_2\cdot F_j\) are multivariate polynomials (not rational fractions) and \(Q_i\) is the polynomial defined by replacing \(X_i\) by \(y_iZ + v_i\). Let \(D'_i(Z)\) be defined from \(D_i(\vec X)\) analogously. Then we have \(\log _{g_{\iota _i}}\!\!\mathbf {Y}_i = Q_i(z)\) and furthermore \(\log _{h_{\iota _i}}\!\!\mathbf {Y}_i = Q_i(z)/D_{\iota _i}(z)\), where \(D_T:=D_1\cdot D_2\).
To answer the oracle query, \(\mathsf {B_{alg}}\) must therefore determine whether the function \(P(Q_1/D_{i_1},\ldots ,Q_n/D_{i_n})\) vanishes at z. Since \(D_1(z),D_2(z)\not \equiv _p 0\), this is the case precisely when \(\overline{P}:= D_1^d\cdot D_2^d\cdot P(Q_1/D_{i_1},\ldots ,Q_n/D_{i_n})\) vanishes at z, where d is the maximal degree of P. Note that \(\overline{P}\) is a polynomial. The reduction distinguishes 3 cases:
-
1.
\(\overline{P}\equiv 0\): in this case, the oracle replies 1.
-
2.
\(\overline{P}\not \equiv 0\): in this case, \(\mathsf {B_{alg}}\) factorizes \(\overline{P}\) to find its roots \(z_1,\ldots \), checks whether \(\mathbf {Z}_1 = g^{z_i}\) for some i. If this is the case, it stops and returns the solution \(z_i\) to its \((q_1,q_2)\)-DLog instance.
-
3.
Else, the oracle replies 0.
Correctness of the simulation is immediate, since the correct oracle reply is 1 if and only if \(\overline{P}(z)\equiv _p 0\). \(\square \)
8 The Flexible Gegenuber Assumption
In this section, we show how to extend the Uber framework even further, by letting the adversary generate its own generators (for the outputs), yielding the GeGenUber assumption. Consider the LRSW assumption
[LRSW99] in Type-1 bilinear groups: given \((X=g^x,Y=g^y)\) (which can be viewed as a signature verification key
[CL04]) and an oracle, which on input (a message)  returns (a signature) \((g^a,g^{ay},g^{a(x+mxy)})\) for a random
returns (a signature) \((g^a,g^{ay},g^{a(x+mxy)})\) for a random  , it is infeasible to return (a signature on a fresh message) \(((g^{a^*},g^{a^*y},g^{a^*(x+m^*xy)},m^*))\) for any \(a^*\) and \(m^*\) different from the queried values. Since the adversary need not return the value \(a^*\), this cannot be cast into the Uber framework. Associating the a-values chosen by the signing oracle to formal variables, in the Uber framework \(\vec X\) would correspond to \((X,Y,A_1,\ldots ,A_\ell )\) and signing queries to the polynomials \(A_i\), \(A_iY\) and \(A_iX+m_iA_iXY\). Now the adversary can choose a fresh generator \(g^*:=g^{a^*}\) and must return \(((g^*)^{R^*_i(\vec X)})_{i=1}^3\) for \(R^*_1\equiv 1, R^*_2=Y\) and \(R^*_3=X+m^*XY\) for some
, it is infeasible to return (a signature on a fresh message) \(((g^{a^*},g^{a^*y},g^{a^*(x+m^*xy)},m^*))\) for any \(a^*\) and \(m^*\) different from the queried values. Since the adversary need not return the value \(a^*\), this cannot be cast into the Uber framework. Associating the a-values chosen by the signing oracle to formal variables, in the Uber framework \(\vec X\) would correspond to \((X,Y,A_1,\ldots ,A_\ell )\) and signing queries to the polynomials \(A_i\), \(A_iY\) and \(A_iX+m_iA_iXY\). Now the adversary can choose a fresh generator \(g^*:=g^{a^*}\) and must return \(((g^*)^{R^*_i(\vec X)})_{i=1}^3\) for \(R^*_1\equiv 1, R^*_2=Y\) and \(R^*_3=X+m^*XY\) for some  of its choice.
of its choice.
Our last generalization now extends the flexible Uber assumption from Sect. 4 by letting the adversary generate its own generators \(\mathbf {U}\), \(\mathbf {V}\) and \(\mathbf {W}\) of \(\mathbb {G}_1\), \(\mathbb {G}_2\) and \(\mathbb {G}_T\), resp., and return polynomials \(R^*, S^*\) and \(F^*\), as well as \((\mathbf {U}^{R^*(\vec x)}, \mathbf {V}^{S^*\left( \vec x \right) },\mathbf {W}^{F^*\left( \vec x\right) })\). The game m
 is defined in Fig. 7. However, this additional freedom for the adversary induces a necessary change in the definition of non-triviality, as illustrated by the following simple (univariate) example: after the challenger chooses
is defined in Fig. 7. However, this additional freedom for the adversary induces a necessary change in the definition of non-triviality, as illustrated by the following simple (univariate) example: after the challenger chooses  , the adversary makes queries \(R_1:=X\) and \(R_2:=X^3\) and receives \(\mathbf {U}_1\) and \(\mathbf {U}_2\). For all Uber assumptions so far, the polynomial \(R^*:=X^2\) would be considered non-trivial. However, in game
, the adversary makes queries \(R_1:=X\) and \(R_2:=X^3\) and receives \(\mathbf {U}_1\) and \(\mathbf {U}_2\). For all Uber assumptions so far, the polynomial \(R^*:=X^2\) would be considered non-trivial. However, in game
 the adversary could return \(\mathbf {U}:=\mathbf {U}_1 = g^x\) and \(\mathbf {U}^* := \mathbf {U}_2 = g^{x^3} = \mathbf {U}^{R^*(x)}\).
the adversary could return \(\mathbf {U}:=\mathbf {U}_1 = g^x\) and \(\mathbf {U}^* := \mathbf {U}_2 = g^{x^3} = \mathbf {U}^{R^*(x)}\).
Whereas until now the target polynomial \(R^*\) was not allowed to be a linear combination of the queried polynomials \(P_1,\ldots ,P_\ell \) (or of products of such polynomials, depending on the group types), for the Gegenuber assumption we also need to exclude fractions of such linear combinations (such as \(X^3/X\) in the example above) to thwart trivial attacks.
For a family E of polynomials, we denote by \(\mathrm{Span}(E)\) all linear combinations of elements of E, which we extend to fractions as
Moreover, by \(E_1*E_2\) we denote the set \(\{P_1\cdot P_2\ |\ (P_1, P_2)\in E_1\times E_2\}\).
Definition 8 (Non-triviality for Gegenuber assumption)
[Non-triviality for Gegenuber assumption] Let \(\mathcal {Q}_1,\mathcal {Q}_2\) and \(\mathcal {Q}_T\) be sets of polynomials and let \(R^{*}, S^{*}\) and \(F^{*}\) be polynomials. We say that \((\mathcal {Q}_1, \mathcal {Q}_2, \mathcal {Q}_T, R^{*}, S^{*}, F^{*})\) is gegenuber-non-trivial for groups of type \(\tau \), if the following holds:

Definition 9
(Degree of non-triviality for Gegenuber assumption). Let \((\mathcal {Q}_1,\mathcal {Q}_2,\mathcal {Q}_T, R^{*}, S^{*}, F^{*})\) be a non-trivial tuple of polynomials in  . For \(i\in \{1,2,T\}\) define \(d'_i := \max \{\deg P \}_{P \in \mathcal {Q}_i}\). We define the type-\(\tau \) degree \(d_{\tau }\) of \((\mathcal {Q}_1, \mathcal {Q}_2, \mathcal {Q}_T, R^{*}, S^{*},F^{*})\) as follows:
. For \(i\in \{1,2,T\}\) define \(d'_i := \max \{\deg P \}_{P \in \mathcal {Q}_i}\). We define the type-\(\tau \) degree \(d_{\tau }\) of \((\mathcal {Q}_1, \mathcal {Q}_2, \mathcal {Q}_T, R^{*}, S^{*},F^{*})\) as follows:

If \((\tau ,i)\) does not hold, set \(d_{\tau ,i}:=\infty \). Define \(d_\tau :=\min \{d_{\tau .1},d_{\tau .2},d_{\tau .T}\}\).
Note that for all Uber variants, the adversary only outputs one element per group \(\mathbb {G}_i\), which is without loss of generality, as a vector of group elements would be non-trivial if at least one component is non-trivial. We defined the Gegenuber assumption analogously, so one might wonder how this covers LRSW, where the adversary must output group elements corresponding to two polynomials Y and \(X+m^*XY\). The reason is that LRSW holds even if the adversary only has to output the latter polynomial: In the GGM this follows from LRSW being an instance of Gegenuber, Theorem 6 (see below for both) and Lemmas 3 and 4.
To show that LRSW is gegenuber-non-trivial, consider the set of queries an adversary can make, namely:
To prove that the stronger variant of LRSW satisfies non-triviality as defined in Definition 8, we show that for \(0\ne m^*\notin \{m_1,\ldots ,m_\ell \}\): \(R^*:=X+m^*XY\notin \mathrm{FrSp}(\mathcal {Q})\). For the sake of contradiction, assume that for some \(\check{P}, \hat{P}\in \mathrm{Span}(\mathcal {Q})\), \(\check{P}\not \equiv 0\):
Since \(\hat{P}\in \mathrm{Span}(\mathcal {Q})\), its total degree in X and Y is at most 2, which implies that \(\check{P}\) must be of degree 0 in X and Y. We can thus write \(\check{P}\) as \(\eta + \sum ^\ell _{j=1} \alpha _jA_j\) for some \(\eta \) and \(\vec \alpha \). Since X is a factor of the left-hand side of (7), \(\hat{P}\) cannot have terms without X and must therefore be of the form \(\hat{P} = \xi X + \sum ^\ell _{j=1} \mu _j A_j\left( X + m_jXY\right) \) for some \(\xi \) and \(\vec \mu \). Equation (7) becomes thus
By equating coefficients, we get: \( \eta = \xi \) (from coeff. X) and \(m^{*} \eta \equiv _p 0\) (from XY) and for all \(j\in [1,\ell ]\): \(\alpha _j=\mu _j\) (from \(A_jX\)) and \(\alpha _j m^{*}\equiv _p\mu _j m_j\) (from \(A_jXY\)). Since \(m^{*} \ne 0\), we have \(\eta =\xi =0\). Furthermore, if \(\alpha _j \ne 0\) for some j, then \(m_j=m^{*}\), meaning it was not a valid solution. If \(\alpha _j=0\) for all j then \(\check{P}\equiv 0\), which shows such \(\hat{P}\) and \(\check{P}\) do not exist and thus \(X+m^*XY\notin \mathrm{FrSp}(\mathcal {Q})\).
Theorem 6
Let \(m\ge 1\), let \(\mathcal {G}\) be a bilinear group of type \(\tau \in \{1,2,3\}\) and let \(\mathsf {A_{alg}}\) be an adversary in game
 . Let \(d'_1,d'_2,d'_T, d^*_1, d^*_2, d^*_T\) be such that \(\mathsf {A_{alg}}\)’s queries \((i,P(\vec X))\) satisfy \(\deg P \le d'_i\) and its output satisfies \(\deg R^*\le d^*_1\), \(\deg S^*\le d^*_2\), \(\deg F^*\le d^*_T\). Let \(q, q_1, q_2\) be such that \(q \ge \max \{d'_1, d'_2, d'_T/2\}\), as well as \(q_1 \ge d'_1 \), \(q_2 \ge d'_2\) and \(q_1+q_2\ge d'_T\). If
. Let \(d'_1,d'_2,d'_T, d^*_1, d^*_2, d^*_T\) be such that \(\mathsf {A_{alg}}\)’s queries \((i,P(\vec X))\) satisfy \(\deg P \le d'_i\) and its output satisfies \(\deg R^*\le d^*_1\), \(\deg S^*\le d^*_2\), \(\deg F^*\le d^*_T\). Let \(q, q_1, q_2\) be such that \(q \ge \max \{d'_1, d'_2, d'_T/2\}\), as well as \(q_1 \ge d'_1 \), \(q_2 \ge d'_2\) and \(q_1+q_2\ge d'_T\). If
-
(Type 1)
 or
or
 is \((\varepsilon ,t)\)-secure in the AGM,
is \((\varepsilon ,t)\)-secure in the AGM, -
(Type 2)
 is \((\varepsilon ,t)\)-secure in the AGM,
is \((\varepsilon ,t)\)-secure in the AGM, -
(Type 3)
 is \((\varepsilon ,t)\)-secure in the AGM,
is \((\varepsilon ,t)\)-secure in the AGM,
then
 is \((\varepsilon '\!,t')\)-secure in the AGM with
is \((\varepsilon '\!,t')\)-secure in the AGM with
with \(d_\tau \) from Definition 9 after replacing \(\deg R^*\), \(\deg S^*\) and \(\deg F^*\) by \(d^*_1, d^*_2\) and \(d^*_T\), respectively.
The proof can be found in the full version. It is an adaptation of the one for the flexible uberassumption, which adapts the proof of Theorem 1.
In the proof of Theorem 6, the adversary also outputs a new generator \(\mathbf {U}\), whose algebraic representation yields a polynomial \(Q\in \mathrm{Span}(\mathcal {Q}_1\cup \mathcal {Q}_2)\) so that \(\mathbf {U}=[Q(\vec x)]_1\). For a valid solution \(\mathbf {U}^*\), we thus have \(\mathbf {U}^* = [R^*(\vec x)\cdot Q(\vec x)]_1\). On the other hand, the representation of \(\mathbf {U}^*\) yields \(\mathbf {U}^* = [Q^*(\vec x)]_1\) for some \(Q^*\in \mathrm{Span}(\mathcal {Q}_1\cup \mathcal {Q}_2)\). We thus have that \(P_1(\vec X):=R^*(\vec X)\cdot Q(\vec X) - Q^*(\vec X)\) vanishes at \(\vec x\). By non-triviality, \(R^*\notin \mathrm{FrSp}(\mathcal {Q}_1\cup \mathcal {Q}_2)\), which implies \(P_1\not \equiv 0\), so the reduction can find the roots of \(P_1(y_1Z + x_1, \dots , y_nZ + x_n)\) and solve q-DLog.
9 Separation of \((q+1)\)-DL from q-DL
Now that we have shown that every Uber assumption falls into a (minimal) class of assumptions that are equivalent to q-DLog, we show that these classes can be separated according to their parameter q. We prove that, assuming that q-DLog is hard, there does not exist an algebraic reduction from q-DLog to \((q+1)\)-DLog. In particular, we show that if there exists a reduction \(\mathsf {R}_\mathsf {alg}\) that has access to a \((q+1)\)-DLog (algebraic) adversary \(\mathsf {A}_\mathsf {alg}\) and can solve q-DLog, then there exists a meta-reduction that uses \(\mathsf {R}_\mathsf {alg}\) to break q-DLog. In the following, we use the notation \(\mathsf {R}_\mathsf {alg}(\mathsf {A}_\mathsf {alg})\) to denote that \(\mathsf {R}_\mathsf {alg}\) has complete access to \(\mathsf {A}_\mathsf {alg}\)’s internal state. In particular, \(\mathsf {R}_\mathsf {alg}\) is allowed to rewind \(\mathsf {A}_\mathsf {alg}\) to any point of an execution and run \(\mathsf {A}_\mathsf {alg}\) on any choice of random coins as many times as it wants.
Theorem 7
Let \(\mathcal {G}_i\) be a group of prime order p. There exists an algorithm \(\mathsf {M}\) such that the following holds. Let \(\mathsf {R}_\mathsf {alg}\) be an algebraic algorithm s.t. for every algorithm \(\mathsf {A}_\mathsf {alg}\) that \((t,\epsilon )\)-breaks  , \(\mathsf {B}=\mathsf {R}_\mathsf {alg}(\mathsf {A}_\mathsf {alg})\) is an algorithm that \((t',\epsilon ')\)-breaks
, \(\mathsf {B}=\mathsf {R}_\mathsf {alg}(\mathsf {A}_\mathsf {alg})\) is an algorithm that \((t',\epsilon ')\)-breaks  . If \(t\ge 2\,(2q+1)\lceil \log _2 p\rceil \) then \(\mathsf {M}^{\mathsf {R}_\mathsf {alg}}\) \((t',\epsilon ')\)-breaks
. If \(t\ge 2\,(2q+1)\lceil \log _2 p\rceil \) then \(\mathsf {M}^{\mathsf {R}_\mathsf {alg}}\) \((t',\epsilon ')\)-breaks  .
.
We start with a proof overview. Consider a reduction \(\mathsf {R}_\mathsf {alg}\), which on input a q-DLog instance \((g,g^x,\ldots ,g^{x^q})\) can run an algebraic adversary \(\mathsf {A}_\mathsf {alg}\) multiple times on \((q+1)\)-DLog instances \((\mathbf {Z},\mathbf {Z}^y,\ldots ,\mathbf {Z}^{y^{q+1}})\); that is, \(\mathsf {R}_\mathsf {alg}\) can choose a new generator \(\mathbf {Z}\) and a new problem solution y. Since \(\mathsf {R}_\mathsf {alg}\) is algebraic, it outputs a representation of the group elements composing its \((q+1)\)-DLog instance in terms of the received q-DLog instance. We distinguish two cases: if (a) y is independent from x then the representation reveals y, which means that a meta-reduction \(\mathsf {M}\) can simulate a successful \(\mathsf {A}_\mathsf {alg}\) to \(\mathsf {R}_\mathsf {alg}\), and the latter must thus find x. On the other hand, if (b) y depends on x, then this yields a non-trivial equation in x, which the meta-reduction can solve and thereby (without needing to simulate \(\mathsf {A}_\mathsf {alg}\)) solve the q-DLog instance. To simplify the probability analysis, we let \(\mathsf {M}\) simulate \(\mathsf {A}_\mathsf {alg}\) even when \(\mathsf {R}_\mathsf {alg}\) behaves as in the second case (as it can compute y from x). To correctly argue about the probability distributions, we ensure that any malformed instance provided by the algebraic reduction \(\mathsf {R}_\mathsf {alg}\) is detected. We will use the following lemma in the proof of Theorem 7:
Lemma 5
Let \(q\ge 1\), let  and let
and let  be of degree at most q. If \(F^{q+1}\!\cdot \! P\) is a polynomial and of degree at most q, then F is constant.
be of degree at most q. If \(F^{q+1}\!\cdot \! P\) is a polynomial and of degree at most q, then F is constant.
Proof
Let  be coprime such that \(F={\hat{F}}/{\check{F}}\). Then \(\hat{F}^{q+1}\) and \(\check{F}^{q+1}\) are coprime as well. From this and the premise that \(\hat{F}^{q+1}\cdot P/\check{F}^{q+1}\) is a polynomial, we get that \(\check{F}^{q+1}\) divides P, and thus \((q+1)\cdot \deg \check{F} \le \deg P\). Since the latter is at most q, we have \(\deg \check{F}=0\).
be coprime such that \(F={\hat{F}}/{\check{F}}\). Then \(\hat{F}^{q+1}\) and \(\check{F}^{q+1}\) are coprime as well. From this and the premise that \(\hat{F}^{q+1}\cdot P/\check{F}^{q+1}\) is a polynomial, we get that \(\check{F}^{q+1}\) divides P, and thus \((q+1)\cdot \deg \check{F} \le \deg P\). Since the latter is at most q, we have \(\deg \check{F}=0\).
Furthermore, we assumed that \(q\ge \deg (F^{q+1}\cdot P) = (q+1)\cdot \deg \hat{F} +\deg P\), and thus \(\deg \hat{F} = 0\). Together, this means F is constant. \(\square \)
Proof (of Theorem 7)
Let \(\mathsf {R}_\mathsf {alg}\) be an algebraic algorithm s.t. for every algorithm \(\mathsf {A}_\mathsf {alg}\) that \((t,\epsilon )\)-breaks  , \(\mathsf {B}=\mathsf {R}_\mathsf {alg}(\mathsf {A}_\mathsf {alg})\) is an algorithm that \((t',\epsilon ')\)-breaks
, \(\mathsf {B}=\mathsf {R}_\mathsf {alg}(\mathsf {A}_\mathsf {alg})\) is an algorithm that \((t',\epsilon ')\)-breaks  . In the following, we describe a meta-reduction \(\mathsf {M}\) s.t. \(\mathsf {M}^{\mathsf {R}_\mathsf {alg}}\) \((t',\epsilon ')\)-breaks
. In the following, we describe a meta-reduction \(\mathsf {M}\) s.t. \(\mathsf {M}^{\mathsf {R}_\mathsf {alg}}\) \((t',\epsilon ')\)-breaks  .
.
-
\(\mathsf {M}(g,\mathbf {X}_1,\ldots ,\mathbf {X}_q)\): Run \(\mathsf {R}_\mathsf {alg}\) on the received q-DLog instance \((g,g^x,\ldots ,g^{x^q})\). Whenever \(\mathsf {R}_\mathsf {alg}\) runs adversary \(\mathsf {A}_\mathsf {alg}\) on \((q+1)\)-DLog input \((\mathbf {Z}_0, \mathbf {Z}_1,\ldots , \mathbf {Z}_{q+1})\), do the following. Let \(\vec {z}_i=(z_{i,0},\ldots ,z_{i,q})\) for \(0\le i\le q+1\) be the representation vectors for \(\mathbf {Z}_0,\dots ,\mathbf {Z}_{q+1}\) provided by \(\mathsf {R}_\mathsf {alg}\); that is, \(\mathbf {Z}_i=\prod _{j=0}^q (g^{x^j})^{z_{i,j}}\).
If \(\mathbf {Z}_0=1\) then return \(\bot .\) \((*)\)
Else define
$$\begin{aligned} P_i(X)&:= \textstyle \sum ^q_{j=0} z_{i,j}X^j \quad \text {for } 0\le i\le q+1 \quad \text {and} \end{aligned}$$(8)$$\begin{aligned} Q_i&:= P_{i+1}P_0 - P_iP_1 \quad \text {for } 0\le i\le q. \end{aligned}$$(9)\(\mathsf {M}\) now distinguishes two cases:
-
(a)
\(Q_i\equiv 0\) for all \(i \in [0,q]\): Then (as we argue below) \(P_1/ P_0\equiv c\), that is, a constant polynomial. \(\mathsf {M}\) returns c as \(\mathsf {A}_\mathsf {alg}\)’s output.
-
(b)
For some \(k\in [0,q]\): \(Q_k\not \equiv 0\): Compute the roots \(x_1,\ldots \) of \(Q_k\) and check if for some j: \(g^{x_j}=\mathbf {X}_1\). If not, then return \(\bot \) as \(\mathsf {A}_\mathsf {alg}\)’s output. \((**)\)
Else let \(y:=P_1(x_j)/P_0(x_j) \bmod p\). (\(1\ne \mathbf {Z}_0 = g^{P_0(x_j)}\), thus \(P_0(x_j)\not \equiv _p0\).) If for some \(i \in [1,q+1]: \mathbf {Z}_i\ne \mathbf {Z}_0^{y^i}\), return \(\bot \) as \(\mathsf {A}_\mathsf {alg}\)’s output. \((*\!*\!*)\)
Else return y.
-
(a)
Correctness of simulation. We now argue that \(\mathsf {M}\) always correctly simulates an adversary \(\mathsf {A}_\mathsf {alg}\) that solves \((q+1)\)-DLog if it received a correct instance, and returns \(\bot \) otherwise. Consider the case where \(\mathsf {R}_\mathsf {alg}\) provides a valid \((q+1)\)-DLog instance, that is \(\mathbf {Z}_0\ne 1\) and

By (8), we have \(\mathbf {Z}_i = g^{P_i(x)}\) for all i. Since \(\mathbf {Z}_0\ne 1\), \(\mathsf {M}\) does not stop in line \((*)\) and \(P_0(x)\not \equiv _p 0\). Moreover, from (10) we have \(y\equiv _p P_1(x)/P_0(x)\) and
in other words, \(Q_i(x)\equiv _p 0\) for all \(i\in [0,q]\).
In case (a), \(Q_i\equiv 0\), and thus, letting \(F:= P_1/P_0\), we have (by Definition (9)) \(P_{i+1} = F\cdot P_i\) for all i, and by induction:
and in particular \(P_{q+1} = F^{q+1} \cdot P_0\). Since \(P_{q+1}\) and \(P_0\) are polynomials of degree at most q, by Lemma 5 we get \(F\equiv c\) for  . The meta-reduction \(\mathsf {M}\) thus returns \(c\equiv _p F(x) \equiv _p P_1(x)/P_0(x) \equiv _p y\).
. The meta-reduction \(\mathsf {M}\) thus returns \(c\equiv _p F(x) \equiv _p P_1(x)/P_0(x) \equiv _p y\).
In case (b), since \(Q_k\not \equiv 0\) but, by (11), \(Q_k(x)\equiv _p 0\), the meta-reduction finds x and \(\mathsf {M}\) does not stop in line \((**)\) and neither in line \((*\!*\!*)\), since \(y\equiv _p P_1(x)/P_0(x)\).
Now consider the case that \(\mathsf {R}_\mathsf {alg}\) sends a malformed instance: if \(\mathbf {Z}_0\) is not a generator then \(\mathsf {A}_\mathsf {alg}\) returns \(\bot \) in line \((*)\). Assume \(\mathbf {Z}_0\) is a generator (and thus \(P_0(x)\not \equiv _p 0\)), but (10) is not satisfied. Using the algebraic representations of \(\mathbf {Z}_0,\dots ,\mathbf {Z}_{q+1}\), this is equivalent to

We first show that the meta-reduction \(\mathsf {M}\) goes to case (b): Indeed, if \(Q_i\equiv 0\) for all \(i\in [0,q]\), then \(P_{i+1}(x) \equiv _p P_1(x)/P_0(x)\cdot P_i(x)\) for all i and, by induction, \(P_i(x) \equiv _p (P_1(x)/P_0(x))^i\cdot P_0(x)\), which, setting \(y:= P_1(x)/P_0(x) \bmod p\), contradicts (12).
Let \(k\in [0,q]\) be such that \(Q_k\not \equiv 0\). If x is not among the roots of \(Q_k\), then \(\mathsf {M}\) returns \(\bot \) in line \((**)\). Otherwise, it sets \(y:=P_1(x)/P_0(x) \bmod p\). If for some \(i\in [1,q+1]\): \(P_i(x) \not \equiv _p y^iP_0(x)\) then \(\mathsf {M}\) returns \(\bot \) in line \((*\!*\!*)\). If not then this contradicts (12). Therefore, the simulation will return \(\bot \) on invalid inputs.
For the simulation of \(\mathsf {A}_\mathsf {alg}\) the meta-reduction needs to compute at most \(2q + 1\) exponentiations, each of which require at most \(2\lceil \log _2 p\rceil \) group operations using square and multiply. The simulation of \(\mathsf {A}_\mathsf {alg}\) is thus perfect and takes at most t steps. The meta-reduction \(\mathsf {M}\) succeeds in winning  whenever \(\mathsf {B}=\mathsf {R}_\mathsf {alg}(\mathsf {A}_\mathsf {alg})\) wins
whenever \(\mathsf {B}=\mathsf {R}_\mathsf {alg}(\mathsf {A}_\mathsf {alg})\) wins  . Therefore, we obtain
. Therefore, we obtain

Moreover, the running time of \(\mathsf {M}\) is that of \(\mathsf {B}\), i.e., \(t'\). This completes the proof. \(\square \)
A similar result can be shown for  , that is,
, that is,  is not implied by
is not implied by  if \(q'_1>q_1\) or \(q'_2>q_2\).
if \(q'_1>q_1\) or \(q'_2>q_2\).
10 Separation of 2-One-More DL from q-DL
We conclude with showing that “one-more”-discrete logarithm (OMDL) assumptions fall outside of our q-DLog taxonomy. While it is known that there is no black-box reduction from DLog to OMDL [BMV08], we show that there is no algebraic reduction either, even one for algebraic adversaries.
To obtain the strongest possible impossibility result, we show that for no \(q\in \mathbb {N}\), there exists an algebraic reduction from q-DLog (a stronger assumption than DLog) to 2-OMDL (the weakest variant of OMDL assumptions), unless q-DLog is easy. The game for 2-OMDL is depicted in Fig. 8. The proof uses the same high-level idea as for Theorem 8. If the representation of the group elements the reduction gives to the adversary is independent of its own q-DLog challenge, then the meta-reduction can directly simulate the adversary. Else, they depend on the q-DLog challenge in a way that allows the meta-reduction to derive a q-DLog solution. Compared to the previous section, we now restrict the algebraic reduction to only have black-box access (according to our notion of black-box) to the adversary. This is because a reduction that can choose the random coins of the adversary in a non-uniform (adaptive) way can make the simulation of the adversary by our meta-reduction fail.
We need to define the adversary’s behavior, that is, its oracle call, beforehand; in particular, it must not depend on the type of representations obtained from the reduction, which makes the proof more complicated and restricts the simulation to adversaries that can fail with negligible probability. The adversary, after receiving a 2-OMDL challenge \((\mathbf {Y}_0,\mathbf {Y}_1,\mathbf {Y}_2)\), makes a query \((\mathbf {Y}_1^{r_1}\mathbf {Y}_2^{r_2})\) for random \(r_1,r_2\) to its DLog oracle and then returns the 2-OMDL solution \((\log _{\mathbf {Y}_0}\!\mathbf {Y}_1,\log _{\mathbf {Y}_0}\!\mathbf {Y}_2)\). We now show how the meta-reduction simulates this adversary.
Since the reduction is algebraic, it provides with its 2-OMDL instance representations \(\vec z_i=(z_{i,0},\ldots ,z_{i,q})\) in terms of its q-DLog challenge \((g,g^x,\ldots ,g^{x^q})\), such that \(\log _g \mathbf {Y}_i \equiv _p \sum _{j=0}^q z_{i,j} x^j\). From the reply \(y\) to the adversary’s single oracle query, we get the following equation: \(0 = \log _g (\mathbf {Y}_1^{r_1}\mathbf {Y}_2^{r_2}) - \log _g\mathbf {Y}_0^y\equiv _p \sum _{j=0}^q \big (r_1z_{1,j}+r_2z_{2,j}-yz_{0,j}\big ) x^j\).
The q-DLog challenge x is thus the root of the polynomial with coefficients \(a_j:=(r_1z_{1,j}+r_2z_{2,j}-yz_{0,j})\bmod p\), and the meta-reduction can find x if one of these coefficients is non-zero. Using x, it can then compute \(\log _g \mathbf {Y}_i\) for all i from the representations and from that the OMDL solution \((\log _{\mathbf {Y}_0}\!\mathbf {Y}_1,\log _{\mathbf {Y}_0}\mathbf {Y}_2)\).
If, on the other hand, \(a_j=0\) for some j then by plugging in the definition of \(y\), we get another polynomial which vanishes at x. We then show that, due to the randomizers \(r_1\) and \(r_2\), with overwhelming probability, the coefficients of this polynomial are non-zero – unless for some \(c_1,c_2\) we have \(\vec z_1=c_1\vec z_0\) and \(\vec z_2=c_2\vec z_0\). But in this case \((c_1,c_2)\) is the solution to the 2-OMDL instance and the meta-reduction can therefore finish the simulation of the adversary.
The proof of the following can be found in the full version.
Theorem 8
Let \(\mathcal {G}_i\) be a group of prime order p. There exists an algorithm \(\mathsf {M}\) such that the following holds: Let \(\mathsf {R}_\mathsf {alg}\) be an algebraic reduction s.t. for every algorithm \(\mathsf {A}_\mathsf {alg}\) that \((t,\epsilon )\)-breaks  , \(\mathsf {B}=\mathsf {R}_\mathsf {alg}^{\mathsf {A}_\mathsf {alg}}\) is an algorithm that \((t',\epsilon ')\)-breaks
, \(\mathsf {B}=\mathsf {R}_\mathsf {alg}^{\mathsf {A}_\mathsf {alg}}\) is an algorithm that \((t',\epsilon ')\)-breaks  . If \(t \ge (6+ 2q)\lceil \log _2 p\rceil + 1 \) and \(\epsilon \le 1-1/p\) then \(\mathsf {M}^{\mathsf {R}_\mathsf {alg}}\) \((t',\epsilon ')\)-breaks
. If \(t \ge (6+ 2q)\lceil \log _2 p\rceil + 1 \) and \(\epsilon \le 1-1/p\) then \(\mathsf {M}^{\mathsf {R}_\mathsf {alg}}\) \((t',\epsilon ')\)-breaks  .
.
Notes
- 1.
E.g., \(\mathsf {B_{alg}}\) can compute \([x_1^q]_1 = [(y_1z+v_1)^q]_1\) as \(\prod _i\psi (\mathbf {Z}_i)^{\left( {\begin{array}{c}q\\ i\end{array}}\right) y_1^i v_1^{q-i}}\) and \([x_1^{2q}]_T\) as \(e\big (\prod _i\psi (\mathbf {Z}_i)^{\left( {\begin{array}{c}q\\ i\end{array}}\right) y_1^i v_1^{q-i}},\prod _i\mathbf {Z}_i^{\left( {\begin{array}{c}q\\ i\end{array}}\right) y_1^i v_1^{q-i}}\big )\) and similarly for terms in more variables.
- 2.
References
Abdalla, M., Benhamouda, F., MacKenzie, P.: Security of the J-PAKE password-authenticated key exchange protocol. In: 2015 IEEE Symposium on Security and Privacy, pp. 571–587. IEEE Press (2015)
Agrikola, T., Hofheinz, D., Kastner, J.: On instantiating the algebraic group model from falsifiable assumptions. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020, Part II. LNCS, vol. 12106, pp. 96–126. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45724-2_4
Deschamps, C., Warusfel, A., Moulin, F.: Mathématiques 1ère année: Cours et exercices corrigés. Editions Dunod (1998)
Boneh, D., Boyen, X.: Short signatures without random oracles and the SDH assumption in bilinear groups. J. Cryptol. 21(2), 149–177 (2008). https://doi.org/10.1007/s00145-007-9005-7
Boneh, D., Boyen, X., Goh, E.-J.: Hierarchical identity based encryption with constant size ciphertext. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 440–456. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_26
Bresson, E., Monnerat, J., Vergnaud, D.: Separation results on the “one-more” computational problems. In: Malkin, T. (ed.) CT-RSA 2008. LNCS, vol. 4964, pp. 71–87. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-79263-5_5
Bartusek, J., Ma, F., Zhandry, M.: The distinction between fixed and random generators in group-based assumptions. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part II. LNCS, vol. 11693, pp. 801–830. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_27
Boyen, X.: The uber-assumption family (invited talk). In: Galbraith, S.D., Paterson, K.G. (eds.) Pairing 2008. LNCS, vol. 5209, pp. 39–56. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85538-5_3
Bellare, M., Rogaway, P.: Code-based game-playing proofs and the security of triple encryption. Cryptology ePrint Archive, Report 2004/331 (2004). http://eprint.iacr.org/2004/331
Camenisch, J., Lysyanskaya, A.: Signature schemes and anonymous credentials from bilinear maps. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 56–72. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_4
Chase, M., Meiklejohn, S.: Déjà Q: using dual systems to revisit q-type assumptions. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 622–639. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_34
Chase, M., Maller, M., Meiklejohn, S.: Déjà Q all over again: tighter and broader reductions of q-type assumptions. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016, Part II. LNCS, vol. 10032, pp. 655–681. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_22
DeMillo, R.A., Lipton, R.J.: A probabilistic remark on algebraic program testing. Technical report, Georgia Inst of Tech Atlanta School of Information and Computer Science (1977)
Fuchsbauer, G., Kiltz, E., Loss, J.: The algebraic group model and its applications. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part II. LNCS, vol. 10992, pp. 33–62. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_2
Fuchsbauer, G., Plouviez, A., Seurin, Y.: Blind Schnorr signatures and signed ElGamal encryption in the algebraic group model. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020, Part II. LNCS, vol. 12106, pp. 63–95. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45724-2_3
Ghadafi, E., Groth, J.: Towards a classification of non-interactive computational assumptions in cyclic groups. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017, Part II. LNCS, vol. 10625, pp. 66–96. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70697-9_3
Groth, J.: On the size of pairing-based non-interactive arguments. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 305–326. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_11
Gabizon, A., Williamson, Z.J., Ciobotaru, O.: PLONK: Permutations over Lagrange-bases for oecumenical noninteractive arguments of knowledge. Cryptology ePrint Archive, Report 2019/953 (2019). https://eprint.iacr.org/2019/953
Lipmaa, H.: Progression-free sets and sublinear pairing-based non-interactive zero-knowledge arguments. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 169–189. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_10
Lipmaa, H.: Simulation-extractable SNARKs revisited. ePrint Cryptogoly Archive, Report 2019/612 (2019)
Loss, J.: New techniques for the modular analysis of digital signature schemes. Ph.D thesis, Ruhr University Bochum, Germany (2019)
Lysyanskaya, A., Rivest, R.L., Sahai, A., Wolf, S.: Pseudonym systems. In: Heys, H., Adams, C. (eds.) SAC 1999. LNCS, vol. 1758, pp. 184–199. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-46513-8_14
Maurer, U.: Abstract models of computation in cryptography (invited paper). In: Smart, N.P. (ed.) Cryptography and Coding 2005. LNCS, vol. 3796, pp. 1–12. Springer, Heidelberg (2005). https://doi.org/10.1007/11586821_1
Maller, M., Bowe, S., Kohlweiss, M., Meiklejohn, S.: Sonic: zero-knowledge SNARKs from linear-size universal and updatable structured reference strings. In: Cavallaro, L., Kinder, J., Wang, X., Katz, J. (eds.) ACM CCS 2019, pp. 2111–2128. ACM (2019)
Mizuide, T., Takayasu, A., Takagi, T.: Tight reductions for Diffie-Hellman variants in the algebraic group model. In: Matsui, M. (ed.) CT-RSA 2019. LNCS, vol. 11405, pp. 169–188. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-12612-4_9
Nechaev, V.I.: Complexity of a determinate algorithm for the discrete logarithm. Math. Notes 55(2), 165–172 (1994). https://doi.org/10.1007/BF02113297
Okamoto, T., Pointcheval, D.: The gap-problems: a new class of problems for the security of cryptographic schemes. In: Kim, K. (ed.) PKC 2001. LNCS, vol. 1992, pp. 104–118. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44586-2_8
Paillier, P., Vergnaud, D.: Discrete-log-based signatures may not be equivalent to discrete log. In: Roy, B. (ed.) ASIACRYPT 2005. LNCS, vol. 3788, pp. 1–20. Springer, Heidelberg (2005). https://doi.org/10.1007/11593447_1
Shoup, V.: Lower bounds for discrete logarithms and related problems. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 256–266. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-69053-0_18
Acknowledgements
This work is funded in part by the MSR–Inria Joint Centre. The second author is supported by the Vienna Science and Technology Fund (WWTF) through project VRG18-002. Parts of this work were done while he was visiting the Simons Institute for the Theory of Computing.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Bauer, B., Fuchsbauer, G., Loss, J. (2020). A Classification of Computational Assumptions in the Algebraic Group Model. In: Micciancio, D., Ristenpart, T. (eds) Advances in Cryptology – CRYPTO 2020. CRYPTO 2020. Lecture Notes in Computer Science(), vol 12171. Springer, Cham. https://doi.org/10.1007/978-3-030-56880-1_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-56880-1_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56879-5
Online ISBN: 978-3-030-56880-1
eBook Packages: Computer ScienceComputer Science (R0)


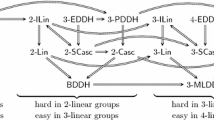


 and all generators
and all generators 
 (left) and
(left) and  (right) relative to group
(right) relative to group 
 or
or
 is
is  is
is  is
is  with
with  for
for  and
and  , implicitly sets
, implicitly sets  . Since
. Since 
 or
or
 is
is  is
is  is
is 
 or
or
 is
is  is
is  is
is 
 or
or
 is
is  is
is  is
is 

 or
or
 is
is  is
is  is
is 
 relative to bilinear group
relative to bilinear group 