Tensor Approximation for Multidimensional and Multivariate Data

Abstract

Tensor decomposition methods and multilinear algebra are powerful tools to cope with challenges around multidimensional and multivariate data in computer graphics, image processing and data visualization, in particular with respect to compact representation and processing of increasingly large-scale data sets. Initially proposed as an extension of the concept of matrix rank for 3 and more dimensions, tensor decomposition methods have found applications in a remarkably wide range of disciplines. We briefly review the main concepts of tensor decompositions and their application to multidimensional visual data. Furthermore, we will include a first outlook on porting these techniques to multivariate data such as vector and tensor fields.

1 Introduction

Data approximation is widely used in the fields of computer graphics and scientific visualizations. One way to achieve it is to decompose the data into a more compact and compressed representation. The general idea is to express a dataset by a set of bases, which are used to reconstruct the dataset to its approximation when needed (see Fig. 1). More specifically, such a representation usually consists of the actual bases and the corresponding coefficients describing the relationship between the original data and the actual bases. Typically, such compact representations consist of less data than the original dataset, capture the most significant features, and, moreover, describe the data in a format that is convenient for adaptive data loading and access.

Fig. 1

Compact data representation for a 3rd-order tensor $\mathcal {A}$ (a volume) by bases and coefficients that can be used to reconstruct the data to its approximation $\widetilde{\mathcal {A}}$

Bases for compact data representation can be classified into two types: pre-defined and learned bases. Pre-defined bases comprise a given function or filter, which is applied to the dataset without any a-priori knowledge of the correlations in the dataset. In contrast, learned bases are generated from the dataset itself. Established examples of the former are the Fourier transform (FT) and the wavelet transform (WT). Well-known examples of the latter are the principal component analysis (PCA), the singular value decomposition (SVD) and vector quantization. Using predefined bases is often computationally cheaper, but learned bases potentially remove more redundancy from a dataset.

Generally, PCA-like methods are able to extract the main data direction of the dataset and represent the data in another coordinate system such that it makes it easier for the user to find the major contributions within the dataset. To exploit this, PCAs higher-order extension—tensor approximation (TA)—can be used for multidimensional datasets. The first occurrence of TA was in [21]. The idea of multi-way analysis, however, is generally attributed to Catell in 1944 [11]. It took a few decades until tensor approximations received more widespread attention, namely by several authors in the field of psychometrics [10, 19, 52].

1.1 Higher-Order Data Decompositions

The matrix SVD works on 2D data arrays and exploits the fact that the dataset can be represented with a few highly significant coefficients and corresponding reconstruction vectors based on the matrix rank reduction concept. The SVD, being a multilinear algebra tool, computes (a) a rank-R decomposition and (b) orthonormal row and column vector matrices. Unlike for 2D, the extension to higher-orders is not unique and these two main properties are captured by two different models that are both called tensor approximations : the Tucker model [14, 15, 25, 49, 52] preserves the orthonormal factor matrices while the CP model (from CANDECOMP [10] and PARAFAC [19]) preserves the rank-R decomposition.

Generally speaking, a tensor is a term for a higher-order generalization of a vector or a multidimensional array. In TA approaches, a multidimensional input dataset in array form, i.e., a tensor, is factorized into a sum of rank-one tensors or into a product of a core tensor (coefficients that describe the relationship to input data) and matrices (bases), i.e., one for each dimension. This factorization process is generally known as tensor decomposition, while the reverse process of the decomposition is the tensor reconstruction.

Tensor decompositions have been widely studied in other fields and were reviewed [13, 25, 34] and summarized [27, 44]. Since TA was emerging from various disciplines, it was developed under multiple names. The CP model was independently developed under the terms CANDECOMP and PARAFAC, therefore, it is sometimes referenced with a single name. The Tucker model takes its name from Tucker, who initially worked on the three-mode factor analysis (3MFA), which is sometimes referred to as the Tucker3 model, also called the three mode PCA (3MPCA) [27, 28, 49]. Similarly the model was referenced to as n-mode PCA [23] since it is equivalent to applying PCA n times, each time along a different mode of the tensor. In [14] all these previous works were captured and written down as generalization of the SVD as multilinear singular SVD, which is usually termed as higher-order SVD or HOSVD. Furthermore, it was also called n-mode SVD in [54, 55].

Given an input tensor, different decompositions capture different types of structures and result in varying numbers of coefficients. For a given accuracy, the number of CP ranks required to decompose a tensor is usually much larger to that of Tucker ranks. On the other hand, CP’s storage cost grows only linearly with respect to its ranks, whereas that relationship becomes exponential in the case of Tucker. In sum, there is no silver bullet: CP is more suitable than Tucker for certain types of data, and vice versa. As a rule of thumb:

• Dense tensors of moderate dimensionality n over continuous variables, for example $n = 3$ or $n = 4$ including spatial and temporal axes, can often be compressed more compactly via the Tucker model.

• Tensors with categorical variables, sparse tensors, and tensors of higher dimensionality (say, $n \ge 5$) often benefit more from the CP model.

The data sets addressed in this chapter fit in the first category, and so we restrict our experiments to the Tucker model. To further illustrate the usual advantage of Tucker over CP for spatial visual data, see Fig. 2, we compare the number of coefficients and root mean squared error (RMSE) obtained with CP vs. Tucker using different numbers of ranks for a $256 \times 256 \times 256$ CT scan of a bonsai.

Fig. 2

RMSE achieved after CP vs. Tucker compression at different ranks R. For Tucker we take $R_1 = R_2 = R_3 = R$. The dataset used is a bonsai CT scan of size $256^3$

1.2 TA Applications in Graphics and Visualization

TA approaches have been applied to a wide range of application domains. Starting from psychometrics, in recent years, TA has been applied to visual data. A highly studied area is TA used for image ensembles [20, 35, 42, 43, 54, 58,59,60, 63] and/or TA used for pattern recognition, e.g., [17, 32, 40, 41, 43, 59]. In (real-time) rendering, tensor decompositions have been used as a method for global illumination models, e.g., for bidirectional reflectance distribution functions (BRDFs) [9, 45] or precomputed radiance transfer (PRT) [45, 50, 51]. Furthermore, TAs have successfully been used in graphics in the context of bidirectional texture functions (BTFs) [3, 18, 38, 39, 51, 55, 61, 62], texture synthesis [62], time-varying visual data [61, 62], 3D face scanning [56] and compression in animation [29, 31, 33, 36, 37, 53, 57].

In scientific visualization, TA methods have first been introduced for interactive multiresolution and multiscale direct volume rendering [6,7,8, 46,47,48]. Additionally, their compact representation power has been exploited for 3D volume data compression [4, 6] with notable advantages over other approaches at extreme compression ratios [2]. In this work, we explore the multiscale feature expressiveness of TA methods for the first time on vector fields, i.e. multidimensional multivariate data . Hence we interpret the vector field as a 4D array, or as a 4th-order data tensor. However, the rank-reduction of TA is only applied to the three spatial dimension.

1.3 Motivation and Contributions

In the results section (Sect. 9) we demonstrate that the feature sensitive approximation power of TA methods carries over from scalar to vector fields. These first results are promising and encourage the extension of tensor compression techniques to multivariate data fields, e.g. for compact storage and quick visualization at variable feature scales of large vector data in the fields of computational fluid dynamics or biomedicine. Moreover, based on the compression-domain data filtering and processing capabilities demonstrated in [5], we expect that important vector-field operators such as divergence or vorticity as well as other feature extraction operations can be analyzed and performed directly in the compressed TA format.

2 Singular Value Decomposition

 

The SVD is a widely used matrix factorization method to solve linear least-square problems. The SVD can be applied to any square or rectangular matrix $\mathbf {A} \in \mathbb {R}^{M \times N}$. Hence, the decomposition is always possible. The aim of the SVD is to produce a diagonalization of the input matrix $\mathbf {A}$. Since the input matrix $\mathbf {A}$ is not symmetric, two bases (matrices) are needed to diagonalize $\mathbf {A}$. Therefore, the SVD produces a matrix factorization into two orthogonal bases $\mathbf {U} \in \mathbb {R}^{M \times M}$ and $\mathbf {V} \in \mathbb {R}^{N \times N}$ and a diagonal matrix $\Sigma \in \mathbb {R}^{M \times N}$, as expressed in Eq. (1) (matrix form) or Eq. (2) (summation form).

$$\begin{aligned} \mathbf {A} =&\mathbf {U} \Sigma \mathbf {V^T} \end{aligned}$$

(1)

$$\begin{aligned} a_{mn} =&\sum \limits _{r = 1}^{R} u_{mr} {\sigma }_r v_{nr} \end{aligned}$$

(2)

The bases $\mathbf {U}$ and $\mathbf {V}$ contain orthogonal unit length vectors $\mathbf {u}_j$ and $\mathbf {v}_j$, respectively, and represent a r-dimensional column space ($\mathbb {R}^{M}$) and a r-dimensional row space ($\mathbb {R}^{N}$). Hence, the bases $\mathbf {U}$ and $\mathbf {V}$ are even orthonormal. The diagonal matrix $\Sigma$ contains the singular values $\sigma _r$, where $\sigma _1 \ge \sigma _2 \ge \dots \ge \sigma _R \ge 0$, where $R = \min (M,N)$. A singular value and a pair of singular vectors of a square or rectangular matrix $\mathbf {A}$ correspond to a non-negative scalar $\sigma$ and two non-zero vectors $\mathbf {u}_j$ and $\mathbf {v}_j$, respectively. The vectors $\mathbf {u}_j$ are the left singular vectors, and the vectors $\mathbf {v}_j$ are the right singular vectors (see Fig. 3). The number of non-zero singular values determines the rank R of the matrix $\mathbf {A}$.

Fig. 3

Visualization of the summed form of the SVD as shown in Eq. (2)—illustrating the singular values with the corresponding left and right singular vector pairs

In applications truncated versions of the SVD are frequently desired. That is, only the first K singular values $\sigma _1 \dots \sigma _K$ and the corresponding K singular vectors $\mathbf {u}_1 \dots \mathbf {u}_K$ and $\mathbf {v}_1 \dots \mathbf {v}_K$ are used for the reconstruction. This approach is referred to as low-rank approximation of a truncated SVD. Basically, each weighted outer vector-product term $\sigma _j \cdot \mathbf {u}_j \circ \mathbf {v}_j$ corresponds to a rank-one component (see also Fig. 4), and the SVD of matrices or images consequently represents a 2D data array eventually as a sum of such rank-one components.

Fig. 4

Simple 2D functions can be represented as an outer product of two 1D functions, and more complex ones as a weighted sum of several such components

3 Tensor Approximation Notation and Definitions

The notation taken here is mostly taken from De Lathauwer et al. [13, 14], Smilde et al. [44], as well as Kolda and Bader [25], who follow the notation proposed by Kiers [24]. To illustrate higher-order extensions we mostly make examples of order three.

3.1 General Notation

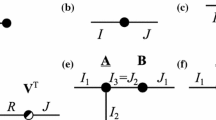
A tensor is a multidimensional array  (or an N-way data array): a 0th-order tensor (tensor0) is a scalar, a 1st-order tensor (tensor1) is a vector, a 2nd-order tensor is a matrix, and a 3rd-order (tensor3) is a volume, see Fig. 5. We consistently use the letter ‘a’ to represent the data, following the notation of, e.g.,  [14, 15, 51, 61, 62]. We use lower case letters for a scalar a, lower case boldface letters for a vector $\mathbf {a}$ in $\mathbb {R}^{I_1}$, capital boldface letters for a matrix $\mathbf {A}$ in $\mathbb {R}^{I_1 \times I_2}$, and calligraphic letters for a 3rd-order tensor $\mathcal {A}$ in $\mathbb {R}^{I_1 \times I_2 \times I_3}$.

Fig. 5

A tensor is a multidimensional array: a 2nd-order tensor is a matrix $\mathbf {A}$ and a 3rd-order tensor is a volume $\mathcal {A}$

The order of a tensor is the number of data directions, also referred as ways or modes. Along a mode n, the index $i_n$ runs from 1 to $I_N$. By using lower script indices for the modes, we can extend the index scheme to any order, i.e., $I_1, I_2, I_3, I_4, \dots$. The ith entry of a vector $\mathbf {a}$ is denoted by $a_{i}$, an element $(i_1,i_2)$ of a matrix $\mathbf {A}$ is denoted by $a_{i_1 i_2}$, and an element $(i_1, i_2, i_3)$ of a 3rd-order tensor $\mathcal {A}$ is denoted by $a_{i_1 i_2 i_3}$.

The general term fibers is used as a generalization for vectors taken along different modes in a tensor. A fiber is defined by fixing every index but one. A matrix column is thus a mode-1 fiber and a matrix row is a mode-2 fiber. 3rd-order tensors have column, row, and tube fibers, denoted by $\mathbf {a}_{i_1}, \mathbf {a}_{i_2}$, and $\mathbf {a}_{i_3}$, respectively. Sometimes, fibers are also called mode-n vectors.

Slices are two-dimensional sub-sections of a tensor (e.g., one fixed index in a 3rd-order tensor). For a 3rd-order tensor $\mathcal {A}$, there are, for example, frontal, horizontal, and lateral slices, denoted by $\mathbf {A}_{i_3}, \mathbf {A}_{i_1}$, and $\mathbf {A}_{i_2}$, respectively as illustrated in Fig. 6.

Fig. 6

Slices of a 3rd-order tensor $\mathcal {A}$

For computations, a tensor is often reorganized into a matrix what we denote as tensor unfolding (sometimes called matricization). There are two main unfolding strategies, backward cyclic unfolding [14] and forward cyclic unfolding [24] as shown in Fig. 7. An unfolded tensor in matrix shape is denoted with a subscript in parentheses, e.g., $\mathbf {A}_{(n)}$.

Fig. 7

Forward cyclic unfolding [24] of a 3rd-order tensor

3.2 Computing with Tensors

While many more operations on tensors exist, here we only outline the most common products used within the scope of this work.

• An Nth-order tensor is defined as $\mathcal {A} \in \mathbb {R}^{I_1 \times I_2 \times \dots \times I_N}$.

• The tensor product is denoted here by $\otimes$: however, other symbols are used in the literature, too. For rank-one tensors, the tensor product corresponds to the vector outer product ($\circ$) of N vectors $\mathbf {b}^{(n)} \in \mathbb {R}^{I_n}$ and results in an Nth-order tensor $\mathcal {A}$. The tensor product or vector outer product for a 3rd-order rank-one tensor is illustrated in Fig. 8: $\mathcal {A} = \mathbf {b}^{(1)} \circ \mathbf {b}^{(2)} \circ \mathbf {b}^{(3)}$, where an element ($i_1, i_2, i_3$) of $\mathcal {A}$ is given by $a_{i_1 i_2 i_3} = {b}^{(1)}_ {i_1} {b}^{(2)} _{i_1} {b}^{(3)} _{i_3}$.

• The inner product of two same-sized tensors $\mathcal {A, B} \in \mathbb {R}^{I_1 \times I_2 \times \dots \times I_N}$ is the sum of the products of their entries, i.e., Eq. (3).

  $$\begin{aligned} (\mathcal {A, B}) = \sum \limits _{i_1 = 1}^{I_1}\sum \limits _{i_2 = 1}^{I_2} \dots \sum \limits _{i_N = 1}^{I_N} a_{i_1i_2\ldots i_N} b_{i_1i_2\ldots i_N} \end{aligned}$$

  (3)

• The n-mode product [14] multiplies a tensor by a matrix (or vector) in mode n. The n-mode product of a tensor $\mathcal {B} \in \mathbb {R}^{I_1 \times I_2 \times \dots \times I_N}$ with a matrix $\mathbf {C} \in \mathbb {R}^{J_n \times I_n}$ is denoted by $\mathcal {B} \times _n \mathbf {C}$ and is of size $I_1 \times \dots \times I_{n-1} \times J_n \times I_{n+1} \times \dots \times I_N$. That is, element-wise we have Eq. (4).

  $$\begin{aligned} (\mathcal {B} \times _n \mathbf {C})_{i_1 \dots i_{n-1} j_n i_{n+1} \dots i_N} = \sum \limits _{i_n = 1}^{I_n} b_{i_1 i_2 \dots i_N} \cdot c_{j_n i_n} \end{aligned}$$

  (4)

  Each mode-n fiber is multiplied by the matrix $\mathbf {C}$. The idea can also be expressed in terms of unfolded tensors (reorganization of a tensor into a matrix as described in Sect. 3.1). The n-mode product of a tensor with a matrix is related to a change of basis in the case when a tensor defines a multilinear operator [25]. The n-mode product is the generalized operand to compute tensor times matrix (TTM) multiplications, and can best be illustrated using unfolded tensors as in Fig. 9.

  $$\begin{aligned} \mathcal {A} = \mathcal {B} \times _n \mathbf {C} \Leftrightarrow \mathbf {A}_{(n)} = \mathbf {C}\mathbf {B}_{(n)} \end{aligned}$$

  (5)

• The norm of a tensor $\mathcal {A} \in \mathbb {R}^{I_1 \times I_2 \times \dots \times I_N}$ is defined analogously to the matrix Frobenius norm $\Vert \mathbf {A}\Vert _F$ and is the square root of the sum squares of all its elements, i.e., Eq. (6).

  $$\begin{aligned} \Vert \mathcal {A}\Vert _F = \sqrt{\sum \limits _{i_1 = 1}^{I_1}\sum \limits _{i_2 = 1}^{I_2} \dots \sum \limits _{i_N = 1}^{I_N} a_{i_1i_2\ldots i_N}^2 } \end{aligned}$$

  (6)

Fig. 8

Three-way outer product for a 3rd-order rank-one tensor $\mathcal {A} =\mathbf {b}^{(1)} \circ \mathbf {b}^{(2)} \circ \mathbf {b}^{(3)}$

Fig. 9

TTM multiplication $\mathbf {C}\cdot \mathbf {B}_{(n)}$, multiplying the unfolded 3rd-order tensor $\mathbf {B}_{(n)}$ with the matrix $\mathbf {C}$

3.3 Rank of a Tensor

 

In order to describe the definitions of the tensor rank, the definition for the matrix rank is recaptured. The matrix rank of a matrix $\mathbf {A}$ is defined over its column and row ranks, i.e., the column and row matrix rank of a matrix $\mathbf {A}$ is the maximal number of linearly independent columns and rows of $\mathbf {A}$ that can be chosen, respectively. For matrices, the column rank and the row rank are always equal and, a matrix rank is therefore simply denoted as rank$(\mathbf {A})$. A tensor rank is defined similarly to the matrix rank, however, there are differences. In fact, the extension of the rank concept is not uniquely defined in higher orders and we review the definitions for the tensor ranks from [14] here.

• The n-rank of a tensor $\mathcal {A}$, denoted by $R_n = {\mathrm rank}_n(\mathcal {A})$, is the dimension of the vector space spanned by mode-n vectors, where the mode-n vectors of $\mathcal {A}$ are the column vectors of the unfolding $\mathbf {A}_{(n)}$, and ${\mathrm rank}_n(\mathcal {A}) = {\mathrm rank}(\mathbf {A}_{(n)})$. Unlike matrices, the different n-ranks of a tensor are not necessarily the same.

• A higher-order tensor has a so called multilinear rank ($R_1, R_2, \dots , R_N$) [21] if its mode-1 rank (row vectors), mode-2 rank (column vectors) until its mode-n rank are equal to $R_1, R_2, \dots , R_N$, e.g., giving rise to a multilinear rank-($R_1, R_2, R_3$) for a 3rd-order tensor.

• A rank-one tensor is an N-way tensor $\mathcal {A} \in \mathbb {R}^{I_1 \times I_2 \times \dots \times I_N}$ under the condition that it can be expressed as the outer product of N vectors, as in Eq. (7) (see also [12, 30]). A rank-one tensor is also known under the term Kruskal tensor.

  $$\begin{aligned} \mathcal {A} = \mathbf {b}^{(1)} \circ \mathbf {b}^{(2)} \circ \dots \circ \mathbf {b}^{(N)} \end{aligned}$$

  (7)

• The tensor rank $R = {\mathrm rank}(\mathcal {A})$ is the minimal number of rank-one tensors that yield $\mathcal {A}$ in a linear combination (see [12, 14, 25, 30]). Except for the special case of matrices, the tensor rank is not necessarily equal to any of its n-ranks, but it always holds that $R_n \le R$.

4 Tensor Decompositions

 

In tensor decompositions an input tensor $\mathcal {A} \in \mathbb {R}^{I_1 \times I_2 \times \dots \times I_N}$ is decomposed into a set of factor matrices $\mathbf {U}^{(n)} \in \mathbb {R}^{I_n \times R_n}$ and coefficients $\mathcal {B} \in \mathbb {R}^{R_1 \times R_2 \times \dots \times R_N}$ that describe the relationship/interactivity between $\mathcal {A}$ and the set of $\mathbf {U}^{(n)}$.

Historically, as seen earlier, tensor decompositions are a higher-order extension of the matrix SVD. The nice properties of the matrix SVD, i.e., rank-R decomposition and orthonormal row-space vectors and column-space vectors, do not extend uniquely to higher orders. The rank-R decomposition can be achieved with the so-called CP model, while the orthonormal row and column vectors are preserved in the so-called Tucker model. An extensive review of the two models and further hybrid models can be found in [25]. Here, we only outline the Tucker model that we apply in our experiments.

4.1 Tucker Model

 

The Tucker model is a widely used approach for tensor decompositions. As given in Eq. (8), any higher-order tensor is approximated by a product of a core tensor $\mathcal {B} \in \mathbb {R}^{R_1 \times R_2 \times \dots \times R_N}$ and its factor matrices $\mathbf {U^{(n)}} \in \mathbb {R}^{I_n \times R_n}$, where the products $\times _n$ denote the n-mode product as outlined in Sect. 3.2. This decomposition can then again be reconstructed to its approximation $\widetilde{\mathcal {A}}$. The missing information of the input tensor $\mathcal {A}$ that cannot be captured by $\widetilde{\mathcal {A}}$ is denoted with the error e. The Tucker decomposition is visualized for a 3rd-order tensor in Fig. 10. Equivalently, a Tucker decomposition can also be represented as a sum of rank-one tensors as in Eq. (9) and illustrated in Fig. 11.

$$\begin{aligned} {\mathcal {A}} = \mathcal {B} \times _1 \mathbf {U}^{(1)} \times _2 \mathbf {U}^{(2)} \times _3 \dots \times _N \mathbf {U}^{(N)} + e \end{aligned}$$

(8)

Fig. 10

Tucker 3rd-order tensor: ${\mathcal {A}} = \mathcal {B} \times _1 \mathbf {U}^{(1)} \times _2 \mathbf {U}^{(2)} \times _3 \mathbf {U}^{(3)}$ + e

$$\begin{aligned} {\mathcal {A}} = \sum _{r_1 = 1}^{R_1} \sum _{r_2 = 1}^{R_2} \dots \sum _{r_N = 1}^{R_N} b_{r_1 r_2 \dots r_N} \cdot \mathbf {u}^{(1)}_{r_1} \circ \mathbf {u}^{(2)}_{r_2} \circ \dots \circ \mathbf {u}^{(N)}_{r_N} + e \end{aligned}$$

(9)

Fig. 11

Tucker 3rd-order tensor as a sum of rank-one tensors: ${\mathcal {A}} = \sum _{r_1 = 1}^{R_1} \sum _{r_2 = 1}^{R_2} \sum _{r_3 = 1}^{R_3} b_{r_1 r_2 r_3} \cdot \mathbf {u}^{(1)}_{r_1} \circ \mathbf {u}^{(2)}_{r_2} \circ \mathbf {u}^{(3)}_{r_3} + e$

The column vectors $\mathbf {u}^{(n)}_{r_n}$ of the factor matrices $\mathbf {U}^{(n)} \in \mathbb {R}^{I_n \times R_n}$ are usually orthonormal and can be thought of as principal components $R_n$ in each mode n [25]. The core tensor $\mathcal {B} \in \mathbb {R}^{R_1 \times R_2 \times \dots \times R_N}$ represents a projection of the original data $\mathcal {A} \in \mathbb {R}^{I_1 \times I_2 \times \dots \times I_N}$ onto its factor matrices and is always of the same order as the input data. The core tensor is computed in general, as shown in Eq. (10), and for orthogonal factor matrices as in Eq. (11). The element-wise core tensor computation is denoted in Eq. (12). In other words, the core tensor coefficients $b_{r_1 r_2 \dots r_N}$ represent the relationship between the Tucker model and the original data.

$$\begin{aligned} {\mathcal {B}} = \mathcal {A} \times _1 {\mathbf {U}^{(1)}}^{(-1)} \times _2 {\mathbf {U}^{(2)}}^{(-1)} \times _3 \dots \times _N {\mathbf {U}^{(N)}}^{(-1)} \end{aligned}$$

(10)

$$\begin{aligned} {\mathcal {B}} = \mathcal {A} \times _1 {\mathbf {U}^{(1)}}^\top \times _2 {\mathbf {U}^{(2)}}^\top \times _3 \dots \times _N {\mathbf {U}^{(N)}}^\top \end{aligned}$$

(11)

$$\begin{aligned} {\mathcal {B}} = \sum _{i_1 = 1}^{I_1} \sum _{i_2 = 1}^{I_2} \dots \sum _{i_N = 1}^{I_N} a_{i_1 i_2 \dots i_N} \cdot {\mathbf {u}^{(1)}_{i_1}}^\top \circ {\mathbf {u}^{(2)}_{i_2}}^\top \circ \dots \circ {\mathbf {u}^{(N)}_{i_N}}^\top \end{aligned}$$

(12)

The Tucker decomposition is not unique, which means that we can modify the core tensor $\mathcal {B}$ without affecting the model fit as long as we apply the same changes to the factor matrices (so-called core tensor rotations), for more details see [25].

Often, we are interested in compact models, which enable a compression of the input data. For example, after computing a (full) Tucker decomposition the core tensor $\mathcal {B}$ has the same size as the original input $\mathcal {A}$ and all the factor matrices are square. However, we are more interested in reduced-size, approximative Tucker decompositions, where $\mathcal {B}$ is an element of $\mathbb {R}^{R_1 \times R_2 \times R_3}$ with $R_1 < I_1$, $R_2 < I_2$ and $R_3 < I_3$. Using so-called rank-reduced tensor decompositions or truncated tensor decompositions one can directly obtain more compact decompositions.

5 Tensor Rank Reduction

 

As seen in Sect. 3.3, the extension of the matrix rank concept to higher orders is not unique and we will mostly follow the rank-($R_1, R_2, \dots , R_N$) tensor decomposition and reduced-rank approximation of the Tucker model here.

5.1 Rank-R and Rank-$(R_1, R_2, \dots , R_N)$ Approximations

A simple rank-one approximation is defined as $\widetilde{\mathcal {A}} = \lambda \cdot \mathbf {u}^{(1)} \circ \mathbf {u}^{(2)} \dots \circ \mathbf {u}^{(N)}$ from the rank-one tensor (vector) product ($\circ$) of its N basis vectors $\mathbf {u}^{(n)} \in \mathbb {R}^{I_n}$ and a weight factor $\lambda$. Hence a tensor $\mathcal {A}$ could be approximated by a linear combination of many rank-one approximations as in Eq. (13). This approximation, also known as a CP model, is called a rank-R approximation.

$$\begin{aligned} \widetilde{\mathcal {A}} = \sum _{r=1}^R \lambda _r \cdot \mathbf {u}^{(1)}_r \circ \mathbf {u}^{(2)}_r \circ \dots \circ \mathbf {u}^{(N)}_r \end{aligned}$$

(13)

Alternatively, if we allow all weighted tensor (vector) products $\mathbf {u}^{(1)}_{i_1} \circ \mathbf {u}^{(2)}_{i_2} \circ \dots \circ \mathbf {u}^{(N)}_{i_N}$ of any arbitrary index combinations $i_1i_2\dots i_N$, we end up with the Tucker model of Sect. 4.1 and Eq. 12 where the weight factors for all index combinations form the core tensor $\mathcal {B}$. Choosing $R_{1,\dots , N} < I_{1,\dots , N}$ we end up with a rank-$(R_1, R_2, \dots , R_N)$ approximation of $\mathcal {A}$, which is given by a decomposition into a lower-rank tensor $\widetilde{\mathcal {A}} \in \mathbb {R}^{I_1 \times I_2 \times \dots \times I_N}$ with ${\mathrm rank}_n(\widetilde{\mathcal {A}}) = R_n \le {\mathrm rank}_n(\mathcal {A})$. The approximated tensor $\widetilde{\mathcal {A}}$ is the n-mode product $\times _n$ of factor matrices $\mathbf {U}^{(n)} \in \mathbb {R}^{I_n \times R_n}$ and a core tensor $\mathcal {B} \in \mathbb {R}^{R_1 \times R_2\times \dots \times R_N}$ in a given reduced rank space (Eq. (14)). This rank-$(R_1, R_2, \dots , R_N)$ approximation was previously introduced as the Tucker model.

$$\begin{aligned} \widetilde{\mathcal {A}} = \mathcal {B} \times _1 \mathbf {U}^{(1)} \times _2 \mathbf {U}^{(2)} \times _3 \dots \times _N \mathbf {U}^{(N)} \end{aligned}$$

(14)

In general, a rank-reduced approximation is sought such that the least-squares cost function of Eq. (15) is minimized.

$$\begin{aligned} \widetilde{\mathcal {A}} = \arg \min _{\widetilde{\mathcal {A}}} \Vert \mathcal {A} - \widetilde{\mathcal {A}}\Vert \ ^2 \end{aligned}$$

(15)

Given that ($R_1, R_2, \dots , R_N$) are sufficiently smaller than the initial dimensions ($I_1, I_2, \dots , I_N$), the core coefficients $\mathcal {B} \in \mathbb {R}^{R_1 \times R_2 \times \dots \times R_N}$ and the factor matrices $\mathbf {U}^{(n)} \in \mathbb {R}^{I_n \times R_n}$ can lead to a compact approximation of $\widetilde{\mathcal {A}}$ of the original tensor $\mathcal {A}$. In particular, the multilinear rank-$(R_1, R_2, \dots , R_N)$ is typically explicitly chosen to be smaller than the initial ranks in order to achieve a compression of the input data (see also [2, 4, 6]).

5.2 Truncated Tensor Decomposition

Similar to matrix SVD, tensor rank reduction can be used to generate lower-rank reconstructions $\widetilde{\mathcal {A}}$ of the input $\mathcal {A}$. The tensor rank parameters $R_n$ are chiefly responsible for the number of TA bases and coefficients that are used for the reconstruction and hence are responsible for the approximation level. In higher orders, the CP decomposition is not directly rank-reducible, however, the truncation of the Tucker decomposition is possible due to the all-orthogonality property of the core tensor.

For a 3rd-order tensor, all-orthogonality means that the different horizontal matrix slices of the core $\mathcal {B}$ (the first index $i_1$ is kept fixed, while the two other indices, $i_2$ and $i_3$, are free) are mutually orthogonal with respect to the scalar product of matrices (i.e., the sum of the products of the corresponding entries vanishes). The same holds for the other slices with fixed indices $i_2$ and $i_3$ (see [14]). Therefore, given an initial sufficiently accurate rank-$(R_1,R_2,R_3)$ Tucker model, we can progressively choose lower ranks $K_n < R_n$ for reduced quality reconstructions. As indicated in Fig. 12, the ranks $K_n$ indicate how many factor matrix columns and corresponding core tensor entries are used for the reconstruction.

Fig. 12

Illustration of a rank reduced Tucker tensor reconstruction: A reduced range of factor matrix columns with corresponding fewer core tensor entries reconstructs a lower quality approximation but at full resolution

Note that the ordering of the coefficients in the Tucker core tensor $\mathcal {B}$ is not strictly decreasing in contrast to the decreasing singular values in the matrix SVD case. However, in practice it can be shown that progressive tensor rank reduction in the Tucker model works very well for adaptive reconstruction of the data at different accuracy levels.

6 Tucker Decomposition Algorithms

There are various strategies for how to compute and generate a tensor decomposition. The most popular and widely used group of algorithms belongs to the alternating least squares (ALS) algorithms, the other group of algorithms uses various Newton methods. The respective algorithms differ for the computation of the different tensor models, and we will mainly focus on the Tucker model in our review.

For the Tucker model, the first decomposition algorithms used were a simple higher-order SVD (HOSVD) (see [14]), the so-called Tucker1 [52], a three-mode SVD. However, the truncated decompositions of higher orders are not optimal in terms of best fit, which is measured by the Frobenius norm of the difference. Starting from a HOSVD algorithm, tensor approximation ALS algorithms [26, 28] were developed, where one of the first Tucker ALS was the so-called TUCKALS [49]. Later various improvements accelerated [1] or optimized the basic TUCKALS method. The higher-order orthogonal iteration (HOOI) algorithm [15] is an iterative algorithm that performs a better fit for a truncated HOSVD version.

Newton methods are also used for the Tucker decomposition or rank-($R_1, R_2, \dots , R_N$) approximation. They typically start with a HOOI initialization and then converge faster to the final point. [16] developed a Newton-Grassman optimization approach, which takes much fewer iterations than the basic HOOI - even though one single iteration is more expensive due to the computation of the Hessian. While the HOOI is not guaranteed to converge, the Newton-Grassmann Tucker decomposition is guaranteed to converge to a stationary point. Another Newton method was proposed by [22], who developed a differential-geometric Newton algorithm with a fast quadratic convergence of the algorithm in a neighborhood of the solution. Since this method is not guaranteed to converge to a global maximum, they support the method by starting with an initial guess of several HOOI iterations, which increases the chances of converging to a solution.

7 Tensor Reconstruction

 

The tensor reconstruction from a reduced-rank tensor decomposition can be achieved in multiple ways. One alternative is a progressive reconstruction: Each entry in the core tensor $\mathcal {B}$ is considered as weight for the outer product between the corresponding column vectors in the factor matrices $\mathbf {U}^{(n)}$. This gives rise to Eq. (16) for the Tucker reconstruction.

$$\begin{aligned} \widetilde{\mathcal {A}} = \sum _{r_1 = 1}^{R_1} \sum _{r_2 = 1}^{R_2} \dots \sum _{r_N = 1}^{R_N} b_{r_1 r_2 \dots r_N} \cdot \mathbf {u}^{(1)}_{r_1} \circ \mathbf {u}^{(2)}_{r_2} \circ \dots \circ \mathbf {u}^{(N)}_{r_N} \end{aligned}$$

(16)

This reconstruction strategy corresponds to forming rank-one tensors and cumulatively summing them up. The accumulated weighted subtensors then form the approximation $\widetilde{\mathcal {A}}$ of the original data $\mathcal {A}$. In particular for the Tucker model, this is an expensive reconstruction strategy since it involves multiple for-loops to run over all the summations, for a total cost of $O(R^N \cdot I^N)$ operations.

7.1 Element-Wise Reconstruction

A simple approach is to reconstruct each required element of the approximated dataset individually, which we call element-wise reconstruction. Each element $\widetilde{a}_{i_1 i_2 i_3}$ is reconstructed, as shown in Eq. (17) for the Tucker reconstruction. That is, all core coefficients multiplied with the corresponding coefficients in the factor matrices are summed up (weighted sum).

$$\begin{aligned} \widetilde{a}_{i_1 i_2 \dots i_N} = \sum _{r_1 r_2 \dots r_N} b_{r_1 r_2 \dots r_N} \cdot {u}^{(1)}_{i_1 r_1} \cdot {u}^{(2)}_{i_2 r_2} \cdot \dots \cdot {u}^{(N)}_{i_N r_N} \end{aligned}$$

(17)

Element-wise reconstruction requires $O(R^N)$ operations on average. It can be beneficial for applications where only a sparse set of reconstructed elements are needed.

7.2 Optimized Tucker Reconstruction

A third reconstruction approach—applying only to the Tucker reconstruction—is to build the n-mode products along every mode, which leads to a TTM multiplication for each mode, e.g., TTM1 along mode 1, (see also Eq. (5)). This is analogous to the Tucker model given by Eq. (14). The intermediate results are then multiplied along the next modes, e.g., TTM2 and finally TTM3. In Fig. 13 we visualize the TTM reconstruction, and the intermediate results $\mathcal {B'}$ and $\mathcal {B}''$ as well as the final approximation $\widetilde{\mathcal {A}}$, applied to a 3rd-order tensor using n-mode products.

Fig. 13

Forward cyclic TTM multiplications after [24] along the three modes (n-mode products)

Since it exploits matrix multiplications, this optimized algorithm is much faster than progressive reconstruction (Eq. (16)). Its cost is dominated by $O(R_1 \cdot I^N)$. In 3D, in particular, it takes $O(R_1 \cdot I_1 \cdot I_2 \cdot I_3 + R_1 \cdot R_2 \cdot I_2 \cdot I_3 + R_1 \cdot R_2 \cdot R_3 \cdot I_3)$ operations.

8 Useful TA Properties for Scientific Visualization

As stated in the introduction, TA is the higher-order generalization of the matrix SVD, which can offer either properties of (a) rank-R decomposition or (b) orthonormal row-space and column-space vectors. In higher orders, the orthonormal row and column vectors are preserved in the Tucker model which thus supports progressive rank-reduced approximations and reconstructions.

8.1 Spatial Selectivity and Subsampling

 

The Tucker model (Sect. 4.1) consists of one factor matrix per mode (data direction) $\mathbf {U^{(n)}} \in \mathbb {R}^{I_n \times R_n}$ and one core tensor $\mathcal {B} \in \mathbb {R}^{R_1 \times R_2\times \dots \times R_N}$. The core tensor $\mathcal {B}$ is in effect a projection of the original data $\mathcal {A}$ onto the basis of the factor matrices $\mathbf {U^{(n)}}$. In case of a volume, the Tucker model has three modes, as illustrated in Fig. 10, and defines an approximation $\widetilde{\mathcal {A}} = \mathcal {B} \times _1 \mathbf {U}^{(1)} \times _2 \mathbf {U}^{(2)} \times _3 \mathbf {U}^{(3)}$ of the original volume $\mathcal {A}$ (using n-mode products $\times _n$).

The row and column axes of the factor matrices represent two different spaces: (1) the rows correspond to the spatial dimension in the corresponding mode, and (2) the columns to the approximation quality. These two properties can be exploited for multiresolution modeling (spatial selection and subsampling of rows) and multiscale approximation (rank reduction on the columns) (see also Fig. 14). In [5, 47] we demonstrated how these features can be exploited for multiresolution and multiscale reconstruction as well as filtering of compressed volume data in the context of interactive visualization.

Fig. 14

Factor matrix properties along the vertical axis supporting: (1.1) spatial selectivity, (1.2) spatial subsampling, and (2) low-rank approximation

8.2 Approximation and Rank Reduction

 

As described earlier, the Tucker model defines a rank-$(R_1,R_2,R_3)$ approximation, where a small $R_n$ corresponds to a low-rank approximation (with details removed) and a large $R_n$ corresponds to a more accurate approximation of the original. The highest rank $R_n$ for the initial Tucker decomposition has to be given explicitly. However, rank reductions can be applied after the initial decomposition (similar to the rank reduction in matrix SVD). Even though the core tensor coefficients are not guaranteed to be in decreasing order, as in matrix SVD, in practice it can be shown that progressive tensor rank reduction in the Tucker model works well for adaptive visualization of the data at different feature scales [2, 4,5,6, 47].

As illustrated in Fig. 12 in Sect. 5.2, the ranks indicate how many factor matrix columns and corresponding core tensor entries are used for a desired reconstruction. Thus, given a rank-$(R_1,R_2,R_3)$ Tucker model, we can specifically or progressively choose lower ranks $K_n < R_n$ for a reduced quality reconstruction, at the original spatial output resolution given by $I_n$ (or also subsampled).

Figure 15 shows the progressive rank reduction from an initial rank-$(256, 256, 256)$ Tucker decomposition of an original $512^3$ example volume. Shown are the visual results and the data reduction of the approximation at variable reduced-rank reconstructions. The numbers of coefficients include all core tensor and factor matrix entries that are used, e.g. a rank-(32, 32, 32) reconstruction corresponds to $32^3 + 3 \cdot 512 \cdot 32 = 81'920$ coefficients. The data reduction ratio can be derived by dividing the number of coefficients by $512^3$, which for $R=32$ results in using only $0.06\%$ of the original amount of data. In particular, Fig. 15 demonstrates the power of low-rank tensor approximations that can be used for multiscale feature visualization or progressive image refinement in volume rendering.

Fig. 15

Multiscale volume visualization by tensor rank reduction, corresponding to 0.02, 0.06, 0.27, 1.71 and 12.79% of the original amount of data used for $R=16,32,64,128,256$

9 Application to Multivariate Data

Encouraged by the data reduction power and the approximation quality of tensor approximations as shown in Fig. 16, we have extended the Tucker decomposition and reduced rank reconstruction to vector field data. Compared to scalar 3D volumes (e.g. from MRI or CT scans), a 3D vector field $\mathcal {V}$ (e.g. of velocities from a weather or fluid simulation) can be interpreted as a multivariate data field with D-dimensional vector-valued entries at each position in a $I_1 \times I_2 \times I_3$ grid. Thus we can interpret $\mathcal {V}$ as a 4th-order tensor $\mathcal {V} \in \mathbb {R}^{I_1 \times I_2 \times I_3 \times D}$. Note that the TA rank-reduction (Sect. 5) is only applied to the three spatial dimension as we are not interested in a dimensionality reduction of the vector-valued field value itself.

Fig. 16

a A $512^3$ isotropic turbulence volume of 512MB, b visually identical compression result using 51.2MB and c result after extreme compression down to only 1.71MB using the TTHRESH method [2]. All the visualizations are generated using ParaView

9.1 Dataset

For our first experiments we used a data set from the Johns Hopkins Turbulence Database http://turbulence.pha.jhu.edu/ representing a direct numerical simulation of incompressible magnetohydrodynamic (MHD) equations (see also Fig. 17). The data set contains, among other output variables, 3 velocity components that we used, hence $D=3$, covers a 3D grid of $256^3$ cells (downsampled subset from the original $1024^3$), hence $I_1 = I_2 = I_3 = 256$, and is the first time step from the output of the simulation.

The vector field therefore covers a 3D cube which we visualize using direct volume and streamline rendering techniques with color-coding of velocity, divergence, vorticity or error magnitudes in ParaView. Transparency is used to reduce clutter and opacity such as to focus the visualizations on the high-magnitude value regions. Note that this cubic vector field is dense and rendered over a black background, thus always appearing as a cube like object in the images.

9.2 Vector Field Magnitude and Angle

As can be seen in Fig. 17, the velocity magnitude and structure of the flow directions is very well maintained down to fairly course reconstructions using $R = 32$. Especially the (important) regions with larger velocity magnitudes are very well preserved with respect to their flow orientation as visible from the streamline visualization. The rendering applies an opacity transfer function setting which is almost linear, slight curve below the diagonal, to the vector field magnitude, highlighting the important high-velocity regions.

Fig. 17

Scalar velocity magnitude (top) and vector field streamline (bottom) visualization of the forced MHD turbulence simulation at variable reduced rank reconstructions $R = 32, 64, 128, 256$

To see how many details are lost after rank reduction of the velocity field data set, we calculated and visualized the error information for both magnitude and angle deviation in Figs. 18 and 19, respectively. For the magnitude, we normalized the error to be the percentage relative to the local vector field magnitude value. The rendering uses an opacity mapping which is almost linear, slight curve below the diagonal, to the vector field magnitude. This makes low magnitude and low opacity areas, and their errors, transparent or dark and highlights any errors in the more critical high-velocity regions. The completely dark images in Fig. 18e–h demonstrate that the magnitude error after rank reduction using Tucker decomposition is close to zero even with for $R=16$, which is 1/16 of the original full rank of 256. The barely noticeable dark blue regions in Fig. 18a–d correspond to low errors in high-velocity regions, with errors in the range of less than $10\%$ down to $10^{-8}\%$ (with $60\%$ being white).

Fig. 18

Relative magnitude error (in $\%$) of the velocity field with reduced rank reconstructions $R = 1, 2, 4, 8, 16, 32, 64, 128$

Compared to the almost negligible relative magnitude errors of the velocity field, however, the angular error of the same data set after rank reduction is more prominent as shown in Fig. 19. The maximum angular error $\pi =180^\circ$ is shown in red while small errors are shown in dark blue ($0^\circ$). The rendering applies an opacity setting almost linear to the angle offset, hence in Fig. 19 large angular errors are highlighted. However, this does not relate to the local strength of the vector field since large angle differences in low-magnitude areas are not that important. Directly comparing Figs 17 and 19, which have the same viewing configuration, one can observe that large angular errors occur mostly in very low-velocity areas and may thus not be that relevant. In particular, since for very short vectors small errors can cause large angular changes.

Fig. 19

Absolute angular error $[0^\circ , 180^\circ ]$ of the velocity field with reduced rank reconstructions $R = 1, 2, 4, 8, 16, 32, 64, 128$

9.3 Vorticity and Divergence

We also inspected the influence of low-rank tensor compression on the two most fundamental features of vector field data: divergence and vorticity. As can be seen in Fig. 20, the global structure of the magnitude from both the divergence field and the vorticity field are still very well preserved with rank $R = 64$, which is 1/4 of the original full rank of 256. The values are given in their absolute ranges of $[0.36, -0.43]$ and $[0.52, 10^{-5}]$ for the divergence and vorticity respectively. The rendering applies an opacity setting which is almost linear, slight curve below the diagonal, to the magnitude values, highlighting the important regions.

Fig. 20

Magnitude of the vector field’s divergence (top) and vorticity (bottom) at variable reduced rank reconstructions $R = 32, 64, 128, 256$

For the vorticity vector field, we also calculated the relative magnitude error as for the velocity vector field data shown in Fig. 18, thus as percentage of the vorticity magnitude, and similar conclusions can also be drawn here for the results shown in Fig. 21. All errors are very low, and barely noticeable for rank-reductions down to $R=16$, which corresponds to 1/16 of the original data volume.

Fig. 21

Relative magnitude error (in $\%$) of the vorticity field with reduced rank reconstructions $R = 1, 2, 4, 8, 16, 32, 64, 128$

Additionally, we also computed the absolute angular error for the vorticity vector field, in this case applying an opacity proportional to the magnitude of the raw vector field, and the results are shown in Fig. 22. We can observe that the angular error almost everywhere is in the color range of dark to light blue which maps to errors from 0 up to $45^\circ$ in this plot, and thus the directional vorticity information seems to be well preserved.

Fig. 22

Absolute angular error $[0^\circ , 130^\circ ]$ of the vorticity field with reduced rank reconstructions $R = 1, 2, 4, 8, 16, 32, 64, 128$

10 Conclusions

In the analysis conducted in this first study on vector fields, we have shown that tensor approximation methods are not only very useful for multidimensional scalar fields but can also be applied to multivariate data, thus extending to vector and possibly tensor fields. In general we can observe that for the important high-velocity vector field regions, the low-rank reconstructions maintain the important overall structures of the flow features, in particular also the vorticity. Furthermore, we note that the MHD simulation model in theory should be divergence-free and thus the numerical results report very low divergence numbers. Therefore, we are very satisfied with the result that the low-rank tensor reconstructions do not result in an unexpected and uncontrolled enlargement of these divergence values, keeping them within the numerical range of the simulation.