Heat Transfer in Pulsating Flow and Its Impact on Temperature Distribution and Damping Performance of Acoustic Resonators

Abstract

A numerical framework for the prediction of acoustic damping characteristics is developed and applied to a quarter-wave resonator with non-uniform temperature. The results demonstrate a significant impact of the temperature profile on the damping characteristics and hence the necessity of accurate modeling of heat transfer in oscillating flow. Large Eddy Simulations are applied to demonstrate and quantify enhancement in heat transfer induced by pulsations. The study covers wall-normal heat transfer in pulsating flow as well as longitudinal convective effects in oscillating flow. A discussion of hydrodynamic and thermal boundary layers provides insight into the flow physics of oscillatory convective heat transfer.

1 Introduction and Placement in SFB

Combustion instabilities jeopardize the structural integrity of rocket combustion chambers. One measure to ensure safe operating conditions is the application of acoustic resonators to suppress the thermo-acoustic feedback. Modern engines such as the Vulcain 2 combustion chamber include L-shaped quarter-wave resonators. Due to regenerative cooling, large temperature differences exist between the hot combustion gases and the cooled chamber walls. The transient heat-up process brings additional uncertainty.

During the first funding period of SFB Transregio 40, A. Cardenas developed analytical correlations for the acoustic damping characteristics of a quarter-wave resonator, which indicate that the impact of temperature inhomogeneities is significant [20]. Thus accurate acoustic predictions require the detailed knowledge of the temperature distribution within a resonator. In this context, the turbulent pulsating nature of the flow in the resonator presents a crucial challenge for the modeling of heat transfer. Experimental results that reported significant enhancement of average heat transfer could not be reproduced in numerical simulations [20]. Low-order network models were developed to evaluate rocket engine combustion stability under the influence of acoustic resonators [11].

During the second funding period, K. Förner identified and quantified significant non-linear effects resulting from large oscillation amplitudes (e.g. vortex shedding) [12, 13]. This implies a high degree of uncertainty for the analytical correlations derived by Cardenas. On the contrary, high-resolution numerical studies are not prone to these inaccuracies.

In the final funding period, S. van Buren merged the two prior lines of study: A numerical framework to predict acoustic damping characteristics was developed and applied to quarter-wave resonators with local temperature inhomogeneities. Subsequently, heat transfer in turbulent pulsation flows was revisited and the range of investigations was extended to larger oscillation amplitudes. Indeed, significant wall-normal enhancement of heat transfer could be confirmed at increased amplitudes. To account for the geometry of a quarter-wave resonator tube, the investigations were extended to convective longitudinal effects in oscillating flows.

Based on the focus on heat transfer, the present project is assigned to the research area Structural Cooling (RA A). The integrated acoustic examination of the resonator in the Combustion Chamber reveals additional close connection to RA C.

2 Impact of Temperature Inhomogeneities on Damping Performance

A variety of analytical correlations to quantify the damping characteristic of acoustic resonators have been derived in analogy to mass-spring-damper systems (e.g. [15, 16, 21]). For the case of a Helmholtz resonator, the acoustically compact fluid in the neck section presents the oscillating mass (velocity fluctuation $u'$, compare Figs. 1 and 2). The compressible fluid in the cavity (volume V) acts as the restoring spring. Damping is induced by either viscous friction in the neck section (losses linear to the velocity perturbation $u'$) or vortex shedding (non-linear losses of higher order). In particular the latter introduces a large degree of uncertainty.

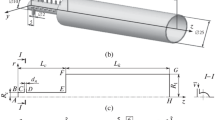
Laudien et al. [19] extended prior studies to the geometry of a quarter-wave resonator (Fig. 3). The difficulty connected to this geometry is the increased axial length scale (quarter-wave length at eigenfrequency) that violates the assumption of acoustic compactness. Laudien’s model is restricted to a homogeneous fluid temperature, as it has a significant impact on the local density $\rho$ and thus on the speed of sound c.

Fig. 1

Redrawn from [20]

Sketch of a Helmholtz resonator, with highlighted oscillating fluid mass in the neck region.

Fig. 2

Redrawn from [20]

Mass-spring-damper system, excited by pressure perturbation ${p}'$, responding in velocity fluctuation ${u}'$.

Fig. 3

Redrawn from [20]

Sketch of a quarter-wave resonator, with highlighted oscillating fluid mass derived by the representative length $l_\mathrm {r}$.

Fig. 4

Polynomial and average temperature profile in the neck and volume regions in a quarter-wave resonator

Resonators used in combustion chambers are generally exposed to significant temperature gradients. Figure 4 shows a schematic axial temperature distribution within a quarter-wave resonator: Hot combustion gas dominates at the front opening, whereas the backing of the cavity is exposed to regenerative cooling. During the first funding period of SFB Transregio 40 Cardenas [20] extended an approach by Kumar and Sujith [17] and introduced temperature inhomogeneities to the model of Laudien et al. [19]. Based on the analytical solution by Kumar and Sujith, applicable temperature profiles T(x) are mathematically restricted to a polynomial form:

$$\begin{aligned} T(x)= (ax + b)^n . \end{aligned}$$

(1)

The analytical model of Cardenas [20] revealed that temperature inhomogeneities have a significant impact on the damping performance, i.e. they cause a shift in eigenfrequency, a reduction of the effective frequency range and the minimum reflection coefficient. The frequency-dependent reflection coefficient $R(\omega )$ quantifies the ratio of the reflected acoustic wave g to the incident wave f:

$$\begin{aligned} R(\omega ) = \frac{g}{f} . \end{aligned}$$

(2)

Subsequently, a numerical framework based on computational fluid dynamics (CFD) for the calculation of the reflection coefficient $R(\omega )$ was presented and applied to quarter-wave resonators with temperature inhomogeneities by van Buren [2, 3]. The resonator is modeled by two- or three-dimensional wedge geometries with an imposed temperature profile. Incident acoustic waves are imposed in the form of harmonic as well as broadband forcing. The time series data generated with the latter approach is post-processed by system identification (SI)—a form of supervised machine learning—and only requires one single simulation to determine results for a wide range of frequencies. Central advantages over the analytical model are the flexibility of arbitrary temperature distributions and the incorporation of non-linear effects. Details on the numerical framework and simulation setup are given in [2, 3].

Fig. 5

Gain of the reflection coefficient for harmonic excitation (squares) and results for three randomly generated broadband excitations obtained by CFD/SI (dashed lines)

Fig. 6

Gain of the reflection coefficient of the analytical model (solid lines) and averaged results obtained by system identification of broadband excitation (dashed lines)

Figure 5 compares numerical results of harmonic and broadband forcing (CFD/SI). Overall, the qualitative and quantitative agreement is very good. This generates confidence in both methods. The plot also illustrates the physical impact of temperature inhomogeneities: All five setups have identical mean temperatures ($T = 647\,\mathrm {K}$) along the resonator tube. As the gradient between cooled backing and hot front opening is increased a significant shift in eigenfrequency is introduced ($\omega \approx 4600\,\mathrm {Hz}$ to $5000\,\mathrm {Hz}$). Furthermore, the effective frequency range of damping narrows and the minimum reflection coefficient R decreases. Both effects reduce the effectiveness of the resonator as a damper of thermo-acoustic instabilities.

Figure 6 compares CFD/SI results with the analytical correlation. There is qualitative agreement but quantitative offset in both frequency and reflection coefficient.

3 Impact of Acoustic Oscillations on Heat Transfer

The accurate computation of the acoustic characteristics of the resonator requires precise knowledge of the local temperature distribution of the working fluid. Therefore, fundamental understanding of heat transfer in the presence of strong acoustic perturbations is indispensable. For the problem at hand, physical boundary conditions define two categories of heat transfer [20]: First, within the combustion chamber, wall normal heat transfer from the hot fluid to the cooled wall occurs in turbulent pulsating flows. The pulsations originate from the superposition of a mean-flow and acoustic velocity perturbations. Second, within the resonator tube, axial heat transfer from the hot front section to the cooled backing of the cavity exists. In contrast to the first category, mean-flow is absent here, one speaks of oscillating flow.

Fig. 7

One-dimensional mode shape of the second harmonic in a channel. Mean flow is driven by the pressure gradient of $P_0(x)$

Fig. 8

Cyclic simulation domain of an acoustically compact channel section at a pressure node

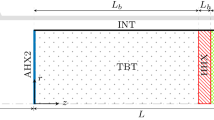
Figure 7 illustrates the modeling of an acoustically compact duct section at the position of a pressure node: In the small domain from $x = X$ to $x = X + \mathrm {d}x$, pressure perturbation p3 are not present, whereas acoustic velocity fluctuations u are maximum. The selection of this domain of interest is consistent with numerous previous studies, which report that enhancement in heat transfer coincides with velocity fluctuations rather than pressure oscillations [8,9,10, 14].

Figure 8 depicts the numerical domain at the location of a pressure node. The channel is confined by two walls of distance 2h. For the investigation of wall-normal heat transfer, these walls are constrained to homogeneous but different temperatures ($T_h$ and $T_c$ as shown in the figure). In the second case of longitudinal heat transfer, constant axial temperature gradients are applied. Cyclic conditions apply to the remaining four boundary patches. One central advantage of this setup is the generation of fully developed turbulent flow without the requirement of turbulent inflow conditions. The flow is driven by a momentum source term $S_{mom}$ that accounts for the acoustic oscillations via the spatial gradient of the pressure perturbation $p'$ and for the mean-flow via the gradient of the overall pressure $P_0$ (compare Fig. 7).

More detailed information of the incompressible Large Eddy Simulation is provided in [1, 4], including the selection of turbulence models, a mesh independence study and the validation against analytical, experimental and numerical results.

3.1 Wall Normal Heat Transfer

In this section, the core findings for wall-normal heat transfer in turbulent pulsating channel flows are presented and discussed. More detailed results are provided in [1, 4].

Fig. 9

Temporal averaged EHT over amplitude $\epsilon$ for various Stokes’ length $l_s^+$ corresponding to different frequencies

The figures in this section show the enhancement in heat transfer (EHT) versus non-dimensional pulsation amplitude $\epsilon$ for various Stokes’ lengths $l_s^+$. The EHT is defined as the enhancement in wall-normal heat flux of the turbulent pulsating flow $\dot{q}_{w,puls}$ over a turbulent but non-pulsation reference $\dot{q}_{w,ref}$:

$$\begin{aligned} \mathrm {EHT} = \frac{\dot{q}_{w,puls}-\dot{q}_{w,ref}}{\dot{q}_{w,ref}} . \end{aligned}$$

(3)

The non-dimensional pulsation amplitude $\epsilon$ relates the pulsating velocity amplitude $a_u$ at the channel center-plane (index $_c$) to the mean velocity of the corresponding non-pulsating reference:

$$\begin{aligned} \epsilon = \left. \frac{a_u}{u_{ref}} \right| _c . \end{aligned}$$

(4)

Lastly, the non-dimensional Stokes’ length $l_s^+$ is introduced as a measure for the pulsation frequency:

$$\begin{aligned} l_s^+ = \frac{u_\tau }{\nu } \delta _s = \frac{\mathrm {Re}_\tau }{h} \delta _s , \end{aligned}$$

(5)

where $\mathrm {Re}_\tau$ is the the turbulent Reynolds number and $\delta _s = (2 \omega / \nu )^{1/2}$ the classical Stokes length.

During the first funding period, numerical simulations by Cardenas [20] could not reproduce experimental results that report EHT of more than $100\%$. To resolve these discrepancies, the present study investigates flows at increased turbulent Reynolds number $\mathrm {Re}_\tau = 350$ (instead of $\mathrm {Re}_\tau \approx 180$). Furthermore, the numerical framework includes the dynamic calculation of locally resolved turbulent Prandtl numbers. Figure 9 depicts the temporal average of enhancement in heat transfer versus pulsation strength $\epsilon$ for various frequencies $l_s^+$. EHT is most pronounced at frequencies around $l_s^+ \approx 14$ and velocity amplitudes close to flow reversal (i.e. $\epsilon \approx 1$). In the parameter range under investigation, only minor effects of EHT confirm the results by Cardenas [20]. A time-resolved investigation over one pulsation period reveals significant variation in EHT, ranging from strong reduction (larger than $50\%$) to clear enhancement (up to $45\%$, Fig. 10)

The local maximum in EHT at $\epsilon \approx 1$ led originally to the conclusion that LES does not capture pronounced EHT [20]. However, this conclusion was premature. Indeed, examination of the time-resolved heat transfer (Fig. 10) strongly indicates the relevance of large flow velocities. This suggested the extension of the parameter range under investigation and to increase the pulsation strength to values beyond $\epsilon = 1.25$. The plateau in Fig. 11 (dashed blue line) shows that no significant enhancement in heat transfer develops below velocity amplitudes corresponding to $\epsilon < 2$, but for larger amplitudes ($\epsilon > 2$), a clear and significant increase in EHT develops. Despite numerous difference in physical modelling and numerical setup, the results qualitatively agree with the work of Wang and Zhang [22]. The significant enhancement in heat transfer is well explained by Fig. 12: At pulsation amplitudes close to flow reversal (e.g. $\epsilon = 1.4$), times of flow velocities close to rest hinder an overall (time-averaged) enhancement. In the case of significant flow reversal, these times of flow stagnation are quickly surpassed, providing longer intervals at large flow velocities.

Fig. 10

Phase related EHT for various non-dimensional Stokes’ length $l_s^+$ at exemplary $\epsilon \approx 0.65$ (depicted by circles in Fig. 9)

Fig. 11

Time averaged enhancement of heat transfer over the pulsation amplitude at $l_s^+ = 14$. Including results of Wang and Zhang [22]

Fig. 12

Ensemble averaged enhancement of heat transfer for four high pulsation amplitudes at $l_s^+ = 14$

3.2 Longitudinal Heat Transfer

The computational setup for the study of wall-normal heat transfer in pulsating turbulent flow is modified to account for a longitudinal convective mechanism first studied by Kurzweg [18]. Kurzweg derived a closed analytical expression for axial heat transfer in oscillatory laminar channel flows constrained by a constant axial temperature gradient. The velocity oscillations enhance the molecular thermal diffusivity by orders of magnitude: The fluid receives a wall heat flux at the hot reversal point, oscillates to the cold reversal point and returns its thermal energy to the walls. During the final funding period of SFB Transregio 40, van Buren applied LES to extend Kurzweg’s investigations to turbulent flows. Details on the numerical setup, results and discussions are given in [5, 7]

Fig. 13

Double-logarithmic presentation of the non-dimensional effective thermal diffusivity $\kappa _e$

Kurzweg [18] proposed an effective thermal diffusivity $\kappa _e$. In its non-dimensional form, this diffusivity is normalized by the angular frequency $\omega$ of the oscillation and the square of the tidal displacement $\Delta x^2$: $\kappa _e / \omega \Delta x^2$. The red line in Fig. 13 shows Kurzweg’s analytical results for effective thermal diffusivity over the Prandtl number $\Pr$ of the fluid. In agreement with the previous numerical study, $l_s^+ = 14$ was selected. This correlates with a Womersley number of $\mathrm {Wo} \approx 35$ and indicates thin hydrodynamic boundary layers compared to the channel width. Numerical results are displayed by the blue, orange, yellow and purple line, which are ordered by increasing oscillation strength. The lower two amplitudes generate laminar flow conditions and show overall agreement with the analytical correlation. At larger amplitudes, deviations appear at high Prandtl numbers, exceeding the location of the peak at $\mathrm {Wo}^2 \Pr \approx \pi$. These differences induced by the onset of turbulence are more apparent in the semi-logarithmic presentation in Fig. 14. The turbulence-induced enhancement of longitudinal heat transfer $\epsilon _\text {turb}$ is defined as the effective thermal diffusivity $\kappa _e$ in respect to its laminar reference. In the spectrum of technically relevant Prandtl numbers (e.g. $\Pr \approx 0.7$ for air), an increase of $100\%$ is expected. Future numerical investigations will extend the range of Prandtl numbers to these values.

Fig. 14

Semi-logarithmic presentation of the enhancement of longitudinal heat transfer $\epsilon _\text {turb}$

Figure 15 provides physical insight for the enhancement in effective thermal diffusivity at large Prandtl numbers approaching unity. To interpret the results, recall that the oscillating fluid is characterized by thin hydrodynamic boundary layers (i.e. $\mathrm {Wo} \approx 35$). The left plot of Fig. 15 shows a fluid Prandtl number of $\Pr = 0.0025$. This indicates a thermal boundary layer clearly exceeding its hydrodynamic counterpart. The plot reveals that the complete cross-sectional area of the channel ($\eta = z/h$) contributes to the longitudinal heat transfer. This is because disturbances in the temperature distribution propagate throughout the entire channel up to its center-plane. For increasing Prandtl numbers (center: $\Pr = 0.025$, right $\Pr = 0.25$), this wall-normal propagation is limited by the thermal conductivity. As a consequence, centered sections of the channel do not contribute to the convective transport anymore. In particular, the laminar setup is restricted to small wall-confined regions. The enhancement induced by turbulence is explained by an increase in wall normal heat flux, which increases the effective cross-sectional area.

van Buren and Polifke [1] also proposed a turbulence-related convective heat transfer coefficient $h_\text {turb}$. In the range of thin hydrodynamic boundary layers, this one-dimensional modeling approach—based on assumptions of bulk velocities and bulk temperatures outside of the boundary layer—predicts a scaling of $\epsilon _\text {turb}$ with the square-root of the Prandtl number $\Pr$. A comprehensive discussion of interactions between hydrodynamic and thermal boundary layers is provided in [6].

Figure 16 shows qualitative agreement of the numerical results (colored lines) and the analytic prediction (black dotted lines). The turbulence-dependent coefficient $h_\text {turb}$ is evaluated at $\Pr = 0.25$. According to its definition (details are given in [1]), the coefficient is zero for laminar flows and increases with oscillation amplitude or turbulence intensity, respectively. This is denoted by the non-dimensional forcing amplitude $\lambda$.

Fig. 15

Space-resolved effective thermal diffusivity over the channel width 2h at $\alpha ^2 \Pr = \pi$ (left), $10\pi$ (center) and $100\pi$ (right) for $\lambda = 100$ (blue), 150 (orange), 200 (yellow) and 250 (purple), $\alpha = 35.4$

Fig. 16

Detailed parametric study of enhancement in longitudinal heat transfer $\epsilon _\text {turb}$ for increasing, equi-spaced oscillation amplitudes ($\lambda = 162.5$ to 250, $\Delta \lambda = 12.5$). The black lines denote the model of van Buren and Polifke [1]

Fig. 17

Comparison of EHT (blue) [1] and the turbulence induced convective heat transfer coefficient $h_\text {turb}$ (orange) plotted over the non-dimensional amplitude $\lambda$. Evaluated at $\Pr = 0.25$

The trend of the turbulent coefficient $h_\text {turb}$ versus the forcing amplitude $\lambda$ is depicted in Fig. 17. Up to the laminar-to-turbulent transition, $h_\text {turb}$ is zero. At this threshold a significant increase is attributed to the initial onset of turbulence. With increasing amplitudes in the turbulent regime, the enhancement continuously decays.

Although there are numerous physical deviations between the setup of wall-normal and longitudinal enhancement in heat transfer (e.g. pulsating vs. oscillating flow, wall-normal vs. longitudinal temperature gradient, ...), results of the wall-normal study are also included in Fig. 17. Note that some characteristic features compare qualitatively: For both flows, there is certain threshold in forcing amplitude (i.e. $\lambda \approx 160$) beyond which overall heat transfer clearly increases. For the longitudinal heat transfer, this is explained by the laminar-to-turbulent transition. Due to the mean-flow, the wall-normal setup is always turbulent. Interestingly—and in agreement with conclusions given in [1]—significant EHT does not develop below this threshold. Furthermore, both results show a declining growth with increasing amplitude in the turbulent regime.

4 Summary and Conclusions

A numerical framework for the quantitative prediction of acoustic damping characteristics was developed and applied to quarter-wave resonators with temperature inhomogeneities. The results confirm the analytical finding of the first funding period, i.e. that the temperature distribution within the resonator has a significant impact and cannot be represented adequately by only the mean temperature. Central advantages of the numerical approach are the flexibility of arbitrary temperature distributions and the resolved investigation of non-linear losses (e.g. vortex shedding). It is self-evident that accurate acoustic predictions require precise knowledge of the present temperature distribution.

First LES-based evidence for significantly enhanced wall-normal heat transfer in turbulent pulsating flow was given. This confirms experimental studies that report enhancement of more than $100\%$. The present work provides quantitative results that cover a wide range of forcing frequencies and pulsation amplitudes. Below velocity amplitudes of significant flow reversals, the time-averaged enhancement of heat transfer is marginal. First with significant flow reversal ($\epsilon \approx 2.5$), periods of flow stagnation quickly pass and allow for major enhancement of more than $100\%$. The present study demonstrates the risk-potential to the thermal integrity of rocket engine combustion chambers: Extreme thermal loads are opposed to restrictions in design and material properties, resulting in little safety margins. Unforeseen enhancement in fluid-to-wall heat transfer during the design process may result in a catastrophic destruction of the chamber.

Within the resonator tube, longitudinal convective effects in oscillating flows are evaluated. In the range of physically relevant Prandtl numbers (e.g. air with $\Pr \approx 0.7$), the effective thermal diffusivity enhances significantly. Based on a comprehensive examination of hydrodynamic and thermal boundary layers, a simple model quantifies the impact of turbulence.

The present study sheds light on the complexity of a comprehensive design process of rocket combustion chambers. In particular, the close interdependence between acoustics and heat transfer requires a holistic treatment: The acoustic amplitude has an impact on heat transfer and thus on the temperature distribution. The local temperature—in turn—influences the damping characteristic of the acoustic resonators. One possible consequence is the shift in effective damping frequency and thus an overall change in acoustic amplitude (closing the feedback-loop at hand). Furthermore, non-linear damping effects present a second direct coupling mechanism between acoustic amplitude and the damping characteristics of the resonator. To conclude, these interdependences do not allow for a decoupled analysis of acoustics and heat transfer. In regards to a numerically supported design process, this finding comes along with major challenges in the selection of length and time scales. On the one hand, highly resolved LES are required to capture effect of EHT and vortex shedding. On the other hand, the length scale of the combustion chamber has to be considered over the time scale of the transient heating process. In future studies, sophisticated approaches that make use of reduced-order models might overcome current restrictions imposed by computational resources. This may include an iterative procedure between the different orders in time scales or an evaluation of EHT by an imposed wall model. From an applied point of view, one is well advised to adhere to the established practice of placing the resonator openings adjacent to cool recirculation zones, where only minor changes in temperature are expected, in order to avoid the complications discussed.