Abstract
Hyperedge replacement (HR) allows to define context-free graph languages, but parsing is NP-hard in the general case. Predictive top-down (PTD) is an efficient, backtrack-free parsing algorithm for subclasses of HR and contextual HR grammars, which has been described and implemented in earlier work, based on a representation of graphs and grammar productions as strings. In this paper, we define PTD parsers for HR grammars by graph transformation rules and prove that they are correct.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Hyperedge replacement (HR, [8]) is one of the best-studied mechanisms for generating graphs. Being context-free, HR grammars inherit most of the favorable structural and computational properties of context-free string grammars. Unfortunately, simplicity of parsing is not one of these, as there are NP-complete HR languages [1, 14]. Hence, efficient parsing can only be done for suitable subclasses. The authors have devised predictive top-down (PTD, [4]) and predictive shift-reduce (PSR, [6]) parsing for subclasses of HR grammars and, in fact, for subclasses of contextual HR grammars (CHR grammars, [2, 3]), which are a modest extension of HR grammars that allows to overcome some of the structural limitations of HR languages.
Although the concepts and implementation of PTD parsers have been described at depth in [4], their correctness has not yet been formally established. We show in this paper how PTD parsing can be defined by graph transformation rules and use this in order to prove the correctness of PTD parsers. Our experience with the correctness proof for PSR parsing in [6] seems to indicate that a graph- and rule-based definition of parsers can make this task easier.
Related work on using graph transformation for defining parsers has dealt with LR string grammars [11] and two-level string grammars [12]. For a broader discussion of related work on parsing algorithms for graph grammars in general we refer to [6, Sect. 10.1].
The paper is structured as follows. After recalling graph transformation concepts (Sect. 2) and HR grammars (Sect. 3), we introduce threaded HR grammars (Sect. 4), which impose a total order on the edges of their derived graphs, which in turn induces a dependency relation on their nodes. In Sect. 5, we define a general top-down parser for HR grammars that respects edge order and node dependencies, and prove it correct. Since this parser is nondeterministic and hence inefficient, we introduce properties that make the parser predictive, and backtrack-free (Sect. 6) and show that this yields correct parsers that terminate for grammars without left recursion.Footnote 1 We conclude the paper by indicating some future work (Sect. 7).
2 Preliminaries
In this paper, \(\mathbb {N}\) denotes the set of non-negative integers and [n] denotes \(\{1,\dots ,n\}\) for all \(n\in \mathbb {N}\). \(A^*\) denotes the set of all finite sequences over a set A; the empty sequence is denoted by \(\varepsilon \), and the length of a sequence \(\alpha \) by \(|\alpha |\). As usual,  and
and  denote the transitive and the transitive reflexive closure of a binary relation
denote the transitive and the transitive reflexive closure of a binary relation  . For a function
. For a function  , its extension
, its extension  to sequences is defined by \(f^*(a_1 \cdots a_n) = f(a_1) \cdots f(a_n)\), for all \(n\in \mathbb {N}\) and \(a_1,\dots ,a_n \in A\). The composition of functions
to sequences is defined by \(f^*(a_1 \cdots a_n) = f(a_1) \cdots f(a_n)\), for all \(n\in \mathbb {N}\) and \(a_1,\dots ,a_n \in A\). The composition of functions  and
and  is denoted as \(g\circ f\) and defined by \((g \circ f) (x) = g(f(x))\) for \(x \in A\). The restriction of f to some subset \(X \subseteq A\) is denoted as \(f|_X\).
is denoted as \(g\circ f\) and defined by \((g \circ f) (x) = g(f(x))\) for \(x \in A\). The restriction of f to some subset \(X \subseteq A\) is denoted as \(f|_X\).
Definition 1
(Hypergraph). An alphabet \(\varSigma \) is a finite set of symbols that comes with an arity function  . A hypergraph (over \(\varSigma \)) is a tuple
. A hypergraph (over \(\varSigma \)) is a tuple  , where
, where  and
and  are finite sets of nodes and hyperedges, respectively, the function
are finite sets of nodes and hyperedges, respectively, the function  attaches hyperedges to sequences of nodes, and the function
attaches hyperedges to sequences of nodes, and the function  labels hyperedges so that
labels hyperedges so that  for every
for every  , i.e., the number of attached nodes of hyperedges is dictated by the arity of their labels.
, i.e., the number of attached nodes of hyperedges is dictated by the arity of their labels.
\(\mathcal {G}_\varSigma \) denotes the class of hypergraphs over \(\varSigma \);  denotes the empty hypergraph, with empty sets of nodes and hyperedges. A set of hyperedges
denotes the empty hypergraph, with empty sets of nodes and hyperedges. A set of hyperedges  induces the subgraph consisting of these hyperedges and their attached nodes.
induces the subgraph consisting of these hyperedges and their attached nodes.
For brevity, we omit the prefix “hyper” in the sequel. Instead of “ or
or  ”, we often write “\(x \in G\)”. We often refer to the functions of a graph G by \( att _G\) and \( lab _G\). An edge carrying a label in an alphabet \(\varSigma \) is also called a \(\varSigma \)-edge. And a node is called isolated if no edge is attached to it.
”, we often write “\(x \in G\)”. We often refer to the functions of a graph G by \( att _G\) and \( lab _G\). An edge carrying a label in an alphabet \(\varSigma \) is also called a \(\varSigma \)-edge. And a node is called isolated if no edge is attached to it.
Definition 2
(Graph Morphism). Given graphs G and H, a graph morphism (morphism, for short)  is a pair
is a pair  of functions
of functions  and
and  that preserve attachments and labels, i.e.,
that preserve attachments and labels, i.e.,  and
and  . The morphism is injective or surjective if both
. The morphism is injective or surjective if both  and
and  are, and a subgraph inclusion of G in H if \(m (x) = x\) for every \(x \in G\); then we write \(G \subseteq H\). If m is surjective and injective, it is called an isomorphism, and G and H are called isomorphic, written as
are, and a subgraph inclusion of G in H if \(m (x) = x\) for every \(x \in G\); then we write \(G \subseteq H\). If m is surjective and injective, it is called an isomorphism, and G and H are called isomorphic, written as  .
.
For transforming graphs, we use the classical approach of [7], with injective matching and non-injective rules [9], but without rules that delete nodes.
Definition 3
(Rule). A graph transformation rule \(r=(P, R, r^\circ )\) consists of a pattern graph P, a replacement graph R, and a mapping  .Footnote 2 We briefly call r a rule and denote it as
.Footnote 2 We briefly call r a rule and denote it as  . An injective morphism
. An injective morphism  into a graph G is a match of r, and r transforms G at m to a graph H as follows:
into a graph G is a match of r, and r transforms G at m to a graph H as follows:
-
Remove all edges m(e),
 , from G to obtain a graph K.
, from G to obtain a graph K. -
Construct H from the disjoint union of K and R by identifying m(x) with \(r^\circ (x)\) for every
 .
.
Then we write  , but may omit m if it is irrelevant, and write
, but may omit m if it is irrelevant, and write  if \(\mathcal {R}\) is a set of rules such that
if \(\mathcal {R}\) is a set of rules such that  for some \(r \in \mathcal {R}\).
for some \(r \in \mathcal {R}\).
Sometimes it is necessary to restrict the application of a rule by requiring the existence or non-existence of certain graphs in the context of its match. Our definition of application conditions is based on [10].
Definition 4
(Conditional Rule). For a graph P, the set of conditions over P is defined inductively as follows: (i) a subgraph relation \(P \subseteq C\) defines a basic condition \(\exists C\) over P. (ii) if \(c,c'\) are conditions over P, then \(\lnot c\), \((c \wedge c')\), and \((c \vee c')\) are conditions over P.Footnote 3
An injective morphism  satisfies a condition c, written \(m \vDash c\), if
satisfies a condition c, written \(m \vDash c\), if
-
\(c = \exists C\) and there is an injective morphism
 so that \(m'|_P = m\);
so that \(m'|_P = m\); -
\(c = \lnot c'\) and
 ;
; -
\(c = (c' \wedge c'')\) and both \(m\vDash c'\) and \(m\vDash c''\);
-
\(c = (c' \vee c'')\) and \(m\vDash c'\) or \(m\vDash c''\).
A conditional rule \(r'=(r,c)\) consists of a rule  and a condition c over P, and is denoted as
and a condition c over P, and is denoted as  . We let
. We let  if \(m \vDash c\) and
if \(m \vDash c\) and  . Note that each rule
. Note that each rule  without a condition can also be seen as a conditional rule
without a condition can also be seen as a conditional rule  . If \({\mathcal {C}}\) is a finite set of conditional rules,
. If \({\mathcal {C}}\) is a finite set of conditional rules,  denotes the conditional transformation relation using these rules.
denotes the conditional transformation relation using these rules.
Examples of graphs and rules, with and without conditions, will be shown below.
3 Hyperedge Replacement Graph Grammars
We recall graph grammars based on hyperedge replacement [8].Footnote 4
Definition 5
(Hyperedge Replacement Grammar). Consider a finite alphabet \(\varSigma \) and a subset \(\mathcal {N}\subseteq \varSigma \) of nonterminals. Edges with labels in \(\mathcal {N}\) are accordingly nonterminal edges; those with labels in \(\varSigma \setminus \mathcal {N}\) are terminal edges.
A rule  is a hyperedge replacement production (production, for short) over \(\varSigma \) if the pattern P consists of a single edge e and its attached nodes, where \( lab _P(e) \in \mathcal {N}\), and the mapping
is a hyperedge replacement production (production, for short) over \(\varSigma \) if the pattern P consists of a single edge e and its attached nodes, where \( lab _P(e) \in \mathcal {N}\), and the mapping  is injective.
is injective.
A hyperedge-replacement grammar (HR grammar)  consists of \(\varSigma \) and \(\mathcal {N}\subseteq \varSigma \) as above, a finite set \(\mathcal {P}\) of productions over \(\varSigma \), and a start graph \(Z \in \mathcal {G}_\varSigma \).
consists of \(\varSigma \) and \(\mathcal {N}\subseteq \varSigma \) as above, a finite set \(\mathcal {P}\) of productions over \(\varSigma \), and a start graph \(Z \in \mathcal {G}_\varSigma \).
The language generated by \(\varGamma \) is given by  .
.
Example 1
(HR Grammars for Trees). As a running example for the constructions in this paper, we use the productions in Fig. 1. They derive n-ary trees like the one in Fig. 2, if the pattern of production  is the start graph. We draw nodes as circles, and nonterminal edges as boxes that contain their labels. Edges are connected to their attached nodes by lines, called tentacles. Tentacles are ordered counter-clockwise around the edge, starting in the north.
is the start graph. We draw nodes as circles, and nonterminal edges as boxes that contain their labels. Edges are connected to their attached nodes by lines, called tentacles. Tentacles are ordered counter-clockwise around the edge, starting in the north.
For the purpose of this paper, we restrict ourselves to this simple example because illustrations would otherwise become too complex. Further examples of well-known HR languages for which PTD parsers can be built include string graph languages such as palindromes, non-context-free ones like \(a^nb^nc^n\), arithmetic expressions, and Nassi-Shneiderman diagrams.
In our running example, edges of shape  with
with  designate root nodes, whereas edges of shape
designate root nodes, whereas edges of shape  with
with  connect parent nodes to their children.
connect parent nodes to their children.
In productions (and later in other rules), nodes of the pattern P have the same identifier ascribed in P as their images in R under \(p^\circ \), like x in our example. In the following, the letters  , and
, and  under the arrows in Fig. 1 are used as identifiers that refer to the corresponding production.
under the arrows in Fig. 1 are used as identifiers that refer to the corresponding production.
Assumption 1
Throughout the remainder of this paper, we consider only HR grammars  that satisfy the following conditions:
that satisfy the following conditions:
-
1.
Z consists of a single edge e of arity 0.
-
2.
\({\mathcal {L}}(\varGamma )\) does not contain graphs with isolated nodes.
These assumptions imply no loss of generality: a new initial nonterminal with a single start production according to Assumption 1 can be added easily. A grammar that violates Assumption 1 and produces isolated nodes can be transformed easily into an equivalent grammar that attaches virtual unary edges to those nodes.
4 Threaded HR Grammars
We now prepare HR grammars for parsing. The edges in graphs, productions and derivations will be ordered linearly with the idea that the parser is instructed to process the symbols of a grammar in this order when it attempts to construct a derivation for a given input graph. The edge order induces a dependency relation between nodes of a graph as follows: for an edge, an attached node is “known” if it is also attached to some preceeding edge, which will be processed earlier by the parser; it is “unknown” otherwise. This defines what we call the profile of an edge: a node is classified as incoming if it is known, and as outgoing otherwise.
Technically, edge order and profiles are represented by extending the structure and labels of a graph: Every edge is equipped with two additional tentacles by which edges are connected to a thread, and the label \(\ell \) of an edge is equipped with a profile \(\nu \subseteq \mathbb {N}\) indicating the positions of its incoming nodes. Unary hyperedges labeled with a fresh symbol distinguish thread nodes from kernel nodes of a graph.
Definition 6
(Threaded Graph). The profiled alphabet of an alphabet \(\varSigma \) is  with
with  and
and  . The profile of an edge labelled by
. The profile of an edge labelled by  is \(\nu \).
is \(\nu \).
Let  . A node
. A node  is called a thread node if a
is called a thread node if a  -edge is attached to it and a kernel node otherwise.
-edge is attached to it and a kernel node otherwise.  and
and  denote the sets of all kernel nodes and thread nodes of G, respectively. An edge
denote the sets of all kernel nodes and thread nodes of G, respectively. An edge  is a profiled edge if
is a profiled edge if  . The set of all profiled edges of G is denoted by
. The set of all profiled edges of G is denoted by  . The profile \(\nu \) divides the set of attached kernel nodes of e into sets \(\textit{in}_G(e) = \{ v_i \mid i \in \nu \}\) and \(\textit{out}_G(e) = \{ v_i \mid i\in [ arity ( lab _G(e))] \setminus \nu \}\) of incoming and outgoing nodes, respectively.
. The profile \(\nu \) divides the set of attached kernel nodes of e into sets \(\textit{in}_G(e) = \{ v_i \mid i \in \nu \}\) and \(\textit{out}_G(e) = \{ v_i \mid i\in [ arity ( lab _G(e))] \setminus \nu \}\) of incoming and outgoing nodes, respectively.
A graph  is threaded if the following hold:
is threaded if the following hold:
-
1.
Each node of G has at most one attached
 -edge.
-edge. -
2.
For every
 with \( lab _G(e) = \ell ^\nu \) and \( att _G(e) = v_1 \dots v_k v_{k+1} v_{k+2}\), the nodes \(v_1,\dots ,v_k\) are kernel nodes of G and \(v_{k+1},v_{k+2}\) are thread nodes of G. (Hence, \(\textit{in}_G(e)\) and \(\textit{out}_G(e)\) partition the kernel nodes of e into incoming and outgoing nodes.)
with \( lab _G(e) = \ell ^\nu \) and \( att _G(e) = v_1 \dots v_k v_{k+1} v_{k+2}\), the nodes \(v_1,\dots ,v_k\) are kernel nodes of G and \(v_{k+1},v_{k+2}\) are thread nodes of G. (Hence, \(\textit{in}_G(e)\) and \(\textit{out}_G(e)\) partition the kernel nodes of e into incoming and outgoing nodes.) -
3.
The profiled edges and thread nodes of G can be ordered as
 and
and  so that, for \(i\in [n]\),
so that, for \(i\in [n]\), -
(a)
\( att _G(e_i)\) ends in \(v_{i-1} v_i\) and
-
(b)
no edge \(e_j\) with \(j\in [i-1]\) is attached to any node in \(\textit{out}_G(e_i)\).
-
(a)
We call \(v_0\) the first and \(v_n\) the last thread node of G, and define furthermore  .
.
The kernel graph of G is the graph  obtained by removing the profiles of edge labels, the
obtained by removing the profiles of edge labels, the  -edges, the thread nodes and their attached tentacles.
-edges, the thread nodes and their attached tentacles.  denotes the set of threaded graphs over
denotes the set of threaded graphs over  ;
;  denotes the empty threaded graph that consists of a single thread node with its attached
denotes the empty threaded graph that consists of a single thread node with its attached  -edge.
-edge.
Remark 1
It is important to note that the profiles of the (profiled) edges of a threaded graph G are uniquely determined by \(\textit{in}(G)\) and the structure of G. To see this, let  , threaded in this order. For every
, threaded in this order. For every  , let
, let
Then \(v\in \textit{in}_G(e_i)\) if \(v\in att _G(e_i)\) and \( first (v)<i\).
Let the concatenation \(H = G \circ G'\) of two threaded graphs G and \(G'\) with  be the threaded graph H that is constructed from the union of G and \(G'\) by identifying the last thread node of G with the first thread node of \(G'\) (and removing one of their attached
be the threaded graph H that is constructed from the union of G and \(G'\) by identifying the last thread node of G with the first thread node of \(G'\) (and removing one of their attached  -edges). Note that kernel nodes of G may also occur in \(G'\).
-edges). Note that kernel nodes of G may also occur in \(G'\).
Definition 7
(Threaded Production and HR grammar). A rule  is a threaded production if P and R are threaded and the following conditions are satisfied:
is a threaded production if P and R are threaded and the following conditions are satisfied:
-
1.
the rule
 , where
, where  is the restriction of \(p^\circ \) to
is the restriction of \(p^\circ \) to  , is a production, called kernel production of p,
, is a production, called kernel production of p, -
2.
\(p^\circ \) maps the first and last thread nodes of P onto the first and last thread nodes of R, respectively, and
-
3.
\(p^\circ (\textit{in}(P))=\textit{in}(R)\).
An application  of a threaded production p to a threaded graph G is called leftmost, written
of a threaded production p to a threaded graph G is called leftmost, written  , if it replaces the first nonterminal on the thread of G.
, if it replaces the first nonterminal on the thread of G.
A HR grammar  over a profiled alphabet
over a profiled alphabet  is threaded if all its productions are threaded.
is threaded if all its productions are threaded.
As in the case of context-free string grammars, the context-freeness of hyperedge replacement implies that derivations can be restricted to leftmost ones:
Fact 1
For every threaded HR grammar  and every
and every  , there is a leftmost derivation
, there is a leftmost derivation  , i.e., a derivation in which all applications of productions are leftmost.
, i.e., a derivation in which all applications of productions are leftmost.
This fact will be important, as top-down parsers for HR grammars attempt to construct leftmost derivations of a graph.
It follows from Remark 1 and condition 3 of Definition 7 that the profiles of edges in the replacement graph of a threaded production are uniquely determined by the profile of the pattern. Hence, given a HR grammar  and an order on
and an order on  for each of its productions
for each of its productions  , a unique threaded version
, a unique threaded version  of \(\varGamma \) is obtained as follows:
of \(\varGamma \) is obtained as follows:
-
1.
The threaded start graph
 of
of  is given by
is given by  (recall that \( arity (Z)=0\)).
(recall that \( arity (Z)=0\)). -
2.
Every production
 of \(\varGamma \) is turned into all threaded productions
of \(\varGamma \) is turned into all threaded productions  where
where  ,
,  , and the edges of
, and the edges of  are threaded according to the chosen order on
are threaded according to the chosen order on  (which defines the profiles of edges in
(which defines the profiles of edges in  uniquely).
uniquely).
While the procedure above creates an exponential number of profiles and thus productions, in most cases many of them will be useless. A more efficient way of constructing  is thus to choose the threading order and then construct the useful threaded productions inductively. The procedure would initially construct the threaded start production (in which \(\textit{in}(P)=\varnothing \)) and then, as long as a replacement graph of one of the constructed productions contains a hitherto unseen profiled nonterminal, continue by constructing the threaded productions for this nonterminal. This leads to the following definition:
is thus to choose the threading order and then construct the useful threaded productions inductively. The procedure would initially construct the threaded start production (in which \(\textit{in}(P)=\varnothing \)) and then, as long as a replacement graph of one of the constructed productions contains a hitherto unseen profiled nonterminal, continue by constructing the threaded productions for this nonterminal. This leads to the following definition:
Definition 8
(Threaded Version of a HR Grammar). Let  be a HR grammar. A threaded version of \(\varGamma \) is a threaded grammar
be a HR grammar. A threaded version of \(\varGamma \) is a threaded grammar  , such that
, such that
-
1.
 and
and  ,
, -
2.
all threaded productions with the same kernel production
 order the edges of R identically, and
order the edges of R identically, and -
3.
 is reduced, i.e., every production
is reduced, i.e., every production  can participate in the generation of a graph in
can participate in the generation of a graph in  : there is a derivation
: there is a derivation  such that
such that  .
.
Example 2
(Threaded Tree Grammar). We consider a threaded version of the tree grammar, given by the threaded productions in Fig. 3. In examples such as this one we draw thread nodes in gray and omit the attached  -edges, and we write profiles as ascending sequences of numbers rather than as sets. The profiles of profiled terminal edges are inscribed into the label symbols, i.e.,
-edges, and we write profiles as ascending sequences of numbers rather than as sets. The profiles of profiled terminal edges are inscribed into the label symbols, i.e.,  for
for  and
and  for
for  Moreover, we distinguish threaded productions with the same kernel productions by the profile of the (unique edge in the) pattern in the production name. The profiled symbols
Moreover, we distinguish threaded productions with the same kernel productions by the profile of the (unique edge in the) pattern in the production name. The profiled symbols  ,
,  ,
,  ,
,  , and
, and  do not appear as they occur only in useless productions.
do not appear as they occur only in useless productions.
It is worthwhile to note that production  merges thread nodes t and n, which we indicate in the drawing by annotating the corresponding node in the replacement graph with “\(t{=}n\)”.
merges thread nodes t and n, which we indicate in the drawing by annotating the corresponding node in the replacement graph with “\(t{=}n\)”.
We arrange thread nodes from left to right and draw thread tentacles in gray so that the kernel graph can be better identified. To make it easier to distinguish incoming from outgoing attached nodes, we draw the former to the left of an edge and the latter to the right of it.
In production  , left-recursion was avoided by choosing the terminal edge to be the first one on the thread. Figure 4 shows a threaded derivation of the tree in Fig. 2, which is leftmost.
, left-recursion was avoided by choosing the terminal edge to be the first one on the thread. Figure 4 shows a threaded derivation of the tree in Fig. 2, which is leftmost.
A leftmost threaded derivation of the tree in Fig. 2
Threaded productions derive threaded graphs to threaded graphs.
Fact 2
If  and G is a threaded graph, H is a threaded graph as well, and \(\textit{in}(H)=\textit{in}(G)\).
and G is a threaded graph, H is a threaded graph as well, and \(\textit{in}(H)=\textit{in}(G)\).
Threaded derivations and unthreaded ones correspond to each other.
Lemma 1
Let  be a HR grammar,
be a HR grammar,  a threaded version of \(\varGamma \), and G a threaded graph such that
a threaded version of \(\varGamma \), and G a threaded graph such that  . Then it holds for all graphs \(G'\) that
. Then it holds for all graphs \(G'\) that  if and only if there is a threaded graph H with
if and only if there is a threaded graph H with  and
and  .
.
Thus the threaded and unthreaded version of a HR grammar generate the same language of kernel graphs.
Theorem 1
If  is a HR grammar and
is a HR grammar and  is a threaded version of \(\varGamma \), then
is a threaded version of \(\varGamma \), then  .
.
Proof
Easy induction on the length of derivations, using Lemma 1. \(\square \)
5 General Top-Down Parsing for HR Grammars
We define top-down parsers for HR grammars as stack automata, which perform transitions of configurations that represent the input graph and a stack. Configurations are graphs, and transitions are described by graph transformation rules. This definition is more precise than the original definition of PTD parsing in [4], but avoids the technical complications occuring in the precise definition of PSR parsing for HR grammars [6], where graphs are represented textually as sequences of literals, and transitions are defined by the transformation of literal sequences, involving substitution and renaming operations on node identifiers. The use of graph transformation and graph morphisms avoids the explicit handling of these technical issues.
A configuration consists of a threaded graph as in Definition 6, which represents its stack and its read input, edges without profile that induce its unread input, and further edges that serve as flags, distinguishing different types of nodes.
Definition 9
(Configuration). Given a HR grammar  and its profiled alphabet
and its profiled alphabet  , let
, let  , \(\otimes \), and
, \(\otimes \), and  be fresh symbols of arity 1. A graph G without isolated nodes is a configuration (of \(\varGamma \)) if the following hold:
be fresh symbols of arity 1. A graph G without isolated nodes is a configuration (of \(\varGamma \)) if the following hold:
-
The subgraph
 induced by its
induced by its  -edges is a threaded graph.
-edges is a threaded graph. -
Exactly one thread node h of
 is attached to a
is attached to a  -edge, representing the top of the stack.
-edge, representing the top of the stack. -
Every kernel node of every profiled edge between the start node of the thread and h is attached to a
 -edge, marking it as read.
-edge, marking it as read. -
Every node of every \(\varSigma \)-edge that is not attached to a profiled edge at the same time is attached to a \(\otimes \)-edge, marking it as unread.
-
No node is attached to several edges with labels in
 .
.
We let  , the read input, denote the subgraph of
, the read input, denote the subgraph of  induced by the profiled edges between the first thread node and h (including the
induced by the profiled edges between the first thread node and h (including the  -edges attached to those nodes). The (threaded) subgraph of
-edges attached to those nodes). The (threaded) subgraph of  induced by the profiled edges between h and the last node of the thread (again including the
induced by the profiled edges between h and the last node of the thread (again including the  -edges attached to those nodes) represents the stack
-edges attached to those nodes) represents the stack  , and the subgraph
, and the subgraph  induced by the \(\varSigma \)-edges represents the unread input. The union of
induced by the \(\varSigma \)-edges represents the unread input. The union of  and the kernel of
and the kernel of  is the input represented by G, denoted by
is the input represented by G, denoted by  .
.
A configuration G is
-
initial if
 and
and  , and
, and -
accepting if
 and
and  .
.
Definition 10
(Top-Down Parser). Let \(\varGamma \) be a HR grammar and \(\mathcal {R}\) a set of conditional rules. A derivation  is a parse if G is an initial configuration. A parse
is a parse if G is an initial configuration. A parse  is successful if H is an accepting configuration. A configuration G is promising (with respect to \(\mathcal {R}\)) if there is an accepting configuration H so that
is successful if H is an accepting configuration. A configuration G is promising (with respect to \(\mathcal {R}\)) if there is an accepting configuration H so that  . \(\mathcal {R}\) is a top-down parser for \(\varGamma \) if, for each initial configuration G,
. \(\mathcal {R}\) is a top-down parser for \(\varGamma \) if, for each initial configuration G,  if and only if G is promising. \(\mathcal {R}\) terminates if there is no infinite parse.
if and only if G is promising. \(\mathcal {R}\) terminates if there is no infinite parse.
Consider in the following a threaded version  of a HR grammar
of a HR grammar  . We define two types of general top-down parsing rules, called match and expand rules.
. We define two types of general top-down parsing rules, called match and expand rules.
Definition 11
(Match and Expand Rules). For every terminal symbol  , the match rule
, the match rule  is given as follows:
is given as follows:
-
The pattern P is a configuration where
-
 ,
, -
 consists of one a-edge
consists of one a-edge  with \(a\in \varSigma \setminus \mathcal {N}\) and
with \(a\in \varSigma \setminus \mathcal {N}\) and  (where \( arity (a)=k\)), with a
(where \( arity (a)=k\)), with a  -edge attached to every
-edge attached to every  with \(i \in \nu \) and a \(\otimes \)-edge attached to every
with \(i \in \nu \) and a \(\otimes \)-edge attached to every 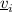 with \(i \not \in \nu \), and
with \(i \not \in \nu \), and -
 consists of one \(a^\nu \)-edge e with \( att _P(e)=v_1 \dots v_k v_{k+1}v_{k+2}\) such that
consists of one \(a^\nu \)-edge e with \( att _P(e)=v_1 \dots v_k v_{k+1}v_{k+2}\) such that  if \(i \in \nu \). If \(i\notin \nu \), then \(v_i\) is not attached to
if \(i \in \nu \). If \(i\notin \nu \), then \(v_i\) is not attached to  .
.
-
-
The replacement R is a configuration where
-
 , with a
, with a  -edge attached to every \(v_i\), for \(i\in [k]\),
-edge attached to every \(v_i\), for \(i\in [k]\), -
 ,
, -
 .
.
-
-
The mapping \(t^\circ _{a^\nu }\) identifies node \(v_i\) with
 if and only if \(i \notin \nu \).
if and only if \(i \notin \nu \).
For each of the threaded productions  in
in  , the expand rule
, the expand rule  is given as follows:
is given as follows:
-
 ,
, -
 ,
, -
 and
and  ,
, -
the mapping \(t^\circ _p\) is the same as in p;
We let \(\mathcal {R}^\mathrm {M}_{\tilde{\varGamma }}\) denote the set of all match rules for terminal symbols, and \(\mathcal {R}^\mathrm {E}_{\tilde{\varGamma }}\) the set of all expand rules for productions of \({\tilde{\varGamma }}\). In the following, we will show that \(\mathcal {R}_{\tilde{\varGamma }}= \mathcal {R}^\mathrm {M}_{\tilde{\varGamma }}\cup \mathcal {R}^\mathrm {E}_{\tilde{\varGamma }}\) is in fact a top-down parser for \(\varGamma \), hence we call  a general top-down parser of \({\tilde{\varGamma }}\) (for \(\varGamma \)).
a general top-down parser of \({\tilde{\varGamma }}\) (for \(\varGamma \)).
Example 3
(General Top-Down Parser for Trees). The expand rules of the general top-down parser for trees in Fig. 5 differ from the threaded productions only in the  -edge marking the top of the stack. (We draw
-edge marking the top of the stack. (We draw  - and
- and  -edges around the nodes to which they are attached, so that they look like distinguished kinds of nodes. Nodes with an attached \(\otimes \)-edge are drawn as \(\otimes \), omitting the attached edge in the drawing.) The match rules for the two edge patterns needed are shown in Fig. 6.
-edges around the nodes to which they are attached, so that they look like distinguished kinds of nodes. Nodes with an attached \(\otimes \)-edge are drawn as \(\otimes \), omitting the attached edge in the drawing.) The match rules for the two edge patterns needed are shown in Fig. 6.
A top-down parse of the tree in Fig. 2
Figure 7 shows snapshots of a successful parse of the tree in Fig. 2 with these rules, where five configurations are omitted for brevity. The parse constructs the leftmost derivation in Fig. 4.
Note that match rules do not change the thread, but just “move” the matched terminal from the unread to the read subgraph of the configuration. In contrast, expand rules do not modify the unread or read subgraphs of the configuration, but just replace the first nonterminal on the thread by the replacement graph of a threaded production for this nonterminal. We can summarize these observations in the following fact:
Fact 3
For a parse  (where
(where  ), the following hold:
), the following hold:
-
1.
 ;
; -
2.
if \(r = t_{a^\nu }\) is a match for some \(a \in \varSigma \setminus \mathcal {N}\), then
 ;
; -
3.
if \(r = t_p\) for some threaded production
 , then
, then 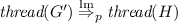 .
.
Thus  constitutes a top-down parser: there is a successful parse if and only if its input graph is in the language of the grammar.
constitutes a top-down parser: there is a successful parse if and only if its input graph is in the language of the grammar.
Theorem 2
For every HR grammar \(\varGamma \) and each threaded version \({\tilde{\varGamma }}\) of \(\varGamma \), \(\mathcal {R}_{\tilde{\varGamma }}\) is a top-down parser for \(\varGamma \).
Proof Sketch
Let  be a successful parse.
be a successful parse.  and
and  hold by Fact 3;
hold by Fact 3;  is the kernel of
is the kernel of  because H is accepting, and hence
because H is accepting, and hence  by Lemma 1.
by Lemma 1.
In order to show the opposite direction, let us consider any configuration G with terminal read input  and \(H'\) a terminal threaded graph with kernel
and \(H'\) a terminal threaded graph with kernel  . It is easy to prove, by induction on the length of the derivation, that
. It is easy to prove, by induction on the length of the derivation, that  implies
implies  where H is an accepting configuration obtained from
where H is an accepting configuration obtained from  by adding a
by adding a  -edge to the last thread node and
-edge to the last thread node and  -edges to all kernel nodes, i.e., G is promising. Now let G be an initial configuration with
-edges to all kernel nodes, i.e., G is promising. Now let G be an initial configuration with  . By Lemma 1, there is a threaded graph \(H'\) with kernel
. By Lemma 1, there is a threaded graph \(H'\) with kernel  and
and  . Hence, G must be promising. \(\square \)
. Hence, G must be promising. \(\square \)
If  is not left-recursive, the general top-down parser terminates. Here, we say that
is not left-recursive, the general top-down parser terminates. Here, we say that  is left-recursive if there is a threaded graph G consisting of a single nonterminal edge labeled A (for some nonterminal A) and there is a derivation
is left-recursive if there is a threaded graph G consisting of a single nonterminal edge labeled A (for some nonterminal A) and there is a derivation  for some graph H such that the first profiled edge of H is also labeled with A.
for some graph H such that the first profiled edge of H is also labeled with A.
Theorem 3
(Termination). Let \({\tilde{\varGamma }}\) be a threaded version of a HR grammar. The general top-down parser \(\mathcal {R}_{\tilde{\varGamma }}\) terminates unless \({\tilde{\varGamma }}\) is left-recursive.
Proof
Assume that there is an infinite parse  with \(t_i \in \mathcal {R}_{\tilde{\varGamma }}\) for \(i \in \mathbb {N}\). Since
with \(t_i \in \mathcal {R}_{\tilde{\varGamma }}\) for \(i \in \mathbb {N}\). Since  is finite and each match operation “removes” an unread edge, there must be a \(k \in \mathbb {N}\) such that \(t_i\) is an expand rule for all \(i > k\). As their number is finite, there must be numbers i and j, \(k< i < j\), such that
is finite and each match operation “removes” an unread edge, there must be a \(k \in \mathbb {N}\) such that \(t_i\) is an expand rule for all \(i > k\). As their number is finite, there must be numbers i and j, \(k< i < j\), such that  and
and  start with edges labeled with the same nonterminal. By Fact 3,
start with edges labeled with the same nonterminal. By Fact 3,  , which proves that \({\tilde{\varGamma }}\) is left-recursive. \(\square \)
, which proves that \({\tilde{\varGamma }}\) is left-recursive. \(\square \)
Inconveniently, the steps of the general top-down parser are nondeterministic:
-
1.
The expansion of a nonterminal \(A^\nu \) may choose any of its productions.
-
2.
The match of an edge \(a^\nu \) may choose any unread edge fitting the profile \(\nu \).
We consider a parse  as a blind alley if the configuration H is not accepting, but does not allow further steps (using \(\mathcal {R}_{\tilde{\varGamma }}\)). This is the case if
as a blind alley if the configuration H is not accepting, but does not allow further steps (using \(\mathcal {R}_{\tilde{\varGamma }}\)). This is the case if
-
 starts with an edge \(a^\nu \), but \(t_{a^\nu }\) does not apply (edge mismatch), or
starts with an edge \(a^\nu \), but \(t_{a^\nu }\) does not apply (edge mismatch), or -
 but
but  (input too big).
(input too big).
Due to nondeterminism, a successful parse may nevertheless exist in such a situation. Exploring the entire search space of parses to determine whether a successful one exists is very inefficient.
6 Predictive Top-Down Parsing for HR Grammars
The aim of predictive top-down parsing for threaded HR grammars is to avoid backtracking, the major source of inefficiency of a straightforward implementation of the general top-down parser. So we have to cope with the nondeterminism identified in the previous section. In every configuration of a parse, it must efficiently be possible to predict which choices of moves are wrong in the sense that they lead into a blind alley, whereas other moves could still lead to a successful parse if there is any. However, this is most likely not achievable for every threaded HR grammar \({\tilde{\varGamma }}\) because Theorem 2 in combination with the known NP-completeness of some HR languages would otherwise imply that P=NP. For such a grammar, certain configurations will allow more than one expansion, and it may be the case that any of them is promising, or just some of them (or none).
Thus backtrack-free parsing only seems to be possible for HR grammars that make correct moves of their top-down parsers predictable.
Let us first define predictive expand rules that will prevent a parser from running into blind alleys by additionally checking so-called lookahead conditions. Henceforth, given a rule  and a condition c over P, we denote the conditional rule
and a condition c over P, we denote the conditional rule  by r[c].
by r[c].
Definition 12
(Predictive expand rules). Let \(\varGamma \) be a HR grammar, \({\tilde{\varGamma }}\) a threaded version of \(\varGamma \), and \(\mathcal {R}_{\tilde{\varGamma }}= \mathcal {R}^\mathrm {M}_{\tilde{\varGamma }}\cup \mathcal {R}^\mathrm {E}_{\tilde{\varGamma }}\) its general top-down parser. For an expand rule  , a condition c over P is a lookahead condition for \(t_{p^\nu }\) if the following holds:
, a condition c over P is a lookahead condition for \(t_{p^\nu }\) if the following holds:
For every derivation
where G is an initial configuration and H is promising,Footnote 5 if \(m\vDash c\) then \(H'\) is promising.
A set \(\mathcal {R}= \{t_{p^\nu }[c_{p^\nu }] \mid t_{p^\nu } \in \mathcal {R}^\mathrm {E}_{\tilde{\varGamma }}\}\) of conditional rules is a set of predictive expand rules for \({\tilde{\varGamma }}\) if \(c_{p^\nu }\) is a lookahead condition for every  .
.
In the following, we briefly describe a simple way to check whether a set of predictive expand rules can be obtained from \(\mathcal {R}^\mathrm {E}_{\tilde{\varGamma }}\). For this purpose, let G be any initial configuration and  any expand rule so that
any expand rule so that  where \(H'\) is promising, i.e., there is an accepting configuration F such that
where \(H'\) is promising, i.e., there is an accepting configuration F such that


Consider case (1) first. There is an isomorphism  because K is obtained from H by expand rules only. Let e be the edge of
because K is obtained from H by expand rules only. Let e be the edge of  that is read by the match operation
that is read by the match operation  and E the subgraph of K induced by e. Clearly, m(P) as well as \( iso (E)\) are both subgraphs of H. Now select a graph C and an injective morphism \(m'\) so that \(P \subseteq C\), \(m = m'|_P\), and \(m'(C) = m(P) \cup iso (E)\). By definition, \(m \vDash \exists C\). In case (2),
and E the subgraph of K induced by e. Clearly, m(P) as well as \( iso (E)\) are both subgraphs of H. Now select a graph C and an injective morphism \(m'\) so that \(P \subseteq C\), \(m = m'|_P\), and \(m'(C) = m(P) \cup iso (E)\). By definition, \(m \vDash \exists C\). In case (2),  is empty and \(m \vDash \exists P\).
is empty and \(m \vDash \exists P\).
We can make use of this as follows. For an expand rule \(t_{p^\nu }\), performing the above analysis for all derivations of types (1) and (2) yields only finitely many distinct graphs C (up to isomorphism). These graphs \(C_1,\dots ,C_n\) can be computed by procedures similar to the construction of FIRST and FOLLOW sets for LL(k) parsing [15, Sect. 5.5]. Defining \(\hat{c}_{p^\nu } = \exists C_1 \vee \exists C_2 \vee \cdots \vee \exists C_n\) we thus obtain for all promising graphs \(H,H'\) that  implies \(m \vDash \hat{c}_{p^\nu }\). Thus, by contraposition, if H is promising and
implies \(m \vDash \hat{c}_{p^\nu }\). Thus, by contraposition, if H is promising and  but
but  , then \(H'\) cannot be promising.
, then \(H'\) cannot be promising.
Note, however, that \(m \vDash \hat{c}_{p^\nu }\) does not necessarily imply that \(H'\) is promising if  and H is promising. Therefore, \(\hat{c}_{p^\nu }\) can in general not directly serve as a lookahead condition. To solve this problem, we define a relation \(\sqsubset \) on expand rules. For this purpose, let us consider two different expand rules \(t_{p_a^\nu }, t_{p_b^\nu } \in \mathcal {R}^\mathrm {E}_{\tilde{\varGamma }}\) with isomorphic left-hand sides. Without loss of generality, we assume that the left-hand sides are identical. We define \(t_{p_a^\nu } \sqsubset t_{p_b^\nu }\) if there is an initial configuration G and a derivation
and H is promising. Therefore, \(\hat{c}_{p^\nu }\) can in general not directly serve as a lookahead condition. To solve this problem, we define a relation \(\sqsubset \) on expand rules. For this purpose, let us consider two different expand rules \(t_{p_a^\nu }, t_{p_b^\nu } \in \mathcal {R}^\mathrm {E}_{\tilde{\varGamma }}\) with isomorphic left-hand sides. Without loss of generality, we assume that the left-hand sides are identical. We define \(t_{p_a^\nu } \sqsubset t_{p_b^\nu }\) if there is an initial configuration G and a derivation  where \(H'\) is promising and \(m \vDash \hat{c}_{p_b^\nu }\). In fact, relation \(\sqsubset \) can be defined while conditions \(\hat{c}_{p_i^\nu }\) are constructed.Footnote 6
where \(H'\) is promising and \(m \vDash \hat{c}_{p_b^\nu }\). In fact, relation \(\sqsubset \) can be defined while conditions \(\hat{c}_{p_i^\nu }\) are constructed.Footnote 6
Note that \(\sqsubset \) is in general not an ordering and that it may even contain cycles \(t_{p_a^\nu } \sqsubset t_{p_b^\nu } \sqsubset \cdots \sqsubset t_{p_a^\nu }\). But if there are no such cycles, one can create (by topological sorting) a linear ordering \(\prec \) on all expand rules with isomorphic left-hand sides (where we again assume that they have in fact identical left-hand sides) so that \(t_{p_a^\nu } \sqsubset t_{p_b^\nu }\) always implies \(t_{p_a^\nu } \prec t_{p_b^\nu }\). We then define, for each expand rule \(t_{p^\nu }\), the condition \(c_{p^\nu } \equiv \hat{c}_{p^\nu } \wedge \lnot c_1 \wedge \lnot c_2 \wedge \cdots \wedge \lnot c_n\) where \(\{c_1, c_2, \ldots c_n\} = \{\hat{c}_{\bar{p}^\nu } \mid t_{\bar{p}^\nu } \prec t_{p^\nu }\}\). The following lemma states that these conditions can serve as lookahead conditions for predictive expand rules:
Lemma 2
Let \(\varGamma \) be a HR grammar, \({\tilde{\varGamma }}\) a threaded version of \(\varGamma \), and \(\mathcal {R}_{\tilde{\varGamma }}= \mathcal {R}^\mathrm {M}_{\tilde{\varGamma }}\cup \mathcal {R}^\mathrm {E}_{\tilde{\varGamma }}\) its general top-down parser. If \(\sqsubset \) is acyclic and the condition \(c_{p^\nu }\) is defined as above for each expand rule \(t_{p^\nu } \in \mathcal {R}^\mathrm {E}_{\tilde{\varGamma }}\), then \(\{t_{p^\nu }[c_{p^\nu }] \mid t_{p^\nu } \in \mathcal {R}^\mathrm {E}_{\tilde{\varGamma }}\}\) is a set of predictive expand rules for \({\tilde{\varGamma }}\).
Proof
Consider any derivation  where G is an initial configuration, and H is promising. Then there is an expand rule \(t_{p^\nu }\) so that
where G is an initial configuration, and H is promising. Then there is an expand rule \(t_{p^\nu }\) so that  and K is promising. By construction, \(m \vDash \hat{c}_{p^\nu }\). If there were a smaller expand rule \(t_{\bar{p}^\nu } \prec t_{p^\nu }\) with \(m \vDash \hat{c}_{\bar{p}^\nu }\), then this would imply \(t_{p^\nu } \sqsubset t_{\bar{p}^\nu }\) because K is promising, and therefore, \(t_{p^\nu } \prec t_{\bar{p}^\nu }\), contradicting the linearity of \(\prec \). Therefore, \(m \vDash \lnot \hat{c}_{\bar{p}^\nu }\) for \(t_{\bar{p}^\nu } \prec t_{p^\nu }\) and \(m \vDash \hat{c}_{p^\nu }\), i.e., \(t_{p^\nu }\) is the only expand rule that satisfies its lookahead condition for H, i.e., \(m \vDash c_{p^\nu }\). \(\square \)
and K is promising. By construction, \(m \vDash \hat{c}_{p^\nu }\). If there were a smaller expand rule \(t_{\bar{p}^\nu } \prec t_{p^\nu }\) with \(m \vDash \hat{c}_{\bar{p}^\nu }\), then this would imply \(t_{p^\nu } \sqsubset t_{\bar{p}^\nu }\) because K is promising, and therefore, \(t_{p^\nu } \prec t_{\bar{p}^\nu }\), contradicting the linearity of \(\prec \). Therefore, \(m \vDash \lnot \hat{c}_{\bar{p}^\nu }\) for \(t_{\bar{p}^\nu } \prec t_{p^\nu }\) and \(m \vDash \hat{c}_{p^\nu }\), i.e., \(t_{p^\nu }\) is the only expand rule that satisfies its lookahead condition for H, i.e., \(m \vDash c_{p^\nu }\). \(\square \)
The proof shows that these lookahead conditions always select a unique expand rule. Clearly, this cannot succeed for situations where expand rules can turn a promising configuration into two or more promising successor configurations.
However, the existence of a set of predictive expand rules is not sufficient for obtaining a predictive top-down parser. The threaded HR grammar must satisfy the following property as well:
Definition 13
(Free edge choice property). Let \(\varGamma \) be a HR grammar, \({\tilde{\varGamma }}\) a threaded version of \(\varGamma \), and \(\mathcal {R}_{\tilde{\varGamma }}= \mathcal {R}^\mathrm {M}_{\tilde{\varGamma }}\cup \mathcal {R}^\mathrm {E}_{\tilde{\varGamma }}\) its general top-down parser. \({\tilde{\varGamma }}\) is said to possess the free edge choice property if, for every derivation  where G is an initial configuration and H is promising, \(H'\) is promising as well.
where G is an initial configuration and H is promising, \(H'\) is promising as well.
Theorem 4
Let \(\varGamma \) be a HR grammar, \({\tilde{\varGamma }}\) a threaded version of \(\varGamma \) without left-recursion, and \(\mathcal {R}_{\tilde{\varGamma }}= \mathcal {R}^\mathrm {M}_{\tilde{\varGamma }}\cup \mathcal {R}^\mathrm {E}_{\tilde{\varGamma }}\) its general top-down parser. \(\mathcal {R}^\mathrm {ptd} = \mathcal {R}^\mathrm {M}_{\tilde{\varGamma }}\cup \mathcal {R}\) is a terminating top-down parser for \(\varGamma \) that cannot run into blind alleys if \(\mathcal {R}\) is a set of predictive expand rules for \({\tilde{\varGamma }}\) and \({\tilde{\varGamma }}\) has the free edge choice property.
Proof
Let \(\varGamma \), \({\tilde{\varGamma }}\), and \(\mathcal {R}^\mathrm {ptd}\) be as in the theorem. Moreover, let \({\tilde{\varGamma }}\) satisfy the free edge choice property, and let \(\mathcal {R}\) be a set of predictive expand rules for \({\tilde{\varGamma }}\). Each derivation  where G and H are initial and accepting configurations, resp., is also a successful parse in \(\mathcal {R}_{\tilde{\varGamma }}\), i.e.,
where G and H are initial and accepting configurations, resp., is also a successful parse in \(\mathcal {R}_{\tilde{\varGamma }}\), i.e.,  by Theorem 2.
by Theorem 2.
Now let G be any initial configuration with  , i.e., G is promising. Any infinite derivation
, i.e., G is promising. Any infinite derivation  would also be an infinite parse
would also be an infinite parse  , contradicting Theorem 3.
, contradicting Theorem 3.
Finally assume that \(\mathcal {R}^\mathrm {ptd}\) runs into a blind alley starting at G, i.e., there is a derivation  , H is not accepting, and there is no configuration \(H'\) so that
, H is not accepting, and there is no configuration \(H'\) so that  . By the free edge choice property and \(\mathcal {R}\) being a set of predictive expand rules, H must be promising, i.e., there is a configuration \(H''\) so that
. By the free edge choice property and \(\mathcal {R}\) being a set of predictive expand rules, H must be promising, i.e., there is a configuration \(H''\) so that  or
or  . In either case, there is a configuration \(H'\) so that
. In either case, there is a configuration \(H'\) so that  , contradicting the assumption. \(\square \)
, contradicting the assumption. \(\square \)
This theorem justifies to call a threaded HR grammar \({\tilde{\varGamma }}\) predictively top-down parsable (PTD for short) if \({\tilde{\varGamma }}\) satisfies the free edge choice property and there is a set of predictive expand rules for \({\tilde{\varGamma }}\).
Example 4
(A Predictive Top-Down Tree Parser). The threaded tree grammar in Example 2 is PTD. To see this, let us construct lookahead conditions for expand rule  and
and  as described above.
as described above.
Inspection of expand rule  shows that choosing this rule cannot produce a promising configuration if the unread part of the input does not contain a
shows that choosing this rule cannot produce a promising configuration if the unread part of the input does not contain a  -edge starting at node x. The existence of this edge is hence requested by the graph condition
-edge starting at node x. The existence of this edge is hence requested by the graph condition  , defined by the supergraph
, defined by the supergraph  of the pattern of
of the pattern of  (see Fig. 8). No such edge can be requested for expand rule
(see Fig. 8). No such edge can be requested for expand rule  ; each match of
; each match of  satisfies
satisfies  since
since  is just the pattern of
is just the pattern of  . Condition
. Condition  is in particular satisfied if choosing
is in particular satisfied if choosing  produces a promising configuration, and therefore
produces a promising configuration, and therefore  . By Lemma 2, we can choose lookahead conditions
. By Lemma 2, we can choose lookahead conditions  and
and  .
.
Figure 9 shows the resulting predictive expand rules for the nonterminal T of the tree parser. For brevity, lookahead conditions show only those subgraphs that must or must not exist in order to apply  or
or  . The match rules and the expand rule
. The match rules and the expand rule  for the start production remain the same as in Example 3. Moreover, it is easy to see that match rule
for the start production remain the same as in Example 3. Moreover, it is easy to see that match rule  produces a promising configuration for each of its matches, i.e., the threaded tree grammar has the free edge choice property. With these modified expand rules, the predictive parser can select the same parse as in Fig. 7. As mentioned earlier, other well-known examples that allow for predictive parsing include palindromes, \(a^nb^nc^n\), arithmetic expressions, and Nassi-Shneiderman diagrams.
produces a promising configuration for each of its matches, i.e., the threaded tree grammar has the free edge choice property. With these modified expand rules, the predictive parser can select the same parse as in Fig. 7. As mentioned earlier, other well-known examples that allow for predictive parsing include palindromes, \(a^nb^nc^n\), arithmetic expressions, and Nassi-Shneiderman diagrams.
7 Conclusions
In this paper, we have defined PTD parsers for HR grammars by graph transformation rules, and shown their correctness. The definition is consistent with the implementation of PTD parsers in the graph parser distiller grappaFootnote 7 described in [4], but some features are still missing: First, productions that merge nodes of the left-hand side have been omitted. Such productions may occur when a HR grammar is “left-factorized” in order to allow for predictive expansion. (This corresponds to left-factorization of CF string grammars for LL-parsing.) Second, PTD parsing for contextual HR grammars [2, 3] has not been considered. Finally, a more sophisticated way of calculating lookahead conditions, by approximating Parikh images, has been ignored.
So our next step will be to extend our definitions and proofs to cover these concepts as well. Our ultimate goal ist to use this definition to relate the power of PTD parsing to that of PSR parsing, probably by using a definition of PSR parsing that is based on graph transformation as well.
Notes
- 1.
Since this paper is dedicated to proving the correctness of PTD parsers, and it has been established in [4] that they run in quadratic time at worst, we shall not dwell on issues of efficiency here.
- 2.
This corresponds to a DPO rule
 , where the interface I is the discrete graph with nodes
, where the interface I is the discrete graph with nodes  , and the morphism
, and the morphism  is given by \((r^\circ ,\varnothing )\).
is given by \((r^\circ ,\varnothing )\). - 3.
We omit nested conditions like “\(\forall (C, \exists C' \wedge \lnot \exists C'')\)” since we do not need them.
- 4.
- 5.
From now on, we call a configuration promising if it is in fact promising with respect to \(\mathcal {R}_{\tilde{\varGamma }}\).
- 6.
\(\hat{c}_{p_i^\nu }\) identifies edges that must occur in H if
 where \(H''\) is promising. And if these edges may also occur in H if \(H'\) is promising, we define \(t_{p_a^\nu } \sqsubset t_{p_b^\nu }\).
where \(H''\) is promising. And if these edges may also occur in H if \(H'\) is promising, we define \(t_{p_a^\nu } \sqsubset t_{p_b^\nu }\). - 7.
Available at www.unibw.de/inf2/grappa. grappa also distills PSR and generalized PSR parsers for CHR grammars [5, 13].
References
Aalbersberg, I., Ehrenfeucht, A., Rozenberg, G.: On the membership problem for regular DNLC grammars. Discrete Appl. Math. 13, 79–85 (1986)
Drewes, F., Hoffmann, B.: Contextual hyperedge replacement. Acta Informatica 52(6), 497–524 (2015). https://doi.org/10.1007/s00236-015-0223-4
Drewes, F., Hoffmann, B., Minas, M.: Contextual hyperedge replacement. In: Schürr, A., Varró, D., Varró, G. (eds.) AGTIVE 2011. LNCS, vol. 7233, pp. 182–197. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34176-2_16
Drewes, F., Hoffmann, B., Minas, M.: Predictive top-down parsing for hyperedge replacement grammars. In: Parisi-Presicce, F., Westfechtel, B. (eds.) ICGT 2015. LNCS, vol. 9151, pp. 19–34. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21145-9_2
Drewes, F., Hoffmann, B., Minas, M.: Extending predictive shift-reduce parsing to contextual hyperedge replacement grammars. In: Guerra, E., Orejas, F. (eds.) ICGT 2019. LNCS, vol. 11629, pp. 55–72. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-23611-3_4
Drewes, F., Hoffmann, B., Minas, M.: Formalization and correctness of predictive shift-reduce parsers for graph grammars based on hyperedge replacement. J. Locical Algebraic Methods Programm. (JLAMP) 104, 303–341 (2019). https://doi.org/10.1016/j.jlamp.2018.12.006
Ehrig, H., Ehrig, K., Prange, U., Taentzer, G.: Implementation of typed attributed graph transformation by AGG. In: Fundamentals of Algebraic Graph Transformation. An EATCS Series, pp. 305–323. Springer, Heidelberg (2006). https://doi.org/10.1007/3-540-31188-2_15
Habel, A.: Hyperedge Replacement: Grammars and Languages. LNCS, vol. 643. Springer, Heidelberg (1992). https://doi.org/10.1007/BFb0013875
Habel, A., Müller, J., Plump, D.: Double-pushout graph transformation revisited. Math. Struct. Comput. Sci. 11(5), 633–688 (2001)
Habel, A., Pennemann, K.H.: Correctness of high-level transformation systems relative to nested conditions. Math. Struct. Comput. Sci. 19(2), 245–296 (2009)
Heilbrunner, S.: A parsing automata approach to LR theory. Theor. Comput. Sci. 15, 117–157 (1981). https://doi.org/10.1016/0304-3975(81)90067-0
Hoffmann, B.: Modelling compiler generation by graph grammars. In: Ehrig, H., Nagl, M., Rozenberg, G. (eds.) Graph Grammars 1982. LNCS, vol. 153, pp. 159–171. Springer, Heidelberg (1983). https://doi.org/10.1007/BFb0000105
Hoffmann, B., Minas, M.: Generalized predictive shift-reduce parsing for hyperedge replacement graph grammars. In: Martín-Vide, C., Okhotin, A., Shapira, D. (eds.) LATA 2019. LNCS, vol. 11417, pp. 233–245. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-13435-8_17
Lange, K.J., Welzl, E.: String grammars with disconnecting or a basic root of the difficulty in graph grammar parsing. Discrete Appl. Math. 16, 17–30 (1987)
Sippu, S., Soisalon-Soininen, E.: Parsing Theroy I: Languages and Parsing. EATCS Monographs in Theoretical Computer Science, vol. 15. Springer, Heidelberg (1988). https://doi.org/10.1007/978-3-642-61345-6
Acknowledgements
The authors thank Annegret Habel for her valuable suggestions in several stages of this work.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Drewes, F., Hoffmann, B., Minas, M. (2020). Graph Parsing as Graph Transformation. In: Gadducci, F., Kehrer, T. (eds) Graph Transformation. ICGT 2020. Lecture Notes in Computer Science(), vol 12150. Springer, Cham. https://doi.org/10.1007/978-3-030-51372-6_13
Download citation
DOI: https://doi.org/10.1007/978-3-030-51372-6_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-51371-9
Online ISBN: 978-3-030-51372-6
eBook Packages: Computer ScienceComputer Science (R0)





 , from G to obtain a graph K.
, from G to obtain a graph K. .
. so that
so that  ;
;

 -edge.
-edge. with
with  and
and  so that, for
so that, for  , where
, where  is the restriction of
is the restriction of  , is a production, called kernel production of p,
, is a production, called kernel production of p, of
of  is given by
is given by  (recall that
(recall that  of
of  where
where  ,
,  , and the edges of
, and the edges of  are threaded according to the chosen order on
are threaded according to the chosen order on  (which defines the profiles of edges in
(which defines the profiles of edges in  uniquely).
uniquely). and
and  ,
, order the edges of R identically, and
order the edges of R identically, and is reduced, i.e., every production
is reduced, i.e., every production  can participate in the generation of a graph in
can participate in the generation of a graph in  : there is a derivation
: there is a derivation  such that
such that  .
.

 induced by its
induced by its  -edges is a threaded graph.
-edges is a threaded graph. is attached to a
is attached to a  -edge, representing the top of the stack.
-edge, representing the top of the stack. -edge, marking it as read.
-edge, marking it as read. .
. and
and  , and
, and and
and  .
. ,
, consists of one a-edge
consists of one a-edge  with
with  (where
(where  -edge attached to every
-edge attached to every  with
with 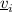 with
with  consists of one
consists of one  if
if  .
. , with a
, with a  -edge attached to every
-edge attached to every  ,
, .
. if and only if
if and only if  ,
, ,
, and
and  ,
,


 ;
; ;
; , then
, then 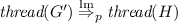 .
. starts with an edge
starts with an edge  but
but  (input too big).
(input too big). where G is an initial configuration and H is promising,
where G is an initial configuration and H is promising,
 and
and  for expand rule
for expand rule  and
and  , resp.
, resp.
 , where the interface I is the discrete graph with nodes
, where the interface I is the discrete graph with nodes  , and the morphism
, and the morphism  is given by
is given by  where
where