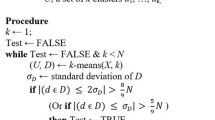k-means Cluster Shape Implications

Abstract

We present a novel justification why k-means clusters should be (hyper)ball-shaped ones. We show that the clusters must be ball-shaped to attain motion-consistency. If clusters are ball-shaped, one can derive conditions under which two clusters attain the global optimum of k-means. We show further that if the gap is sufficient for perfect separation, then an incremental k-means is able to discover perfectly separated clusters. This is in conflict with the impression left by an earlier publication by Ackerman and Dasgupta. The proposed motion-transformations can be used to the new labeled data for clustering from existent ones.

1 Introduction

Sufficiently diverse corpora of test data for the development and implementation of algorithms, in particular of clustering algorithms, constitute an immanent challenge [9]. While various efforts like crowdsourcing produce considerable resources, tasks like fine-tuning or prevention of overfitting require still bigger sets of labeled data. Therefore, ways are sought on how to derive a new tagged set from an existent one without violating clustering algorithm assumptions.

Therefore, the axiomatization of clustering algorithm properties are of interest. Kleinberg [5] introduced interesting clustering invariant properties like scaling-invariance and consistency. Scaling invariance means that the cluster structure should be preserved if all distances between data points are multiplied by a constant. Consistency means that the clustering should be preserved if distances between data points in the cluster are not increased, and distances between data points from distinct clusters are not decreased. Regrettably, the consistency transform (CT) cannot be applied to data being subject of k-means clustering to generate a new labeled data set because this algorithm does not have the consistency property [8]. Hence other properties like the inner or outer consistency [1] need to be investigated. The inner-consistency transform is identical with CT except for distances between data points from distinct clusters are unchanged. The outer-consistency transform is identical with CT except for distances between data points within each cluster are unchanged. But inner-consistency property is not possessed by k-means [1] and what is worse, in a fixed-dimensional space the inner CT reduces typically to identity transform [7] which is of no value for test data generation. The outer consistency, on the other hand, with respect to k-means is of little value under continuous setting because it requires synchronized motion of all clusters – one cluster alone cannot be moved. This paper investigates how the outer-consistency constraints can be relaxed to what we call motion-consistency. It shall be defined as follows:

Definition 1

Cluster area is any solid body containing all cluster data points. Gap between two clusters is the minimum distance between the cluster areas, i.e., Euclidean distance between the closest points of both areas.

Definition 2

Given a clustered data set embedded in a fixed dimensional Euclidean space, the motion-transformation is any continuous transformation of the data set in the fixed dimensional space that (1) preserves the cluster areas (the areas may only be subject of isomorphic transformations) and (2) keeps the minimum required gaps between clusters (the minimum gaps being fixed prior to transformation). By continuous we mean: there exists a continuous trajectory for each data point such that the conditions (1) and (2) are kept all the way.

Definition 3

A clustering method has the property of motion-consistency, if it returns the same clustering after motion-transformation.

Compared to outer-consistency, or even the consistency, we weaken the constraints imposed on the distances between points, because the distances between data points of different data sets do not need to be increased, but only the distances between cluster areas (gaps) should not be decreased below certain values.

We demonstrate for k-means that it is advantageous to define the cluster area as a ball centered at its gravity center and encompassing all the data points of a cluster. Wherever we speak about a ball, we mean a hyper-ball that is the region enclosed by a hyper-sphere, that is an n-ball for n-dimensional Euclidean space $\mathbb {R}^n$. k-means, one of the most popular algorithms, exists in a multitude of versions. For an extensive overview of the general concept of k-means and versatile versions of it, see e.g., [11]. We refer here to the following ones: (1) random-seed k-means, that is one with random initial seeding of cluster centers, (2) random-set k-means, that is one with the random initial assignment of data points to clusters, (3) k-means++, that is one with seeding of clusters according to a heuristic minimizing the distance to the closest cluster (4) k-means-ideal that is an “oracle” algorithm that finds the clustering minimizing absolutely the k-means objective. We consider so-called batch versions.

2 Moving Clusters – Motion-Consistency

As was observed in [4], clustering algorithms make implicit assumptions about the clusters’ definition, shape, and other characteristics and/or require some predetermined free parameters. The shape of the clusters may constitute the foundation for choosing the right number of clusters to split the data into [3]. In this section, let us ask what should be the shape of the area covered by the k-means clusters. The usual way to look at the k-means clusters is one of the so-called Voronoi regions [10]. These regions are polyhedrons such that any point within the area of the polyhedron is closer to its cluster center than to any other cluster center. Obviously, the outer polyhedrons (at least one of them) can be moved away continuously from the rest without overlapping any other region so that at least the motion-transformation is applicable non-trivially. However, does the motion-consistency hold? A closer look at the issue tells us that it is not. As k-means terminates, the neighboring clusters’ polyhedra touch each other via a hyperplane such that the straight line connecting centers of the clusters is orthogonal to this hyperplane. This causes that points on the one side of this hyperplane lie more closely to the one center, and on the other to the other one. But if we move the clusters in such a way that both touch each other along the same hyperplane, then it happens that some points within the first cluster will become closer to the center of the other cluster and vice versa.

Generally, moving the clusters will change their structure (points switch clusters) unless the points lie actually not within the polyhedrons but rather within paraboloids with appropriate equations. Then moving along the border, hyperplane will not change cluster membership (locally, that is, the data points of the two considered clusters will not switch cluster membership given that we fixed all other clusters and consider reclustering of these two clusters only). But the intrinsic cluster borders are now paraboloids. The problem will occur again if we relocate the clusters allowing for touching along the paraboloids.

Hence the question can be raised: What shape should the k-means clusters have in order to be (locally) immune to movement of whole clusters?

Assume that only one cluster would move. Let us consider the problem of susceptibility to class membership change within a 2D plane containing the two cluster centers and the motion vector of the moving cluster. Let the one cluster center be located (for simplicity) at the point (0,0) in this plane and the other at $(2x_0,2y_0)$ for some $x_0, y_0$. Let further the border of the first cluster be characterised by a (symmetric) function f(x) and let the shape of the border of the other one g(x) be the same, but rotated by $180^{\circ }$ around $(x_0,y_0)$: $g(x)=2y_0-f(2x_0-x)$. Let both have a touching point (we excluded already a straight line and want to have convex smooth borders). From the symmetry conditions one easily sees that the touching point must be $(x_0, y_0)$. As this point lies on the surface of f(), $y_0=f(x_0)$ must hold. Any point (x, f(x)) of the border of the first cluster must be closer to its centre (0, 0) than to the centre $(2x_0,2y_0)$ of the other:

$$\begin{aligned} (x-2x_0)^2+(f(x)-2f(x_0))^2-x^2-f^2(x)\ge 0 \end{aligned}$$

(1)

That is

$$- x_0( x- x_0)- f(x_0)\left( f(x)- f(x_0)\right) \ge 0$$

Let us consider only positions of the center of the second cluster below the X axis ($y_0<0$). In this case $f(x_0)< 0$. Further let us concentrate on $x>x_0$. We get $\frac{ f(x)-f(x_0)}{x-x_0} \ge \frac{x_0}{-f(x_0)}$. In the limit, when x approaches $x_0$, $f'(x_0) \ge \frac{x_0}{-f(x_0)}$. By analogy for $x< x_0$ in the limit $x\rightarrow x_0$ we get: $f'(x_0) \le \frac{x_0}{-f(x_0)}$ This implies

$$\begin{aligned} f'(x_0) = \frac{-1}{ \frac{f(x_0)}{x_0}} \end{aligned}$$

(2)

$\frac{f(x_0)}{x_0}$ is the directional tangent of the straight line connecting both cluster centres. $f'(x_0)$ is tangential of the borderline of the first cluster at the touching point of both clusters. The equation above means both are orthogonal. But this property implies that f(x) must define (a part of) a circle centred at (0, 0). As the same reasoning applies at any touching point of the clusters, a k-means cluster would have to be (hyper)ball-shaped in order to allow the movement of the clusters without elements switching cluster membership.

We know that most k-means versions tend to stick at local minima. We see here immediately that some kind of local minima is preserved under motion-consistency transform.

Theorem 1

If random-set k-means has a local minimum in ball form that is such that the clusters are enclosed into equal radius balls centered at the respective cluster centers, and gaps are fixed at zero, then the motion-transform preserves this local minimum.

Proof

For $k=2$, this is obvious from the above consideration. For $k>2$ consider just each pair of clusters to see that no cluster change occurs.

The tendency of k-means to recognize best ball-shaped clusters has been known long ago, but we are not aware of presenting such an argument for it.

Fig. 1.

Possible alternatives to the basic clustering into {$C_1,C_2$}. Left figure: one cluster is split into two clusters. Central figure: upon this split, one cluster takes over a subcluster of the other cluster. Right figure: both clusters are split into subclusters that form new clusters, as indicated in Fig. 2.

3 Motion-Consistency Property for Two Clusters

The preservation of local minima does not guarantee the preservation of the global minimum even if the global minimum has the above-mentioned ball form.

A sufficient separation between the enclosing balls is needed, as we will show again for $k=2$.

Let us consider, under which circumstances a cluster $C_1$ of radius $r_1$ containing $n_1$ elements would take over $n_{21}$ elements (i.e. subcluster $C_{21}$) of a cluster $C_2$ of radius $r_2$ of cardinality $n_{2}$, if we perform the motion-consistency transform. As only (sub)cluster centres are of interest in our investigation, we can concentrate on the plane spanned by the gravity centres c1, c21, c22 of $C_1, C_{21}, C_{22}$, see left most Fig. 1. The enclosing (hyper)balls of both clusters $C_1,C_2$ intersect with this plane as circles, indicated as black lines. In worst case, either c21 or c22 would lie on the respective circle, which implies the other centre lying on a circle with smaller radius, drawn in grey. Generally, both will lie closer to $C_2$ gravity centre. Let $n_{22}=n_2-n_{21}$ be the number of the remaining elements (subcluster $C_{22}$ of the second cluster. Let the enclosing balls of both clusters be separated by the distance (gap) g. Let us consider the worst case that is that the center of the $C_{21}$ subcluster lies on a straight line segment connecting both cluster centers. The centre of the remaining $C_{22}$ subcluster would lie on the same line but on the other side of the second cluster centre. Let $r_{21}$, $r_{22}$ be the distances of centres of $n_{21}$ and $n_{22}$ from the centre of the second cluster. The relations

$$n_{21}\cdot r_{21}= n_{22}\cdot r_{22}, \ r_{21}\le r_2, \ r_{22}\le r_2$$

must hold. Let us denote with SSC(C) the sum of squared distances of elements of the set C to the center of this set.

Fig. 2.

Extreme cases to be considered when looking for a sufficient gap to avoid alternative clustering with a split of both clusters.

So in order for the clusters $C_1,C_2$ to constitute the global optimum

$$SSC(C_1)+SSC(C_2) \le SSC(C_1\cup C_{21})+SSC(C_{22}) $$

must hold. But

$$SSC(C_2)=SSC(C_{21})+SSC(C_{22})+n_{21}\cdot r_{21}^2+n_{22}\cdot r_{22}^2$$

$$SSC(C_1\cup C_{21})=SSC(C_1)+SSC(C_{21})+\frac{n_1 n_{21}}{n_1+ n_{21}}(r_1+r_2+g-r_{21})^2$$

Hence

$$ \sqrt{ ( r_{21}^2+ r_{21}\cdot r_{22} ) (n_{21}/n_1+ 1 )} -r_1-r_2+r_{21} \le g $$

As $r_{22}= \frac{r_{21} n_{21}}{n_2-n_{21}}$

$$ r_{21} \sqrt{ \frac{ n_2}{n_1} \frac{n_1+n_{21}}{n_2-n_{21}}} -r_1-r_2+r_{21} \le g $$

Let us consider the worst-case when the elements to be taken over are at the edge of the cluster region ($r_{21}=r_2$). Then

$$ r_2 \sqrt{ \frac{ n_2}{n_1} \frac{n_1+n_{21}}{n_2-n_{21}}} -r_1 \le g $$

The lower limit on g will grow with $n_{21}$, but $n_{21}\le 0.5 n_2$, because otherwise $r_{22}$ would exceed $r_2$. Hence in the worst case

$$ r_2 \sqrt{ \frac{ n_2}{n_1} \frac{n_1+n_2/2}{n_2/2}} -r_1 \le g $$

$$\begin{aligned} r_2 \sqrt{ 2 (1+0.5n_2/n_1) } -r_1 \le g \end{aligned}$$

(3)

In case of clusters with equal sizes and equal radius this amounts to

$$g\ge r_1(\sqrt{3}-1)\approx 0.7r_1 $$

But there exists the theoretical possibility that both clusters are split into subclusters, which then may form pairwise clusters different from the original $C_1, C_2$. This is symbolically illustrated in the right Fig. 1. As only (sub)cluster centres are of interest in our investigation, we can concentrate on the 3D subspace spanned by the gravity centres c11, c12, c21, c22 of subclusters $C_{11},C_{12}, C_{21}, C_{22}$. Furthermore, distances between subcluster gravity centers from different clusters will decrease if we rotate the lines c11, c12 and c21, c22, so that they lie in a 2D plane. So we need in fact to consider this 2D plane in worst-case analysis, as in Fig. 1, though the results apply to any high-dimensional space. In an analogous way as above, we can derive (as a simple exercise) explicit requirements on minimum gap g needed in order to ensure that such a re-clustering will not happen. The worst cases of subcluster center positions to be considered are depicted in Fig. 2. In each case, the 50%–50% split of a cluster into subclusters turns out to be requiring the biggest gap. We conclude

Theorem 2

k-means algorithm with $k=2$ possesses the property of motion-consistency if (1) the k-means clustering global minimum $\varGamma {}$ has the property that each cluster can be enclosed in a ball and (2) the gaps between balls fulfil the condition of taking the maximum of the gaps derived from Fig. 2, Fig. 1 and (3) the gap between clusters would not be decreased below the gap value from (2) during the motion.

Note that under k-means objective, the globally optimal clustering is also pairwise optimal, but the inverse does not hold.

This means that Motion-Consistency transform can turn an optimal clustering to an unoptimal one for $k>2$.

It should be emphasized that we consider here about the local optimum of k-means. With the aforementioned gap size, the global k-means minimum may lie elsewhere, in a clustering possibly without gaps. Also, the motion-transformation preserves as a local minimum the partition it is applied to. Other local minima and global minimum can change.

Note that the motion-consistency (applicable for $k=2$ in k-means) is more flexible for the creation of new labeled data sets than outer-consistency.

4 Perfect Ball Clusterings

The problem with k-means (-random and ++) is the discrepancy between the theoretically optimized function (k-means-ideal) and the actual approximation of this value. It appears to be problematic even for well-separated clusters.

First, let us point to the fact that well-separatedness may keep the algorithm in a local minimum.

It is commonly assumed that a good initialization of a k-means clustering is one where the seeds hit different clusters. It is well-known that under some circumstances, the k-means does not recover from poor initialization, and as a consequence, a natural cluster may be split even for well-separated data.

Hitting each cluster may not be sufficient as neighboring clusters may be able to shift the cluster center away from its cluster. Hence let us investigate what kind of well-separability would be sufficient to ensure that once clusters are hit by one seed each, they would never lose the cluster center.

Let us investigate the working hypothesis that two clusters are well separated if we can draw a ball of some radius $\rho$ around true cluster center of each of them, and there is a gap between these balls. We claim (see [6]) that

Theorem 3

If the distance between any two cluster centres A, B is at least $4\rho _{AB}+\epsilon$, $\epsilon >0$, where $\rho _{AB}$ is the radius of a ball centred at A and enclosing its cluster (that is cluster lies in the interior of the ball) and it also is the radius of a ball centred at B and enclosing its cluster, then once each cluster is seeded the clusters cannot loose their cluster elements for each other during k-means-random and k-means++ iterations.

Before starting the proof, let us introduce related definitions.

Definition 4

We shall say that clusters centred at A and B and enclosed in balls centred at A, B and with radius $\rho _{AB}$ each are nicely ball-separated, if the distance between A, B is at least $4\rho _{AB}+\epsilon$, $\epsilon >0$. If all pairs of clusters are nicely ball separated with the same ball radius, then we shall say that they are perfectly ball-separated.

Obviously, if there exists a perfect ball clustering into k-clusters in the data set, then after invariance transform as well as after consistency transform, there exists a perfect ball clustering into k-clusters in the data set. Let us restrict ourselves to clusterings with at least three data points in a cluster (violation of the most general richness, but nonetheless a reasonable richness, let us call it reachness-$3{++}$. In this case, it is obvious that if the perfect ball clustering exists then, it is unique. This means automatically that if k-means would be able to detect the perfect ball clustering into k clusters, then it would be consistent in the sense of Kleinberg. Therefore it is worth investigating whether or not k-means can detect a perfect ball clustering.

If the data set had a perfect ball clustering into k clusters (of at least 2 elements), but not into $k-n_1$ nor into $k+n_2$ clusters, where $1\le n_1 \le k-2 ,1\le n_2\le n/2-k$ are natural numbers, then under application of Kleinberg’s consistency transform, the new data set can both have a perfect ball clustering into $k-n_1$ and into $k+n_2$ clusters. Hence the Kleinberg’s impossibility theorem holds also within the realm of perfect ball clusterings.

Fig. 3.

An illustrative figure for proof of 4 radius distance ensuring good separability.

Proof

For the illustration of the proof see Fig. 3.

Consider two points A, B be two ball centers and two points, X, Y, one being in each ball (presumably the cluster centers at some stage of the k-means algorithm). To represent their distances faithfully, we need at most a 3D space.

Let us consider the plane established by the line AB and parallel to the line XY. Let $X'$ and $Y'$ be projections of X, Y onto this plane. Now let us establish that the hyperplane $\pi$ orthogonal to X, Y, and passing through the middle of the line segment XY, that is the hyperplane containing the boundary between clusters centered at X and Y does not cut any of the balls centered at A and B. This hyperplane will be orthogonal to the plane of the Fig. 3 and so it will manifest itself as an intersecting line l that should not cross circles around A and B, being projections of the respective balls. Let us draw two solid lines k, m between circles $O(A,\rho )$ and $O(B,\rho )$ tangential to each of them. Line l should lie between these lines, in which case the cluster center will not jump to the other ball. Let the line $X'Y'$ intersect with the circles $O(A,\rho )$ and $O(B,\rho )$ at points C, D, E, F as in the figure. It is obvious that the line l would get closer to circle A, if the points X’, Y’ would lie closer to C and E, or closer to circle B if they would be closer to D and F.

Therefore, to show that the line l does not cut the circle $O(A,\rho )$, it is sufficient to consider $X'=C$ and $Y'=E$. (The case with ball $Ball(B,\rho )$ is symmetrical).

Let O be the center of the line segment AB. Let us draw through this point a line parallel to CE that cuts the circles at points $C', D', E'$ and $F'$. Now notice that centric symmetry through point O transforms the circles $O(A,\rho )$, $O(B,\rho )$ into one another, and point $C'$ into $F'$ and $D'$ into $E'$. Let $E^*$ and $F^*$ be images of points E and F under this symmetry. In order for the line l to lie between m and k, the middle point of the line segment CE shall lie between these lines.

Let us introduce a planar coordinate system centered at O with $\mathcal {X}$ axis parallel to lines m, k, such that A has both coordinates non-negative, and B non-positive. Let us denote with $\alpha$ the angle between the lines AB and k. As we assume that the distance between A and B equals $4\rho$, then the distance between lines k and m amounts to $2\rho (2\sin (\alpha )-1)$. Hence the $\mathcal {Y}$ coordinate of line k equals $\rho (2 \sin (\alpha )-1)$. So the $\mathcal {Y}$ coordinate of the center of the line segment CE shall be not higher than this. Let us express this in vector calculus:

$$4(y_{OC}+y_{OE})/2 \le \rho (2\sin (\alpha )-1)$$

Note, however that

$$y_{OC}+y_{OE}=y_{OA}+y_{AC}+y_{OB}+y_{BE}= y_{AC}+y_{BE} = y_{AC}-y_{AE^*} =y_{AC}+y_{E^*A}$$

So let us examine the circle with center at A. Note that the lines CD and $E^*F^*$ are at the same distance from the line C’ D’. Note also that the absolute values of direction coefficients of tangentials of circle A at C’ and D’ are identical. The more distant these lines are, as line CD gets closer to A, the $y_{AC}$ gets bigger, and $y_{E^*A}$ becomes smaller. But from the properties of the circle, we see that $y_{AC}$ increases at a decreasing rate, while $y_{E^*A}$ decreases at an increasing rate. So the sum $y_{AC}+y_{E^*A}$ has the biggest value when C is identical with $C'$ and we need hence to prove only that

$$(y_{AC'}+y_{D'A} )/2=y_{AC'} \le \rho (2\sin (\alpha )-1)$$

Let M denote the middle point of the line segment $C'D'$. As point A has the coordinates $(2\rho \cos (\alpha ), 2\rho \sin (\alpha ))$, the point M is at distance of $2\rho \cos (\alpha )$ from A. But $C'M^2= \rho ^2-(2\rho \cos (\alpha ))^2$.

So we need to show that $\rho ^2-(2\rho \cos (\alpha ))^2 \le ( \rho (2\sin (\alpha )-1))^2$. In fact we get from the above $0 \le 1 - \sin (\alpha )$ which is an obvious trigonometric relation.

5 Incremental k-means

It is not hard to demonstrate that if the perfect-ball separation was found, it does not suffice to state that we reached a global minimum of k-means. Moreover, even if the global minimum of k-means is a perfectly ball separated set of clusters, it does not mean that motion-transformation keeping this property will yield a new clustering being optimal for k-means.

However, there exists a version of k-means for which a perfectly ball separated set of clusters is the global optimum. Hence the motion-transform keeping the perfect ball separation keeps the optimum. We will introduce this algorithm in this section and demonstrate the respective property.

Ackerman and Dasgupta [2] study clusterability properties of incremental clustering algorithms. They introduce an incremental version of a very popular k-means algorithm (for an extensive overview of k-means versions see [11]).

They introduced the perfect clustering with the property that the smallest distance between elements of distinct clusters is larger than the distance between any two elements of the same cluster. They demonstrate that there exists an incremental algorithm discovering the perfect clustering that is linear in k with respect to space. But their incremental (sequential) k-means fails to do so.

Their case study is interesting because it demonstrates that the cluster shape plays a role - each cluster has to be enclosed into a convex envelope. The problem of incremental k-means is caused by the fact that this envelope is not ball-shaped.

Let us discuss at this point a bit the notions of perfect separation. In their Theorem 4.4. Ackerman and Dasgupta [2] show that the incremental k-means algorithm, as introduced in their Algorithm 2.2, is not able to cluster correctly data that is perfectly clusterable (their Definition 4.1). The reason is quite simple. The perfect separation refers only to separation of data points, and not to points in the convex hull of these points. But during the clustering process, the candidate cluster centres are moved in the convex hulls, so that they can occasionally get too close to data points of the other cluster. To avoid this effect, we will use the just introduced concept of perfect ball separation (see Definition 4)

Under the perfect-ball-separation as introduced here their incremental k-means Algorithm 2.2. (Sequential k-means) will discover the structure of the clusters after a modification (Algorithm 1):

The reason is as follows. Perfect ball separation ensures that there exists an r of the enclosing ball such that the distance between any two points within the same ball is lower than 2r, and between them is bigger than 2r. So whenever Ackerman’s incremental k-mean merges two points, they are the points of the same ball. Upon merging, the resulting point lies again within the ball.

Theorem 4

The incremental k-means algorithm will discover the structure of perfect-ball-clustering.

Proof

If $t_i,t_j$ are points within the ball enclosing a single cluster, then also $(t_in_i+t_jn_j)/(n_i+n_j)$ will lie within the same ball. If $t_{k+1}$ stems from a cluster not represented by $t_1,\dots ,t_k$, then $k+1$ will not be in the pair (i, j) of closest elements, because their distance is more than $2\rho$, while those within a cluster at most $2\rho$. On the other hand, $t_i,t_j$ would not stem from two different clusters because $t_1,\dots ,t_k$, because the distance within a cluster is at most $2\rho$, while the distance between elements from distinct clusters is at most $2\rho$. In this way, no $t_l$, $l=1,\dots ,k$ will lie outside of balls representing clusters. Furthermore, its position will be calculated only based on data points from the same cluster. Furthermore, it will be the average position of those points, so finally, after the full pass, all $t_l$ will represent the k different cluster centers.

The incremental k-means algorithm returns only a set of cluster centers without stating whether or not we got a perfect ball clustering. However, if we are allowed to inspect the data for the second time, such information can be provided. See Algorithm 2: A second pass for other algorithms from Ackerman and Dasgupta Sect. 2 would not yield such a decision.

6 Conclusions

We derived in this paper the intended shape of a k-means cluster (a ball centered at cluster gravity center) as a necessary condition of clustering preserving motion-transformation of the dataset. This shape preserves ball-shaped local minima for k-means algorithm with random initial partition. We have also derived, for ball-shaped clusters for $k=2$, gap condition for motion-transformation that preserves the global minimum of k-means. We have also shown that incremental k-means is able to find the perfect ball-shaped clustering. Therefore the motion-transform keeping the perfect ball separation will preserve the incremental-k-means clustering. Thus we have discovered a couple of transformations that preserve various aspects of clustering, suitable for deriving new labeled datasets from existent ones, as implied by our Theorems 1, 3, 2, 4.