Keywords

1 Introduction

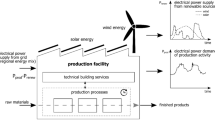
The Electronic Components and Systems industry (ECS) is characterized by large lead times and high market volatility. Besides fast technological development within this industry, cyclic market up- and downturns are influencing the semiconductor market (Mönch et al. 2011). Therefore, proper capacity and inventory management are key success factors for semiconductor companies to survive. The effects of rapidly advancing technology cause goods in inventory to depreciate very fast, which may lead to considerable losses in case of a steep market downturn. On the other hand, too little inventory of required products can cause a loss in terms of opportunity costs by not reaching customer satisfaction, service level and product availability if the customer demand cannot be satisfied due to the long term manufacturing lead times. In addition, the majority of fixed assets consists of very expensive front-end equipment. In this context this leads to high costs of wasted capacity (e.g., idling, bad product quality) in fab. Consequently, maximized front-end capacity utilization is an important constraint in semiconductor planning.

Above, Fig. 1 shows that the internal semiconductor supply chain struggles with a high degree of supply and demand uncertainty. A key success factor of this highly competitive environment is process improvement. Within this work, the authors focus on a manufacturing excellence approach to increase front-end supply reliability and the availability of inventory within the customer order decoupling point (CODP). Manufacturing excellence is represented by superior key performance indicators, i.e. development and manufacturing processes must be designed in a way to reach an optimum between product quality, flexibility, time and costs (Yasin et al. 1999; Plunkett and Dale 1988).

Fig. 1.
figure 1

Uncertainty in semiconductor manufacturing environment

Full size image

To analyze the effects of process improvements we propose an advanced “return on quality” approach (Rust et al. 1995) considering,

  • the accountability of quality efforts to reach a stable process (monitor, control, improve) and the related impact on product quality and process performance (lead time, service level, etc.),

  • the complexity of the processes have the risk to spend too much on quality (over engineering) if the root cause of quality problems are not understood,

  • quality investments are not equally valid and sometimes a repair process can be used to reach a Zero-Failure Culture (Schneiderman 1986), and

  • non-quality costs, i.e., failure costs, productivity losses (material, energy, human resources) or customer dissatisfaction related costs can be high.

The need for scientific research in the field of an efficient and effective process improvement for the Electronic Components and Systems industry is motivated by the following research questions:

  • RQ1: Can production costs be reduced, when critical process deviation are identified at an earlier stage?

  • RQ2: How does an early detection of defective products affect the lead-time, process quality and performance?

  • RQ3: Understand the interaction between quality problems and lot sizing.

2 Theoretical Foundations

For more realistic queueing models, exact analytical solutions become very difficult to achieve. Therefore, researchers usually use approximations to estimate cycle time. Accuracy of approximation models depends greatly on the actual distribution of the inter-arrival times and the service times. Accordingly, various approximations may exist for the same queueing model. For example, Buzacott and Shanthikumar (1993) listed three approximations for the G/G/1 queues. M/M/1 Models for example are not sufficient to accurately describe fab performance because of the oversimplified modelling assumptions. However, these models provide general insight on the relationship between WIP level, capacity and throughput, and provides intuitive directions on how to improve performance. Little’s law (Little 1961) can describe a simple and stable process, where the inflow and outflow rates are identical. However, to analyse complex operation processes, require more than the long-run average values set by Little’s law. For example, Wu (2005) applied Little’s law and the G/G/1 queueing formula to estimate the variance of a simple factory with single toolsets. He found some basic properties that provide managerial insight on how variability affects the production performances. He also pointed out that the variability of bottleneck toolsets should be reduced to achieve fast cycle time. The following conditions apply for a stable process:

$$ \rho = \frac{\lambda }{\mu } < 1, $$
(1)

where \( \rho \) is the utilization, \( \lambda \) is the unit arrival rate and \( \mu \) is the service rate. The arrival and service rate is defined by

$$ \lambda = \frac{1}{{t_{a} }} , $$
(2)
$$ \mu = \frac{1}{{t_{e} }} , $$
(3)

where \( t_{a} \) is the inter-arrival time of units and \( t_{e} \) is the effective process time. The approximation for waiting time (\( CT_{q} \)) of a single process, is given by

$$ CT_{q} = \frac{\rho }{{\left( {1 - \rho } \right)}}\left( {\frac{{c_{a}^{2} + c_{e}^{2} }}{2}} \right) t_{e} , $$
(4)

where \( c_{a}^{2} \) is the squared-coefficient-of-variation (SCV) of the inter-arrival time (\( t_{a} \)), and \( c_{e}^{2} \) is the SCV of the effective process time (\( t_{e} \)). The effective process time include the raw process time (\( t_{s} \)) and all time losses due to setup, breakdown, unavailability of operator, and any other source of variability (Wu 2005; Kingman 1961). The throughput rate of a single server is defined by

$$ r = \frac{\rho }{{t_{e} }} , $$
(5)

and the cycle time is defined by

$$ CT = CT_{q} + t_{s} . $$
(6)

The raw process time includes all the times a unit spends on a server, such as load/unload and processing (Fig. 2).

Fig. 2.
figure 2

Cycle time of a single server process

Full size image

Analytical approaches based on queuing theory serve as a fundamental instrument to explore what-if questions. Queuing models make cycle time estimation based on the assumption of stochastic arrival and service processes. The arrivals (demand) of a unit to the workstation is a stochastic process where inter-arrival times are random variables following specific (unknown) distributions. Based on machine configuration and process requirements, processing times are also stochastic. Products that have already arrived but cannot be processed directly are placed in the waiting queue.

Most operational processes are characterized by dynamic operating conditions and complex interrelationships that cause changes in inputs, operations and outputs. Variability results in non-conformities that have a negative impact on an operations process. Product characteristics and product quality, as well as process attributes (e.g., process time, set-up time, process quality, equipment breakdowns and repairs) are subject to non-conformance (Klassen and Menor 2007). Thus, the reduction of variability improves operational performance, such as throughput, lead-time, customer service, quality, etc. (Hopp and Spearman 2001). Figure 3 shows examples of the effect of variability reduction on the cycle time and capacity utilization:

Fig. 3.
figure 3

Impact of process variability

Full size image
  1. a)

    Lower variability leads to a reduced cycle time be unchanged capacity utilization.

  2. b)

    Lower variability enables higher capacity utilization and therefore a higher throughput rate.

3 Modelling Approach

The purpose of this article is to explore the meaning of return on quality in manufacturing systems. To accomplish this purpose a general model consisting of discrete-event simulation (DES) and system dynamics (SD) simulation models is described. In order to better understand the challenges and benefits of each simulation type the paper starts by reviewing the related work on the different simulation approaches. In general SD can be used to model problems at a strategic level, whereas DES is used at operational and tactical level (Tako and Robinson 2012). Different simulation approaches such as discrete event simulation (DES) and system Dynamics (SD) are excellent tool for visualizing, understanding and analysing the dynamics of manufacturing systems and thus supporting the decision-making process (Borshchev 2013). Both simulation approaches enhance the understanding of how systems behave over time (Sweetser 1999). However, contradictory statements are made regarding the level of understanding that users can gain from using these models. DES is more concerned with detailed complexity, while SD with dynamic complexity (Lane 2000).

These methods tend to be appropriate as long as changing circumstances and time have no significant impact on the managerial problem issue. However, the influence of certain elements on the overall problem definition forces scientists to take a dynamic system into consideration when applying solution methods. In practice, most problems derive from complex and dynamic systems which requires solution methods that are capable of handling these challenges. In the late 1950s MIT professor Jay W. Forrester developed a methodology for modelling and analysing the behaviour of complex social systems. The term “system dynamics” was introduced to the scientific world and attracted particular attention in recent years with the development of high-performance computer software (Rodrigues and Bowers 1996). The basic idea behind system dynamics is the identification and analysis of information feedback structures within a system and their representation with differential and algebraic equations in a simulation modelling environment (Homer and Hirsch 2006). This methodology has been applied to a number of problem domains, such as economic behaviour, biological and medical modelling, energy and the environment, theory development in the natural and social sciences, dynamic decision making, complex non-linear dynamics, software engineering and supply chain management (Angerhofer and Angelides 2000).

System dynamics models consist of feedback loops that represent information based interaction between elements of the simulated system. Feedback loops create a dynamic behaviour of a system, influence the values of stocks and flows and often lead to new unanticipated reactions of the system. They can either be positive (or self-reinforcing) or negative (or balancing). For example the inventory level in a production plant is increased by the flow of produced goods and decreased by the flow of shipped goods. The interaction between feedback loops, stocks and flows enables to replicate dynamic systems in a simulation environment (An and Jeng 2005).

Simulation modelling offers a great potential in modelling and analysing a systems behaviour. In our work, we use DES to simulate the improvement of early quality control. Furthermore, the impact on the holistic system shall be shown by improving the throughput time and the reduction of variability in process stability and quality. The approach presented in this paper not only enables accurate performance evaluation, but also suggests simple real time control rules under which the flexible manufacturing system has a regular and stable behavior when no major breakdown occurs, the production requirements are satisfied, and the bottleneck machines are fully utilized.

First results based on the theoretical background information led to the following selected expected impacts:

  • Internal & external improvements based on overall framework.

  • Reduction of variability influences the process stability, lead-time and gives potential improvements due to customer satisfaction.

  • The company can react faster to uncertainty of order fulfilments and give adequate information to the customer, which results in better service performance and customer satisfaction.

  • The company can reduce operating costs, production costs and enhances overall speed of production performance if the inspection and fault detection operations are improved (Felsberger et al. 2018).

Based on the above presented theoretical foundations we now illustrate the developed modelling framework. Our process improvement evaluation model is based on successively using a discrete event simulation model of the relevant processes that provides the basis for estimating the changes of input parameters for a system dynamics model (Fig. 4). The purpose of the discrete-event simulation model is to conduct experiments regarding these processes (e.g., Impact of early detection of systematic errors based on machine data). The DES model can be used to quantify relevant performance indicators (e.g., lead-time, equipment utilization, waiting times, WIP, throughput, service-level). In addition, our discrete-event simulation model analyzes risks such as front-end demand uncertainty as well as the impacts of these uncertainties. Furthermore, the methodology of system dynamics will be taken in consideration to present the dynamic changeovers of quality aspects by improving selected manufacturing processes (Reiner 2005). Existing system dynamics models already focus on the dynamics of quality improvement and quality costs in manufacturing companies (Mahanty et al. 2012; Kiani et al. 2009). Our model approach will be used to analyze the effects of process improvements (development and manufacturing) and analyze its dynamic behavior based on a Systems Dynamics approach in combination with process simulation for manufacturing processes for high-risk environments (Felsberger et al. 2018). This system dynamic model will have the ability to evaluate the impact of input parameters to production process performance as well as stability.

Fig. 4.
figure 4

System Dynamics approach in combination with process simulation

Full size image

Inspired by a real front-end production process in the ECS industry we first start to develop a simplified model (Fig. 5) that highlights three so-called work centers or tool groups (PG,1, PG,2, PG,3). Between these three selected work centers, additional activities such as transport activities and further processing steps take place. In our model, we consider these additional activities as a black box. The nature of such systems is characterized by several re-entrant flows at different stages in the manufacturing cycle. Single tools are the smallest unit of a work center (Ps). The machines within a work center provide similar processing capabilities. Therefore, the machines of a single work center can be often modeled as identical or unrelated parallel machines (Mönch et al. 2011). Contrariwise, jobs (Lots) cannot always be processed on all machines within a work center related to different process requirements. Finally, the last activity is the wafer test, were every circuit (die) is tested for its functionality. It is performed on the not yet divided wafer to detect faulty circuits. If the defective number of dies per wafer exceeds a certain limit, the entire wafer is discarded. If several wafers of a lot are faulty, the entire batch is discarded. Causes of yield reduction may consist of a common (random) or special (systematic) nature. Incorrect electrical parameters, faulty layers, poor alignment of the layers or poor matching of the chip design to the technology are examples of systematic errors (Hilsenbeck 2005).

Fig. 5.
figure 5

Topology of the process model

Full size image

4 Conclusion and Future Outlook

The model can be extended with several details showing effects of process improvement and variability reduction through an increased level of technology, i.e. the early detection of faulty items potentially leads to decrease of cycle times and therefore to an overall improved process performance. We expect that an investment in quality improvement, e.g. appraisal and prevention efforts leads to a positive impact on process quality (Zero Failure Culture) and performance (lead-time, service level). Furthermore, the benefits of investing in return on quality along with process improvement lead to significant impacts on overall manufacturing performance and therefore in profitability and customer satisfaction (Mahanty et al. 2012). Our process model therefore analyses these impacts on a strategical (SD) as well as on a tactical level (DES). Based on the DES model we intend to generate input data for the SD model, which will be subject of future work. In detail, this includes the development of the SD model and linking it to the DES model.

For example, the input parameters for productivity measures might be the potential increase of the overall improvement of speed lead-time. Finally, this improvement eventually ends up in a better customer satisfaction and retention. Costs for example are determined by earlier scrap detection and the reduction of expensive defect density test equipment. Considering Rust et al. (1995) we intend to measure:

  • the impact on product quality and process performance (lead time, service level, etc.),

  • the risk of over engineering if the root cause of quality problems are not understood,

  • the justification of quality investments to reach a Zero-Failure Culture and

  • the impact on non-quality costs, i.e., failure costs, productivity losses or customer dissatisfaction related costs.