Abstract
Real-time embedded systems are information processing systems that require both functional and timing correctness.
Such systems usually interact with the physical world, where time naturally processes. Therefore, safe bounds of deterministic or probabilistic timing properties are required. Existing analyses and optimizations for scheduling algorithms and resource management policies in complex real-time systems are usually ad hoc solutions for a specific studied problem. In this chapter, we challenge this design and analytical practice, since the future design of real-time systems will be more complex, not only in the execution model but also in the parallelization, communication, and synchronization models. We strongly believe that the future design of real-time systems requires formal properties that can be used modularly to compose safe and tight analysis as well as optimization for the scheduler design and schedulability test problems. This chapter summarizes our recent progress at TU Dortmund in this regard with respect to both deterministic and probabilistic properties.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
- Property-based real-time analysis
- Formalism for complex models
- Deterministic timing properties
- Probabilistic timing properties
4.1 Introduction
The advanced development of embedded computing devices, accessible networks, and sensor devices has triggered the emergence of complex cyber-physical systems (CPS). In such systems, advanced embedded computing and information processing systems heavily interact with the physical world. Cyber-physical systems are integrations of computation, networking, and physical processes to achieve high stability, performance, reliability, robustness, and efficiency [26]. A cyber-physical system continuously monitors and affects the physical environment which also interactively imposes feedback to the information processing system. The applications of CPS include healthcare, automotive systems, aerospace, power grids, water distribution, disaster recovery, etc.
Due to their intensive interaction with the physical world, in which time naturally progresses, timeliness is an essential requirement of correctness for CPS. Communication and computation of safety-critical tasks should be finished within a specified amount of time, called deadline. Otherwise, even if the results are correctly delivered from the functional perspective, the reaction of the CPS may be too late and have catastrophic consequences. One example is the release of an airbag in a vehicle, which only functions properly if the bag is filled with the correct amount of air in the correct time interval after a collision, even in the worst-case timing scenario. While in an entertainment gadget a delayed computation result is inconvenient, in the control of a vehicle it can be fatal. Therefore, a modern society cannot adopt a technological advance when it is not safe.
Cyber-physical systems that require both functional and timing correctness are called cyber-physical real-time systems. Since cyber-physical real-time systems are replacing mechanical and control units that are traditionally operated manually, providing both predictability and efficiency for such systems is crucial to satisfy the safety and cost requirements in our society. Real-time computing for such systems is to provide safe bounds for deterministic or probabilistic timing properties. For providing deterministic timing guarantees, worst-case bounds are pursued. Specifically, the worst-case execution time (WCET) of a program (when it is executed exclusively in the system, i.e., without any interference) has to be safely calculated, for details the reader is referred to [31]. The WCETs of multiple programs are then used for analyzing the worst-case response time (WCRT) when multi-tasking in the system.
The strongest deterministic timing guarantee ensures that there is no deadline miss of a task by validating whether the WCRT is less than or equal to the specified relative deadline. When the deadlines of all tasks in a system are satisfied, the hard real-time requirements are met and the system is a hard real-time system. The assumption behind the requirements of hard real-time guarantees is that a deadline miss can result in fatal errors of the system. Ensuring worst-case timing properties has been an important topic for decades. Initially, such worst-case guarantees were achieved by constructing cyclically repetitive static schedules. The timing properties of static schedules can be analyzed easily, but the constructed real-time systems were inflexible to accommodate any upgrades or changes that were not planned in advance.
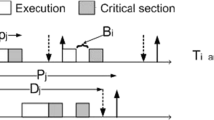
The seminal work by Liu and Layland [23] provided fundamental knowledge to ensure timeliness and allow flexibility for scheduling periodic real-time tasks in a uniprocessor system. A periodic task τ i is an infinite sequence of task instances, called jobs, where two consecutive jobs of a task should arrive recurrently with a period T i (i.e., the time interval length between the arrival times of two consecutive jobs is always T i), all jobs of a task have the same relative deadline D i = T i (i.e., the absolute deadline of a job arriving at time t is t + D i), and each job has the same worst-case execution time (WCET) C i [23]. The utilization U i of a task τ i is hence defined as U i = C i∕T i. Although the periodic real-time task model is not always suitable for industrial applications, the exploration of the fundamental knowledge in the past decades provides significant insights. Specifically, Liu and Layland proved the applicability of preemptive dynamic-priority and fixed-priority scheduling algorithms and provided worst-case utilization analysis. To be precise, they showed that as long as the utilization \(\sum _{i=1}^{n} C_i/T_i\) of the given n tasks is no more than \(n(2^{\frac {1}{n}}-1)\), which is ≥ 69.3%, then the worst-case response time of a task τ i is guaranteed to be no longer than T i if the priorities are assigned in the rate-monotonic (RM) order, i.e., τ i has a higher priority when its period is shorter. Similarly, under preemptive earliest-deadline-first (EDF) scheduling, the utilization bound is guaranteed to be 100%.
However, in many scenarios occasional deadline misses are possible and acceptable. Systems that can still function correctly under these conditions are called soft real-time systems. When the deadline misses are bounded and limited, the term weakly hard real-time system is used. For such cases, safe and tight quantitative properties of deadline misses have to be analyzed so that the system designers can verify whether the occasional deadline misses are acceptable from the system’s perspective. For this purpose, probabilistic timing properties can be very useful, in which the probability of deadline misses or miss rates are pursued. In safety standards, e.g., IEC-61508 and ISO-26262, the probability of failure has to be proved to be sufficiently low. Probabilistic timing properties are important to assure the service level agreements in many applications that require real-time communication and real-time decision-making, such as autonomous driving, smart building, internet of things, and industry 4.0. Deterministic guarantees of interest for weakly hard real-time systems include the quantification of the number of deadline misses within a specified time window length, the worst-case tardiness, and the worst-case number of consecutive deadline misses. Such deadline misses may be allowed and designed on purpose, especially to verify the controller for the physical plant in a CPS. With potential deadline misses in mind, suitable control approaches that can systematically account for data losses can be applied. Such weakly hard real-time systems have been proposed as a feature towards timing-aware control software design for automotive systems in [33].
To design a timing predictable and rigorous cyber-physical real-time system, two separate but co-related problems have to be considered:
-
1.
how to design scheduling policies to feasibly schedule the tasks on the platform and system model, referred to as the scheduler design problem, and
-
2.
how to validate the schedulability of a task system under a scheduling algorithm, referred to as the schedulability test problem, to ensure deterministic and/or probabilistic timing guarantees.
The real-time systems research results in the past half-century have a significant impact on the design of cyber-physical systems. Allowing system design flexibility by using dynamic schedules (either fixed-priority or dynamic-priority schedules) has not only academic values but also industrial penetration. Nowadays, most real-time operating systems support fixed-priority schedulers and allow periodic as well as sporadic task activations. When task synchronization or resource sharing is necessary, the priority inheritance protocol and the priority ceiling protocol developed by Sha et al. [27] are part of the POSIX Standards (in POSIX.1-2008).
Existing analyses and optimizations for scheduling algorithms and resource management policies in complex real-time systems are usually ad-hoc solutions for a specific studied problem. In this chapter, we challenge this design and analytical practice, since the future design of real-time systems will be more complex, not only in the execution model but also in the parallelization, communication, and synchronization models.
Our Conjecture
We strongly believe that the future design of real-time systems require formal properties that can be used modularly to compose safe and tight analysis as well as optimization for the scheduler design and schedulability test problems. This chapter summarizes our recent progress at TU Dortmund for property-based analyses of real-time embedded systems with respect to both deterministic and probabilistic properties.
4.2 Formal Analysis Based on Schedule Functions
For uniprocessor systems, at most one job is executed at a time. Therefore, a scheduling algorithm (or scheduler) determines the order, in which jobs are executed on the processor, called a schedule. A schedule is an assignment of the given jobs to the processor, such that each job is executed (not necessarily consecutively) until completion. Suppose that J = {J
1, J
2, … J
n} is a set of n given jobs. A schedule for J can be defined as a function  , where σ(t) = J
j denotes that job J
j is executed at time t, and
, where σ(t) = J
j denotes that job J
j is executed at time t, and  denotes that the system is idle at time t.
denotes that the system is idle at time t.
If σ(t) changes its value at some time t, the processor performs a context switch at time t. For a schedule σ to be valid with respect to the arrival time, the absolute deadline, and the execution time of the given jobs, we need to have the following conditions for each J j in J for hard real-time guarantees:
-
σ(t) ≠ J j for any t ≤ r j and t > d j and
-
 , where
, where  is a binary indicator. If the condition holds, the value is 1; otherwise, the value is 0.
is a binary indicator. If the condition holds, the value is 1; otherwise, the value is 0.
Note that the integration
\(\int \)
of
 over time used in this chapter is only a symbolic representation for summation.
over time used in this chapter is only a symbolic representation for summation.
For a given sporadic task set T, each task τ i in T can generate an infinite number of jobs as long as the temporal conditions of arrival times of the jobs generated by task τ i can satisfy the minimum inter-arrival time constraint.
Suppose that the jth job generated by task τ i is denoted as J i,j. Let the set of jobs generated by task τ i be denoted as FJ i. A feasible set of jobs generated by a sporadic real-time task τ i satisfies the following conditions:
-
By the definition of the WCET of task τ i, the actual execution time C i,j of job J i,j is no more than C i, i.e., C i,j ≤ C i.
-
By the definition of the relative deadline of task τ i, we have d i,j = r i,j + D i for any integer j with j ≥ 1.
-
By the minimum inter-arrival time constraint, we have r i,j ≥ r i,j−1 + T i for any integer j with j ≥ 2.
A feasible set of jobs generated by a periodic real-time task τ i should satisfy the first two conditions above and the following condition:
-
By periodic releases, we have r i,1 = O i and r i,j = r i,j−1 + T i for any integer j with j ≥ 2.
A feasible collection FJ of jobs generated by a task set T is the union of the feasible sets of jobs generated by the sporadic (or periodic) tasks in T, i.e., \(\mathbf {FJ} = \cup _{\tau _i \in \mathbf {T}} \mathbf {FJ}_i\). It should be obvious that there are infinite feasible collections of jobs generated by a sporadic real-time task set T.
For a feasible collection FJ of jobs generated by T, a uniprocessor schedule for FJ can be defined as a function  , where σ(t) = J
i,j denotes that job J
i,j is executed at time t, and
, where σ(t) = J
i,j denotes that job J
i,j is executed at time t, and  denotes that the system is idle at time t. Recall that we assume that the jobs of task τ
i should be executed in the FCFS manner. Therefore, if σ(t) = J
i,j then \(\sigma (t') \notin \left \{{J_{i,h} | h=1,2,\ldots ,j-1}\right \}\), for any t′ > t and j ≥ 2.
denotes that the system is idle at time t. Recall that we assume that the jobs of task τ
i should be executed in the FCFS manner. Therefore, if σ(t) = J
i,j then \(\sigma (t') \notin \left \{{J_{i,h} | h=1,2,\ldots ,j-1}\right \}\), for any t′ > t and j ≥ 2.
The feasibility and optimality of scheduling algorithms should be defined based on all possible feasible collections of jobs generated by T.
Definition 4.1
Suppose that we are given a set T of sporadic real-time tasks on a uniprocessor system. A schedule σ of a feasible collection FJ of jobs generated by T is feasible for hard real-time guarantees if the following conditions hold for each J i,j in FJ:
-
σ(t) ≠ J i,j for any t ≤ r i,j and t > d i,j,
-
 , and
, and -
if σ(t) = J i,j, then \(\sigma (t') \notin \left \{{J_{i,h} | h=1,2,\ldots ,j-1}\right \}\), for any t′ > t and j ≥ 2.
A sporadic real-time task set T is schedulable for hard real-time guarantees under a scheduling algorithm if the resulting schedule of any feasible collection FJ of jobs generated by T is always feasible. A scheduling algorithm is optimal for hard real-time guarantees if it always produces feasible schedule(s) when the task set T is schedulable under a scheduling algorithm. □
4.2.1 Preemptive EDF
For the preemptive earliest-deadline-first (EDF) scheduling algorithm, the job in the ready queue whose absolute deadline is the earliest is executed on the processor. To validate the schedulability of preemptive EDF, the demand bound function DBFi(t), defined by Baruah et al. [1], has been widely used to specify the maximum demand of a sporadic (or periodic) real-time task τ i to be released and finished in a time interval with length equal to t:
To prove the correctness of such a demand bound function, we focus on all possible feasible sets of jobs generated by a sporadic/periodic real-time task τ i. Recall that a feasible set FJ i of jobs generated by a sporadic/periodic real-time task τ i should satisfy the following conditions:
-
The actual execution time C i,j of job J i,j satisfies C i,j ≤ C i.
-
d i,j = r i,j + D i for any integer j with j ≥ 1.
-
r i,j ≥ r i,j−1 + T i for any integer j with j ≥ 2.
Lemma 4.1
For a given feasible set FJ i of jobs generated by a sporadic/periodic real-time task τ i, let FJ i,[r,r+t] be the subset of the jobs in FJ i arriving no earlier than r and have absolute deadlines no later than r + t. That is,
For any r and any t > 0,
Proof
By definition, DBFi(t) ≥ 0. Therefore, if FJ i,[r,r+t] is an empty set, we reach the conclusion.
We consider that FJ i,[r,r+t] is not empty for the rest of the proof. Let J i,j∗ be the first job generated by task τ i in FJ i,[r,r+t]. By the definition of FJ i,[r,r+t] in Eq. (4.2), the arrival time \(r_{i,j^*}\) of job \(J_{i,j^*}\) is no less than r, i.e., \(r_{i,j^*} \geq r\). Since FJ i,[r,r+t] is not empty, \(r_{i,j^*}+D_i \leq r+t\).
Since r i,j ≥ r i,j−1 + T i for any integer j with j ≥ 2 for the jobs in FJ i as well as the jobs in FJ i,[r,r+t], the absolute deadlines of the subsequent jobs in FJ i,[r,r+t] are at least \(r_{i,j^*}+T_i+D_i, r_{i,j^*}+2T_i+D_i, r_{i,j^*}+3T_i+D_i, \ldots \). Therefore, there are at most \(\left \lfloor {\frac {r+t-(r_{i,j^*}+D_i)}{T_i}}\right \rfloor +1 \leq \left \lfloor {\frac {t-D_i}{T_i}}\right \rfloor +1 \) jobs in FJ i,[r,r+t] since \(r \leq r_{i,j^*}\). Since the actual execution time C i,j of each job J i,j is no more than C i by the definition of the jobs in FJ i, we reach the conclusion. □
With the help of Lemma 4.1, the following theorem holds.
Theorem 4.1
A set T of sporadic tasks is schedulable under uniprocessor preemptive EDF if and only if
Proof
Only-if part, i.e., the necessary schedulability test. We prove the condition by contrapositive. Suppose that there exists a t > 0 such that \(\sum _{\tau _i \in \mathbf {T}} \mathrm {DBF}_i(t) > t\), for contrapositive.
For each task τ i, we create a feasible set of jobs generated by task τ i by releasing the jobs periodically starting from time 0, and their actual execution times are all set to C i. By the definition of a uniprocessor system in our scheduling model, at most one job is executed at a time. Therefore, the demand of the jobs that are released no earlier than 0 and must be finished no later than t is strictly more than the amount of available time since \(\sum _{\tau _i \in \mathbf {T}} \mathrm {DBF}_i(t) > t\). Therefore, (at least) one of these jobs misses its deadline no matter which uniprocessor scheduling algorithm is used.
Therefore, we can conclude that if the task set T is schedulable under EDF-P, then \(\sum _{\tau _i \in \mathbf {T}} \mathrm {DBF}_i(t) \leq t, \forall t > 0\).
If part, i.e., the sufficient schedulability test: We prove the condition by contrapositive. Suppose that the given task set T is not schedulable under EDF-P for contrapositive.
Then, there exists a feasible collection of jobs generated by T which cannot be feasibly scheduled under EDF-P. Let FJ be such a collection of jobs, where FJ
i is its subset generated by a sporadic real-time task τ
i in T. Let  be the schedule of EDF-P for FJ. Since at least one job misses its deadline in σ, let job J
k,ℓ be the first job which misses its absolute deadline d
k,ℓ in schedule σ. That is,
be the schedule of EDF-P for FJ. Since at least one job misses its deadline in σ, let job J
k,ℓ be the first job which misses its absolute deadline d
k,ℓ in schedule σ. That is,

Let t
0 be the earliest instant prior to d
k,ℓ, i.e., t
0 < d
k,ℓ, such that the processor only executes jobs with absolute deadlines no later than d
k,ℓ in time interval (t
0, d
k,ℓ] under EDF-P. That means, immediately prior to time t
0, i.e., t = t
0 − 𝜖 for an infinitesimal 𝜖, σ(t) is either  or a job whose absolute deadline is (strictly) greater than d
k,ℓ. We note that t
0 exists since it is at least the earliest arrival time of the jobs in FJ. Moreover, since EDF-P does not let the processor idle unless there is no job in the ready queue, t
0 ≤ r
k,ℓ.
or a job whose absolute deadline is (strictly) greater than d
k,ℓ. We note that t
0 exists since it is at least the earliest arrival time of the jobs in FJ. Moreover, since EDF-P does not let the processor idle unless there is no job in the ready queue, t
0 ≤ r
k,ℓ.
Let \(\mathbf {FJ}_{i,[t_0, d_{k,\ell }]}\) be the subset of the jobs in FJ i arriving no earlier than t 0 and have absolute deadlines no later than d k,ℓ. That is, we define \(\mathbf {FJ}_{i,[t_0, d_{k,\ell }]}\) by setting r to t 0 and t to d k,ℓ − t 0 in Eq. (4.2). Let \(\mathbf {FJ}_{[t_0, d_{k,\ell }]}\) be \(\cup _{\tau _i \in \mathbf {T}}\; \mathbf {FJ}_{i,[t_0, d_{k,\ell }]}\) for notational brevity.
By the definition of t 0, d k,ℓ, and EDF-P, the processor executes only the jobs in \(\mathbf {FJ}_{[t_0, d_{k,\ell }]}\), i.e., \(\sigma (t) \in \mathbf {FJ}_{[t_0, d_{k,\ell }]}\) for any t 0 < t ≤ d k,ℓ. Therefore,

where the condition \(\overset {1}{=}\) is due to \(\sigma (t) \in \mathbf {FJ}_{[t_0, d_{k,\ell }]}\) for any t 0 < t ≤ d k,ℓ, the condition \(\overset {2}{\leq }\) is due to the definition of a schedule of the jobs in \(\mathbf {FJ}_{[t_0, d_{k,\ell }]} \setminus \left \{{J_{k,\ell }}\right \}\), the condition \(\overset {3}{=}\) is due to t 0 ≤ r k,ℓ, and σ(t) ≠ J k,ℓ for t 0 < t ≤ r k,ℓ. Hence, there is a certain Δ = d k,ℓ − t 0 with \(\sum _{\tau _i \in \mathbf {T}}\mathrm {DBF}_i(\Delta ) > \Delta \). We reach our conclusion by contrapositive. □
4.2.2 Preemptive Fixed-Priority Scheduling Algorithms
Under preemptive fixed-priority (FP-P) scheduling, each task is assigned a unique priority before execution and does not change over time. The jobs generated by a task always have the same priority defined by the task. Here, we define hp(τ k) as the set of higher-priority tasks than task τ k and lp(τ k) as the set of lower-priority tasks than task τ k. When task τ i has a higher priority than task τ j, we denote their priority relationship as τ i > τ j. We assume that the priority levels are unique.
For FP scheduling algorithms, we need another notation
That is, for a given feasible set FJ i of jobs generated by a sporadic/periodic real-time task τ i, let FRJ i,[r,r+ Δ) be the subset of the jobs in FJ i arriving in time interval [r, r + Δ). By extending the proofs like in Sect. 4.2.1, we can also prove the following lemma and theorem.
Lemma 4.2
The total amount of execution time of the jobs of τ i that are released in a time interval [r, r + Δ) for any Δ ≥ 0 is
Theorem 4.2
Let \(\Delta _{\min } > 0\) be the minimum value that satisfies
The WCRT R k of task τ k in a preemptive fixed-priority uniprocessor scheduling algorithm is
-
\(R_k = \Delta _{\min }\) , if \(\Delta _{\min } \leq T_k\) , and
-
R k > T k, otherwise.
Theorem 4.2 can be re-written into a more popular form, called time-demand analysis (TDA) proposed by Lehoczky et al. [21]: A (constrained-deadline) task τ k is schedulable under FP-P scheduling if and only if
Theorem 4.2 is a very interesting and remarkable result, widely used in the literature. It suggests to validate the worst-case response time of task τ k by
-
releasing the first jobs of the higher-priority tasks in hp(τ k) together with a job of τ k and
-
releasing the subsequent jobs of the higher-priority tasks in hp(τ k) as early as possible by respecting their minimum inter-arrival times.
To explain the above phenomena, Liu and Layland in their seminal paper [23] in 1973 defined two terms (according to their wording):
-
A critical instant for task τ k is an instant at which a job of task τ k released at this instant has the largest response time.
-
A critical time zone for task τ k is a time interval starting from a critical instant of τ k to the completion of the job of task τ k released at the critical instant.
Liu and Layland [23] concluded the famous critical-instant theorem as follows: “A critical instant for any task occurs whenever the task is requested simultaneously with requests for all higher-priority tasks.” Their proof was in fact incomplete. Moreover, their definition of the critical-instant theorem was incomplete since the condition \(\Delta _{\min } > T_k\) was not considered in their definition. A precise definition of the critical-instant theorem is revised as follows:
-
A critical instant for task τ k is an instant such that
-
a job of task τ k released at this instant has the largest response time if it is no more than T k or
-
the worst-case response time of a job of task τ k released at this instant is more than T k.
-
-
A critical time zone for task τ k is a time interval starting from a critical instant of τ k to the completion of the job of task τ k released at the critical instant.
-
In a critical time zone for task τ k, all the tasks release their first jobs at a critical instant for task τ k and their subsequent jobs as early as possible by respecting their minimum inter-arrival times.
4.3 Utilization-Based Analyses for Fixed-Priority Scheduling
The TDA in Eq. (4.8) requires pseudo-polynomial-time complexity to check the time points in (0, D k] for Eq. (4.8), which can be further generalized for verifying the schedulability of task τ k under fixed-priority scheduling:
where σ > 0 and b ≥ 0. Equation (4.10) can be used in many cases if D k ≤ T k, such as
-
σ = 1 and b = 0 in Eq. (4.10) for uniprocessor sporadic task systems [21],
-
σ = 1 and b = 1 in Eq. (4.10) for uniprocessor self-suspending sporadic task systems [22] (under the assumption that task τ k does not suspend itself), and
-
σ = 1∕M and b = 1 in Eq. (4.10) for multiprocessor global rate-monotonic scheduling [2] on M identical processors.
Although testing Eq. (4.10) takes pseudo-polynomial time, it is not always necessary to test all possible time points to derive a safe worst-case response time or to provide sufficient schedulability tests. The general and key concept to obtain sufficient schedulability tests in k2U in [7, 8] and k2Q in [6, 10] is to test only a subset of such points for verifying the schedulability. Traditional fixed-priority schedulability tests often have pseudo-polynomial-time (or even higher) complexity. The idea implemented in the k2U and k2Q frameworks is to provide a general k-point schedulability test, which only needs to test k points under any fixed-priority scheduling when checking schedulability of the task with the kth highest priority in the system. Suppose that there are k − 1 higher-priority tasks, indexed as τ 1, τ 2, …, τ k−1, than task τ k. Recall that the task utilization is defined as U i = C i∕T i. The success of the k2U framework is based on a k-point effective schedulability test, defined as follows:
Definition 4.2 (Chen et al. [7, 8])
A k-point effective schedulability test is a sufficient schedulability test of a fixed-priority scheduling policy that verifies the existence of \(t_j \in \left \{{t_1, t_2, \ldots t_k}\right \}\) with 0 < t 1 ≤ t 2 ≤⋯ ≤ t k such that
where C k > 0, α i > 0, U i > 0, and β i > 0 are dependent upon the setting of the task models and task τ i. □
The properties in Definition 4.2 lead to the following lemmas for the k2U framework which are proven in [8].
Lemma 4.3
For a given k-point effective schedulability test of a scheduling algorithm, defined in Definition 4.2, in which 0 < t k and 0 < α i ≤ α, and 0 < β i ≤ β for any i = 1, 2, …, k − 1, task τ k is schedulable by the scheduling algorithm if the following condition holds:
Lemma 4.4
For a given k-point effective schedulability test of a scheduling algorithm, defined in Definition 4.2, in which 0 < t k and 0 < α i ≤ α and 0 < β i ≤ β for any i = 1, 2, …, k − 1, task τ k is schedulable by the scheduling algorithm if
Example 4.1
Suppose that D k = T k and the tasks are indexed by the periods, i.e., T 1 ≤⋯ ≤ T k. When T k ≤ 2T 1, task τ k is schedulable by preemptive rate-monotonic (RM) scheduling if there exists \(j \in \left \{{1,2,\ldots ,k}\right \}\) where
Therefore, the coefficients in Definition 4.2 for this test are α i = β i = 1 and t i = T i for i = 1, 2, …, k − 1, and t k = T k. Based on Lemma 4.3, the schedulability of task τ k under preemptive RM is guaranteed if
Based on Lemma 4.4, the schedulability condition of task τ k under preemptive RM is
The schedulability test in Eq. (4.15) was originally proposed by Bini and Buttazzo [3], called hyperbolic bound, as an improvement of the utilization bound in Eq. (4.16) by Liu and Layland in [23]. We note that the original proof in [23] was incomplete, pointed out and fixed by Goossens [15].
The success of the k2Q framework is based on a k-point effective schedulability test, defined as follows:
Definition 4.3
A k-point last-release schedulability test under a given ordering π of the k − 1 higher-priority tasks is a sufficient schedulability test of a fixed-priority scheduling policy that verifies the existence of 0 ≤ t 1 ≤ t 2 ≤⋯ ≤ t k−1 ≤ t k such that
where C k > 0, for i = 1, 2, …, k − 1, α i > 0, U i > 0, C i ≥ 0, and β i > 0 are dependent upon the setting of the task models and task τ i.
The properties in Definition 4.3 lead to the following lemmas for the k2Q framework which are proven in [10].
Lemma 4.5
For a given k-point last-release schedulability test of a scheduling algorithm in Definition 4.3, in which 0 < α i, and 0 < β i for any i = 1, 2, …, k − 1, 0 < t k, \(\sum _{i=1}^{k-1}\alpha _i U_i \leq 1\), and \(\sum _{i=1}^{k-1} \beta _i C_i \leq t_k\), task τ k is schedulable by the fixed-priority scheduling algorithm if the following condition holds:
Example 4.2
Suppose that D k = T k and the tasks are indexed by the periods, i.e., T 1 ≤⋯ ≤ T k. When T k ≤ 2T 1, task τ k is schedulable by rate-monotonic (RM) scheduling if there exists \(j \in \left \{{1,2,\ldots ,k}\right \}\) where
Therefore, the coefficients in Definition 4.3 for this test are α i = β i = 1 and t i = T i for i = 1, 2, …, k − 1, and t k = T k. Based on Lemma 4.5, the schedulability of task τ k under preemptive RM is
The test in Eq. (4.20) is a quadratic form. The first quadratic bound (QB) by Davis and Burns in Equation (26) in [14] and Bini et al. in Equation (11) in [4] is
The test in Eq. (4.20) is superior to the test in Eq. (4.21).
The generality of the k2Q and k2U frameworks has been demonstrated in [8, 10]. We believe that these two frameworks, to be used for different cases, have great potential in analyzing many other complex real-time task models, where the existing analysis approaches are insufficient or cumbersome.
For the k2Q and k2U frameworks, their characteristics and advantages over other approaches have been already discussed in [8, 10]. In general, the k2U framework is more precise by using only the utilization values of the higher-priority tasks. If we can formulate the schedulability tests into the k2U framework, it is also usually possible to model it into the k2Q framework. In such cases, the same pseudo-polynomial-time test is used. When we consider the worst-case quantitative metrics like utilization bounds, resource augmentation bounds, or speedup factors, the result derived from the k2U framework is better for such cases. However, there are also cases, in which formulating the test by using the k2U framework is not possible. These cases may even start from schedulability tests with exponential-time complexity. We have successfully demonstrated three examples in [6] by using the k2Q framework to derive polynomial-time tests. In those demonstrated cases, either the k2U framework cannot be applied or with worse results (since different exponential-time or pseudo-polynomial-time schedulability tests are applied).
The automatic procedure to derive the parameters in the k2U can be found in [9]. Previously, the parameters in all the examples in [8] were manually constructed. This automation procedure significantly empowers the k2U framework to automatically handle a wide range of classes of real-time execution platforms and task models, including uniprocessor scheduling, multiprocessor scheduling, self-suspending task systems, real-time tasks with arrival jitter, services and virtualizations with bounded delays, etc. We believe that the k2U framework and the automatic parameter derivations together can be a very powerful tool for researchers to construct utilization-based analyses almost automatically. Depending on the needs of the use scenarios, a more suitable schedulability test class should be chosen for deriving better results.
Utilization-Based Analysis for Dynamic-Priority Scheduling Algorithms
The k2U and k2Q frameworks provide general utilization-based timing analyses for fixed-priority scheduling. One missing building block is the utilization-based timing analyses for dynamic-priority scheduling algorithms, like EDF. The analytical framework in [8, 10] is based on analytical solutions of linear programming. However, such formulations do not work for EDF.
4.4 Probabilistic Schedulability Tests
In many real-time systems, it is tolerable that at least some of the tasks in the system miss their deadline in rare situations. Regardless, these deadline misses must be quantified to ensure the system’s safety. We examine the problem of determining the deadline miss probability of a task under uniprocessor static-priority preemptive scheduling for an uncertain execution behavior, i.e., when each task has distinct execution modes and a related known probability distribution.
One important assumption for real-time systems is that a deadline miss, i.e., a job that does not finish its execution before its deadline, will be disastrous and thus the WCET of each task is always considered during the analysis. Nevertheless, if a job has multiple distinct execution schemes, the WCETs of those schemes may differ significantly. Examples are software-based fault-recovery techniques which rely on (at least partially) re-executing the faulty task instance, mixed-criticality systems, and a reduced CPU frequency to prevent overheating. In all these cases, it is reasonable to assume that schemes with smaller WCET are the common case, while larger WCETs happen rarely.
We use the example of software-based fault-recovery in the following discussion. When such techniques are applied, the probability that a fault occurs and thus has to be corrected is very low, since otherwise hardware-based fault-recovery techniques would be applied. If re-execution may happen multiple times, the resulting execution schemes have an increased related WCET, while the probability decreases drastically. Therefore, solely considering the execution scheme with the largest WCET at design time would lead to largely overdesigning the system resources. Furthermore, many real-time systems can tolerate a small number of deadline misses at runtime as long as these deadline misses do not happen too frequently. This holds true especially if some of the tasks in the system only have weakly hard or soft real-time constraints. Hence, being able to predict the probability of a deadline miss is an important property when designing real-time systems.
We focus on the probability of deadline misses for a single task here, which is defined as follows:
Definition 4.4 (Probability of Deadline Misses)
Let R k,j be the response time of the jth job of τ k. The probability of deadline misses (DMP) of task τ k, denoted by Φk, is an upper bound on the probability that a job of τ k is not finished before its (relative) deadline D k, i.e.,
It was shown in [24] that the DMP of a job of a constrained- or implicit-deadline task is maximized when τ k is released at its critical instant. Hence, the time-demand analysis (TDA) in Eq. (4.8) can be applied to determine the worst-case response time of a task when the execution time of each job is known. This implicitly assumes that no previous job has an overrun that interferes with the analyzed job, i.e., we are searching for the probability that the first job of τ k misses its deadline after a longer interval where all deadlines were met.
When probabilistic WCETs are considered, the WCET obtains a value in (C i,1, …, C i,h) with a certain probability \(\mathbb {P}_i(j)\) for each job of each task τ i. Therefore, TDA for a given t is not looking for a binary decision anymore. Instead, we are interested in the probability that the accumulated workload S t over an interval of length t is at most t. The probability that τ k cannot finish in this interval is denoted accordingly with \(\mathbb {P}(S_t > t)\). The situation where S t is larger than t is called an overload for an interval of length t and hence \(\mathbb {P}(S_t > t)\) is the overload probability at time t. Since TDA only needs to hold for one t with 0 < t ≤ D k to ensure that τ k is schedulable, the probability that the test fails is upper bounded by the minimum probability among all time points at which the test could fail. As a result, the probability of a deadline miss Φk can be upper bounded by
The number of points considered in the TDA can be reduced by only considering the points of interest, i.e., D k and the releases of higher-priority tasks.
Therefore, testing the schedulability efficiently requires an efficient routine to calculate \(\mathbb {P}(S_t > t)\) for a given t and a combination of given random variables S t. The research results at TU Dortmund have recently achieved efficient calculations as follows:
-
Chernoff bound in [5, 13]: The calculation of \(\mathbb {P}(S_t > t)\) is based on the moment generating function of the classical Chernoff bound.
-
Multinomial-based approach in [30]: The calculation of \(\mathbb {P}(S_t > t)\) uses the multinomial distribution.
We note that the DMP is not identical to the deadline miss rate of a task and that the deadline miss rate may be even higher than this probability, as detailed by Chen et al. [11]. However, the approach in [11] utilizes approaches to approximate the deadline miss probability as a subroutine when calculating the rate.
Generality of Using \(\mathbb {P}(S_t > t)\)
The efficient calculation of \(\mathbb {P}(S_t > t)\) results in efficient probabilistic schedulability tests and deadline miss rate analyses for preemptive fixed-priority uniprocessor systems. The general question is whether this holds also for other scheduling problems and platforms, like multiprocessor systems. Whether the applicability can be generalized is an open problem.
4.5 Conclusion
The critical-instant theorem has been widely used in many research results. Some of the extensions of the critical-instant theorem are correct, e.g., the level-i busy window concept in [20], and some are unfortunately incorrect, e.g., for self-suspending tasks in [18, 25]. Specifically, the misconception of modeling self-suspension time of a higher-priority task as its release jitter in the worst-case response time analysis in [25] and [19] had become a standard approach in multiprocessor locking protocols in real-time systems since 2009 until the error was found in 2016, summarized in Section 6 in [12].
In addition to the lack of formalism, the existing properties that have been widely used in analyzing timing satisfactions in cyber-physical real-time systems are also biased towards computation. One key assumption used in computation is that the execution of one cycle on a processor reduces the execution of a task by one cycle. If the problem under analysis does not have such a property, the workload characterized by using uniprocessor systems cannot be used at all. To explain this mismatch, consider the preemptive worm-hole switching protocol in communication as an example. Suppose that a message has to be sent from node A to node B by using two switches, called S 1 and S 2. Namely, the message has to follow the path A → S 1 → S 2 → B. Suppose that the message is divided into f communication units, in which a communication unit can be sent and received in every time unit. A fast transmission plan is to fully parallelize the communication if possible. That is, one communication unit from A to S 1 for the first time unit, one communication unit from A to S 1 and S 1 to S 2 for the second time units, etc. Therefore, the communication time of the message can be modeled as f + 2. This analysis is correct under the assumption that S 1 and S 2 are not used by other flows. However, if the usage of S 1 or S 2 is blocked during the transmission of the message flow, using f + 2 time units for analysis is problematic. For the fast transmission plan with f + 2 communication time, it is actually possible that the message is transmitted in 3f time units as the links are blocked for any communication parallelism. To handle the increase of time, several factors have been introduced into the real-time analyses for priority-preemptive worm-hole networks, including direct interference, indirect interference, backpressure, non-zero critical instant, sub-route interference, and downstream multiple interference (summarized in Table VII in [17]). However, since the problem under analysis is essentially not the same as a uniprocessor schedule, applying the uniprocessor timing analysis with extensions is in my opinion only possible after a rigorous proof of equivalence. This mismatch leads to a significant amount of flaws in the literature in this topic. Specifically, the analysis in [28] had been considered safe for a few years until a counterexample was provided in [32].
To successfully tackle complex cyber-physical real-time systems that involve computation, parallelization, communication, and synchronization, we believe that new, mathematical, modulable, and fundamental properties for property-based (schedulability) timing analyses and scheduling optimizations are strongly needed. They should capture the pivotal properties of cyber-physical real-time systems and thus enable mathematical and algorithmic research on the topic. The view angles should not be limited to the processor- or computation-centric perspective. When there are abundant cores/processors, the bottleneck of the system design becomes the synchronization and the communication among the tasks [16, 29]. Different flexibility and tradeoff options to achieve real-time guarantees should be provided in a modularized manner to enable tradeoffs between execution efficiency and timing predictability.
References
S.K. Baruah, A.K. Mok, L.E. Rosier, Preemptively scheduling hard-real-time sporadic tasks on one processor, in Proceedings of the 11th Real-Time Systems Symposium RTSS, pp. 182–190 (1990). https://doi.org/10.1109/REAL.1990.128746
M. Bertogna, M. Cirinei, G. Lipari, New schedulability tests for real-time task sets scheduled by deadline monotonic on multiprocessors, in 9th International Conference on Principles of Distributed Systems, OPODIS, pp. 306–321 (2005)
E. Bini, G. Buttazzo, G. Buttazzo, A hyperbolic bound for the rate monotonic algorithm, in 13th Euromicro Conference on Real-Time Systems, 2001 (2001), pp. 59–66. https://doi.org/10.1109/EMRTS.2001.bini01
E. Bini, T.H.C. Nguyen, P. Richard, S.K. Baruah, A response-time bound in fixed-priority scheduling with arbitrary deadlines. IEEE Trans. Comput. 58(2), 279–286 (2009)
K.H. Chen, J.J. Chen, Probabilistic schedulability tests for uniprocessor fixed-priority scheduling under soft errors, in 12th IEEE International Symposium on Industrial Embedded Systems, SIES (2017), pp. 1–8. https://doi.org/10.1109/SIES.2017.7993392
J.J. Chen, W.H. Huang, C. Liu, k2Q: a quadratic-form response time and schedulability analysis framework for utilization-based analysis. CoRR (2015)
J.J. Chen, W.H. Huang, C. Liu, k2U: a general framework from k-point effective schedulability analysis to utilization-based tests. CoRR abs/1501.07084 (2015). http://arxiv.org/abs/1304.1590
J.J. Chen, W.H. Huang, C. Liu, k2u: a general framework from k-point effective schedulability analysis to utilization-based tests, in IEEE Real-Time Systems Symposium, RTSS (2015), pp. 107–118. https://doi.org/10.1109/RTSS.2015.18
J.J. Chen, W.H. Huang, C. Liu, Automatic parameter derivations in k2U framework. Computing Research Repository (CoRR) (2016). http://arxiv.org/abs/1605.00119
J.J. Chen, W.H. Huang, C. Liu, k2q: a quadratic-form response time and schedulability analysis framework for utilization-based analysis, in IEEE Real-Time Systems Symposium, RTSS (2016), pp. 351–362. https://doi.org/10.1109/RTSS.2016.041
K.H. Chen, G. von der Brüggen, J.J. Chen, Analysis of deadline miss rates for uniprocessor fixed-priority scheduling, in 24th IEEE International Conference on Embedded and Real-Time Computing Systems and Applications, RTCSA 2018, Hakodate, August 28–31, 2018 (2018), pp. 168–178. https://doi.org/10.1109/RTCSA.2018.00028
J.J. Chen, G. Nelissen, W.H. Huang, M. Yang, B. Brandenburg, K. Bletsas, C. Liu, P. Richard, F. Ridouard, N. Audsley, R. Rajkumar, D. de Niz, G. von der Brüggen, Many suspensions, many problems: a review of self-suspending tasks in real-time systems. Real-Time Syst. 55, 144–207 (2019). https://doi.org/10.1007/s11241-018-9316-9
K.H. Chen, N. Ueter, G. von der Bruggen, J.J. Chen, Efficient computation of deadline-miss probability and potential pitfalls, in Design, Automation & Test in Europe Conference & Exhibition, DATE 2019, Florence, March 25–29, 2019 (2019), pp. 896–901. https://doi.org/10.23919/DATE.2019.8714908
R.I. Davis, A. Burns, Response time upper bounds for fixed priority real-time systems, in Real-Time Systems Symposium, 2008 (2008), pp. 407–418. https://doi.org/10.1109/RTSS.2008.18
J. Goossens, Scheduling of hard real-time periodic systems with various kinds of deadline and offset constraints. Ph.D. Thesis, Universite Libre de Bruxelles (1999). http://di.ulb.ac.be/ssd/goossens/Thesis.pdf
W.H. Huang, M. Yang, J.J. Chen, Resource-oriented partitioned scheduling in multiprocessor systems: how to partition and how to share? in Real-Time Systems Symposium (RTSS) (2016), pp. 111–122
L.S. Indrusiak, A. Burns, B. Nikolic, Analysis of buffering effects on hard real-time priority-preemptive wormhole networks. CoRR abs/1606.02942 (2016). http://arxiv.org/abs/1606.02942
K. Lakshmanan, R. Rajkumar, Scheduling self-suspending real-time tasks with rate-monotonic priorities, in Real-Time and Embedded Technology and Applications Symposium (RTAS) (2010), pp. 3–12. https://doi.org/10.1109/RTAS.2010.38
K. Lakshmanan, D. de Niz, R. Rajkumar, Coordinated task scheduling, allocation and synchronization on multiprocessors, in Real-Time Systems Symposium (RTSS) (2009), pp. 469–478. http://dx.doi.org/10.1109/RTSS.2009.51
J. Lehoczky, Fixed priority scheduling of periodic task sets with arbitrary deadlines, in Proceedings Real-Time Systems Symposium (RTSS) (1990), pp. 201–209. https://doi.org/10.1109/REAL.1990.128748
J.P. Lehoczky, L. Sha, Y. Ding, The rate monotonic scheduling algorithm: exact characterization and average case behavior, in IEEE Real-Time Systems Symposium’89 (1989), pp. 166–171
C. Liu, J. Chen, Bursty-interference analysis techniques for analyzing complex real-time task models, in Real-Time Systems Symposium (RTSS) (2014), pp. 173–183
C.L. Liu, J.W. Layland, Scheduling algorithms for multiprogramming in a hard-real-time environment. J. ACM 20(1), 46–61 (1973). https://doi.org/10.1145/321738.321743
D. Maxim, L. Cucu-Grosjean, Response time analysis for fixed-priority tasks with multiple probabilistic parameters, in Proceedings of the IEEE 34th Real-Time Systems Symposium, RTSS 2013, Vancouver, December 3–6, 2013 (2013), pp. 224–235. https://doi.org/10.1109/RTSS.2013.30
L. Ming, Scheduling of the inter-dependent messages in real-time communication, in Proceedings of the First International Workshop on Real-Time Computing Systems and Applications (1994)
R. Rajkumar, I. Lee, L. Sha, J. Stankovic, Cyber-physical systems: the next computing revolution, in Proceedings of the 47th Design Automation Conference (ACM, New York, 2010), pp. 731–736. https://doi.org/10.1145/1837274.1837461
L. Sha, R. Rajkumar, J.P. Lehoczky, Priority inheritance protocols: an approach to real-time synchronization. IEEE Trans. Comput. 39(9), 1175–1185 (1990). http://dx.doi.org/10.1109/12.57058
Z. Shi, A. Burns, Real-time communication analysis for on-chip networks with wormhole switching, in Proceedings of the Second ACM/IEEE International Symposium on Networks-on-Chip (NOCS) (2008), pp. 161–170. https://doi.org/10.1109/NOCS.2008.4492735. http://dl.acm.org/citation.cfm?id=1397757.1397996
G. von der Brüggen, J.J. Chen, W.H. Huang, M. Yang, Release enforcement in resource-oriented partitioned scheduling for multiprocessor systems, in Proceedings of the 25th International Conference on Real-Time Networks and Systems, RTNS’17 (ACM, New York, 2017), pp. 287–296. https://doi.org/10.1145/3139258.3139287
G. von der Brüggen, N. Piatkowski, K.H. Chen, J.J. Chen, K. Morik, Efficiently approximating the probability of deadline misses in real-time systems, in Euromicro Conference on Real-Time Systems, ECRTS (2018), pp. 6:1–6:22. https://doi.org/10.4230/LIPIcs.ECRTS.2018.6
R. Wilhelm, J. Engblom, A. Ermedahl, N. Holsti, S. Thesing, D. Whalley, G. Bernat, C. Ferdinand, R. Heckmann, T. Mitra, F. Mueller, I. Puaut, P. Puschner, J. Staschulat, P. Stenström, The worst-case execution-time problem–overview of methods and survey of tools. ACM Trans. Embed. Comput. Syst. 7(3), 36:1–36:53 (2008). http://doi.acm.org/10.1145/1347375.1347389
Q. Xiong, Z. Lu, F. Wu, C. Xie, Real-time analysis for wormhole NoC: revisited and revised, in 2016 International Great Lakes Symposium on VLSI (GLSVLSI), (2016), pp. 75–80. https://doi.org/10.1145/2902961.2903023
D. Ziegenbein, A. Hamann, Timing-aware control software design for automotive systems, in Proceedings of the 52Nd Annual Design Automation Conference, DAC’15 (2015), pp. 56:1–56:6. http://doi.acm.org/10.1145/2744769.2747947
Acknowledgements
Part of this work has been supported by European Research Council (ERC) Consolidator Award 2019, PropRT (Number 865170), and Deutsche Forschungsgemeinschaft (DFG), as part of the priority program “Dependable Embedded Systems”—SPP1500, project GetSURE, and the Collaborative Research Center SFB 876 (http://sfb876.tu-dortmund.de/), subprojects A1, A3, and B2.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Chen, JJ., Huang, WH., Brüggen, G.v.d., Chen, KH., Ueter, N. (2021). On the Formalism and Properties of Timing Analyses in Real-Time Embedded Systems. In: Chen, JJ. (eds) A Journey of Embedded and Cyber-Physical Systems. Springer, Cham. https://doi.org/10.1007/978-3-030-47487-4_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-47487-4_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-47486-7
Online ISBN: 978-3-030-47487-4
eBook Packages: EngineeringEngineering (R0)




 , where
, where  is a binary indicator. If the condition holds, the value is 1; otherwise, the value is 0.
is a binary indicator. If the condition holds, the value is 1; otherwise, the value is 0. , and
, and