Reversible Languages and Incremental State Saving in Optimistic Parallel Discrete Event Simulation

Abstract

Optimistic parallel discrete event simulation (PDES) requires to do a distributed rollback if conflicts are detected during a simulation due to the massively parallel optimistic execution approach. When a rollback of a simulation is performed each node that is determined to be in a wrong state must be restored to one of its previous states. This can be achieved through reverse computation or by restoring a previous checkpoint. In this paper we investigate and compare both approaches, reverse computation and a variant of checkpointing, incremental state saving (also called incremental checkpointing), to restore a previous program state as part of an optimistic parallel discrete event simulation. We present a benchmark model that is specifically designed for evaluating the performance of approaches to reversibility in PDES. Our benchmarking model has mathematical properties that allow to tune the amount of arithmetic operations relative to the amount of memory operations. These tuning opportunities are the basis for our systematic performance evaluation.

1 Introduction

Discrete event simulation (DES) is a simulation paradigm suitable for systems whose states are modeled as changing discontinuously and irregularly at discrete moments of simulation time. State changes occur at simulation times that are calculated dynamically rather than determined statically as typical in time-stepped simulations. Most irregular systems whose behavior is not describable by continuous equations and do not happen to be suitable for simple time-stepped models are candidates for DES. Efficient parallel discrete event simulation (PDES) is much more complicated than the sequential version. There are two broad approaches to resolving the PDES synchronization issue, called conservative and optimistic [1]. Recently Omelchenko and Karimabadi have developed an asynchronous flux-conserving DES technique for physical simulations [2]. Their preemptive event processing approach to parallel synchronization complements standard optimistic and conservative strategies for PDES. In this paper we will discuss optimistic PDES, which requires reversibility, in more detail.

In particular, we will focus on PDES using the Time Warp optimistic synchronization method [3]. The optimistic classification of Time Warp implies that it employs speculative execution to enable parallelism. In order to allow roll-backs needed to resolve incorrect speculation, the original formulation of Time Warp utilized checkpointing of the entire system state. This can be very wasteful, so in recent years reverse computation has become a key concept in optimistic parallel discrete event simulation [4, 5], as it allows one to reduce the overhead in the forward execution in comparison to checkpointing and, thus, improve the performance. Fundamentally, there are two ways to achieve reversibility: (1) incremental state saving and (2) reverse execution. Incremental state saving (also called incremental checkpointing in [5]) is a well-established approach, which has the advantage that only a few language constructs need to be augmented to establish reversibility of an arbitrary piece of code. However, it (often) results in a high runtime overhead as any checkpointing is a memory-heavy method. Reverse execution is based on the idea that for many programs there exists an inverse program that can uncompute all results of the (forward) computed program. The inverse program can be achieved either through implementation of reverse code from a given forward code, or by implementing the program in a reversible programming language that offers the capability to automatically generate the inverse program: the imperative reversible language Janus [6] has such functionality.¹

In this paper we systematically evaluate the generation of forward and reverse C++ code from Janus code (Sect. 4) as well as automatically generated code based on incremental state saving (Sect. 5). We also discuss the differences in methodology, whether a model code is written in a “destructive” language such as C/C++ or in the reversible language Janus, and its applications when implementing (and debugging) a model for PDES.

For this purpose and in order to validate the simulator and also check correctness of generated code, we have developed a new discrete event benchmark model that can be scaled in various dimensions. For execution of our model codes we use the ROSS general purpose discrete event simulator. Our new discrete event benchmark model is similar to the classic PHOLD benchmark model, but includes some extra state variables and computations that aid in detecting simulation errors. In our new model each event involves non-commutative matrix algebra, and the matrix that results from the simulation of the model serves as a checksum or hash of the simulation, and is sensitive to the order of events. The size of this matrix can be controlled by the user, as can the number of bits in its elements. This new benchmark is particularly useful for debugging simulations that are computed with the Time Warp Algorithm as its mathematical properties allow for checking of various assertions.

In our new model we can also tune the amount of arithmetic operations relative to the amount of memory modifying operations. This enables a systematic comparison of hand-written reverse code with multiple approaches of automatically generated reverse code and code instrumented for incremental state saving.

In our performance evaluation we use several different versions of the model code: (1) the original forward code with hand written reverse code, (2) Backstroke instrumented code to perform incremental state saving [7], and (3) Janus generated code for forward/reverse functions.

The forward/reverse code generated from Janus is particularly interesting because it allows to get forward code with no memory overhead and in some cases no runtime overhead, whereas for instrumented code one can only try to reduce the runtime and memory overhead in the forward code.

To the best of our knowledge this is the very first runtime comparison of the two approaches to reversible computation: generating reverse code and incremental state saving. In the optimistic PDES setting incremental state saving is suitable because optimistic PDES follows the Forward-Reverse-Commit (FRC) paradigm. In that paradigm, after an event has been executed in the forward direction, it can either be reversed (e.g. in the case it was incorrect to run it forward in the first place), or committed (when it has been proved that it was a correct event). When an event is committed its associated data is no longer needed, which allows to dispose recorded traces with every commit. In this paper we also investigate whether the combination of both the reversible language and incremental checkpointing approaches can be beneficial.

After giving a brief overview of PDES in Sect. 2, we describe our benchmark model and its properties in Sect. 3. In Sect. 4 we describe the reversible language Janus and how we generated forward/reverse function from Janus code. In Sect. 5 we briefly describe what source code transformations are applied to code to support incremental state saving with the Forward-Reverse-Commit paradigm. In Sect. 6 we describe the discrete event simulator that we use for optimistic parallel discrete event simulation and some adaptations that we implemented to better support the Forward-Reverse-Commit paradigm. The performance evaluation results are presented in Sect. 7. In Sect. 8 we discuss previous work that is related to our evaluated approaches and in Sect. 9 we discuss conclusions from the observed performance results.

2 Optimistic Parallel Discrete Event Simulation (PDES)

In this section we give a brief overview of PDES. A more detailed overview can be found in our previous work [7]. The general approach is to divide the simulation and its state into semi-independent units called LPs (logical processes) that can execute concurrently and communicate asynchronously, each maintaining its own state. A simulated event generally triggers a state change in one LP and affects only that LP’s state. Any event may schedule other events to happen in the future of the current LP’s simulation time. Events scheduled for other LPs must be transmitted to them as event messages with a timestamp indicating the simulation time when the event happens. Arriving event messages get enqueued in the event queues of the receiving LPs in increasing time stamp order. The LP has to allocate enough memory to store these queues.

Every LP must execute all of its events in strictly non-decreasing timestamp order irrespective of the order in which events may arrive or what timestamps they may carry. This poses a synchronization problem.

In contrast to optimistic PDES, conservative synchronization in conservative PDES uses conventional process blocking primitives along with extra knowledge about the simulation model (called lookahead information) to prevent the execution from ever getting into a situation in which an event message arrives at an LP with a timestamp in its past. Conservative synchronization is limited to models with static communication graphs.

Optimistic synchronization, by contrast, employs speculative execution to allow dynamic communication graphs and exposure of more parallelism. As a result, there is the danger of a causality violation when an LP that is behind in simulation time, e.g. at $t_1$, sends an event message with a (future) timestamp $t_2 > t_1$ that arrives at a receiver that has already simulated to time $t_3 > t_2$ due to its optimistic execution. In that case the receiver has already simulated past the simulation time when it should have executed the event at $t_2$, but it would be incorrect to execute events out of order because this may produce different results. Whenever that occurs, the simulator needs to roll back the LP from $t_3$ to the state it was in at time $t_2$, cancel all event messages the LP had sent after $t_2$, execute the arriving event, and then re-execute forward from time $t_2$ to $t_3$ and beyond. All event executions are therefore speculative or provisional, and are subject to rollback if the simulator detects a local causality conflict.

Each LP computes its local virtual time (LVT) based on the time stamps of event messages it receives. Because of rollbacks the LVT can also be reset to an earlier point in time. The global virtual time (GVT) is defined to be the minimum of all of the LVTs. Several algorithms exist to compute an estimate of the GVT during the simulation. Any events with time stamps older than GVT can be committed because it is guaranteed that they never need to be reversed. For more detail see [3, 5]. That events are committed once they are older than GVT, allows to delete all information that may have been stored to enable reversibility. This commit operation is the same that we also use for incremental state saving, described in Sect. 5, to dispose recorded execution traces of memory modifying operations.

3 PDES Model Benchmark

In order to validate the simulator and also check the correctness of automatically generated code suitable for reversible computation, we have developed a new discrete event benchmark model. It is similar to the classic PHOLD benchmark model, but includes some extra state variables and computations which aid in detecting simulation errors. The state of each LP contains two square matrices: an accumulation matrix A, and a transformation matrix T, each of size $n\times n$, where n is an integer constant chosen by the user. Each event message contains the transformation matrix of the sender, and upon execution of an event the receiving LP multiplies its accumulation matrix to the right with the received transformation matrix. When an event is executed the receiving LP schedules a new event for a randomly selected LP at an exponentially distributed time delay.

At the end of the simulation, the matrices of all LP’s are multiplied together, in LP ID (rank) order. The resulting matrix is the output of the simulation. Since matrix multiplication is in general non-commutative, the output depends on the individual events being executed in the correct order. The output serves as a check sum or hash of the simulation, and its size can be controlled by choosing the matrix size and the number of bits in the matrix elements.

The kernel of the event execution is a matrix multiplication, which (in the conventional implementation that we use) takes $O(n^3)$ arithmetic operations for $n\times n$ matrices. Reverse computation involves calculating a matrix inverse (or solving a matrix equation $A' = A\times T$ for A), which also requires $O(n^3)$ arithmetic operations. Each event or event message contains an $n\times n$ matrix and requires $n^2$ words of storage, and the same amount of data to be transmitted if communicated over a network. For bench-marking studies we can tune the ratio of arithmetic operations to memory/communication needs. This ratio is O(n) for $n\times n$ matrices. We want to emphasize that this model is perfectly reversible, in the sense that no extra state besides the event itself is needed to undo the forward event: We simply invert the matrix in the event message and multiply the accumulation matrix to the right with this inverse.

We let the matrix elements be of a standard unsigned integral data type (e.g. 8, 16, 32, or 64 bits). For each of these types, the standard computer multiplication, addition, and subtraction perform arithmetic in an associated finite integer ring; $Z_{2^k}$ where k is the number of bits in the data type, e.g. $k\in \{8,16,32,64\}$. In these finite rings, all odd numbers have an inverse, and so half of the numbers in each ring can be used as denominators in division.

In this chapter we are interested in comparing different approaches to generate reversal of events to support roll-back. One of these approaches is reverse computation. In order for reverse computation to be applicable, events execution need to be reversible. To guarantee that, we select the transformation matrices to be non-singular over the integer ring of their elements. To simplify the expression of reversible multiplication, we additionally pick the transformation matrices so that Gaussian elimination can be completed successfully without pivoting.

3.1 Ring Inverses and Non-singular Matrices

The C++ language provides us with addition, subtraction, and multiplication in the relevant integer rings. We also need a division, which can be implemented as multiplication with the inverse. In order to find a ring inverse, we can use Euclid’s extended algorithm. To be specific, we use the following implementation:

The function in Listing 1.1 returns the inverse of b if b is invertible in $Z_{2^k}$, otherwise it returns zero. We have the relation $b \equiv 1 \mod 2\Rightarrow b*\text {intinv}(b) = b$.

One might initially worry that it can be hard to find non-singular matrices over $Z_{2^k}$. It turns out that a significant fraction of such matrices where the elements are picked from a uniformly random distribution are non-singular. We can determine this as follows. First, a matrix is non-singular if and only if Gaussian elimination with row pivoting can be completed successfully. We note that since we work with a finite set of numbers (ring), there is no need to worry about stability – all calculations are exact and there are no round-off errors. Let M be an $n\times n$ matrix with elements independently selected uniformly from $Z_{2^k}$, where $k > 0$ is an integer. To perform Gaussian elimination on a M we first need to find a pivot element p in the first row. Any invertible element will do. The probability that we find one is $1-\left( \frac{1}{2}\right) ^n$. Assume p is in column j. Now swap column j and column 1. For all rows r and for all columns c in M, set $M_{rc}' = M_{rc} - M_{r1}p^{-1}M_{1c}$. Gaussian elimination proceeds by recursively performing elimination of the submatrix S of $M'$ resulting from removing its first row and first column. For $r>1$ and $c>1$, the parity (oddness) of $M_{rc}'$ is swapped if $M_{r1}M_{1c}$ is odd, and unchanged otherwise. The parity of $M_{rc}$ is uniformly random, and the parity of $M_{r1}M_{1c}$ is independent of $M_{rc}$. Therefore the parity of $M_{rc}'$ is also uniformly random, since an independent flip does not change the distribution. By induction, the probability of finding a pivot element in S is $1-\left( \frac{1}{2}\right) ^{n-1}$, and carrying out the recursion to the end, yields the probability of M being non-singular to be

$$\prod _{i=1}^n \left( 1-\left( \frac{1}{2}\right) ^n\right) \approx 0.288788\ldots .$$

This means that a little bit over one quarter of all uniformly random matrices over $Z_{2^k}$ are non-singular. Therefore we can find suitable ones relatively efficiently by trial and error. Further, in order to create matrices for which we can do Gaussian elimination without pivoting, we pick a non-singular matrix T, and then permute the columns in the schedule dictated by the pivot columns given by computing Gaussian elimination with row pivoting on (a copy of) T.

4 Forward/Backward Code from Reversible Programs

The defining property of reversible programming languages is their forward and backward determinism, that is, in each computation state not only the successor state is uniquely defined, but also the predecessor state [8]. The computation is information preserving. In contrast, mainstream (irreversible) programming languages, such as C, are forward, but not backward deterministic.

In a reversible imperative programming language, such as Janus, every assignment statement is non-destructive, that is a reversible update, such as x -= e, where variable x may not occur in expression e on the right side (e.g., x -= x is not backward deterministic). In case of an assignment to an array element, for example a[i,j] -= a[k,l], a runtime check ensures that i $\ne$ k or j $\ne$ l.

All control-flow statements, such as conditionals and loops, are equipped with assertions, in one way or another, to ensure their backward determinism. The variant of Janus used for the programs in this paper has a two-way deterministic loop iterate i = e1 to e2; s; end, where neither the index variable i nor the variables occurring in expressions e1 and e2, defining the start- and end-values of i, may be modified in the body statement s, which is executed once per iteration. Hence, the number of iterations is known before and after the loop.

An advantage of reversible programming languages is that their programs do not require instrumentation to restore a previous computation state from the current state, which is usually necessary in irreversible languages. Backward determinism opens new opportunities for program development because a procedure p cannot only be called by a usual call p, but its inverse semantics can be invoked by an uncall p. Forward and backward execution of a procedure are equally efficient, thus is makes no difference which direction is implemented in a program, which therefore is usually the one that is easier to write. We will make use of this possibility to reuse code by uncalling a procedure.

Translation from Janus to C++. Reversible programs can be translated to a mainstream (irreversible) programming language, which in this paper is C++. Usually, this requires the implementation of additional runtime checks in the target program to preserve the semantics of the source program. Assuming that the source program is correct and only applied to values for which it is well defined, the runtime checks in the target program can be turned off. The translation of Janus into C++ which we use for the benchmarks is straightforward, e.g., iterate is translated into a for-loop, and no further optimizations are performed by the Janus-to-C++ translator.

Only the translation of an uncall p requires an unconventional step in the translator, namely first the program inversion of procedure p into its inverse procedure p-inv, both p and p-inv written in Janus, followed by the translation of p-inv into the target language and the replacement of every uncall p by the functionally equivalent call p-inv. The target program then contains the C++ implementation of p and its inverse p-inv. Program inversion is straightforward in a reversible language (cf. [6]), e.g., a reversible assignment x -= e is inverted to x += e and a statement sequence is inverted to the reversed sequence of its inverted statements.

As a non-trivial example, Listing 1.2 shows the Janus implementation of the Crout algorithm for LDU matrix decomposition. The translation from Janus into C++ for the forward code is straightforward, and a uncall mult in Janus becomes a call to mult-inv in C++. To illustrate the generated inverted code, its C++ translation can be found in Listing 1.3. The iteration is translated into nested for-loops and the reversible assignment in Janus requires only a minor adaptation to the C++ syntax. In the C++ listing the mult(a,b) is effectively a standard integer product $a:=a\times b$ with appropriate assertions that it can be inverted, i.e. the inverse of b exists. mult-inv uses intinv from Listing 1.1 to compute the ring inverse.

Matrix Multiplication in Janus. A conventional matrix-matrix multiplication needs temporary storage, and the individual steps are not reversible. Since a reversible language requires each operation to be reversible we need a different approach. One approach is to use LU or LDU decomposition, which can be performed in place, and is step-wise reversible. Multiplication with the resulting triangular matrices can also be done in-place and step-wise reversible. In the approach here, to compute $A := A\times B$, we perform the Crout algorithm for LDU decomposition, $B = L\times D\times U$ in place, then the sequence $A:=A\times L$, $A:=A\times D$, $A:=A\times U$. Finally we reverse the LDU decomposition in place, to recover the original input B. For a Janus implementation of the in-place matrix multiplication, see Listing 1.4. The code for multiplication with triangular matrices is shown in Listing 1.5. This approach needs no temporary storage and is step-wise reversible. The price for this reversibility and in-place operation is more arithmetic operations than a standard matrix product by a factor of about 5/3 (for sufficiently large n, say $n>10$). In the full implementation, we used a local temporary variable to reduce the number of calls to the ring-inverse function for speed optimization, since it is much more costly than a multiplication or addition. This does not change any of the reversibility features.

5 Automatic Generation of Reversible Code for the Forward-Reverse-Commit Paradigm

In the forward-reverse-commit (FRC) paradigm [5] the original code is transformed such that during its forward execution it stores all information required to reverse all effects of the forward execution and restore the previous state of the program, or commit (possibly deferred) operations at a later point in time. Hence, we add the history of the computation to each saved state, which is usually called a Landauer’s embedding. In both reverse and commit functions the additional information stored in the forward code is eventually disposed. Before that the reverse function uses the stored data to undo all memory modifying operations, in the commit function performs the deferred memory deallocation.

We generate transformed forward code to implement incremental state saving. The idea is to only store information about what changes in the program state because of a state transition, not the entire state. This approach is also briefly described in [5] for the programming language C (called “incremental check pointing” by the author). After performing a forward execution of the transformed program followed by a corresponding reverse operation, the program is restored to its original state, i.e. the exact same state as the original program was before performing any operation. Therefore, the execution of a forward function and a reverse operation is equivalent to executing no code (i.e. a no-op).

After performing a forward execution of the transformed program followed by a commit operation, the program is in the exact same state as executing the original program. Therefore, the execution of a forward function and its corresponding commit operation performs the same changes to the program state as the execution of the original function.

This transformation can also be considered to turn the program into a transactional program, where each execution step can be reversed (undone) or committed after which it cannot be reversed since all information necessary to reverse it is disposed by the commit operation. This is an important aspect when performing long running discrete event simulations: the forward-commit pairs ensures that no additional memory is consumed after a commit has been performed. As we shall see, the optimistic parallel discrete event simulation ensures that such a point in time at which all events can be committed up to a certain point in the past, can always be computed during the simulation.

In [9] we have shown how this approach can be extended to address C++ without templates. In [10] we have applied this approach to all of C++98, including templates and in [7] we have shown that this approach is general enough to be applied to C++11 standard containers and algorithms.

Our approach to generating reversible forward code introduces one additional function call, an instrumentation, for each memory modifying operation. Memory modifying operations are destructive assignments and memory allocation and deallocation. We only instrument operations of built-in types. For user-defined types either the existing user-provided assignment operator is instrumented (like any other code), or we generate a reversible default assignment operator if it is not user-provided. This is sufficient to cover all forms of memory modifying operations – of built-in types as well as user-defined types – because our runtime library that is linked with the instrumented code performs all necessary book-keeping at run-time. In particular, it also contains C++11 compile-time predicates. Those predicates check whether a provided type is a built-in type or a user-defined type and handle assignments of user-defined types (e.g. entire structs) as fall-through cases because they are handled component-wise by the respective overloaded assignment operator (which is either user-provided and automatically instrumented or generated). For a formal definition of the semantics of the instrumentations we refer the reader to [7].

We have implemented our approach in a tool called Backstroke² as source-to-source transformation based on the compiler infrastructure ROSE³. The Backstroke compiler for generating reversible programs from C$++$ was released to the public in March 2017 (version 2.1.0). This was the first public release of Backstroke V2 using incremental state saving.

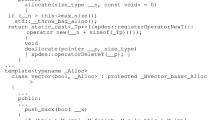
5.1 Backstroke Instrumented Code

Three variants of the matrix multiplication are shown: (1) the original C++ code in Listing 1.6 for the matrix multiplication, (2) the non-optimized Backstroke generated code in Listing 1.7, and (3) the optimized Backstroke generated code in Listing 1.8. Backstroke’s optimization detects local variables and ensures that direct accesses to local variables are not instrumented because those never need to be restored since memory for local variables is reserved on the runtime stack. Backstroke instrumented code records memory modifications only for heap allocated data since only this data persists across event function calls. In the presence of pointers the accesses to memory locations on the stack may be instrumented, but a runtime check in the Backstroke library ensures that only heap allocated data is stored.

This runtime check is always performed in the xpdes::avpush function because due to pointer aliasing, in general it is not known at compile time where the data that a pointer is referring to may be allocated. This check is performed based on the memory addresses of the argument passed to avpush and the stack boundaries determined as part of the initialization of the Backstroke runtime library.

In the presented model only C++ assignments are instrumented because no memory allocation happens in the event functions. The memory for the matrices is allocated in the initialization of the simulation, i.e. in the initialization function for each LP.

The avpush function passes a reference to the memory section denoted by the respective expression as argument and stores a pair of the address (of the denoted memory location) and the value at that address in a queue in the Backstroke runtime library. It returns the very same address such that the code can execute as usual and perform the write access. Consequently, avpush always stores the old value before the assignment happens. When a previous state needs to be restored, the reverse function simply iterates over all those address-value pairs stored by the avpush function and restores the memory locations at those addresses to the stored value. The avpush functions are strictly typed, and restoration follows in exact reverse order, which is important in case a memory location is written more than once or any forms of aliasing occur. For more details on the instrumentation functions we refer the reader to [7].

The difference of the non-optimized version to the optimized version is that the instrumentation in the innermost loop is not necessary because it is a write to a local variable s. In Listing 1.8 the innermost loop is not instrumented and therefore the number of instrumentations is only executed $n^2$ times where n is the size of the quadratic matrices. Without this optimization the Backstroke generated code would always be slower than the Janus generated code as we will discuss in more detail in Sect. 7. In general, accesses to memory which only holds temporary data, not defining the state of an LP, need not be instrumented. The more precise a static analysis is that determines this property, the more instrumentations to temporary memory locations can be avoided.

Backstroke also offers program annotations (through pragmas) for users to manually minimize the number of instrumentations and interface functions to turn on/off the recording of data at runtime. For example, with this feature one can add conditions in loops to only record data in the very first iteration, but not in subsequent iterations that write to the same memory location. Alternatively, one can unroll a loop and only instrument the first (unrolled) iteration and exclude the remaining loop from instrumentation. Thus, with Backstroke one can also manually optimize the recording of data.

6 ROSS Simulator

For execution of our model codes we use the ROSS general purpose discrete event simulator, developed at RPI by C. Carothers et al. [11]. ROSS has been developed for more than a decade. It has the capability of running simulations both sequentially and in parallel using either the YAWNS conservative or Time Warp optimistic mechanism. Time Warp is an optimistic approach, where each processor employs speculative execution to process any event messages it is aware of. Causality conflicts, such as when a previously unknown message which should already have been processed is received, are handled through local roll back. During roll back the effects of messages that were processed in error are undone.

In order to use Time Warp in a ROSS model, a reverse event function must be provided, which is responsible for undoing the state changes that the forward event function incurred for the same event.

6.1 Adaptations of the ROSS Simulator for the FRC Paradigm

For our evaluation we are using the same ROSS implementation as in [7]. This version offers a commit method. Whenever an event is committed (during fossil collection) a commit function is called for the corresponding LP with the event as an argument. This is a time when non-reversible functions such as file I/O can be called safely. In particular, this is very useful for Backstroke, since commit time is the earliest known moment at which the state saved by the Backstroke instrumented forward code can be released, and memory deallocated by the forward event can be returned to the system. In addition to the commit methods, we extended ROSS to support a C++ class for the simulation time data structure, as opposed to the default double data type for representing time. This allows the sender to encode additional bits in the message timestamp to help with tie breaking of events.

Fig. 1.

Top: Performance of original, Backstroke, and Janus versions of the matrix model code. The graph shows the execution time per event for the three approaches. The inset shows execution time relative to the original code. Bottom: The time for the event function for the Backstroke code separated into event setup time, forward event time, and commit time costs.

7 Evaluation

We have evaluated the performance of three different implementations for the forward and reverse code of the matrix mode: Original code with hand written reverse code, forward code implemented in Janus with reverse code generated by the Janus compiler, and forward code instrumented by Backstroke. For these performance evaluations we used the Backstroke code with local variable optimization.

First we focus on forward event code, which consists of three phases: event setup, forward computation, and commit. It is only the Backstroke instrumented code that has any significant work to perform in the setup and commit phases. We ran the matrix model sequentially using 8000 LP’s and running up to 20 time units.

Figure 1 shows the matrix model performance as a function of matrix size for the four different reverse code approaches. The upper panel shows total event execution time, while the lower panel shows the relative cost of the three event execution phases for the Backstroke instrumented code.

The standard procedure, which we employ in the original code, for multiplying two $n\times n$ matrices performs $n^3$ multiplications and additions, and thus in general the execution time for an event should scale as $O(n^3)$ for sufficiently large n.

The Janus code must perform an LU factorization before carrying out the multiplications, and undo the factorization after the multiplication is complete. The total number of operations is about $\frac{5}{3}$ times as many as for the standard procedure. We can thus expect the Janus code to be almost twice as slow as the original code for large matrices. For very small matrices the number of operations of the Janus implementation is similar to the original code.

The Backstroke instrumented code with local variable optimization instruments $2n^2$ memory operations ($n^2$ for the matrix multiplication, and another $n^2$ for copying the result into the destination memory). Since there are $O(n^3)$ arithmetic operations, we expect the Backstroke instrumented code to incur negligible overhead for sufficiently large matrices.

We performed the runs using matrix sizes ranging from 2 to 640. The simulations were run on an cluster with Infiniband interconnect and 2.6GHz Intel Xeon E5-2670 cpus, 16 cores per node. We used the GNU g++ compiler with version 4.9.3, and the “-O3” optimization switches.

In the evaluation results we see that Janus performs best for small matrix sizes, whereas the Backstroke generated incremental state saving code performs better the larger the matrix size becomes, with a cross-over point at the size of a matrix size of 20 and for a matrix size of 640 the performance becomes almost the same as the non-instrumented version of the original forward code. The reason is that the Backstroke generated code only instruments those memory modifications that actually change the state of the simulation, i.e. elements in the matrix, whereas the computation of the intermediate results is not instrumented. This optimization is straightforward because this corresponds to not instrumenting accesses to local (stack-allocated) variables. Since optimistic PDES follows the forward-reverse-commit paradigm the trace only grows to a certain size, until the commit function is invoked by the simulator. The simulator guarantees that this happens in reasonable time intervals. The non-monotonic performance behavior for small matrices in Backstroke, and for intermediate size matrices in Janus (see inset in Fig. 1), is likely due to simulator and timing overhead, and cache effects, respectively.

The advantage of Janus generated forward/reverse code is that it does not need to store any additional data since the Janus implementation of the forward code is reversible. Saving memory is useful particularly in Time Warp simulations, since the amount of memory available dictates how much speculation can be performed. A challenge to implementing an algorithm in Janus is that it requires to writing assertions at the end of constructs that enable reverse execution to take the right execution path (i.e. reverse conditionals). In addition, reversibility may require algorithms that use inherently more operations than the most efficient ones available in traditional non-reversible computing.

8 Related Work

Jefferson started the subject of rollback-based synchronization in 1984 [3]. The paper discusses rollback implemented by restoring a snapshot of an old state, but today we are interested in using reverse computation and/or incremental state saving for that purpose. Also, that paper is written as if discrete event simulation is one of several applications of virtual time, but in fact it was then and is now the primary application. Although the term “virtual time” is used, you can safely read it as “simulation time”.

In 1999 Carothers et al. published the first paper [4], that suggests using reverse computation instead of snapshot restoration as the mechanism for rollback, but it does not contemplate using a reversible language. It is written in terms of very simple and conventional programming constructs (C-like rather than C++ -like) and instrumenting the forward code to store near minimal trace information to allow rollback of side effects by reverse computation.

Barnes et al. demonstrated in 2013 [12], how important reverse computation can be in a practical application area. The fastest and most parallel discrete event simulation benchmark ever executed was done at LLNL on one of the world’s largest supercomputers using reverse computation as its rollback method for synchronization. The reverse code was hand-generated, and methodologically we know that this is unsustainable. For practical applications we need a way of automatically generating reverse code from forward code, and this is what we address with the work presented in this paper - to have a tool available, Backstroke (version 2), for generating reverse code that can be applied to the full C++ language.

Kalyan Perumalla and Alfred Park discuss the use of Reverse Computation for scalable fault tolerant computations [13]. The paper is limited in a number of ways, but they make a fundamental point, which is that Reverse Computation can be used to recover from faults by mechanisms that are much faster than check pointing mechanisms.

In [14] Justin LaPre et al. discuss reverse code generation for PDES. The presented method is similar to one of our previous approaches in the work on Backstroke [15] as it takes control flow into account and generates code for computing additional information required to reconstruct the execution path that had been taken in the forward code. The approach we evaluate in this paper is different as it does not need to take control flow information into account. Our initial discussion of incremental state saving was presented in [9], but was limited to C++ without templates. In this paper we evaluate a model that is implemented using C++ templates as well. The automatic optimization that we evaluate was also not present in [9].

An example for an optimistic PDES simulation with an automatically generated code using incremental state saving running thousands of LPs was published for a Kinetic Monte-Carlo model in [10]. In this crystal grain simulation, a piece of solid is modeled as a grid of unit elements. Each unit element represents a microscopic piece of material, big enough to be able to exhibit a well defined crystal orientation, but much smaller than typical grain sizes. These unit elements are commonly called spins, since the nature of grain evolution resembles evolution of magnetic domains. In the experiment the biggest model was run with a size of 768 $\times$ 768 spins divided into a grid of 96 $\times$ 96 = 9216 LPs with a slow-down factor in comparison to the hand-written reverse code of 4.7 to 4.3. In a new experiment presented in [7], the model was run at a much bigger scale with $1536\times 1536$ spins in $256\times 256$ logical processes (LPs) and implemented using C++ Standard containers and algorithms and user-defined types. After the transformation by Backstroke the model was run for 2 time units, or a total of 47633718 events on LLNL’s IBM BlueGene/Q supercomputer with 16 cores per node, using up to 8192 cores. This version showed a penalty of 2.7. to 2.9 in comparison to the hand-written reverse code.

In [16] an autonomic system is presented that can utilize both an incremental and a full checkpointing mode. At run time both code variants are available and the system switches between the two variants, trying to select the more efficient checkpointing version. With our approach to incremental checkpointing we aim to reduce the number of instrumentations based on static analysis and offer a directive to the user for enabling or disabling the recording of data at runtime, allowing to also manually optimize instrumented code.

In [17] an instrumentation technique is applied to relocatable object files. Specifically, it operates on the Executable and Linkable Format (ELF). It uses the tool Hijacker [18] to instrument the binary code to generate a cache of disassembly information. This allows to avoid disassembly of instructions at run time. In contrast to our approach, the reverse instructions are built on-the-fly at runtime, and using pre-compiled tables of instructions. Similar to our approach there is also an overhead for each instrumentation. The information that it extracts from instructions, the target address and the size of a memory write, is similar to our address-value pairs. Recently progress has been made also in utilizing hardware transactional memory for further optimizing single node performance [19].

9 Conclusion

We have presented a new benchmark model for evaluating approaches to optimistic parallel discrete event simulation. We evaluated the performance of using Janus generated forward/reverse code and incremental state saving (also called incremental checkpointing). The benchmark model has as its core operation a matrix multiplication.

From the results for our presented benchmark model we can conclude that depending on the matrix size either the Janus generated code or the Backstroke generated code performs best. Therefore, an implementation could include both codes and call the respective implementation dependent on the matrix size. If memory consumption becomes a limiting factor, the Janus implementation could be favored over the Backstroke implementation as well, since the Janus code does not store any additional data.

It also could be interesting to further explore how the Janus translator can be optimized and how this impacts the native C++ compiler. The Janus translator used in the benchmarks is non-optimizing, which means it implements every Janus statements in the target program, even when irreversible alternatives provide a faster implementation and some statements may be redundant in C++. Depending on the architecture, locality can be exploited to improve the runtime behavior, e.g., when translating summation iterate... A[i,j]+=e end the use of a temporary variable in conventional assignments is an option: s=A[i,j]; for... s+=e end; A[i,j]=s;. Some optimizations are performed by the native C++ compiler, others are better done by the Janus translator. Also, Janus may be extended with translator hints that allow a programmer to mark compute-uncompute pairs, which makes it easier to determine redundant statements.