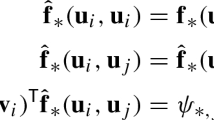Abstract
Summation-by-parts operators can be used in the context of finite difference and discontinuous Galerkin methods to create discretisations mimicking properties given at the continuous level such as entropy conservation. Recently, there has been some interest in schemes for the Euler equations that additionally preserve the kinetic energy. However, some these methods resulted in undesired and unexpected changes of the kinetic energy in numerical experiments of Gassner et al. (J Comput Phys 327:39–66, 2016). Here, analytical insights into kinetic energy preservation are given and new entropy conservative and kinetic energy preserving numerical fluxes are proposed.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Considering the solution of hyperbolic conservation laws, high order methods can be very efficient, providing accurate numerical solutions with relatively low computational effort [21]. In order to make use of this accuracy, stability has to be established. Mimicking estimates obtained on the continuous level via integration-by-parts, summation-by-parts (SBP) operators [22, 37] can be used. In short, SBP operators are discrete derivative operators equipped with a compatible quadrature providing a discrete analogue of the L 2 norm. The compatibility of discrete integration and differentiation mimics integration-by-parts on a discrete level. Combined with the weak enforcement of boundary conditions via simultaneous approximation terms (SATs) [1], highly efficient and stable semidiscretisations can be obtained at least for linear problems, see e.g. [6, 14, 39] and references cited therein.
In recent years, there has been an enduring and increasing interest in the basic ideas of SBP operators and their application in various frameworks including finite volume (FV) [25, 26], discontinuous Galerkin (DG) [2, 4, 10, 11, 13, 20, 27, 28, 30], and the recent flux reconstruction/correction procedure via reconstruction framework [15, 16, 42] as described in [31, 32]. While there is only a limited amount of well-posedness theory for nonlinear conservation laws, mimicking properties such as entropy stability semidiscretely has received much interest. Building on the seminal work of Tadmor [40, 41], entropy stability of second order schemes using symmetric numerical fluxes has been investigated, resulting in well-defined properties that numerical fluxes have to satisfy in order to result in entropy conservative schemes. Decomposing general semidiscretisations into a non-dissipative central part and an additional dissipative part, suitable artificial dissipation or filtering can be added afterwards, cf. [7, 9, 38]. Second order methods based on symmetric numerical fluxes can be extended to high order in a conservative way, cf. [4, 7, 28] and [8, 23, 34,35,36].
Another property of numerical methods for the Euler equations that has received much interest in the literature concerns the kinetic energy. A structural property of numerical fluxes described by Jameson [18] has been used to construct so-called kinetic energy preserving (KEP) numerical fluxes inter alia by Chandrashekar [3]. However, schemes using these fluxes do not preserve the kinetic energy as expected in numerical experiments by Gassner et al. [12]. They had to change the discretisation of the pressure to reduce undesired changes of the kinetic energy. However, this resulted in a loss of entropy conservation. Motivated by these results, some analytical insights into this behaviour have been developed in [29, Section 7.4] and will be presented here.
This chapter is structured as follows. At first, some basic results about SBP operators and corresponding semidiscretisations of hyperbolic conservation laws are reviewed in Sect. 2. Afterwards, the Euler equations are considered in Sect. 3. After demonstrating that the property that has been used to characterise numerical fluxes as KEP is not well-defined, the new concept of KEP numerical methods is introduced. Moreover, a numerical flux that is both entropy conservative and kinetic energy preserving in the new sense is developed. Thereafter, results of a numerical experiment comparing entropy conservative numerical fluxes are described in Sect. 4. Finally, a brief summary is given in Sect. 5.
2 Discretisations Using Summation-by-Parts Operators
Consider the Euler equations in two space dimensions
where ρ is the density, v the velocity, e the specific total energy, and p the pressure. For a perfect gas, \(p = (\gamma -1) \bigl ( \rho e - \frac {1}{2} \rho v^2 \bigr )\). The usual entropy is \(U = - \frac {\rho s}{\gamma - 1}\), where \(s = \log p - \gamma \log \rho \) is the specific (physical) entropy.
With the entropy fluxes F j fulfilling ∂ u U ⋅ ∂ u f j = ∂ u F j, smooth solutions of the Euler equations in d space dimensions satisfy \(\partial _t U(u) + \sum _{j=1}^d \partial _j F^j(u) = 0\) and the entropy inequality
is used as additional admissibility criterion for weak solutions, cf. [5].
In order to discretise (1), the domain Ω is divided into several non-overlapping sub-domains Ω l ⊆ Ω and SBP operators will be used on each element. SBP operators consist of discrete derivative operators D j, approximating the partial derivative in direction j, and a symmetric and positive definite mass/norm matrix M, approximating the L 2(Ω l) scalar product via \(u^T M v = \langle u, v, \rangle _M \approx \langle u, v, \rangle _{L^2(\varOmega _l)} = \int _{\varOmega _l} u \, v\). Moreover, an interpolation operator R approximates the restriction of functions on Ω l to the boundary ∂Ω l and a symmetric and positive definite boundary mass matrix B approximate the L 2(∂Ω l) scalar product. Representing the multiplication by the j-th component of the outer unit normal ν at ∂Ω l by the diagonal matrix n j, the SBP property
has to be satisfied in order to mimic integration-by-parts discretely via

Semidiscretisation of (1) will be constructed as follows. Each sub-domain Ω l ⊆ Ω is mapped onto a reference element and all computations are performed there. On each element, the resulting semidiscretisation is of the form
where the volume terms VOL discretise the flux divergence in the interior of Ω l and the surface terms SURF couple elements or impose boundary conditions. Here, u is the vector of the nodal values of the numerical solution at specified nodes ξ i in Ω l and a collocation approach is used. Thus, nonlinear operations are performed pointwise and the discrete fluxes f j are given by their nodal values \(f^j_i = f^j(u_i) = f^j( u(\xi _i) )\). As in (nodal) discontinuous Galerkin methods, the surface terms will be built using numerical fluxes f num, j in the j-th coordinate direction as
Finally, the volume terms are constructed using symmetric (two-point) numerical fluxes f vol, j (volume fluxes) that are consistent with f j as
where VOLi is the volume term at ξ i [7]. If f vol, j are smooth fluxes, the discretisation (7) is of the same order of accuracy as the derivative matrices D j [4, 28]. Moreover, if the mass matrix M is diagonal, this approximation can be written in a conservative form [7]. Finally, if the boundary operators R T Bn j R are also diagonal and f vol, j are entropy conservative in the sense of Tadmor [40, 41], the semidiscretisation (5) is entropy conservative/stable across elements if the numerical surface fluxes f num, j are entropy conservative/stable. Moreover, some results on the kinetic energy can be transferred as well [12]. In the following, the focus will lie on the fluxes f vol, j.
3 Euler Equations and Kinetic Energy
The kinetic energy \(E_{\mathrm {kin}} = \frac {1}{2} \rho v^2\) fulfils (for sufficiently smooth solutions)
Jameson [18] investigated the kinetic energy in a one-dimensional semidiscrete setting using finite volume methods. To simplify the notation, this setup will be used in the following; its extension to multiple dimensions is straightforward. Jameson proposed to mimic (8) semidiscretely by using numerical momentum fluxes of the form \(f^{\mathrm {num}}_{\rho v} = f^{\mathrm {num}}_{\rho v}(u_-, u_+) = \{\!\{ v \}\!\} f^{\mathrm {num}}_\rho + p^{\mathrm {num}}\), where { {v} } is the arithmetic mean of v − and v +, \(f^{\mathrm {num}}_\rho \) is the numerical density flux, and p num is a consistent numerical approximation of the pressure. Later, this has been used as a kind of “definition” of kinetic energy preserving (KEP) numerical fluxes, e.g. in [3, 12]. However, this is not a well-defined concept, cf. [28, 29]. Indeed, every numerical momentum flux can be written as
Since the numerical fluxes are consistent, \(p^{\mathrm {num}} := f^{\mathrm {num}}_{\rho v} - \{\!\{ v \}\!\} f^{\mathrm {num}}_\rho \) is a consistent approximation of the pressure. The insufficiency of the condition \(f^{\mathrm {num}}_{\rho v} = \{\!\{ v \}\!\} f^{\mathrm {num}}_\rho + p^{\mathrm {num}}\) is in accordance with observations of Gassner et al. [12]. They investigated a Taylor-Green vortex problem and compared several numerical fluxes for the Euler equations. There, numerical fluxes of the form \(f^{\mathrm {num}}_{\rho v} = \{\!\{ v \}\!\} f^{\mathrm {num}}_\rho + p^{\mathrm {num}}\) with p num ≠ { {p} } resulted in a clear loss of kinetic energy compared to other KEP fluxes using the arithmetic average p num = { {p} } as approximation of the pressure. They observed that “the discretisation of the pressure plays a crucial role for the kinetic energy” and that the choice of the arithmetic average p num = { {p} } “seems to be important for the kinetic energy equation” [12, Section 4.2]. However, they had no (theoretical) explanations for this observation.
3.1 New Approach to Kinetic Energy Preservation
By a heuristic argument, the balance law (8) may not be suitable in the incompressible limit: Indeed, for smooth solutions, (8) can be rewritten as
which becomes a conservation law for smooth solutions of the incompressible Euler equations due to \(\operatorname {div}(v) = 0\) or an energy inequality similar to the entropy inequality (2). Since the kinetic energy is plays a crucial role in the incompressible limit [24], the second form (10) might be considered the “better” one. Thus, a semidiscretisation mimicking this equation might be desirable near the incompressible limit.
Definition 1
A numerical flux \(f^{\mathrm {num}} = (f^{\mathrm {num}}_{\rho }, f^{\mathrm {num}}_{\rho v}, f^{\mathrm {num}}_{\rho e})\) for the Euler equations is called kinetic energy preserving (KEP), if the momentum flux can be written as \(f^{\mathrm {num}}_{\rho v} = \{\!\{ v \}\!\} f^{\mathrm {num}}_{\rho } + \{\!\{ p \}\!\}\).
Definition 1 results in a well-defined concept of KEP numerical fluxes.
Theorem 1 (Corollary 7.5 of [29])
If a kinetic energy preserving numerical flux is used in a semidiscrete FV method, the resulting semidiscrete kinetic energy equation mimics both the conservative and the non-conservative terms of Eq.(10).
Proof (Sketch)
Using the chain rule in a one dimensional finite volume setting, the time derivative of the kinetic energy in cell i becomes
where \(\bigl ( \frac {1}{2} \rho v^2 v + p v \bigr )^{\mathrm {\!num}}(u_i, u_j) = v_i v_j f^{\mathrm {num}}_\rho (u_i, u_j) + \frac { p_{i} v_{j} + p_{j} v_{i} }{2}\). □
Using the momentum flux \(f^{\mathrm {num}}_{\rho v} = \{\!\{ v \}\!\} f^{\mathrm {num}}_{\rho } + \{\!\{ p \}\!\}\) in the volume terms (7) in one dimension, the arithmetic average of the pressure yields the volume term Dp, i.e. a straightforward discretisation of ∂ x p. Analogous results hold in multiple space dimensions, cf. Sect. 2.
The kinetic energy preserving DG methods presented in [11, 27] use volume terms corresponding to the numerical fluxes \(f^{\mathrm {num}}_{\rho } = \{\!\{ \rho v \}\!\}\), \(f^{\mathrm {num}}_{\rho v} = \{\!\{ \rho v \}\!\} \{\!\{ v \}\!\} + \{\!\{ p \}\!\}\), which are kinetic energy preserving in the sense of Definition 1.
3.2 Entropy Conservative and KEP Numerical Fluxes
Since entropy stability has received much interest and the entropy conservative numerical fluxes of [3, 17] are not KEP in the sense of Definition 1, it is interesting whether both concepts can be fulfilled simultaneously. The logarithmic mean value \(\{\!\{ \rho \}\!\}_{\mathrm {log}} = [\![ \rho ]\!] / [\![ \log \rho ]\!]\) has been proposed by Roe [33] in the context of entropy conservative numerical fluxes and is described in [17]. Many useful entropy conservative numerical density fluxes are of the form \(f^{\mathrm {num}}_\rho = \{\!\{ \rho \}\!\}_{\mathrm {log}} \{\!\{ v \}\!\}\), e.g. the one presented in [3]. This form seems to be preferable, since positivity preservation of the density can be achieved using local Lax-Friedrichs/Rusanov dissipation operators [28, Section 6.2]. Using this ansatz for \(f^{\mathrm {num}}_\rho \) and Definition 1, the following entropy conservative and kinetic energy preserving numerical flux (f num, y analogously) has been constructed in [29, Section 7.4]
4 Numerical Results
Since the kinetic energy is an important quantity for the incompressible Euler equations, a Taylor-Green vortex given by
for (x, y) ∈ [0, 2π]2 with periodic boundary conditions is considered, which is a stationary solution of the incompressible Euler equations. Using tensor product Lobatto bases for polynomials of degree p = 5 on N = 16 elements per coordinate direction, the numerical solutions have been computed in the time interval t ∈ [0, 30] with the fourth order, ten-stage, strong stability preserving Runge-Kutta method of [19]. The time step Δt has been chosen as \(\varDelta t = \mathrm {cfl} \, \min \{ \varDelta x / (2p+1) \lambda \}\), where λ is the greatest absolute value of the eigenvalues of f′ and the minimum is taken over all cells and nodes. As in [12], the given numerical fluxes have been used for both the volume terms (7) and as surface fluxes in (6), without additional dissipation.
The evolution of the entropy U and the kinetic energy E kin using a CFL number cfl = 0.9 for the entropy conservative fluxes of Ismail and Roe [17], Chandrashekar [3], and the new flux (11) are visualised in Fig. 1. As can be seen there, the entropy remains approximately constant and the kinetic energy oscillates uniformly until t ≈ 20. Afterwards, the kinetic energy drops for the fluxes of [3, 17] and there is a relative change of the entropy of order 10−5. Contrary, there is no visible change for the new flux (11).
The entropy loss for the fluxes of Ismail and Roe [17] and Chandrashekar [3] is caused by the time integration scheme, as can be seen in Fig. 2, where the time step is reduced by an order of magnitude (cfl = 0.09). However, the behaviour of the kinetic energy is nearly unchanged.
5 Summary and Discussion
Using summation-by-parts operators, high order numerical schemes with specific properties can be constructed using symmetric (two-point) numerical fluxes. While several “kinetic energy preserving” methods have been proposed, they have been characterised by a property of the numerical fluxes that is not well-defined. Such numerical fluxes resulted in schemes that did not preserve the kinetic energy as expected [12]. Here, a new approach to kinetic energy preservation inspired by the incompressible Euler equations and developed in [29, Section 7.4] has been described. This results in a well-defined property numerical fluxes have to satisfy in order mimic the balance law for the kinetic energy more reliably. Moreover, new entropy conservative numerical fluxes have been developed that are kinetic energy preserving in the new sense.
References
Carpenter, M.H., Gottlieb, D., Abarbanel, S.: Time-stable boundary conditions for finite-difference schemes solving hyperbolic systems: methodology and application to high-order compact schemes. J. Comput. Phys. 111(2), 220–236 (1994). https://doi.org/10.1006/jcph.1994.1057
Chan, J.: On discretely entropy conservative and entropy stable discontinuous Galerkin methods. J. Comput. Phys. 362, 346–374 (2018). https://doi.org/10.1016/j.jcp.2018.02.033
Chandrashekar, P.: Kinetic energy preserving and entropy stable finite volume schemes for compressible Euler and Navier-Stokes equations. Commun. Comput. Phys. 14(5), 1252–1286 (2013). https://doi.org/10.4208/cicp.170712.010313a
Chen, T., Shu, C.W.: Entropy stable high order discontinuous Galerkin methods with suitable quadrature rules for hyperbolic conservation laws. J. Comput. Phys. 345, 427–461 (2017). https://doi.org/10.1016/j.jcp.2017.05.025
Dafermos, C.M.: Hyperbolic Conservation Laws in Continuum Physics. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-04048-1
Fernández, D.C.D.R., Hicken, J.E., Zingg, D.W.: Review of summation-by-parts operators with simultaneous approximation terms for the numerical solution of partial differential equations. Comput. Fluids 95, 171–196 (2014). https://doi.org/10.1016/j.compfluid.2014.02.016
Fisher, T.C., Carpenter, M.H.: High-order entropy stable finite difference schemes for nonlinear conservation laws: finite domains. J. Comput. Phys. 252, 518–557 (2013). https://doi.org/10.1016/j.jcp.2013.06.014
Fisher, T.C., Carpenter, M.H., Nordström, J., Yamaleev, N.K., Swanson, C.: Discretely conservative finite-difference formulations for nonlinear conservation laws in split form: theory and boundary conditions. J. Comput. Phys. 234, 353–375 (2013). https://doi.org/10.1016/j.jcp.2012.09.026
Fjordholm, U.S., Mishra, S., Tadmor, E.: Arbitrarily high-order accurate entropy stable essentially nonoscillatory schemes for systems of conservation laws. SIAM J. Numer. Anal. 50(2), 544–573 (2012). https://doi.org/10.1137/110836961
Gassner, G.J.: A skew-symmetric discontinuous Galerkin spectral element discretization and its relation to SBP-SAT finite difference methods. SIAM J. Sci. Comput. 35(3), A1233–A1253 (2013). https://doi.org/10.1137/120890144
Gassner, G.J.: A kinetic energy preserving nodal discontinuous Galerkin spectral element method. Int. J. Numer. Methods Fluids 76(1), 28–50 (2014). https://doi.org/10.1002/fld.3923
Gassner, G.J., Winters, A.R., Kopriva, D.A.: Split form nodal discontinuous Galerkin schemes with summation-by-parts property for the compressible Euler equations. J. Comput. Phys. 327, 39–66 (2016). https://doi.org/10.1016/j.jcp.2016.09.013
Gassner, G.J., Winters, A.R., Kopriva, D.A.: A well balanced and entropy conservative discontinuous Galerkin spectral element method for the shallow water equations. Appl. Math. Comput. 272, 291–308 (2016). https://doi.org/10.1016/j.amc.2015.07.014
Gustafsson, B., Kreiss, H.O., Oliger, J.: Time-Dependent Problems and Difference Methods. Wiley, Hoboken (2013)
Huynh, H.T.: A flux reconstruction approach to high-order schemes including discontinuous Galerkin methods. In: 18th AIAA Computational Fluid Dynamics Conference. American Institute of Aeronautics and Astronautics (2007). https://doi.org/10.2514/6.2007-4079
Huynh, H.T., Wang, Z.J., Vincent, P.E.: High-order methods for computational fluid dynamics: a brief review of compact differential formulations on unstructured grids. Comput. Fluids 98, 209–220 (2014). https://doi.org/10.1016/j.compfluid.2013.12.007
Ismail, F., Roe, P.L.: Affordable, entropy-consistent Euler flux functions II: entropy production at shocks. J. Comput. Phys. 228(15), 5410–5436 (2009). https://doi.org/10.1016/j.jcp.2009.04.021
Jameson, A.: Formulation of kinetic energy preserving conservative schemes for gas dynamics and direct numerical simulation of one-dimensional viscous compressible flow in a shock tube using entropy and kinetic energy preserving schemes. J. Sci. Comput. 34(2), 188–208 (2008). https://doi.org/10.1007/s10915-007-9172-6
Ketcheson, D.I.: Highly efficient strong stability-preserving Runge-Kutta methods with low-storage implementations. SIAM J. Sci. Comput. 30(4), 2113–2136 (2008). https://doi.org/10.1137/07070485X
Kopriva, D.A., Gassner, G.J.: An energy stable discontinuous Galerkin spectral element discretization for variable coefficient advection problems. SIAM J. Sci. Comput. 36(4), A2076–A2099 (2014). https://doi.org/10.1137/130928650
Kreiss, H.O., Oliger, J.: Comparison of accurate methods for the integration of hyperbolic equations. Tellus 24(3), 199–215 (1972). https://doi.org/10.1111/j.2153-3490.1972.tb01547.x
Kreiss, H.O., Scherer, G.: Finite element and finite difference methods for hyperbolic partial differential equations. In: de Boor, C. (ed.) Mathematical Aspects of Finite Elements in Partial Differential Equations, pp. 195–212. Academic, New York (1974)
LeFloch, P.G., Mercier, J.M., Rohde, C.: Fully discrete, entropy conservative schemes of arbitrary order. SIAM J. Numer. Anal. 40(5), 1968–1992 (2002). https://doi.org/10.1137/S003614290240069X
Lions, P.L.: Mathematical topics in fluid mechanics. Incompressible Models, vol. 1. Oxford University, Oxford (1996)
Nordström, J., Björck, M.: Finite volume approximations and strict stability for hyperbolic problems. Appl. Numer. Math. 38(3), 237–255 (2001). https://doi.org/10.1016/S0168-9274(01)00027-7
Nordström, J., Forsberg, K., Adamsson, C., Eliasson, P.: Finite volume methods, unstructured meshes and strict stability for hyperbolic problems. Appl. Numer. Math. 45(4), 453–473 (2003). https://doi.org/10.1016/S0168-9274(02)00239-8
Ortleb, S.: A kinetic energy preserving DG scheme based on Gauss-Legendre points. J. Sci. Comput. 71(3), 1135–1168 (2017). https://doi.org/10.1007/s10915-016-0334-2
Ranocha, H.: Comparison of some entropy conservative numerical fluxes for the Euler equations. J. Sci. Comput. (2017). https://doi.org/10.1007/s10915-017-0618-1
Ranocha, H.: Generalised summation-by-parts operators and entropy stability of numerical methods for hyperbolic balance laws. Ph.D. Thesis, TU Braunschweig (2018)
Ranocha, H.: Generalised summation-by-parts operators and variable coefficients. J. Comput. Phys. 362, 20–48 (2018). https://doi.org/10.1016/j.jcp.2018.02.021
Ranocha, H., Öffner, P., Sonar, T.: Summation-by-parts operators for correction procedure via reconstruction. J. Comput. Phys. 311, 299–328 (2016). https://doi.org/10.1016/j.jcp.2016.02.009
Ranocha, H., Öffner, P., Sonar, T.: Summation-by-parts and correction procedure via reconstruction. In: Bittencourt, M.L., Dumont, N.A., Hesthaven, J.S. (eds.) Spectral and High Order Methods for Partial Differential Equations ICOSAHOM 2016. Lecture Notes in Computational Science and Engineering, vol. 119, pp. 627–637. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-65870-4_45
Roe, P.L.: Affordable, entropy-consistent Euler flux functions. In: Talk presented at the Eleventh International Conference on Hyperbolic Problems: Theory, Numerics, Applications (2006). http://www2.cscamm.umd.edu/people/faculty/tadmor/references/files/Roe_Affordable_entropy_Hyp2006.pdf
Sjögreen, B., Yee, H.C.: On skew-symmetric splitting and entropy conservation schemes for the Euler equations. In: Kreiss, G., Lötstedt, P., Målqvist, A., Neytcheva, M. (eds.) Numerical Mathematics and Advanced Applications 2009: Proceedings of ENUMATH 2009, the 8th European Conference on Numerical Mathematics and Advanced Applications, Uppsala, July 2009, pp. 817–827. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11795-4_88
Sjögreen, B., Yee, H.: High order entropy conservative central schemes for wide ranges of compressible gas dynamics and MHD flows. J. Comput. Phys. 364, 153–185 (2018). https://doi.org/10.1016/j.jcp.2018.02.003
Sjögreen, B., Yee, H.C., Kotov, D.: Skew-symmetric splitting and stability of high order central schemes. In: Journal of Physics: Conference Series, vol. 837, p. 012019. IOP Publishing, Philadelphia (2017). https://doi.org/10.1088/1742-6596/837/1/012019
Strand, B.: Summation by parts for finite difference approximations for d∕dx. J. Comput. Phys. 110(1), 47–67 (1994). https://doi.org/10.1006/jcph.1994.1005
Svärd, M., Mishra, S.: Shock capturing artificial dissipation for high-order finite difference schemes. J. Sci. Comput. 39(3), 454–484 (2009). https://doi.org/10.1007/s10915-009-9285-1
Svärd, M., Nordström, J.: Review of summation-by-parts schemes for initial-boundary-value problems. J. Comput. Phys. 268, 17–38 (2014). https://doi.org/10.1016/j.jcp.2014.02.031
Tadmor, E.: The numerical viscosity of entropy stable schemes for systems of conservation laws. I. Math. Comput. 49(179), 91–103 (1987). https://doi.org/10.1090/S0025-5718-1987-0890255-3
Tadmor, E.: Entropy stability theory for difference approximations of nonlinear conservation laws and related time-dependent problems. Acta Numer. 12, 451–512 (2003). https://doi.org/10.1017/S0962492902000156
Wang, Z.J., Gao, H.: A unifying lifting collocation penalty formulation including the discontinuous Galerkin, spectral volume/difference methods for conservation laws on mixed grids. J. Comput. Phys. 228(21), 8161–8186 (2009). https://doi.org/10.1016/j.jcp.2009.07.036
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2020 The Author(s)
About this paper
Cite this paper
Ranocha, H. (2020). Entropy Conserving and Kinetic Energy Preserving Numerical Methods for the Euler Equations Using Summation-by-Parts Operators. In: Sherwin, S.J., Moxey, D., Peiró, J., Vincent, P.E., Schwab, C. (eds) Spectral and High Order Methods for Partial Differential Equations ICOSAHOM 2018. Lecture Notes in Computational Science and Engineering, vol 134. Springer, Cham. https://doi.org/10.1007/978-3-030-39647-3_42
Download citation
DOI: https://doi.org/10.1007/978-3-030-39647-3_42
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-39646-6
Online ISBN: 978-3-030-39647-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)