1 Introduction

In this paper we focus on isogeometric Galerkin discretizations of the weighted curl-div operator

$$\displaystyle \begin{aligned} \mathcal{L}_{\alpha, \beta} \boldsymbol{u} := \alpha \nabla \times \nabla \times \boldsymbol{u} - \beta \nabla \nabla \cdot \boldsymbol{u}, \quad 0<\alpha,\beta. \end{aligned} $$
(1)

This parameter-dependent operator appears in several problems, including the Stokes equation and Maxwell equations [1]. Moreover, containing a weighting of the curl and div operators, it captures the essential features of the so-called Alfvén-like operator [14], which is of interest in magnetohydrodynamics [15]. We note that \(\mathcal {L}_{\alpha , \beta }\) can be seen as a weighted Laplacian for vector fields (equivalently, Hodge Laplace for 1-forms). Indeed, when α = β = 1, it is equal to the standard (negative) vector Laplace operator, i.e.,

$$\displaystyle \begin{aligned} \nabla \times \nabla \times \boldsymbol{u} -\nabla \nabla \cdot \boldsymbol{u} = -\nabla^2 \boldsymbol{u}. \end{aligned}$$

We assume that (1) is defined on a sufficiently smooth domain \(\Omega \in {\mathbb R}^2\) that can be described through a geometry map \(\boldsymbol {G}:[0,1]^2\rightarrow \overline {\Omega }\), and we consider homogeneous Dirichlet (no-slip) boundary conditions, i.e., u = 0 on ∂ Ω. This leads us to the following variational formulation

$$\displaystyle \begin{aligned} (\mathcal{L}_{\alpha,\beta} \boldsymbol{u}, \boldsymbol{v}) = \alpha(\nabla \times\boldsymbol{u},\nabla \times\boldsymbol{v}) +\beta(\nabla \cdot\boldsymbol{u},\nabla \cdot\boldsymbol{v}), \quad \boldsymbol{u},\boldsymbol{v} \in \big(H_0^1(\Omega)\big)^2. \end{aligned} $$
(2)

We refer the reader to [2, 15] for a discussion about well-posedness.

To find an approximate solution of the problem \(\mathcal {L}_{\alpha , \beta } \boldsymbol {u}={\boldsymbol {f}}\), with the stated boundary conditions, we consider the variational formulation (2) in a finite dimensional vector space \(\mathbb {V}_h \subset \big (H_0^1(\Omega )\big )^2\), i.e.,

$$\displaystyle \begin{aligned} (\mathcal{L}_{\alpha,\beta} \boldsymbol{u}_h, \boldsymbol{v}_h) = \alpha(\nabla \times\boldsymbol{u}_h,\nabla \times\boldsymbol{v}_h) +\beta(\nabla \cdot\boldsymbol{u}_h,\nabla \cdot\boldsymbol{v}_h), \quad \boldsymbol{u}_h,\boldsymbol{v}_h \in \mathbb{V}_h. \end{aligned} $$
(3)

We focus on isogeometric analysis (IgA) as discretization technique, where the approximation space \(\mathbb {V}_h\) is chosen to be composed of vector fields whose components are linear combinations of tensor-product B-splines mapped according to G.

The discretization (3) leads to solving linear systems, which turn out to be severely ill-conditioned and require ad hoc fast solvers for a proper treatment [4, 6, 15]. This requires a deep understanding of the spectral properties of the related matrices. They depend on many factors: the problem parameters α, β, the basic curl and div operators, the mesh-size, the degree of the B-spline approximation, and the map G used to describe the geometry of the computational domain.

In this paper we provide a spectral study of these matrices using the theory of (multilevel block) Toeplitz [13, 17, 19] and generalized locally Toeplitz [10,11,12] sequences. More precisely, we show that such matrices admit a spectral distribution which can be described in terms of a so-called spectral symbol. We determine this spectral symbol and we reveal its dependence on the characteristic parameters of the problem listed above. The spectral analysis presented in this paper extends the results of [15] to the case of non-trivial geometry and relies on the spectral theory developed for isogeometric discretizations of elliptic problems in [7, 8]. We also refer the reader to [16] for a spectral analysis of the curl-curl operator.

The remainder of the paper is organized as follows. In Sect. 2 we introduce notations and definitions relevant for our spectral analysis, and we recall the basics of B-splines. In Sect. 3 we detail the IgA discretization matrices and we perform a spectral analysis of them. We numerically illustrate those results in Sect. 4. Finally, we conclude the paper in Sect. 5.

2 Preliminaries

In this section we collect some preliminary tools on spectral analysis and IgA discretizations. In particular, we recall the formal definition of spectral distribution for a general matrix-sequence and the definition of (cardinal) B-splines.

2.1 Spectral Distribution

Throughout the paper, we follow the standard convention for operations with multi-indices (see, e.g. [9, 18]). Given a multi-index \(\boldsymbol {n}:=(n_1,\ldots ,n_d)\in {\mathbb N}^d\), we say n →∞ if n i →∞, i = 1, …, d. Let \(\mathcal C_0({\mathbb C})\) be the set of continuous functions \(F:{\mathbb C}\rightarrow {\mathbb C}\) with compact support.

Definition 1

Let \(f:D\to \mathbb {C}^{s\times s}\) be a measurable matrix-valued function, defined on a measurable set \(D\subset {\mathbb R}^q\) with q ≥ 1, 0 < μ q(D) < ∞, where μ q is the Lebesgue measure. Let {A n}n be a matrix-sequence with dim(A n) =: d n and d n →∞ as n →∞. {A n}n is distributed like the pair (f, D) in the sense of the eigenvalues, denoted by {A n}n ∼λ(f, D), if the following limit relation holds for all \(F\in \mathcal C_0(\mathbb C)\):

$$\displaystyle \begin{aligned} \lim_{\boldsymbol{n}\to\infty}\frac{1}{d_{\boldsymbol{n}}}\sum_{j=1}^{d_{\boldsymbol{n}}}F(\lambda_j(A_{\boldsymbol{n}}))= \frac 1{\mu_q(D)}\int_D \frac{\sum_{i=1}^{s}F(\lambda_i(f({\boldsymbol t})))}{s} {\mathrm{d}}{\boldsymbol t}, \end{aligned} $$
(4)

where λ j(A n), j = 1, …, d n are the eigenvalues of A n and λ i(f), i = 1, …, s are the eigenvalues of f. We say that f is the (spectral) symbol of the matrix-sequence {A n}n.

If f is smooth enough and the matrix-size of A n is sufficiently large, then the limit relation (4) has the following informal meaning: a first set of d n∕s eigenvalues of A n is approximated by a sampling of λ 1(f) on a uniform equispaced grid of the domain D, a second set of d n∕s eigenvalues of A n is approximated by a sampling of λ 2(f) on a uniform equispaced grid of the domain D, and so on, up to few outliers.

In general, understanding whether a matrix-sequence admits a symbol and how to compute it is not an easy task. On the other hand, any “reasonable” approximation of partial differential equations by local methods leads to matrix-sequences that are in the so-called generalized locally Toeplitz (GLT) algebra, and so admit a symbol [10,11,12]. The IgA discretization of our curl-div problem (3) fits in this frame.

2.2 B-Splines

For p ≥ 0 and n ≥ 1, consider the uniform knot sequence

$$\displaystyle \begin{aligned} \xi_1=\cdots=\xi_{p+1}:=0<\xi_{p+2}<\cdots<\xi_{p+n}<1=:\xi_{p+n+1}=\cdots=\xi_{2p+n+1}, \end{aligned}$$

where \(\xi _{i+p+1}:=\frac {i}{n}\), i = 0, …, n. This knot sequence allows us to define n + p B-splines of degree p. Let χ I denote the characteristic function on the interval I.

Definition 2

The B-splines of degree p over a uniform mesh of [0, 1], consisting of n intervals, are denoted by \(N_{i}^p:[0,1]\rightarrow {\mathbb R}\), i = 1, …, n + p, and defined recursively as follows: for 1 ≤ i ≤ n + 2p,

$$\displaystyle \begin{aligned} N_i^0(x):=\chi_{[\xi_i,\xi_{i+1})}(x); \end{aligned}$$

for 1 ≤ k ≤ p and 1 ≤ i ≤ n + 2p − k,

$$\displaystyle \begin{aligned} N_i^k(x):=\frac{x-\xi_i}{\xi_{i+k}-\xi_i}N_{i}^{k-1}(x)+\frac{\xi_{i+k+1}-x}{\xi_{i+k+1}-\xi_{i+1}}N_{i+1}^{k-1}(x), \end{aligned}$$

where a fraction with zero denominator is assumed to be zero.

It is well known (see, e.g. [3]) that the B-splines \(N_{i}^p\), i = 1, …, n + p, form a basis, and

$$\displaystyle \begin{aligned} N_{i}^p(0)=N_{i}^p(1)=0, \quad i=2,\ldots,n+p-1. \end{aligned} $$
(5)

The central B-splines \(N_i^p\), i = p + 1, …, n, are uniformly shifted and scaled versions of a single shape function, the so-called cardinal B-spline \(\phi _p:{\mathbb R}\rightarrow {\mathbb R}\),

$$\displaystyle \begin{aligned} \phi_0(t) := \chi_{[0, 1)}(t), \quad \phi_p(t) := \frac{t}{p} \phi_{p-1}(t) + \frac{p+1-t}{p} \phi_{p-1}(t-1), \quad p \geq 1. \end{aligned}$$

More precisely, we have

$$\displaystyle \begin{aligned} N^{p}_i(x) =\phi_{p}(nx-i+p+1), \quad i=p+1,\ldots,n. \end{aligned}$$

The cardinal B-spline ϕ p is a C p−1 function which is locally supported on the interval [0, p + 1].

Finally, we recall the definition of tensor-product B-splines.

Definition 3

The tensor-product B-splines of bi-degree p:= (p 1, p 2) over a uniform mesh of [0, 1]2, consisting of n:= (n 1, n 2) intervals in each direction, are denoted by \(N_{\boldsymbol {i}}^{\boldsymbol {p}}:[0,1]^2\rightarrow {\mathbb R}\), i = 1, …, n + p, and defined as

$$\displaystyle \begin{aligned} N_{\boldsymbol{i}}^{\boldsymbol{p}}:=N_{i_1}^{p_1}\otimes N_{i_2}^{p_2}, \end{aligned}$$

where 1:= (1, 1) and \(\boldsymbol {i}:=(i_1,i_2)\in {\mathbb N}^2\).

We define the tensor-product spline space \(\mathbb {S}^{\boldsymbol {p}}_{\boldsymbol {n}}\) as

$$\displaystyle \begin{aligned} \mathbb{S}^{\boldsymbol{p}}_{\boldsymbol{n}}:={\mbox{span}}\left\{N_{\boldsymbol{i}}^{\boldsymbol{p}}:\boldsymbol{i}=\boldsymbol{2},\ldots,\boldsymbol{n+p-1}\right\}. \end{aligned} $$
(6)

Note that all the elements of this space vanish at the boundary of [0, 1]2; see (5). Hence, the space incorporates homogeneous Dirichlet boundary conditions.

3 Spectral Analysis of Isogeometric Discretizations in 2D

Suppose that the physical domain Ω can be described by a global geometry map, G:= [G 1, G 2]T, \(\boldsymbol {G}:\widehat {\Omega }\rightarrow \overline {\Omega }\), which is invertible in the parametric domain \(\widehat {\Omega }:=[0,1]^2\) and satisfies \(\boldsymbol {G}(\partial \widehat {\Omega })=\partial {\Omega }\). Let

$$\displaystyle \begin{aligned} \mathbb{V}_h ={\mbox{span}}\left\{\phi^{p,1}_{i_1,i_2},\phi^{p,2}_{j_1,j_2}:i_l,j_l=2,\ldots,n+p-1; \ l=1,2\right\}, \end{aligned} $$
(7)

where

$$\displaystyle \begin{aligned} \phi^{p,1}_{i_1,i_2}:=\begin{bmatrix} \varphi_{i_1,i_2} \\[.1cm] 0 \end{bmatrix}, \quad \phi^{p,2}_{j_1,j_2}:=\begin{bmatrix} 0 \\ \varphi_{j_1,j_2} \end{bmatrix}, \end{aligned}$$

and for k l ∈{i l, j l}, l = 1, 2,

$$\displaystyle \begin{aligned} \varphi_{k_1,k_2}(x_1,x_2):={\hat{\varphi}}_{k_1,k_2}(\boldsymbol{G}^{-1}(x_1,x_2))=\hat{\varphi}_{k_1,k_2}(\hat{x}_1,\hat{x}_2), \quad (x_1,x_2)=\boldsymbol{G}(\hat{x}_1,\hat{x}_2). \end{aligned}$$

Then, we set \(\hat {\varphi }_{k_1,k_2}=N^p_{k_1}\otimes N^p_{k_2}\), i.e., the tensor-product B-splines in (6). For simplicity of notation, we have taken n 1 = n 2 = n and p 1 = p 2 = p. Also note that

$$\displaystyle \begin{aligned} \nabla \varphi_{k_1,k_2} &= (J_{\boldsymbol{G}})^{-T}\nabla (N^p_{k_1}\otimes N^p_{k_2})\\ &= \frac{1}{\det(J_{\boldsymbol{G}})} \begin{bmatrix} \frac{\partial{G_2}}{\partial \hat{x}_2} (N^p_{k_1})^{\prime}\otimes N^p_{k_2} -\frac{\partial{G_2}}{\partial \hat{x}_1}N^p_{k_1}\otimes (N^p_{k_2})^{\prime}\\[0.1cm] -\frac{\partial{G_1}}{\partial \hat{x}_2} (N^p_{k_1})^{\prime}\otimes N^p_{k_2} +\frac{\partial{G_1}}{\partial \hat{x}_1}N^p_{k_1}\otimes (N^p_{k_2})^{\prime} \end{bmatrix}, \end{aligned} $$

where

$$\displaystyle \begin{aligned} J_{\boldsymbol{G}}:= \begin{bmatrix} \frac{\partial{G_1}}{\partial \hat{x}_1} & \frac{\partial{G_1}}{\partial \hat{x}_2}\\[0.1cm] \frac{\partial{G_2}}{\partial \hat{x}_1} & \frac{\partial{G_2}}{\partial \hat{x}_2} \end{bmatrix}. \end{aligned}$$

In the following, we start by discussing the coefficient matrices arising from the IgA discretization of a generalized Poisson problem. Then, we construct the coefficient matrices related to the IgA discretization of our curl-div problem (3) using (7), and we perform a spectral analysis.

3.1 Matrices Related to a Generalized Poisson Problem

Let us focus on the following bivariate generalized Poisson operator:

$$\displaystyle \begin{aligned} \mathcal{L}_{K} u := -\nabla \cdot K\nabla u, \end{aligned} $$
(8)

where \(K:\Omega \to {\mathbb R}^{2\times 2}\), and consider homogeneous Dirichlet boundary conditions, i.e., u = 0 on ∂ Ω. From [8] we know that the Galerkin discretization of (8) using one component of the space (7) leads to the coefficient matrix \(\mathcal {A}^{p,K}_{\boldsymbol {n},\boldsymbol {G}}\) defined by

$$\displaystyle \begin{aligned} \left[\mathcal{A}^{p,K}_{\boldsymbol{n},\boldsymbol{G}}\right]_{\boldsymbol{i},\boldsymbol{j}} := \int_{\widehat{\Omega}} \left[\nabla (N^p_{j_1+1}\otimes N^p_{j_2+1})^T\, K_{\boldsymbol{G}}\, \nabla (N^p_{i_1+1}\otimes N^p_{i_2+1})\right] |\det(J_{\boldsymbol{G}})|, \end{aligned} $$

where

$$\displaystyle \begin{aligned} K_{\boldsymbol{G}}:=(J_{\boldsymbol{G}})^{-1}K(\boldsymbol{G})(J_{\boldsymbol{G}})^{-T}. \end{aligned}$$

It has been proved in [8] that such matrices admit a spectral distribution according to Definition 1. To this end, let us define

$$\displaystyle \begin{aligned} H_p := \begin{bmatrix} \mathfrak{s}_p\otimes \mathfrak{m}_p & & \mathfrak{a}_p\otimes \mathfrak{a}_p\\ \mathfrak{a}_p\otimes \mathfrak{a}_p & & \mathfrak{m}_p\otimes \mathfrak{s}_p \end{bmatrix}, \end{aligned}$$

with

$$\displaystyle \begin{aligned} \mathfrak{m}_p(\theta) &:= \phi_{2p+1}(p+1) + 2 \sum_{k=1}^p \phi_{2p+1}(p+1-k) \cos{}(k \theta),\\[-0.15cm] \mathfrak{a}_p(\theta) &:= - 2 \sum_{k=1}^p {\phi}^{\prime}_{2p+1}(p+1-k) \sin{}(k \theta),\\[-0.15cm] \mathfrak{s}_p(\theta) &:= - {\phi}^{\prime\prime}_{2p+1}(p+1) - 2 \sum_{k=1}^p {\phi}^{\prime\prime}_{2p+1}(p+1-k) \cos{}(k \theta). \end{aligned} $$

Theorem 1

Let G be a regular geometry map, i.e., G ∈ C 1([0, 1]2) and \(\det (J_{\boldsymbol {G}})\ne 0\) in [0, 1]2 , and let K be a symmetric matrix. Then, the matrix-sequence \(\{\mathcal {A}^{p,K}_{\boldsymbol {n},\boldsymbol {G}}\}_n\) with n = (n, n) is distributed, in the sense of the eigenvalues, like the function

$$\displaystyle \begin{aligned} f^{p,K}_{\boldsymbol{G}}(\hat{\boldsymbol{x}},\boldsymbol{\theta}):= [1\, 1]\left(|\det(J_{\boldsymbol{G}}(\hat{\boldsymbol{x}}))|\,K_{\boldsymbol{G}}(\hat{\boldsymbol{x}}) \circ H_p(\boldsymbol{\theta}) \right)[1\, 1]^T, \end{aligned} $$
(9)

where \(\hat {\boldsymbol {x}}\in [0,1]^2\) , θ ∈ [−π, π]2 , and ∘ is the Hadamard matrix product.

We refer the reader to [8, 9] for a detailed discussion about the symbol (9).

3.2 Matrices Related to Our Curl-Div Problem

We can reformulate (1) in 2D as

$$\displaystyle \begin{aligned} {\mathcal{L}}_{\alpha,\beta}\boldsymbol{u}= \alpha\begin{bmatrix} \frac{\partial^2{u_2}}{\partial {x}_1{x}_2}-\frac{\partial^2{u_1}}{\partial {x}_2^2}\\ \frac{\partial^2{u_1}}{\partial {x}_1{x}_2}-\frac{\partial^2{u_2}}{\partial {x}_1^2} \end{bmatrix} -\beta\begin{bmatrix} \frac{\partial^2{u_2}}{\partial {x}_1{x}_2}+\frac{\partial^2{u_1}}{\partial {x}_1^2} \\ \frac{\partial^2{u_1}}{\partial {x}_1{x}_2}+\frac{\partial^2{u_2}}{\partial {x}_2^2} \end{bmatrix}, \end{aligned} $$
(10)

where u(x 1, x 2):= [u 1(x 1, x 2), u 2(x 1, x 2)]T. When discretizing the weak form (3) using the space (7) we arrive at the 2 × 2 block matrix

$$\displaystyle \begin{aligned} \mathcal{A}^{p,\alpha,\beta}_{\boldsymbol{n},\boldsymbol{G}}:= \alpha\begin{bmatrix} \mathcal{A}^{p,{\mathrm{curl}}}_{\boldsymbol{n},11} & \mathcal{A}^{p,{\mathrm{curl}}}_{\boldsymbol{n},12} \\ \mathcal{A}^{p,{\mathrm{curl}}}_{\boldsymbol{n},21} & \mathcal{A}^{p,{\mathrm{curl}}}_{\boldsymbol{n},22} \end{bmatrix} + \beta \begin{bmatrix} \mathcal{A}^{p,{\mathrm{div}}}_{\boldsymbol{n},11} & \mathcal{A}^{p,{\mathrm{div}}}_{\boldsymbol{n},12} \\ \mathcal{A}^{p,{\mathrm{div}}}_{\boldsymbol{n},21} & \mathcal{A}^{p,{\mathrm{div}}}_{\boldsymbol{n},22} \end{bmatrix}. \end{aligned}$$

The blocks related to the curl-curl operator (∇×⋅, ∇×⋅) are given by

$$\displaystyle \begin{aligned} \left[\mathcal{A}^{p,{\mathrm{curl}}}_{\boldsymbol{n},11}\right]_{\boldsymbol{i},\boldsymbol{j}} &= \int_{\widehat{\Omega}} \left[\textstyle-\frac{\partial{G_1}}{\partial \hat{x}_2} (N^p_{j_1+1})^{\prime}\otimes N^p_{j_2+1} +\frac{\partial{G_1}}{\partial \hat{x}_1}N^p_{j_1+1}\otimes (N^p_{j_2+1})^{\prime}\right] \\ &\quad \left[\textstyle-\frac{\partial{G_1}}{\partial \hat{x}_2} (N^p_{i_1+1})^{\prime}\otimes N^p_{i_2+1} +\frac{\partial{G_1}}{\partial \hat{x}_1}N^p_{i_1+1}\otimes (N^p_{i_2+1})^{\prime}\right] \frac{1}{|\det(J_{\boldsymbol{G}})|}, \\[0.1cm] \left[\mathcal{A}^{p,{\mathrm{curl}}}_{\boldsymbol{n},12}\right]_{\boldsymbol{i},\boldsymbol{j}} &= -\int_{\widehat{\Omega}} \left[\textstyle \frac{\partial{G_2}}{\partial \hat{x}_2} (N^p_{j_1+1})^{\prime}\otimes N^p_{j_2+1} -\frac{\partial{G_2}}{\partial \hat{x}_1}N^p_{j_1+1}\otimes (N^p_{j_2+1})^{\prime}\right] \\ &\quad \left[-\textstyle\frac{\partial{G_1}}{\partial \hat{x}_2} (N^p_{i_1+1})^{\prime}\otimes N^p_{i_2+1} +\frac{\partial{G_1}}{\partial \hat{x}_1}N^p_{i_1+1}\otimes (N^p_{i_2+1})^{\prime}\right] \frac{1}{|\det(J_{\boldsymbol{G}})|}, \\[0.1cm] \left[\mathcal{A}^{p,{\mathrm{curl}}}_{\boldsymbol{n},22}\right]_{\boldsymbol{i},\boldsymbol{j}} &= \int_{\widehat{\Omega}} \left[\textstyle\frac{\partial{G_2}}{\partial \hat{x}_2} (N^p_{j_1+1})^{\prime}\otimes N^p_{j_2+1} -\frac{\partial{G_2}}{\partial \hat{x}_1}N^p_{j_1+1}\otimes (N^p_{j_2+1})^{\prime}\right] \\ &\quad \left[\textstyle\frac{\partial{G_2}}{\partial \hat{x}_2} (N^p_{i_1+1})^{\prime}\otimes N^p_{i_2+1} -\frac{\partial{G_2}}{\partial \hat{x}_1}N^p_{i_1+1}\otimes (N^p_{i_2+1})^{\prime}\right] \frac{1}{|\det(J_{\boldsymbol{G}})|}, \end{aligned} $$

and \(\mathcal {A}^{p,{\mathrm {curl}}}_{\boldsymbol {n},21} = \mathcal {A}^{p,{\mathrm {curl}}}_{\boldsymbol {n},12}\). Note that all those blocks are symmetric matrices. Similarly, the blocks related to the div-div operator (∇⋅, ∇⋅) are given by (see also (10))

$$\displaystyle \begin{aligned} \mathcal{A}^{p,{\mathrm{div}}}_{\boldsymbol{n},11} = \mathcal{A}^{p,{\mathrm{curl}}}_{\boldsymbol{n},22}, \quad \mathcal{A}^{p,{\mathrm{div}}}_{\boldsymbol{n},12} = \mathcal{A}^{p,{\mathrm{div}}}_{\boldsymbol{n},21} = -\mathcal{A}^{p,{\mathrm{curl}}}_{\boldsymbol{n},12}, \quad \mathcal{A}^{p,{\mathrm{div}}}_{\boldsymbol{n},22} = \mathcal{A}^{p,{\mathrm{curl}}}_{\boldsymbol{n},11}. \end{aligned}$$

In the next subsection we compute the symbol of the matrix-sequence \(\{\mathcal {A}^{p,\alpha ,\beta }_{\boldsymbol {n},\boldsymbol {G}}\}_n\).

3.3 Spectral Symbol of Curl-Div Matrices \(\mathcal {A}^{p,\alpha ,\beta }_{\boldsymbol {n},\boldsymbol {G}}\)

We are now ready for the main contribution of the paper: we show that the matrix-sequence \(\{\mathcal {A}^{p,\alpha ,\beta }_{\boldsymbol {n},\boldsymbol {G}}\}_n\) admits a spectral distribution according to Definition 1. This extends the symbol computation in [15] to the case of non-trivial geometry.

Theorem 2

Let G be a regular geometry map, i.e., G ∈ C 1([0, 1]2) and \(\det (J_{\boldsymbol {G}})\ne 0\) in [0, 1]2 . Then, the matrix-sequence \(\{\mathcal {A}^{p,\alpha ,\beta }_{\boldsymbol {n},\boldsymbol {G}}\}_n\) with n = (n, n) is distributed, in the sense of the eigenvalues, like the 2 × 2 matrix-valued function

$$\displaystyle \begin{aligned} f^{p,\alpha,\beta}_{\boldsymbol{G}}(\hat{\boldsymbol{x}},\boldsymbol{\theta}):=\alpha f^{p,{\mathrm{curl}}}_{\boldsymbol{G}}(\hat{\boldsymbol{x}},\boldsymbol{\theta})+\beta f^{p,{\mathrm{div}}}_{\boldsymbol{G}}(\hat{\boldsymbol{x}},\boldsymbol{\theta}), \end{aligned} $$
(11)

where \(\hat {\boldsymbol {x}}\in [0,1]^2\) , θ ∈ [−π, π]2 , and

$$\displaystyle \begin{aligned} f^{p,{\mathrm{curl}}}_{\boldsymbol{G}}(\hat{\boldsymbol{x}},\boldsymbol{\theta}) &:= \frac{1}{|\det(J_{\boldsymbol{G}}(\hat{\boldsymbol{x}}))|}\,J_{\boldsymbol{G}}(\hat{\boldsymbol{x}}) \,P\, H_p(\boldsymbol{\theta})\,P^T\, (J_{\boldsymbol{G}}(\hat{\boldsymbol{x}}))^T, \quad P:=\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}, \\[0.1cm] f^{p,{\mathrm{div}}}_{\boldsymbol{G}}(\hat{\boldsymbol{x}},\boldsymbol{\theta}) &:= {|\det(J_{\boldsymbol{G}}(\hat{\boldsymbol{x}}))|}\,(J_{\boldsymbol{G}}(\hat{\boldsymbol{x}}))^{-T}\, H_p(\boldsymbol{\theta})\, (J_{\boldsymbol{G}}(\hat{\boldsymbol{x}}))^{-1}. \end{aligned} $$

Proof

From (10) it follows that the block \(\mathcal {A}^{p,{\mathrm {curl}}}_{\boldsymbol {n},11}\) corresponds to the isogeometric discretization of \(-\frac {\partial ^2{u_1}}{\partial {x}_2^2}\). By means of a direct computation we can verify that Theorem 1, with

$$\displaystyle \begin{aligned} K=\begin{bmatrix} 0 & 0 \\ 0 & 1 \end{bmatrix}, \end{aligned}$$

ensures that the matrix-sequence \(\{\mathcal {A}^{p,{\mathrm {curl}}}_{\boldsymbol {n},11}\}_n\) is distributed in the sense of the eigenvalues like the entry (1, 1) of the matrix \(f^{p,{\mathrm {curl}}}_{\boldsymbol {G}}\). The same argument (using a suitable matrix K) can also be applied to the remaining blocks. Then, it can be checked that all the considered blocks satisfy the hypotheses of [10, Theorem 5], which implies that \(\mathcal {A}^{p,\alpha ,\beta }_{\boldsymbol {n},\boldsymbol {G}}\) is similar, via a proper permutation matrix, to a matrix \(\mathcal {T}^{p,\alpha ,\beta }_{\boldsymbol {n},\boldsymbol {G}}\) such that the matrix-sequence \(\{\mathcal {T}^{p,\alpha ,\beta }_{\boldsymbol {n},\boldsymbol {G}}\}_n\) has its symbol given by (11). □

In the context of IgA, the geometry map G is expressed in terms of the same B-spline basis as used for the discretization space. However, as can be seen from the proof, the spectral result in the above theorem holds for any (smooth enough) geometry map.

Finally, we remark that the p-dependence of the symbol in (11) is completely captured by the matrix H p(θ). As described in Sect. 3.1 this matrix also appears in the symbol expression of a generalized Poisson problem; its properties have been discussed in [5, 8].

4 Numerical Example

In this section we numerically illustrate the spectral results obtained in Sect. 3.3, using the same test problem as in [15, Section 5]. More precisely, we consider (3) defined on a quarter of an annulus,

$$\displaystyle \begin{aligned} \Omega=\{(x_1,x_2)\in{\mathbb R}^2:\ r^2<x_1^2+x_2^2<R^2,\ x_1>0,\ x_2>0\},\quad r=1,\quad R=4, \end{aligned}$$

with

$$\displaystyle \begin{aligned} \boldsymbol{G}(\hat x_1,\hat x_2)= \begin{cases} x_1=[r+\hat x_1(R-r)]\cos\left(\frac\pi2\hat x_2\right) \\[0.1cm] x_2=[r+\hat x_1(R-r)]\sin\left(\frac\pi2\hat x_2\right) \end{cases} \hspace{-0.4cm}, \quad (\hat x_1,\hat x_2)\in [0,1]^2. \end{aligned}$$

Let us fix \(\boldsymbol {n}:=(n,n)\in {\mathbb N}^2\), \(\boldsymbol {p}:=(p,p)\in {\mathbb N}^2\) and \(\boldsymbol {m}\in {\mathbb N}^2\) such that m 2 = n + p −2. We start by defining two equispaced grids on [0, 1]2 and [0, π]2:

$$\displaystyle \begin{aligned} \boldsymbol{x}_{\boldsymbol{j}}:=\frac{\boldsymbol{j}}{\boldsymbol{m}-{\boldsymbol 1}}, \quad \boldsymbol{\theta}_{\boldsymbol{k}}:=\frac{\boldsymbol{k}\pi}{\boldsymbol{m}-{\boldsymbol 1}}, \quad \boldsymbol{j},\boldsymbol{k}={\boldsymbol 0}, \dots, \boldsymbol{m}-{\boldsymbol 1}. \end{aligned} $$

Then, we denote by Λi the set of all evaluations of \(\lambda _i(f_{\boldsymbol {G}}^{p,\alpha ,\beta })\) on Γ:= {(x j, θ k), j, k = 0, …, m −1} for a fixed i ∈{1, 2}. Note that it suffices to consider only [0, π]2 because the symbol (11) is symmetric on [−π, π]2, and hence also its eigenvalue functions.

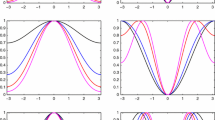
In Fig. 1 we numerically check relation (11) by comparing the eigenvalues of \(\mathcal {A}^{p,\alpha ,\beta }_{\boldsymbol {n},\boldsymbol {G}}\) with the values collected in Λ = { Λ1, Λ2}, ordered in ascending way, for α = 1 and β = 0.1. We observe that, in a complete agreement with the theory, the considered sampling of \(\lambda _i(f^{p,\alpha ,\beta }_{\boldsymbol {G}})\), i = 1, 2, describes quite accurately the behavior of the eigenvalues of \(\mathcal {A}^{p,\alpha ,\beta }_{\boldsymbol {n},\boldsymbol {G}}\), also for relatively small matrix-sizes, up to few outliers.

Fig. 1
figure 1

Comparison of the eigenvalues of \(\mathcal {A}^{p,\alpha ,\beta }_{ \boldsymbol {n}, \boldsymbol {G}}\) (open circle) with Λ = { Λ1, Λ2} collecting uniform samples of \(\lambda _i(f^{p,\alpha ,\beta }_{ \boldsymbol {G}})\), i = 1, 2 (asterisk), ordered in ascending way, varying both n and p, and fixing α = 1 and β = 0.1. (a) p = 3, n = 15. (b) p = 3, n = 35. (c) p = 4, n = 14. (d) p = 4, n = 34. (e) p = 5, n = 13. (f) p = 5, n = 33

Full size image

5 Conclusions

We have analyzed the spectral properties of matrix-sequences arising from isogeometric Galerkin methods for weighted curl-div operators on general planar domains, considering a non-trivial geometry map. More precisely, we have shown that an (asymptotic) spectral distribution exists and it is compactly described by a 2 × 2 spectral symbol. In other words, the eigenvalues of the matrices we are dealing with can be approximated accurately by a uniform sampling of the two eigenvalue functions of the 2 × 2 symbol matrix. The symbol depends on the characteristic parameters of the problem and on the geometry of the physical domain. Its formal structure nicely mimics the structure of the differential problem. The numerical results show a very good matching between the true eigenvalues and the estimates provided by the symbol, already for relatively small matrix-sizes.

The convergence of iterative solvers for linear systems strongly depends on the spectral behavior of the corresponding coefficient matrices. Since the symbol gives a precise description of the spectrum of the curl-div matrix \(\mathcal {A}^{p,\alpha ,\beta }_{\boldsymbol {n},\boldsymbol {G}}\), it could be helpful in the design of good preconditioners that lead to better performance than current solution strategies, like the one in [15, Section 5].