Symmetry Violations and Quark Flavour Physics

Abstract

One of the surprising facts in our present understanding of the development of the Universe is the complete absence of “primordial” antimatter from the Big Bang about 13.7 billion years ago. The detection of charged cosmic-ray particles by magnetic spectrometers borne by balloons, satellites, and the space shuttle has shown no evidence for such primordial (high-energy) antibaryons; nor has the search for gamma rays from antimatter–matter annihilation yielded any such observation. In the early phases of the expanding Universe , a hot (10³² K) and dense plasma of quarks, antiquarks, leptons, antileptons and photons coexisted in equilibrium. This plasma expanded and cooled down, and matter and antimatter could recombine and annihilate into photons. If all interactions were symmetric with respect to matter and antimatter, and if baryon and lepton numbers were conserved, then all particles would finally convert to photons, and the expansion of the Universe would shift the wavelength of these photons to the far infrared region.

9.1 Introduction

9.1.1 Matter–Antimatter Asymmetry in the Universe

One of the surprising facts in our present understanding of the development of the Universe is the complete absence of “primordial” antimatter from the Big Bang about 13.7 billion years ago. The detection of charged cosmic-ray particles by magnetic spectrometers borne by balloons, satellites, and the space shuttle has shown no evidence for such primordial (high-energy) antibaryons; nor has the search for gamma rays from antimatter–matter annihilation yielded any such observation. In the early phases of the expanding Universe , a hot (10³² K) and dense plasma of quarks, antiquarks, leptons, antileptons and photons coexisted in equilibrium. This plasma expanded and cooled down, and matter and antimatter could recombine and annihilate into photons. If all interactions were symmetric with respect to matter and antimatter, and if baryon and lepton numbers were conserved, then all particles would finally convert to photons, and the expansion of the Universe would shift the wavelength of these photons to the far infrared region.

This cosmic microwave background radiation was indeed observed by Penzias and Wilson in 1965 [1], and its wavelength distribution corresponds exactly to Planck black-body radiation at a temperature of 2.73 K (see Fig. 9.1). The density of this radiation is about 5 × 10² photons/cm³.

Fig. 9.1

Frequency distribution of the cosmic microwave background variation, as measured by the COBE satellite and earth-based experiments

However, this radiation is not the only remnant of the Big Bang; there is also a small amount of baryonic matter left over, at a density of 6 × 10⁻⁸ nucleons/cm³, about 10⁻¹⁰ of the photon density. This phenomenon can only be explained if the three conditions of Sakharov [2] are fulfilled:

• there must be an interaction violating $\mathcal {C}\mathcal {P}$ invariance, where ${\mathcal {C} }$ is the particle–antiparticle transformation and $\mathcal {P}$ the space inversion operation;

• there must be an interaction violating the conservation of baryon number ;

• there must be phases of the expansion without thermodynamic equilibrium.

The first condition was shown to be fulfilled when, in 1964, J. Christenson, J. Cronin, V. Fitch and R. Turlay discovered $\mathcal {C}\mathcal {P}$ violation [3] in decays of neutral K mesons. The second criterion would imply that protons are not stable; searches for such a decay have been unsuccessful, showing that the lifetime of the proton is longer then 10³¹ years. The third condition can be met in cosmological models by inflationary fast expansion or by a first-order phase transition in the electroweak interaction of the Standard Model.

In the following, we shall concentrate on the observed $\mathcal {C}\mathcal {P}$ violation, which could in principle lead to a small surplus of matter, the observed baryon asymmetry of 10⁻¹⁰ in the Universe.

9.2 Discrete Symmetries

Symmetries and conservation laws have long played an important role in physics. The simplest examples of macroscopic relevance are the laws of conservation of energy and momentum, which are due to the invariance of forces under translation in time and space, respectively. Both are continuous transformations. In the domain of quantum phenomena, there are also conservation laws corresponding to discrete transformations. One of these is reflection in space (the “parity operation”) $\mathcal {P}$ [4]. The second discrete transformation is particle–antiparticle conjugation ${\mathcal {C} }$ [5]. This transforms each particle into its antiparticle, whereby all additive quantum numbers change their sign. A third transformation of this kind is time reversal ${\mathcal {T}}$, which reverses momenta and angular momenta [6]. This corresponds formally to an inversion of the direction of time. According to the ${\mathcal {C}\mathcal {P}\mathcal {T} }$ theorem of Lüders and Pauli [7,8,9], there is a connection between these three transformations such that, under rather weak assumptions, in a local field theory all processes are invariant under the combined operation $\mathcal {C} \cdot \mathcal {P} \cdot \mathcal {T}$.

9.2.1 Discrete Symmetries in Classical Physics

9.2.1.1 Parity ${\mathcal {P}}$

The parity operation consists in reversing the direction of the position vector $\vec {r} = (X, Y, Z)$ in Cartesian coordinates. This corresponds to reflection in a plane mirror, followed by a rotation by 180^∘. Symmetry under parity operation is therefore also called mirror symmetry.

The parity operation reverses the direction of all polar vectors derived from the position vector; in particular, this is the case for the momentum $\vec {p}$ = $m\vec {v}$ = $m \mathrm {d}\vec {r}/\mathrm {d} t$ and the acceleration $\vec {a}$ = $\mathrm {d}^{2} \vec {r}/\mathrm {d} t^{2}$. Therefore, the Newtonian force $\vec {F}$ = $\mathrm {d}\vec {p}/\mathrm {d} t$ is also reversed under the parity operation.

This must be also the case for the Lorentz and Coulomb forces on a particle with charge q moving with velocity $\vec {v}$:

$$\displaystyle \begin{aligned} \vec{F}\, =\, q ( \vec{E} + \vec{v} \times \vec{B})\;. \end{aligned} $$

(9.1)

Since the charge q is invariant under $\mathcal {P}$, and the force $\vec {F}$ and the velocity $\vec {v}$ change sign, the electric field strength $\vec {E}$ must change sign and the magnetic field strength $\vec {B}$ must remain unchanged.

For the electric potential $\vec {A}$, we obtain from the relations

$$\displaystyle \begin{aligned} \vec{E}\, =\, - \mathrm{grad}\, V - \partial \vec{A}/\partial t, \end{aligned} $$

(9.2)

$$\displaystyle \begin{aligned} \vec{B}\, =\, \mathrm{rot}\, \vec{A}, \end{aligned} $$

(9.3)

the result that $\vec {A}$ changes sign and V  remains invariant, since the spatial differential operator changes sign under the parity operation.

We therefore have four classes of quantities with different transformation behavior under ${\mathcal {P}}$: axial vectors or pseudovectors such as $\vec {B}$ and the angular momentum $\vec {J} = \vec {r} \times \vec {p}$, and scalars such as V , which remain invariant under ${\mathcal {P}}$; and polar vectors such as $\vec {r},\, \vec {p}, \,\vec {F}, \,\vec {E} \,\mathrm {and} \,\vec {A}$, and pseudoscalars such as $\vec {E} \cdot \vec {B}$, which change sign under ${\mathcal {P}}$.

9.2.1.2 Time Reversal ${\mathcal {T}}$

This operation consists in reversing the sign of the time axis t. Under this operation t →−t, the velocity $\vec {v}$, the momentum $\vec {p}$ and the angular momentum $\vec {J}$ change sign, while the force $\vec {F}$ remains unchanged under ${\mathcal {T}}$. From the fact that the Coulomb and Lorentz forces are invariant, we derive the result that $\vec {E} \rightarrow \vec {E}$ and $\vec {B} \rightarrow \vec {B}$ under ${\mathcal {T}}$; for the potentials, V → V  but $\vec {A} \rightarrow - \vec {A}$.

9.2.1.3 Dipole Moments

Elementary particles with spin may have electric or magnetic dipole moments. The spin $\vec {s}$ has the dimensions of an angular momentum, and therefore remains unchanged under parity and changes sign under time reversal.

The potential energy of an electric or magnetic dipole in an external field is proportional to the scalar product of the electric or magnetic moment with the strength of the external electromagnetic field. Since the moments must be parallel to the spin, the potential energy is given by

$$\displaystyle \begin{aligned} - d_{\mathrm{e}} \vec{s} \cdot \vec{E} \quad \mbox{for the electric case} \end{aligned} $$

(9.4)

and

$$\displaystyle \begin{aligned} - d_{\mathrm{m}} \vec{s} \cdot \vec{B} \quad \mbox{for the magnetic case} \end{aligned} $$

(9.5)

Here d _e and d _m are the electric and magnetic dipole moments, respectively. If we consider the transformation properties of $\vec {s}$, $\vec {E}$ and $\vec {B}$ under $\mathcal {P}$ and ${\mathcal {T}}$, it turns out that for both operations d _m → d _m and d _e →−d _e. This means that observation of a nonvanishing electric dipole moment would violate any invariance under parity and time-reversal transformations.

In classical physics, all processes are invariant under parity and under time reversal. In the case of mirror symmetry, this means that a physical experiment will lead to the same result as a mirror-imaged experiment, since the equations of classical physics are left-right symmetric. In a similar way, the classical motion of one particle can be reversed, e.g. by playing a film backwards, and this inversion of the motion corresponds formally to time reversal. Again, the laws of motion are invariant under ${\mathcal {T}}$, and the reversed motion follows the same path backwards as forwards.

Of course, this is no longer the case if many particles move and interact with each other; in this case the second law of thermodynamics ensures that entropy is increasing, thus defining an arrow of time.

9.2.2 Discrete Symmetries in Quantum Systems

9.2.2.1 Particle–Antiparticle Conjugation

In relativistic quantum mechanics, the Dirac equation requires that for each solution describing a particle, there is a second solution with opposite charge, describing the antiparticle. The antiparticle of the electron, the positron, was found in 1933 [10], and the antiproton was found in 1955 [11]. The particle–antiparticle conjugation ${\mathcal {C} }$ transforms the field ϕ of the particle into a related field ϕ ^† which has opposite quantum numbers: the charge, lepton number, baryon number, strangeness, beauty, etc., for the antiparticle are opposite in sign to the values for the particle.

Invariance under the ${\mathcal {C} }$ transformation is always valid in the strong and electromagnetic interactions. This means, in particular, that the visible spectral lines from atoms and their antiatom partners are identical, and we cannot use these lines to identify antimatter in the Universe.

This would be especially important in the science-fiction scenario in which a man-made spacecraft sets out to meet a distant civilization, where it would be advisable to know whether the other planet was made of matter or antimatter. In this case another means of differentiation would have to be found.

9.2.2.2 Violation of Mirror Symmetry: Parity Violation in Weak Interactions

Lee and Yang [13] suggested that of the four interactions—strong, electromagnetic, weak and gravitational—the weak interaction might violate mirror symmetry when it was described by a combination of vector and axial-vector currents in the Lagrangian (V–A theory). The interference of these two currents could lead to pseudoscalar observables which would change sign under the parity operation. One such observable is the scalar product of an axial vector (such as the spin of a particle) with a polar vector (such as the momentum of another particle in the final state). If the expectation value of this pseudoscalar is measured to be nonvanishing, then parity is violated.

An experiment on the beta decay of cobalt-60 [14] measured exactly such an observable, the scalar product of the spin 5ħ of the⁶⁰Co nucleus and the direction of the electron from its beta decay into an excited state of ⁶⁰Ni with nuclear spin 4ħ. The ⁶⁰Co nuclei were polarized by embedding them in a cerium–magnesium crystal, where the magnetic moments were aligned by a weak external magnetic field of about 0.05 T. In the strong magnetic field inside this paramagnet, the ⁶⁰Co nuclei are polarized through hyperfine interactions if the temperature is low enough (0.01 K) to avoid thermal demagnetization. The polarization was measured through the asymmetry of γ rays from the cascade decay of the ⁶⁰Ni state. The measurement then required the detection of the electron direction relative to the polarization of the Co nuclei. The experimenters found that the electron was emitted preferentially in a direction opposite to the external magnetic field, and that this effect disappeared when the crystal was warmed and the nuclear polarization disappeared. Thus, at low temperature, a nonzero pseudoscalar is observed, demonstrating parity violation.

By comparing nuclear beta decays having an electron and an antineutrino in the final state with their counterpart with emission of a positron-neutrino pair, it was shown that the helicity ${h =\vec {s}\cdot \vec {p}/|\vec {s}\cdot \vec {p}|}$ of neutrinos is opposite to the one of antineutrinos [18].

Other experiments lead to similar results. The helicity ${h =\vec {s}\cdot \vec {p}/|\vec {s}\cdot \vec {p} |}$ of the neutrino emitted in the weak electron capture by ¹⁵²Eu was measured in an experiment by Goldhaber and Grodzins [19] to be negative; the neutrino is “left-handed”, i.e. the spin is aligned antiparallel to the momentum. Similarly, measurements of the polarization of electrons from β ⁻ decay showed a negative value, with a modulus increasing with the velocity of the electron, v∕c. Positrons from β ⁺ decay were found to have a positive polarization that increases with v∕c.

9.2.2.3 Violation of ${\mathcal {C} }$ Symmetry, and $\mathcal {C}\mathcal {P}$ Invariance

In the realm of weak decays of particles, supporting evidence for the violation of mirror symmetry came from the observation that parity is violated in the decay π ⁺ → μ ⁺ν _μ, and that the muon neutrino from this decay is left-handed [15, 16]. The ${\mathcal {P}}$-conjugate process, i.e. π ⁺ → ν _μμ ⁺, with a right-handed neutrino, does not occur. The same is true for the ${\mathcal {C}}$-conjugate process, ${\pi ^-\rightarrow \mu ^-\overline {\nu _\mu }}$, with a left-handed antineutrino. However, if we combine the ${\mathcal {C} }$ and $\mathcal {P}$ operations, we arrive at a process ${\pi ^- \rightarrow \mu ^-\overline {\nu _\mu }}$ with a right-handed antineutrino, which proceeds at the same rate as the original π ⁺ decay, with a left-handed muon neutrino. Evidently, in weak interactions, ${\mathcal {P} }$ and ${\mathcal {C} }$ are violated, while it seemed at the time of those experiments that the process was invariant under the combined operation ${\mathcal {C} }$ ⋅ ${\mathcal {P}}$. This argument can be visualized as in Fig. 9.2. Here the ${\mathcal {P} }$ mirror and the ${\mathcal {C} }$ mirror act on a left-handed neutrino , both leading to unphysical states, a right-handed neutrino and a left-handed antineutrino . Only the combined $\mathcal {C}\mathcal {P}$ mirror leads to a physical particle, the right-handed antineutrino. This argument was made by Landau [17], suggesting that the real symmetry was $\mathcal {C}\mathcal {P}$ invariance.

Fig. 9.2

The mirror image of a left-handed neutrino under ${\mathcal {P}}$, ${\mathcal {C} }$ and $\mathcal {C}\mathcal {P}$ mirror operations

9.2.2.4 $\mathcal {C}\mathcal {P}$ Invariance and Neutral K Mesons

One consequence of this postulated $\mathcal {C}\mathcal {P}$ invariance was predicted by Gell-Mann and Pais [12] for the neutral K mesons: there should be a long-lived partner to the known $\mathrm {V}^0\left ( \mathrm {K}^0_1\right )$ particle of short lifetime (10⁻¹⁰s). According to this proposal, these two particles are mixtures of the two strangeness eigenstates ${\mathrm {K^0}(\mathbb {S} = +1)}$ and ${\overline {\mathrm {K^0}}(\mathbb {S} = -1)}$ produced in strong interactions. Weak interactions do not conserve strangeness , and the physical particles should be eigenstates of $\mathcal {C}\mathcal {P}$ if the weak interactions are ${\mathcal {C}\mathcal {P}}$-invariant. These eigenstates are described as follows (where we choose the phases such that $\overline {\mathrm {K^0}}=\mathcal {C}\mathcal {P} {\mathrm {K^0}}$):

$$\displaystyle \begin{aligned} \mathcal{C}\mathcal{P} \mathrm{K_1}\, =\, \mathcal{C}\mathcal{P} \left[\frac{1}{\sqrt{2}} \left({\mathrm{K^0}} + \overline{\mathrm{K^0}}\right)\right]\, =\, \frac{1}{\sqrt{2}} \left(\overline{\mathrm{K^0}} + {\mathrm{K^0}}\right)\, =\, \mathrm{K_1} \;, \end{aligned} $$

(9.6)

$$\displaystyle \begin{aligned} \mathcal{C}\mathcal{P} \mathrm{K_2}\, =\, \mathcal{C}\mathcal{P} \left[\frac{1}{\sqrt{2}} \left({\mathrm{K^0}} - \overline{\mathrm{K^0}}\right)\right]\, =\, \frac{1}{\sqrt{2}} \left(\overline{\mathrm{K^0}} - {\mathrm{K^0}}\right)\, =\, - \mathrm{K_2} \;. \end{aligned} $$

(9.7)

Because $\mathcal {C}\mathcal {P}$ |π ⁺π ⁻〉 = |π ⁺π ⁻〉 for π mesons in a state with angular momentum zero, i.e. the two-pion state has a positive $\mathcal {C}\mathcal {P}$ eigenvalue, a decay into π ⁺π ⁻ is allowed for the K₁ but forbidden for the K₂; hence the longer lifetime of K₂, which was indeed confirmed when the K₂ was discovered [20, 21].

9.2.2.5 Discovery of $\mathcal {C}\mathcal {P}$ Violation

In 1964, however, Christenson et al. [22] discovered that the long-lived neutral K meson also decays to two charged pions with a branching ratio of 2 × 10⁻³.

The motivation of this experiment was twofold: the experimenters wanted to check on an effect found by Adair et al. [23] when the latter observed interactions of long-lived kaons (K₂) in hydrogen, and they wanted to test $\mathcal {C}\mathcal {P}$ invariance by searching for the decay of K₂ into two pions. Adair et al. had found anomalous regeneration of short-lived kaons (K₁) above expectation. “Regeneration ” is an effect due to the different strong interactions of the two components of a long-lived kaon, K⁰ and ${\overline {\mathrm {K^0}}}$. This leads to a creation of a coherent K₁ component when a K₂ beam traverses matter. The anomalous effect above expectation was still observed in the experiment of Christenson et al. when the (K₂) beam hit a hydrogen target.

Therefore, Christenson et al. emptied the target and looked for K₂ → π ⁺π ⁻ decays from the vacuum. To their surprise, they found such decays, which meant that $\mathcal {C}\mathcal {P}$ invariance was broken in this decay.

The magnetic spectrometer used by Christenson et al. is shown in Fig. 9.3. On each side of the spectrometer, one charged particle is detected through spark chambers in front of and behind the magnet. The two vector momenta ${\vec {p}_i\; (i = 1,2)}$ of the two particles are measured. Assuming the mass of the particles to be the pion rest mass m _π their energies can be obtained from

$$\displaystyle \begin{aligned} E^2_i\, =\, \vec{p}^2_i + m^2_\pi\; . \end{aligned} $$

(9.8)

The invariant mass of the pair is

$$\displaystyle \begin{aligned} m_{\pi\pi}\, =\, \sqrt{\left[(E_1 + E_2)^2 - (\vec{p}_1 + \vec{p}_{2})^2\right]} \; , \end{aligned} $$

(9.9)

and the kaon momentum is

$$\displaystyle \begin{aligned} \vec{p}_{\mathrm{K}}\, =\, \vec{p}_1 + \vec{p}_2\; . \end{aligned} $$

(9.10)

From the reconstructed kaon momentum, the intersection of the kaon flight path with the target plane gives an indication of whether this was a two-body decay coming from the target or a three-body decay with an escaping neutrino.

Fig. 9.3

The experimental setup used by Christenson et al. [22] for the discovery of $\mathcal {C}\mathcal {P}$ violation

In the latter case, the direction of ${\vec {p}_{\mathrm {K}}}$ does not point back to the target source. The result of the experiment is shown in Fig. 9.4. A significant peak of K → π ⁺π ⁻ decays coming from the target direction ($\cos \theta = 1$) is seen, while the background of three-body decays outside the peak can be extrapolated under the signal, and represents only ∼20% of the data in the signal region: there is a signal at the level of 2 × 10⁻³ of all decays, and ${\mathcal {C}\mathcal {P} }$ is violated.

Fig. 9.4

(a) Experimental distribution of m ^∗ compared with Monte Carlo calculation. The calculated distribution is normalized to the total number of observed events. (b) Angular distribution of those events in the range 490 < m ^∗ < 510 MeV. The calculated curve is normalized to the number of events in the total sample

From then on the long-lived K meson state was called K_L because it was no longer identical to the ${\mathcal {C}\mathcal {P} }$ eigenstate K₂. However, the physical long-lived state K_L was a superposition of a predominant K₂ amplitude and a small admixture of a K₁ amplitude, $\mathrm {K_L} = (\mathrm {K_2} + \varepsilon \mathrm {K_1}) / \sqrt {1+ |\varepsilon |{ }^2}$ where the admixture parameter ε is determined by experiment to satisfy |ε|∼ 2 × 10⁻³ . Similarly, the short-lived state was called K_S, and $\mathrm {K_S} = (\mathrm {K_1} + \varepsilon \mathrm {K_2}) / \sqrt {1 + |\varepsilon |{ }^2}$. The ${\mathcal {C}\mathcal {P} }$ violation that manifested itself by the decay K_L → π ⁺π ⁻ was confirmed subsequently in the decay K_L → π ⁰π ⁰ [24, 25], and by a charge asymmetry in the decays K_L → π ^±e ^∓ν and K_L → π ^±μ ^∓ν [26, 27].

9.2.3 Discrete Symmetries in Quantum Mechanics

The three discrete symmetries ${\mathcal {P}}$, ${\mathcal {C} }$ and ${\mathcal {T} }$ are described by the operators ${\mathcal {P} }$ for the parity transformation, ${\mathcal {C} }$ for particle–antiparticle conjugation and ${\mathcal {T} }$ for time reversal. Invariance of an interaction described by a Hamiltonian ${\mathcal {H} }$ under a symmetry operation means that ${\mathcal {H} }$ commutes with the relevant operator, e.g. [${\mathcal {H} }$, ${\mathcal {P} }$] = 0. According to experimental evidence, the strong and electromagnetic interactions are ${\mathcal {P}}$- and ${\mathcal {C}}$-invariant. The corresponding operators are unitary, i.e. the Hermitian conjugate is equal to the inverse:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathcal{C}^{\dag}\, =\, \mathcal{C}^{-1}\; , \end{array} \end{aligned} $$

(9.11)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathcal{P}^{\dag}\, =\, \mathcal{P}^{-1}\; . \end{array} \end{aligned} $$

(9.12)

For two states |ψ〉 and |φ〉, such a unitary transformation does not change the product:

$$\displaystyle \begin{aligned} \langle\psi\mid\varphi\rangle\, =\, \langle\psi'\mid\varphi'\rangle \; ,\end{aligned} $$

(9.13)

where |ψ′〉 and |φ′〉 are the transformed states.

By defining the intrinsic parity of the proton as +1, a phase convention for the fields can be chosen, such that the parity operator ${\mathcal {P} }$ has only eigenvalues of +1 or − 1, and all particles have intrinsic parities ±1 as quantum numbers. These conserved quantities, which correspond to discrete symmetries, are multiplicative quantum numbers.

The third discrete symmetry, time reversal , is a special case. The corresponding operator ${\mathcal {T} }$ is not unitary, but antiunitary . Here the bracket 〈ψ|φ〉 is not conserved by the ${\mathcal {T} }$ transformation, but rather

$$\displaystyle \begin{aligned} \langle\psi'|\varphi'\rangle\, =\, \langle\psi|\varphi\rangle^{\ast}\; . \end{aligned} $$

(9.14)

Probability is still conserved, i.e.

$$\displaystyle \begin{aligned} |\langle\psi'|\varphi'\rangle|\, =\, |\langle\psi|\varphi\rangle| \; , \end{aligned} $$

(9.15)

but the phases are not. The fact that ${\mathcal {T} }$ is antiunitary can be deduced from the Schrödinger equation for a free particle, where the time derivative is odd under ${\mathcal {T}\;}$ while the Laplace operator Δ is even. This can be reconciled with ${\mathcal {T} }$ invariance only if ${\mathcal {T}\;}$ makes the changes i →−i and ψ → ψ ^∗.

${\mathcal {C}\mathcal {P}\mathcal {T}}$ , the product of all three discrete transformations, being a product of two unitary and one antiunitary operator, is also antiunitary. According to the ${\mathcal {C}\mathcal {P}\mathcal {T} }$ theorem of Lüders [7] and Pauli [8], and Jost [9], a field theory with Lorentz invariance, locality, and the commutation relations given by the spin-statistics theorem, is ${\mathcal {C}\mathcal {P}\mathcal {T}}$-invariant. At present there is no realistic field theory which violates ${\mathcal {C}\mathcal {P}\mathcal {T} }$ invariance.

As a consequence of this theorem, violation of one of the three discrete symmetries implies a violation of a complementary one. If ${\mathcal {C}\mathcal {P} }$ is violated, then ${\mathcal {T} }$ is also violated.

The experimental consequences of ${\mathcal {C}\mathcal {P}\mathcal {T} }$ invariance are the equality of the masses, lifetimes and magnetic dipole moments of a particle and its antiparticle. These equalities have been tested with great precision, as shown in Table 9.1.

Table 9.1 Comparison of masses m, lifetimes τ, and magnetic g-factors of particle and antiparticles

A very special case in this context is that of the masses of the neutral K mesons. The mass difference between the long-lived K_L and the short-lived K_S can be measured in interference experiments. This difference is due to second-order weak interactions and, therefore, is very small, about Δm = (3.480 ± 0.007) × 10⁻⁶ eV, which means that Δm∕m _K < 10⁻¹⁴. From this, one can deduce very stringent limits on the mass difference between the K⁰ and ${\overline {\mathrm {K^0}}}$, of order 10⁻¹⁸.

Thus, from experimental evidence, there is no doubt about the validity of ${\mathcal {C}\mathcal {P}\mathcal {T} }$ invariance .

9.3 Mixing and Decay of Neutral Flavoured Mesons

9.3.1 Particle–Antiparticle Mixing

Neutral mesons (represented by N⁰ in this chapter) with a characteristic quantum number, such as the strangeness ${\mathbb {S}\;}$ for K⁰ mesons, charm ${\mathbb {C}\;}$ for D⁰ mesons and beauty ${\mathbb {B}\;}$ for $\mathrm {B_s^0}$ and $\mathrm {B_d^0}$ mesons, have the particular property that they can mix with their antiparticles, which carry an opposite-sign quantum number. Weak interactions do not conserve any of these quantum numbers ($\mathbb {S}$, $\mathbb {C}$, $\mathbb {B}$); consequently N⁰ and ${\overline {\mathrm {N^0}}}$ can mix by second-order weak transitions through intermediate states such as 2π, 3π, πμν, πeν (for K⁰), or πK (for B⁰). The states that obey an exponential decay law are linear superpositions of N⁰ and ${\overline {\mathrm {N^0}}}$,

$$\displaystyle \begin{aligned} \alpha \, |\mathrm{N^0}\rangle + \beta \, |\overline{\mathrm{N^0}}\rangle = { \alpha \choose \beta}\; . \end{aligned} $$

(9.16)

The time-dependent Schrödinger equation then becomes a matrix equation

$$\displaystyle \begin{aligned} \mathrm{i} \frac{\mathrm{d}}{\mathrm{d} t}{ \alpha \choose \beta } = X { \alpha \choose \beta}\; , \end{aligned} $$

(9.17)

where X _ik = M _ik −iΓ _ik∕2, and M _ik and Γ _ik are Hermitian matrices , called mass matrix and decay matrix , respectively. Both of the latter two matrices are Hermitian : M = M ^† and Γ = Γ ^†. However, X is not Hermitian. The elements of the matrix X are

$$\displaystyle \begin{aligned} X_{11}\, =\, \langle {\mathrm{N^0}}|\mathcal{H}|\mathrm{N^0}\rangle \;, \quad X_{22}\, =\, \langle\overline{\mathrm{N^0}}|\mathcal{H}|\overline{\mathrm{N^0}}\rangle \;, \end{aligned}$$

$$\displaystyle \begin{aligned} X_{12}\, =\, \langle{\mathrm{N^0}}|\mathcal{H}|\overline{\mathrm{N^0}}\rangle \;, \quad X_{21}\, =\, \langle\overline{\mathrm{N^0}}|\mathcal{H}|\mathrm{N^0}\rangle\, \end{aligned} $$

(9.18)

where ${\mathcal {C}\mathcal {P}\mathcal {T} }$ invariance requires the diagonal elements to be equal: X ₁₁ = X ₂₂. The matrix has the form

$$\displaystyle \begin{aligned} X = \begin{pmatrix} m - \frac{\mathrm{i}}{2} {\varGamma} & m_{{}_{12}} - \frac{\mathrm{i}}{2} {\varGamma}_{{}_{12}} \\ m_{{}_{12}}^{*} - \frac{\mathrm{i}}{2} {\varGamma}_{{}_{12}}^{*}& m - \frac{\mathrm{i}}{2} {\varGamma} \\ \end{pmatrix}\; . \end{aligned} $$

(9.19)

The off-diagonal elements of the matrices are given by

$$\displaystyle \begin{aligned} {\varGamma}_{21} = 2\pi \sum \varrho_{{}_F} \langle{\overline {\mathrm{N^0}}}|\mathcal{H}_{\mathrm{W}}|F \rangle \langle F|\mathcal{H}_{\mathrm{W}}|\mathrm{N^0} \rangle\; , \end{aligned} $$

(9.20)

where the sum runs over all possible physical intermediate states F, which have a phase space density ${\varrho _{{ }_F}}$. Similarly,

$$\displaystyle \begin{aligned} M_{21} = \langle \overline {\mathrm{N^0}}|\mathcal{H}_{\mathrm{W}}|\mathrm{N^0} \rangle + \sum_n \frac{\langle\overline {\mathrm{N^0}}|\mathcal{H}_{\mathrm{W}}| n\rangle \langle n|\mathcal{H}_{\mathrm{W}}|\mathrm{N^0}\rangle}{m_{{}_{\mathrm{N^0}}} - m_n}\; , \end{aligned} $$

(9.21)

where the sum extends over all possible virtual intermediate states n.

The eigenvalue equations for X yield two eigenstates , which can be labeled by their mass: h for the higher mass, l for the lower mass. These eigenstates are the physical particles with a definite mass and an exponential lifetime distribution. The eigenvalues M _h and M _l of the matrix X are

$$\displaystyle \begin{aligned} \begin{array}{rcl} M_h &\displaystyle =&\displaystyle m_h - \frac{\mathrm{i}}{2} {\varGamma}_h \; , \\ M_l &\displaystyle =&\displaystyle m_l - \frac{\mathrm{i}}{2} {\varGamma}_l \end{array} \end{aligned} $$

(9.22)

We denote the differences between the physical quantities by ΔΓ = Γ _h − Γ _l and Δm = m _h − m _l > 0 and denote the average values by

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\varGamma} &\displaystyle =&\displaystyle \frac{{\varGamma}_h + {\varGamma}_l}{2} \; , \end{array} \end{aligned} $$

(9.23)

$$\displaystyle \begin{aligned} \begin{array}{rcl} m &\displaystyle =&\displaystyle \frac{m_h + m_l}{2} \; . \end{array} \end{aligned} $$

(9.24)

For the B⁰—$\overline {\mathrm {B^0}}$ system and the D ⁰—$\overline {\mathrm {{D^0}}}$ system, the two decay widths Γ _h and Γ _l are expected to be nearly equal (because the numbers of final states for the decay are very similar). In these cases it is customary to introduce the dimensionless quantities

$$\displaystyle \begin{aligned} x = \frac{\Delta m}{{\varGamma}} \end{aligned} $$

(9.25)

and

$$\displaystyle \begin{aligned} y = \frac{\Delta{\varGamma}}{2{\varGamma}} \; . \end{aligned} $$

(9.26)

Here x is positive by definition, and y varies between −1 and +1. For heavy systems such as B⁰, |y| is expected to be much less than 1, while for the K⁰ system, y is found experimentally to be close to − 1, since here the decay width of the lighter state is 600 times larger then that of the heavier state. Therefore, for the K⁰ system, the lighter state is called K_S (“short-lived”) and the heavier state K_L (“long-lived”). Table 9.2 gives a summary of various parameters of oscillating meson pairs .

Table 9.2 Parameters of the four neutral oscillating meson pairs [28] (see Sects. 9.5.5.7 and 9.6.4)

9.3.2 Decays of Neutral Mesons

9.3.2.1 Time-Dependent Schrödinger Equation

From the time-dependent Schrödinger equation for mixed states given above, it follows that

$$\displaystyle \begin{aligned} \frac{\mathrm{d}}{\mathrm{d} t} \left(|\alpha|{}^2 + |\beta|{}^2\right) = - \left(\alpha^* \beta^* \right) {\varGamma} {\alpha\choose\beta} \;. \end{aligned} $$

(9.27)

Since both of the neutral mesons N⁰ and ${\overline {\mathrm {N^0}}}$ decay, the left-hand side of this equation is negative for any α or β. Therefore Γ is positive definite, in particular Γ ₁₁, Γ ₂₂ and $\det {\varGamma }$ are positive.

The physical particles, which have a definite mass and lifetime, are mixtures of the eigenstates N⁰ and $\overline {\mathrm {N^0}}$ of the strong interaction, which carry definite values of their characteristic quantum numbers strangeness $\mathbb {S}$, charm $\mathbb {C}$, and beauty $\mathbb {B}$.

If the weak interaction through which these particles decay is invariant under a discrete symmetry, say $\mathcal {C}\mathcal {P}$, then the physical particles are eigenstates of this symmetry because ${\mathcal {H}_{\mathrm {W}}}$ commutes with $\mathcal {C}\mathcal {P}$.

The effect of discrete symmetries on N⁰ and ${\overline {\mathrm {N^0}}}$ is the following: ${\mathcal {C}\mathcal {P} }$ is unitary, and there is an arbitrary phase a:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathcal{C}\mathcal{P} | \mathrm{N^0} \rangle &\displaystyle =&\displaystyle \mathrm{e}^{\mathrm{i} a} |\overline{\mathrm{N^0}} \rangle \; , \\ \mathcal{C}\mathcal{P} | \overline{\mathrm{N^0}}\rangle &\displaystyle =&\displaystyle \mathrm{e}^{-\mathrm{i} a} |\mathrm{N^0} \rangle \; . \end{array} \end{aligned} $$

(9.28)

${\mathcal {C}\mathcal {P}\mathcal {T} }$ , however, is antiunitary, and, with an arbitrary phase b,

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathcal{C}\mathcal{P}\mathcal{T} | \mathrm{N^0} \rangle &\displaystyle =&\displaystyle \mathrm{e}^{\mathrm{i} b} | \overline{\mathrm{N^0}} \rangle \; , \\ \mathcal{C}\mathcal{P}\mathcal{T} | \overline{\mathrm{N^0}} \rangle &\displaystyle =&\displaystyle \mathrm{e}^{\mathrm{i} b} | \mathrm{N^0} \rangle \; . \end{array} \end{aligned} $$

(9.29)

For ${\mathcal {T} }$, which is also antiunitary, we obtain

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathcal{T} | \mathrm{N^0} \rangle &\displaystyle =&\displaystyle \mathrm{e}^{\mathrm{i} (b-a)} |\overline{\mathrm{N^0}} \rangle \\ \mathcal{T} | \overline{\mathrm{N^0}} \rangle &\displaystyle =&\displaystyle \mathrm{e}^{\mathrm{i} (b+a)} |\mathrm{N^0} \rangle \end{array} \end{aligned} $$

(9.30)

We choose the arbitrary phase a to be equal to 0 here, such that the eigenstates of ${\mathcal {C}\mathcal {P} }$ are

$$\displaystyle \begin{aligned} \begin{array}{rcl} | \mathrm{N_+} \rangle &\displaystyle =&\displaystyle \frac{1}{\sqrt{2}} \left( | \mathrm{N^0} \rangle + | \overline{\mathrm{N^0}}\rangle \right) \; , \\ | \mathrm{N_-} \rangle &\displaystyle =&\displaystyle \frac{1}{\sqrt{2}} \left( | \mathrm{N^0} \rangle - | \overline{\mathrm{N^0}}\rangle \right) \; , \end{array} \end{aligned} $$

(9.31)

with the property that they have ${\mathcal {C}\mathcal {P} }$ eigenvalues +1 and − 1:

$$\displaystyle \begin{aligned} \sqrt{2}\, \mathcal{C}\mathcal{P} | \mathrm{N_+} \rangle\, =\, \mathcal{C}\mathcal{P} | \mathrm{N^0} \rangle + \mathcal{C}\mathcal{P} |\overline{\mathrm{N^0}}\rangle\, =\, |\overline{\mathrm{N^0}} \rangle + |\mathrm{N^0}\rangle\, =\, \sqrt{2} \, | \mathrm{N_+} \rangle \end{aligned}$$

$$\displaystyle \begin{aligned} \sqrt{2}\, \mathcal{C}\mathcal{P} | \mathrm{N_-} \rangle\, =\, \mathcal{C}\mathcal{P} | \mathrm{N^0} \rangle - \mathcal{C}\mathcal{P} |\overline{\mathrm{N^0}}\rangle\, =\, |\overline{\mathrm{N^0}} \rangle - |\mathrm{N^0}\rangle\, =\, -\sqrt{2} \, | \mathrm{N_-} \rangle \end{aligned} $$

(9.32)

Historically, in the K⁰ system, |N₊〉 was designated by |K₁〉, and |N₋〉 by |K₂〉.

Discrete symmetries impose certain conditions on the elements of the mass and decay matrix. ${\mathcal {C}\mathcal {P}\mathcal {T} }$ invariance requires the masses and lifetimes of the particle and antiparticle to be equal, i.e. X ₁₁ = X ₂₂, or M ₁₁ = M ₂₂ and Γ ₁₁ = Γ ₂₂, for the diagonal elements. ${\mathcal {C}\mathcal {P} }$ invariance requires that |X ₁₂| = |X ₂₁|. In the following, we assume ${\mathcal {C}\mathcal {P}\mathcal {T} }$ invariance.

The eigenvalue equation for the matrix X yields

$$\displaystyle \begin{aligned} \Delta \mu = \Delta m - \frac{i}{2} \Delta {\varGamma} = 2 \sqrt{X_{12} X_{21}} \; . \end{aligned} $$

(9.33)

The corresponding eigenvectors of X are written

$$\displaystyle \begin{aligned} \begin{array}{rcl} |\mathrm{N}_h \rangle &\displaystyle =&\displaystyle p |\mathrm{N^0}\rangle - q |\overline{\mathrm{N^0}} \rangle\; , \\ |\mathrm{N}_l \rangle &\displaystyle =&\displaystyle p |\mathrm{N^0}\rangle + q |\overline{\mathrm{N^0}} \rangle\; , {} \end{array} \end{aligned} $$

(9.34)

or in the form of the corresponding relations

$$\displaystyle \begin{aligned} \begin{array}{rcl} |\mathrm{N^0}\rangle &\displaystyle =&\displaystyle \frac{1}{2p} \left( |\mathrm{N}_h \rangle + |\mathrm{N}_l \rangle \right) \; , \\ |\overline{\mathrm{N^0}} \rangle &\displaystyle =&\displaystyle \frac{-1}{2q} \left( |\mathrm{N}_h \rangle - |\mathrm{N}_l \rangle \right) \; . \end{array} \end{aligned} $$

(9.35)

Unitarity requires |p|² + |q ²| = 1, and ${\mathcal {C}\mathcal {P} }$ invariance would mean ${p = q = 1/\sqrt {2}}$. In the case of ${\mathcal {C}\mathcal {P} }$ noninvariance, an asymmetry parameter can be defined by

$$\displaystyle \begin{aligned} \varepsilon = \frac{p-q}{p+q} \quad \mbox{ or } \quad \frac{p}{q} = \frac{1 + \varepsilon}{1 - \varepsilon} {} \end{aligned} $$

(9.36)

and we obtain

$$\displaystyle \begin{aligned} \varepsilon = \frac{\frac{1}{2} \,\Im m \,{\varGamma}_{12} + \mathrm{i} \, \Im m \, M_{12}}{\Delta m - \frac{i}{2} \Delta {\varGamma}} \; , {} \end{aligned} $$

(9.37)

where ℑmM ₁₂ ≫ℑmΓ ₁₂ for the K meson system, and therefore

$$\displaystyle \begin{aligned} \arg \, \varepsilon \simeq \arctan \frac{2\, \Delta m}{{\varGamma}_{\mathrm{S}}} {} \end{aligned} $$

(9.38)

In this case the two physical states are not orthogonal, and we obtain

$$\displaystyle \begin{aligned} \langle \mathrm{N}_l |\mathrm{N}_h \rangle = \frac{2\, \Re e\, \varepsilon}{1 + |\varepsilon|{}^2}\;. {} \end{aligned} $$

(9.39)

For the eigenstates of the time-dependent Schrödinger equation, the time evolution obeys an exponential decay law, as can be shown in the Wigner–Weisskopf approximation . Here, the time t is measured in the rest frame given by the common mass defined by the strong and electromagnetic interactions. The time evolution is given by

$$\displaystyle \begin{aligned} \begin{array}{rcl} |\mathrm{N}_h(t) \rangle &\displaystyle =&\displaystyle \mathrm{e}^{-\mathrm{i} m_h t - \frac{1}{2}{\varGamma}_h t} \, |\mathrm{N}_h(0)\rangle \; , \\ |\mathrm{N}_l(t) \rangle &\displaystyle =&\displaystyle \mathrm{e}^{-\mathrm{i} m_l t - \frac{1}{2}{\varGamma}_l t} \, |\mathrm{N}_l(0)\rangle \; . {} \end{array} \end{aligned} $$

(9.40)

In this way, N_h decays as exp(−Γ _ht) and N_l as exp(−Γ _lt), while the phases of the two states evolve with different frequency, and this difference will show up in any interference effect between the two decaying mesons.

On the other hand, if initially a pure flavor state N⁰ or $\overline {\mathrm {N^0}}$ is produced, the decay law is not exponential but shows oscillations. If we define the complex quantities

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\gamma}_h\quad =\quad \mathrm{i} m_h + \frac{{\varGamma}_h}{2}\; ,\\ {\gamma}_l\quad =\quad \mathrm{i} m_l + \frac{{\varGamma}_l}{2}\; , {} \end{array} \end{aligned} $$

(9.41)

for the heavy (h) and light (l) meson states, respectively, then the amplitude for an initially pure state N⁰ at time t = 0 is given by (9.34), and at a finite time t the two components evolve according to (9.40). At this time, the state is

$$\displaystyle \begin{aligned} \psi_{\mathrm{N}} = \frac{1}{2} \left(\mathrm{N^0} \left(\mathrm{e}^{-{\gamma}_h t} + \mathrm{e}^{-{\gamma}_l t} \right) - \frac{q}{p} \overline{\mathrm{N^0}} \left(\mathrm{e}^{-{\gamma}_h t} - \mathrm{e}^{-{\gamma}_l t}\right) \right) \; . {} \end{aligned} $$

(9.42)

The probability of finding an $\overline {\mathrm {N^0}}$ after a time t, starting from an initially pure N⁰ state is

$$\displaystyle \begin{aligned} P (\mathrm{N^0} \rightarrow \overline{\mathrm{N^0}}) = \frac{1}{4} \left|\frac{q}{p}\right|{}^2 \left[\mathrm{e}^{-{\varGamma}_h t} + \mathrm{e}^{-{\varGamma}_l t} - 2 \mathrm{e}^{-{\varGamma} t} \cos \left(\Delta m\, t\right) \right] \; . {} \end{aligned} $$

(9.43)

If we express this in the unified variables T = Γt, x and y, this reads

$$\displaystyle \begin{aligned} P (\mathrm{N^0} \rightarrow \overline{\mathrm{N^0}}) = \frac{1}{2}\left|\frac{q}{p} \right|{}^2 \mathrm{e}^{-T}\left(\cosh y T - \cos x T \right) \; . {} \end{aligned} $$

(9.44)

Similarly, the probability of finding an N⁰ in an initially pure N⁰ state is

$$\displaystyle \begin{aligned} P(\mathrm{N^0} \rightarrow \mathrm{N^0}) = \frac{1}{2} \mathrm{e}^{-T} \left( \cosh y T + \cos x T \right) \; . {} \end{aligned} $$

(9.45)

The difference between these two probabilities is then

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle {}{}{}&\displaystyle {P(\mathrm{N^0} \rightarrow \mathrm{N^0}) - P(\mathrm{N^0} \rightarrow \overline{\mathrm{N^0}})} \\ &\displaystyle &\displaystyle =\, \frac{1}{2} \mathrm{e}^{-T} \left(\cosh y T + \cos x T\right) - \frac{1}{2} \mathrm{e}^{-T} \left(\left|\frac{q}{p}\right|{}^2 \cosh y T - \left|\frac{q}{p}\right|{}^2 \cos x T \right)\\ &\displaystyle &\displaystyle =\, \frac{1}{2} \mathrm{e}^{-T} \left[ \cosh y T \left(1- \left|\frac{q}{p} \right|{}^2\right) + \cos x T \left( 1 + \left| \frac{q}{p} \right|{}^2 \right) \right] \,. \end{array} \end{aligned} $$

(9.46)

However, the two states N _h and N _l are not orthogonal, but their overlap δ is

$$\displaystyle \begin{aligned} \delta = \langle N_h|N_l \rangle = |p|{}^2 - |q|{}^2 = \frac{1 - \left|\frac{q}{p}\right|{}^2}{1 + \left|\frac{q}{p}\right|{}^2} = \frac{2 \, \Re e\, \varepsilon}{1 + |\varepsilon|{}^2}\,.\end{aligned} $$

(9.47)

From this result, we obtain

$$\displaystyle \begin{aligned} P(\mathrm{N^0} \rightarrow \mathrm{N^0}) - P (\mathrm{N^0} \rightarrow \overline{\mathrm{N^0}}) = \frac{1}{2} \mathrm{e}^{-T} \left(1 + \left|\frac{q}{p}\right|{}^2\right) \left(\delta \cosh y T + \cos x T \right) \; .\end{aligned} $$

(9.48)

Similarly,

$$\displaystyle \begin{aligned} P(\mathrm{N^0} \rightarrow \mathrm{N^0}) + P (\mathrm{N^0} \rightarrow \overline{\mathrm{N^0}}) = \frac{1}{2} \mathrm{e}^{-T} \left(1 + \left|\frac{q}{p}\right|{}^2 \right) \left(\cosh y T + \delta \cos x T \right) \; ,\end{aligned} $$

(9.49)

and the flavor asymmetry at time T in an initially pure flavor state becomes

$$\displaystyle \begin{aligned} A (T) = \frac{P(\mathrm{N^0} \rightarrow \mathrm{N^0}) - P (\mathrm{N^0} \rightarrow \overline{\mathrm{N^0}})}{P(\mathrm{N^0} \rightarrow \mathrm{N^0}) + P (\mathrm{N^0} \rightarrow \overline{\mathrm{N^0}})} = \frac{\cos x T + \delta \cosh y T}{\cosh y T + \delta \cos x T} \; . {} \end{aligned} $$

(9.50)

This function behaves very differently for the neutral K, D, and B meson systems.

9.3.2.2 Decay Asymmetries and ${\mathcal {C}\mathcal {P} }$

We define the decay amplitudes of neutral mesons to a final state f as

$$\displaystyle \begin{aligned} \begin{array}{rcl} A_f &\displaystyle =&\displaystyle \langle f | T | \mathrm{N^0}\rangle \; , \\ \overline{A_f} &\displaystyle =&\displaystyle \langle f | T | \overline{\mathrm{N^0}}\rangle \; . {} \end{array} \end{aligned} $$

(9.51)

The decay amplitudes of the mass eigenstates are then

$$\displaystyle \begin{aligned} \begin{array}{rcl} A^{h}_{f} &\displaystyle =&\displaystyle p A_f - q \overline{A_f} \; , \\ A^{l}_{f} &\displaystyle =&\displaystyle p A_f + q \overline{A_f} \; , \end{array} \end{aligned} $$

(9.52)

and we define the complex quantity

$$\displaystyle \begin{aligned} \lambda_f = \frac{q\overline{A_f}}{pA_f} \; . {} \end{aligned} $$

(9.53)

The moduli for the decay of N⁰ to f and the decay of $\overline {\mathrm {N^0}}$ to its ${\mathcal {C}\mathcal {P} }$ conjugate state ${\overline f}$ are equal if ${\mathcal {C}\mathcal {P} }$ is conserved, and vice versa:

$$\displaystyle \begin{aligned} \begin{array}{rcl} |A_f| &\displaystyle =&\displaystyle |\overline{A\overline{{}_f}}| \; , \\ |A\overline{{}_f}| &\displaystyle =&\displaystyle |\overline{A_f}| \; . {} \end{array} \end{aligned} $$

(9.54)

(If f is a ${\mathcal {C}\mathcal {P} }$ eigenstate, this is simplified to ${|A_f| = |\overline {A_f}|}$).

Now ${\mathcal {C}\mathcal {P} }$ violation may occur in three different ways:

• 1. ${\mathcal {C}\mathcal {P} }$ violation in the mixing, if |q∕p|≠ 1, called “indirect ${\mathcal {C}\mathcal {P} }$ violation ”.

• 2. ${\mathcal {C}\mathcal {P} }$ violation in the decay amplitudes, when (9.54) is not valid, called “direct ${\mathcal {C}\mathcal {P} }$ violation”.

• 3. ${\mathcal {C}\mathcal {P} }$ violation in the interference , when the phase of the expression

  $$\displaystyle \begin{aligned} {A_f \overline{A_f^*} A_{\overline{f}} \overline {A_{\overline{f}}^*} \, p^2/q^2} \end{aligned} $$

  (9.55)

  is not zero.

These three types of ${\mathcal {C}\mathcal {P} }$ violation are characterized by the following details:

• 1. ${\mathcal {C}\mathcal {P} }$violation in the mixing. This type of ${\mathcal {C}\mathcal {P} }$ violation will show up if the mass eigenstates of a neutral meson system are different from the ${\mathcal {C}\mathcal {P} }$ eigenstates, i.e. if |q∕p|≠ 1 (or ε ≠ 0) and if there is a relative phase between M ₁₂ and Γ ₁₂. For the neutral kaon system, this is evident from the existence of the decay K_L → π ⁺π ⁻, where |ε|∼ 2 × 10⁻³, and from the charge asymmetry in semileptonic decays δ _L which is proportional to $2 \, \Re e\, \varepsilon$. For the neutral B system, this effect could be seen also in the charge asymmetry of semileptonic decays

  $$\displaystyle \begin{aligned} a_{\mathrm{S}\mathrm{L}} = \frac{{\varGamma} (\overline{\mathrm{B^0}} (t)\rightarrow l^+ \nu X) - {\varGamma} (\mathrm{B^0} (t) \rightarrow l^- \bar{\nu} X)} {{\varGamma} (\overline{\mathrm{B^0}} (t)\rightarrow l^+ \nu X )+ {\varGamma} (\mathrm{B^0}(t) \rightarrow l^- \bar{\nu} X)} \; . {} \end{aligned} $$

  (9.56)

  This asymmetry is expected to be small in the Standard Model of order ΔΓ∕ Δm or $\mathcal {O}(10^{-3})$.

• 2. ${\mathcal {C}\mathcal {P} }$violation in the decay amplitude. This effect appears if the decay amplitude A _f of the neutral meson N⁰ to a final state f is different from the amplitude $\overline {A_{\overline {f}}}$ of the antiparticle $\overline {\mathrm {N^0}}$ to the charge-conjugate state $\overline {f}$, i.e. $|\overline {A_{\overline {f}}}/A_f|\neq 1$. In the neutral-kaon decay to two π mesons, this is realized by the interference of two decay amplitudes, one with ΔI = 1∕2 to an isospin I = 0 state, and another with ΔI = 3∕2 to an isospin I = 2 state. The amplitude of direct ${\mathcal {C}\mathcal {P} }$ violation is denoted by ε′ and proceeds through penguin diagram processes. The observed magnitude of this amplitude is |ε′|∼ 4 × 10⁻⁶. In the neutral B meson system, the required two decay amplitudes with different weak phases and different strong phases could be a penguin diagram and a tree diagram, e.g. for the decay to the final state K⁻π ⁺ or K⁺π ⁻. The b → s penguin diagram has a dominant contribution from a top quark loop, with a weak coupling $V^*_{tb} V_{ts}$ and an isospin-1∕2 (Kπ) state. The tree diagram for $b \rightarrow u + (\overline {u}s)$ has a coupling $V^*_{ub} V_{us}$ and leads to I = 1∕2 or 3∕2 states. The observed quantity is the decay asymmetry:

  $$\displaystyle \begin{aligned} a = \frac{N(\overline{\mathrm{B^0}} \rightarrow \mathrm{K^-} \pi^+) - N(\mathrm{B^0} \rightarrow \mathrm{K^+} \pi^-)} {N(\overline{\mathrm{B^0}} \rightarrow \mathrm{K^-} \pi^+) + N(\mathrm{B^0} \rightarrow \mathrm{K^+} \pi^-)}\; . \end{aligned} $$

  (9.57)

  Asymmetries in the order of 10% and 025% have been observed for the B⁰ and the $\mathrm {B}^0_{\mathrm {s}}$ meson respectively.

• 3. ${\mathcal {C}\mathcal {P} }$violation in the interference. Here the time dependence of the decay of an initially pure flavor state to a final state f is different for an initial particle or antiparticle. The final state can be a ${\mathcal {C}\mathcal {P} }$ eigenstate such as $\pi ^+ \pi ^- \;(\mathcal {C}\mathcal {P} = +1)$ or $J/\varPsi \mathrm {K_S}\; (\mathcal {C}\mathcal {P} = -1)$. In the kaon system the observed effect is ℑmε ∼ 1.6 × 10⁻³, while in the B⁰ system it is a very large asymmetry of order $\mathcal {O}(1)$.

9.4 Models of ${\mathcal {C}\mathcal {P} }$ Violation

After the discovery of ${\mathcal {C}\mathcal {P} }$ violation in K decay, a host of theoretical models was proposed to allocate this phenomenon to known interactions. Assuming ${\mathcal {C}\mathcal {P}\mathcal {T} }$ invariance of all interactions, the observed ${\mathcal {C}\mathcal {P}}$-violating effects in K decay imply also ${\mathcal {T} }$ violation (the experimental data of Sect. 9.5 are even sufficient to prove ${\mathcal {T} }$ violation without ${\mathcal {C}\mathcal {P}\mathcal {T} }$ invariance). In general, with ${\mathcal {C}\mathcal {P}\mathcal {T} }$ invariance, there are four combinations of violations possible:

• (a) ${\mathcal {T}}$-conserving, ${\mathcal {C}}$-violating and ${\mathcal {P}}$-violating;

• (b) ${\mathcal {T}}$-violating, ${\mathcal {C}}$-conserving and ${\mathcal {P}}$-violating;

• (c) ${\mathcal {T}}$-violating, ${\mathcal {C}}$-violating and ${\mathcal {P}}$-conserving;

• (d) ${\mathcal {T}}$-violating, ${\mathcal {C}}$-violating and ${\mathcal {P}}$-violating.

Parity conservation in strong and electromagnetic interactions has been tested, for example by looking for a circular polarization in γ rays from nuclear transitions. The presence of a wrong-parity admixture in one of the nuclear states involved will cause a small amplitude for a γ transition with abnormal multipolarity that can interfere with the dominant amplitude and cause such a circular polarization. In the experiments of Lobashov et al. [46], polarizations of the order of 10⁻⁵ have been measured. These are consistent with being due to the two-nucleon force np  → pn induced by the weak interaction (see [47] for a review).

From many experiments of a similar nature, one can infer that the strong and electromagnetic interactions are not of type (a), (b) or (d). Therefore, if the source of the ${\mathcal {C}\mathcal {P}}$-violating phenomena is located in the strong or the electromagnetic interaction, there must be a part of one of those interactions that belongs to class (c), i.e. ${\mathcal {C}}$- and ${\mathcal {T}}$-violating, but ${\mathcal {P}}$-conserving.

The proposed models can be grouped into the following four categories:

• 1. Millistrong ${\mathcal {C}\mathcal {P} }$ violation models [29,30,31] postulate the existence of ${\mathcal {C}}$- and ${\mathcal {T}}$-violating terms of order 10⁻³ in the strong interaction. The process K_L → π ⁺π ⁻ is supposed to occur by the interference of two amplitudes: first, the K_L decays via the normal ${\mathcal {C}\mathcal {P}}$-conserving weak interaction, with ${\Delta \mathbb {S} = 1}$, into an intermediate state X, and then this state decays into π ⁺π ⁻ by a ${\mathcal {T}}$-violating strong interaction. The amplitude of the process is of order ${G_{{ }_{\mathrm {F}}} \, a}$, where ${G_{{ }_{\mathrm {F}}}}$ is the Fermi coupling constant and a is the coupling of this ${\mathcal {C}\mathcal {P}}$-violating strong interaction. From the experimental value of |η ₊₋|, one can conclude that a ≈ 10⁻³.

• 2. Electromagnetic ${\mathcal {C}\mathcal {P} }$ violation models [32,33,34,35] require large parts of the electromagnetic interaction of hadrons to be ${\mathcal {C}}$- and ${\mathcal {T}}$-violating, but ${\mathcal {P}}$-conserving. A two-step process K_L →X → 2π could then occur through the interference of a weak and an electromagnetic ${\mathcal {C}\mathcal {P}}$-violating amplitude. The product of ${G_{{ }_{\mathrm {F}}}}$ with the fine structure constant α is not too far from ${G_{{ }_{\mathrm {F}}} \times 10^{-3}}$, as required by the magnitude of |η ₊₋|.

• 3. Milliweak models assume that a part, of the order of 10⁻³, of the weak interaction is ${\mathcal {C}\mathcal {P}}$-violating and is responsible for the observed effects. The decay K_L → 2π is then a one-step process, hence the name “direct ${\mathcal {C}\mathcal {P} }$ violation ”, and ${\mathcal {C}\mathcal {P} }$ or ${\mathcal {T} }$ violations of the order of 10⁻³ should show up in other weak processes [36,37,38,39,40,41,42,43,44]. In these models, based on two doublets of quarks, ${\mathcal {C}\mathcal {P} }$ violation is introduced in different ways. In one example [44], ${\mathcal {C}\mathcal {P} }$ violation is due to the Higgs couplings , with flavor-changing neutral currents allowed; in another one [42], it is due to right-handed weak currents. A bold alternative was considered in 1973 by Kobayashi and Maskawa [48]: they saw that if there are three doublets of quarks, there is a possibility of ${\mathcal {C}\mathcal {P} }$ violation in the 3 × 3 weak quark mixing. Today, with six quarks observed, this seems the most natural model as discussed below.

• 4. The superweak model [45] postulates a new ${\Delta \mathbb {S} = 2}$ ${\mathcal {C}\mathcal {P}}$-violating interaction that has a coupling (coupling constant g) smaller than the second-order weak interaction. This interaction could induce a transition K_L →K_S, with a subsequent decay K_S → 2π. More precisely, this interaction would cause a first-order transition matrix element

  $$\displaystyle \begin{aligned} \mathcal{M}_{{}_{\mathrm{SW}}} = \langle {\overline K}|{\mathcal{H}}_{{}_{\mathrm{SW}}}| K \rangle \sim g G_{{}_{\mathrm{F}}}\; . \end{aligned} $$

  (9.58)

  The mass difference itself is related to the second-order weak matrix element

  $$\displaystyle \begin{aligned} \mathcal{M}_{{\overline{\mathrm{K}}}\mathrm{K}} = \sum_n \frac{\langle \overline{\mathrm{K}}|{\mathcal{H}}_{{}_{\mathrm{W}}}| n \rangle\langle n|{\mathcal{H}}_{{}_{\mathrm{W}}}| K \rangle}{E_{{}_{\mathrm{K}}} - E_n + i\varepsilon}\; . \end{aligned} $$

  (9.59)

  where n is an intermediate state with energy E _n and ${{\mathcal {H}}_{{ }_{\mathrm {W}}}}$ is the weak Hamiltonian. In order that the ${\mathcal {C}\mathcal {P}}$-violating amplitude for K_L → 2π relative to the ${\mathcal {C}\mathcal {P}}$-conserving amplitude should be of the observed magnitude, the ratio ${{\mathcal {M}}_{{ }_{\mathrm {SW}}}/{\mathcal {M}}_{{\overline {\mathrm {K}}}\mathrm {K}}}$ must be of the order of 10⁻³. Since ${{\mathcal {M}}_{{ }_{\mathrm {SW}}} \approx gG_{{ }_{\mathrm {F}}}}$ and ${{\mathcal {M}}_{{\overline {\mathrm {K}}}\mathrm {K}} \sim G^2_{{ }_{\mathrm {F}}}m^2_p}$ where the proton mass m _p is used as a cutoff in the integration, this yields ${g \sim G_{{ }_F}m^2_p \approx 10^{-8}}$.

  This superweak interaction can be detected only in the K_L–K_S and B⁰–$\overline {\mathrm {B}^0}$ systems because these are the only known pairs of states with such a small difference in energy that they are sensitive to forces weaker than the second-order weak interaction. The clear prediction of this model is that there is no direct ${\mathcal {C}\mathcal {P} }$ violation in the decay.

For models other than the superweak one, violations of ${\mathcal {C}\mathcal {P} }$ or ${\mathcal {T} }$ should manifest themselves in other reactions of particles or nuclei. One observable is the electric dipole moment (EDM) of the neutron. Most milliweak models predict this EDM to be of order 10⁻²³ ecm to 10⁻²⁴ ecm, while the superweak model predicts 10⁻²⁹ ecm. The present experimental upper limit is 0.63  × 10⁻²⁵ ecm.

One of the milliweak models mentioned above under item 3 of the enumeration which is rather clear in its predictions should be noted: this is the idea of Kobayashi and Maskawa (KM) dating from 1973 [48]. At the time of the discovery of ${\mathcal {C}\mathcal {P} }$ violation, only three quarks were known, and there was no possibility of explaining ${\mathcal {C}\mathcal {P} }$ violation as a genuine phenomenon of weak interactions with left-handed charged currents and an absence of flavor-changing neutral currents. This situation remained unchanged with the introduction of a fourth quark because the 2×2 unitary weak quark mixing matrix has only one free parameter, the Cabibbo angle, and no nontrivial complex phase. However, as remarked by Kobayashi and Maskawa, the picture changes if six quarks are present. In this case the 3×3 unitary mixing matrix V _ik naturally contains a phase δ, in addition to three mixing angles (Sect. 9.7). It is then possible to construct ${\mathcal {C}\mathcal {P}}$-violating weak amplitudes from “box diagrams ” of the form shown in Fig. 9.5.

Fig. 9.5

Box diagram for K⁰–$\overline {\mathrm {K^0}}$ mixing connected with the ${\mathcal {C}\mathcal {P}}$-violating parameter ε

In the K⁰–$\overline {\mathrm {K^0}}$ system, this amplitude is proportional to the product of the four weak coupling constants $G^2_{{ }_{\mathrm {F}}} V_{ts} V_{ts}^* V_{td} V_{td}^*$. If there is a nontrivial phase δ in the unitary mixing matrix, then the product is a complex number, with the imaginary part depending on the phase δ. This leads to time-reversal (${\mathcal {T}}$) violation and to ${\mathcal {C}\mathcal {P} }$ violation. The ${\mathcal {C}\mathcal {P}}$-violating mixing parameter for the kaon system, ε, is given by

$$\displaystyle \begin{aligned} \varepsilon = \frac{G^2_{{}_{\mathrm{F}}} \, f^2_{\mathrm{K}} \, m_{\mathrm{K}} \, m^2_{\mathrm{W}}}{G{\sqrt{2}}\,\pi^2 \Delta m}B_{\mathrm{K}} \,\Im m (V_{td} \, V^*_{ts}) F (m^2_t, m^2_c) \; . \end{aligned} $$

(9.60)

Here $G_{{ }_{\mathrm {F}}}$ is the Fermi constant, f _K the kaon decay constant, B _K the kaon bag factor (0.80 ± 0.15), and $F(M^2_t, m^2_c)$ the loop function due to interference of the top and charm graphs, given by

$$\displaystyle \begin{aligned} F (m^2_t, m^2_c) = \Re e \left(V^*_{cs} V_{cd}\right) \left[\eta_1 S_0\left(m^2_c\right) - \eta_3 S_0\left(m^2_c, m^2_t\right)\right] - \Re e \left(V^*_{ts} V_{td}\right) \eta_2 S_0\left(m^2_t\right) \; , \end{aligned} $$

(9.61)

where $S_0(m^2_t)$ is a kinematical factor, and η ₁, η ₂, and η ₃ are QCD correction factors.

For the $\mathrm {B}^0_d$–$\overline {\mathrm {B}^0_d}$ mixing, a similar box graph applies, with the s quark replaced by a b quark. Here the amplitude is proportional to $G^2_{{ }_{\mathrm {F}}} V_{tb} V_{tb}^* V_{td} V_{td}^*$. Analogous diagrams can be calculated for $\mathrm {B}^0_{\mathrm {s}}$ ($b\overline {s}$) mixing and for D⁰ ($c\overline {d}$) mixing.

All ${\mathcal {C}\mathcal {P}}$-violating amplitudes in the KM model are proportional to the following product of the three mixing angles and the phase δ (Sect. 9.7),

$$\displaystyle \begin{aligned} J = |V_{us} V_{ub} V_{cb}\, \sin \delta| \end{aligned} $$

(9.62)

A necessary consequence of this model of ${\mathcal {C}\mathcal {P} }$ violation is the non-equality of the relative decay rates for K_L → π ⁺π ⁻ and K_L → π ⁰π ⁰. This “direct ${\mathcal {C}\mathcal {P} }$ violation ” is due to “penguin diagrams ” of the form given in Fig. 9.6 for kaon decays. The amplitude for this direct ${\mathcal {C}\mathcal {P} }$ violation is denoted by ε′. In kaon decays, it will show up in the interference of two decay amplitudes, with the final two-pion state having isospin 0 or 2 (A ₀ and A ₂ in (9.91)). With six quarks, the weak quark mixing through flavor change can carry a nontrivial phase δ in the mixing matrix, and therefore can induce a ${\mathcal {C}\mathcal {P}}$-violating difference between weak decay amplitudes, such that ${|A_f| \neq |\overline {A_f}|}$. This model gives an explicit origin of direct ${\mathcal {C}\mathcal {P} }$ violation with a predictable size. In the kaon system, these asymmetries are very small because of the small value of |J|∼ 3 × 10⁻⁵, the suppression of ΔI = 3∕2 currents, and the partial cancellation of two penguin graphs, called Q ₆ and Q ₈, shown in Fig. 9.6. However, in the B⁰ system, the asymmetries of the decay rates to ${\mathcal {C}\mathcal {P} }$ eigenstates can be very large. Examples are the decays B⁰ → J∕ΨK_S and B⁰ → π ⁺π ⁻.

Fig. 9.6

Penguin diagrams for K⁰ → 2π decay with direct ${\mathcal {C}\mathcal {P} }$ violation (amplitude ε′). The graphs correspond to the Wilson operators Q ₈ and Q ₆ and give rise to amplitudes with opposite signs

The main models which could be tested experimentally were the KM model and the superweak model, and the decisive question was the existence or non-existence of direct ${\mathcal {C}\mathcal {P} }$ violation. For the kaon system in the superweak model ε′ = 0, and the decay rates of K_L to π ⁺π ⁻ and to π ⁰π ⁰ are equal. The predicted value of ε′ within the KM model can be estimated if one infers the magnitude of the mixing angles from other experiments and if the hadronic matrix elements for box graphs and penguin graphs are calculated. Typical values of |ε′∕ε| are in the range +(0.05–2.0)× 10⁻³ for three generations of quarks. A measurement of this quantity to this level of precision therefore becomes the experimentum crucis for our understanding of ${\mathcal {C}\mathcal {P} }$ violation . If ε′ is orthogonal to ε, then a measurement of the phases of η ₊₋ and of η ₀₀ (see Eqs. (9.79) and (9.80), respectively) can help to detect a finite value of ℑm(ε′∕ε). If, however, the phase of ε′ is close to that of ε, and since |ε′∕ε|≪ 1 to a good approximation, we obtain

$$\displaystyle \begin{aligned} \frac{\varepsilon'}{\varepsilon} \simeq \Re e \left(\frac{\varepsilon'}{\varepsilon}\right) = \frac{1}{6} \left( 1 - \frac{|\eta_{00}|{}^2}{|\eta_{+-}|{}^2} \right) \; . \end{aligned} $$

(9.63)

Various methods have been used to calculate the value of $\Re e (\varepsilon '/\varepsilon )$. Owing to the difficulties in calculating hadronic matrix elements in the penguin diagrams, which involve long-distance effects, the task turns out to be very difficult. In particular, the electroweak penguin diagram (corresponding to the Wilson operator Q ₈) and the QCD penguin diagram (operatir Q ₈) yield contributions of opposite sign and lead to a partial cancellation in the result ε′∕ε. At the time of this review, great progress has been made by lattice calculations which now can be compared to the two groups of earlier analytic calculations.

The lattice calculation of the RBC-UKQCD-collaboration [49, 50] imply the following values of the penguin graph matrix elements [51, 52]:

$$\displaystyle \begin{aligned} B_6 = 0.57 \pm 0.19 ~~~\mbox{and}~~~ B_8 = 0.76 \pm 0.05 \, . \end{aligned} $$

(9.64)

From this the lattice method obtains:

$$\displaystyle \begin{aligned} \varepsilon '/\varepsilon = \left(1.9 \pm 4.5 \right) \times 10^{-4} \end{aligned} $$

(9.65)

On the side of analytic calculations, one method was based on the limit of large N, where N is the numbers of colours in QCD [53] (“dual QCD” or “DQCD”). At large N, QCD becomes a theory of three mesons. Here one gets B ₆ = B ₈ = 1 at the pion mass scale. Considering the meson evolution of these matrix elements to the mass scale of 1 GeV [54], Buras and Gerard obtain a suppression of both B ₆ and B ₈. At the scale of the charm quark mass, they find

$$\displaystyle \begin{aligned} B_6 \le 0.6 ~~~\mbox{and}~~~ B_8 = 0.8 \pm 0.1 \, , \end{aligned} $$

(9.66)

in agreement with the lattice results. using the lattice values for B ₈ and the relation B ₆ ≤ B ₈, they find an upper bound;

$$\displaystyle \begin{aligned} \varepsilon '/\varepsilon \le \left(6.0 \pm 2.4 \right) \times 10^{-4} \end{aligned} $$

(9.67)

However, an alternative analytic calculation [55] based on chiral perturbation theory which emphasizes final state interactions and neglects the meson evolution, obtains a much larger value

$$\displaystyle \begin{aligned} \varepsilon '/\varepsilon = \left(15 \pm 7 \right) \times 10^{-4} \, . \end{aligned} $$

(9.68)

Further improvement of the lattice calculations will hopefully clear-up this important discrepancy of the standard model prediction for ε′∕ε.

9.5 The Neutral K Meson System

9.5.1 Mass Eigenstates and ${\mathcal {C}\mathcal {P} }$ Eigenstates

The eigenstates of strangeness are ${\mathrm {K^0}\; (\mathbb {S} = +1)}$ and ${\overline {\mathrm {K^0}}\; (\mathbb {S} = -1)}$, the $\mathcal {C}\mathcal {P}$ eigenstates are K₁ (with ${\mathcal {C}\mathcal {P} }$ eigenvalue + 1) and K₂ (${\mathcal {C}\mathcal {P} }$ eigenvalue − 1), and the mass eigenstates are

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} |\mathrm{K_S}\rangle &\displaystyle =&\displaystyle p\, |\mathrm{K^0}\rangle + q |\overline{\mathrm{K^0}}\rangle \quad (\mathbf{S}\mbox{hort-lived)} \; , \end{array} \end{aligned} $$

(9.69)

$$\displaystyle \begin{aligned} \begin{array}{rcl} |\mathrm{K_L}\rangle &\displaystyle =&\displaystyle p\, |\mathrm{K^0}\rangle - q |\overline{\mathrm{K^0}}\rangle \quad (\mathbf{L}\mbox{ong-lived)} \; , {} \end{array} \end{aligned} $$

(9.70)

where, from experiment, K_L is the heavier state (h). The lifetimes of the two eigenstates are very different. While the short-lived particle (K_S) has a mean lifetime of (0.8959 ± 0.0004) × 10⁻¹⁰ s, the long-lived particle K_L has a lifetime of (5.17 ± 0.04) × 10⁻⁸ s, i.e. 600 times larger. This is due to the fact that the dominant ${\mathcal {C}\mathcal {P}}$-conserving decays are K_S → 2π and K_L → 3π, πeν, πμν, with a much smaller phase space for the three-body decays. Using the parameter ε = (p − q)∕(p + q), (9.69) and (9.70) can also be written

$$\displaystyle \begin{aligned} \begin{array}{rcl} |\mathrm{K_S}\rangle &\displaystyle =&\displaystyle \frac{1}{\sqrt{1+|\varepsilon|{}^2}} (|\mathrm{K_1} \rangle + \varepsilon |\mathrm{K_2} \rangle) \; , \end{array} \end{aligned} $$

(9.71)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} |\mathrm{K_L}\rangle &\displaystyle =&\displaystyle \frac{1}{\sqrt{1+|\varepsilon|{}^2}} (|\mathrm{K_2} \rangle + \varepsilon |\mathrm{K_1} \rangle) \; . {} \end{array} \end{aligned} $$

(9.72)

The long-lived state is therefore mainly a state with ${\mathcal {C}\mathcal {P} }$ eigenvalue − 1, with a small (2 × 10⁻³) admixture of a ${\mathcal {C}\mathcal {P} }$ +1 state K₁. The two mass eigenstates are not orthogonal if ${\mathcal {C}\mathcal {P} }$ is violated, because ${\langle \mathrm {K_S} | \mathrm {K_L} \rangle = 2\, \Re e\, \varepsilon }$.

If the validity of ${\mathcal {C}\mathcal {P}\mathcal {T} }$ symmetry is not assumed, the expressions are generalized to

$$\displaystyle \begin{aligned} \begin{array}{rcl} |\mathrm{K_S}\rangle &\displaystyle =&\displaystyle \frac{1}{\sqrt{1+|\varepsilon + \delta|{}^2}} (|\mathrm{K_1} \rangle + (\varepsilon + \delta) |\mathrm{K_2} \rangle) \; , \end{array} \end{aligned} $$

(9.73)

$$\displaystyle \begin{aligned} \begin{array}{rcl} |\mathrm{K_L}\rangle &\displaystyle =&\displaystyle \frac{1}{\sqrt{1+|\varepsilon - \delta|{}^2}} (|\mathrm{K_2} \rangle + (\varepsilon - \delta) |\mathrm{K_1} \rangle) \; . \end{array} \end{aligned} $$

(9.74)

with a ${\mathcal {C}\mathcal {P}\mathcal {T} }$ violating parameter δ.

9.5.2 Isospin Decomposition

In K_S,L → 2π decays, the angular momentum of the pions vanishes. The spatial part of the wave function is therefore symmetric, and since pions are bosons, the isospin wave function must be symmetric too. The two symmetric combinations of two I = 1 states have I = 0 and I = 2, and the four transition amplitudes that exist are

(9.75)

These can be reduced to three complex numbers by normalizing to the amplitude 〈0|T|K_S〉:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \varepsilon_0 &\displaystyle =&\displaystyle \frac{\langle 0|T|\mathrm{K_L}\rangle}{\langle 0|T|\mathrm{K_S}\rangle}\; , \end{array} \end{aligned} $$

(9.76)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \varepsilon_2 &\displaystyle =&\displaystyle \frac{1}{\sqrt{2}}\frac{\langle 2|T|\mathrm{K_L}\rangle }{ \langle 0|T|\mathrm{K_S}\rangle}\; , \end{array} \end{aligned} $$

(9.77)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \omega &\displaystyle =&\displaystyle \frac{\langle 2|T|\mathrm{K_S}\rangle}{\langle 0|T|\mathrm{K_S}\rangle}\; . \end{array} \end{aligned} $$

(9.78)

The experimentally observable quantities are

$$\displaystyle \begin{aligned} \begin{array}{rcl} \eta _{+-} &\displaystyle =&\displaystyle \frac{\langle \pi^+\pi^-|T|\mathrm{K_L}\rangle }{ \langle \pi^+\pi^-|T|\mathrm{K_S}\rangle}\; ,{} \end{array} \end{aligned} $$

(9.79)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \eta _{00} &\displaystyle =&\displaystyle \frac{\langle \pi^0\pi^0|T|\mathrm{K_L}\rangle }{ \langle \pi^0\pi^0|T|\mathrm{K_S}\rangle}\; ,{} \end{array} \end{aligned} $$

(9.80)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \delta_{\mathrm{L}} &\displaystyle =&\displaystyle \frac{{\varGamma} (\mathrm{K_L} \rightarrow \pi^-l^+\nu) - {\varGamma} (\mathrm{K_L} \rightarrow \pi^+l^-\bar{\nu})}{{\varGamma} (\mathrm{K_L} \rightarrow \pi^-l^+\nu) + {\varGamma} (\mathrm{K_L} \rightarrow \pi^+l^-\bar{\nu})}\; . \end{array} \end{aligned} $$

(9.81)

Relating the isospin states to the physical 2π states

$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle 0| &\displaystyle =&\displaystyle \frac{1}{\sqrt{3}} \langle \pi^-\pi^+| - \frac{1}{\sqrt{3}} \langle \pi^0 \pi^0| + \frac{1}{\sqrt{3}}\langle \pi^+\pi^-|\; , \end{array} \end{aligned} $$

(9.82)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle 2| &\displaystyle =&\displaystyle \frac{1}{\sqrt{6}} \langle \pi^-\pi^+| + \sqrt{\frac{2}{3}} \langle \pi^0 \pi^0| + \frac{1}{\sqrt{6}}\langle \pi^+\pi^-| \; . \end{array} \end{aligned} $$

(9.83)

we obtain

$$\displaystyle \begin{aligned} \begin{array}{rcl} \renewcommand{\arraystretch}{1.3} \eta_{+-} &\displaystyle =&\displaystyle \frac{\varepsilon_0 + \varepsilon_2}{1 + (1/\sqrt{2})\omega}, \end{array} \end{aligned} $$

(9.84)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \eta_{00} &\displaystyle =&\displaystyle \frac{\varepsilon_0 - 2 \varepsilon_2}{1 - \sqrt{2} \omega}. \renewcommand{\arraystretch}{1.0} \end{array} \end{aligned} $$

(9.85)

Because of the validity of the ΔI = 1∕2 rule for ${\mathcal {C}\mathcal {P}}$-conserving weak nonleptonic decays, ω ≪ 1 and therefore can be neglected.

A suitable choice for the phase of the K⁰ → 2π(I = 0) amplitude is obtained by choosing this amplitude to be real except for final-state interactions between two pions, leading to a phase shift δ ₀:

$$\displaystyle \begin{aligned} \langle 0|T|\mathrm{K^0} \rangle = \mathrm{e}^{\mathrm{i} \delta_0} A_0 \qquad \mathrm{and} \ A_0 \ \mathrm{ real}. \end{aligned} $$

(9.86)

Similarly,

$$\displaystyle \begin{aligned} \langle 2|T|\mathrm{K^0}\rangle = \mathrm{e}^{\mathrm{i} \delta_2} A_2\; . \end{aligned} $$

(9.87)

With these choices, we obtain

$$\displaystyle \begin{aligned} \begin{array}{rcl} \varepsilon_0 &\displaystyle =&\displaystyle \varepsilon\; , \end{array} \end{aligned} $$

(9.88)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \varepsilon_2 &\displaystyle =&\displaystyle \frac{\mathrm{i}}{\sqrt{2}} \mathrm{e}^{\mathrm{i}(\delta_2 - \delta_0)} \frac{\Im m \,A_2}{A_0}= \varepsilon '\; . \end{array} \end{aligned} $$

(9.89)

Therefore, representing ε and ε′ in the complex plane, we obtain the triangle relations

(9.90)

In this way, η ₊₋, η ₀₀ and 3𝜖′ form a triangle in the complex plane, the Wu–Yang triangle . The ${\mathcal {C}\mathcal {P}}$-violating decay amplitude ε′ is due to interference of ΔI = 1∕2 (A ₀) and ΔI = 3∕2 (A ₂) amplitudes:

$$\displaystyle \begin{aligned} \varepsilon' = \frac{\mathrm{i}\, \Im m\, A_2}{2 A_0} \mathrm{e}^{\mathrm{i} (\delta_2 - \delta_0)}\; . {} \end{aligned} $$

(9.91)

Its phase is given by the ππ phase shifts in the I = 0 and I = 2 states, δ ₀ and δ ₂, respectively, assuming ${\mathcal {C}\mathcal {P}\mathcal {T} }$ invariance:

$$\displaystyle \begin{aligned} \arg(\varepsilon') = (\delta_2 - \delta_0)+\frac{\pi}{2} \; . {} \end{aligned} $$

(9.92)

The ππ phase shifts have been measured precisely in pion-scattering experiments. The results obtained are δ ₂ = (−7.2 ± 1.3)^∘ [151] and δ ₀ = (39 ± 5)^∘ [152]. Using dispersion relation calculations or chiral perturbation theory, these results can be used to extract $\arg (\varepsilon ')$. The results are (42.3 ± 1.5)^∘ [149] and (46.0 ± 3.6)^∘ [150].

The decomposition of the observable decay amplitude into ε and ε′ corresponds to a separation of the ${\mathcal {C}\mathcal {P}}$-violating effects due to the mass and decay matrices (represented by ε), which are seen also in the impurity of the K_L and K_S states, from ${\mathcal {C}\mathcal {P} }$ violation in the transition matrix element (represented by ε′).

The phase of ε is given by (9.37) and (9.38):

$$\displaystyle \begin{aligned} \arg \varepsilon = \varPhi_{\mathrm{D}} + \arctan \left(\frac{2\Delta m}{{\varGamma}_{\mathrm{S}}}\right) \; , \end{aligned} $$

(9.93)

where Δm = m _L − m _S and

$$\displaystyle \begin{aligned} \varPhi_{\mathrm{D}} = - \arctan \left(\frac{\Im m\, {\varGamma}_{12}}{2\, \Im m\, M_{12}}\right). \end{aligned} $$

(9.94)

If there is no strong ${\mathcal {C}\mathcal {P} }$ violation in the channels K → 2π (I = 2), K → πlν, and K → 3π, Φ _D is very small. This can be deduced from the Bell–Steinberger unitarity relation [156]. If the final states of the K_L and K_S decays are designated by |F〉, then

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\varGamma}_{\mathrm{S}} &\displaystyle =&\displaystyle \sum_F \left| \langle F|T|\mathrm{K_S}\rangle\right|{}^2\; , \end{array} \end{aligned} $$

(9.95)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\varGamma}_{\mathrm{L}} &\displaystyle =&\displaystyle \sum_F \left| \langle F|T|\mathrm{K_L}\rangle\right|{}^2\; . \end{array} \end{aligned} $$

(9.96)

Unitarity leads to the relation

$$\displaystyle \begin{aligned} \mathrm{i}\left( M_{\mathrm{S}}-M_{\mathrm{L}}^{*}\right) \langle\mathrm{K_S}|\mathrm{K_L}\rangle = \sum_F \langle F|T|\mathrm{K_L}\rangle^{*} \langle F|T|\mathrm{K_S}\rangle\; . \end{aligned} $$

(9.97)

If ${\mathcal {C}\mathcal {P}\mathcal {T} }$ invariance is not assumed, the left side of this unitarity relation includes a contribution of the ${\mathcal {C}\mathcal {P}\mathcal {T} }$ violating parameter δ. It then has the form [156]:

$$\displaystyle \begin{aligned} (1 + \mathrm{i} \tan \varPhi_{SW}) [\Re e\, \varepsilon -\mathrm{i} \Im m\, \delta] \end{aligned} $$

(9.98)

The mass matrix elements are then (with ${\mathcal {C}\mathcal {P}\mathcal {T} }$ invariance assumed)

$$\displaystyle \begin{aligned} \begin{array}{rcl} X_{11} &\displaystyle =&\displaystyle X_{22} = \frac{M_{\mathrm{S}}+M_{\mathrm{L}}}{2} \end{array} \end{aligned} $$

(9.99)

$$\displaystyle \begin{aligned} \begin{array}{rcl} X_{12} &\displaystyle =&\displaystyle \frac{(M_{\mathrm{S}}-M_{\mathrm{L}})(1 + \varepsilon)}{2 (1 - \varepsilon)} \end{array} \end{aligned} $$

(9.100)

$$\displaystyle \begin{aligned} \begin{array}{rcl} X_{21} &\displaystyle =&\displaystyle \frac{(M_{\mathrm{S}}-M_{\mathrm{L}})(1 - \varepsilon)}{2 (1 + \varepsilon)}. \end{array} \end{aligned} $$

(9.101)

Ignoring all final states but 2π or assuming ℑmΓ ₁₂ = 0, we obtain the following from the unitarity relation or from (9.37):

$$\displaystyle \begin{aligned} \arg \, \varepsilon = \arctan\left(\frac{2\Delta m}{{\varGamma}_{\mathrm{S}}} \right)= \varPhi_{{}_{\mathrm{SW}}} {} \end{aligned} $$

(9.102)

where $\varPhi _{{ }_{\mathrm {SW}}}$ designates the phase in the superweak model

When we add other final states of ${\mathcal {C}\mathcal {P}}$-violating decays, the phase is shifted by Φ _D, and an upper limit can be obtained from the unitarity relation :

$$\displaystyle \begin{aligned} \varPhi_{\mathrm{D}} \leq \frac{0.75}{{\varGamma}_{\mathrm{S}} |\eta_{+-}|} \sum_F \sqrt{{\varGamma}_{{F,\mathrm{CPV}}} \cdot {\varGamma}_{{F,\mathrm{CPC}}}} \end{aligned} $$

(9.103)

where the sum runs over all states F ≠ 2π and the root is taken of the product of the ${\mathcal {C}\mathcal {P}}$-violating (CPV) and ${\mathcal {C}\mathcal {P}}$-conserving (CPC) decay rates.

Present limits on ${\mathcal {C}\mathcal {P}}$-violating processes in these decays show that contributions from semileptonic decays are negligible. Using the limits on ($\Delta Q = \Delta \mathbb {S}$)-violating amplitudes, we obtain

$$\displaystyle \begin{aligned} |\varPhi_{\mathrm{D}} (\mathrm{K_{e3}})| < 0.07^{\circ}\; , \hspace {1 cm} |\varPhi_{\mathrm{D}} (\mathrm{K}_{\mu 3})| < 0.05^{\circ} \; . \end{aligned} $$

(9.104)

In the same way, the measurement of the ${\mathcal {C}\mathcal {P}}$-violating part of the K_S → π ⁺π ⁻π ⁰ decay [153,154,155],

$$\displaystyle \begin{aligned} \frac{{\varGamma}(\mathrm{K_S} \rightarrow \pi^+ \pi^-\pi^0) }{{\varGamma}_{\mathrm{S}}} = 3.5 ^{+1.1}_{-0.9}\times 10^{-7}\; , \end{aligned} $$

(9.105)

allows us to set the limit

$$\displaystyle \begin{aligned} |\varPhi_{\mathrm{D}} (\pi^+ \pi^-\pi^0) | < 0.05^{\circ}\;. \end{aligned} $$

(9.106)

Similarly, from the limit [158, 159] Γ(K_S → 3π ⁰)∕Γ _S < 2.8 × 10⁻⁸ it follows that

$$\displaystyle \begin{aligned} |\varPhi_{\mathrm{D}} (3 \pi^0)| < 0.02^{\circ}\; . \end{aligned} $$

(9.107)

New, more sensitive experiments will improve this limit. If we use the experimental values of Δm and Γ _S from Sect. 9.5.5, then ${\arg \varepsilon = (43.4 \pm 0.1 \pm 0.17)^{\circ }}$, where the first error comes from the uncertainties of Δm and Γ _S and the second error from the uncertainty of Φ _D.

Another independent observable is the charge asymmetry

$$\displaystyle \begin{aligned} \delta_{\mathrm{L}} = \frac{1-|x|{}^2}{|1 - x|{}^2} 2\, \Re e\, \varepsilon\; , {} \end{aligned} $$

(9.108)

where x = g∕f is the ratio of the ${\Delta Q = - \Delta \mathbb {S}}$ to the ${\Delta Q = \Delta \mathbb {S}}$ amplitude (Sects. 9.5.3.2 and 9.5.5.6).

9.5.3 Interference Between Decay Amplitudes of K_L and K_S

An arbitrary coherent mixture of K_L and K_S states will show interference phenomena when decaying into 2π and in other common decay channels. According to Sect. 9.3.2.1 the eigentime development of K_L is

$$\displaystyle \begin{aligned} |\mathrm{K_L} \rangle\rightarrow |\mathrm{K_L} \rangle \, \mathrm{e}^{- \mathrm{i} M_{\mathrm{L}} {\tau}} \; , \end{aligned} $$

(9.109)

where M _L = m _L − (i∕2)Γ _L, and correspondingly for K_S. An arbitrary mixture

$$\displaystyle \begin{aligned} |\psi(0)\rangle = a_{\mathrm{S}}|\mathrm{K_S} \rangle + a_{\mathrm{L}}|\mathrm{K_L} \rangle \end{aligned} $$

(9.110)

will develop into

$$\displaystyle \begin{aligned} |\psi(\tau)\rangle = a_{\mathrm{S}}\, \mathrm{e}^{- \mathrm{i} M_{\mathrm{S}} {\tau}}\, |\mathrm{K_S} \rangle + a_{\mathrm{L}}\, \mathrm{e}^{- \mathrm{i} M_{\mathrm{L}} {\tau}} \,|\mathrm{K_L} \rangle\; . {} \end{aligned} $$

(9.111)

We call the ratio a _S∕a _L = V .

9.5.3.1 2π Decay

The 2π decay amplitude is therefore

$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle 2\pi|T|\psi(\tau)\rangle &\displaystyle =&\displaystyle a_{\mathrm{S}} \, \mathrm{e}^{- \mathrm{i} M_{\mathrm{S}} \tau}\, \langle 2\pi|T|\mathrm{K_S} \rangle + a_{\mathrm{L}} \, \mathrm{e}^{- \mathrm{i} M_{\mathrm{L}} \tau}\, \langle 2\pi|T|\mathrm{K_L} \rangle \\ &\displaystyle =&\displaystyle \langle 2\pi|T|\mathrm{K_S}\rangle{a_{\mathrm{S}} \, \mathrm{e}^{- \mathrm{i} M_{\mathrm{S}} \tau} + a_{\mathrm{L}} \eta \, \mathrm{e}^{-\mathrm{i} M_{\mathrm{L}} \tau}}\; , \end{array} \end{aligned} $$

(9.112)

where η = η ₊₋ for π ⁺π ⁻ decay and η = η ₀₀ for π ⁰π ⁰ decay. The observed decay rate is proportional to

$$\displaystyle \begin{aligned} R(\tau) = |a_{\mathrm{S}}|{}^2 \, \mathrm{e}^{-{\varGamma}_{\mathrm{S}} { \tau}} + |a_{\mathrm{L}} \, \eta|{}^2 \, \mathrm{e}^{- {\varGamma}_{\mathrm{L}}{\tau}} + 2 |a_{\mathrm{S}}| |a_{\mathrm{L}}| |\eta| \, \mathrm{e}^{-\left({\varGamma}_{\mathrm{L}} + {\varGamma}_{\mathrm{S}}\right) ({\tau}/{2})} \cos \left(\Delta m\, \tau + \varPhi\right) \; . \end{aligned} $$

(9.113)

where $\varPhi = \arg (a_{\mathrm {S}}) - \arg (\eta a_{\mathrm {L}})$. We obtain for various initial conditions of the mixture:

• 1. For an initially pure K⁰ state (a _S = 1 = a _L),

  $$\displaystyle \begin{aligned} \!R_1(\tau) = \mathrm{e}^{-{\varGamma}_{\mathrm{S}} {\tau}} + |\eta|{}^2 \, \mathrm{e}^{-{\varGamma}_{\mathrm{L}} {\tau}} + 2|\eta| \, \mathrm{e}^{- \left({\varGamma}_{\mathrm{L}} + {\varGamma}_{\mathrm{S}}\right) ({\tau}/{2})} \cos \left(\Delta m\, \tau - \arg \eta\right)\; . \end{aligned} $$

  (9.114)

• 2. For an initially pure $\overline {\mathrm {K^0}}$ state, the interference term changes sign.

• 3. For an incoherent mixture of K⁰ (intensity $N_{{ }_{\mathrm {K}}}$) and $\overline {\mathrm {K^0}}$ (intensity $N_{{ }_{\overline {\mathrm {K}}}}$), the interference term is multiplied by the “dilution factor”

  $$\displaystyle \begin{aligned} \frac{N_{{}_{\mathrm{K}}} - N_{{}_{\overline{\mathrm{K}}}}}{N_{{}_{\mathrm{K}}} + N_{{}_{\overline{\mathrm{K}}}}}\,. \end{aligned} $$

  (9.115)

  Measurement of the interference term under these conditions is called the vacuum interference method .

• 4. For the coherent mixture behind a regenerator, a _S = ϱ, a _L = 1, and we obtain

  $$\displaystyle \begin{aligned} R_2(\tau) = |\varrho|{}^2 \, \mathrm{e}^{- {\varGamma}_{\mathrm{S}} {\tau}} + |\eta|{}^2 \, \mathrm{e}^{- {\varGamma}_{\mathrm{L}} {\tau}} + 2|\varrho| |\eta| \, \mathrm{e}^{- \left({\varGamma}_{\mathrm{L}} + {\varGamma}_{\mathrm{S}}\right) ({\tau}/{2})} \cos \left(\Delta m\, \tau + \varPhi_\varrho - \arg \eta\right). {} \end{aligned} $$

  (9.116)

9.5.3.2 Semileptonic Decays

Interference phenomena and ${\mathcal {C}\mathcal {P} }$ violation can also be observed in the decay of a coherent mixture of K⁰ and $\overline {\mathrm {K^0}}$ mesons into semileptonic final states. In particular the time-dependent charge asymmetry δ(τ) = (N ⁺ − N ⁻)∕(N ⁺ + N ⁻) shows an oscillatory behavior, where N ⁺ denotes decays into π ⁺e ⁻ν final states and N ⁻ into π ⁻e ⁺ν. Assuming ${\mathcal {C}\mathcal {P}\mathcal {T} }$ invariance, we obtain

$$\displaystyle \begin{aligned} \delta(\tau) = 2 \frac{1-|x|{}^2}{|1-x|{}^2}\left[\Re e\, \varepsilon + |V| \,\mathrm{e}^{-(1/2) ({\varGamma}_{\mathrm{S}} - {\varGamma}_{\mathrm{L}}){\tau}} \cos \left(\Delta m\, \tau + \varPhi_V\right)\right]. {} \end{aligned} $$

(9.117)

where x is the ratio of amplitudes with ΔS = − ΔQ and ΔS =  ΔQ. x is consistent with zero, in agreement with the ΔS =  ΔQ rule.

For an initially pure K_L beam (R = 0), the asymmetry is independent of the decay time:

$$\displaystyle \begin{aligned} \delta_{\mathrm{L}} = 2\, \Re e\, \varepsilon\, \frac{1 - |x|{}^2}{|1 - x|{}^2}\; . \end{aligned} $$

(9.118)

For an initial incoherent mixture of $\mathrm {K^0}\, (N_{{ }_{\mathrm {K}}})$ and $\overline {\mathrm {K^0}} \; (N_{{ }_{\overline {\mathrm {K}}}})$ the quantity |R| has to be replaced by $(N_{{ }_{\mathrm {K}}} - N_{{ }_{\overline {\mathrm {K}}}})/(N_{{ }_{\mathrm {K}}} + N_{{ }_{\overline {\mathrm {K}}}})$, i.e. by the same dilution factor as for 2π interference in a short-lived beam.

For the coherent mixture created by a regenerator, R is given by the regeneration amplitude ϱ, and Φ _R by the regeneration phase Φ _ϱ.

9.5.4 Detection of K⁰ Decays

The main decay modes originating from K⁰’s in a neutral beam and their respective branching ratios are [163]

$$\displaystyle \begin{aligned} \begin{array}{lllll} \mathrm{K_L} \rightarrow \pi^\pm e^\mp \nu &(40.55 \pm 0.11)\% &&&\mathrm{K}_{\mathrm{e}3}\; ; \\ \mathrm{K_L} \rightarrow \pi^\pm \mu^\mp \nu &(27.07 \pm 0.07)\% &&&\mathrm{K}_{\mu3}\; ; \\ \mathrm{K_L} \rightarrow \pi^+ \pi^- \pi^0 &(12.54 \pm 0.05)\% &&&\mathrm{K}_{\pi3}\; ; \\ \mathrm{K_L} \rightarrow \pi^0 \pi^0 \pi^0 &(19.52 \pm 0.12)\% &&&\mathrm{K}_{\pi3}\; ; \\ \mathrm{K_S} \rightarrow \pi^+ \pi^- &(69.20 \pm 0.05)\% &&&\mathrm{K}_{\pi2}\; ; \\ \mathrm{K_S} \rightarrow \pi^0 \pi^0 &(30.69 \pm 0.05)\% &&&\mathrm{K}_{\pi2}\; . \\ \end{array} \end{aligned}$$

The experimental problem is to detect the rare ${\mathcal {C}\mathcal {P}}$-violating decay modes K_L → π ⁺π ⁻ and K_L → π ⁰π ⁰, with branching ratios of order 10⁻³, in this overwhelming background of other decays, and to measure their decay rate, and, by interference, their phase relation to ${\mathcal {C}\mathcal {P}}$-conserving decay amplitudes. In addition, the ${\mathcal {C}\mathcal {P} }$ impurity in the K_L state can be obtained by measuring the charge asymmetry in the semileptonic decay modes.

9.5.4.1 Charged Decay Modes

The two charged decay products in π ⁺π ⁻ and semileptonic decays are usually recorded in a magnetic spectrometer consisting of a wide-aperture magnet and at least three layers of position-measuring detectors. The vector momenta $\vec p_i\; (i = 1,2)$ of the charged decay products are measured and the energies of the particles are obtained from the calculated vector momenta $\vec p_i$, assuming their rest mass to be m _π, as

$$\displaystyle \begin{aligned} E_i = \sqrt{\vec{p}^2_i + m^2_\pi}\; . \end{aligned} $$

(9.119)

The invariant mass of the pair is

$$\displaystyle \begin{aligned} m_{\pi\pi} = \sqrt{(E_1 + E_2)^2 - (\vec p_1 + \vec p_2)^2}\; , \end{aligned} $$

(9.120)

and the kaon momentum $\vec {p_{{ }_{\mathrm {K}}}} = \vec {p_1} + \vec {p_2}$. The lifetime of the kaon from the target to the decay vertex (z _V) in the kaon rest system is given by $\tau = (z_{\mathrm {V}} - z_{\mathrm {T}}) m_{{ }_{\mathrm {K}}}/(c p_z)$, where $m_{{ }_{\mathrm {K}}}$ is the kaon mass, c the light velocity, and p _z the component of $\vec p_{{ }_{\mathrm {K}}}$ along the beam line.

Two sets of information can be used to separate 2π and leptonic decays. First, the invariant mass m _ππ is required to be equal to $m_{{ }_{\mathrm {K}}}$ within the experimental resolution. Second, all experimenters use lepton identification.

The most frequently used methods for electron identification at intermediate energies, around 10 GeV, are Cerenkov counters , and identification through comparison of the energy deposition in electromagnetic and hadronic showers. At high energies, i.e. for electrons with energies between 10 GeV and 100 GeV, electron identification in calorimetric detectors works on the principle that for a particle of momentum p, the energy E deposited in a calorimeter by an electron (or photon) is much higher than for a hadron of the same momentum.

For the identification of muons one uses their penetration through several (∼8) interaction lengths of material in order to distinguish them from pions interacting in this absorber.

Once the 2π decay mode has been identified, one has to know, in general, whether the K_S or K_L from which the decay products originate has undergone scattering on its way from its production to the decay point. In the case of a short-lived beam produced by protons interacting in a target near to the detector, this is done by calculating the distance of the intercept of the reprojected kaon momentum $p_{{ }_{\mathrm {K}}}$ in the target plane from the target center, p _t. Unscattered events cluster around p _t = 0. In the case of a long-lived beam, one uses the component of $p_{{ }_{\mathrm {K}}}$ transverse to the beam, p _t, or the angle θ between the kaon direction $p_{{ }_{\mathrm {K}}}$ and the beam direction in order to separate transmitted and coherently regenerated (θ = 0 = p _t) kaons from events due to kaons that have undergone scattering, or diffractive, or inelastic, regeneration.

9.5.4.2 Neutral Decay Modes

The detection of the neutral decay mode K_L → π ⁰π ⁰ → 4γ is complicated by the presence of the decay K_L → 3π ⁰ → 6γ with a 21% branching ratio. This decay can simulate 4γ events for kinematic reasons, e.g. if two γ rays are missed by the detector. Very specific kinematic features of the 2π ⁰ decay were therefore used in the early medium-energy experiments in order to obtain a clean K_L → 2π ⁰ signal [167,168,169,170, 172].

For kaon energies between 40 GeV and 200 GeV, totally absorbing electromagnetic calorimeters are used. These calorimeters consist of scintillating crystals, Cerenkov lead glass counters, or liquid-noble-gas detectors with or without lead radiators. Their longitudinal thickness is around 25 radiation lengths, and their transverse segmentation corresponds to the transverse width of an electromagnetic shower, given by the Moli$\grave {\mathrm {e}}$re radius R _M of the material. In this way, the energies E _i and the transverse positions (x _i, y _i) of each of the four photon-induced showers are measured in the calorimeter. This is the only information available for reconstructing all variables describing the decay. In principle, the invariant mass of the four photons can be calculated using the relation

$$\displaystyle \begin{aligned} \begin{array}{rcl} M^2 &\displaystyle =&\displaystyle E^2 - \vec{p}^2 = \left(\sum_{i=1}^{4}E_i\right)^{2} - \left(\sum_{i=1}^{4}\vec{p}_i \right)^{2} \end{array} \end{aligned} $$

(9.121)

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle =&\displaystyle \sum_{i\neq j} (E_i E_j - E_i E_j \cos \theta_{ij}) \end{array} \end{aligned} $$

(9.122)

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle =&\displaystyle 2 \sum_{i<j} E_i E_j \frac{\theta_{ij}^2}{2}\; . \end{array} \end{aligned} $$

(9.123)

The opening angle θ _ij between two photons can be obtained from the transverse distance r _ij between the impact points in the calorimeter,

$$\displaystyle \begin{aligned} r_{ij}=\sqrt{(x_i - x_j)^2 + (y_i - y_j)^2}\; , \end{aligned} $$

(9.124)

and the distance z of the K meson decay point from the calorimeter. Using these variables, the invariant four-photon mass can be written as

$$\displaystyle \begin{aligned} M = \frac{1}{z} \sqrt{\sum_{i<j} E_i E_j r_{ij}^2}\; . \end{aligned} $$

(9.125)

This relation can be used to calculate the distance of the decay point of the kaon from the calorimeter by using the kaon mass as a constraint:

$$\displaystyle \begin{aligned} z = \frac{1}{M_{{}_{\mathrm{K}}}} \sqrt{\sum_{i<j} E_i E_j r_{ij}^2}\; . \end{aligned} $$

(9.126)

With this knowledge about the decay point, the invariant mass of any pair (i, j) of photons can then be calculated:

$$\displaystyle \begin{aligned} M_{ij} = \frac{1}{z} r_{ij} \sqrt{E_i E_j} \; . \end{aligned} $$

(9.127)

Of the three possible combinations, the one where both masses are closest to the π ⁰ mass is chosen. A scatter plot of m ₁₂ versus m ₃₄ shows a signal at ($m_{\pi ^0}, m_{\pi ^0}$) if the four photons come from the decay K_L → π ⁰π ⁰, while for events from the decay K_L → 3π ⁰, with four detected photons, the invariant masses are spread over a large region around this point (Fig. 9.20). It is possible to extract the amount of background in the signal region by extrapolating the observed level of background events into this signal region, with the help of Monte Carlo simulations of the K_L → 3π ⁰ background. In high-energy experiments, the background can then be reduced to a level below one percent.

9.5.4.3 Detectors Measuring Charged and Neutral Decay Modes Simultaneously

For the measurement of the parameter ε′ of direct ${\mathcal {C}\mathcal {P} }$ violation, the ratio of the decay rates of K_L into charged (π ⁺π ⁻) and neutral (π ⁰π ⁰) two-pion states has to be measured with great precision. For this purpose, experimentalists reduce systematic normalization uncertainties by measuring charged and neutral decays (from K_L and K_S mesons) simultaneously.

Four such experiments have been constructed for high-energy K meson beams, two of them at CERN (NA31 and NA48 ) and two at Fermilab (E731 and kTeV ).

One experiment has been designed to detect K mesons of a few hundred MeV/c momentum arising from the annihilation of stopping antiprotons in a hydrogen target at the Low Energy Antiproton Ring (LEAR) at CERN (CPLEAR).

9.5.4.4 NA31

This detector (Fig. 9.7) [171], situated in a K_L or K_S beam from the CERN SPS, was based on calorimetry and was designed for good stability and high efficiency. The K_L and the K_S beam were produced by a 450 GeV proton beam with a production angle of 3.6 mrad.

Fig. 9.7

Beam layout and detector in the NA31 experiment. The setup contains a movable target for the production of the K_S mesons, and a liquid-argon calorimeter; it does not contain a magnet

Fig. 9.8

Beam layout and detector in the NA48 experiment

A schematic illustration of the beam layout and the apparatus is shown in Fig. 9.7.

The principal features can be summarized as follows:

• to adjust the steeply falling vertex distribution of the K_S decays to the almost flat vertex distribution of the K_L decays, the K_S target is located on a train that can be positioned at 41 stations in the decay volume;

• an anticounter with a 7 mm lead converter in the K_S beam is used to veto decays in the collimator, defines the upstream edge of the decay region, and provides for the relative calibration of the 2π ⁰ and π ⁺π ⁻ energy scales to a precision better than ± 10⁻³;

• two wire chambers spaced 25 m apart, with ± 0.5 mm resolution in each projection, track charged pions;

• a liquid-argon/lead sandwich calorimeter with strip readout detects photons with ± 0.5 mm position resolution and an energy resolution of$\sigma _{E}/E=10\%/E \oplus 7.5\%/\sqrt {E} \oplus 0.6\%$ (E in GeV);

• an iron/scintillator sandwich calorimeter measures the energy of charged pions with $\pm 65\%/\sqrt {E}$ (E in GeV) energy resolution.

The energies of the two pions and their opening angle are used to measure the invariant mass of the charged pair.

The NA31 experiment collected K_L and K_S decays in alternating time periods. In each case the charged and neutral decays were collected simultaneously.

9.5.4.5 NA48

This experiment (Fig. 9.8) was also built at CERN [201]. The detector was exposed to a simultaneous nearly collinear K_L∕K_S beam, derived from a 450 GeV/c proton beam from the SPS.

Fig. 9.9

kTeV beam and detector

The K_S beam was produced by using a fraction of the protons that did not interact with the K_L target.

Charged particles were measured by a magnetic spectrometer composed of four drift chambers with a dipole magnet between the second and the third chamber. The average efficiency per plane was 99.5%, with a radial uniformity better than ±0.2%. The space point resolution was ≈95 μm. The momentum resolution was σ _p∕p = 0.48% ⊕ 0.009% × p, where the momentum p is in GeV/c. The ππ invariant mass resolution is 2.5 MeV.

A liquid-krypton (LKr) calorimeter was used to reconstruct K → 2π ⁰ decays. Cu–Be–Co ribbon electrodes of size 40 μm × 18 mm × 125 cm defined 13212 cells (each with a 2 cm × 2 cm cross section) in a structure of longitudinal projective towers pointing to the center of the decay region. The calorimeter was ∼27 radiation lengths long and fully contained electromagnetic showers with energies up to 100 GeV. The energy resolution of the calorimeter was $\sigma _{E}/E=(3.2 \pm 0.2)\%/E \oplus (9 \pm 1)\%/\sqrt {E} \oplus (0.42 \pm 0.05)\%$ where E is in GeV.

9.5.4.6 kTeV

The kTeV experiment at the 800 GeV/c Tevatron [180] uses a regeneration technique to produce the K_S beam (Fig. 9.9). The K_L “double beam” entered from the left, one half continuing as K_L, the other half producing a K_S beam by regeneration. The regenerator in the kTeV experiment was made of blocks of plastic scintillator. These blocks were viewed by photomultiplier tubes to reject inelastically or quasi-elastically scattered kaons.

Fig. 9.10

CPLEAR detector

The evacuated decay volume extended over 40 m, or about 7 K_S mean lifetimes at 100 GeV/c, followed by the first drift chamber. The analysis magnet was located between the second and the third drift chamber. Each of the four drift chambers had two horizontal and two vertical planes of sense wires. The typical single-hit position resolution of the drift chambers was about 110 μm in either direction, which lead to a mean mass resolution of 2.2 MeV for the reconstructed kaon mass obtained from the π ⁺π ⁻ decay mode. The momentum resolution for a charged particle was σ _p∕p = 0.17% ⊕ 0.0071% × p (in GeV/c).

The four photons from the 2π ⁰ were detected in an electromagnetic calorimeter made of pure cesium iodide. The calorimeter consisted of 3100 blocks arranged in a square array of 1.9 m side length. The blocks had two sizes: 2.5 × 2.5 cm² in the central region and 5 × 5 cm² in the outer region. All blocks are 50 cm, or ∼27 radiation lengths, long. Two 15 cm square holes allowed the passage of the K_L and the K_S beam through the calorimeter. The calorimeter had an energy resolution of $\sigma _{E}/E= 2\%/\sqrt {E} \oplus 0.4\%$ (E in GeV). The average position resolution for electrons was about 1.2 mm for clusters in the smaller crystals and 2.4 mm for the larger crystals.

9.5.4.7 CPLEAR

In contrast to the detectors described in the previous sections, the CPLEAR detector measured decays from kaons produced in $\bar {p} p$ annihilations at rest obtained from the low energy $\bar {p}$ ring LEAR at CERN. The antiprotons were stopped in a 16 bar hydrogen gas target and formed a protonium before annihilation. In annihilation reactions of the type $\bar {p} p \rightarrow \mathrm {K^0} \mathrm {K^-} \pi ^+$ and $\bar {p} p \rightarrow \overline {\mathrm {K^0}} \mathrm {K^+} \pi ^-$, the charged kaon was identified through the time of flight and track curvature in a solenoidal magnetic field (“tagging”). This tag was used as a trigger for detecting the decay products of the neutral K meson associated with the K⁺ or K⁻. A unique property of this scheme is that the strangeness of the neutral K meson is known from the charge of the tagged K⁺ or K⁻.

As shown in Fig. 9.10, the experiment had a cylindrical, onion-type, setup. Six cylindrical drift chambers, starting at a radius of 25.46 cm and going out to a radius of 50.95 cm, provided the main tracking information for charged particles. The offline track-finding efficiency was better than 99% and the wire positions were determined with an accuracy of about 10 μm. The mean mass resolution achieved for the invariant kaon mass in the π ⁺π ⁻ final state was 13.6 MeV/c ². By applying kinematically and/or geometrically constrained fits, the K⁰ momentum resolution $\sigma _{p_{{ }_t}}/p_{\mathrm t}$ was improved from 5.5% to 0.25%.

Fig. 9.11

z decay distribution of K → π ⁺π ⁻ decays in the regenerator beam, for the restricted momentum range 40–50 GeV/c. The Monte Carlo prediction (dashed line) is without the interference term that is proportional to “2|ϱ||η|” (kTeV experiment [180])

The tracking detectors were followed by the particle identification detector (PID), used for charged-kaon identification and e∕π separation. It was located at radii between 62.5 cm and 75.0 cm. and was composed of two layers of plastic scintillators with an 8 cm thick liquid threshold Cerenkov detector in between. The two charged tracks from the decays $\overline {\mathrm {K^0}} \rightarrow \pi ^+ \pi ^-,\, \pi ^+ e^- \nu ,\, \pi ^+ \mu ^- \nu$ were reconstructed and the decay vertex was calculated. Using this vertex and the annihilation point in the hydrogen target, the proper time for decay of the kaon was obtained.

The electromagnetic calorimeter had the form of a barrel and was an assembly of 18 lead plates alternating with sampling chambers. It was located at radii between 75 cm and 100 cm. The calorimeter had a total thickness of ∼6 radiation lengths, an energy resolution of $\sigma _{E}/E \approx 13\%/\sqrt {E}$ (E in GeV) and a position resolution of ∼5 mm for the photon conversion points. The photon detection efficiency was (90 ± 1)% for photon energies above 200 MeV. For photons with energies below 200 MeV the efficiency dropped significantly and was only about 60% for 100 MeV photons.

All subdetectors were embedded in a 3.6 m long, 2 m diameter solenoid magnet, which provided a 0.44 T uniform field.

9.5.5 Elucidation of ${\mathcal {C}\mathcal {P} }$ Violation in K⁰ Decays (I): Search for ℑm(ε′∕ε)

9.5.5.1 The Significance of the Phase Φ ₊₋

The phase of η ₊₋, $\varPhi _{+-} = \arg (\eta _{+-})$, was a possible clue that would help to disentangle the two components of ${\mathcal {C}\mathcal {P} }$ violation, since

$$\displaystyle \begin{aligned} \eta_{+-} = \varepsilon + \varepsilon'\; . \end{aligned} $$

(9.128)

If ε′, the parameter of direct ${\mathcal {C}\mathcal {P} }$ violation, was comparable in size to ε, and if its phase was orthogonal to ε, then the phase of η ₊₋ would deviate in a detectable way from the phase of ε, which is mainly determined by the experimentally measurable values of Δm and Γ _S = 1∕τ _S (see Sect. 9.5.2):

$$\displaystyle \begin{aligned} \arg (\varepsilon) = \arctan \left(\frac{2\Delta}{{\varGamma}_{\mathrm{S}}}\right) + \varPhi_{\mathrm{D}} = \varPhi_{{}_{\mathrm{SW}}} + \varPhi_{\mathrm{D}} \end{aligned} $$

(9.129)

With the present values of Δm and Γ _S (Sect. 9.5.5.7), $\varPhi _{{ }_{\mathrm {SW}}} = (43.4 \pm 0.1)^{\circ }$.

A significant deviation of the measured value of Φ ₊₋ from $\varPhi _{{ }_{\mathrm {SW}}}$ would be evidence for a nonvanishing component ℑm(ε′∕ε) and against the superweak model of ${\mathcal {C}\mathcal {P} }$ violation.

9.5.5.2 Measurements of the Phase Φ ₊₋ in Interference Experiments Behind a Regenerator

The relative phase between the two amplitudes of the decays K_L → π ⁺π ⁻ and K_S → π ⁺π ⁻ has been measured by two distinct methods.

The first consists of measuring the interference of the K_L → π ⁺π ⁻ amplitude with the coherently regenerated K_S → π ⁺π ⁻ amplitude behind a slab of material (the regenerator). The experiments require (a) the measurement of the π ⁺π ⁻ intensity as a function of the K⁰ eigentime behind the regenerator, which is given in Sect. 9.5.3.1, and (b) an independent determination of the regeneration phase.

The latest and most precise experiment of this type has been done by the kTeV collaboration [180] (see also [176]) in an experiment at Fermilab with an 800 GeV/c proton beam. The detector is described in Sect. 9.5.4.6; 5 × 10⁹ events were recorded in 1996–1997, among those were about 9 × 10⁶ K⁰ → π ⁺π ⁻ events. Their z decay distribution in the restricted kaon momentum interval from 40 to 50 GeV/c is shown in Fig. 9.11. The corresponding decay time distribution was fitted with the formula (9.116). The nuclear regeneration amplitude $F= \mathrm {i} (f(0) - \overline {f}(0))/k$ was assumed to decrease with the kaon momentum $\vec {p}$ according to a power law F(p) = F(70 GeV/c)× (p/70 GeV/c)^α. This was motivated by a Regge model where the difference between the K and $\overline {\mathrm {K}}$ scattering amplitudes would be described by one single ω meson exchange trajectory. In this model, the phase of the regeneration amplitude is given by Φ _F = −(π∕2)(1 + α). In the fit, Φ ₊₋, Δm, Γ _S and α were free parameters, and Φ _F was assumed to be given by the Regge model. The results are

$$\displaystyle \begin{aligned} \begin{array}{rcl} \varPhi_{+-} &\displaystyle =&\displaystyle 44.12^\circ \pm 0.72^\circ\; (\mbox{stat}) \pm 1.20^\circ\; (\mbox{syst}) = 44.12^\circ \pm 1.40^\circ\; , \end{array} \end{aligned} $$

(9.130)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \Delta m &\displaystyle =&\displaystyle (5288 \pm 23) \times 10^6\,\mbox{s}^{-1}\; , \end{array} \end{aligned} $$

(9.131)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \tau_{\mathrm{S}} &\displaystyle =&\displaystyle (89.58 \pm 0.08 \; (\mbox{stat})) \times 10^{-12}\,\mbox{ s} \; , \end{array} \end{aligned} $$

(9.132)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \chi^2 &\displaystyle =&\displaystyle \mbox{223.6 for 197 degrees of freedom} \; . \end{array} \end{aligned} $$

(9.133)

The systematic error in Φ ₊₋ includes a 0.25^∘ uncertainty from the fact that the relation between the regeneration phase and the momentum dependence of the regeneration amplitude through a dispersion relation integral is incomplete. It has been argued [178] that this uncertainty is larger, more than one degree, because of the limited momentum range in which the regeneration amplitude was measured.

Fig. 9.12

Time distribution of K → π ⁺π ⁻ events from a coherent mixture of K_L and K_S produced in pure strangeness states [166]. Curve a: events (histogram) and fitted distribution (dots). Curve b: events corrected for detection efficiency (histogram), and fitted distribution with interference term (dots) and without interference term (curve). Inset: interference term as extracted from data (dots) and fitted term (line). (CERN–Heidelberg experiment [166])

9.5.5.3 Measurements of Φ ₊₋ in Vacuum Interference Experiments

The other method for measuring Φ ₊₋ is the vacuum interference method mentioned above (Sect. 9.5.3.1), where one observes the K → π ⁺π ⁻ distribution obtained from an initially pure strangeness state. The information on Φ ₊₋ is contained in the interference term proportional to $\cos {}(\Delta m\, \tau - \varPhi _{+-})$, and the time at which the two interfering amplitudes are equal is ∼ 12τ _S, so that the correlation of Φ ₊₋ with Δm is rather strong.

Three experiments of this type have been done in the intermediate-energy domain [166, 182, 183]. An analysis of the latest and most precise of those has been performed by the CERN–Heidelberg group [166]. The apparatus was situated in a 75 mrad short neutral beam derived from 24 GeV/c protons. The time distribution of 6 × 10⁶ K_S,L → π ⁺π ⁻ decays is shown in Fig. 9.12: (curve a), together with the fitted time distribution, as given in Sect. 9.5.3.1. The result of this fit is

$$\displaystyle \begin{aligned} \begin{array}{rcl} \varPhi_{+-} &\displaystyle =&\displaystyle (49.4^\circ \pm 1.0^\circ) + 305^{\circ}\frac{(\Delta m - 0.540\times 10^{10} \; \mathrm{s}^{-1})}{\Delta m}\; , \end{array} \end{aligned} $$

(9.134)

$$\displaystyle \begin{aligned} \begin{array}{rcl} |\eta_{+-}| &\displaystyle =&\displaystyle (2.30 \pm 0.035) \times 10^{-3}\; , \end{array} \end{aligned} $$

(9.135)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\varGamma}_{\mathrm{S}} &\displaystyle =&\displaystyle (1.119 \pm 0.006) \times 10^{-10} \; \mathrm{s}^{-1}\; , \end{array} \end{aligned} $$

(9.136)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \chi^2 &\displaystyle =&\displaystyle \mbox{421 for 444 degrees of freedom} \; . \end{array} \end{aligned} $$

(9.137)

Fig. 9.13

(a) Measured decay-rate asymmetry, $A_{+-}^{\mathrm {exp}}(\tau )$; the data points include residual background. (b) Decay-rate asymmetry, A ₊₋(τ); the data points are background subtracted. In both cases the continuous curve is the result of the fit (CPLEAR experiment, [185])

In the high-energy domain, this method has also been used by the NA31 collaboration [184]. In a 3.6 mrad neutral beam derived from 450 GeV protons, kaons of mean momentum around 100 GeV were allowed to decay. Two different target positions were chosen, at distances of 48 m and 33.6 m from the defining collimator of the neutral beam, which marked the upstream end of the decay volume. Kaons that decayed along 50 m in an evacuated tank were detected further downstream at about 120 m from the final collimator by the NA31 detector (Sect. 9.5.4.4, Fig. 9.7). The measured time distribution of π ⁺π ⁻ decays is similar to the one in Fig. 9.12. There are 2.24 × 10⁶ and 0.57 × 10⁶π ⁺π ⁻ events in the data for the target in the near and far positions, respectively; the corresponding numbers of π ⁰π ⁰ events are 1.81 × 10⁶ and 0.31 × 10⁶. The phases were extracted from a fit to the time distribution of the ratio of the data in the near and far positions of the target.

The results are

$$\displaystyle \begin{aligned} \begin{array}{rcl} \varPhi_{+-} = (46.9^\circ \pm 1.4^\circ) &\displaystyle +&\displaystyle 310^\circ \frac{(\Delta m - 0.5351 \times 10^{10}\,\mathrm{s}^{-1})}{\Delta m}\\ &\displaystyle +&\displaystyle 270^\circ \frac{(\tau_{\mathrm{S}} - 0.8922 \times 10^{-10}\;\, \mathrm{s})}{\tau_{\mathrm{S}}} \end{array} \end{aligned} $$

(9.138)

and

$$\displaystyle \begin{aligned} \begin{array}{rcl} \varPhi_{00} = (47.1^\circ \pm 2.1^\circ) &\displaystyle +&\displaystyle 310^\circ \frac{(\Delta m - 0.5351 \times 10^{10} \mathrm{s}^{-1})}{\Delta m}\\ &\displaystyle +&\displaystyle 225^\circ \frac{(\tau_{\mathrm{S}} - 0.8922 \times 10^{-10}\;\, \mathrm{s})}{\tau_{\mathrm{S}}}\; . \end{array} \end{aligned} $$

(9.139)

The difference between the two phases comes out to be

$$\displaystyle \begin{aligned} \varPhi_{00} - \varPhi_{+-} = 0.2^\circ \pm 2.6^\circ \pm 1.2^\circ \; . {} \end{aligned} $$

(9.140)

9.5.5.4 Measurements of the Phase Difference Φ ₀₀ − Φ ₊₋

For small |ε′∕ε|, this phase difference is related to ε′∕ε by the equation

$$\displaystyle \begin{aligned} \varPhi_{00} - \varPhi_{+-} = - 3 \, \Im m \left(\frac{\varepsilon'}{\varepsilon}\right)\; . \end{aligned} $$

(9.141)

In this way, the component of ε′ orthogonal to the direction of ε can be measured. In the absence of ${\mathcal {C}\mathcal {P}\mathcal {T} }$ violation and for small |ε′∕ε|, both of the phases Φ ₀₀ and Φ ₊₋ are close to the superweak phase $\varPhi _{{ }_{\mathrm {SW}}}$ (9.102).

The measurement of this phase difference by the NA31 experiment (Sect. 9.5.5.3) was improved by the simultaneous measurement of the time distributions of π ⁺π ⁻ and π ⁰π ⁰ decays behind a regenerator in the kTeV experiment [180] (Sect. 9.5.5.2). Here, the uncertainty arising from the phase of coherent regeneration (which is the determining uncertainty in the Φ ₊₋ measurement) cancels in the comparison of the two decay modes. The authors of [180] conclude that

$$\displaystyle \begin{aligned} \varPhi_{00} - \varPhi_{+-} = (0.39 \pm 0.50)^\circ\; . \end{aligned} $$

(9.142)

Together with an earlier measurement by E731/E773 [179] and the NA31 measurement (9.140), this gives

$$\displaystyle \begin{aligned} \varPhi_{00} - \varPhi_{+-} = (0.36 \pm 0.43)^\circ \; . \end{aligned} $$

(9.143)

9.5.5.5 Measurement of Φ ₊₋ from a Tagged Pure Strangeness State

The CPLEAR experiment (Sect. 9.5.4.7) offers the unique feature of tagging a pure neutral strangeness state K⁰ or $\overline {\mathrm {K^0}}$ produced in a $\overline {p}p$ annihilation at rest by identifying a charged kaon produced in the same reaction. Compared with the vacuum interference experiments (Sect. 9.5.5.3), this offers the advantage of a full-size interference term, whereas in the vacuum interference experiments, an incoherent mixture of (predominantly) K⁰ and $\overline {\mathrm {K^0}}$ forms the initial state, and the interference term is diluted.

The interference term is visualized by measuring the decay-rate asymmetry for decays into π ⁺π ⁻,

$$\displaystyle \begin{aligned} \begin{array}{rcl} A_{+-} (\tau) &\displaystyle =&\displaystyle \frac{\overline{N}(\tau)- N(\tau)}{\overline{N} (\tau)+ N (\tau)} \end{array} \end{aligned} $$

(9.144)

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle =&\displaystyle 2 \, \Re e \,\varepsilon - 2 \,|\eta_{+-}| \mathrm{e}^{-(1/2){\varGamma}_{\mathrm{S}}\tau} \cos (\Delta m\, \tau - \varPhi_{+-})\; . \end{array} \end{aligned} $$

(9.145)

In the corresponding experimental distribution, the background was subtracted and the events were appropriately weighted taking into account the tagging efficiencies for K⁰ and $\overline {\mathrm {K^0}}$. The result is shown in Fig. 9.13 [181]. The result of a fit to these data gives values for Φ ₊₋ and |η ₊₋|, which are correlated with the values chosen for Δm and τ _S, respectively.

Fig. 9.14

Number of accepted 4γ events as a function of χ ² for the K_S → π ⁰π ⁰ (left) and K_L → π ⁰π ⁰ (right) data, and a Monte Carlo calculation of the background originating from K_L → 3π ⁰ decays (dotted). The signal region was taken as χ ² < 9 (NA31 experiment [191])

The correlation parameters are

$$\displaystyle \begin{aligned} \delta \varPhi_{+-} = 0.30 (\Delta m - 0.5301 \times 10^{10} \mbox{ s}^{-1}) \end{aligned} $$

(9.146)

and

$$\displaystyle \begin{aligned} \delta |\eta_{+-}| = 0.09 (\tau_{\mathrm{S}} - 0.8934 \times 10^{-10} \mbox{ s} )\; . \end{aligned} $$

(9.147)

For the values of Δm and τ _S chosen by the authors of [181], the results are

$$\displaystyle \begin{aligned} \begin{array}{rcl} \varPhi_{+-} &\displaystyle =&\displaystyle 43.19^\circ \pm 0.53^\circ\; (\mbox{stat}) \pm 0.28^\circ\; (\mbox{syst}) \pm 0.42^\circ\; (\Delta m)\; , \end{array} \end{aligned} $$

(9.148)

$$\displaystyle \begin{aligned} \begin{array}{rcl} |\eta_{+-}| &\displaystyle =&\displaystyle [2.264 \pm 0.023\; (\mbox{stat}) \pm 0.026\; (\mbox{syst})] \times 10^{-3} \; . \end{array} \end{aligned} $$

(9.149)

A similar asymmetry is obtained for decays to π ⁰π ⁰, although with less statistical weight.

The following values of the ${\mathcal {C}\mathcal {P} }$ parameters in the neutral mode have been extracted:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \varPhi_{00} &\displaystyle =&\displaystyle 42.0^\circ \pm 5.6^\circ\; \mbox{(stat)} \pm 1.9^\circ\; \mbox{(syst)}\; , \end{array} \end{aligned} $$

(9.150)

$$\displaystyle \begin{aligned} \begin{array}{rcl} |\eta_{00}| &\displaystyle =&\displaystyle [2.47 \pm 0.31\; (\mbox{stat}) \pm 0.24 \; \mbox{(syst)}] \times 10^{-3}\; . \end{array} \end{aligned} $$

(9.151)

9.5.5.6 Charge Asymmetry in Semileptonic Decays

This asymmetry δ _L is the third manifestation of ${\mathcal {C}\mathcal {P} }$ violation (9.108). This asymmetry measures the ${\mathcal {C}\mathcal {P} }$ impurity of the long-lived kaon state: $\delta _{\mathrm {L}} = 2 \Re e \, \varepsilon (1-|x|{ }^2)/(|1 - x|{ }^2)$, where x is the $\Delta \mathbb {S} = \Delta Q$ violation parameter. Considerable precision was achieved in the first ten years of experimentation after 1964: for the K_e3 mode, two experiments, by the Princeton group [186] and by the CERN–Heidelberg group [187], have been reported; for the K_μ3 mode, results have been obtained from Stanford [189] and one from the CERN–Heidelberg group [187], and a Brookhaven–Yale group [190] obtained a result for a mixture of both decay modes. Recently, two new results on this asymmetry have been reported by the kTeV and NA48 collaborations. The most significant features of these results are:

• 1. Event numbers of up to 298 million events in the K_e3 mode and 15 million events in the K_μ3 mode.

• 2. An apparatus design such that the decay products (π and electron) traverse only minute amounts of matter (about 0.3–0.4 g cm⁻²), thus diminishing corrections due to secondary interactions of these particles.

• 3. The precision of the K_μ3 asymmetry measurements is a factor of 4 below the value for K_e3, making a comparison between the two possible. Table 9.3 gives the results; the average δ _L = (3.316 ± 0.053) × 10⁻³.

  Table 9.3 Charge asymmetry measurements in K_l3 decays

The charge asymmetries for K_e3 and K_μ3 decays are equal to within 8%: $\delta ^e_{\mathrm {L}}/\delta ^\mu _{\mathrm {L}} = 1.04 \;\pm \; 0.08$. Assuming the validity of the $\Delta Q = \Delta \mathbb {S}$ rule, which is supported by the present experiments, we obtain $\Re e \, \varepsilon = (1.658 \pm 0.026) \times 10^{-3}$. If we use the most precise tests of the $\Delta Q = \Delta \mathbb {S}$ rule by the CPLEAR experiment [185], there is a small correction

$$\displaystyle \begin{aligned} \frac{1 - |x|{}^2}{|1 - x|{}^2} = 0.996 \pm 0.012\,. \end{aligned} $$

(9.152)

9.5.5.7 Parameters of ${\mathcal {C}\mathcal {P} }$ Violation in the K⁰ System: ℑm(ε′∕ε)

K _S Lifetime

We take the average of the older measurements combined with the two most recent measurements by the kTeV collaboration, (0.8965 ± 0.0007) × 10⁻¹⁰ s [180], and by the NA48 collaboration, (0.89598 ± 0.0007) × 10⁻¹⁰ s [197]. Our grand average is

$$\displaystyle \begin{aligned} \tau_{\mathrm{S}} = (0.8959 \pm 0.0004) \times 10^{-10}\;\mathrm{s}\;. \end{aligned} $$

(9.153)

We use this value in the following sections.

Mass Difference Δm

Combining the values from the CERN–Heidelberg experiments [173,174,175] with those from Fermilab E731 and E773 [176, 179], from CPLEAR [181, 198, 199] and from the most precise single measurement by kTeV [180], we obtain

$$\displaystyle \begin{aligned} \Delta m = (0.5286 \pm 0.0011) \times 10^{10}\mbox{ s}^{-1}\;. \end{aligned} $$

(9.154)

Superweak Phase

From the two parameters given above, we obtain the phase of ε in the superweak model,

$$\displaystyle \begin{aligned} \varPhi_{{}_{\mathrm{SW}}} = \arctan \left(\frac{2 \,\Delta m}{{\varGamma}_{\mathrm{S}}}\right) = (43.4 \pm 0.1)^\circ\; . \end{aligned} $$

(9.155)

Moduli of the Amplitudes η ₊₋ and η ₀₀

New measurements of η ₊₋ from the ratio of π ⁺π ⁻ decays and semileptonic decays yield precise values of η ₊₋. We combine these with previous results and obtain [160,161,162].

$$\displaystyle \begin{aligned} |\eta_{+-}| = (2.230 \pm 0.006) \times 10^{-3}\; . \end{aligned} $$

(9.156)

Absolute measurements of the amplitude η ₀₀ are much less precise. A recent average including the CPLEAR result is

$$\displaystyle \begin{aligned} |\eta_{00}| = (2.23 \pm 0.11) \times 10^{-3} \; . \end{aligned} $$

(9.157)

Phase Φ ₊₋

In all measurements, this phase is extracted from an interference term with a beat frequency Δm. Taking the results from NA31 [184], E731 [176], E773 [179], and kTeV [180], together with the pre-1975 data and the result from CPLEAR [181], we obtain the world average

$$\displaystyle \begin{aligned} \varPhi_{+-} = (43.3 \pm 0.4)^\circ \end{aligned} $$

(9.158)

using the values for Δm and τ _S above. This result is in excellent agreement with the value of $\varPhi _{{ }_{SW}} = (43.4 \pm 0.1)^\circ$. Since the interference experiments were evaluated without assuming ${\mathcal {C}\mathcal {P}\mathcal {T} }$ invariance, this constitutes a stringent test of ${\mathcal {C}\mathcal {P}\mathcal {T} }$ invariance. The difference is $\varPhi _{+-} - \varPhi _{{ }_{\mathrm {SW}}} = - (0.1\; \pm \; 0.4)^\circ$. At the same time, this result can again be used to constrain the component of ε′ orthogonal to ε:

$$\displaystyle \begin{aligned} \Im m \left(\frac{\varepsilon'}{\varepsilon}\right) = - (1.7 \pm 7.0) \times 10^{-3}\; . \end{aligned} $$

(9.159)

Therefore, at this level of 10⁻² relative to the amplitude for ${\mathcal {C}\mathcal {P} }$ violation by mixing, ε, there is no evidence for a direct ${\mathcal {C}\mathcal {P} }$ violation amplitude ε′ orthogonal to ε. Our interest now shifts to the component of ε′ parallel to ε, i.e. $\Re e (\varepsilon '/\varepsilon )$.

9.5.6 Elucidation of ${\mathcal {C}\mathcal {P} }$ Violation in K⁰ Decays (II): Discovery of Direct ${\mathcal {C}\mathcal {P} }$ Violation in $\Re e (\varepsilon '/\varepsilon )$

9.5.6.1 Significance of the Double Ratio R

The real part of ε′∕ε is connected with the amplitude ratios η ₀₀ and η ₊₋ of ${\mathcal {C}\mathcal {P}}$-violating K_L decays to ${\mathcal {C}\mathcal {P}}$-conserving K_S decays. A measurement of decay rates with the required precision of 10⁻³ is only possible by measuring the ratio of rates in the same beam in the same time interval. From the Wu–Yang triangle relations (9.90) η ₀₀ = ε − 2ε′ and η ₊₋ = ε + ε′, we obtain

$$\displaystyle \begin{aligned} \Re e \left(\frac{\varepsilon'}{\varepsilon}\right) = \frac{1}{6} \left(1 - \left|\frac{\eta_{00}}{\eta_{+-}}\right|{}^2\right)\; . \end{aligned} $$

(9.160)

A measurement of the double ratio

$$\displaystyle \begin{aligned} R = \frac{|\eta_{00}|{}^2}{|\eta_{+-}|{}^2} = \frac{{\varGamma} (\mathrm{K_L} \rightarrow 2 \pi^0)/{\varGamma} (\mathrm{K_L} \rightarrow \pi^+ \pi^-)}{{\varGamma}(\mathrm{K_S} \rightarrow 2 \pi^0)/{\varGamma}(\mathrm{K_S} \rightarrow \pi^+ \pi^-)} \end{aligned} $$

(9.161)

to a precision of about 0.3% is therefore required to distinguish between the two remaining models, the KM milliweak model and the superweak model. Since the KM model predicts values of $\Re e (\varepsilon '/\varepsilon )$ in the range between 0.2  × 10⁻³ and 3  × 10⁻³, the precision required for detecting a signal of direct ${\mathcal {C}\mathcal {P} }$ violation depends on the actual value. If the largest prediction is realized in nature, a precision of δR  =  5  × 10⁻³ would be sufficient for a three-standard-deviation observation. If, however, the lowest value is realized, a precision of δR  =  0.4  × 10⁻³ would be needed, corresponding to samples of several million events for each of the four decay modes.

9.5.6.2 The NA31 Experiment : First Evidence for Direct ${\mathcal {C}\mathcal {P} }$ Violation

The first observation of direct ${\mathcal {C}\mathcal {P} }$ violation was made by a collaboration of physicists at CERN in 1988 [191]. The experiment, called “North Area No. 31”, or NA31, was based on the concurrent detection of 2π ⁰ and π ⁺π ⁻ decays. Collinear beams of K_L and K_S were employed alternately. The beam layout and the apparatus were described in Sect. 9.5.4.4. The K⁰ → 2π ⁰ → 4γ decays were reconstructed and separated from the background primarily due to K_L → 3π ⁰ → 6γ decays as described in Sect. 9.5.4.2. This background is uniformly distributed in a two-dimensional scatter plot of photon-pair masses, while the 2π ⁰ signal peaks at a point S where both photon pairs have the π ⁰ mass, with a 2 MeV resolution. Signal and background events were counted in equal-area χ ² contours around S. Figure 9.14 shows the χ ² distribution of events in the K_S beam and in the K_L beam. The signal region was taken as χ ² < 9. Background in the K_L data was subtracted by linear extrapolation into the signal region, and amounts to about 4%, while it is negligible in the K_S data.

Fig. 9.15

Event distribution for charged decays as a function of the distance d _T (in cm) between the decay plane and the production target for K_S (left) and K_L (right) decays, and for various background components (right) (NA31 experiment [191])

The K⁰ → π ⁺π ⁻ decays were reconstructed from the four space points of the two pion tracks in two wire chambers. From these tracks, the position of the decay vertex along the beam was reconstructed with a precision of better than 1 m. The energies E ₁ and E ₂ of the two pions were obtained from the energies deposited in the liquid-argon electromagnetic calorimeter and the iron-scintillator hadronic calorimeter. The K⁰ energy was then calculated using the kaon mass and the opening angle θ of the two tracks as constraints from the ratio E ₁∕E ₂:

$$\displaystyle \begin{aligned} E_{{}_{\mathrm{K}}} = \sqrt{\frac{A}{\theta^2} \left( m_{{}_{\mathrm{K}}}^2 - A m_{\pi}^2 \right) } \, , \end{aligned} $$

(9.162)

where

$$\displaystyle \begin{aligned} A = \frac{E_1}{E_2} + \frac{E_2}{E_1} + 2\,. \end{aligned} $$

(9.163)

Background from K⁰ → πeν (K_e3) decay was reduced by comparing, for each track, the energy deposited in the front half of the electromagnetic calorimeter with the energy deposited in the hadron calorimeter.

After cuts on the invariant π ⁺π ⁻ mass and on the transverse location of the center of energy relative to the center of the neutral beam, a residual background of three-body decays was subtracted.

Figure 9.15 shows the transverse distance d _T between the decay plane, as reconstructed from the two tracks, and the K⁰ production target, at the longitudinal position of the target. For K_S decays, this distributions peaks at d _T = 0 with a resolution given by the measurement error and multiple scattering. For K_L decays, in addition to this component of two-body decays from the target, there is a broader distribution mixed in due to three-body decays. The signal region was taken to be d _T < 5 cm, and the three-body background was extrapolated from a control region 7 < d _T < 12 cm. This background amounts to (6.5 ± 2.0) × 10⁻³ of the signal, including systematic uncertainties.

Fig. 9.16

(a) z vertex distribution for reconstructed K → π ⁺π ⁻ decays for the vacuum beam (thick) and regenerator beam (thin histogram). (b) z vertex distribution for reconstructed K → π ⁰π ⁰ decays. (c) Kaon momentum distribution for reconstructed K → π ⁺π ⁻ decays. (d) Kaon momentum distribution for reconstructed K → π ⁰π ⁰ decays. All K → ππ analysis cuts have been applied and background has been subtracted (see [180])

The remaining event sample contained 109  × 10³ of K_L → π ⁰π ⁰, 295  × 10³ of K_L → π ⁺π ⁻, 932  × 10³ of K_S → π ⁰π ⁰, and 2300  × 10³ of K_S → π ⁺π ⁻. In order to equalize the acceptance for K_S decays (with an average decay length of 6 m) to that for the uniformly distributed K_L decays, the K_S data were taken with the K_S target displaced in 1.2 m steps over 48 m such that the distribution of K_S decays became effectively uniform in the fiducial region. This makes the double ratio essentially insensitive to acceptance corrections. The double ratio was evaluated in 10 × 32 bins in energy and vertex position. The weighted average, after all corrections, is

$$\displaystyle \begin{aligned} R = 0.980 \pm 0.004 \;\mbox{(stat)} \pm 0.005 \;\mbox{(syst)}\; . \end{aligned} $$

(9.164)

The corresponding result for the direct-${\mathcal {C}\mathcal {P}}$-violation parameter is [191]

$$\displaystyle \begin{aligned} \Re e \left(\frac{\varepsilon'}{\varepsilon}\right) = (33.0 \pm 11.0) \times 10^{-4}\; . \end{aligned} $$

(9.165)

This, with three-standard-deviation significance, shows that the ${\mathcal {C}\mathcal {P}}$-odd K₂ decays to two pions, and was the first evidence of direct ${\mathcal {C}\mathcal {P} }$ violation .

In further measurements with the NA31 detector, the event numbers recorded were considerably increased, by a factor of four, thus decreasing the statistical error. In addition, the background from K_e3 decays was reduced by introducing a two-stage transition radiation detector as an additional identifier for electrons. With these improved data, the double ratio was measured with reduced uncertainty. Including the former result, the double ratio obtained is

$$\displaystyle \begin{aligned} R = 0.982 \pm 0.0039\; , \end{aligned} $$

(9.166)

leading to a value

$$\displaystyle \begin{aligned} \Re e \left(\frac{\varepsilon'}{\varepsilon}\right) = (23.0 \pm 6.5) \times 10^{-4}\; , \end{aligned} $$

(9.167)

or 3.5 standard deviations from zero.

9.5.6.3 The Experiment E731 at Fermilab

In this experiment [177] charged and neutral decays were registered in separate runs with a slightly different detector. On the other hand, in E731 K_L and K_S decays were collected simultaneously using a split beam: in one half of the beam cross section, K_L mesons from the target were allowed to decay over a long decay region of 27 m (charged decays) or 42 m (neutral decays), while in the other half, the K_L beam hit a block of B₄C, whereby a beam of K_S mesons was regenerated.

The vertex distribution of the events from regenerated K_S was concentrated in a small region behind the regenerator, positioned at 123 m from the target, owing to the typical K_S decay length of 5 m. On the other hand, the vertex distribution of K_L → π ⁰π ⁰ decays extended from 110 to 152 m from the target. The detector acceptances for K_L and K_S decays therefore were very different, and since the decay volumes for K_L → π ⁺π ⁻ and K_L → π ⁰π ⁰ were different, this acceptance correction does not cancel in the double ratio.

The π ⁺π ⁻ decays were selected by requiring the invariant ππ mass to be near the kaon mass and the transverse kaon momentum to satisfy ${p^2_{\mathrm t} < 250 \mbox{ MeV}^2/c^2}$. The background from incoherent kaon regeneration amounted to (0.155 ± 0.014)%. The extrapolated 3π ⁰ background under the peak is 1.78% and 0.049% in the vacuum and regenerator beams, respectively. Neutral background from incoherent scattering in the regenerator was subtracted by evaluating the distribution of the transverse center of energy of each event around the center of each beam. After this background subtraction, the event numbers in the vacuum beams were 327  × 10³ (π ⁺π ⁻) and 410  × 10³ (π ⁰π ⁰). In the regenerator beams, there were 1.06 × 10⁶π ⁺π ⁻ events and 0.800 × 10⁶ 2π ⁰ events. The regeneration amplitude was assumed to fall in accordance with a power of the kaon momentum, p ^α. In the fit, the parameter α, the regeneration amplitude at 70 GeV/c momentum, and $\Re e (\varepsilon '/\varepsilon )$ were varied. The results were

$$\displaystyle \begin{aligned} \alpha = - 0.6025 \pm 0.0065 \end{aligned} $$

(9.168)

and

$$\displaystyle \begin{aligned} \Re e \left(\frac{\varepsilon'}{\varepsilon}\right) = \left(7.4 \pm 5.2\; \mbox{(stat)} \pm 2.9\; \mbox{(syst)}\right) \times 10^{-4}\; , \end{aligned} $$

(9.169)

where the systematic uncertainty includes a part from acceptance calculations (1.19  × 10⁻⁴) and from the energy calibration (1.6  × 10⁻⁴). The authors of [177] deduce an upper limit $\Re e (\varepsilon '/\varepsilon ) < 17 \times 10^{-4}\; (95\% \mbox{ C.L.})$, which is at variance with the observation of the NA31 experiment.

9.5.6.4 The kTeV Experiment at Fermilab

The disagreement between the positive result of NA31 and the null result of E731 left an unsatisfactory state of affairs. For this reason, new experiments with a tenfold increase in data-taking capacity and reduced systematic uncertainty were designed, at both Fermilab and CERN.

The Fermilab experiment at the 800 GeV Tevatron, called kTeV, was described in Sect. 9.5.4.6 [180]. The main improvements compared with E731 were:

• all four decay modes were measured concurrently;

• the electromagnetic calorimeter was made of CsI, with much improved energy resolution;

• the regenerator at 123 m from the target was made of plastic scintillator, viewed by photomultipliers such that inelastic regeneration could be detected by the recoiling nucleus;

• the kaon momentum range from 40 to 160 GeV/c and the decay vertex region from 110 m to 158 m from the target were the same for all decay modes.

As in the E731 experiment, a double beam of K_L and regenerated K_S entered the decay volume. K⁰ → π ⁺π ⁻ decays were identified by their invariant mass. Semileptonic K_e3 events were reduced by a factor of 1000 by requiring the ratio of the calorimetric energy E of a track to its momentum p to be less than 0.85. K_μ3 events were rejected by registering the muon penetrating the 4 m iron wall. The invariant-ππ-mass shows a rms mass resolution of 1.6 MeV, and events in the range 488–508 MeV were selected. Background from K_S produced in incoherent regeneration was suppressed mainly by vetoing events with a signal generated in the active regenerator indicating the recoil of a nucleus in the scattering process. Further reduction of this background was achieved by extrapolating the kaon direction back to the regenerator exit face and calculating the transverse momentum of the kaon relative to the line connecting this intercept with the target position. After a cut against the backgrounds from semileptonic decays and from collimator scattering, 11.1 million and 19.29 million π ⁺π ⁻ events remain in the vacuum beam and regenerator beam samples, respectively.

The selection of 2π ⁰ events follows the lines described in Sect. 9.5.4.2. Events with an invariant π ⁰π ⁰ mass between 490 and 505 MeV were selected. Events in which a kaon scatters in the collimator or the regenerator were reduced by a cut in the ring number (RING), defined by the maximum deviation Δx _coe or Δy _coe (in cm) of the center of energy of all showers from the center of the corresponding beam spot at the CsI position, to which the event was assigned by use of the x-position of the center of energy:

$$\displaystyle \begin{aligned} \mathrm{RING} = 4 \times \mathrm{Max} (\Delta x^2_{\mathrm{coe}}, \Delta y^2_{\mathrm{coe}})\;. \end{aligned} $$

(9.170)

The signal was selected by the cut RING < 110 cm². The largest background comes from regenerator scattering in the regenerator beam, 1.13%, adding up to a total of 1.235% in that beam. Also, in the vacuum beam, the events scattered in the nearby regenerator make the largest contribution to the background, 0.25%, which is 0.48% in total. After all cuts and background subtraction, the remaining signal consists of 3.3 million and 5.55 million events in the vacuum and regenerator beams, respectively. The 3.3 million K_L → π ⁰π ⁰ events are the limiting factor in the statistical uncertainty in the double ratio .

Since the vertex distributions of K_L decays (flat) and K_S decays (concentrated behind the regenerator) are very different, the raw double ratio has to be corrected by the double ratio of acceptances (Fig. 9.16). The quality of the Monte Carlo simulations for the acceptances was checked by reproducing the z vertex distributions of the vacuum beam data for different decay modes (Fig. 9.17). In general the agreement is good, except that the π ⁺π ⁻ data show a slope of (−0.70 ± 0.30) × 10⁻⁴∕m.

Fig. 9.17

(a) Comparison of the vacuum beam z distributions for data (dots) and MC calculations (histograms). The data-to-MC ratios (b) have been fitted to a line, and the z slopes are shown. The neutral distributions are for the combined 1996 + 1997 samples; the charged distributions are for 1997 only (kTeV experiment [180])

Fig. 9.18

(a), (c) Minimal difference between tagger time and event time (Δt _min). (b) Δt _min for charged K_L and K_S events. (d) Comparison between charged and neutral event times. For this measurement, decays with tracks selected by the neutral trigger were used (γ conversion and Dalitz decays $\mathrm {K_S} \rightarrow \pi ^0 \pi ^0_{\mathrm {D}} \rightarrow \gamma \gamma \gamma e^+ e^-$) (NA48 experiment [201])

The result for $\Re e (\varepsilon '/\varepsilon )$ is [180]

$$\displaystyle \begin{aligned} \Re e \left(\frac{\varepsilon'}{\varepsilon}\right) = (20.71 \pm 1.48\; \mbox{(stat)} \pm 2.39\; \mbox{(syst)}) \times 10^{-4} = (20.7 \pm 2.8) \times 10^{-4}\; . \end{aligned} $$

(9.171)

The systematic uncertainty for the neutral decays is mainly due to background, CsI energy calibration and acceptance corrections; for the charged decays, it is mainly due to uncertainties in the acceptance and trigger efficiency.

The acceptance correction that has to be applied is about 5 × 10⁻² for R, or ∼ 80 × 10⁻⁴ for $\Re e (\varepsilon '/\varepsilon )$, four times larger than the signal.

9.5.6.5 The NA48 Experiment

When the NA31 observation of a nonvanishing $\Re e (\varepsilon '/\varepsilon )$ was not confirmed by the result from the E731 experiment, the CERN-based collaboration set out to construct a new, improved detector with the goal of achieving a precision measurement of $\Re e (\varepsilon '/\varepsilon )$ with a total uncertainty of 0.2 × 10⁻⁴.

The new experiment was designed

• to measure all four decay modes concurrently by using two incident proton beams;

• to improve on neutral-background rejection by developing a liquid-krypton electromagnetic calorimeter with substantially better energy resolution;

• to improve on charged-background rejection by using a magnetic spectrometer.

The resulting beam and detector have been described in Sect. 9.5.4.5. Data were taken in 1997, 1998 and 1999 with 450 GeV protons. In the design of the NA48 detector, the cancellation of systematic uncertainties in the double ratio was exploited as much as possible [201]. Important properties of the experiment are

• two almost collinear beams , which lead to almost identical illumination of the detector, and

• the K_S lifetime weighting of the events defined as K_L events.

The K_L target was located 126 m upstream of the beginning of the decay region, and the K_S target 6 m upstream of the decay region. The beginning of the K_S decay region was defined by an anti-counter used to veto kaon decays occurring upstream of the counter and defining the global kaon energy scale.

The identification of K_S decays was done by a detector (tagger ) consisting of an array of scintillators situated in the proton beam directed on to the K_S target. To identify events coming from the K_S target a coincidence window of ± 2 ns between the proton signal in the tagger and the event time was chosen (see Fig. 9.18). Owing to inefficiencies in the tagger and in the proton reconstruction, a fraction $\alpha _{{ }_{\mathrm {SL}}}$ of true K_S events are misidentified as K_L events. On the other hand, there is a constant background of protons in the tagger which have not led to a good K_S event. If those protons accidentally coincide with a true K_L event, this event is misidentified as a K_S decay. This fraction $\alpha _{{ }_{\mathrm {LS}}}$ depends only on the proton rate in the tagger and the width of the coincidence window.

Fig. 9.19

Comparison of the $p_{\mathrm {t}}^{\prime 2}$ tail of the K_L → π ⁺π ⁻ candidates with the sum of all known components (NA48 experiment [201])

Both effects, $\alpha ^{+-}_{{ }_{\mathrm {SL}}}$ and $\alpha ^{+-}_{{ }_{\mathrm {LS}}}$, can be measured (see Fig. 9.18b) in the charged mode, as K_S and K_L events can be distinguished by the vertical position of the decay vertex. The results are $\alpha ^{+-}_{{ }_{\mathrm {SL}}} = (1.63 \pm 0.03)\times 10^{-4}$ for the data from 1998/1999 and (1.12 ± 0.03) × 10⁻⁴ for the data from 2001. For the accidental-tagging rate, the value measured was $\alpha ^{+-}_{{ }_{\mathrm {LS}}}=(10.649 \pm 0.008)$% for the 1998/1999 data sample and (8.115 ± 0.010)% for the 2001 sample, owing to the lower instantaneous beam intensity. This means that about 11% or 8% of true K_L events are misidentified as K_S events; however, this quantity is precisely measured to the 10⁻⁴ level here. For the measurement of R the difference between the charged and the neutral decay modes, $\Delta \alpha _{{ }_{\mathrm {LS}}} = \alpha ^{00}_{{ }_{\mathrm {LS}}} - \alpha ^{+-}_{{ }_{\mathrm {LS}}}$, is important. Proton rates in the sidebands of the tagging window were measured in both modes to determine $\Delta \alpha _{{ }_{\mathrm {LS}}}$. The result is $\Delta \alpha _{{ }_{\mathrm {LS}}} = (4.3 \pm 1.8) \times 10^{-4}$ for the 1998/1999 event sample and (3.4 ± 1.4) × 10⁻⁴ for the 2001 event sample. Several methods have been used to measure $\Delta \alpha _{{ }_{\mathrm {SL}}}$, leading to the conclusion that there is no measurable difference between the mistaggings measured by different methods within an uncertainty of ± 0.5 × 10⁻⁴.

Another important correction is the background subtraction. Decays of the types K_L → πeν and K_L → πμν can be misidentified as K → π ⁺π ⁻ decays, as the ν is undetectable. These events were identified by their high transverse momentum $p_{\mathrm {t}}^{\prime }$ and their reconstructed invariant mass. The remaining background can be measured by extrapolating the shape of the background in the $p_{\mathrm {t}}^{\prime 2}$ distribution into the signal region (Fig. 9.19). In this way, the charged background fraction leads to an overall correction to R of (16.9 ± 3.0) × 10⁻⁴ for the 1998/1999 data and (14.2 ± 3.0) × 10⁻⁴ for the 2001 sample.

Fig. 9.20

Distribution of the K_S → π ⁰π ⁰ candidates in the space of two reconstructed values of m _γγ. The contours correspond to increments of one standard deviation (NA48 experiment [201])

The reconstruction of π ⁰π ⁰ decays followed the principles described in Sect. 9.5.4.2. The two γγ masses for the best pairing are anticorrelated because of the constraint of the kaon mass (Fig. 9.20). The ellipses in Fig. 9.20 designate contours with increments of one standard deviation. The background from 3π ⁰ decays with two undetected photons is distributed with constant probability over each ellipse, as shown by Monte Carlo calculations. This leads to a correction to R of (−5.9 ± 2.0) × 10⁻⁴ for the 1998/1999 sample and (−5.6 ± 2.0) × 10⁻⁴ for the 2001 sample.

The numbers of signal events after these corrections are summarized in Table 9.4.

Table 9.4 Event numbers of the NA48 experiment after tagging correction and background subtraction [201, 202]

The efficiency of the triggers used to record neutral and charged events has been determined. In the neutral decay mode the efficiency was measured to be 0.99920 ± 0.00009, without any measurable difference between K_S and K_L decays. The π ⁺π ⁻ trigger efficiency was measured to be (98.319 ± 0.038)% for K_L and (98.353 ± 0.022)% for K_S decays. Here, a small difference between the trigger efficiencies for K_S and K_L decays was found. This leads to a correction to the double ratio of (−4.5 ± 4.7) × 10⁻⁴ for the 1998/1999 sample and (5.2 ± 3.6) × 10⁻⁴ for the 2001 sample.

Other systematic uncertainties include the limited knowledge of the energy scale, nonlinearities in the calorimeter, and small acceptance corrections.

Summing all corrections to and systematic uncertainties in R, the authors find the amount to (35.9 ± 12.6) × 10⁻⁴ for the 1998/1999 data and (35.0 ± 11.0) × 10⁻⁴ for the 2001 data.

The corresponding result for the direct-${\mathcal {C}\mathcal {P}}$-violation parameter is

$$\displaystyle \begin{aligned} \Re e \left(\frac{\varepsilon'}{\varepsilon}\right) = (15.3 \pm 2.6) \times 10^{-4} \end{aligned} $$

(9.172)

for the data from 1997 [203] and 1998/1999 [201], and

$$\displaystyle \begin{aligned} \Re e \left(\frac{\varepsilon'}{\varepsilon}\right) = (13.7 \pm 3.1) \times 10^{-4} \end{aligned} $$

(9.173)

for the data from 2001 [202].

A comparison of these two values is significant because they were obtained at different average beam intensities. The combined final result from the NA48 experiment is

$$\displaystyle \begin{aligned} \Re e \left(\frac{\varepsilon'}{\varepsilon}\right) = (14.7 \pm 1.4\; \mbox{(stat)} \pm 0.9\; \mbox{(syst)} \pm 1.5\; \mbox{(MC)}) \times 10^{-4} = (14.7 \pm 2.2) \times 10^{-4}\;. \end{aligned} $$

(9.174)

9.5.6.6 Conclusions About Direct ${\mathcal {C}\mathcal {P} }$ Violation, $\Re e (\varepsilon '/\varepsilon )$ and the Wu–Yang Triangle

The two experiments kTeV and NA48 have definitively confirmed the original observation of the NA31 team that direct ${\mathcal {C}\mathcal {P} }$ violation exists. The results of all published experiments on 𝜖′∕𝜖 are shown in Fig. 9.21. Therefore, ${\mathcal {C}\mathcal {P} }$ violation as observed in the K meson system is a part of the weak interaction due to weak quark mixing. Exotic, new interactions such as the superweak interaction are not needed. We therefore have a very precise experimental result for ε′∕ε. The theoretical calculations of ε′∕ε within the Standard Model, however, are still not very precise. This does not change the main conclusion of the experiments that ε′ is different from zero and positive, i.e. direct ${\mathcal {C}\mathcal {P} }$ violation exists.

Fig. 9.21

Time sequence of published measurements of the parameter $\Re e (\varepsilon '/\varepsilon )$ of direct ${\mathcal {C}\mathcal {P} }$ violation. The experiments at CERN are marked by filled circles and the experiments at Fermilab are marked by open squares. The kTeV result from 2003 is a reanalysis of the data from the kTeV 1999 result (see [204] and also [180, 200,201,202,203])

If we take into account the four relevant experiments NA31, E731, NA48, and kTeV, the weighted average comes out to be

$$\displaystyle \begin{aligned} \Re e \left(\frac{\varepsilon'}{\varepsilon}\right) = (16.7 \pm 1.6) \times 10^{-4}\; . {} \end{aligned} $$

(9.175)

The consistency of the result is not completely satisfactory, since χ ²∕ndf = 6.3∕3. If the phase of ε′ as defined in (9.92), $\arg \varepsilon ' = (42.3 \pm 1.5)^\circ$ [149], is inferred, then a more precise value for the component of ε′ transverse to ε can be derived.

We have done a complete fit to the Wu–Yang triangle (9.90), using as input

$$\displaystyle \begin{aligned} \Re e \left(\frac{\varepsilon'}{\varepsilon}\right) = (16.7 \pm 1.6) \times 10^{-4} ,\quad \Re e \, \varepsilon = (1.658 \pm 0.0265) \times 10^{-3} \; , \end{aligned}$$

$$\displaystyle \begin{aligned} \varPhi_{+-} = 43.3^\circ \pm 0.4^\circ ,\quad \varPhi_{00} - \varPhi_{+-} = (0.36 \pm 0.43)^\circ \; , \end{aligned}$$

$$\displaystyle \begin{aligned} |\eta_{+-}| = (2.230 \pm 0.006)\times 10^{-3} ,\quad |\eta_{00}|=(2.225 \pm 0.007) \times 10^{-3} \; , \end{aligned}$$

$$\displaystyle \begin{aligned} \arg \, \varepsilon = 43.4 \pm 0.1^\circ,\quad \arg \, \varepsilon' = 42.3^\circ \pm 1.5^\circ \,. \end{aligned}$$

The result of this fit is, with χ ²∕ndf = 3∕4

$$\displaystyle \begin{aligned} \Im m \left(\frac{\varepsilon'}{\varepsilon}\right) = (-3.2 \pm 4.4)\times 10^{-5} \end{aligned} $$

(9.176)

and

$$\displaystyle \begin{aligned} \Im m \, \varepsilon = (1.530 \pm 0.005)\times 10^{-3} \; . \end{aligned} $$

(9.177)

Also, the real part of ε is constrained by the fit:

$$\displaystyle \begin{aligned} \Re e \, \varepsilon = (1.619 \pm 0.005)\times 10^{-3} \end{aligned}$$

The result of this fit is expressed in correlation plots for $\Re e\, \varepsilon$ and ℑmε, and for $\Re e (\varepsilon '/\varepsilon )$ and ℑm(ε′∕ε), in Fig. 9.22.

Fig. 9.22

Result of the fit to the Wu–Yang triangle relations between η ₊₋, η ₀₀, ε and ε′. (a) Correlation of $\Re e\, \varepsilon$ and ℑmε ; (b) correlation of $\Re e (\varepsilon '/\varepsilon )$ and ℑm(ε′∕ε). The boundaries of the black areas correspond to one-standard-deviation uncertainties

The result for direct ${\mathcal {C}\mathcal {P} }$ violation (9.175) can also be quoted as a decay asymmetry between the K⁰ and $\overline {\mathrm {K^0}}$ decay rates to a π ⁺π ⁻ final state. If the amplitudes are called a = amp(K⁰ → π ⁺π ⁻) and $\overline {a} = \mathrm {amp}(\overline {\mathrm {K^0}} \to \pi ^+ \pi ^-)$, then this asymmetry is

$$\displaystyle \begin{aligned} A = \frac{{\varGamma}(\mathrm{K^0} \rightarrow \pi^+ \pi^-) - {\varGamma}(\overline{\mathrm{K^0}} \rightarrow \pi^+ \pi^-)}{{\varGamma}(\mathrm{K^0} \rightarrow \pi^+ \pi^-) + {\varGamma}(\overline{\mathrm{K^0}} \rightarrow \pi^+ \pi^-)} = \frac{|a|{}^2 - |\overline{a}|{}^2}{|a|{}^2 + |\overline{a}|{}^2}\; . \end{aligned} $$

(9.178)

Since $\overline {a}/a = 1 - 2 \varepsilon '$, we obtain

$$\displaystyle \begin{aligned} \left|\frac{\overline{a}}{a}\right|{}^2 = 1 - 4\, \Re e\, \varepsilon' \end{aligned} $$

(9.179)

and

$$\displaystyle \begin{aligned} A = 2\, \Re e\, \varepsilon' = 2 \left( \Re e\, \varepsilon \; \Re e \left(\frac{\varepsilon'}{\varepsilon} \right) - \Im m\, \varepsilon \; \Im m \left(\frac{\varepsilon'}{\varepsilon} \right) \right) = (5.5 \pm 0.6) \times 10^{-6}\; . \end{aligned} $$

(9.180)

This very small decay rate asymmetry can be compared with the large values of some similar observables in the B system.

9.6 The Neutral B Meson System

The KM model today often also referred as CKM¹ mechanism of the Standard Model predicts direct ${\mathcal {C}\mathcal {P} }$ violation for the neutral K meson system and it was thus a strong support for the theory when a finite value of $\Re e(\varepsilon '/\varepsilon )$ was observed. The ultimate test of the quark-mixing paradigm however was the precise study of ${\mathcal {C}\mathcal {P} }$ violation in the neutral B meson system for which the theory predicted large ${\mathcal {C}\mathcal {P} }$ violation. The discovery of $\mathrm {B^0} - \overline {\mathrm {B^0}}$ mixing in 1987 [58] made the B⁰ system the prime candidate for observing ${\mathcal {C}\mathcal {P} }$ violation in a physical system different from the neutral kaon. The observation of large time-dependent ${\mathcal {C}\mathcal {P} }$ asymmetries in B⁰ decays in 2001 by the B-factories [59, 60] allowed the determination of the complex phase δ of the CKM matrix and as a consequence provided a first sensitive test of the unitarity of the quark mixing matrix. With the observation of the $\mathrm {B}^0_{\mathrm {s}}$ meson mixing in 2006 [61] a second B meson system became available for precise mixing studies and studies of ${\mathcal {C}\mathcal {P} }$ violating effects. With the start of the LHCb experiment [62] the focus of the B meson studies have changed. Precision measurements no longer aim to prove the CKM paradigm but look for small deviations from the theory predictions as possible smoking-guns for physics beyond the description of the Standard Model.

9.6.1 Phenomenology of Mixing in the Neutral B Meson System

The parameters of mixing in the two neutral B mesons—the B⁰ with quark content ($\bar {b}d$) and the $\mathrm {B}^0_{\mathrm {s}}$ with quark content ($\bar {b}s$), in the following they are called both generically B⁰—are very different from those observed in the neutral K meson system. In Sect. 9.3 the complex decay parameters γ _h and γ _l are defined for the heavy (h) and light (l) meson states (see Eq. (9.41)):

$$\displaystyle \begin{aligned} \begin{array}{rcl} \gamma_h &\displaystyle =&\displaystyle i m_h + \frac{\Gamma_h}{2} \; , \\ \gamma_l &\displaystyle =&\displaystyle i m_l + \frac{\Gamma_l}{2} \; . \ \end{array} \end{aligned} $$

With these parameters the time evolution of the neutral B states can be written as (see Eqs. (9.34) and (9.40))

$$\displaystyle \begin{aligned} \begin{array}{rcl} \left|\mathrm{B}_h (t)\right\rangle &\displaystyle =&\displaystyle (p \left|\mathrm{B^0} \right\rangle- q \left|\overline{\mathrm{B^0}}\right\rangle) \mathrm{e}^{-\gamma_h t} \; , \\ \left|\mathrm{B}_l (t)\right\rangle &\displaystyle =&\displaystyle (p \left|\mathrm{B^0}\right\rangle + q \left|\overline{\mathrm{B^0}}\right\rangle) \mathrm{e}^{-\gamma_l t}\; . {} \end{array} \end{aligned} $$

(9.181)

The two initial states at t = 0, with a definite quantum number ${\mathbb {B}\;}$, are

$$\displaystyle \begin{aligned} \psi_{{}_{\mathrm{B}}} (0) = \mathrm{B^0} \mbox{ and } \psi_{{}_{\overline{B}}}(0) = \overline{\mathrm{B^0}}\; . \end{aligned} $$

(9.182)

Their decay law is not any longer exponential and results to a finite probability P for a flavor change given by Eqs. (9.44) and (9.45). In the Standard Model, the ${\mathcal {C}\mathcal {P} }$ violation in mixing of neutral B mesons is expected to be very small, such that |q∕p| = 1 within $\mathcal {O}(10^{-4})$ and $\mathcal {O}(10^{-5})$ for the B⁰ and the $\mathrm {B}^0_{\mathrm {s}}$ system respectively [63]. In this approximation the mixing probabilities for the two B⁰ and $\overline {\mathrm {B^0}}$ are equal, i.e.

$$\displaystyle \begin{aligned} P (\mathrm{B^0} \rightarrow \overline{\mathrm{B^0}}) = P (\overline{\mathrm{B^0}} \rightarrow \mathrm{B^0})\; , \end{aligned} $$

(9.183)

and Eq. (9.44) can be written as

$$\displaystyle \begin{aligned} P (\mathrm{B^0} \rightarrow \overline{\mathrm{B^0}}) =\frac{1}{2} \mathrm{e}^{-T} \left(\cosh y T - \cos x T \right) = \frac{1}{2} \mathrm{e}^{-\varGamma t} \left( \cosh \frac{\Delta\Gamma t}{2} - \cos (\Delta m\, t) \right)\, . {} \end{aligned} $$

(9.184)

Correspondingly, the probability for remaining in the original beauty state is,

$$\displaystyle \begin{aligned} P (\mathrm{B^0} \rightarrow \mathrm{B^0}) = P (\overline{\mathrm{B^0}} \rightarrow \overline{\mathrm{B^0}}) = \frac{1}{2} \mathrm{e}^{-\varGamma t} \left( \cosh \frac{\Delta\Gamma t}{2} + \cos (\Delta m\, t) \right)\, . {} \end{aligned} $$

(9.185)

One thus obtains for the flavor asymmetry at time t of an initially pure flavor state (see Eq. (9.50)):

$$\displaystyle \begin{aligned} A(t) = \frac{P (\mathrm{B^0} \rightarrow \mathrm{B^0}) - P (\mathrm{B^0} \rightarrow \overline{\mathrm{B^0}})} {P (\mathrm{B^0} \rightarrow \mathrm{B^0}) + P (\mathrm{B^0} \rightarrow \overline{\mathrm{B^0}})} = \frac{\cos (\Delta m\, t) }{\cosh \frac{\Delta\Gamma t}{2} } {} \end{aligned} $$

(9.186)

The mixing parameter x is determined through short-range interactions given by box diagrams of the type shown in Fig. 9.23. For the B⁰ mixing the diagrams with a virtual t quark dominate and one obtains [63, 65] for the mixing parameter x,

$$\displaystyle \begin{aligned} x \equiv \frac{\Delta m}{\varGamma} = \frac{G^2_{{}_{\mathrm{F}}}}{6{\pi^2}} \mathcal{ B}_{{}_{\mathrm{B_q}}} f^2_{{}_{\mathrm{B_q}}} m_{{}_{\mathrm{B_q}}} \tau_{{}_{\mathrm{B_q}}} |V_{tb}^{*} V_{tq}|{}^2 M_{\mathrm{W}}^2 F\left(\frac{m_t^2}{M_{\mathrm{W}}^2}\right) \eta_{{}_{\mathrm{QCD}}} {} \end{aligned} $$

(9.187)

with index q = d(s) for the B⁰ ($\mathrm {B}^0_{\mathrm {s}}$) respectively. Here, $m_{{ }_{\mathrm {B_q}}}$ and $\tau _{{ }_{\mathrm {B_q}}}$ are the mass and the lifetime of the neutral B meson, $\mathcal {B}_{\mathrm {B_q}}$ is the bag factor parametrizing the probability that the d (s) and the $\overline {b}$ quarks will form a B⁰ ($\mathrm {B}^0_{\mathrm {s}}$) hadron, $f_{\mathrm {B_q}}$ is the B meson decay constant, F is the calculated loop function, increasing with the top quark mass squared $m^2_t$, and $\eta _{{ }_{\mathrm {QCD}}} \approx 0.8$ is a QCD correction. The parameters $G_{{ }_{\mathrm {F}}}$ and M _W are the Fermi coupling constant and the mass of the W boson and V _ij are the CKM matrix elements (see Sect. 9.7).

Fig. 9.23

Feynman diagrams of the B⁰ mixing

For the B⁰ meson the lifetimes of the heavy and light state are approximately equal, Γ _h = Γ _l = Γ , and y =  ΔΓ∕2Γ ≈ 0. In this case the flavor asymmetry simplifies to $A(t) = \cos \left ( \Delta m t\right )$. For the $\mathrm {B}^0_{\mathrm {s}}$ meson a significant lifetime difference between the heavy and light states arises due to different decay channels as result of the different ${\mathcal {C}\mathcal {P} }$ eigenvalues of the two mass states. The lifetime or width difference can thus be measured using final states with defined ${\mathcal {C}\mathcal {P} }$ values.² From recent theory calculations one expects for the $\mathrm {B}_{\mathrm {s}}^0$ meson Δ Γ∕ Γ ≈ 13% [64, 66]. It should further be noted that applying the definition of Sect. 9.3 for Δ Γ leads to a negative width differences for the $\mathrm {B}^0_{\mathrm {s}}$ mesons. It is therefore common practice [67] to redefine Δ Γ to be positive,

$$\displaystyle \begin{aligned} \Delta\Gamma = \Gamma_l - \Gamma_h \, . {} \end{aligned} $$

(9.188)

To test the approximation |q∕p|≈ 1, i.e. the assumption of vanishing ${\mathcal {C}\mathcal {P} }$ violation in the mixing,

$$\displaystyle \begin{aligned} a_{\mathrm{mix}} = \frac{ P (\overline{\mathrm{B^0}} \rightarrow \mathrm{B^0}) - P (\mathrm{B^0} \rightarrow \overline{\mathrm{B^0}}) }{ P (\overline{\mathrm{B^0}} \rightarrow \mathrm{B^0}) + P (\mathrm{B^0} \rightarrow \overline{\mathrm{B^0}}) } = \frac{1 - \left| q/p\right|{}^4}{1 + \left| q/p\right|{}^4} \approx 0 \, , \end{aligned}$$

one can measure the semi-leptonic ${\mathcal {C}\mathcal {P} }$ asymmetry for the two B⁰ species (see Eq. (9.56)),

$$\displaystyle \begin{aligned} a_{\mathrm{S}\mathrm{L}} = \frac{ \Gamma(\overline{B^0}(t)\rightarrow \ell^+ \nu X) - \Gamma(B^0(t)\rightarrow \ell^- \overline{\nu} X) }{ \Gamma(\overline{B^0}(t)\rightarrow \ell^+ \nu X) + \Gamma(B^0(t)\rightarrow \ell^- \overline{\nu} X)} = a_{\mathrm{mix}} \, , {} \end{aligned} $$

(9.189)

where the detection of a B⁰ decaying into a wrong-sign muon $B^0 \rightarrow \overline {B^0} \rightarrow \ell ^- \overline {\nu } X$ indicates mixing.

The measurement of the time-dependent ${\mathcal {C}\mathcal {P} }$ asymmetry between the decays of a B⁰ and a $\overline {\mathrm {B^0}}$ to a common final state f probes the ${\mathcal {C}\mathcal {P} }$ violation in the interference between the decay with and without mixing. Following Eq. (9.51) one introduces the decay amplitudes

$$\displaystyle \begin{aligned} \begin{array}{rcl} A_f &\displaystyle =&\displaystyle \langle f |T|\mathrm{B^0} \rangle\;, \;\;\; A_{\bar{f}} = \langle \bar{f}|T|\mathrm{B^0} \rangle\; ,\\ \overline{A_f} &\displaystyle =&\displaystyle \langle f|T|\overline{\mathrm{B^0}}\rangle\;, \;\;\; \overline{A_{\bar{f}}} = \langle \bar{f}|T|\overline{\mathrm{B^0}}\rangle\;. \end{array} \end{aligned} $$

(9.190)

The theoretical description simplifies if decays to ${\mathcal {C}\mathcal {P} }$ eigenstates B → f _CP are used. These final states fulfill $\mathcal {C}\mathcal {P} \left | f_{CP} \right \rangle = \left | \overline {f_{CP}} \right \rangle = \eta _{CP} \left | f_{CP} \right \rangle$ with η _CP = ±1 and $\overline {A_f} = \eta _{CP} \overline {A_{\bar {f}}}$.

Using Eq. (9.42), one obtains the decay rates of initially pure B⁰ and $\overline {\mathrm {B^0}}$ states,

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{\mathrm{d}N(t)}{\mathrm{d}t} &\displaystyle =&\displaystyle \frac{1}{4} \left| \left( \mathrm{e}^{-\gamma_h t} + \mathrm{e}^{-\gamma_l t}\right)A_f - \frac{q}{p} \left( \mathrm{e}^{-\gamma_h t} - \mathrm{e}^{-\gamma_l t}\right)\overline{A_f}\right|{}^2 \; , \\ \frac{\mathrm{d}\overline{N}(t)}{\mathrm{d}t} &\displaystyle =&\displaystyle \frac{1}{4} \left| \left( \mathrm{e}^{-\gamma_h t} + \mathrm{e}^{-\gamma_l t}\right)\overline{A_f} - \frac{p}{q} \left( \mathrm{e}^{-\gamma_h t} - \mathrm{e}^{-\gamma_l t}\right){A_f}\right|{}^2 \,. \end{array} \end{aligned} $$

(9.191)

The time dependent ${\mathcal {C}\mathcal {P} }$ asymmetry is defined as

$$\displaystyle \begin{aligned} a_{CP}(t) = \frac{\mathrm{d}\overline{N}-\mathrm{d}N}{\mathrm{d}\overline{N}+\mathrm{d}N} \, . {}\end{aligned} $$

(9.192)

Neglecting the very small deviation of $\left |q/p\right |$ from unity (i.e. ${\mathcal {C}\mathcal {P} }$ violation in mixing) and using the ratio defined in Eq. (9.53),

$$\displaystyle \begin{aligned} \lambda_f = \frac{q \overline{A_f}}{p A_f} \;, {}\end{aligned} $$

(9.193)

one obtains for a _CP(t) [68],

$$\displaystyle \begin{aligned} a_{CP}(t) = - \frac{ A_{CP}^{dir} \cos{}(\Delta m t) + A_{CP}^{mix} \sin{}(\Delta m t) } { \cosh(\frac{\Delta \Gamma}{2} t ) + A_{\Delta\Gamma} \sinh(\frac{\Delta \Gamma}{2} t ) } {}\end{aligned} $$

(9.194)

with

$$\displaystyle \begin{aligned} A_{CP}^{dir} = \frac{1 -\left| \lambda_f \right|{}^2}{1 + \left| \lambda_f \right|{}^2}\;, \;\;\; A_{CP}^{mix} = -\frac{2 \Im \lambda_f }{1 + \left| \lambda_f \right|{}^2}\;, \;\;\; A_{\Delta\Gamma} = -\frac{2 \Re \lambda_f }{1 + \left| \lambda_f \right|{}^2}\;. {}\end{aligned} $$

(9.195)

The first term accounts for possible direct ${\mathcal {C}\mathcal {P} }$ violation while the other two terms encode properties of the mixing. Experimentally, by measuring the time dependent ${\mathcal {C}\mathcal {P} }$ violation a _CP(t) one can determine the coefficients of $\cos {}(\Delta m t )$ and $\sin {}(\Delta m t)$ and thus determine $\left | \lambda _f \right |$ and ℑλ _f. In general, non-perturbative QCD effects prevent to relate these quantities to ${\mathcal {C}\mathcal {P} }$ phases originating from the quark mixing. However, in case of so called golden modes which are dominated by a single decay amplitude and thus a single combination $\mathcal {V}_{\mathrm {CKM}}$ of CKM elements such an association is possible. Since the strong interaction respects the ${\mathcal {C}\mathcal {P} }$ symmetry, golden modes fulfill:

$$\displaystyle \begin{aligned} \frac{\overline{A}_f}{A_f} = \eta_{CP} \frac{ \overline{A}_{\bar{f}}} {A_f} = \eta_{CP} \frac{\mathcal{V}_{{}_{\mathrm CKM}}^\ast}{\mathcal{V}_{{}_{\mathrm CKM}}} {} \end{aligned} $$

(9.196)

From this equation one sees that $\left | \overline {A_f} \right | = \left | A_f \right |$ and that assuming $\left |q/p\right |=1$, one obtains $\left | \lambda _f \right | = 1$. Thus golden modes satisfy

$$\displaystyle \begin{aligned} A_{CP}^{dir} = 0 \; , \;\;\; A_{CP}^{mix} = -\Im \lambda_f \, . {} \end{aligned} $$

(9.197)

For golden decays of B⁰ mesons for which the decay width difference Δ Γ is negligible, expression (9.194) further simplifies to

$$\displaystyle \begin{aligned} a_{CP}(t) = - \Im \lambda_f \sin{}(\Delta m t) \; . {} \end{aligned} $$

(9.198)

Thus, if λ _f carries a non-trivial weak phase ϕ (ℑλ _f ≠ 0) the time dependent ${\mathcal {C}\mathcal {P} }$ asymmetry will show a sinusoidal time behaviour with an amplitude given by $\sin \phi$.

9.6.2 Production and Detection of B-Mesons

The precise measurement of oscillation and ${\mathcal {C}\mathcal {P} }$ violation in the neutral B meson system requires a high number of produced B mesons. A good reconstruction of the B meson decay vertex, necessary for an excellent decay time resolution, is needed to resolve the time-dependent effects. To perform the ${\mathcal {C}\mathcal {P} }$ measurements the determination of the production flavor of the B meson, often referred as flavor-tagging, is necessary.

9.6.2.1 e ⁺e ⁻ B-Factories

The first experiments which have systematically addressed these requirements are the BABAR experiment [69] at the e ⁺e ⁻ collider PEP-II at Stanford and the Belle experiment [70] at the Japanese e ⁺e ⁻ collider KEKB. Both e ⁺e ⁻ machines were operating at a centre-of-mass energy of $\sqrt {s}=10.58$ GeV, corresponding to the mass of the Υ(4S), an excited $b\bar {b}$ resonance which decays to $\mathrm {B^0}\overline {\mathrm {B^0}}$ (∼ 50%) and B⁺B⁻ (∼50%). The cross section for the Υ(4S) production is 1.1 nb which is about a quarter of the total hadronic cross section.

BABAR was operated from 1999 to 2008 and collected a data set corresponding to an integrated luminosity of 550 fb⁻¹. The Belle experiment has also been started in 1999 and was taking data until the end of 2009, collecting about 1 ab⁻¹ of data. Due to the large number of B mesons the two experiments have recorded, they are often referred as B-factories.³ To continue this successful path, the KEKB collider as well as the Belle experiment have both undergone an upgrade. The new Belle-II experiment has started data-taking in 2018 and will be operated at a 40 times larger instantaneous luminosity [72].

The mass of the Υ(4S) lies only 11 MeV/c² above the sum of the two produced B mesons which would therefore be produced essentially at rest and would not fly. The vanishing decay length would prevent a measurement of the decay time. To overcome this problem both machines have been operated with slightly asymmetric beam energies resulting in a small boost of the Υ(4S) and thus of the produced B mesons. The boost factor βγ was 0.56 (0.425) for the BABAR (Belle) experiment, resulting into typical decay lengths of about 250 μm for the two B mesons with lifetimes of 1.5 ps.

If the Υ(4S) with J ^P = 1⁻ decays into a pair of neutral B mesons, the two mesons are produced in a coherent $\mathrm {B}^0 \overline {\mathrm {B}^0}$ state with negative parity,

$$\displaystyle \begin{aligned} \mathrm{B^0} (\theta_1) \overline{\mathrm{B^0}} (\theta_2) - \mathrm{B^0} (\theta_2) \overline{\mathrm{B^0}}(\theta_1)\; , \end{aligned} $$

(9.199)

where θ _1,2 are the B meson production angles relative to the e ⁺ direction. The flavors of the two mesons are thus fully correlated until the first meson decays at time t ₁. If at that time this meson is a B⁰ the flavor of the second meson is fixed to be a $\overline {\mathrm {B^0}}$ and vice versa. The time evolution of the second B meson with decay time t ₂ is then given by

$$\displaystyle \begin{aligned} \psi_2(t_2) = \overline{\mathrm{B^0}} \left(\mathrm{e}^{-\gamma_h(t_2 - t_1)} + \mathrm{e}^{-\gamma_l(t_2 - t_1)}\right) - \frac{q}{p}\mathrm{B^0} \left(\mathrm{e}^{-\gamma_h (t_2 - t_1)} - \mathrm{e}^{-\gamma_l (t_2 - t_1)} \right) \; , \end{aligned} $$

(9.200)

i.e. the time evolution of the flavor of the second B meson is defined by the time difference Δt = t ₂ − t ₁ between the two decays. Depending on which of the two B mesons is studied, Δt can also be negative.

The decay topology of a $\mathrm {B^0}\overline {\mathrm {B^0}}$ pair produced at t = 0 from the decay of the Υ(4S) is illustrated in Fig. 9.24, where one of the neutral B mesons (signal B) is decaying at t ₂ into the golden mode J∕ψK_S used to measure the time-dependent ${\mathcal {C}\mathcal {P} }$ violation, and the other B meson (tagging B) decays at t ₁ into a flavor-specific final state. The charge of the electron indicates the flavor of the B meson at the time of the decay (B⁰). At this time the signal B was thus a $\overline {\mathrm {B^0}}$.

Fig. 9.24

Decay topology of $\mathrm {B^0} \overline {\mathrm {B^0}}$ pairs

Due to the boost of the Υ(4S) the different decay times result into different z-positions of the two decay vertices along the beam direction. The difference Δz is about 250 μm and is related to the decay time difference Δt:

$$\displaystyle \begin{aligned} \Delta z = z_2 - z_1 = \beta \gamma c \, (t_2 - t_1) = \beta \gamma c \, \Delta t\; . {} \end{aligned} $$

(9.201)

Both B-factories are very similar. Therefore only the Belle experiment at the KEKB collider in Tsukuba is discussed here. To produce a boost βγ = 0.425 of the Υ(4S) in the laboratory, the KEKB electron beam has an energy of 8 GeV while the positrons collide with an energy of 3.5 GeV. The highest instantaneous luminosity achieved at KEKB was $\mathcal {L} = 2\times 10^{34}$s⁻¹ cm⁻² [71].

The Belle detector (Fig. 9.25) followed the typical onion-shape design. After an exchange in 2003, a silicon vertex detector (SVD) made from four layers of double-sided silicon strip sensors was used as inner component. The innermost (outermost) SVD layer was located at a radial distance of only 20 (88) mm from the collision point. The impact parameter resolution for charged particle tracks obtained is [71]

$$\displaystyle \begin{aligned} \begin{array}{rcl} \sigma_{r} &\displaystyle =&\displaystyle \left[21.9 \oplus \frac{35.5}{p}\right]\, \upmu\mbox{m} ~~~\left[p~~\mbox{in GeV/c}\right] \;,\\ \sigma_{z} &\displaystyle =&\displaystyle \left[27.8 \oplus \frac{31.9}{p}\right]\, \upmu\mbox{m}\;. \end{array} \end{aligned} $$

The SVD was followed by the central drift chamber (CDC) which extended to a radial distances of 88 cm. The combined tracking system of SVD and CDC provided a good momentum resolution, especially for low momentum tracks, thanks to the minimization of material. For the transverse momentum a resolution of $\sigma _{p_T}/p_T = 0.0019\cdot p_T \oplus 0.0030/\beta$ $\left [p_T~\mbox{in GeV/c}\right ]$ was achieved [71]. Particle identification was provided by the time-of-flight (TOF) system and by the aerogel Cherenkov counter (ACC). Photon and electron energies were measured in the electromagnetic calorimeter (ECL) consisting of thallium-doped CsI crystals. The energy resolution varied from 4% at 100 MeV to about 1.6% at 8 GeV [71]. All detector components were placed inside a super-conducting solenoid magnet of cylindrical shape which was providing a magnetic field of 1.5 T. The iron return yoke is instrumented with resistive plate chambers (KLM) and served to identify muons and K_L with a momentum above 600 MeV/c.

Fig. 9.25

Belle detector with the silicon vertex detector (SVD), the central drift chamber (CDC), the time-of-flight-system (TOF) and the aerogel Cherenkov counter (ACC), the CsI electromagnetic calorimeter and the K_L∕μ detector (KLM). The detector is embedded in a magnetic field of 1.5 T produced by a solenoid with a length of 4.4 m and a diameter of 3.4 m [70]

9.6.2.2 The LHCb Experiment at the Large Hadron Collider

The multi-purpose experiments CDF and D0 [73,74,75,76] operated at the $p\bar {p}$ collider Tevatron at Fermilab established that—despite of the harsh and high-multiplicity environment of the hadron collisions—precision measurements of B mesons competitive with those performed at e ⁺e ⁻ B-factories are possible at hadron machines. Both experiments have pioneered studies of the $\mathrm {B}_{\mathrm {s}}^0$ system which was hardly studied at the e ⁺e ⁻ machines, as kinematically the heavier $\mathrm {B}_{\mathrm {s}}^0$ system is only accessible through the decays of the Υ(5S). Only the Belle collaboration collected a small data sample of Υ(5S) decays.

At the Large Hadron Collider (LHC) at CERN, the LHCb experiment [77] and to a lesser extent also the ATLAS and CMS experiments [78, 79] followed the successful path of precision B meson studies explored at Tevatron. The cross section for $b\bar {b}$ pair production in the pp collision of the LHC is huge, about 500 μb for proton-proton center-of-mass energies of 13 TeV. As only small fractions of the proton energies are needed to produce the $b\bar {b}$ pair, the momentum factions x ₁ and x ₂ of the colliding partons are in general very different and the relatively light $b\bar {b}$ system is boosted in the laboratory frame into either the forward or the backward direction. The LHCb experiment has therefore been designed as a single-arm forward spectrometer. With a pseudo-rapidity coverage of 2 < η < 5 about 35% of all produced $b\bar {b}$ pairs lie within the detector acceptance. The average boost of the b hadrons is large, βγ ≈ 25, resulting into average flight distances of about 1 cm. Although the $b\bar {b}$ cross section at the LHC is large, the total inelastic cross section is about a factor 200 larger. The huge rate of non b events together with the fact that the decay products of the b hadrons are comparably soft makes the trigger to the primary challenge for any B meson experiment. Typical combined trigger and reconstruction efficiencies vary between 0.1 and 10% depending on the decay channel. Channels with muons in the final state are in general easier to trigger and reconstruct.

At a hadron collider the two produced b quarks hadronise separately and no quantum correlation between the two b hadrons exists. It is therefore harder to conclude from the flavor of the second b hadron (tagging B), which for the case that it is a neutral B meson oscillates independently, on the production flavor of the signal B. Effective tagging efficiencies therefore stay significantly below 10%.

The LHCb forward spectrometer is shown in Fig. 9.26 and includes a high-precision tracking system consisting of a silicon-strip vertex detector (Velo) surrounding the pp interaction region, a large-area silicon-strip detector (TT) located upstream of a dipole magnet with a bending power of about 4 Tm, and three stations of silicon-strip detectors (IT) and straw drift tubes (OT) placed downstream of the magnet. The tracking system provides a measurement of momentum of charged particles with a relative uncertainty that varies from 0.5% at low momentum to 1.0% at 200 GeV/c. The minimum distance of a track to the primary proton-proton vertex, the impact parameter (IP), is measured with a resolution of

$$\displaystyle \begin{aligned} \sigma_{IP} = (15 + 29/p_T) \upmu\mbox{m} \;\,\; \left[p_T~\mbox{in GeV/c}\right] \end{aligned}$$

The average boost and the vertex resolution translates into a decay-time resolution of about 50 fs. Different types of charged hadrons are distinguished using information from two ring-imaging Cherenkov detectors (RICH). Photons, electrons and hadrons are identified by a calorimeter system consisting of scintillating pads (SPD) and a preshower detector (PS), an electromagnetic calorimeter (ECAL) and a hadronic calorimeter (HCAL). Muons are identified by a system composed of alternating layers of iron and multiwire proportional chambers. The online event selection is performed by a trigger system consisting of a hardware stage, based on information from the calorimeter and the muon systems, followed by a software stage, which applies full event reconstruction.

Fig. 9.26

LHCb detector consisting of a vertex detector (Vertex Locator), a first Cherenkov detector (RICH1), a large-area silicon-strip detector (TT), the main tracking stations (T1, T2, T3) with an inner part built from silicon-strip detectors and outer part build with straw drift tubes, a second Cherenkov detector (RICH2), a scintillating-pad detector (SPD) and a preshower detector (PS) in front of an electromagnetic (ECAL) and hadronic calorimeter (HCAL, and the muon system with 5 stations (M1 to M5). A dipole magnet (4 Tm) is placed between the large-area silicon-strip detector and the main tracking stations [77]

The displacement of the B decay vertex from the primary interaction vertex is an important identification requirement of B events. However, due to the large boost in forward direction, the association of b hadrons to their production vertex is challenging, in particular if the number of primary vertices is large. In order to keep the average number of primary proton-proton interactions per bunch crossing at the most optimal value (below 2) the instantaneous luminosity for the LHCb interaction point was leveled by displacing the centres of the colliding beams slightly. Until 2018 LHCb has recorded data corresponding to an integrated luminosity of 3 fb⁻¹ at 7 and 8 TeV, and 6 fb⁻¹ at 13 TeV proton-proton centre-of-mass energy. This data sample corresponds to more than 1 × 10¹² $b\bar {b}$ events produced inside the LHCb acceptance.

9.6.3 Measurements of B Oscillations

Mixing in the $\mathrm {B^0}{-}\overline {\mathrm {B^0}}$ system was discovered in 1987 by the ARGUS collaboration [80] and the first time-integrated determinations of the mixing parameter x _d have been performed by the ARGUS and the CLEO collaborations [81, 82]. Time-dependent measurements of the mixing frequency Δm _d became possible at the electron-positron collider LEP. The silicon vertex detectors and the large boost of the B mesons produced at the Z resonance allowed to observe the B⁰ oscillations. With their high statistics and low background B samples the BABAR and Belle experiments improved the errors on the mixing frequency Δm _d significantly [83, 84]. Exploiting the excellent time resolution as well as the large statistics of recorded B mesons the LHCb experiment performed the so far most precise measurement of Δm _d [88].

After the first B⁰ mixing measurement it was clear that mixing was an important effect also in the $\mathrm {B}^0_{\mathrm {s}} - \overline {\mathrm {B}^0_{\mathrm {s}}}$ system and theory predicted a much faster oscillation of the $\mathrm {B}^0_{\mathrm {s}}$ meson. While limits on x _s existed from LEP and the two Tevatron experiments it took until 2006 that the CDF collaboration resolved the fast mixing and performed the first measurement of the mixing frequency [85]. The measurement was repeated with much smaller uncertainties by the LHCb collaboration in 2012 [86].

The oscillation frequency of neutral B mesons is measured using flavor-specific final states, i.e. final states like B⁰ → D ^(∗)−ℓ ⁺ν _ℓ or B⁰ → D ⁻π ⁺ where the charge of one of the final-state particles (e.g. the lepton or pion charge) indicate the flavor of the decaying signal B⁰ (e.g. $\bar {b}\rightarrow \bar {c} \ell ^+ \nu _{\ell }$). In case of incoherent production of the two b hadrons, a flavor-specific decay of the second B (B _tag) is used to tag the flavor at the time t = 0 of the production. For the coherent production at the B factories the tagging B defines the flavor of the signal B at time Δt with respect to its decay—see Fig. 9.24 and Eq. (9.201). B-factory experiments have also used explicitly so called dilepton events where both B mesons decay semi-leptonically. Flavor-mixing of one of the B mesons is indicated by the presence of same-sign lepton events.

For LHCb, where the boost factor of the decaying B is not known and must be reconstructed from the final-state particles, semi-leptonic signal decays with an undetected neutrino present an additional complication compared to full hadronic decays. To account for the missing neutrinos in the calculation of the proper decay-time correction factors are used.

An important performance number for the mixing measurement and even more for ${\mathcal {C}\mathcal {P} }$ violation measurements is the tagging power or effective tagging efficiency $Q=\epsilon _{tag}D_{tag}^2$ which corresponds to the efficiency to correctly tag the flavor of the signal B meson. The tagging power is the product of the tagging efficiency 𝜖 _tag, the probability that a specific algorithm delivers tagging information, and the square of the dilution factor D _tag = 1 − 2ω, where ω is the mistag probability, i.e. the probability that a tagging decision is wrong. At a hadron collider, B mesons are produced independently of each other and mistag probabilities are large (about 40%). The B-factories profit from the coherent $\mathrm {B^0}\overline {\mathrm {B^0}}$ production and mistag probabilities of only a few percents are achieved for some tagging algorithms. Consequently, the tagging power at the B-factories is as high as 30% while for LHCb values only up to 6% are obtained.

If one considers the effect of the tagging dilution D _tag as well as the effect of a finite time resolution expressed by a dilution factor D _t one expects that the measured flavor asymmetry A _meas parameterizes as,

$$\displaystyle \begin{aligned} A_{meas}(t) = \frac{ N_{unmixed}(t) - N_{mixed}(t)} {N_{unmixed}(t) + N_{mixed}(t)} = D_{tag} D_t \frac{\cos \Delta m t}{\cosh \Delta \Gamma/2 t} \, , {} \end{aligned} $$

(9.202)

where t is the decay time of the signal B. For the measurement at BABAR and Belle with coherently produced B mesons the time difference Δt = t _sig − t _tag between the decay times of the signal and the tagging B needs to be used instead. N _unmixed and N _mixed are the observed numbers of unmixed ($\mathrm {B^0}\overline {\mathrm {B^0}}$) or mixed (B⁰B⁰ or $\overline {\mathrm {B^0}}\overline {\mathrm {B^0}}$) events for different decay times. The effect of the finite time resolution is treated in the fit by a convolution with a resolution function. For LHCb, the effect of the time resolution on the measurement of the slow B⁰-$\overline {\mathrm {B^0}}$ mixing is negligible (D _t ≈ 1). For the fast oscillating $\mathrm {B}^0_{\mathrm {s}}$-$\overline {\mathrm {B}^0_{\mathrm {s}}}$ the measured decay-time resolution of 44 fs leads to a dilution factor of ≈ 0.73.

9.6.3.1 Measurement of the B⁰-$\overline {\mathrm {B^0}}$ Oscillation Frequency

BABAR and Belle have used large event samples of dilepton events where both B mesons decay leptonically with either a muon or an electron in the final-state to measure Δm _d . Figure 9.27 shows the measured decay time difference Δt (t ₂ − t ₁, see above) of opposite-sign and same-sign di-lepton events as measured by BABAR, as well as the mixing asymmetry A _meas( Δt). The fit to the data resulted in a value of Δm _d = (0.493 ± 0.012 ± 0.009) ps⁻¹ [83]

Fig. 9.27

Distributions of time difference Δt of the two neutral B mesons for (a) opposite- sign and (b) same-sign dilepton events; (c) asymmetry between opposite- and same-sign dilepton events. Points are data and the lines correspond to result of a fit. Figure taken from [83]

The most precise determination of Δm _d at the B-factories was performed by Belle analyzing simultaneously semi-leptonic decays B⁰ → D ^∗−ℓν and a set of four different hadronic decays in a data sample of 140 fb⁻¹ and resulting into the value Δm _d = (0.511 ± 0.005 ± 0.006) ps⁻¹ [84]. The various Δm _d measurements at the B-factories have been averaged [87] to

$$\displaystyle \begin{aligned} \Delta m_d = ( 0.509 \pm 0.003 \pm 0.003 )~{\mathrm{ps}^{-1}} \, . \end{aligned}$$

LHCb has performed a mixing measurement using fully reconstructed hadronic final states as well as semi-leptonic decays. The most precise LHCb measurement was performed using semi-leptonic B⁰ decays. A total of 1.923 × 10⁶ B⁰ → D ⁻μ ⁺ν _μX candidates and 0.829 × 10⁶ B⁰ → D ^∗−μ ⁺ν _μX candidates (charge conjugated decays included) are used [88] and yield

$$\displaystyle \begin{aligned} \Delta m_d = (0.5050 \pm 0.0021 \pm 0.0010) ~{\mathrm{ps}^{-1}} \, . \end{aligned}$$

Dominated by the LHCb result, the current world average of the existing Δm _d measurements yields

Using the B⁰ lifetime average of 1.520 ± 0.004 ps [130] one obtains the mixing parameter,

which is of similar magnitude as the value of the neutral K system, x _K = 0.945 ± 0.002 (see Sect. 9.5). As predicted, the decay width difference of the B⁰ turns out to be very small. The world average [130] of y _d is,

$$\displaystyle \begin{aligned} y_d = \frac{\Delta \Gamma_d}{2 \Gamma_d} = -0.001 \pm 0.005 \end{aligned}$$

compared to y _K = −0.9965 for the K meson.

9.6.3.2 Measurement of the $\mathrm {B}^0_{\mathrm {s}}{-}\overline {\mathrm {B}^0_{\mathrm {s}}}$ Oscillation Frequency

Inserting the corresponding CKM elements in Eq. (9.187) one expects that the oscillation of the neutral $\mathrm {B}^0_{\mathrm {s}}$ meson is by a factor $\left | V_{ts}\right |{ }^2 / \left | V_{td}\right |{ }^2$ faster than the oscillation of the B⁰. To resolve the fast oscillation pattern represented a challenge and the first measurement of Δm _s was achieved only in 2006 by the CDF experiment [85].

The by far most precise determination of Δm _s was performed by LHCb [86] using about 34,000 $\mathrm {B}^0_{\mathrm {s}}\rightarrow D_s^- \pi ^+$ decays (charge conjugated decays are included). Figure 9.28 shows the decay time distribution dependent number of observed $\mathrm {B}^0_{\mathrm {s}}$ meson decays which decay with the same (unmixed) or the different flavor (mixed) with respect to their production. One can nicely observe the rather fast oscillation pattern. A fit accounting for the tagging dilution and for the finite time resolution results into

This value agrees well with the theoretical prediction Δm _s = (18.3 ± 2.5) ps⁻¹ which however, exhibits large errors due to the uncertainties of the hadronic parameters $f_{B_s}\sqrt {B_{B_s}}$ [66]. With the mean $\mathrm {B}^0_{\mathrm {s}}$ life-time, τ = 1.509 ± 0.004 ps⁻¹, one obtains for the mixing parameter

Fig. 9.28

Decay time distribution for $\mathrm {B}^0_{\mathrm {s}}$ candidates tagged as mixed (different flavour at decay and production; red, continuous line) or unmixed (same flavour at decay and production; blue, dotted line). Figure adopted from [86]

9.6.4 CP Violation in Neutral B Meson Mixing

${\mathcal {C}\mathcal {P} }$ violation in mixing, a _mix ≠ 0, is predicted to be $\mathcal {O}(10^{-4})$ for B⁰ mesons and $\mathcal {O}(10^{-5})$ for $\mathrm {B}^0_{\mathrm {s}}$ mesons [66]. As the ${\mathcal {C}\mathcal {P} }$ violation in mixing is probed using semi-leptonic B decays it is often also referred to as a _SL (see Eq. (9.56)). In 2010, the D0 collaboration reported an anomalous charge asymmetry in the inclusive production rates of like-sign dimuon events [89] indicating a significant deviation from the prediction. Their most recent study [90] shows a discrepancy to the theory prediction of about three standard deviations .

B mesons containing a $\bar {b}$ quark undergo decays with a positively charged leptons in the final-state ($\bar {b} \rightarrow \bar {c} \,\ell ^+ \nu _\ell$), while $\bar {\mathrm {B}}$ mesons decay into negatively charged leptons ($b \rightarrow c \,\ell ^- \bar {\nu _\ell }$). In case of pair production of B mesons with subsequent semi-leptonic decay, a pair of negatively charged leptons indicates the mixing of B⁰ into a $\overline {\mathrm {B^0}}$, while the observation of a positively charged lepton pair signals the transformation of $\overline {\mathrm {B^0}}$ into B⁰. The dilepton asymmetry is measured with dimuon events and is defined as

$$\displaystyle \begin{aligned} \mathcal{A}_{\ell\ell} = \frac{N(\mu^+\mu^+) - N(\mu^-\mu^-)}{N(\mu^+\mu^+) + N(\mu^-\mu^-)}, \end{aligned} $$

(9.203)

where N(μ ⁺μ ⁺) and N(μ ⁻μ ⁻) are the number of events with two positively or two negatively charged muons, respectively. At a hadron collider the detection of two muons does not distinguish between initial B⁰ or initial $\mathrm {B}^0_{\mathrm {s}}$ meson and the above dimuon asymmetry as determined by the D0 experiment measures a combination of the B⁰ and $\mathrm {B}^0_{\mathrm {s}}$ mixing asymmetries $a_{\mathrm {S}\mathrm {L}}^d$ and $a_{\mathrm {S}\mathrm {L}}^s$ defined in Eq. (9.189).

Measurements performed by BABAR, Belle, D0 and LHCb determine separately the mixing asymmetries $a_{\mathrm {S}\mathrm {L}}^d$ and $a_{\mathrm {S}\mathrm {L}}^s$ for the two neutral B mesons by using partially reconstructed semi-leptonic decays or with fully reconstructed hadronic decays. Measuring the expected very tiny ${\mathcal {C}\mathcal {P} }$ asymmetries requires a precise understanding of various experimental and instrumental effects, e.g. asymmetries arising from different detection efficiencies ($\mathcal {A}_D$) or different material interaction ($\mathcal {A}_{I}$) for the two charge-conjugated final states. The so far most precise determination of both mixing asymmetries has been performed by the LHCb experiment. At the LHC the initial proton-proton collision is not a particle-antiparticle symmetric state. The number of produced b and $\bar {b}$ hadrons of a given species is not necessarily the same and the production asymmetry $\mathcal {A}_P$ has also to be taken into account when the measurement of the mixing asymmetry is performed. The measured asymmetry of a neutral B meson, independent whether it is a B⁰ or a $\overline {\mathrm {B^0}}$, into a final state f or its conjugated state $\bar {f}$ can be expressed by the mixing asymmetry $a_{\mathrm {S}\mathrm {L}}^q$,

$$\displaystyle \begin{aligned} \mathcal{A}_{meas} &= \frac{ N(\overline{B^0_q}/B^0_q \rightarrow f)(t) - N(\overline{B^0_q}/B^0_q \rightarrow \bar{f})(t) }{ N(\overline{B^0_q}/B^0_q \rightarrow f)(t) + N(\overline{B^0_q}/B^0_q \rightarrow \bar{f})(t)}\\ &= \frac{a_{\mathrm{S}\mathrm{L}}^q}{2} - \left( \mathcal{A}_P + \frac{a_{\mathrm{S}\mathrm{L}}^q}{2} \right) \cdot \frac{\cos\left(\Delta m_q t\right)} {\cosh\left( \Delta \Gamma_q t / 2\right) } + \mathcal{A}_D + \mathcal{A}_{I} \, . \end{aligned} $$

(9.204)

By omitting the flavor tagging of the decaying neutral B the sensitivity to a _SL is a factor 1∕2 smaller with respect to a tagged measurement. At the same time one dramatically wins in statistical power as no tagging is required.

For the B⁰ system the time dependent analysis together with the precise determination of $\mathcal {A}_D$ and $\mathcal {A}_{I}$ allows to eliminate the production asymmetry $\mathcal {A}_P$. LHCb has performed this complicated analysis [91] and obtained for the mixing asymmetry of the B⁰ system the value

$$\displaystyle \begin{aligned} a_{\mathrm{S}\mathrm{L}}^{d} = \left( -0.02 \pm 0.19 \pm 0.30 \right)~\% \end{aligned}$$

with a total precision of 3.6 per mill. In case of the fast oscillating $\mathrm {B}^0_{\mathrm {s}}$ system the measurement simplifies as the term involving the production asymmetry cancels in a time integrated measurement. Furthermore, the measurement was performed using $D_s^- \mu ^+ \nu _\mu X$ final states with the $D_s^-$ meson decaying to ϕ(→ K ⁺K ⁻)π ⁻ [92]. For the charge symmetric K ⁺K ⁻ state the interaction asymmetry is negligible and one only needs to correct for the pion detection asymmetry. The final result obtained for $a_{\mathrm {S}\mathrm {L}}^s$ is

with a total precision of 3 per mill.

Figure 9.29 shows the different a _SL measurements [91,92,93,94,95,96,97] for the two neutral B systems as well as the averages. The D0 measurement indicating large mixing asymmetries is not confirmed by the other experiments. The measured a _SL values can be used to determine the deviation of $\left | q/p\right |$ from unity,

$$\displaystyle \begin{aligned} a_{\mathrm{S}\mathrm{L}} = \frac{1 - \left| q/p\right|{}^4}{1 + \left| q/p\right|{}^4} \approx 2 \left( 1 - \left| q/p \right| \right) \, , \end{aligned} $$

(9.205)

or equivalently

$$\displaystyle \begin{aligned} \left|\frac{q}{p} \right| \approx 1 - \frac{a_{\mathrm{S}\mathrm{L}}}{2} \, . \end{aligned} $$

(9.206)

Fig. 9.29

Mixing asymmetries $a_{\mathrm {S}\mathrm {L}}^s$ and $a_{\mathrm {S}\mathrm {L}}^d$ as measured by the different experiments [91,92,93,94,95,96,97]. The D0 dimuon measurement (contour) [90] determines a combination of $a_{\mathrm {S}\mathrm {L}}^s$ and $a_{\mathrm {S}\mathrm {L}}^d$. Green bands show the averages. The theory prediction is marked by the black dot. Figure adopted from [92]

The most recent world averages as provided by the HFLAV group⁴ and published in [130] are for the B⁰ system,

$$\displaystyle \begin{aligned} \begin{array}{rcl} a_{\mathrm{S}\mathrm{L}}^d &\displaystyle = &\displaystyle 0.0021 \pm 0.0017 \, ,\\ \left|q/p \right| &\displaystyle = &\displaystyle 1.0010 \pm 0.0008 \, , \end{array} \end{aligned} $$

and correspondingly for the $\mathrm {B}^0_{\mathrm {s}}$ system,

$$\displaystyle \begin{aligned} \begin{array}{rcl} a_{\mathrm{S}\mathrm{L}}^2 &\displaystyle = &\displaystyle 0.0006 \pm 0.0028 \, , \\ \left|q/p \right| &\displaystyle = &\displaystyle 1.0003 \pm 0.0014 \, . \end{array} \end{aligned} $$

The values so far show no evidence for ${\mathcal {C}\mathcal {P} }$ violation in mixing and are consistent with the theory prediction of very small ${\mathcal {C}\mathcal {P} }$ asymmetries [66].

9.6.5 CP Violation in the Interference of Mixing and Decay

The B-factories BABAR and Belle were built with the primary goal to discover ${\mathcal {C}\mathcal {P} }$ violation in the interference of B⁰ decays to the ${\mathcal {C}\mathcal {P} }$ eigenstate B⁰ →J∕ψK_S with and without mixing. Large ${\mathcal {C}\mathcal {P} }$ violation had been predicted for this channel. Shortly after the start of data-taking the two collaborations presented first measurements in summer 2000. A clear evidence of the first ${\mathcal {C}\mathcal {P} }$ violation outside the neutral K meson was established in 2001 [59, 60].

9.6.5.1 B⁰ Meson

The expected time-dependent ${\mathcal {C}\mathcal {P} }$ asymmetry is defined in Eq. (9.192) and parametrised by Eq. (9.194). Taking into account the negligible width difference, Δ Γ ≈ 0, for B⁰ mesons the time-dependent ${\mathcal {C}\mathcal {P} }$ asymmtery for the channel B⁰ →J∕ψK_S can be written as

$$\displaystyle \begin{aligned} \mathcal{A}_{J/\psi K_S}(t) = A_{J/\psi K_S}^{mix}\sin{}(\Delta m_d t) - A_{J/\psi K_S}^{dir} \cos{}(\Delta m_d t) \, , {} \end{aligned} $$

(9.207)

where the coefficients $A^{mix}_{J/\psi K_S}$ and $A^{dir}_{J/\psi K_S}$ have been introduced in Eq. (9.195). The decay B⁰ →J∕ψK_S is a golden mode, dominated by a single tree-level amplitude. ${\mathcal {C}\mathcal {P} }$ violation in the decay amplitudes can therefore be neglected, i.e. $A_{J/\psi K_S}^{dir} \approx 0$. The coefficient $A_{J/\psi K_S}^{mix}$ is given by the CKM matrix elements involved in the short range box diagrams responsible for the B⁰ mixing and by the CKM matrix elements appearing in the decay amplitudes. With $A_{J/\psi K_S}^{mix} = -\Im \lambda _{J/\psi K_S}$ (see Eq. (9.195)) and the definition of $\lambda _{J/\psi K_S}$ of Eq. (9.193),

$$\displaystyle \begin{aligned} \lambda_{J/\psi K_S} = \frac{q}{p} \frac{\overline{A}_{J/\psi K_S}}{A_{J/\psi K_S}} \;, \end{aligned}$$

one can calculate the time-dependent CP asymmetry according to Eq. (9.197). For the decay B⁰ →J∕ψK_S one finds for the ratio q∕p describing the mixing and for the ratio of the amplitudes the following CKM factors,⁵

$$\displaystyle \begin{aligned} \frac{q}{p} = \frac{V_{tb}^\ast V_{td}}{V_{tb} V_{td}^\ast}~~\mbox{and}~~ \frac{\overline{A}_{J/\psi K_S}}{A_{J/\psi K_S}} = \eta_{J/\psi K_S} \left( \frac{V_{cb} V_{cs}^\ast}{V_{cb}^\ast V_{cs}}\right) \left( \frac{V_{cs} V_{cd}^\ast}{V_{cs}^\ast V_{cs}}\right) \, , \end{aligned} $$

(9.208)

The second CKM term in the expression for the amplitude ratio is a result of the K ⁰–$\overline {K^0}$ mixing necessary to produce the K_S. As the V _cs terms all cancel one obtains for the $A_{J/\psi K_S}^{mix}$

$$\displaystyle \begin{aligned} A_{J/\psi K_S}^{mix} = -\Im \left\{ \eta_{J/\psi K_S} \left( \frac{V_{tb}^\ast V_{td}}{V_{tb} V_{td}^\ast} \right) \left( \frac{V_{cb} V_{cd}^\ast}{V_{cb}^\ast V_{cd}}\right) \right\} = - \eta_{J/\psi K_S} \sin{}(2\beta) \, , \end{aligned} $$

(9.209)

where the last equality uses the definition of the CKM angle β of Sect. 9.7. Finally one obtains for the time-dependent ${\mathcal {C}\mathcal {P} }$ asymmetry,

$$\displaystyle \begin{aligned} \mathcal{A}_{J/\psi K_s^0}(t) = - \eta_{J/\psi K_S} \sin \left(2 \beta \right) \sin \left( \Delta m_d t \right) \, . \end{aligned} $$

(9.210)

For the decay B⁰ →J∕ψK_S the ${\mathcal {C}\mathcal {P} }$ eigenvalue of the final state is $\eta _{J/\psi \mathrm {K_S}}=-1$. Due to opposite CP eigenvalue of the K_L the ${\mathcal {C}\mathcal {P} }$ eigenvalue of the decay B⁰ →J∕ψK_L is $\eta _{J/\psi \mathrm {K_L}}=+1$. Both statements are strictly true only if one ignores the very small CP violation in the $K^0\overline {K}^0$ mixing. The decay B⁰ →J∕ψK_L is interesting as one expects exactly the same magnitude of the ${\mathcal {C}\mathcal {P} }$ violation as for B⁰ →J∕ψK_S but an opposite time behavior due to the opposite ${\mathcal {C}\mathcal {P} }$ eigenvalue.

Experimentally the decay $\mathrm {B^0} \rightarrow J / \psi K_s^0$ is easy to access. The J∕ψ meson decays into two leptons and can be easily triggered and selected. Additional requirements on the displacement of the B vertex from the primary vertex allow an almost background-free reconstruction even at a hadron collider. The measurement has been extended to include other ($c\bar {c}$) resonances for which the same ${\mathcal {C}\mathcal {P} }$ behavior as for the golden mode is expected.

At the B-factories the time-dependent ${\mathcal {C}\mathcal {P} }$ asymmetry is measured as function of the time difference Δt = t ₂ − t ₁. The most precise determination of the quantity $\sin \left ( 2\beta \right )$ has been performed by the Belle experiment using about 32,000 signal candidates with an average signal purity of 79% [98],

$$\displaystyle \begin{aligned} \sin \left( 2\beta \right) = 0.667 \pm 0.023 \pm 0.012 \, . \end{aligned}$$

The time-dependent CP asymmetry for the CP-odd and CP-even final states as measured by Belle are shown in Fig. 9.30. The BABAR experiment has recorded less signal candidates (15,481 candidates with a purity of 76% ) and obtained [99],

$$\displaystyle \begin{aligned} \sin \left( 2\beta \right) = 0.687 \pm 0.028 \pm 0.012 \, , \end{aligned}$$

with a slightly larger statistical error than the Belle measurement.

Fig. 9.30

Flavor-tagged Δt distributions and raw CP asymmetries for the Belle measurements of $\sin 2\beta$. The top plots show the $\mathrm {B^0}\rightarrow (c\bar {c})\mathrm {K_S}$ (η _f = −1) measurement and the bottom plots show the measurement for B⁰ →J∕ψK_L (η _f = +1) The distributions are background subtracted. Figure adapted from [98]

The LHCb collaboration has also performed the measurement of $\sin \left ( 2\beta \right )$ by analysing the time dependent ${\mathcal {C}\mathcal {P} }$ violation in B⁰ →J∕ψK_S and B⁰ → ψ(2S)K_S decays with 52,000 and 8000 signal candidates, respectively [100, 101]. As for the measurement of the ${\mathcal {C}\mathcal {P} }$ violation in mixing the observed time dependent asymmetry has to be corrected for the production asymmetry between B⁰ and $\overline {\mathrm {B^0}}$ of about 1%. The resulting value $\sin \left ( 2 \beta \right ) = 0.760 \pm 0.034$ [101] is slightly larger than the ones measured at the B-factories. It is important to notice that despite the much larger number of signal candidates used for the LHCb measurement the total error is comparable with the ones of Belle and BABAR. The reason is the significantly larger mistag probability at a hadron collider which leads to a reduction of the statistical power of the events. Using all available measurements of $\sin \left ( 2\beta \right )$ an average value of

$$\displaystyle \begin{aligned} \sin \left( 2\beta\right) = 0.691 \pm 0.017 \end{aligned}$$

is obtained [87] which corresponds to a value of the phase β of,

$$\displaystyle \begin{aligned} \beta = (21.9 \pm 0.7)^\circ ~~\mbox{or}~~ \beta = (68.1 \pm 0.7)^\circ \, , \end{aligned}$$

where the ambiguity is not resolved.

9.6.5.2 $\mathrm {B}^0_{\mathrm {s}}$ Meson

Analogue to the measurement of the CKM phase β in the B⁰ system, the measurement of a corresponding ${\mathcal {C}\mathcal {P} }$ violating phase β _s, defined in Sect. 9.7, can be performed in the $\mathrm {B}^0_{\mathrm {s}}$ system, assuming that the $\mathrm {B}^0_{\mathrm {s}}$ oscillation can be resolved. The golden channel used is the decay $\mathrm {B}^0_{\mathrm {s}} \rightarrow \mathrm {J}/\psi \phi$. Due to its higher mass the $\mathrm {B}^0_{\mathrm {s}}$ system cannot be produced at the Υ(4S) resonance and β _s was therefore not accessible at the B-factories.

The two Tevatron experiments CDF and D0 have performed explorative studies of the decay $\mathrm {B}^0_{\mathrm {s}} \rightarrow \mathrm {J}/\psi \phi$ [102, 103] and also first measurements [104, 105] but the results have been limited by the number of recorded signal events. The first significant measurement of the phase⁶ϕ _s = −2β _s has been presented by the LHCb experiment in 2011 [106].

In the decay $\mathrm {B}^0_{\mathrm {s}} \rightarrow \mathrm {J}/\psi \phi$ the final-state is composed of two vector particles and angular momentum conservation allows for the relative angular momentum values L = 0, 1 or 2. The final-state J∕ψϕ is thus not a pure ${\mathcal {C}\mathcal {P} }$-state but a linear combination of ${\mathcal {C}\mathcal {P} }$-even and ${\mathcal {C}\mathcal {P} }$-odd eigenstates depending on the relative angular momentum L of the two vector mesons: η _CP = η _CP(J∕ψ)η _CP(ϕ)(−1)^L = (−1)^L. The measurement of the time dependent CP asymmetry requires a separate treatment of the CP-odd and CP-even states which can be achieved statistically by analyzing the angular distribution of the final-state particles J∕ψ → μ ⁺μ ⁻ and ϕ → K ⁺K ⁻. To measure the angular distribution of the final state particles it is common to use the helicity basis. The three decay angles necessary to describe the decay are denoted by (θ _K, θ _μ, φ _h) and are defined in Fig. 9.31. The polar angle θ _K (θ _μ) is the angle between the K ⁺ (μ ⁺) momentum and the direction opposite to the $\mathrm {B}^0_{\mathrm {s}}$ momentum in the K ⁺K ⁻ (μ ⁺μ ⁻) centre-of-mass system. The azimuthal angle between the K ⁺K ⁻ and μ ⁺μ ⁻ planes is φ _h.

Fig. 9.31

Definition of helicity angles as discussed in the text. Figure taken from [107]

The analysis of the $\mathrm {B}^0_{\mathrm {s}} \rightarrow \mathrm {J}/\psi \phi$ events is further complicated by a small fraction of non-resonant $\mathrm {B}^0_{\mathrm {s}} \rightarrow \mathrm {J}/\psi \mathrm {K}^+\mathrm {K}^-$ decays (${\mathcal {C}\mathcal {P} }$-odd) which interfere with the ϕ meson decaying to two charged kaons. These non-resonant events need to be considered. Effectively one therefore studies $\mathrm {B}^0_{\mathrm {s}}$ decays to J∕ψK ⁺K ⁻.

In the absence of ${\mathcal {C}\mathcal {P} }$ violation in mixing the ${\mathcal {C}\mathcal {P} }$-odd and ${\mathcal {C}\mathcal {P} }$-even decays of the $\mathrm {B}^0_{\mathrm {s}}$ meson correspond to the heavy and light mass eigenstates. Thus separating statistically the polarization amplitudes in an angular analysis allows the measurement of the decay width Γ_H and Γ_L and thus the measurement of the different lifetimes of the two $\mathrm {B}^0_{\mathrm {s}}$ mass states.

With a data-sample of 96,000 $\mathrm {B}^0_{\mathrm {s}} \rightarrow \mathrm {J}/\psi \mathrm {K}^+\mathrm {K}^-$ events LHCb has performed a simultaneous analysis of the measured decay time and the three decay angles to determine the time-dependent ${\mathcal {C}\mathcal {P} }$ asymmetry and the related ${\mathcal {C}\mathcal {P} }$ phase ϕ _s [108]. Figure 9.32 shows the decay time distribution as well as the distributions of the three decay angles. One clearly sees how the ${\mathcal {C}\mathcal {P} }$-odd and ${\mathcal {C}\mathcal {P} }$-even components can be statistically separated using the decay angles. The decay time distribution shows the different decay behavior of the two ${\mathcal {C}\mathcal {P} }$ components with the ${\mathcal {C}\mathcal {P} }$-even component decaying visibly faster. For the average decay width Γ_s and for the decay width difference Δ Γ_s one obtains [108],

$$\displaystyle \begin{aligned} \Gamma_s = (\Gamma_L + \Gamma_H)/2 = 0.6603 \pm 0.0027 \pm 0.0015~\mathrm{ps}^{-1}\, , \end{aligned}$$

$$\displaystyle \begin{aligned} \Delta \Gamma_s = \Gamma_L - \Gamma_H = 0.0805 \pm 0.0091 \pm 0.0032~\mathrm{ps}^{-1} \, . \end{aligned}$$

Fig. 9.32

Decay-time and helicity-angle distributions for $\mathrm {B}^0_{\mathrm {s}} \rightarrow \mathrm {J}/\psi \mathrm {K}^+\mathrm {K}^-$ decays (data points). The solid blue line shows the total signal contribution, which is composed of ${\mathcal {C}\mathcal {P} }$-even (long-dashed red), ${\mathcal {C}\mathcal {P} }$-odd (short-dashed green) and S-wave (dotted-dashed purple) contributions. Figure taken from [108]

The simultaneous determination of the time-dependent ${\mathcal {C}\mathcal {P} }$ asymmetry results in the following value for the ${\mathcal {C}\mathcal {P} }$ violating phase ϕ _s,

$$\displaystyle \begin{aligned} \phi_s = -0.058 \pm 0.049 \pm 0.006 \, . \end{aligned}$$

The time-dependent ${\mathcal {C}\mathcal {P} }$ violation in the $\mathrm {B}^0_{\mathrm {s}}$ system is thus very small and within the sensitivity of the measurement no ${\mathcal {C}\mathcal {P} }$ violation has been seen. The phase ϕ _s can also be measured in the mode $\mathrm {B}^0_{\mathrm {s}} \rightarrow \mathrm {J}/\psi \pi ^+\pi ^-$. The J∕ψπ ⁺π ⁻ final-state has been shown to be an almost pure (97.7%) CP-odd final state [109] and the CP violating phase can thus be extracted without the complication of an angular analysis. A much smaller signal sample with 27,000 events results into a comparable precision for ϕ _s, ϕ _s = −0.070 ± 0.068 ± 0.008 [110]. The analysis of these events however, requires the knowledge Δ Γ_s as external input. Performing a combined analysis of the two decay channels [108] LHCb reports a value of ϕ _s of

$$\displaystyle \begin{aligned} \phi_s = -0.010 \pm 0.039 \, . \end{aligned}$$

The ATLAS and CMS collaborations have also performed measurements of the phase ϕ _s and of the width difference Δ Γ_s [111, 112]. The overall experimental situation is summarized in Fig. 9.33 where also the theoretical expectation is shown. It should be noted that there is no ab-initio theory prediction for the phase ϕ _s. The prediction results from the measurement of $\sin \left ( 2\beta \right )$ and exploits the unitarity of the CKM matrix, see also Sect. 9.7. The average value for ϕ _s, ϕ _s = −0.021 ± 0.031 [130], agrees very well with the expectation ϕ _s = −0.0370 ± 0.0006 [113].

Fig. 9.33

68% confidence level contours in the ϕ _s-Δ Γ_s plane, showing the measurements from CDF, D0, ATLAS, CMS and LHCb together with their combination (white ellipse). The thin black line represents the Standard Model predictions. Figure taken from [130]

9.6.6 Direct CP Violation

B meson decays offer a broad decay phenomenology and are an ideal system to look also for large direct ${\mathcal {C}\mathcal {P} }$ violation. Topologically very different tree-level and penguin decay amplitudes can result into the same final state and their interference can cause significant ${\mathcal {C}\mathcal {P} }$ asymmetries. Considering the B meson decay B → f and its ${\mathcal {C}\mathcal {P} }$ conjugates ${\bar {B} \rightarrow \bar {f}}$, direct ${\mathcal {C}\mathcal {P} }$ violation or ${\mathcal {C}\mathcal {P} }$ violation in the decay is measured as time-integrated asymmetry of the observed signal yields:

$$\displaystyle \begin{aligned} A_{CP} = \frac{\Gamma({B \rightarrow f}) - \Gamma({\bar{B} \rightarrow \bar{f}})}{\Gamma({B \rightarrow f}) + \Gamma({\bar{B} \rightarrow \bar{f}})} \end{aligned} $$

For a given B decay B → f, direct ${\mathcal {C}\mathcal {P} }$ violation can only arise if at least two interfering decay amplitudes A ₁ and A ₂ exist and if these decay amplitudes carry different weak and strong phases, φ _i and δ _i. The total decay amplitude A _f is given as sum

$$\displaystyle \begin{aligned} A_f = \left| A_1 \right| e^{\varphi_1 + \delta_1} + \left| A_2 \right| e^{\varphi_2 + \delta_2} \, . \end{aligned} $$

For the amplitudes of the charge conjugated process $\bar {A}_{\bar {f}}$ the weak phases change sign while the strong phases stay unchanged,

$$\displaystyle \begin{aligned} \bar{A}_{\bar{f}} = \left| A_1 \right| e^{-\varphi_1 + \delta_1} + \left| A_2 \right| e^{-\varphi_2 + \delta_2} \, . \end{aligned}$$

The expected signal yields depend on the interference of the amplitudes and the observable ${\mathcal {C}\mathcal {P} }$ asymmetry is determined by the difference of the interference terms. The ${\mathcal {C}\mathcal {P} }$ asymmetry is a function of the weak and strong phases as well as a function of the ratio R of the decay amplitudes,

$$\displaystyle \begin{aligned} A_{CP} = \frac{2\sin{}(\phi_1 -\phi_2)\sin{}(\delta_1 -\delta_2)} {R + R^{-1} + \cos{}(\phi_1 -\phi_2)\cos{}(\delta_1 -\delta_2)} ~\mbox{with}~R\equiv\left|\frac{A_1}{A_2} \right| \, . \end{aligned} $$

(9.211)

To observe large asymmetries the interfering amplitudes should have different weak and strong phases. While the weak phases, and in particular the weak phase difference, are determined by the CKM parameters, the theoretical determination of the strong phases is difficult. The B meson are subject to both, short and long-distance QCD effects which cannot be treated perturbatively.

In the following, two classes of B decays exhibiting large direct ${\mathcal {C}\mathcal {P} }$ violation will be discussed: B decays to charmless final-states, i.e. to final-states without D mesons, and decays to charmed final-states of the type B → DK.

9.6.6.1 Direct ${\mathcal {C}\mathcal {P} }$ Violation in Charmless B Decays

As sketched in Fig. 9.34 charmless two-body B decays such as B ⁰ → K ⁺π ⁻ can proceed via two topologically very different classes of decay amplitudes, tree and penguin processes, which carry different weak and in generally also different strong phases. Large direct ${\mathcal {C}\mathcal {P} }$ violation is therefore expected for these decays.

Fig. 9.34

Tree-level (left) and penguin (right) contribution to the charmless two-body decay B ⁰ → K ⁺π ⁻

First experimental evidence for direct ${\mathcal {C}\mathcal {P} }$ violation in B meson decays was reported by the Belle collaboration in 2004 for the decay B ⁰ → π ⁺π ⁻ [114]. As the neutral B meson decays here to a ${\mathcal {C}\mathcal {P} }$ eigenstate the formalism of (9.194) and (9.207) has to be applied, i.e. the observable time dependent asymmetry can be parametrized by the coefficient $A^{dir}_{\pi \pi }$ describing the effect of direct ${\mathcal {C}\mathcal {P} }$ asymmetry and the coefficient $A^{mix}_{\pi \pi }$ to describe the effect of indirect ${\mathcal {C}\mathcal {P} }$ violation through interference of diagrams with and without mixing. Belle observed a deviation of the coefficient $A^{dir}_{\pi \pi }$ from zero, i.e. direct ${\mathcal {C}\mathcal {P} }$ violation, at the level of 3.2σ. The result suggested large interference effects between the relevant tree and penguin diagrams and was confirmed by subsequent measurements. Today, the most recent value of this coefficient is $A^{dir}_{\pi \pi } = 0.32 \pm 0.04$ [87] and confirms the early hints for direct ${\mathcal {C}\mathcal {P} }$ violation in B ⁰ → π ⁺π ⁻.

The two B-factory experiments, BABAR and Belle, also studied B ⁰ → K ⁺π ⁻ decays where large penguin contributions were expected. Both collaborations performed time-independent analyses and reported the observation of large direct ${\mathcal {C}\mathcal {P} }$ violations for B ⁰ → K ⁺π ⁻ decays ( Babar: A _CP = −0.133 ± 0.030 ± 0.009 [115]; Belle: A _CP = −0.101 ± 0.025 ± 0.005 [116]). Both measurements represent the first doubtless observation of large direct ${\mathcal {C}\mathcal {P} }$ violation in the B⁰ system. It is useful to remember that direct ${\mathcal {C}\mathcal {P} }$ violation in the neutral kaon system is many orders smaller (O(10⁻⁶)). It is the effect of the large weak phases entering the B⁰ decay amplitudes which produces the much larger direct ${\mathcal {C}\mathcal {P} }$ violation.

Already with the very first data-set recorded in 2011 and corresponding to only 0.35 fb⁻¹ of data, the LHCb experiment has repeated the measurement of A _CP for the channel B ⁰ → K ⁺π ⁻ [117]. LHCb’s excellent resolution of the reconstructed K ^±π ^∓ invariant mass allows to distinguish between a decaying B⁰ and $\mathrm {B}^0_{\mathrm {s}}$ and thus also probed the decay ${B^0_s \rightarrow K^-\pi ^+}$. The measurement of $A_{CP}({B^0_s \rightarrow K^-\pi ^+}) = 0.27 \pm 0.08 \pm 0.02$ provided the first evidence (3.3σ ) for direct ${\mathcal {C}\mathcal {P} }$ violation in the $\mathrm {B}^0_{\mathrm {s}}$ system. The measurement was repeated with more data and the observed direct ${\mathcal {C}\mathcal {P} }$ violation $A_{CP}({B^0_s \rightarrow K^-\pi ^+}) = 0.27 \pm 0.04 \pm 0.01$ [118] confirmed the earlier result. Figure 9.35 shows the invariant mass distribution for the recorded ${ B^0_{(s)} \rightarrow K \pi }$ decays. Clear differences in the number of recorded decays for the B and the anti-B decays are observed.

Fig. 9.35

Invariant mass spectra of (a, b) B ⁰ → K ⁺π ⁻ the recorded decays and zoomed in (c, d) to show the ${B^0_s \rightarrow K^-\pi ^+}$ decays. Panels (a) and (c) represent the K ⁺π ⁻ invariant mass, whereas panels (b) and (d) represent the K ⁻π ⁺ invariant mass. The results of a mass fit describing the signals are overlaid. The main components contributing to the fit model are also shown. Figure taken from [118]

9.6.6.2 Direct ${\mathcal {C}\mathcal {P} }$ Violation in B → DK Decays and Measurement of CKM Phase γ

While direct ${\mathcal {C}\mathcal {P} }$ violation in B decays is large and experimentally easy accessible, the theoretical interpretation is non-trivial. The calculation of the non-perturbative hadronic effects and the resulting strong phases is difficult. A way to use direct ${\mathcal {C}\mathcal {P} }$ asymmetries to constrain the CKM parameters is therefore a simultaneous determination of the weak (CKM) phases and the hadronic nuisance parameters including the strong phases. This approach is followed to determine the CKM phase γ as defined in Sect. 9.7. Ignoring higher order terms, γ is in good approximation equal to the phase of the CKM matrix element V _ub ($V_{ub}=\left | V_{ub}\right | e^{-i\gamma }$).

The phase can be probed using ${B^- \rightarrow D^0 (\overline {D}^0) K^-}$ decays with either a $b\rightarrow u \bar {c}s$ ($\overline {D}^0 K^-$) or $b\rightarrow c \bar {u}s$ (D ⁰K ⁻) tree-level quark transition as depicted in Fig. 9.36. The two decays can be described by three parameters: r _B (≈ O(0.1)), the absolute value of the ratio of both amplitudes; δ _B the strong phase difference; and the CKM phase γ. In order to observe the ${\mathcal {C}\mathcal {P} }$ violating interference between the two amplitudes the D ⁰ and the $\overline {D}^0$ mesons emerging in case of the two different amplitudes should decay into a common final state f _D, i.e. $D, \bar {D} \rightarrow f_D$. The size of the ${\mathcal {C}\mathcal {P} }$ violating interference which provides the sensitivity to γ is proportional to r _B.

Fig. 9.36

Tree-level Feynman diagrams of the decays ${B^- \rightarrow D^0 (\overline {D}^0) K^-}$. The left diagram implies a $b\rightarrow u \bar {c}s$ transition, and is strongly suppressed by the small value of $\left | V_{ub} \right |$. The right diagram proceeds via a transition $b\rightarrow c \bar {u}s$

The possibility of observing direct ${\mathcal {C}\mathcal {P} }$ violation in B ⁻→ DK ⁻ decays was first discussed in the 1980s [119, 120] using decays of the $D (\bar {D})$ to neutral kaons and pions. Since then, several methods have been proposed which can be grouped according to the choice of the final state.

• The Gronau-London-Wyler (GLW) method [121, 122] considers the decays of D mesons to ${\mathcal {C}\mathcal {P} }$ eigenstates, such as the ${\mathcal {C}\mathcal {P} }$-even decays D ⁰ → K ⁺K ⁻ and D ⁰ → π ⁺π ⁻.

• The Atwood-Dunietz-Soni (ADS) approach [123, 124] extends this to include final states that are not ${\mathcal {C}\mathcal {P} }$ eigenstates, for example D ⁰ → K ⁺π ⁻ together with its doubly Cabibbo-suppressed counterpart D ⁰ → K ⁻π ⁺. The interference between Cabibbo-allowed and doubly Cabibbo-suppressed decay modes in both the B and D decays gives rise to large charge asymmetries. However, the different D decays require additional parameters r _D and δ _D to describe the ratio of suppressed and favored D decay amplitudes as well as their phase difference.

• The Grossman-Ligeti-Soffer (GLS) method [125] is similar to the ADS method but uses singly Cabibbo-suppressed decays such as D →K_SK⁺π ⁻ decays.

• The Giri-Grossman-Soffer-Zupan (GGSZ) method [126] uses self-conjugate multibody D meson decay modes like K_Sπ ⁺π ⁻ or K_SK⁺K⁻ and requires an analysis of the Dalitz plot to account for the varying D decay parameters. A model-dependent analysis assumes specific D decay amplitudes while a model-independent approach uses external input for the strong-phase difference δ _D and the D amplitude ratio r _D in bins of the Dalitz space.

Simultaneous fits to several observables, ${\mathcal {C}\mathcal {P} }$ asymmetries or ratios of suppressed to favored modes, allow the determination of the decay parameters including the CKM phase γ. The main issue with all methods is the small overall branching fraction of the observable decays which range from 5 × 10⁻⁵ to 5 × 10⁻⁹ [127]. The precise determination of the CKM phase γ therefore requires a very large data-sample. The B factories have pioneered different methods to determine γ, however the achieved overall statistical precision on γ was limited. Combining the different methods and quoting a single result for γ, BABAR and Belle report the following values [127]:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \gamma &\displaystyle =&\displaystyle (69 \pm 17)^\circ~~\mbox{(BABAR)} \, ,\\ \gamma &\displaystyle =&\displaystyle (68 \pm 14)^\circ~~\mbox{(Belle)} \, . \end{array} \end{aligned} $$

The breakthrough towards a precision determination of the phase γ came when the LHCb experiment was able to measure even very rare doubly Cabibbo-suppressed decays such as $B^- \rightarrow \left [ \pi ^- K^+\right ]_D K^-$ and its charge-conjugated counter-parts with sufficiently high statistics to observe ${\mathcal {C}\mathcal {P} }$ asymmetries. Figure 9.37 shows as an example the decay $B^- \rightarrow \left [ \pi ^- K^+\right ]_D K^-$ as well as the decay $B^- \rightarrow \left [ \pi ^- K^+\right ]_D \pi ^-$ which also provides sensitivity to γ together with the corresponding charge conjugated decays [128]. The observed yields clearly signal direct ${\mathcal {C}\mathcal {P} }$ violation for both channels. LHCb has analysed B ⁺ → DK ⁺ decays with a multitude of different decay modes of the neutral D, B ⁺ → D ^∗K ⁺ and B ⁺ → DK ^∗+ decays and B ⁰ → DK ^∗ decays. In addition time-dependent analyses of $B_s^0 \rightarrow D_s^\mp K^\pm$ and B ⁰ → D ^∓π ^± are performed and measure combinations of the CKM phases γ and β _s or β, respectively. The combination of the different LHCb measurements [129] finally result into a value of

$$\displaystyle \begin{aligned} \begin{array}{rcl} \gamma &\displaystyle =&\displaystyle (74.0^{+5.0}_{-5.8})^\circ~~\mbox{(LHCb)} \, , \end{array} \end{aligned} $$

(9.212)

in perfect agreement with the early measurements by BABAR and Belle. For the average of all γ measurements one finds [87],

$$\displaystyle \begin{aligned} \begin{array}{rcl} \gamma &\displaystyle =&\displaystyle (73.5^{+4.2}_{-5.1})^\circ \, . \end{array} \end{aligned} $$

(9.213)

Fig. 9.37

Invariant mass distributions of selected $B^\pm \rightarrow \left [ \pi ^\pm K^\mp \right ]_D h^\pm$ decays, separated by charge. The dashed pink line left of the signal peak shows partially reconstructed $B_s^0 \rightarrow \left [ K^+\pi ^- \right ]_D K^-\pi ^+$ decays, where the bachelor pion is missed. For the two channels, one clearly observes a yield difference, i.e. ${\mathcal {C}\mathcal {P} }$ asymmetry, between the two charge-conjugated channels. Figure taken from [128]

9.7 Weak Quark Mixing and the CKM Matrix

The observation of direct ${\mathcal {C}\mathcal {P} }$ violation in the neutral K meson and the confirmation of large ${\mathcal {C}\mathcal {P} }$ violating effects in the neutral B meson system provided the experimental evidence of weak quark-mixing as the primary source of ${\mathcal {C}\mathcal {P} }$ violation in the hadron sector. A multitude of precision measurements confirmed the prediction of the quark-mixing paradigm of the Standard Model [57] and led to the Nobel prize for Kobayshi and Maskawa. Despite this success of experimental and theoretical quark flavor physics we know today that other sources of ${\mathcal {C}\mathcal {P} }$ violation must exists to explain the baryon asymmetry of our universe.

9.7.1 Quark-Mixing Matrix

Historically quark-mixing was introduced by Cabibbo [56] to explain the different coupling strength of hadronic currents in weak decays of neutrons and pions compared to strangeness changing processes, such as the decay of K mesons and Λ hyperons. Cabibbo postulated—expressed in today’s notation—that the weak eigenstates of the then known quarks with charge − 1∕3 were not the flavor eigenstates d and s but a linear combination, rotated by an angle θ, the Cabibbo angle:

$$\displaystyle \begin{aligned} d_c = d \, \cos\,\theta + s \sin\,\theta\;. \end{aligned} $$

(9.214)

The GIM mechanism [131], introduced to cancel the K_L → μ ⁺μ ⁻ amplitude, required the orthogonal state

$$\displaystyle \begin{aligned} s_c = - d \, \sin\,\theta + s \, \cos\,\theta\;, \end{aligned} $$

(9.215)

and an additional charge + 2∕3 quark, the charm quark, complementing the two quark doublets.

We know today that three generations of up-type quarks u ⁱ (i = 1, 2, 3: u-, c-, t-quark) with electrical charge + 2∕3 and three generations of down-type quarks d ⁱ (i = 1, 2, 3: d-, s-, b-quark) with electrical charge − 1∕3 exist. In the Standard Model, the masses and mixing of quarks arise from the Yukawa interaction with the Higgs condensate which couples the left-handed quark fields u _L and d _L to the right-handed quark fields u _R and d _R (for better readability the generation index is suppressed). After spontaneous breaking of the electroweak symmetry the Yukawa terms give rise to masses and mixing:

$$\displaystyle \begin{aligned} \mathcal{L}_{\mbox{Yukawa}} = -\frac{v}{\sqrt{2}} \left( \bar{d}_L \mathbf{Y_d} d_R + \bar{u}_L \mathbf{Y_u} u_R\right) + h.c. \end{aligned}$$

The Yukawa matrices Y _d and Y _u are complex 3 × 3 matrices in generation or flavor space and do not need to be diagonal. Indeed, in the Standard Model they are not, and as a consequence the flavor states are not equal to the mass eigenstates of the quarks. The mass eigenstates $\tilde {u}_{L,R}$ and $\tilde {d}_{L,R}$ are obtained by unitary transformations of the above quark flavor states: $\tilde {u}_{A}= \mathbf {V_{A,u}} u_A$ and $\tilde {d}_{A}= \mathbf {V_{A,d}} d_A$ (with chirality index A = L, R for left and right-handed quark fields, and suppressed generation indices). The unitary matrices V _A,u and V _A,d diagonalize the Yukawa matrices and one obtains the diagonal quark mass matrices for the up- and down-type quarks,

$$\displaystyle \begin{aligned} \mathbf{M_u} = \mbox{diag}(m_u, m_c, m_t) = \frac{v}{\sqrt{2}} \mathbf{V_{L,u}{Y_u}V^\dagger _{R,u}} \, , \end{aligned}$$

$$\displaystyle \begin{aligned} \mathbf{M_d} = \mbox{diag}(m_d, m_s, m_b) = \frac{v}{\sqrt{2}} \mathbf{V_{L,d}{Y_d}V ^\dagger _{R,d}}. \end{aligned}$$

The quark masses will appear as usual Dirac mass terms in the above Yukawa part of the Lagrangian:

$$\displaystyle \begin{aligned} \mathcal{L}_{\mbox{Yukawa}} = - \bar{\tilde{d}}_L \mathbf{M_d} \tilde{d}_R - \bar{\tilde{u}}_L \mathbf{M_d} \tilde{u}_R + h.c. \end{aligned}$$

If the up-type and and down-type Yuakawa matrices Y _u and Y _d cannot be diagonalized simultaneously by the same transformations there is a net effect of the change of the quark basis. The charged current terms of the Standard Model Lagrangian combining left-handed up and down-type quarks therefore get a flavor structure imprinted which is described by the Cabibbo Kobayshi Maskawa (CKM) quark-mixing matrix

$$\displaystyle \begin{aligned} \mathbf{V_{CKM} \equiv V_{L,u}V^\dagger_{L,d} }\; . \end{aligned}$$

The charge current terms expressed in the mass eigenstates have the form

$$\displaystyle \begin{aligned} \mathcal{L}_{\mathcal{C}\mathcal{C} } = -\frac{g}{\sqrt{2}} \left( \bar{\tilde{u_L}} \gamma^\mu W_\mu^+ \mathbf{ V_{CKM}} \tilde{d_L} + \bar{\tilde{d_L}} \gamma^\mu W_\mu^- \mathbf{V_{CKM}}^\dagger \tilde{u_L} \right) \; . \end{aligned}$$

Here, the matrix element (V _CKM)_ij connects a left-handed up-type quark of the ith generation to a left-handed down-type quark of the jth generation. The matrix elements are therefore expressed using flavor indices:

For a non-diagonal CKM matrix the charged quark currents are thus inter-generation flavor changing currents. In analogy to the flavor eigenstates introduced by Cabibbo it is usual to absorb the CKM matrix by introducing for the down-type quarks the weak quark eigenstates $\tilde {d}^\prime = \mathbf {V_{CKM}} \tilde {d_L}$.

Since it is the product of unitary matrices the CKM matrix itself is unitary, i.e. V _CKMV _CKM ^† = 1, and its elements are in general complex. The number of parameters of a general unitary 3 × 3 matrix is nine, three rotation angles and six phases. By rephasing the quark mass eigenstates $\tilde {q}\rightarrow e^{i\alpha _q} \tilde {q}$ one can remove five phases, corresponding to the five independent phase differences between the quarks, and leaving one ${\mathcal {C}\mathcal {P} }$ violating phase δ. The usual parametrization of the CKM matrix uses the three rotation angles θ ₁₂, θ ₂₃, θ ₁₃ and the phase δ:

(9.216)

where $s_{{ }_{ij}} = \sin \theta _{ij}$ and $c_{{ }_{ij}} = \cos \theta _{ij}$. in the Standard Model, the phase δ is responsible for all ${\mathcal {C}\mathcal {P} }$ violating phenomena in quark-flavor changing processes.

The rotation angles are defined and labeled in a way which relates to the mixing of two specific generations. In the limit θ ₂₃ = θ ₁₃ = 0 the third generation decouples, and the situation reduces to the usual Cabibbo mixing of the first two generations, with θ ₁₂ identified as the Cabibbo angle. The angles θ ₁₂, θ ₂₃, θ ₁₃ can all be chosen to lie in the first quadrant, i.e. $s_{{ }_{ij}},c_{{ }_{ij}} >0$, by appropriate redefinition of the quark field phases.

From measurements it is known that $1 \gg s_{{ }_{12}} \gg s_{{ }_{23}} \gg s_{{ }_{13}}$. It is therefore common to use a parametrization of the CKM matrix that emphasizes this hierarchy. In the Wolfenstein parametrization one defines

$$\displaystyle \begin{aligned} \lambda = s_{{}_{12}} = \frac{\left| V_{us}\right|}{\sqrt{\left| V_{ud}\right|{}^2+\left| V_{us}\right|{}^2}} \; , \;\;\; A \lambda^2 = s_{{}_{23}} = \lambda \left| \frac{V_{cb}}{V_{us}} \right| \; , \;\;\; A \lambda^3 \left( \rho + i \eta \right) = s_{{}_{13}} e^{i\delta} = V_{ub}^\ast \, , \end{aligned}$$

where λ is the sine of the Cabibbo angle ($\sin \theta \approx 0.22$) and the real numbers A, ρ and η are of order unity. With these parameters the CKM matrix can be expressed in powers of λ and takes the convenient form

$$\displaystyle \begin{aligned} V = \begin{pmatrix} 1 - {\lambda}^2 /2 & \lambda & A {\lambda}^3 (\rho - \mathrm{i} \eta ) \\ -\lambda & 1 - {\lambda}^2 /2 & A {\lambda}^2 \\ A {\lambda}^3 (1 - \rho - \mathrm{i} \eta ) & -A {\lambda}^2 & 1 \\ \end{pmatrix} + \mathcal{O}(\lambda^4 ) ~. {} \end{aligned} $$

(9.217)

As the definition of (ρ + iη) depends on the phase convention, one often introduces the parameters $(\bar {\rho } + i \bar {\eta } )$, defined by

$$\displaystyle \begin{aligned} A \lambda^3 \left( \rho + i \eta \right) = \frac{A \lambda^3 (\bar{\rho} + i \bar{\eta} ) \sqrt{1-A^2 \lambda^4}}{\sqrt{1-\lambda^2}\left[ 1- A^2 \lambda^4 (\bar{\rho} + i \bar{\eta} )\right] } \, . \end{aligned} $$

(9.218)

This definition ensures that $(\bar {\rho } + i \bar {\eta } ) = -(V_{ud}V_{ub}^\ast )(V_{cd}V_{cb}^\ast )$ is phase convention independent and the CKM matrix written in the parameters λ, A, $\bar {\rho }$ and $\bar {\eta }$ is unitary to all orders in λ.⁷

The elements of the CKM matrix are fundamental parameters of the Standard Model and need to be experimentally determined. The unitarity condition of the CKM matrix imposes a set of relations between the matrix elements:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_i{V_{ij}V_{ik}^\ast} &\displaystyle = &\displaystyle \delta_{jk} \;\;\mbox{with} \;\; jk=\{dd, ds, db, ss, sb, bb \} \end{array} \end{aligned} $$

(9.219)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_j{V_{ij}V_{kj}^\ast} &\displaystyle = &\displaystyle \delta_{ik} \;\;\mbox{with} \;\; ik=\{uu, uc, ut, cc, ct, tt \} \end{array} \end{aligned} $$

(9.220)

The six vanishing combinations (j ≠ k, i ≠ k) describe triangles in the complex plane. The area of all triangles is given by half of the Jarlskog invariant J [132],

$$\displaystyle \begin{aligned} \Im \left[ V_{ij} V_{kl} V_{il}^\ast V_{kj}^\ast \right] = J \sum_{m,n=1}^{3} \epsilon_{ikm}\epsilon_{jln} \; , {} \end{aligned} $$

(9.221)

where one representation of Eq. (9.221) reads for instance $J = \Im \left [ V_{us} V_{cb} V_{ub}^\ast V_{cs}^\ast \right ]$. Expressed in the parameters of the standard CKM representation one finds $J = -c_{{ }_{12}} c_{{ }_{13}} c_{{ }_{23}} s_{{ }_{12}} s_{{ }_{13}} s_{{ }_{23}} \sin \delta$. A nonvanishing CKM phase and hence ${\mathcal {C}\mathcal {P} }$ violation requires J ≠ 0.

While four of the six unitarity triangles are degenerated and rather slim, only two triangles have approximately equal sides, of which one is usually referred as the Unitarity Triangle (UT),

$$\displaystyle \begin{aligned} V_{ud}V_{ub}^\ast + V_{cd}V_{cb}^\ast + V_{td}V_{tb}^\ast = 0 \; . \end{aligned} $$

(9.222)

Commonly one normalizes the triangle basis to unity by dividing each side by $V_{cd}V_{cb}^\ast$ to obtain a triangle with vertices exactly at (0, 0), (0, 1) and the apex at $(\bar {\rho }, \bar {\eta })$. The UT is sketched in Fig. 9.38. As can be seen from Fig. 9.38 the angles of the UT are

$$\displaystyle \begin{aligned} \begin{array}{rcl} \alpha &\displaystyle = &\displaystyle \arg \left( - \frac{V_{td} V_{tb}^\ast} {V_{ud} V_{ub}^\ast } \right) \end{array} \end{aligned} $$

(9.223)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \beta &\displaystyle = &\displaystyle \arg \left( - \frac{V_{cd} V_{cb}^\ast} {V_{td} V_{tb}^\ast } \right) \end{array} \end{aligned} $$

(9.224)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \gamma &\displaystyle = &\displaystyle \arg \left( - \frac{V_{ud} V_{ub}^\ast} {V_{cd} V_{cb}^\ast } \right) {} \end{array} \end{aligned} $$

(9.225)

Fig. 9.38

Sketch of the Unitarity Triangle (UT). Figure taken from [133]

Often a different naming convention, also shown in Fig. 9.38, is used to label the three angles. The UT angles are constraint by the ${\mathcal {C}\mathcal {P} }$ observables discussed in Sect. 9.6:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \beta &\displaystyle = &\displaystyle (21.9\pm 0.7)^\circ \end{array} \end{aligned} $$

(9.226)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \gamma &\displaystyle =&\displaystyle (73.5^{+4.2}_{-5.1})^\circ \end{array} \end{aligned} $$

(9.227)

The measurement of the angle α has not been discussed in Sect. 9.6. It is measured using the observation of time-dependent ${\mathcal {C}\mathcal {P} }$ violation in the decays B ⁰ → ππ, ρρ, and πρ by BABAR and Belle. The average of this measurements result into [133, 134],

$$\displaystyle \begin{aligned} \begin{array}{rcl} \alpha &\displaystyle = &\displaystyle ( 84.5^{+5.9}_{-5.2} )^\circ \; . \end{array} \end{aligned} $$

(9.228)

The sum of three angles, $\alpha +\beta + \gamma = \left ( 180 \pm 7\right )^\circ$, is consistent with the expectation and represents a first test of the unitarity of the CKM matrix. An additional constraint of the CKM phases and thus of the UT angles comes from the measurement of time-dependent ${\mathcal {C}\mathcal {P} }$ violation in $\mathrm {B}^0_{\mathrm {s}}$ decays and the measurement of the phase β _s (with ϕ _s = −2β _s, see Sect. 9.6),

$$\displaystyle \begin{aligned} \beta_s = \arg \left( - \frac{V_{ts} V_{tb}^\ast} {V_{cs} V_{cb}^\ast } \right) = (0.60 \pm 0.89)^\circ \, . \end{aligned} $$

(9.229)

In addition to the measurements of ${\mathcal {C}\mathcal {P} }$ violation in the B meson systems also the measurements of ${\mathcal {C}\mathcal {P} }$ violation in the $K^0\bar {K}^0$ mixing, |𝜖 _K| = (2.233 ± 0.015) × 10⁻³ (see Sect. 9.5) provides information about the CKM matrix. The measurement of |𝜖 _K| can be translated into an approximate hyperbolic constraint on the apex ($\bar {\rho }$, $\bar {\eta }$) of the UT [135].

The sides of the unitarity triangle are accessible by measuring decay rates and mixing frequencies. In the following the experimental determination of the CKM elements as well as a test of the unitarity of the CKM matrix is discussed.

9.7.2 Determination of the CKM Matrix Elements

• 1. |V _ud|. Precise determinations of |V _ud| are available from nuclear beta decays, from the decay of the free neutron and from semileptonic pion decays (π ⁺ → π ⁰e ⁺ν). The most precise value results from an analysis of superallowed 0⁺ → 0⁺ nuclear beta decays which are pure vector transitions. The measurements of the transition energies, the partial branching fractions, and the half-lives of the parent nuclei together with radiative and isospin-symmetry-breaking corrections allow the determination of the corrected $\mathcal {F}t$-value, from which, by using the muon life-time, |V _ud| can be determined. The average of the fourteen most precise determinations yield [136],

  $$\displaystyle \begin{aligned} |V_{ud}| = 0.97417 \pm 0.00021 \, , \end{aligned}$$

  where the error is dominated by the theoretical uncertainty stemming from the nuclear structure and radiation correction.

  The theoretical uncertainties in extracting a value of |V _ud| from neutron decays are significantly smaller than those for the superallowed decays, however the value depends on the ratio between axial-vector and vector couplings (g _A ≡ G _A∕G _V) and on the neutron lifetime. Using the most recent measurements [133] the following value for |V _ud| is obtained,

  $$\displaystyle \begin{aligned} |V_{ud}| = 0.9763 \pm 0.0016 \, , \end{aligned}$$

  with the error dominated by the g _A uncertainty.

  An alternative approach is the measurement of the very small ($\mathcal {O}(10^{-8})$) branching ratio of the pion beta-decay π ⁺ → π ⁰e ⁺ν. The value normalized by a very precise theoretical prediction for π ⁺ → e ⁺ν and yields [137]

  $$\displaystyle \begin{aligned} |V_{ud}| = 0.9749 \pm 0.0026 \, . \end{aligned}$$

  The error here stems mainly from the measurement of the rare process.

• 2. |V _us|. Earlier measurements of |V _us| from kaon decays have used K_L → πeν to extract the product of |V _us| and the form factor |V _us|f ₊(0) at q ² = 0. The most recent data provide enough experimental constraints to also use decays to muons as well as decays of K_S and K^±. Averaging results from K_L → πeν, K_L → πμν, K^±→ π ⁰e ^±ν, K^±→ π ⁰μ ^±ν and K_S → πeν yields the value |V _us|f ₊(0) = 0.2165 ± 0.0004 [133]. Lattice QCD calculations of f ₊(0) have been carried out for different numbers of quark flavors. The form-factor average, f ₊(0) = 0.9704 ± 0.0032, of the (2+1)-flavor lattice calculations [138] is in good agreement with a classical calculation [139]. With this value one obtains,

  $$\displaystyle \begin{aligned} |V_{us}| = 0.2231 \pm 0.0008 \, . \end{aligned}$$

  The lattice calculation of the ratio of kaon and pion decay constant, f _K∕f _π = 1.1933 ± 0.0029 [138], allows the determination of the ratio |V _us∕V _ud| from K → μν and π → μν decays. Using the precise measurement of the K → μν branching fraction by the KLOE collaboration [140] results in |V _us| = 0.2253 ± 0.0007.

  An alternative determination of |V _us| uses hadronic τ decays to strange hadrons. The average of the measured inclusive and exclusive branching fractions yields |V _us| = 0.2216 ± 0.0015 [134].

• 3. |V _cd|. First determinations of $\left | V_{cd}\right |$ came from neutrino scattering experiments. The difference of the ratio of double-muon to single-muon production for neutrino and antineutrino scattering is depending on the charm production cross section and thus on |V _cd|², as well as on the semileptonic (muonic) branching ratio of the produced charm mesons, $\bar {\mathcal {B}}_\mu$. The method was first used by the CDHS group [141] but has also been applied by CCFR [142] and by CHARM II [143]. Averaging the results is complicated, also because $\bar {\mathcal {B}}_\mu$ is an effective quantity which depends on the specific neutrino beam characteristics. One finds $\bar {\mathcal {B}}_\mu |V_{cd}|{ }^2 = (0.463\pm 0.034) \times 10^{-2}$ [144] and using the average value of $\bar {\mathcal {B}}_\mu = 0.087 \pm 0.005$ one obtains [133]

  $$\displaystyle \begin{aligned} |V_{cd}| = 0.230 \pm 0.011 \, . \end{aligned}$$

  Similar to $\left | V_{us} \right |$, $\left | V_{cd} \right |$ can also be extracted from semileptonic (D → πℓν) and leptonic (D ⁺ → μ ⁺ν) charm decays. Also here, QCD lattice calculations are used to determine the relevant form factors $f_+^{D\pi }(q^2=0)$ and f _D [138]. Using the average of the branching fraction measurements from BABAR, Belle, BES III and CLEO-c for D → πℓν [134] results into [133]

  $$\displaystyle \begin{aligned} |V_{cd}| = 0.2140 \pm 0.0029 \pm 0.0093, \end{aligned}$$

  where the first uncertainty is experimental and the second stems from the theoretical uncertainty of the form factor calculation. The measurements of the leptonic branching ratio D ⁺ → μ ⁺ν by BES III and a CLEO-c results into [134]

  $$\displaystyle \begin{aligned} |V_{cd}| = 0.2164 \pm 0.0050 \pm 0.0015 \, , \end{aligned}$$

  where also here the first error is experimental while the second describes the uncertainty of the form factor calculation. For the average of the three different determinations of $\left |V_{cd} \right |$ the Particle Data Group [133] quotes a value of

  $$\displaystyle \begin{aligned} |V_{cd}| = 0.218 \pm 0.004 \, . \end{aligned}$$

• 4. |V _cs|. Measurements of semileptonic decays of D mesons to kaons D →Kℓν as well as the measurement of leptonic decays of D _s mesons, $D_s^+\rightarrow \mu ^+ \nu$, together with the corresponding form factors from lattice calculations allow the determination of |V _cs|. Branching fraction measurements have been performed by Belle, BABAR, CLEO-c and BES III, and are averaged in [134]. From the semileptonic measurements one obtains |V _cs| = 0.967 ± 0.025 where the error is dominated by the theoretical uncertainty of the form factor calculations. The average of the leptonic measurements results into |V _cs| = 1.006 ± 0.019 where the dominating uncertainty is experimental. For the average of both values the Particle Data Group [133] reports a values of

  $$\displaystyle \begin{aligned} |V_{cs}| = 0.997 \pm 0.017. \end{aligned}$$

• 5. |V _cb|. This matrix element is determined from semileptonic B decays to D or D ^∗ mesons. Two experimentally and theoretically different approaches are used. The inclusive approach measures the inclusive semileptonic decay rate to any charmed final state together with the moments of the leptonic energy and the hadronic invariant mass spectra. An operator product expansion within the Heavy Quark Effective Theory (HQET) allows the calculation of decay rates and the energy and mass spectra in dependence of expansion parameters α _s and the inverse of the heavy quark mass. The simultaneous measurement of several distributions over-constrains the physical parameters and allows a determination of |V _cb|. An analysis and an averaging of existing measurements is performed in [145] and leads to |V _cb| = (42.2 ± 0.8) × 10³ with uncertainties arising mainly from higher-order perturbative and non-perturbative corrections.

  In the exclusive approach semileptonic B decays to exclusive channels containing D and D ^∗ mesons are studied. In the infinite quark mass limit with m _b , m _c ≫ Λ _QCD, heavy quark symmetry predicts that all form-factors are given by a single function which depends on the product of the four-velocities v of the B and v ^′ of the D ^(∗) (mesons) and are normalized at the point of maximum momentum transfer to the lepton system (v ⋅ v ^′ = 1). The matrix element |V _cb| is obtained from an extrapolation to this point. The precise determination of normalization and the shape of the form factor function requires additional corrections calculated using HQET. Reference [145] quotes |V _cb| = (41.9 ± 2.0) × 10³ as the average exclusive value of |V _cb|.

  The inclusive and the exclusive determination of |V _cb| are in agreement and [145] performs the average of both values:

  $$\displaystyle \begin{aligned} |V_{cb}| = (42.2 \pm 0.8) \times 10^{3}. \end{aligned}$$

• 6. |V _ub|. Similar to |V _cb| also |V _ub| is determined analysing inclusive and exclusive semileptonic B decays with a $b \rightarrow u \ell \bar {\nu }$ transition. The determination of |V _ub| from inclusive decays however suffers experimental and theoretical difficulties. The total inclusive decay rate is hard to measure due to the large background from CKM-favored $b \rightarrow c \ell \bar {\nu }$ transitions. Therefore, strong kinematic cuts are introduced to suppress these background contributions. The restriction to tight kinematic regions however complicates the theoretical description. The calculation of partial decay rates in the various kinematic regions requires the introduction of non-perturbative distribution functions—the so called shape functions—to describe the effect of hadronic physics. At leading order there is only a single shape function which can be determined using inclusive $\bar {B}\rightarrow X_s \gamma$ decays. Subleading effects are considered using different theoretical models based on Heavy Quark Expansion (HQE). A recent summary of the |V _ub| values extracted within different models from measurements by BABAR, BELLE and CLEO can be found in [145]. All calculations give similar values for |V _ub| and similar error estimates. As average [145] quotes

  $$\displaystyle \begin{aligned} |V_{ub}| = (4.49 \pm 0.15^{+0.16}_{-0.17} ) \times 10^{-3} \, . \end{aligned}$$

  To consider different theoretical treatments the authors assign an additional quadratic error of ± 0.17 × 10⁻³.

  The determination of |V _ub| from exclusive decays, such as B → πℓν decays, suffers experimentally from very small signal yields and requires the theoretical determination of the corresponding form factors. Lattice form factor calculations are available for the high q ² regions. So called light-cone QCD sum rules (LCSR) are applicable for the low q ² region. A simultaneous fit to experimental B → πℓν data and lattice results as function of q ² together with additional constraints from LCSR results into

  

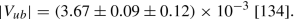
  The inclusive and exclusive determinations of |V _ub| are largely independent and the large discrepancy between both methods remains a puzzle. Inflating the errors to account for this discrepancy [145] quotes an average of

  $$\displaystyle \begin{aligned} |V_{ub}| = (3.94 \pm 0.36) \times 10^{-3} \end{aligned}$$

  The LHCb experiment has used the ratio of the two baryonic decays $\varLambda _b \rightarrow p \mu ^- \bar {\nu }$ and $\varLambda _b \rightarrow \varLambda _c \mu ^- \bar {\nu }$ to extract the ratio |V _ub∕V _cb| = 0.083 ± 0.006 [146]. The q ²-dependent form factor ratio had to be taken into account to consider the different kinematical ranges of the two decays. Using the above average for |V _cb| one obtains

  $$\displaystyle \begin{aligned} |V_{ub}|=(3.50 \pm 0.26)\times 10^{-3} \, . \end{aligned}$$

• 7. |V _tb|. An experimental determination of |V _tb| without assuming unitarity is possible using the production of single-top quarks. Single-top quark production cross-sections have been measured by the Tevatron experiments CDF and D0, and at LHC by ATLAS and CMS. Using these measurements [133] quotes the value

  $$\displaystyle \begin{aligned} |V_{tb}| = 1.019 \pm 0.025 \, . \end{aligned}$$

• 8. |V _td| and |V _ts|. The two CKM elements |V _td| and |V _ts| are expected to be very tiny and tree-level decays of the top-quark to a d-quark or s-quark will be very difficult to measure. However, both elements are accessible through the measurements of the mixing frequency of B⁰ and $\mathrm {B}^0_{\mathrm {s}}$ mesons (see Sect. 9.6). Using the most recent lattice QCD results for the hadronic factors, $f_{B_d}\sqrt {\hat {B}_{B_d}}= (219\pm 14)$ MeV and $f_{B_s}\sqrt {\hat {B}_{B_s}}= (270\pm 16)$ MeV [138], together with the world averages for the mixing frequencies Δm _d and Δm _s results into [133]

  $$\displaystyle \begin{aligned} |V_{td}| = (8.1 \pm 0.5) \times 10^{-3} ~~~\mbox{and} \end{aligned}$$
  $$\displaystyle \begin{aligned} |V_{ts}| = (39.4 \pm 2.3) \times 10^{-3} \; , \end{aligned}$$

  where the uncertainties are dominated by the lattice uncertainties of the hadronic factors. Several uncertainties are reduced when calculating the ratio

  $$\displaystyle \begin{aligned} \xi = \left( f_{B_s}\sqrt{\hat{B}_{B_s}} \right) / \left( f_{B_d}\sqrt{\hat{B}_{B_d}} \right) = 1.239 \pm 0.046 \, . \end{aligned}$$

  The ratio |V _td|∕|V _ts| is therefore stronger constraint [133],

  $$\displaystyle \begin{aligned} |V_{td}|/|V_{ts}| = 0.210 \pm 0.001 \pm 0.008 \, . \end{aligned}$$

Using the independent measurements of the CKM elements the unitarity of the CKM matrix can be checked. One obtains for the first two rows [133],

$$\displaystyle \begin{aligned} \begin{array}{rcl} |V_{ud}|{}^2 + |V_{us}|{}^2 + |V_{ub}|{}^2 &\displaystyle = &\displaystyle 0.9994 \pm 0.0005 \, ,\\ |V_{cd}|{}^2 + |V_{cs}|{}^2 + |V_{cb}|{}^2 &\displaystyle = &\displaystyle 1.043 \pm 0.034 \, , \end{array} \end{aligned} $$

which agrees well with the unitarity assumption. In addition, the direct measurement of |V _tb| leaves little room for mixing of the top into unknown other states.

9.7.3 Global Analysis and Test of the Unitarity of the CKM Matrix

The available information on the magnitude and the phases of the CKM elements can be analysed by a global fit to all CKM parameters. The most precise information is obtained imposing Standard Model constraints such as the unitarity of the CKM matrix and the existence of exactly three quark generations. Input parameters of the global analysis are, beside the experimental measurements, also theoretically determined hadronic parameters with sometimes large errors.

Different approaches exist to combine the experimental data and to treat the experimental and theoretical errors. The CKM-Fitter group [135, 147] is using a frequentist’s framework based on a χ ² analysis. In these fits the frequentist’s treatment is also applied to the theoretical errors. The UTfit group [148] uses a baysian approach for all errors. The two different statistical approaches lead to very similar results and here only the results of [135] are presented.

Figure 9.39 shows the experimental constraints in the $(\bar {\rho },\bar {\eta })$ plane. Indicated is the unitarity triangle with its angles α, β and γ. The different measurements clearly limit the apex of the triangle to a small (dashed) region. For the Wolfenstein parameters introduced in Eq. (9.217) the global fit [133, 135] gives

(9.230)

(9.231)

Alternatively one can give the fit results of the magnitudes of all nine elements of the CKM matrix:

(9.232)

Fig. 9.39

Experimental constraints of the unitarity triangle. Shaded areas correspond to 95% C.L. Figure taken from [133]

Figure 9.39 represents an impressive confirmation of the CKM paradigm which describes the flavor transition and the ${\mathcal {C}\mathcal {P} }$ violation in the quark sector. The global fit currently does not point to deviations from the Standard Model picture. However, the effect of New Physics might be small. Over-constraining measurements of ${\mathcal {C}\mathcal {P} }$ asymmetries, mixing and flavor changing decays will put further bounds on possible New Physics contributions.

9.8 Conclusion

Nearly 40 years after the discovery of ${\mathcal {C}\mathcal {P} }$ violation, the nature of the phenomenon has been clarified experimentally. In the K meson system, ${\mathcal {C}\mathcal {P} }$ violation has been discovered in the mixing (ε), in the decay (ε′∕ε, direct ${\mathcal {C}\mathcal {P} }$ violation), and in the interference between mixing and decay (ℑmε); in the B meson system, ${\mathcal {C}\mathcal {P} }$ violation in the interference between mixing and decay (sin 2β) as well as ${\mathcal {C}\mathcal {P} }$ violation in the decay have been observed. While finishing this article, the LHCb collaboration has also reported the first observation of ${\mathcal {C}\mathcal {P} }$ violation in the decay of neutral D mesons to K ⁺K ⁻ and π ⁺π ⁻ ($\mathcal {O}(1.5\times 10^{-3})$) [205]. All observations are consistent⁸ with the model of Kobayashi and Maskawa where the 3 × 3 mixing matrix of six quarks has one non-trivial complex phase δ = (71.0 ± 0.3)^∘. This leads to complex weak coupling constants of quarks, and to ${\mathcal {T} }$ and ${\mathcal {C}\mathcal {P} }$ violation.

In cosmology , ${\mathcal {C}\mathcal {P} }$ violation together with a large departure from thermal equilibrium via a first-order electroweak phase transition [206] and a baryon number violation by instanton processes [207] could explain the observed baryon asymmetry . The source would be the asymmetric interactions of quarks and antiquarks with the Higgs field [208]. The size of the observed ${\mathcal {C}\mathcal {P} }$ violation in the quark sector, expressed by the Jarlskog determinant, however is insufficient to explain the matter asymmetry by several orders of magnitude [209]. Moreover, the low mass of the Higgs boson disfavours baryogenesis during the electroweak phase transition [210]. A way out of this dilemma is the hypothesis that ${\mathcal {C}\mathcal {P} }$ violation in the neutrino sector could cause a lepton asymmetry . (B+L)-violating processes before the electroweak phase transition could then convert the lepton asymmetry into a baryon asymmetry. Leptogenesis would proceed through the production of heavy Majorana neutrinos in the early Universe [211]. While the experimental proof of leptogenesis is difficult, the observation of ${\mathcal {C}\mathcal {P} }$ violation in the neutrino sector and the exploration of the nature of the neutrino (Dirac or Majorana fermion) could establish strong hints.

In quark flavor physics the focus has changed after the successful establishment of the Kobayashi-Maskawa paradigm. Today, the precise measurement of flavor changing processes and ${\mathcal {C}\mathcal {P} }$ asymmetries are used as tools to test the Standard Model predictions. Tiny deviations between observations and theory predictions could hint to additional quantum corrections modifying the size and the phase of flavor changing amplitudes. The origin of these additional corrections could be new heavy particles at mass scales much higher than the energies accessible by today’s collider experiments. Experimental results on neutral meson mixing already constrain the ratio between mass scale and the coupling strength of new particles to values above 10² to 10⁴ TeV, where the strongest bounds come from the neutral K meson system [212]. The next generation of precision quark-flavor experiments will thus open a window to New Physics complementary to the direct searches at highest energies.