Evaluating the Complexity of Deriving Adaptive Homing, Synchronizing and Distinguishing Sequences for Nondeterministic FSMs

Abstract

Homing, synchronizing and distinguishing sequences (HSs, SSs, and DSs) are used in FSM (Finite State Machine) based testing for state identification and can significantly reduce the size of a returned test suite with guaranteed fault coverage. However, such preset sequences not always exist for nondeterministic FSMs and are rather long when existing. Adaptive HSs, SSs and DSs are known to exist more often and be much shorter that makes them attractive for deriving test suites and adaptive checking sequences. As nowadays, a number of specifications are represented by nondeterministic FSMs, the deeper study of such sequences, their derivation strategies, and related complexity estimations/reductions is in great demand. In this paper, we evaluate the complexity of deriving adaptive HSs and SSs for noninitialized FSMs, the complexity of deriving DSs for noninitialized merging-free FSMs.

This work is partially supported by RFBR project N 19-0700327/19.

1 Introduction

Many problems in automata theory, for example, such as automata/Finite State Machine (FSM) based test derivation methods (see, for example, [1, 2, 4, 5, 12, 13]), rely on the state identification sequences in the specification FSM, namely, on distinguishing, homing, and synchronizing sequences (DSs, HSs, and SSs) that can be preset or adaptive [3]. Distinguishing sequences are derived to identify the initial state of the machine of interest, while homing and synchronizing sequences allow identifying its final state. Preset input sequences are derived before being applied to the system of interest (FSM, implementation under test, etc.), while for adaptive sequences the next input depends on the outputs produced for the previous inputs. Adaptive sequences can be represented by a tree or an acyclic FSM [14] called a test case. Adaptive distinguishing and homing sequences exist more often than the preset ones and are usually shorter.

When deriving adaptive DSs/HSs/SSs for deterministic FSMs one can consider a successor or a spanning tree [12, 18]. However, based on the above trees for nondeterministic FSMs, for all types of sequences there are no necessary and sufficient conditions when an adaptive sequence exists. Another approach [8] constructs an adaptive HS for the case when each pair of states has such an adaptive HS and these conditions are necessary and sufficient for a noninitialized complete observable FSM to have an HS. However, for a weakly initialized FSM with a proper subset of initial states the conditions become only sufficient. The same situation holds for adaptive DSs if an FSM under study is merging-free, i.e., an FSM where for each input, the FSM cannot move from two different states to the same state with equal outputs. The pairwise ‘homeability’ for the set of states can be also effectively used for deriving an adaptive SS for a given nondeterministic FSM. Indeed, it was shown in [11] that such adaptive SS exists for a noninitialized FSM if and only if each state pair is adaptively homing and the FSM has a state that is definitely reachable from any other state. The obtained results allowed to evaluate the upper bound on the length of a shortest adaptive HS/SS for complete noninitialized possibly nondeterministic FSMs; however, the question of the complexity for deriving such corresponding test cases remained open.

The main contribution of this paper is therefore the complexity evaluation of derivation of an adaptive HS/SS for noninitialized complete FSMs and an adaptive DS for noninitialized complete merging-free FSMs. We show that given the FSM under study having n states and q outputs, a corresponding test case has at most $(n-1)^2n/2 + n + 1$ states and the complexity of deriving such a test case is $\mathrm {O}(qn^5)$.

The rest of the paper has the following structure. Section 2 contains the preliminaries. The procedure for deriving adaptive HSs and DSs based on those for each pair of states is presented in Sect. 3 along with its complexity estimation while Sect. 4 describes the construction of SSs. Section 5 briefly describes the related work and Sect. 6 concludes the paper.

2 Preliminaries

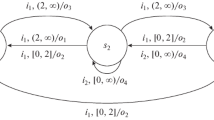
A finite state machine (FSM), or simply a machine, is a 5-tuple $\mathbf {S} \,=\, {<}S, I, O, h_S, S_{in}{>}$ where S is a finite nonempty set of states with the set $S_{in} \subseteq S$ of initial states, I and O are finite input and output alphabets, and $h_S \subseteq S \times I \times O \times S$ is a transition relation. FSM $\mathbf {S}$ is noninitialized if $S_{in} = S$ and in this case, we omit the set $S_{in}$ of initial states and a noninitialized FSM is denoted as a 4-tuple ${<}S, I, O, h_S{>}$. FSM $\mathbf {S}$ is an initialized FSM if $|S_{in}| = 1$ and FSM $\mathbf {S}$ with the initial state $s_j$ is denoted $\mathbf {S}/s_j$. If $1< |S_{in}| < |S|$ then FSM $\mathbf {S}$ often is called weakly initialized. FSM $\mathbf {S}$ is nondeterministic if for some pair $(s, i) \in S \times I$, there exist several pairs $(o, s') \in O \times S$ such that $(s, i, o, s') \in h_S$; otherwise, the FSM is deterministic. FSM $\mathbf {S}$ is observable if for every two transitions $(s, i, o, s_1)$, $(s, i, o, s_2) \in h_S$ it holds that $s_1 = s_2$. FSM $\mathbf {S}$ is complete if for every pair $(s, i) \in S \times I$, there exists a transition $(s, i, o, s') \in h_S$. In the following, we consider complete observable possibly nondeterministic FSMs unless something different is explicitly stated. An example of a complete nondeterministic FSM is shown in Fig. 1. A complete observable FSM is merging-free [20] if for every two different states $s_1$ and $s_2$ and any input i it holds that if $(s_1, i, o, s_1')$, $(s_2, i, o, s_2') \in h_S$, then $s_1' \ne s_2'$.

Fig. 1.

A complete observable nondeterministic FSM $\mathbf {S}$

The behavior relation $h_S$ is extended to input and output sequences in usual way and given an input sequence $i_1 \dots i_l$, we say that an output sequence $o_1 \dots o_l \in out(s, i_1 \dots i_l)$ if and only if there exists a state $s'$ such that $(s, i_1 \dots i_l, o_1 \dots o_l, s') \in h_S$. Given an input/output pair io and a state s of a complete observable FSM $\mathbf {S}$, state $s'$ is the io-successor of state s of FSM $\mathbf {S}$ if $(s, i, o, s') \in h_S$. The io-successor of state s not necessarily exists and in this case, we say that the io-successor of state s is the empty set. A trace of FSM $\mathbf {S}$ at state s is a sequence of input/output pairs which label consecutive transitions starting from state s, $tr = i_1o_1 \dots i_lo_l$ (or $i_1/o_1 \dots i_l/o_l$). A sequence $i_1 \dots i_l$ is an input sequence of the trace while $o_1 \dots o_l$ is an output sequence. Since FSM $\mathbf {S}$ is observable, given state s and a trace $\gamma$ of the FSM, the $\gamma$-successor of state s is state $s'$ which is reached from s via the trace $\gamma$. If $\gamma$ is not a trace at state s then the $\gamma$-successor of state s is empty or sometimes we say that in this case the $\gamma$-successor of state s does not exist. Given non-empty subset $S'$ of states and a trace $\gamma$ of the FSM, the $\gamma$-successor of $S'$ is the union of $\gamma$-successors over all states of the set $S'$.

Test Case Definition. An input sequence $\alpha$ is called adaptive if the next input depends on the output to the previous one. An adaptive input sequence can be represented by a tree or a special FSM that is called a test case [14]. Given an input alphabet I and an output alphabet O, a test case $\mathbf {TC}(I, O)$ over an input alphabet I and an output alphabet O is an initialized initially connected observable single-input output-complete FSM that has an acyclic transition graph. In other words, at each state either only one input with all possible outputs is defined or there are no outgoing transitions, and in the latter case, the state is a deadlock state. A test case is a partial FSM once $|I| > 1$. By definition, a test case $\mathbf {TC}(I, O)$ represents an adaptive experiment with a complete FSM $\mathbf {S}$ over alphabets I and O in the following way. If input $i_1$ is a defined input at the initial state $t_0$ of $\mathbf {TC}(I, O)$ then first, the input $i_1$ is applied to the FSM $\mathbf {S}$ under investigation and $\mathbf {TC}(I, O)$ moves to the $i_1o$-successor $t_1$ of state $t_0$ if $\mathbf {S}$ produces the output o as the response to the input $i_1$. The next input to apply is the input defined at state $t_1$, etc. The procedure terminates when a deadlock state is reached. The height of the test case $\mathbf {TC}(I, O)$ is the length of a longest trace from the initial state to a deadlock state of $\mathbf {TC}(I, O)$ and it specifies the length of the longest input sequence that can be applied to an FSM $\mathbf {S}$ during the adaptive experiment.

Given FSM $\mathbf {S} \,=\, {<}S, I, O, h_S{>}$, a test case $\mathbf {TC}(I, O)$ is a homing test case (HTC) for $\mathbf {S}$ if for every trace $\gamma$ from the initial state to a deadlock state, the $\gamma$-successor of the set $S_{in}$ in $\mathbf {S}$ is a singleton or the empty set. FSM $\mathbf {S}$ is homing if $\mathbf {S}$ has a homing test case. A homing test case is a synchronizing test case (STC) for the FSM $\mathbf {S}$, if there exists a state s such that for every trace $\gamma$ of $\mathbf {TC}(I, O)$ from the initial to a deadlock state, $\gamma$-successor of $S_{in}$ is either $\{s\}$ or the empty set. A homing test case represents an adaptive homing sequence and a homing test case for machine $\mathbf {S}$ in Fig. 1 is shown in Fig. 3. By direct inspection, one can assure that an HTC in Fig. 3 is not an STC for $\mathbf {S}$.

A test case $\mathbf {TC}(I, O)$ is a distinguishing test case (DTC) if every trace $\gamma$ from the initial state to a deadlock state can be a trace at most at a single state of the set $S_{in}$. A distinguishing test case represents an adaptive distinguishing sequence.

In [8], it is shown that a noninitialized observable FSM has a homing test case if and only if each pair of states is homing while in [20] it is it is shown that a noninitialized observable merging-free FSM has a distinguishing test case if and only if each pair of states has such test case. For a STC corresponding necessary and sufficient conditions are established in [11]. Given a complete observable noninitialized FSM, there exists a synchronizing test case if and only if the FSM has a homing test case and there exists a state definitely reachable from any other state. State $s' \in S$ is definitely-reachable (d-reachable) from state $s \in S$ if there exists a test case $\mathbf {P}(s, s')$ over alphabets I and O such that for every trace $\gamma$ of $\mathbf {P}(s, s')$ from the initial state to a deadlock state, the $\gamma$-successor of state s in FSM $\mathbf {S}$ is either the empty set or is the set $\{s'\}$. We hereafter refer to such a test case as a d-transfer test case. In [15], necessary and sufficient conditions are established that allow to check if state $s \in S$ is definitely reachable from the initial state $s_0$ of the initialized FSM $\mathbf {S}$. In particular, it is proven that state s of an initialized FSM $\mathbf {S}$ is definitely reachable from state $s_0$ if and only if $\mathbf {S}$ has a single-input acyclic submachine $\mathbf {S}'$ with the initial state $s_0$ and the only deadlock state s such that for each input defined in some state of $\mathbf {S}'$, the state has all the transitions of $\mathbf {S}$ labeled with this input. Moreover, in the same paper, an efficient method is proposed for checking whether a state s is definitely reachable from the initial state of an initialized complete FSM, and in [11], this procedure is adjusted for arbitrary states s and $s'$.

Note that since any d-transfer test case $\mathbf {P}(s, s')$ is an acyclic submachine of the machine $\mathbf {S}$, then the length of any trace in $\mathbf {P}(s, s')$ does not exceed the number n of states of $\mathbf {S}$; in other words, one needs at most $n-1$ inputs to adaptively transfer the possibly nondeterministic machine from state s to state $s'$. Therefore, the length of a longest trace in a shortest test case $\mathbf {P}(s, s')$ is polynomial and is at most $n-1$.

Given a uninitialized complete observable FSM $\mathbf {S}$, if there is no state s that is definitely reachable from any other state then FSM $\mathbf {S}$ has no synchronizing test case. On the other hand, if there exists state s that is definitely reachable for any other state then this condition does not guarantee that the FSM has a synchronizing test case; the FSM must also be homing.

As an example, consider an FSM $\mathbf {P}$ in Fig. 2. By direct inspection, one can assure that state 3 is d-reachable from state 1 via input b while being d-reachable from state 2 via input a. Note that, for FSM $\mathbf {S}$ in Fig. 1, there is no state that is d-reachable from any other state.

Fig. 2.

A complete observable nondeterministic FSM $\mathbf {P}$ where state 3 is d-reachable from states 1 and 2

Despite the fact that there are many research papers on evaluating the complexity of the existence check of adaptive HS/SS/DS and their length (see Sect. 5), the complexity of their derivation even for noninitialized complete nondeterministic FSM is unknown. We furthermore utilize the above cited criteria to estimate the complexity of deriving HTCs, STCs and DTCs for noninitialized nondeterministic FSMs. For the sake of simplicity, we hash states, inputs and outputs by integers; however, for simplifying the reading we still use characters s, i, o.

3 Deriving Homing and Distinguishing Test Cases

We first come back to the definition of k-homing pairs of different states [7]. Given a noninitialized complete observable possibly nondeterministic FSM $\mathbf {S} = {<}S, I, O, h_S{>}$ and two different states $s_a$ and $s_b$, the pair $\{s_a, s_b\}$ is 1-homing if there exists an input $i_{\{s_a, s_b\}}$ such that for every $o \in O$, the $i_{\{s_a, s_b\}}o$-successor of the pair $\{s_a, s_b\}$ has at most one state. Let all the pairs of k-homing states be determined for some $k > 0$. Then the pair $\{s_a, s_b\}$ is $(k+1)$-homing if it is not k-homing and there exists an input $i_{\{s_a, s_b\}}$ such that for every $o \in O$, the pair of $i_{\{s_a, s_b\}}o$-successors of states $s_a$ and $s_b$ either is at most k-homing or the $i_{\{s_a, s_b\}}o$-successor of the pair $\{s_a, s_b\}$ has at most one state. The pair $\{s_a, s_b\}$ is homing if $\{s_a, s_b\}$ is k-homing for some $k > 0$.

In fact, the above definition for checking if a pair of different states is homing is constructive and can be used for deriving a homing test case for a homing pair of states. Moreover, when each pair of different states is homing a partial order relation can be established over pairs of different states when $\{s_a, s_b\} > \{s_p, s_m\}$ if and only if $\{s_a, s_b\}$ is a j-homing pair while $\{s_p, s_m\}$ being k-homing for $k < j$. Let the pair $\{s_a, s_b\}$ be j-homing, $j > 0$. If $j = 1$ then there exists an input $i_{\{s_a, s_b\}}$ such that for every $o \in O$, the $i_{\{s_a, s_b\}}o$-successor of $\{s_a, s_b\}$ has at most one state. If $j > 1$ then there exists an input $i_{\{s_a, s_b\}}$ such that for every $o \in O$, the pair of $i_{\{s_a, s_b\}}o$-successors of states $s_a$ and $s_b$ either is at most $(j-1)$-homing or the $i_{\{s_a, s_b\}}o$-successor of the pair $\{s_a, s_b\}$ has at most one state. Correspondingly, we propose to derive an array Input where for each pair $\{s_a, s_b\}$ the corresponding input $i_{\{s_a, s_b\}}$ is saved.

Consider FSM $\mathbf {S}$ in Fig. 1. There are 1-homing pairs $\{2,3\}$ and $\{2,4\}$ with $i_{\{2,3\}} = a$ and $i_{\{2,4\}} = b$. Pairs $\{1,2\}$, $\{1,3\}$ and $\{1,4\}$ are 2-homing with the inputs $i_{\{1,2\}}$, $i_{\{1,3\}}$, $i_{\{1,4\}}$ such that for every $o \in O$, $i_{\{1,2\}}o$-successor ($i_{\{1,3\}}o$-successor or $i_{\{1,4\}}o$-successor) of the corresponding pair is either 1-homing or those successors are singletons. Correspondingly, $i_{\{1,2\}} = b$, $i_{\{1,3\}} = i_{\{1,4\}} = a$. Pair $\{3,4\}$ is 3-homing with the input $i_{\{3,4\}}$ such that for every $o \in O$, the $i_{\{3,4\}}o$-successor of this pair is at most 2-homing or is a singleton and thus, $i_{\{3,4\}} = b$. The array Input is shown in Table 1.

Table 1. Array input for FSM $\mathbf {S}$ in Fig. 1

The main operation when constructing homing test cases is determining an io-successor for a given state (pair of different states). For this reason, we first assume that an FSM is given as a two-dimensional array IOsuc. Columns of IOsuc correspond to states of the given FSM while the rows correspond to possible io-pairs, i.e., given a state and an io-pair, the related cell has either the corresponding io-successor or it is empty (the transition is not defined). With the help of such structure, the calculation of an io-successor of a given state can be considered as an elementary operation. Table 2 has the array IOsuc for FSM $\mathbf {S}$ in Fig. 1. If FSM $\mathbf {S}$ is homing then we also prepare in advance the array Input where for each pair of different states $\{s_a, s_b\}$ the corresponding input $i_{\{s_a, s_b\}}$ is saved as described above. In fact, given these structures, the calculation of an io-successor will be reduced to a proper indexing in a certain array.

Table 2. The array IOsuc for FSM $\mathbf {S}$ in Fig. 1

Given a pair $\{s_1, s_2\}$ of different states of a homing complete observable FSM, the following algorithm returns a special homing test case $\mathbf {HTC}_{\{s_1, s_2\}}$ for the pair $\{s_1, s_2\}$. Indeed, in test case $\mathbf {HTC}_{\{s_1, s_2\}}$ returned by Algorithm 1 each state pair is listed only once. The reason is that the algorithm constructs a HTC for a state pair in such a way that each state pair representing its current state has a bigger degree of the ‘homeability’ than its successors (see Proposition 1).

Given FSM $\mathbf {S}$ in Fig. 1, the test case is derived by the use of the array Input and following partial order over the FSM state pairs: $\{1, 3\} > \{2, 3\}$, $\{1, 3\} > \{2, 4\}$.

Fig. 3.

A homing test case $\mathbf {HTC}_{\{1,3\}}$

By construction of a test case $\mathbf {HTC}_{\{s_1, s_2\}}$, the following statement holds.

Proposition 1

Given an FSM $\mathbf {S}$ with n states and a homing pair $\{s_1, s_2\}$ of $\mathbf {S}$, there exists a homing test case $\mathbf {HTC}_{\{s_1, s_2\}}$ such that states of $\mathbf {HTC}_{\{s_1, s_2\}}$ are pairs of different states of FSM $\mathbf {S}$ in the union with singletons of S and the deadlock state D. Moreover, given a j-homing state $q_1$ and an m-homing state $q_2$, if $j \le m$, then state $q_2$ is unreachable from state $q_1$ in $\mathbf {HTC}_{\{s_1, s_2\}}$.

Corollary 1

The number of states of $\mathbf {HTC}_{\{s_1, s_2\}}$ does not exceed $n(n-1)/2 + n + 1$ while the number of transitions of the test case $\mathbf {HTC}_{\{s_1, s_2\}}$ does not exceed $|O|n(n-1)/2$.

We now discuss the complexity of deriving the array Input and test case $\mathbf {HTC}_{\{s_1, s_2\}}$.

For deriving the set of all 1-homing pairs, for each pair of different states all input/output pairs io have to be studied, i.e., the complexity of this step is $\mathrm {O}(|I||O||S|^2)$ and each test case for a 1-homing pair has at most $(n+2)$ states and is constructed according to Algorithm 1. If k is the maximum integer such that there exists a pair of states that is k-homing then k is at most $\mathrm {O}(|S|^2)$. For deriving the set of all j-homing pairs, $j \le k$, the same check should be performed, and thus, the complexity of the check whether each pair of states is homing is $\mathrm {O}(|I||O||S|^2k)$ or at most $\mathrm {O}(|I||O||S|^4)$. The array Input is constructed during this check and thus, the derivation of the array Input has the same complexity. Therefore, the following proposition holds.

Proposition 2

Given an FSM $\mathbf {S} \,=\, {<}S, I, O, h_S{>}$ with n states, the (time) complexity of checking whether this FSM is homing is $\mathrm {O}(|I||O||S|^4)$. The problem of deriving the array Input has the same complexity.

If each pair of states is homing then the noninitialized FSM $\mathbf {S}$ is homing and at the next step, an HTC for the FSM has to be constructed. Here we notice that in [8], [7], a procedure for deriving HTC was proposed but the complexity of the HTC derivation was not evaluated. In this paper, we propose a modification of that algorithm that allows us evaluating the size of a returned HTC as well as the (time) complexity of the HTC derivation.

We now investigate some properties of the FSM $\mathbf {HTC}$ returned by Algorithm 2.

Proposition 3

An FSM $\mathbf {HTC}$ returned by Algorithm 2 is a homing test case for the FSM $\mathbf {S}$.

Proof

We first show that the FSM $\mathbf {HTC}$ returned by Algorithm 2 has an acyclic transition graph. By construction, given a state $\{s_a, s_b\}^r$, only states $\{s_k, s_p\}^j$, $j \ge r$, can be reached from state $\{s_a, s_b\}^r$. Moreover, if $r = j$, then due to Proposition 1, if state $\{s_a, s_b\}^r$ is reachable from state $\{s_k, s_p\}^r$ and the pair $\{s_a, s_b\}$ is j-homing, then the pair $\{s_k, s_p\}$ is at most l-homing for $l < r$ and thus, state $\{s_k, s_p\}^r$ is unreachable from state $\{s_a, s_b\}^r$ in $\mathbf {HTC}$ as only $\mathbf {HTC}_{\{s_p, s_m\}}$, $\{s_p, s_m\} \subseteq S$, are used when deriving $\mathbf {HTC}$ at the r-th iteration of Algorithm 2. The FSM under construction is indeed single-input as at each iteration of Algorithm 2 the transitions added to h refer to a single input $i_{\{s_a, s_b\}}$. Output completeness is handled by the last instruction at each iteration.

We now should show that when a singleton $s_k$ is reached then for this trace only $s_k$ can be reached from any state of $\mathbf {S}$. The statement holds for states $s_1$ and $s_2$ by construction of the test case $\mathbf {HTC}_{\{s_1, s_2\}}$. When states $s_3, \dots , s_n$ are added at the next iterations, if some trace at some of these states does not take the FSM $\mathbf {S}$ to state $s_k$ then the singleton $\{s_k\}$ would not be a deadlock state in the HTC.

Proposition 4

Given the FSM $\mathbf {S}$ with n states and the maximum integer k such that FSM $\mathbf {S}$ has a pair of different states that is k-homing but is not $(k - 1)$-homing, the FSM $\mathbf {HTC}$ returned by Algorithm 2 has at most $(n - 1)^2n/2 + n + 1$ states and the height at most $(n - 1)k$.

Indeed, Algorithm 2 has at most $(n - 1)$ iterations and at each iteration at most $(n - 1)n/2$ pairs of states are added. Moreover, there can be at most n singletons and a deadlock state D reached by traces which are not traces at some state of FSM $\mathbf {S}$. The height of $\mathbf {HTC}$ under construction does not exceed the maximal height k of $\mathbf {HTC}_{\{s_p, s_m\}}$, $\{s_p, s_m\} \subseteq S$, attached at most $(n - 1)$ times.

Since there is only one defined input with all possible outputs at each intermediate state of $\mathbf {HTC}$ returned by Algorithm 2, the following statement holds.

Corollary 2

Given a homing FSM $\mathbf {S}$ with n states, the FSM $\mathbf {HTC}$ returned by Algorithm 2 has at most $|O|(n - 1)^2n/2$ transitions.

Proposition 5

The (time) complexity of Algorithm 2 is $\mathrm {O}(|O|n^5)$.

Proof

The proof is performed by evaluating the complexity at an iteration step of Algorithm 2. At the iteration j we have at most $(j - 2)n(n - 1)/2$ states which are pairs of different states in $\mathbf {HTC}$ under construction. Correspondingly, the analysis of transitions at this step requires $\mathrm {O}(|O|(j - 2)n(n - 1)/2)$ operations.

At the same time, at the iteration j we perform the intersection of $\mathbf {HTC}$ under construction and $\mathbf {S}/s_j$, the former having $jn(n - 1)/2$ states which are pairs of different states and |O| transitions to process at each state while the latter having n states. Correspondingly, the complexity of checking all the transitions of the intersection needs $\mathrm {O}(|O|njn(n - 1)/2)$ operations and this number is higher than that for analyzing states of $\mathbf {HTC}$ under construction. Adding up the number of operations for $j = 2, \dots , n - 1$ we obtain the complexity $\mathrm {O}(|O|n^5)$ for Algorithm 2.

As a corollary to the above propositions and keeping in mind Proposition 2, the following statement can be established.

Theorem 1

Given a homing FSM $\mathbf {S}\, =\, {<}S, I, O, h_S{>}$, $|S| = n$, and the maximum integer k such that FSM $\mathbf {S}$ has a pair of different states that is k-homing but is not $(k - 1)$-homing, there exists a homing test case of the height at most $(n - 1)k$ with at most $(n - 1)^2n/2 + n + 1$ states, at most $|O|(n - 1)^2n/2$ transitions; the (time) complexity of deriving this test case is $\mathrm {O}(|O|n^5)$ when $\mathbf {S}$ is represented by arrays IOsuc and Input.

Note that the complexity of $\mathbf {HTC}$ derivation depends only on the number of states of the FSM under experiment as well as its number of outputs. However, differently from other approaches for deriving homing/synchronizing/distinguishing sequences, it does not directly depend on the number of inputs when the array Input is already derived.

Corollary 3

Given an FSM where all pairs of different states are at most 1-homing, there exists a homing test case $\mathbf {HTC}$ for the FSM $\mathbf {S}$ that has the height at most $(n - 1)$.

Consider an example of FSM $\mathbf {S}$ in Fig. 1 for illustrating Algorithm 2. We start with a pair $\{1, 2\}^2$; the b0-successor is $\{1\}$ while the b1-successor is $\{2, 3\}^2$. According to the array Input we consider input a for the pair $\{2, 3\}$ and obtain the a0-successor $\{2\}$ and the a1-successor $\{4\}$. After adding state 3 as an initial state the b0-successor $\{1\}$ of $\{1, 2\}^2$ becomes a new state $\{1, 3\}^3$. Since input a corresponds to the pair $\{1, 3\}$ in the array Input, we add corresponding transitions to states $\{2, 3\}^3$ and $\{2, 4\}^3$ and to singletons $\{1\}$, $\{2\}$, $\{4\}$. Adding state 4 as an initial state does not add more transitions to the test case.

We also notice that $\mathbf {HTC}$ returned by Algorithm 2 can be minimized. For example, in $\mathbf {HTC}$ in Fig. 4 states $\{2, 3\}^2$ and $\{2, 3\}^3$ can be merged into a single state since $\{2, 3\}^3$ is not reachable from any state reachable from $\{2, 3\}^2$ but generally it is not the case and such optimization is out of the scope of this paper.

Fig. 4.

$\mathbf {HTC}$ for FSM $\mathbf {S}$ in Fig. 1

It also should be mentioned that the observability and completeness of an FSM under investigation are the necessary conditions when using Algorithms 1 and 2 for deriving a homing test case. If the FSM is nonobservable then it can well happen that when adding a new state at the j-th iteration of Algorithm 2 not pairs of states but bigger subsets can be obtained when deriving the intersection $\mathbf {HTC} \cap \mathbf {S}/s_j$. If the FSM is partially specified then as it is shown in [19], even the problem of checking the existence of an adaptive homing sequence is PSPACE-complete.

Another interesting fact is that both above algorithms can be applied for deriving a distinguishing test case for a merging-free FSM. This relies on the following proposition.

Proposition 6

Given a complete merging-free noninitialized observable possibly nondeterministic FSM $\mathbf {S}$, a test case $\mathbf {TC}$ is a homing test case for $\mathbf {S}$ if and only if the $\mathbf {TC}$ is a distinguishing test case for $\mathbf {S}$.

Indeed, due to properties of merging free FSMs, given a merging-free FSM $\mathbf {S}$, a pair of different states of a complete FSM $\mathbf {S}$ is j-homing, $j > 0$, if and only if this pair is j-distinguishing for $\mathbf {S}$.

Note that the FSM in Fig. 2 is merging-free and thus, a homing test case, i.e., the test case in Fig. 5 without transitions from singletons is also a distinguishing test case¹.

Fig. 5.

$\mathbf {STC}$ for FSM $\mathbf {S}$ in Fig. 2

In the next section, the complexity of the derivation of an adaptive synchronizing sequence is evaluated based on the complexity for deriving an HTC for a homing FSM.

4 Deriving Synchronizing Test Cases

As mentioned above, there exists a synchronizing test case for a complete noninitialized observable FSM $\mathbf {S}$ if and only if the FSM $\mathbf {S}$ has a homing test case and there exists a state $s \in S$ that is definitely-reachable state from any other state. Moreover, in [11], the authors propose just appending the singletons of the HTC with d-transfer test cases. In this paper, we discuss this procedure more detailed in order to evaluate whether the complexity will be increased when a HTC is appended for deriving a STC.

The complexity of the procedure for checking if there exists a state that is d-reachable from any other state requires again considering all pairs of states. Similar to the check of homing pairs, we check each pair $\{i, 1\}$, $i = 2, 3, \dots , n$, of different states to conclude whether state 1 is d-reachable from any other state. If state 1 does not possess this property we check state pairs $\{i, 2\}$, $i = 1, 3, \dots , n$, etc. If there is no state that is d-reachable from any other state then the FSM has no synchronizing test case. The complexity of this check is $\mathrm {O}(|I||O||S|^2|S|)$ or at most $\mathrm {O}(|I||O||S|^3)$. If there exists state s that is d-reachable from any other state then in order to append a HTC with the corresponding transfer test cases, we define the relation of j-d-reachability that also is a partial order over the FSM states.

Given state $s'$ that is d-reachable from any other state, we say that $s'$ is 1-d-reachable from state s if there exists an input $i_s$ such that for each $o \in O$, the $i_so$-successor of s is empty or is a singleton $\{s'\}$. Given a subset of states from which state $s'$ is j-d-reachable, $j > 0$, we say that state $s'$ is $(j + 1)$-d-reachable from state s if there exists an input $i_s$ that for each $o \in O$, the $i_so$-successor of state $s'$ is l-d-reachable from state s for $l < j$. In other words, similar to j-homing pairs we establish a partial order relation over states due to the d-reachability of state $s'$. Similar to the array Input, we derive an array Input-d where for each state s of the FSM $\mathbf {S}$ the corresponding input $i_s$ is stored.

Correspondingly, we propose Algorithm 3 for deriving a STC for a complete observable FSM $\mathbf {S}$.

As an example, consider an FSM in Fig. 2. The corresponding array Input-d is shown in Table 3.

Table 3. Array Input-d for FSM in Fig. 2; state 3 is d-reachable from states 1 and 2

The corresponding synchronizing test case for the FSM in Fig. 2 is presented in Fig. 5. Note that, in Fig. 5 we omitted the transitions to the deadlock state D; some of these transitions are added at the third step of Algorithm 3 for preserving the output completeness of the returned test case. Indexes for state pairs indicate the number of j-th iteration of Algorithm 2 for deriving the corresponding HTC.

Since the d-reachability is a partial order relation and the array Input-d inherits the corresponding property, the following statement holds.

Proposition 7

An FSM $\mathbf {STC}$ returned by Algorithm 3 is a synchronizing test case for the FSM $\mathbf {S}$.

Similar to HTC derivation, the following statements estimate the complexity of the STC derivation taking advantage of the Input-d utilization.

Proposition 8

Given a FSM $\mathbf {S}$ with n states, the FSM $\mathbf {STC}$ returned by Algorithm 3 has the same set of states as the initial HTC while the number of transitions can be increased at most by |O|n.

Proposition 9

Given a homing FSM $\mathbf {S}$ with n states and its HTC, the complexity of Algorithm 3 is $\mathrm {O}(|O|n^4)$.

As a corollary to Propositions 4 and 9, the following statements hold.

Proposition 10

Given a homing FSM $\mathbf {S}$ with n states and the FSM $\mathbf {HTC}$ returned by Algorithm 2 of height l, the FSM $\mathbf {STC}$ returned by Algorithm 3 has at most $(n - 1)^2n/2 + n + 1$ states, at most $|O|(n - 1)^2n/2 + |O|n$ transitions and its height is at most $(l + n)$.

Theorem 2

Given a homing FSM $\mathbf {S}$ with n states where there exists a state that is d-reachable from any other state and the maximal integer k such that FSM $\mathbf {S}$ has a pair of different states that is k-homing but is not $(k - 1)$-homing, there exists a synchronizing test case with at most $(n - 1)^2n/2 + n + 1$ states, at most $|O|((n - 1)^2n/2 + n)$ transitions, of the height at most $(n - 1)k + n$, and the complexity of deriving this test case is $\mathrm {O}(|O|n^5)$ when $\mathbf {S}$ is represented by arrays IOsuc, Input and Input-d.

Note again, that similar to homing test case derivation, the complexity of deriving a STC for a noninitialized observable FSM does not directly depend on the cardinality of its input alphabet when $\mathbf {HTC}$ and the array Input-d are given.

5 Related Work

The problems of checking the existence and derivation of homing, synchronizing and distinguishing sequences have been widely investigated in the past seventy years. Major results obtained in this area mainly concern the deterministic FSM case: for noninitialized complete deterministic minimal machines the existence decision and derivation of an appropriate sequence for the final state identification (HS and SS) can be performed in polynomial time [16]. However, whenever the machine is weakly initialized or partial [19] the corresponding decision problems become PSPACE-complete. There is the same complexity for the existence check of a distinguishing sequence for a uninitialized deterministic machine [12]. However, even for the ‘good’ case of HS and SS for deterministic FSMs the problem becomes much harder when constructing a shortest HS or SS. Indeed, the problem of deriving a shortest HS/SS is NP-hard even for complete noninitialized deterministic minimal FSMs [16].

In some cases, the complexity of the existence check or derivation of a corresponding state identification sequence can be reduced via adaptive strategy. A remarkable example of such complexity reduction has been considered in [12] where the existence check of an adaptive DS has been proven to be solved in polynomial time with respect to the number of FSM states.

For nondeterministic machines, the problems listed above become harder. Indeed, as homing, synchronizing and distinguishing sequences have exponential length in this case [6, 9, 17], their existence check and derivation cannot be performed in polynomial time. The adaptive test case length however can be reduced: for homing and synchronizing sequences when considering complete noninitialized FSMs, while for distinguishing sequences for merging-free FSMs. Related decision problems have been considered in [8, 10, 11, 20] and have been proven to have polynomial complexity, as well as polynomial length of the corresponding sequences (with respect to the number of FSM states). In [8], an algorithm for deriving an adaptive homing sequence has been proposed, while [11] presents a similar contribution for synchronizing sequences. Nevertheless, to the best of our knowledge, the complexity of the derivation of such adaptive sequences for nondeterministic FSMs has not been investigated yet. Therefore, the contributions of the current paper are inline with the current state of the art and moreover, are rather promising as they establish the polynomial complexity of the derivation of adaptive SS and HS for nondeterministic noninitialized FSMs, as well as for adaptive DS for merging-free FSMs.

6 Conclusion

In this paper, we have investigated the complexity of deriving adaptive homing and synchronizing sequences for a complete observable noninitialized possibly non-deterministic FSM as well as the complexity of deriving an adaptive distinguishing sequence for merging-free FSMs. In fact, this complexity can be polynomial with respect to the product of the number of FSM states and the cardinality of its output alphabet. The main trick consists of the proposed data structures for representing the FSM under experiment, that allow considering an io-successor calculation as an elementary operation. Another important contribution lies in the proposal of a partial order over the FSM state pairs identifying the degree of homeability.

We note however, that the reachability of the upper bound $\mathrm {O}(|O|n^5)$ for an FSM with n states and |O| outputs, for deriving a homing/synchronizing test case might not be tight similar to distinguishing test cases for merging-free nondeterministic FSMs. For the future work, we thus would like to specify the FSM classes where worst theoretical upper bounds are reached while for other classes, we would like to investigate some potential optimizations of the proposed algorithms. We also note that in this work we only consider noninitialized FSMs, and there is still an open problem of evaluating the complexity of adaptive HS/SS/DS derivation for weakly initialized nondeterministic FSMs. The corresponding research is also left for the future work, together with the identification of the class of FSMs where the worst theoretical upper bounds are reached.