Local Least Squares Analysis of Auroral Currents

Abstract

Multi-spacecraft probing of geospace allows the study of physical structures on spatial scales dictated by orbital and instrumental parameters. This chapter highlights multi-point array analysis methods for constellations of two or three spacecraft such as Swarm, and also discusses multi-scale techniques for the geometrical characterisation of auroral current structures using observations of stationary or weakly time-dependent current structures along the tracks of individual satellites. Linear estimators are based on a least squares approach which is local in the sense that only few measurements around a reference point are considered for the reconstruction of geometrical and physical parameters. Local least squares estimators for field-aligned currents are compared with non-local counterparts and also local estimators based on finite differences. Uncertainties, implementation and other practical aspects are discussed. The techniques are illustrated using selected Swarm crossings of the auroral zone.

4.1 Introduction

Coupling processes in the auroral zone are to a large extent controlled by electric currents flowing parallel to the ambient magnetic field lines (e.g., Lysak 1990; Paschmann et al. 2002; Vogt 2002). Auroral field-aligned currents (FACs) connect remote plasmas in geospace and are associated with global magnetospheric dynamics such as large-scale convection and substorms. The type of electrodynamic coupling in the auroral current circuit depends on the spatial scale L of FACs. Quasi-static coupling of the equatorial magnetosphere and the auroral ionosphere is expected on large scales $L \gtrsim \lambda _P \sim 100$ km (Lyons 1980; Lotko et al. 1987). Alfvénic coupling should be important on intermediate scales $L \gtrsim \lambda _A \sim 10$ km (Vogt and Haerendel 1998). On even smaller spatial scales in the kilometre range or below, auroral phenomena are typically very dynamic and short-lived, and not correlated with long-range magnetosphere–ionosphere coupling processes. The importance of spatial scales in FACs and their association with auroral processes and coupling regimes was confirmed by Lühr et al. (2015) using data from the initial phase of ESA’s three-spacecraft Swarm mission when a range of inter-spacecraft distances was covered, see also Chap. 6 of this volume. Since April 2014, two Swarm satellites SwA and SwC orbit side-by-side in the auroral ionosphere, while the third Swarm satellite SwB moves at a higher altitude and lines up only occasionally with the lower pair to form a three-spacecraft constellation. SwA and SwC can be understood as a two-satellite array that allows the study of auroral FACs on a regular basis but restricted to the spatial scale given by their orbital separation.

To resolve electric current systems or other geospace structures by means of single-spacecraft data or multi-spacecraft observations, analysis methods must provide an adequate spatial resolution. The single-spacecraft approach where an individual satellite is assumed to move across a stationary or at most weakly time-dependent structure may resolve spatial scales given by the product of relative speed V and sampling interval $\varDelta t$. Satellite constellations such as Cluster and Swarm allow to adopt a multi-point array perspective with the spatial resolution given by the inter-spacecraft distance scale $\varDelta r$. For geospace phenomena and missions, $V \varDelta t$ is typically smaller than $\varDelta r$. Single-spacecraft methods allow the study of smaller scales but only in the along-track direction. Multi-point array techniques provide information also about the across-track variability (and possibly temporal changes) but only on larger spatial scales (e.g., Russell et al. 1983; Dunlop et al. 1988; Neubauer and Glassmeier 1990; Pinçon and Lefeuvre 1991; Chanteur and Mottez 1993; Dudok de Wit et al. 1995; Bauer et al. 2000; Balikhin et al. 2001; Dunlop et al. 2002; De Keyser et al. 2007; Vogt et al. 2008a), see also the ISSI Scientific Reports SR-1 and SR-8 (Paschmann and Daly 1998, 2008).

The category of analysis methods addressed in this report may be termed local least squares (LS) techniques. We are concerned mainly with multi-point array estimation of auroral FACs using vector magnetometer data from satellite missions such as Swarm, but also with multi-scale geometrical characterisation of current structures in the data of individual spacecraft. In local LS analysis, the least squares principle is applied to a confined region of interest, typically comprising only a few measurement points, equivalent to general (non-local) least squares modelling with localised basis functions but requiring less computational effort. Compared to local estimators based on finite differencing, local LS estimators turn out to be more robust with regard to non-regular (skewed or stretched) satellite constellations. To cover the multi-scale nature of auroral processes, in particular also intermediate and possibly even smaller scales, a multi-scale analysis technique developed by Bunescu et al. (2015, 2017) is included here as a localised version of the popular single-spacecraft minimum variance analysis or MVA that has its roots also in the least squares approach (Sonnerup and Scheible 1998).

Multi-spacecraft array techniques based on the local LS principle are presented in Sect. 4.2 (methodology) and Sect. 4.3 (implementation and applications). The multi-scale variant of MVA is discussed in Sect. 4.4 before we conclude in Sect. 4.5 with a summary.

4.2 Methodology of Multi-spacecraft Array Techniques

Multi-spacecraft estimation of spatial gradients, electric currents, or boundary parameters is based on a set of satellite positions and corresponding observations that are interpreted as array measurements. In the simplest and most straightforward case, each satellite of a constellation contributes one position vector to the array, and all measurements are taken at the same time. This perspective was adopted, e.g., by Dunlop et al. (1988), Chanteur (1998), Harvey (1998), as well as Vogt and Paschmann (1998) in the preparation phase of ESA’s four-spacecraft mission Cluster to develop analysis methods for electric currents and spatial gradients. The corresponding three-spacecraft case of the LS approach was addressed by Vogt et al. (2009). The resulting estimators are instantaneous, thus perfectly localised in time, and also local in space at the lower resolution limit given by the inter-spacecraft separation scale that for Cluster ranged between 100 km and 10,000 km.

For the Swarm mission with only two satellites SwA and SwC close enough to be considered a multi-point array on a regular basis, the instantaneous approach was relaxed to include additional measurements shifted in time, thus generating a virtual planar four-point satellite array (Ritter and Lühr 2006; Ritter et al. 2013; Shen et al. 2012a; Vogt et al. 2013). Virtual along-track separations approximately equal to the distance between SwA and SwC of somewhat less than 100 km in the auroral zone are obtained using time shifts of about 10 s, considerably smaller than the variation time scales of FACs associated with quasi-static coupling. Localisation in space is characterised by the effective inter-spacecraft separation in the virtual quad, typically of the order of 100 km. In the context of this report, we refer to this class of methods as local analysis techniques.

When spatial distributions of electrodynamic variables for large parts of or even the entire auroral region are to be reconstructed from satellite crossings (e.g., He et al. 2012; Amm et al. 2015), possibly in combination with other ground-based data, the methodology is usually termed modelling rather than analysis, and should be referred to as a regional method (spatial extent of the order of 1000 km), applicable to structures that do not vary on time scales less than the satellite crossing time of the order of a few minutes. The most popular modelling approach is based on the least squares principle that we choose as a starting point for our discussion.

4.2.1 General Linear Least Squares

Least squares modelling can be characterised as a statistical technique to find the parameters of a model (m) that gives the best approximation of a given data set (d) of S measurements contaminated by random errors (residuals r). The measurements $d_\sigma$ form the components of a data vector $\mathbf {d}$. If all parameters $a_1,a_2,\ldots ,a_N$ enter the model function m linearly, then $m = \sum _\nu a_\nu f_\nu$ with basis functions $f_\nu$. The model parameters $a_\nu$ are also called amplitudes and can be cast into a vector $\mathbf {a}$. The estimation problem can be written in the form ${\mathsf {M}}\mathbf {a} = \mathbf {d}$ with a matrix ${\mathsf {M}}$ and the solution $\mathbf {a} = {\mathsf {M}}^\text {ils} \mathbf {d}$ where ${\mathsf {M}}^\text {ils}$ is the pseudo-inverse of ${\mathsf {M}}$ in the least squares sense. For technical details of the general linear least squares approach, see Appendix A.

Fig. 4.1

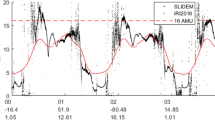
Sample output of MFACE, an empirical model of auroral FAC based on 10 years of CHAMP magnetic field measurements. Model results are generated for 02:48:00 UT on 24 July 2014 and for 13:40:30 UT on 29 May 2014, corresponding to the centre times of two Swarm auroral crossings used for demonstrating FAC analysis techniques in Sects. 4.3.2 and 4.4.1

Regional least squares modelling of auroral field-aligned currents was carried out by He et al. (2012, 2014) who condensed ten years of CHAMP (Reigber et al. 2002) magnetic field measurements into the empirical FAC model MFACE using a set of data-adaptive basis functions called empirical orthogonal functions (EOFs). In the first modelling step, the set of EOFs was constructed from the data in a coordinate frame centred on the dynamic auroral oval to capture its magnetic local time-dependent expansion and contraction during magnetospheric activity. The EOFs then serve as basis functions in an expansion of the form $j_\Vert (\varDelta \beta | \mathbf {p}) = \sum _\nu a_\nu (\mathbf {p}) f_\nu (\varDelta \beta )$ where the parameter vector $\mathbf {p}$ is formed by a set of predictor variables (magnetic local time, seasonal and solar wind parameters, AE), and $\varDelta \beta = \beta - \beta _\text {ACC}$ is magnetic latitude in auroral oval coordinates, i.e. relative to the latitude of the auroral current centre $\beta _\text {ACC}$. In a second step, the functional dependences $\beta _\text {ACC} = \beta _\text {ACC} (\mathbf {p})$ and $a_\nu = a_\nu (\mathbf {p})$ were determined also through least squares regression. The geophysical parameters that drive the model (such as the IMF, solar wind parameters and geomagnetic indices) are obtained from NASA’s OMNIWeb service. Two sample outputs are shown in Fig. 4.1. The times chosen for producing the diagrams correspond to selected Swarm auroral crossings that are used also for demonstrating multi-point FAC estimators in Sect. 4.3.2 and multi-scale MVA analysis of FACs in Sect. 4.4.1.

With regard to the discussion below of gradient and curl estimation from multi-spacecraft magnetic field measurements, it is important to note that the normal equations produce parameter estimates that are linear in the data: we may write

$$\begin{aligned} \mathbf {a} \; = \; \sum _\sigma \mathbf {q}_\sigma d_\sigma \end{aligned}$$

(4.1)

where the vectors $\mathbf {q}_\sigma$ are the rows of ${\mathsf {M}}^\text {ils}$. They depend only on the array geometry but not on the measurements $d_\sigma$, and may be termed generalised reciprocal vectors, see below. Linearity in the data applies also to any aspect of the model that can be expressed through a linear operation acting on the model function. Since differential operators like grad or curl are linear, least squares estimators of gradients and currents from linear magnetic field models based on multi-spacecraft vector measurements are linear in the data. The representation $\mathbf {a} = \sum _\sigma \mathbf {q}_\sigma d_\sigma$ facilitates error analyses and comparisons of the linear least squares technique with linear estimators derived form other principles such as finite differencing or boundary integrals, see Sect. 4.2.4.

4.2.2 Local LS Estimators of Spatial Gradients

The position vectors in an array of S spacecraft are denoted as $\mathbf {r}_\sigma , \sigma = 1, \ldots , S$, and the difference vectors are $\mathbf {r}_{\sigma \tau } = \mathbf {r}_\tau - \mathbf {r}_\sigma$. The average position or mesocentre $\mathbf {r}_*\; = \; (1/S) \, \sum _\sigma \mathbf {r}_\sigma$ may be chosen to coincide with the origin. In such a mesocentric coordinate system, the position tensor ${\mathsf {R}} = \sum _\sigma (\mathbf {r}_\sigma - \mathbf {r}_*) (\mathbf {r}_\sigma - \mathbf {r}_*)^\mathsf {T}$ simplifies to ${\mathsf {R}} = \sum _\sigma \mathbf {r} \, \mathbf {r}^\mathsf {T}$. Note that the volumetric tensor introduced by Harvey (1998) differs by a factor of 1/S from the position tensor defined here.

To estimate the gradient vector of a scalar field h, we consider the model $h (\mathbf {r}) = h_*+ (\mathbf {r}-\mathbf {r}_*) \varvec{\cdot }\nabla h$ (or $h (\mathbf {r}) = h_*+ \mathbf {r} \varvec{\cdot }\nabla h$ in a mesocentric frame). The function is linear in its four parameters, namely, the value $h_*$ of h at the mesocentre and the three components of the gradient $\nabla h$. Using S measurements $h_\sigma$ at positions $\mathbf {r}_\sigma$, the least squares estimates are $h_*\simeq (1/S) \sum _\sigma h_\sigma$ and

$$\begin{aligned} \nabla h \; \simeq \; \mathbf {g} \; = \; \sum _\sigma \mathbf {q}_\sigma h_\sigma ~. \end{aligned}$$

(4.2)

The local LS estimate of the gradient matrix of a vector field $\mathbf {B}$ is given by

$$\begin{aligned} \nabla \mathbf {B} \; \simeq \; {\mathsf {G}} \; = \; \sum _\sigma \mathbf {q}_\sigma \mathbf {B}_\sigma ^\mathsf {T}~. \end{aligned}$$

(4.3)

The vectors $\mathbf {q}_\sigma$ are solutions of

$$\begin{aligned} {\mathsf {R}} \mathbf {q}_\sigma = \mathbf {r}_\sigma \end{aligned}$$

(4.4)

Vogt et al. (2008b). Based on the rank of the ($3 \times 3$) position tensor ${\mathsf {R}}$, we distinguish two cases.

Invertible position tensor

If $S \ge 4$, and the position vectors are not all in one plane, the position tensor is non-singular (full rank 3), and we obtain $\mathbf {q}_\sigma = {\mathsf {R}}^{-1} \mathbf {r}_\sigma$ (Vogt et al. 2008b). The vectors $\mathbf {q}_\sigma$ can be understood as generalised reciprocal vectors, because in the special case $S=4$ they coincide with the (tetrahedral) reciprocal vectors (Chanteur 1998; Chanteur and Harvey 1998; Vogt et al. 2008b) defined through

$$\begin{aligned} \mathbf {k}_{\rho } \; = \; \frac{ \mathbf {r}_{\sigma \tau } \times \mathbf {r}_{\sigma \nu } }{ \mathbf {r}_{\sigma \rho } \cdot ( \mathbf {r}_{\sigma \tau } \times \mathbf {r}_{\sigma \nu } ) } \end{aligned}$$

(4.5)

where $(\rho , \sigma , \tau , \nu )$ is a cyclic permutation of (1, 2, 3, 4).

Singular position tensor, planar spacecraft array

If $S \ge 3$, and the spacecraft are in all one plane but not co-linear, the position tensor has only rank 2. Measurements allow to determine the component $\nabla _{\!\!p}\,h$ of the gradient in the plane spanned by the three spacecraft (in-plane or perpendicular gradient) but not the component $\nabla _{\!\!n}\,h$ normal to that plane (out-of-plane or normal component). Additional information in the form of geometrical or physical assumptions (conditions, constraints) is required to determine $\nabla _{\!\!n}\,h$. The vectors $\mathbf {q}_\sigma$ are the minimum-norm solutions of ${\mathsf {R}} \mathbf {q}_\sigma = \mathbf {r}_\sigma$ (Vogt et al. 2013), and may be termed planar reciprocal vectors. In the special case $S=3$, they can be written in the form (Vogt et al. 2009)

$$\begin{aligned} \mathbf {q}_\sigma \; = \; \frac{\mathbf {n} \times \mathbf {r}_{\tau \nu }}{|\mathbf {n}|^2} ~,~ \sigma = 1,2,3 ~, \end{aligned}$$

(4.6)

where $(\sigma , \tau , \nu )$ is a cyclic permutation of (1, 2, 3), $\mathbf {n} = \mathbf {r}_{12} \times \mathbf {r}_{13} = \mathbf {r}_{\sigma \tau } \times \mathbf {r}_{\sigma \nu }$, and the corresponding unit vector is $\hat{\mathbf {n}} = \mathbf {n} / |\mathbf {n}|$. The geometry of planar reciprocal vectors for a three-spacecraft configuration is sketched in Fig. 4.2. The relationships of planar reciprocal vectors to the eigenvalues and eigenvectors of the volumetric tensor $(1/S) {\mathsf {R}}$ are discussed in detail by Shen et al. (2012b).

Fig. 4.2

Geometry of planar reciprocal vectors for a three-spacecraft configuration. Each vector $\mathbf {q}_\sigma$ is perpendicular to the line segment $L_\sigma$ facing satellite no. $\sigma$ at position vector $\mathbf {r}_\sigma$. The length $|\mathbf {q}_\sigma |$ is inversely proportional to the distance between $L_\sigma$ and $\mathbf {r}_\sigma$

The singular position tensor case is most relevant for the Swarm mission: here the gradient vector cannot be resolved fully from the measurements, and additional information has to be taken into account to reconstruct its out-of-plane component. Constraints may in principle be incorporated in the least squares framework using Lagrange multipliers. The approach chosen by Vogt et al. (2009) is based on geometrical considerations, and offers the possibility to choose between three types of constraints: (1) gradient parallel to a given direction $\hat{\mathbf {e}}$, (2) gradient perpendicular to a given direction $\hat{\mathbf {e}}$, (3) the physical structure is stationary in a reference frame moving with a known velocity relative to the spacecraft array. Of particular importance for studies of field-aligned currents is a fourth constraint that combines the force-free condition $\mathbf {B} \varvec{\times }(\nabla \varvec{\times }\mathbf {B}) = \mathbf {0}$ with $\nabla \varvec{\cdot }\mathbf {B} = 0$ to estimate the full magnetic gradient matrix from spacecraft measurements in one plane (Shen et al. 2012a; Vogt et al. 2013).

4.2.3 Local LS Estimators of Electric Currents

In the invertible position tensor case (spacecraft are not all in one plane), the local LS estimate of the curl $\nabla \varvec{\times }\mathbf {B}$ can be written as

$$\begin{aligned} \nabla \varvec{\times }\mathbf {B} \; \simeq \; \mathbf {c} \; = \; \sum _\sigma \mathbf {q}_\sigma \varvec{\times }\mathbf {B}_\sigma ~. \end{aligned}$$

(4.7)

In the singular position tensor case (spacecraft are in one plane but not co-linear), one may incorporate an adequate constraint to reconstruct the full gradient matrix $\nabla \mathbf {B}$ first, and then take its skew-symmetric part $\frac{1}{2} ( \nabla \mathbf {B} - \nabla \mathbf {B}^\mathsf {T})$ to obtain the curl (Vogt et al. 2009). If the curl is known to be parallel to a given direction as in the case of auroral FACs, one may also start from the density $j_n$ of the normal current (i.e. the component perpendicular to the plane spanned by the spacecraft positions) that is fully determined by the measurements through

$$\begin{aligned} \mu _0 j_n \; = \; ( \nabla \varvec{\times }\mathbf {B} )_n \; \simeq \; c_n \; = \; \hat{\mathbf {n}} \varvec{\cdot }\sum _\sigma \mathbf {q}_\sigma \varvec{\times }\mathbf {B}_\sigma \; = \; \sum _\sigma \left( \hat{\mathbf {n}} \varvec{\times }\mathbf {q}_\sigma \right) \varvec{\cdot }\mathbf {B}_\sigma \; = \; \sum _\sigma \left( \hat{\mathbf {n}} \varvec{\times }\mathbf {q}_\sigma \right) \varvec{\cdot }\mathbf {B}_{p,\sigma } \end{aligned}$$

(4.8)

Here $\hat{\mathbf {n}}$ is a unit vector normal to the spacecraft plane, and $\mathbf {B}_{p,\sigma }$ are the planar components of the measured vectors $\mathbf {B}_\sigma$. The field-aligned current density is then given by $j_\Vert \simeq j_n / \hat{\mathbf {n}} \varvec{\cdot }\hat{\mathbf {B}}_0$ where $\hat{\mathbf {B}}_0$ is the direction of the ambient magnetic field.

4.2.4 Related Local Estimators of Gradients and Currents

In preparation of the Cluster mission, gradient analysis methods were derived from several different principles such as discretised boundary integration (Dunlop et al. 1988), spatial interpolation (Chanteur 1998), and least squares estimation (Harvey 1998). For the Swarm mission, curl estimators based on finite differences (FD) and also on discretised boundary integrals (BI) were developed by Ritter and Lühr (2006), see also Shen et al. (2012a) and Ritter et al. (2013). Although the underlying principles differ, the resulting estimators may still turn out to be identical. Chanteur and Harvey (1998) demonstrated that in the regular (tetrahedral) four-spacecraft case, spatial interpolation yields the same analysis scheme as unconstrained least squares. Considering virtual four-point almost planar configurations relevant for the Swarm mission, (Vogt et al. 2013) compared different estimators for the normal component of the curl (corresponding to the radial current density) and found that the FD and BI estimators are algebraically identical.

Inter-comparisons of gradient and curl analysis schemes are facilitated by the observation that (to our knowledge) all the proposed multi-spacecraft methods yield estimators that are linear in the data. Using general results from linear algebra, (Vogt et al. 2008b) demonstrated that the problem of linear and consistent four-point gradient estimation has a unique solution. The same argumentation can be applied to three-spacecraft arrays: the number of free parameters (mesocentre value $h_*$ and two components of the planar gradient $\nabla _{\!\!p}\,h$) is the same as the number of measurements (values $h_\sigma$ at three-spacecraft positions), therefore there is a unique three-point linear and consistent estimator for the planar gradient that can be expressed explicitly, e.g., using the formalism of Vogt et al. (2009).

Fig. 4.3

From Vogt et al. (2013), Fig. 4.1

Virtual four-point configuration produced by two satellites on close orbits such as SwA (corresponding to satellite a) and SwC (satellite b). The shape of the four-point array can be characterised by the dimensionless parameters $\mu = M/L$ (stretching parameter, ratio of along-track to across-track distance), $\lambda = \ell /L$ (skewness parameter, ratio of relative offset $2\ell$ to across-track distance 2L), and $\varepsilon = m/M$ (deviation of the two velocity directions from the perfectly parallel case).

All linear estimators for the gradient of a scalar variable h can be represented in the form $\nabla h \simeq \sum _\sigma \mathbf {p}_\sigma h_\sigma$ with a specific set of vectors $\mathbf {p}_\sigma$, termed canonical base vectors by Vogt et al. (2013). For vector measurements, we obtain $\nabla \mathbf {B} = \sum _\sigma \mathbf {p}_\sigma \mathbf {B}_\sigma ^\mathsf {T}$. The corresponding linear curl estimator can then be written in the form $\nabla \varvec{\times }\mathbf {B} = \sum _\sigma \mathbf {p}_\sigma \varvec{\times }\mathbf {B}$. The FD/BI and LS estimators for planar four-point configurations produced from the SwA–SwC pair yield canonical base vectors that differ only in terms proportional to a small configurational parameter $\varepsilon = m/M \sim 10^{-2}$ with m and M as in Fig. 4.3, see Vogt et al. (2013) for a detailed description. The FD/BI estimator of the normal curl component $( \nabla \varvec{\times }\mathbf {B} )_n$ can be written in the compact form

$$\begin{aligned} \mu _0 j_n \; = \; ( \nabla \varvec{\times }\mathbf {B} )_n \; \simeq \; \frac{1}{2 A} \left[ \left( \mathbf {B}_c^+ - \mathbf {B}_a^- \right) \cdot \left( \mathbf {r}_a^+ - \mathbf {r}_c^- \right) \, - \, \left( \mathbf {B}_a^+ - \mathbf {B}_c^- \right) \cdot \left( \mathbf {r}_c^+ - \mathbf {r}_a^- \right) \right] \end{aligned}$$

(4.9)

where the A is the modulus of the oriented area

$$\begin{aligned} \mathbf {A} \; = \; \frac{1}{2} \left( \mathbf {r}_a^- - \mathbf {r}_a^+ \right) \times \left( \mathbf {r}_c^+ - \mathbf {r}_a^+ \right) \, + \, \frac{1}{2} \left( \mathbf {r}_c^+ - \mathbf {r}_c^- \right) \times \left( \mathbf {r}_a^- - \mathbf {r}_c^- \right) ~, \end{aligned}$$

(4.10)

see also Appendix B in Vogt et al. (2013). Subscripts a and c indicate SwA and SwC, respectively, and superscripts ± denote the two time-shifted measurements.

4.2.5 Errors and Limitations

Spatial gradient estimates produced from multi-point measurements are affected by several errors and limitations: (a) measurement errors, (b) positional errors, (c) imperfections of the assumed linear model. In the planar spacecraft array case when additional information has to be considered to reconstruct the normal gradient, and (d) uncertainties in the imposed geometrical or physical conditions give rise to additional errors.

Measurement errors

Random uncertainties produced by limitations of the experimental setup (instrumental noise) are called measurement errors or physical errors. They can be quantified by means of error covariances $\left\langle \delta h_\sigma \, \delta h_\tau \right\rangle$ for scalar observables, and $\left\langle \delta \mathbf {B}_\sigma \, \delta \mathbf {B}_\tau ^\mathsf {T} \right\rangle$ for vectors such as the magnetic field. Representations such as $\nabla h \simeq \mathbf {g} = \sum _\sigma \mathbf {q}_\sigma h_\sigma$ for linear gradient estimators offer a coherent framework for an assessment of the resulting uncertainties (Chanteur 1998; Vogt and Paschmann 1998; Vogt et al. 2008b, 2009, 2013). The special case of isotropic and uncorrelated measurement errors yields $\left\langle \delta h_\sigma \, \delta h_\tau \right\rangle = \delta _{\sigma \tau } (\delta h)^2$ where $\delta _{\sigma \tau }$ is the Kronecker delta symbol, and $\delta h$ is a measure of instrumental sensitivity, resulting in the parameter covariant matrix

$$\begin{aligned} \left\langle \delta \mathbf {g} \, \delta \mathbf {g}^\mathsf {T} \right\rangle \; = \; (\delta h)^2 {\mathsf {Q}} \end{aligned}$$

(4.11)

with the tensor ${\mathsf {Q}} = \sum _\sigma \mathbf {q}_\sigma \mathbf {q}_\sigma ^\mathsf {T}$ (reciprocal tensor). For planar arrays of spacecraft positions, $\mathbf {g}$ is an estimator of the in-plane gradient component. The square magnitude error is given by the trace

$$\begin{aligned} \left\langle |\delta \mathbf {g}|^2 \right\rangle \; = \; (\delta h)^2 \, \text {trace} ({\mathsf {Q}}) \; = \; (\delta h)^2 \, \sum _\sigma |\mathbf {q}_\sigma |^2 ~. \end{aligned}$$

(4.12)

In both the invertible and the singular position tensor case, the term $\text {trace} ({\mathsf {Q}}) = \sum _\sigma |\mathbf {q}_\sigma |^2$ is the square of an inverse length scale and can be understood as an error amplification factor that depends on the geometry (extension and shape) of the spacecraft array, see Vogt et al. (2008b, 2009, 2013). Normalisation using the mean square inter-spacecraft distance $(1/S) \sum _\sigma |\mathbf {r}_\sigma |^2$ yields a scaled version of the geometrical error amplification factor. The case of gradient matrix estimators $\nabla \mathbf {B} \simeq {\mathsf {G}} = \sum _\sigma \mathbf {q}_\sigma \mathbf {B}_\sigma ^\mathsf {T}$, based on vector measurements is discussed in detail by Chanteur (1998) and Vogt et al. (2009).

Using the same approach and assumptions, the accuracy of linear curl estimators $\nabla \varvec{\times }\mathbf {B} \simeq \mathbf {c} = \sum _\sigma \mathbf {q}_\sigma \varvec{\times }\mathbf {B}_\sigma$ is studied in Appendix B. The parameter covariance matrix is given by

$$\begin{aligned} \left\langle \delta \mathbf {c} \, \delta \mathbf {c}^\mathsf {T} \right\rangle \; = \; (\delta B)^{2} \left\{ \sum _\sigma |\mathbf {q}_\sigma |^2 {\mathsf {E}} - \sum _\sigma \mathbf {q}_\sigma \mathbf {q}_\sigma ^\mathsf {T}\right\} \; = \; (\delta B)^{2} \left\{ \text {trace} ({\mathsf {Q}}) {\mathsf {E}} - {\mathsf {Q}} \right\} \end{aligned}$$

(4.13)

where ${\mathsf {E}}$ denotes the identity matrix. For a planar spacecraft array with normal unit vector $\hat{\mathbf {n}}$ we obtain

$$\begin{aligned} \left\langle | \delta c_n |^2 \right\rangle \; = \; (\delta B)^{2} \sum _\sigma |\mathbf {q}_\sigma |^2 ~. \end{aligned}$$

(4.14)

This case applies to Swarm field-aligned current estimates with the vectors $\mathbf {q}_\sigma$ being the canonical base vectors of the respective LS or FD/BI estimator (Vogt et al. 2013).

Fig. 4.4

From Vogt et al. (2013), Fig. 3

Logarithm of the ratio $L_r^2/L_q^2$ as defined by Eq. (4.16), an effective error amplification factor controlled by the shape of the planar four-point configuration sketched in Fig. 4.3, as a function of the stretching parameter $\mu = M/L$ and the skewness parameter $\lambda = \ell /L$.

Defining $L_q = \left( \sum _\sigma |\mathbf {q}_\sigma |^2 \right) ^{-1/2}$ (gradient estimation error length) for a planar four-point configuration, we may express the mean square error of the radial (normal) current $j_n$ as $\left\langle | \delta j_n |^2 \right\rangle \, = \, (\delta B)^{2} / (\mu _0^2 L_q^2)$. Using the mean square inter-spacecraft distance $L_r = \left( \frac{1}{4} \sum _\sigma |\mathbf {r}_\sigma |^2 \right) ^{1/2}$ as a measure of the extent of the spacecraft array, one may further rearrange to obtain the form

$$\begin{aligned} \left\langle | \delta j_n |^2 \right\rangle \; = \; \frac{(\delta B)^{2}}{\mu _0^2 L_r^2} \, \frac{L_r^2}{L_q^2} ~. \end{aligned}$$

(4.15)

The first term is a reference error for field-aligned current density controlled only by the array size. The second term

$$\begin{aligned} \frac{L_r^2}{L_q^2} \; = \; \left( \sum _\sigma |\mathbf {q}_\sigma |^2 \right) \cdot \frac{1}{4} \left( \sum _\sigma |\mathbf {r}_\sigma |^2 \right) \end{aligned}$$

(4.16)

gives the influence of the array shape. Figure 4.4 displays the logarithm of $L_r^2/L_q^2$ for $m/M = \varepsilon = 10^{-2}$ in terms of the configurational parameters $\mu = M/L$ and $\lambda = \ell /L$ (see Fig. 4.3). Error amplification is smallest (close to unity) for equal-sided ($\mu \approx 1$) and non-skewed ($\lambda \approx 0$) quads. Significantly skewed configurations ($\lambda \gtrsim 3$) give rise to substantial error amplification.

Positional errors

Random uncertainties in spacecraft positions are called positional errors or geometrical errors. Isotropic and uncorrelated positional errors can be incorporated in the parameter covariances obtained from considering only measurement errors by replacing $(\delta h)^2 \rightarrow (\delta h)^2 + |\nabla h|^2 (\delta r)^2$ (Vogt and Paschmann 1998; Vogt et al. 2009). In the case of magnetic gradient and electric current estimates based on Swarm magnetic field data, positional errors have a much smaller impact than measurement errors because $|\nabla \mathbf {B}| \delta r \ll \delta B$ and can thus be neglected. This statement remains valid if positional inaccuracies in virtual four-point configurations imposed by time-shift errors $\delta t$ (in the order of ms) are taken into account, then $\delta r \sim V \delta t$ where V is the spacecraft speed.

Model imperfections

Nonlinear variations of the observable over the spatial region covered by the spacecraft array cause deviations from the assumed linear model, and the spatial gradient is not perfectly uniform. In contrast to the statistical nature of measurement errors and positional errors which become less important for larger inter-spacecraft separation distances, gradient estimation errors due to deviations from linearity tend to increase with spacecraft separations (Robert et al. 1998). In the auroral zone the problem implies that current structures with variation scales (sheet widths) smaller than the array extension cannot be resolved and are effectively smeared out.

Uncertainties of imposed conditions

In the planar spacecraft array case (position tensor has rank 2) where only the in-plane component can be directly estimated from the measurements, the constraint equations used to reconstruct the normal gradient may not be perfectly satisfied, producing additional errors. The quality of the normal gradient can be assessed by means of error indicators (Vogt et al. 2009, 2013). The assumption that the full gradient is aligned with a given direction $\hat{\mathbf {e}}$ (parallel constraint) can lead to large uncertainties if $|\hat{\mathbf {e}} \varvec{\times }\hat{\mathbf {n}}|$ is small. The normal gradient estimate resulting from the perpendicular constraint (full gradient perpendicular to a given direction $\hat{\mathbf {e}}$) should be taken with care if the error indicator $|\hat{\mathbf {e}} \varvec{\cdot }\hat{\mathbf {n}}|$ is small. An error indicator for the force-free case that should not become too small is $|\hat{\mathbf {B}}_0 \varvec{\cdot }\hat{\mathbf {n}}|$. Since in the auroral zone the magnetic field forms a small angle with the radial vector, the error indicator for the virtual four-point configuration constructed from Swarm dual-spacecraft positions is close to unity and thus well-behaved. Larger uncertainties are expected at low latitudes.

4.3 Multi-spacecraft Array Techniques in Practice

The multi-point array techniques of Sect. 4.2 rest on the choice of canonical base vectors. For local LS estimators in the invertible position tensor case and a mesocentric coordinate frame, the canonical base vectors are generalised reciprocal vectors $\mathbf {q}_\sigma = {\mathsf {R}}^{-1} \mathbf {r}_\sigma$. Estimators of the magnetic gradient matrix $\nabla \mathbf {B}$ and the curl vector $\nabla \varvec{\times }\mathbf {B}$ are given by

$$\begin{aligned} \nabla \mathbf {B}\simeq & {} {\mathsf {G}} \; = \; \sum _\sigma \mathbf {q}_\sigma \mathbf {B}_\sigma ^\mathsf {T}~, \end{aligned}$$

(4.17)

$$\begin{aligned} \nabla \varvec{\times }\mathbf {B}\simeq & {} \mathbf {c} \; = \; \sum _\sigma \mathbf {q}_\sigma \varvec{\times }\mathbf {B}_\sigma ~. \end{aligned}$$

(4.18)

Practical aspects of four-spacecraft LS estimators were discussed, e.g., by Chanteur and Harvey (1998), Vogt et al. (2008b), and Vogt (2014).

This section is concerned with the implementation and applications of local LS estimators for the planar array case, i.e. three-spacecraft arrays and virtual four-point configuration constructed from the positions of SwA and SwC. Then the canonical base vectors $\mathbf {q}_\sigma$ are minimum-norm solutions of ${\mathsf {R}} \mathbf {q}_\sigma = \mathbf {r}_\sigma$, and Eqs. (4.17) and (4.18) produce the in-plane gradient and the normal curl component directly from the measurements. The three-spacecraft LS gradient estimator was tested by Vogt et al. (2009) and applied to Cluster pressure measurements in the magnetail. The dual-satellite LS FAC estimator was validated by Vogt et al. (2013) using Cluster observations of a force-free plasma structure in the solar wind that had previously been studied and characterised in detail by means of multi-spacecraft timing analysis (Vogt et al. 2011). Below in Sect. 4.3.2 we present selected applications of the three-spacecraft and the dual-satellite LS FAC estimator to Swarm magnetic field measurements, after discussing the implementation of local LS estimators for planar arrays in Sect. 4.3.1.

4.3.1 Implementation of Planar Multi-point Array Estimators

Local LS gradient and/or curl estimation using measurements of a planar spacecraft array involves the following steps.

Construction of canonical base vectors

In the planar array case with the position vectors of all spacecraft located in one plane, we first compute the eigenvalues and eigenvectors of the position tensor ${\mathsf {R}}$, and then construct the pseudo-inverse ${\mathsf {Q}}$ from the two largest eigenvalues $\rho _1,\rho _2$ and the corresponding eigenvectors $\hat{\mathbf {e}}_1$ and $\hat{\mathbf {e}}_2$ as

$$\begin{aligned} {\mathsf {Q}} \; = \; \rho _1^{-1} \hat{\mathbf {e}}_1 \hat{\mathbf {e}}_1^\mathsf {T}\, + \, \rho _2^{-1} \hat{\mathbf {e}}_2 \hat{\mathbf {e}}_2^\mathsf {T}~. \end{aligned}$$

(4.19)

The eigenvalues are assumed to be in descending order, $\rho _1 \ge \rho _2 \ge 0$, and $\rho _3 = 0$ because the spacecraft array is planar. The canonical base vectors are $\mathbf {q}_\sigma = {\mathsf {Q}} \mathbf {r}_\sigma$ (in a mesocentric frame). The procedure works for both the virtual four-point configurations formed by positions of SwA and SwC as well as for three-spacecraft arrays. In the latter case the canonical base vectors are planar reciprocal vectors (Vogt et al. 2009) that can also be computed using Eq. (4.6). For a thorough discussion of volumetric tensor $(1/S)\,{\mathsf {R}}$ eigenvectors and eigenvalues in the three-spacecraft case, see Appendix D of Shen et al. (2012b).

Estimation of planar gradient and/or normal current components

Array magnetic field data $\mathbf {B}_\sigma$ allow to estimate directly the in-plane component of the gradient matrix as $\nabla _{\!\!p}\,\mathbf {B} = \sum _\sigma \mathbf {q}_\sigma \mathbf {B}^\mathsf {T}$, and also the normal component $c_n$ of the curl:

$$\begin{aligned} c_n \; = \; \hat{\mathbf {n}} \varvec{\cdot }\sum _\sigma \mathbf {q}_\sigma \varvec{\times }\mathbf {B}_\sigma \; = \; \sum _\sigma \left( \hat{\mathbf {n}} \varvec{\times }\mathbf {q}_\sigma \right) \varvec{\cdot }\mathbf {B}_\sigma ~. \end{aligned}$$

(4.20)

The normal (out-of-plane) current density is given by $j_n = c_n / \mu _0$.

Quality indicators of planar gradient and normal current estimates

The stability of the (constrained) matrix inversion that yields the canonical base vectors is controlled by the effective condition number $\text {CN} ({\mathsf {R}}) = \rho _1/\rho _2$ of the position tensor ${\mathsf {R}}$.

Error amplification due to the array shape is controlled by the ratio of square length scales $L_r^2/L_q^2$ defined by Eq. (4.16), and directly related to the condition number through

$$\begin{aligned} \frac{L_r^2}{L_q^2}= & {} \frac{1}{4} \left( 2 + \text {CN} ({\mathsf {R}}) + \frac{1}{\text {CN} ({\mathsf {R}})} \right) ~, \end{aligned}$$

(4.21)

$$\begin{aligned} \text {CN} ({\mathsf {R}})= & {} \exp \left[ \text {arcosh} \left( 2 \frac{L_r^2}{L_q^2} - 1 \right) \right] ~, \end{aligned}$$

(4.22)

see Appendix C for a proof. Hence, $\text {CN} ({\mathsf {R}})$ and $L_r^2/L_q^2$ contain essentially the same information, and for moderately large values are related linearly: $\text {CN} ({\mathsf {R}}) \simeq 4 L_r^2/L_q^2 - 2$. When also the array size is taken into account, error amplification is measured by the square inverse length scale $L_q^{-2} = \sum _\sigma |\mathbf {q}_\sigma |^2$. The uncertainty of both planar gradient and normal curl estimation is simply given by $\delta B / L_q$. Hence in addition to $\text {CN} ({\mathsf {R}})$ also $L_q$ should be computed and checked to assess the quality of the estimated derivative.

Construction of the full gradient matrix and/or the full current vector

In order to obtain the full gradient, the component normal to the spacecraft plane has to be constructed in addition to the planar gradient estimate. This can be achieved by means of suitable constraint equations as discussed in Sect. 4.2.2, see also Vogt et al. (2009). The curl vector $\nabla \varvec{\times }\mathbf {B}$ can then be read directly from the components of the skew-symmetric part of $\nabla \mathbf {B}$. In the special case of the force-free condition, the current is parallel to the ambient magnetic field $\mathbf {B}_0$, and the field-aligned current density $j_\Vert$ can be computed directly from the normal current density $j_n$ through $j_\Vert \simeq j_n / \hat{\mathbf {n}} \varvec{\cdot }\hat{\mathbf {B}}_0$. The construction of normal gradients and planar curl components should be critically assessed using error indicators as discussed in Sect. 4.2.5.

4.3.2 Application to Swarm Auroral Crossings

To demonstrate local LS estimation of FACs for planar spacecraft arrays, we select two auroral crossings of the Swarm satellites when SwB was close enough to the SwA–SwC pair for the application of three-spacecraft techniques.

Fig. 4.5

Panels 1–3: magnetic field measurements of SwA, SwB, and SwC on 24 July 2014, 02:44–02:50 UT. Panel 4: logarithmic condition numbers for the three-spacecraft array (CN_ABC) and the virtual four-point configuration generated by SwA and SwC (CN_AC). Panel 5: angle between the ambient magnetic field direction $\hat{\mathbf {B}}_0$ and the normal vector of the three-spacecraft plane. Panel 6: comparison of the dual-satellite (virtual four-point) LS FAC estimator J_LS_AC and the three-spacecraft LS FAC estimator J_LS_ABC with the Level-2 dual-satellite FAC product J_L2_AC

Figure 4.5 shows magnetic field measurements of the three Swarm satellites in the Southern hemisphere on 24 July 2014, 02:44–02:50 UT, together with different FAC estimates and quality indicators. Clearly visible are negative parallel (downward) currents between $\sim$02:47:30 and $\sim$02:48:00 followed by positive parallel (upward) current until $\sim$02:48:30. The dual-satellite LS FAC estimates are very close to the Level-2 FAC product J_L2_AC apart from several smaller-scale deviations. They are due to the fact that the Level-2 dual-satellite FAC product is based on filtered Swarm magnetic field observations whereas here the least squares estimator processed unfiltered data as input. The smaller-scale deviations are much less pronounced if the dual-satellite LS estimate of the FAC profile is also computed after application of a suitable filter. The output produced by the three-spacecraft LS estimator, also based on unfiltered magnetic field measurements, also shows smaller-scale variability but otherwise follows the other two profiles quite well apart from an apparent time shift, caused by different mesocentres of the three-spacecraft array and the four-point configuration. Condition numbers for the current structure crossing are moderate (below 5 for the dual-satellite estimator, and not much larger than 10 for the three-spacecraft array). The angle between the ambient magnetic field and the normal direction of the three-spacecraft plane assumes tolerable values far from $90^\circ$.

The geometry of the current structure can be further studied using minimum variance analysis (MVA), discussed in more detail in Sect. 4.4 where the analysis procedure and key variables are explained. An important MVA parameter is the eigenvalue ratio that can be interpreted as a measure of planarity. For sufficiently large eigenvalue ratios we can think of the current structure as a sheet, with the eigenvector to the largest eigenvalue being tangential to the sheet. The auroral crossing considered here yields large eigenvalue ratios 29, 20 and 37 for SwA, SwB and SwC, respectively, and sheet orientations that are very consistent within a few degrees for all three satellites.

Fig. 4.6

Panels 1–3: magnetic field measurements of SwA, SwB, and SwC on 29 May 2014, 13:36–13:44 UT. Panel 4: logarithmic condition numbers for the three-spacecraft array (CN_ABC) and the virtual four-point configuration generated by SwA and SwC (CN_AC). Panel 5: angle between the ambient magnetic field direction $\hat{\mathbf {B}}_0$ and the normal vector of the three-spacecraft plane. Panel 6: comparison of the dual-satellite (virtual four-point) LS FAC estimator J_LS_AC and the three-spacecraft LS FAC estimator J_LS_ABC with the Level-2 dual-satellite FAC product J_L2_AC

Data from the second Swarm auroral crossing on 29 May 2014, 13:36–13:44 UT, are displayed in Fig. 4.6. The largest current densities are observed between $\sim$13:39:30 and $\sim$13:41:30. Again apart from smaller-scale deviations due to differences in filtering of the input magnetic field measurements, the two dual-satellite FAC estimates (both based on data from SwA and SwC) are very similar. The FAC profile produced by the three-spacecraft LS estimator differs significantly at around 13:41, despite reasonable values of the quality indicators. Closer inspection of the SwB magnetic field profile reveals a substructure at 13:41 that is not present in the measurements of SwA and SwC, indicating non-uniform currents on the inter-spacecraft separation scale that are inconsistent with the linear model assumption. Eigenvalue ratios are 11, 16, 13 and thus somewhat smaller than for the first crossing, and also the sheet orientations obtained from single-spaceraft MVA show larger differences up to about 10 degrees.

4.4 Single-Spacecraft Multi-scale Analysis

Satellite measurements of the magnetic field allow the study of planar geospace structures such as current sheets or boundary layers through the eigenvalues and eigenvectors of the data covariance matrix. This type of principal axis decomposition is known as principal component analysis (PCA) or empirical orthogonal function (EOF) analysis in the statistical literature, and as minimum variance analysis (MVA) in space physics (Sonnerup and Cahill 1967). MVA can be derived using constrained least squares estimation (Sonnerup and Scheible 1998) and is usually applied to the entire geospace structure of interest. (Bunescu et al. 2015, 2017) introduced a multi-scale version by applying the MVA procedure using a range of sliding windows, thus producing local estimates of key MVA parameters such as the eigenvalue ratio and the angle characterising sheet orientation. The novel multi-scale version of MVA is described below in Sect. 4.4.2, followed by an application to Swarm magnetic field measurements in Sect. 4.4.3. The starting point of our discussion are the principles of MVA as summarised in Sect. 4.4.1.

4.4.1 MVA Applied to Auroral Current Sheets

Since the magnetic field $\mathbf {B}$ is solenoidal (divergence-free), planar magnetic structures varying only in one spatial direction $\hat{\mathbf {n}}$ satisfy

$$\begin{aligned} 0 \; = \; \nabla \varvec{\cdot }\mathbf {B} \; = \; \hat{\mathbf {n}} \varvec{\cdot }\nabla B_n ~, \end{aligned}$$

(4.23)

thus $B_n = \hat{\mathbf {n}} \varvec{\cdot }\mathbf {B}$ is constant. Assuming that any observed variability along $\hat{\mathbf {n}}$ is due to sufficiently small random errors, the eigenvector to the smallest eigenvalue of the data covariance matrix is a proxy of $\hat{\mathbf {n}}$. MVA applied to magnetic field data is sometimes termed MVAB. The method can be used also for other conserved plasma variables, see Sonnerup and Scheible (1998).

The quality of $\hat{\mathbf {n}}$ estimates is associated with eigenvalue ratios. In the case of auroral FAC sheets, magnetic perturbations are in the plane perpendicular to the ambient magnetic field. The problem reduces to two spatial dimensions with two relevant eigenvalues $\lambda _1 \ge \lambda _2$ and two eigenvectors $\hat{\mathbf {e}}_1,\hat{\mathbf {e}}_2$. The eigenvalue ratio $\lambda _1 / \lambda _2$ can be understood as a measure of planarity and should be sufficiently large. The sheet orientation is given by tangential vectors $\hat{\mathbf {B}}_0$ (direction of the ambient magnetic field) and $\hat{\mathbf {e}}_1$, and the normal unit vector $\hat{\mathbf {n}} = \hat{\mathbf {e}}_2$. The orientation of auroral current sheets can be concisely characterised by the (inclination) angle formed by the sheet normal with magnetic north, or the spacecraft velocity vector (approximately geographic north for polar orbiting satellites such as CHAMP or Swarm).

4.4.2 Multi-scale Field-Aligned Current Analyzer

The multi-scale and continuous (local) variant of MVAB introduced by Bunescu et al. (2015, 2017), termed MS-MVA, can be summarised as follows:

• A range of window widths w with linear resolution $\mathrm {d}w$ is defined.

• At each time t of the magnetic field series, MVA is applied to an array of data segments of width w within a predefined range and centred at t, thus yielding a series of key MVA parameters $\lambda _1 = \lambda _\text {max}$, $\lambda _2 = \lambda _\text {min}$, $R_\lambda = \lambda _1/\lambda _2$ (eigenvalue ratio), and an inclination angle. All parameters are functions of time t and scale w.

• In addition to these MVA parameters, the derivative of the largest eigenvalue $\lambda _1 = \lambda _\text {max}$ with respect to scale w is computed numerically to yield $\partial _w \lambda _\text {max}$.

• The continuous and multi-scale MVA parameters are displayed as functions of time t and scale w in a suitable two-dimensional graphical representation, either as a contour plot and/or using an appropriate colour bar. Important scales are found to show up well in colour plots of $\partial _w \lambda _\text {max}$.

MS-MVA was validated using synthetic data and measurements of the Cluster and FAST satellites.

Fig. 4.7

Swarm magnetic measurements and MS-MVA parameters for two selected auroral crossings. Panels 1–4: 24 July 2014, 02:45-02:50 UT. Panels 5–8: 29 May 2014, 13:37-13:43 UT. Shown are the magnetic field measurements of SwA (panels 1 and 5), the eigenvalue ratio $R_\lambda$ (panels 2 and 6), the $R_\lambda$ (panels 2 and 6), the derivative $\partial _w \lambda _\text {max}$ (panels 3 and 7) and the current sheet inclination (panels 4 and 8)

4.4.3 Application of MS-MVA to Swarm Auroral Crossings

Figure 4.7 shows the MS-MVA results for the two Swarm auroral crossings considered already in Sect. 4.3.2. In both cases, MS-MVA was applied to magnetic field data from SwA (panels 1 and 5), here given in the mean-field-aligned (MFA) coordinate frame (note that in Figs. 4.5 and 4.6 the magnetic field was displayed in NEC coordinates). The eigenvalue ratio $R_\lambda$ is displayed in panels 2 and 6. The current sheet inclination is shown in panels 4 and 8. The multi-scale nature of the FAC sheets is visualised very clearly in the panels 3 and 7 showing $\partial _w \lambda _\text {max}$.

4.5 Summary

The local least squares approach to the estimation of spatial derivatives from multi-spacecraft magnetic field measurements yields a generic framework for the analysis for auroral FACs and their errors. This report reviewed the underlying principles, estimation procedures, uncertainties, limitations, and practical aspects. The array geometry defines the position tensor with eigenvalues controlling the quality of gradient and curl estimates. Linear estimators can be uniquely qualified through their set of canonical base vectors, facilitating error analysis and comparison with alternative approaches. In planar spacecraft array configurations, reconstruction of the full gradient and curl vectors requires additional information that can be supplemented in the form of geometrical or physical constraints. The multi-scale nature of auroral currents can be investigated using a multi-scale version of the well-established minimum variance analysis. Analysis techniques were illustrated using selected auroral crossings of the Swarm satellites.

Appendix

4.1.1 Appendix A: General Linear Least Squares Modeling

Least squares modelling can be characterised as a statistical technique to find the parameters of a model (m) that gives the best approximation of a given data set (d) of S measurements contaminated by random errors (residuals r). The measurements $d_\sigma$ form the components of a data vector $\mathbf {d}$ that can be understood as an object in S-dimensional data space $\mathscr {D}$. The corresponding model predictions yield another vector $\mathbf {m}$, and the best approximation in the least squares sense is given by minimising the total square deviation $\chi ^2 \, \propto \, |\mathbf {d} - \mathbf {m} |^2 \, = \, |\mathbf {r} |^2 ~,$ where the square norm derives from a scalar product that may be designed to account for non-constant errors and possibly correlated observations through an error covariance matrix. In this sense, the best model vector minimises the (square) distance to the data vector. Furthermore, the best model satisfies the orthogonality principle: the residual vector $\mathbf {r} = \mathbf {d} - \mathbf {m}$ is orthogonal to the space $\mathscr {M}$ formed by all admissible model vectors. The effective dimension of the model space is the number N of model parameters.

Suppose all parameters $a_1,a_2,\ldots ,a_N$ enter the model function m linearly, then $m = \sum _\nu a_\nu f_\nu$ with basis functions $f_\nu$, and the $a_\nu$ are called amplitudes. The space $\mathscr {M}$ of all admissible models forms a linear subspace of the data space $\mathscr {D}$. Casting the model parameters into an amplitude vector $\mathbf {a}$, and the predictions of individual basis functions into a $S \times N$ matrix ${\mathsf {M}}$ (design matrix), the model vector can be written in the form $\mathbf {m} = {\mathsf {M}} \mathbf {a}$. Parameter estimation is reduced to a linear inverse problem. In the overdetermined case ($S > N$), the solution is given by the so-called normal equations

$$\begin{aligned} \mathbf {a} \; = \; \left( {\mathsf {M}}^\mathsf {T}{\mathsf {M}} \right) ^{-1} {\mathsf {M}}^\mathsf {T}\mathbf {d} \; = \; {\mathsf {M}}^\text {ils} \mathbf {d} \quad \text {with}\quad {\mathsf {M}}^\text {ils} \; = \; \left( {\mathsf {M}}^\mathsf {T}{\mathsf {M}} \right) ^{-1} {\mathsf {M}}^\mathsf {T}~. \end{aligned}$$

(4.24)

The matrix ${\mathsf {M}}^\text {ils}$ is the pseudo-inverse of ${\mathsf {M}}$ in the least squares sense. The problem simplies further in the case of mutually orthogonal basis functions, then the amplitudes are given by $a_\nu = \left( \mathbf {f}_\nu / | \mathbf {f}_\nu |^2 \right) \varvec{\cdot }\mathbf {d}$ where a vector $\mathbf {f}_\nu$ comprises the predictions of the basis function $f_\nu$, typically obtained through evaluation at the S independent variables (usually spatial coordinates, possibly combined with auxiliary parameters) corresponding to the measurements.

4.1.2 Appendix B: Accuracy of Linear Curl Estimators

Consider a linear estimator of the form

$$\begin{aligned} \mathbf {c} \; = \; \nabla \varvec{\times }\mathbf {B} \; = \; \sum _\sigma \mathbf {q}_\sigma \varvec{\times }\mathbf {B}_\sigma \end{aligned}$$

(4.25)

with vectors $\mathbf {q}_\sigma$ that are functions of the spacecraft positions but do not depend on the measurements $\mathbf {B}_\sigma$. The associated linear variation is given by

$$\begin{aligned} \delta \mathbf {c} \; = \; \sum _\sigma \left( \mathbf {q}_\sigma \varvec{\times }\delta \mathbf {B}_\sigma + \delta \mathbf {q}_\sigma \varvec{\times }\mathbf {B}_\sigma \right) ~. \end{aligned}$$

(4.26)

In the case of Swarm, the typical positional inaccuracy $\delta r$ and instrumental error $\delta B$ are such that the second term can be dropped because in the auroral zone $|\nabla \mathbf {B} | \delta r \ll \delta B$, see Vogt et al. (2013).

Defining the tensor ${\mathsf {X}}_\sigma$ through ${\mathsf {X}}_\sigma \mathbf {u} = \mathbf {q}_\sigma \varvec{\times }\mathbf {u}$ yields $\delta \mathbf {c} = \sum _\sigma {\mathsf {X}}_\sigma \delta \mathbf {B}_\sigma$. The parameter covariance tensor is then given by

$$\begin{aligned} \left\langle \delta \mathbf {c} \, \delta \mathbf {c}^\mathsf {T} \right\rangle \; = \; \left\langle \left( \sum _\sigma {\mathsf {X}}_\sigma \delta \mathbf {B}_\sigma \right) \left( \sum _\nu {\mathsf {X}}_\nu \delta \mathbf {B}_\nu \right) ^\mathsf {T} \right\rangle \; = \; \sum _{\sigma ,\nu } {\mathsf {X}}_\sigma \left\langle \delta \mathbf {B}_\sigma \delta \mathbf {B}_\nu ^\mathsf {T} \right\rangle {\mathsf {X}}_\nu ^\mathsf {T}\end{aligned}$$

(4.27)

Assuming isotropic and uncorrelated errors $\left\langle \delta \mathbf {B}_\sigma \, \delta \mathbf {B}_\nu ^\mathsf {T} \right\rangle \; = \; (\delta B)^2 \delta _{\sigma \nu } {\mathsf {E}}$, we may write

$$\begin{aligned} \left\langle \delta \mathbf {c} \, \delta \mathbf {c}^\mathsf {T} \right\rangle \; = \; (\delta B)^2 \sum _\sigma {\mathsf {X}}_\sigma {\mathsf {X}}_\sigma ^\mathsf {T}\end{aligned}$$

(4.28)

Since ${\mathsf {X}}_\sigma \mathbf {u} = \mathbf {q}_\sigma \varvec{\times }\mathbf {u}$, ${\mathsf {X}}_\sigma ^\mathsf {T}\mathbf {u} = - \mathbf {q}_\sigma \varvec{\times }\mathbf {u}$, and thus

$$\begin{aligned} {\mathsf {X}}_\sigma {\mathsf {X}}_\sigma ^\mathsf {T}\mathbf {u} \; = \; - \mathbf {q}_\sigma \varvec{\times }( \mathbf {q}_\sigma \varvec{\times }\mathbf {u} ) \; = \; \left\{ |\mathbf {q}_\sigma |^2 {\mathsf {E}} - \mathbf {q}_\sigma \mathbf {q}_\sigma ^\mathsf {T}\right\} \mathbf {u} \end{aligned}$$

(4.29)

we obtain

$$\begin{aligned} (\delta B)^{-2} \left\langle \delta \mathbf {c} \, \delta \mathbf {c}^\mathsf {T} \right\rangle \; = \; \sum _\sigma |\mathbf {q}_\sigma |^2 {\mathsf {E}} - \sum _\sigma \mathbf {q}_\sigma \mathbf {q}_\sigma ^\mathsf {T}\; = \; \text {trace} ({\mathsf {Q}}) {\mathsf {E}} - {\mathsf {Q}} \end{aligned}$$

(4.30)

where ${\mathsf {Q}} = \sum _\sigma \mathbf {q}_\sigma \mathbf {q}_\sigma ^\mathsf {T}$.

The error covariance of the curl component $c_n = \hat{\mathbf {n}} \varvec{\cdot }\mathbf {c} = \hat{\mathbf {n}}^\mathsf {T}\mathbf {c}$ orthogonal to a given unit vector $\hat{\mathbf {n}}$ can be expressed in the form

$$\begin{aligned} (\delta B)^{-2} \left\langle | \delta c_n |^2 \right\rangle= & {} (\delta B)^{-2} \left\langle \delta c_n \, \delta c_n \right\rangle \; = \; (\delta B)^{-2} \hat{\mathbf {n}}^\mathsf {T}\left\langle \delta \mathbf {c} \, \delta \mathbf {c}^\mathsf {T} \right\rangle \hat{\mathbf {n}} \nonumber \\= & {} \text {trace} ({\mathsf {Q}}) \hat{\mathbf {n}}^\mathsf {T}\hat{\mathbf {n}} \, - \, \hat{\mathbf {n}}^\mathsf {T}{\mathsf {Q}} \hat{\mathbf {n}} \; = \; \sum _\sigma |\mathbf {q}_\sigma |^2 \, - \, \sum _\sigma |\hat{\mathbf {n}} \varvec{\cdot }\mathbf {q}_\sigma |^2 \nonumber \\= & {} \sum _\sigma |\hat{\mathbf {n}} \varvec{\times }\mathbf {q}_\sigma |^2 ~. \end{aligned}$$

(4.31)

In the planar spacecraft array case, and if $\hat{\mathbf {n}}$ is the normal unit vector to the spacecraft plane, $\hat{\mathbf {n}} \varvec{\cdot }\mathbf {q}_\sigma = 0$ and thus $\left\langle | \delta c_n |^2 \right\rangle = (\delta B)^{2} \sum _\sigma |\mathbf {q}_\sigma |^2$.

4.1.3 Appendix C: Condition Number of a Planar Position Tensor

In order to show that the product of $L_q^{-2} = \sum _\sigma |\mathbf {q}_\sigma |^2$ (inverse square gradient estimation error length) and $L_r^2 = \frac{1}{4} \left( \sum _\sigma |\mathbf {q}_\sigma |^2 \right) ^{1/2}$ (mean square inter-spacecraft distance) is in the planar spacecraft array case related to the effective condition number of the position tensor ${\mathsf {R}}$ through Eq. (4.22)

$$\begin{aligned} \text {CN} ({\mathsf {R}}) \; = \; \exp \left[ \text {arcosh} \left( 2 \frac{L_r^2}{L_q^2} - 1 \right) \right] ~, \end{aligned}$$

(4.32)

we work in a mesocentric coordinate frame to express the position vectors $\mathbf {r}_\sigma$ and the position tensor ${\mathsf {R}} = \sum _\sigma \mathbf {r}_\sigma \mathbf {r}_\sigma ^\mathsf {T}$, thus $L_r^2 = \frac{1}{4} \text {trace} ({\mathsf {R}})$. The eigenvalues $\rho _1 \ge \rho _2 \ge \rho _3$ and corresponding eigenvectors $\hat{\mathbf {e}}_1,\hat{\mathbf {e}}_2,\hat{\mathbf {e}}_3$ of ${\mathsf {R}}$ yield the alternative representation ${\mathsf {R}} = \sum _k \rho _k \hat{\mathbf {e}}_k \hat{\mathbf {e}}_k^\mathsf {T}$. Since the spacecraft configuration is assumed to be planar, ${\mathsf {R}}$ has rank 2, thus the third eigenvalue $\rho _3$ is zero,

$$\begin{aligned} {\mathsf {R}} \; = \; \rho _1 \hat{\mathbf {e}}_1 \hat{\mathbf {e}}_1^\mathsf {T}\, + \, \rho _2 \hat{\mathbf {e}}_2 \hat{\mathbf {e}}_2^\mathsf {T}~, \end{aligned}$$

(4.33)

and $L_r^2 = \frac{1}{4} \text {trace} ({\mathsf {R}}) = \frac{1}{4} \left( \rho _1 + \rho _2\right)$. The effective condition number $\text {CN} ({\mathsf {R}})$ in the construction of the pseudo-inverse

$$\begin{aligned} {\mathsf {Q}} \; = \; \rho _1^{-1} \hat{\mathbf {e}}_1 \hat{\mathbf {e}}_1^\mathsf {T}\, + \, \rho _2^{-1} \hat{\mathbf {e}}_2 \hat{\mathbf {e}}_2^\mathsf {T}\end{aligned}$$

(4.34)

is $\text {CN} ({\mathsf {R}}) = \rho _1/\rho _2$. We further note that by defintion of $\mathbf {q}_\sigma = {\mathsf {Q}} \mathbf {r}_\sigma$,

$$\begin{aligned} \sum _\sigma \mathbf {q}_\sigma \mathbf {q}_\sigma ^\mathsf {T}\; = \; \sum _\sigma {\mathsf {Q}} \mathbf {r}_\sigma \mathbf {r}_\sigma ^\mathsf {T}{\mathsf {Q}}^\mathsf {T}\; = \; {\mathsf {Q}} {\mathsf {R}} {\mathsf {Q}}^\mathsf {T}\; = \; {\mathsf {Q}} \end{aligned}$$

(4.35)

because the operator ${\mathsf {Q}} = {\mathsf {Q}}^\mathsf {T}$ acts only in the spacecraft plane (spanned by the two eigenvectors $\hat{\mathbf {e}}_1$ and $\hat{\mathbf {e}}_2$), and ${\mathsf {Q}} {\mathsf {R}}$ yields the identity operation on that plane. Therefore,

$$\begin{aligned} \rho _1^{-1} + \rho _2^{-1} \; = \; \text {trace} ({\mathsf {Q}}) \; = \; \sum _\sigma | \mathbf {q}_\sigma |^2 \; = \; L_q^{-2} ~, \end{aligned}$$

(4.36)

and

$$\begin{aligned} \frac{L_r^2}{L_q^2} \; = \; \frac{1}{4} \left( \rho _1 + \rho _2 \right) \left( \rho _1^{-1} + \rho _2^{-1} \right) \; = \; \frac{1}{4} \left( 2 + \frac{\rho _1}{\rho _2} + \frac{\rho _2}{\rho _1} \right) \; = \; \frac{1}{4} \left( 2 + \text {CN} ({\mathsf {R}}) + \frac{1}{\text {CN} ({\mathsf {R}})} \right) ~. \end{aligned}$$

(4.37)

With $x = \ln \text {CN} ({\mathsf {R}}) = \ln (\rho _1/\rho _2)$ we obtain

$$\begin{aligned} \frac{L_r^2}{L_q^2} \; = \; \frac{1}{4} \left( 2 + \mathrm {e}^x + \mathrm {e}^{-x} \right) \; = \; \frac{1}{2} \left( 1 + \text {cosh} x \right) ~, \end{aligned}$$

(4.38)

and finally $\text {cosh} \left[ \ln \text {CN} ({\mathsf {R}}) \right] = 2 L_r^2/L_q^2 - 1$.