Skip to main content
SpringerLink
Log in

Motion Planning for PDEs

  • Living reference work entry
  • Latest version View entry history
  • First Online:
Encyclopedia of Systems and Control

  • 48 Accesses

Abstract

Motion planning or trajectory planning, respectively, refers to the design of an open-loop control to achieve desired trajectories for the system states or outputs. Given distributed parameter systems that are governed by partial differential equations (PDEs), this requires to take into account the spatial-temporal system dynamics. In this case flatness-based techniques provide a systematic motion planning approach, which is based on the parametrization of any system variable by means of a flat or basic output. With this, the motion planning problem can be solved rather intuitively as is illustrated subsequently for linear and semi-linear PDEs. In addition constraints on system input or states can be taken into account systematically by introducing a dynamic optimization problem for the computation of the flat output trajectory.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Institutional subscriptions

Similar content being viewed by others

Notes

  1. 1.

    Expressions are for the sake of simplicity in the following only written for the input parametrization. The state parametrization follows accordingly.

  2. 2.

    Classically stationary solutions are to be defined in terms of stationary input values .

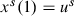Bibliography

  • Andrej J, Meurer T (2018) Flatness-based constrained optimal control of reaction-diffusion systems. In: American control conference (ACC), Milwaukee, pp 2539–2544

    Google Scholar 

  • Boas R (1954) Entire functions. Academic, New York

    MATH  Google Scholar 

  • Böhm T, Meurer T (2017) Trajectory planning and tracking control for the temperature distribution in a deep drawing tool. Control Eng Pract 64:127–139

    Article  Google Scholar 

  • Delaleau E, Rudolph J (1998) Control of flat systems by quasi-static feedback of generalized states. Int J Control 71(5):745–765 https://doi.org/10.1080/002071798221551

    Article  MathSciNet  Google Scholar 

  • Fliess M, Lévine J, Martin P, Rouchon P (1995) Flatness and defect of non–linear systems: introductory theory and examples. Int J Control 61:1327–1361

    Article  MathSciNet  Google Scholar 

  • Fliess M, Mounier H, Rouchon P, Rudolph J (1997) Systèmes linéaires sur les opérateurs de MikusiÅ„ski et commande d’une poutre flexible. ESAIM Proceedings 2:183–193

    Article  Google Scholar 

  • Fliess M, Lévine J, Martin P, Rouchon P (1999) A Lie-Bäcklund approach to equivalence and flatness of nonlinear systems. IEEE Trans Autom Control 44(5): 922–937

    Article  Google Scholar 

  • Freudenthaler G, Meurer T (2016) PDE–based tracking control for multi-agent deployment. IFAC–PapersOnLine 49(18):582–587; 10th IFAC symposium on nonlinear control systems (NOLCOS 2016), Monterey, 23–25 Aug 2016

    Article  Google Scholar 

  • Kater A, Meurer T (2019) Motion planning and tracking control for coupled flexible beam structures. Control Eng Pract 84:389–398

    Article  Google Scholar 

  • Knüppel T, Woittennek F, Rudolph J (2010) Flatness-based trajectory planning for the shallow water equations. In: Proceedings of 49th IEEE conference on decision and control (CDC), Altanta, pp 2960–2965

    Google Scholar 

  • Meurer T (2011) Flatness–based trajectory planning for diffusion–reaction systems in a Parallelepipedon – a spectral approach. Automatica 47(5):935–949

    Article  MathSciNet  Google Scholar 

  • Meurer T (2013) Control of higher–dimensional PDEs: flatness and backstepping designs. Communications and control engineering series. Springer

    Book  Google Scholar 

  • Meurer T, Andrej J (2018) Flatness-based model predictive control of linear diffusion–convection–reaction processes. In: IEEE conference on decision and control (CDC), Miami Beach, pp 527–532

    Google Scholar 

  • Meurer T, Krstic M (2011) Finite–time multi–agent deployment: a nonlinear PDE motion planning approach. Automatica 47(11):2534–2542

    Article  MathSciNet  Google Scholar 

  • Meurer T, Kugi A (2009) Trajectory planning for boundary controlled parabolic PDEs with varying parameters on higher-dimensional spatial domains. IEEE T Automat Control 54(8):1854–1868

    Article  MathSciNet  Google Scholar 

  • Petit N, Rouchon P (2001) Flatness of heavy chain systems. SIAM J Control Optim 40(2):475–495

    Article  MathSciNet  Google Scholar 

  • Petit N, Rouchon P (2002) Dynamics and solutions to some control problems for water-tank systems. IEEE Trans Autom Control 47(4):594–609

    Article  MathSciNet  Google Scholar 

  • Qi J, Vazquez R, Krstic M (2015) Multi–agent deployment in 3–D via PDE control. IEEE Trans Autom Control 60(4):891–906

    Article  MathSciNet  Google Scholar 

  • Rodino L (1993) Linear partial differential operators in Gevrey spaces. World Scientific Publishing Co. Pte. Ltd., Singapore

    Book  Google Scholar 

  • Rouchon P (2001) Motion planning, equivalence, and infinite dimensional systems. Int J Appl Math Comp Sci 11:165–188

    MathSciNet  MATH  Google Scholar 

  • Rudolph J (2003a) Beiträge zur flachheitsbasierten Folgeregelung linearer und nichtlinearer Systeme endlicher und unendlicher Dimension. Berichte aus der Steuerungs– und Regelungstechnik, Shaker–Verlag, Aachen

    Google Scholar 

  • Rudolph J (2003b) Flatness Based Control of Distributed Parameter Systems. Berichte aus der Steuerungs– und Regelungstechnik, Shaker–Verlag, Aachen

    Google Scholar 

  • Rudolph J, Woittennek F (2008) Motion planning and open loop control design for linear distributed parameter systems with lumped controls. Int J Control 81(3):457–474

    Article  MathSciNet  Google Scholar 

  • Schörkhuber B, Meurer T, Jüngel A (2013) Flatness of semilinear parabolic PDEs – a generalized Cauchy-Kowalevski approach. IEEE T Automat Control 58(9):2277–2291

    Article  MathSciNet  Google Scholar 

  • Schröck J, Meurer T, Kugi A (2013) Motion planning for Piezo–actuated flexible structures: modeling, design, and experiment. IEEE T Control Sys Tech 21(3): 807–819

    Article  Google Scholar 

  • Woittennek F, Mounier H (2010) Controllability of networks of spatially one-dimensional second order p.d.e. – an algebraic approach. SIAM J Control Optim 48(6):3882–3902

    Article  MathSciNet  Google Scholar 

  • Woittennek F, Rudolph J (2003) Motion planning for a class of boundary controlled linear hyperbolic PDE’s involving finite distributed delays. ESAIM: Control Optim Calcul Var 9:419–435

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Automatic Control Chair, Faculty of Engineering, Kiel University, Kiel, Germany

    Thomas Meurer

Authors
  1. Thomas Meurer
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Thomas Meurer .

Editor information

Editors and Affiliations

  1. Electrical and Computer Engineering, Boston University, Boston, MA, USA

    John Baillieul

  2. Automation and Control Solutions, Honeywell, Golden Valley, MN, USA

    Tariq Samad

Section Editor information

  1. Department of Mechanical and Aerospace Engineering, University of California, San Diego, La Jolla, CA, USA

    Miroslav Krstic

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer-Verlag London Ltd., part of Springer Nature

About this entry

Check for updates. Verify currency and authenticity via CrossMark

Cite this entry

Meurer, T. (2020). Motion Planning for PDEs. In: Baillieul, J., Samad, T. (eds) Encyclopedia of Systems and Control. Springer, London. https://doi.org/10.1007/978-1-4471-5102-9_14-2

Download citation

  • DOI: https://doi.org/10.1007/978-1-4471-5102-9_14-2

  • Published:

  • Publisher Name: Springer, London

  • Print ISBN: 978-1-4471-5102-9

  • Online ISBN: 978-1-4471-5102-9

  • eBook Packages: Springer Reference EngineeringReference Module Computer Science and Engineering

Publish with us

Policies and ethics

Chapter history

  1. Latest

    Motion Planning for PDEs
    Published:
    20 November 2019

    DOI: https://doi.org/10.1007/978-1-4471-5102-9_14-2

  2. Original

    Motion Planning for PDEs
    Published:
    14 March 2014

    DOI: https://doi.org/10.1007/978-1-4471-5102-9_14-1

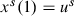Search

Navigation