Keywords

1 Introduction

The geoid, being the natural mathematical figure of the earth, serves as height reference surface for geodetic, geophysical and many engineering applications. It is directly connected with the theory of equipotential surfaces (Heiskanen and Moritz 1967; Hofmann-Wellenhof and Moritz 2006), and its determination needs sufficient coverage of observation data related to the earth’s gravity field, such as gravity anomalies. In this investigation, a geoid model for Africa will be determined. The challenge we face here consists in the available data set, which suffers from significantly large gaps, especially on land.

The available data for this investigation is a set of gravity anomalies, both on land and sea. The geoid is computed using the Stokes’ integral, which requires interpolating the available data into a regular grid. In order to reduce the interpolation errors, especially in areas of large data gaps, the window remove-restore technique (Abd-Elmotaal and Kühtreiber 1999, 2003) is used. The window technique doesn’t suffer from the double consideration of the topographic-isostatic masses in the neighbourhood of the computational point, and accordingly produces un-biased reduced gravity anomalies with minimum variance.

In order to control the gravity interpolation in the large data gaps, these gaps are filled-in, prior to the interpolation process, with an underlying grid employing the EIGEN-6C4 geopotential model (Förste et al. 2014a,b). Hence the interpolation process took place using the unequal weight least-squares prediction technique (Moritz 1980).

Finally, the computed geoid within the current investigation is fitted to the DIR_R5 GOCE satellite-only model by applying an offset and two tilt parameters. This adjustment reduces remaining tilts and a vertical offset in the model. Previous studies (Abd-Elmotaal 2015) have shown that the DIR_R5 GOCE model is best suited for this purpose on the African continent.

The first attempt to compute a geoid model for Africa has been made by Merry (2003) and Merry et al. (2005). A 5′× 5′ mean gravity anomaly grid developed at Leeds University was used to compute that geoid model. We regret that this data set has never become available since then again. For the geoid computed by Merry et al. (2005), the remove-restore method, based on the EGM96 geopotential model (Lemoine et al. 1998), was employed. Another geoid model for Africa has been computed by Abd-Elmotaal et al. (2019). This geoid model employed the window remove-restore technique with the EGM2008 geopotential model (Pavlis et al. 2012), up to degree and order 2160, and a tailored reference model (computed through an iterative process), up to degree and order 2160, to fill in the data gaps.

Due to problems with a data set in Morocco, used in the former solution AFRgeo_v1.0 (Abd-Elmotaal et al. 2019), the computed geoid has been compared only to the AGP2003 model (Merry et al. 2005) in the present paper.

2 The Data

2.1 Gravity Data

The available gravity data set for the current investigation comprises data on land and sea. The sea data consists of shipborne point data and altimetry-derived gravity anomalies along tracks. The latter data set was derived from the average of 44 repeated cycles of the satellite altimetry mission GEOSAT by the National Geophysical Data Center NGDC (www.ngdc.noaa.gov) (Abd-Elmotaal and Makhloof 2013, 2014). The goal of the African Geoid Project is the calculation of the geoid on the African continent. Data within the data window which are located on the oceans (shipborne and altimetry data) are used to stabilize the solution at the continental margins to avoid the Gibbs phenomenon.

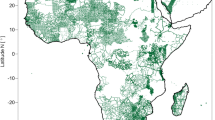
The land point gravity data, being the most important data set for the geoid at the continent, have passed a laborious gross-error detection process developed by Abd-Elmotaal and Kühtreiber (2014) using the least-squares prediction technique (Moritz 1980). This gross-error detection process estimates the gravity anomaly at the computational point using the neighbour points and defines a possible gross-error by comparing it to the data value. The gross-error detection process deletes the point from the data set if it proves to be a real gross-error after examining its effect to the neighbourhood points. Furthermore, a grid-filtering scheme (Abd-Elmotaal and Kühtreiber 2014) on a grid of 1′× 1′ is applied to the land data to improve the behaviour of the empirical covariance function especially near the origin (Kraiger 1988). The statistics of the land free-air gravity anomalies, after the gross-error detection and the grid-filtering, are illustrated in Table 2. Figure 1a shows the distribution of the land gravity data set.

Fig. 1
figure 1

Distribution of the (a) land, (b) shipborne and (c) altimetry free-air gravity anomaly points for Africa

Full size image

The shipborne and altimetry-derived free-air anomalies have passed a gross-error detection scheme developed by Abd-Elmotaal and Makhloof (2013), also based on the least-squares prediction technique. It estimates the gravity anomaly at the computational point utilizing the neighbourhood points, and defines a possible blunder by comparing it to the data value. The gross-error technique works in an iterative scheme till it reaches 1.5 mgal or better for the discrepancy between the estimated and data values. A combination between the shipborne and altimetry data took place (Abd-Elmotaal and Makhloof 2014). Then a grid-filtering process on a grid of 3′× 3′ has been applied to the shipborne and altimetry-derived gravity anomalies to decrease their dominating effect on the gravity data set. The statistics of the shipborne and altimetry-derived free-air anomalies, after the gross-error detection and grid-filtering, are listed in Table 2. The distribution of the shipborne and altimetry data is given in Fig. 1b and c, respectively. More details about the used data sets can be found in Abd-Elmotaal et al. (2018).

2.2 Digital Height Models

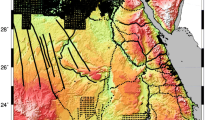
If the computation of the topographic reduction is carried out with a software such as TC-program, a fine DTM for the near-zone and a coarse one for the far-zone are required. The TC-software originates from Forsberg (1984). In this investigation a program version was used which was modified by Abd-Elmotaal and Kühtreiber (2003). A set of DTMs for Africa covering the window (− 42∘≤ ϕ ≤ 44∘;−22∘≤ λ ≤ 62∘) are available for the current investigation. The AFH16S30 30′′× 30′′ and the AFH16M03 3′× 3′ models (Abd-Elmotaal et al. 2017) have been chosen to represent the fine and coarse DTMs, respectively. Figure 2 illustrates the AFH16S30 30′′× 30′′ fine DTM for Africa. The heights range between − 8291 and 5777 m with an average of − 1623 m.

Fig. 2
figure 2

The 30′′× 30′′ AFH16S30 DTM for Africa. Units in [m]

Full size image

2.3 A Short History of Used Data

The data used to calculate the current geoid solution for Africa have been described in Sects. 2.1 and 2.2. Data acquisition is a continuous tedious task, especially for point gravity values on land. As can be seen in Fig. 1, significant data gaps still need to be closed despite great efforts. In fact, since the first basic calculation of an African geoid by Merry (2003) and Merry et al. (2005), the point gravity data situation is continuously improving, although the original data of Merry et al. (2005) are no longer available. This can be concluded from Table 1. It should be mentioned that no ocean data had been used in the former AGP2003 solution.

Table 1 Used data and techniques in the African Geoid Project
Full size table
Table 2 Statistics of the free-air and reduced gravity anomalies
Full size table

3 Gravity Reduction

As stated earlier, in order to get un-biased reduced anomalies with minimum variance, the window remove-restore technique is used. The remove step of the window remove-restore technique when using the EIGEN-6C4 geopotential model (Förste et al. 2014a,b), complete to degree and order 2190, as the reference model can be expressed by (Abd-Elmotaal and Kühtreiber 1999, 2003) (cf. Fig. 3)

(1)

where refers to the window-reduced gravity anomalies, ΔgF refers to the measured free-air gravity anomalies, stands for the contribution of the global reference geopotential model, ΔgTIwin is the contribution of the topographic-isostatic masses for the fixed data window, \(\varDelta g_{winco\!f}\) stands for the contribution of the harmonic coefficients of the topographic-isostatic masses of the same data window and nmax is the maximum degree (nmax = 2, 190 is used).

Fig. 3
figure 3

The window remove-restore technique

Full size image

For the underlying grid, which is intended to support the boundary values, particularly in areas of data gaps, the free-air gravity anomalies are computed by

(2)

on a 15′× 15′ grid. This is three times the resolution of the output grid. To avoid identical grid points between the underlying grid and the output grid, the underlying grid is shifted by 2.5′ relative to the output grid. Therefore both grids are called unregistered.

The contribution of the topographic-isostatic masses ΔgTIwin for the fixed data window (− 42∘≤ ϕ ≤ 44∘; − 22∘≤ λ ≤ 62∘) is computed using TC-program (Forsberg 1984; Abd-Elmotaal and Kühtreiber 2003). The following commonly used parameter set (cf. Kaban et al. 2016; Braitenberg and Ebbing 2009; Heiskanen and Moritz 1967, p. 327) is implemented

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} T_{\circ} & = &\displaystyle 30 \mbox{ km} \, , \\ \rho_{\circ} & = &\displaystyle 2.67 \mbox{ g/cm}^3 \, ,\\ \varDelta \rho & = &\displaystyle 0.40 \mbox{ g/cm}^3 \, , \end{array} \end{aligned} $$
(3)

where T∘ is the normal crustal thickness, ρ∘ is the density of the topography and Δρ is the density contrast between the crust and the mantle.

The contribution of the involved harmonic models is computed by the technique developed by Abd-Elmotaal (1998). Alternative techniques can be found, for example, in Rapp (1982) or Tscherning et al. (1994). The potential harmonic coefficients of the topographic-isostatic masses for the data window are computed using the rigorous expressions developed by Abd-Elmotaal and Kühtreiber (2015).

Table 2 illustrates the statistics of the free-air and reduced anomalies for each data category. The great reduction effect using the window remove-restore technique in terms of both the mean and the standard deviation for all data categories is obvious. What is very remarkable is the dramatic drop of the standard deviation of the most important data source, the land gravity data, by about 84%. This indicates that the used reduction technique works quite well. Table 2 also shows that the underlying grid has a compatible statistical behaviour with the other data categories, which is needed for the interpolation process.

4 Interpolation Technique

An unequal weight least-squares interpolation technique (Moritz 1980) on a 5′× 5′ grid covering the African window (40∘S ≤ ϕ ≤ 42∘N, 20∘W ≤ λ ≤ 60∘E) took place to generate the gridded window-reduced gravity anomalies from the pointwise window-reduced gravity anomalies . The following standard deviations have been fixed after some preparatory investigations:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \begin{aligned} \sigma_{land} & = &\displaystyle 1 \;\mbox{mgal} \, , \\ \sigma_{shipborne} & = &\displaystyle 3 \;\mbox{mgal} \, , \\ \sigma_{altimetry} & = &\displaystyle 5 \;\mbox{mgal} \, , \\ \sigma_{underlying \:grid} & = &\displaystyle 20 \;\mbox{mgal} \, . \end{aligned}{} \end{array} \end{aligned} $$
(4)

The generalized covariance model of Hirvonen has been used for which the estimation of the parameter p (related to the curvature of the covariance function near the origin) has been made through the fitting of the empirically determined covariance function by employing a least-squares regression algorithm developed by Abd-Elmotaal and Kühtreiber (2016). A value of p = 0.364 has been estimated. The values of the empirically determined variance C∘ and correlation length ξ for the empirical covariance function are as follows:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \begin{aligned} C_{\circ} & = &\displaystyle 81.30 \; \mbox{mgal}^2 \, ,\\ \xi & = &\displaystyle 10.38\; \mbox{km} \, . \end{aligned}{} \end{array} \end{aligned} $$
(5)

Figure 4 shows the excellent fitting of the empirically determined covariance function performed by the above described process.

Fig. 4
figure 4

Fitting of the empirically determined covariance function using the least-squares regression algorithm developed by Abd-Elmotaal and Kühtreiber (2016)

Full size image

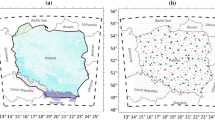
Figure 5 illustrates the 5′× 5′ interpolated window-reduced anomalies generated using the unequal weight least-squares interpolation technique employing the relative standard deviations described above and specified in Eq. (4). In most areas, the anomalies are less than 10 mgal, indicating that the modelling is appropriate for the remove step. This is particularly evident in the regions on the African mainland and there especially in the areas with large data gaps. Thus it can be concluded that the reduction and interpolation methods, especially developed for this data situation, have not led to any irregularities in the reduced anomalies. The efficiency of the used reduction and interpolation method has been validated by Abd-Elmotaal and Kühtreiber (2019), employing independent point gravity data not used in the interpolation process; this validation proved an external precision of about 7 mgal over various test areas on the African continent indicating the good feasibility of the applied approach.

Fig. 5
figure 5

Interpolated 5′× 5′ window-reduced anomalies for Africa. Units in [mgal]

Full size image

5 Geoid Determination

For a better combination of the different wavelengths of the earth’s gravity field (e.g., Featherstone et al. 1998; Abd-Elmotaal and Kühtreiber 2008), the contribution of the reduced gridded gravity anomalies to the geoid is determined on a 5′× 5′ grid covering the African window using Stokes’ integral employing Meissl (1971) modified kernel, i.e.,

(6)

where KM(ψ) is the Meissl modified kernel, given by

$$\displaystyle \begin{aligned} K^{M}(\psi) = \left\{ \begin{array}{lll} S(\psi) - S(\psi_{\circ}) & \mbox{for} & 0 < \psi \leq \psi_{\circ}\\ 0 & \mbox{for} & \psi > \psi_{\circ} \end{array} \right. \, . \end{aligned} $$
(7)

A value of the cap size ψ∘ = 3∘ has been used. S(⋅) is the original Stokes function. The choice of the Meissl modified kernel has been made because it proved to give good results (cf. Featherstone et al. 1998; Abd-Elmotaal and Kühtreiber 2008).

The full geoid restore expression for the window technique reads (Abd-Elmotaal and Kühtreiber 1999, 2003)

(8)

where NTIwin gives the contribution of the topographic-isostatic masses (the indirect effect) for the same fixed data window as used for the remove step, gives the contribution of the EIGEN-6C4 geopotential model, \(\zeta _{winco\!f}\) stands for the contribution of the dimensionless harmonic coefficients of the topographic-isostatic masses of the data window, and (N − ζ)win is the conversion from quasi-geoid to geoid for the terms related to the quasi-geoid, i.e., and \(\zeta _{winco\!f}\). The term (N − ζ)win can be determined by applying the quasi-geoid to geoid conversion given by Heiskanen and Moritz (1967, p. 327) (see also Eq. (11)). This gives immediately

(9)

where and \(\varDelta g_{winco\!f}\) are the free-air gravity anomaly contributions of the EIGEN-6C4 geopotential model and the harmonic coefficients of the topographic-isostatic masses of the data window, respectively, and \(\bar {\gamma }\) is a mean value of the normal gravity.

In order to fit the gravimetric geoid model for Africa to the individual height systems of the African countries, one needs some GNSS stations with known orthometric height covering the continental area. Unfortunately, despite our hard efforts, this data is still not available to the authors. As an alternative, the computed geoid is embedded using the GOCE DIR_R5 satellite-only model (Bruinsma et al. 2014), which is complete to degree and order 300. It represents the best available global geopotential model approximating the gravity field in Africa; this has been investigated by Abd-Elmotaal (2015). In the present application, the DIR_R5 model was evaluated up to d/o 280, since the signal-to-noise ratio for higher degrees is greater than one, and thus the coefficients of higher degrees are not considered. The general discrepancies between the GOCE DIR_R5 geoid and our calculated geoid solution have been represented by a trend model consisting of a vertical offset and two tilt parameters. These parameters have been estimated through a least-squares regression technique from the residuals between the two geoid solutions. This parametric model has been used to remove the trend which may be present in the computed geoid within the current investigation. This trend may be caused by errors in the long-wavelength components of the used reference model EIGEN-6C4 or the point gravity data. The Dir_R5 geoid undulations \(N_{Dir\_R5}\) can be computed by

$$\displaystyle \begin{aligned} N_{Dir\_R5} = \zeta_{Dir\_R5} + (N-\zeta) \, , \end{aligned} $$
(10)

where \(\zeta _{Dir\_R5}\) refers to the contribution of the Dir_R5 geopotential model, and the term (N − ζ) is computed by (Heiskanen and Moritz 1967, p. 327)

$$\displaystyle \begin{aligned} (N-\zeta) = \frac{\varDelta g_{Dir\_R5}-2\pi\rho_{\circ} G H}{\bar{\gamma}} H \, , {} \end{aligned} $$
(11)

where \(\varDelta g_{Dir\_R5}\) refers to the free-air gravity anomalies computed by using the Dir_R5 geopotential model, G is Newton’s gravitational constant, and ρ∘ is the density of the topography, given by Eq. (3).

Figure 6 shows the AFRgeo2019 African de-trended geoid as stated above. The values of the AFRgeo2019 African geoid range between − 55.34 and 57.34 m with an average of 11.73 m.

Fig. 6
figure 6

The AFRgeo2019 African de-trended geoid model. Contour interval: 2 m

Full size image

6 Geoid Comparison

As stated earlier, the first attempt to determine a geoid model for Africa “AGP2003” has been carried out by Merry (2003) and Merry et al. (2005). Since then, the data base has been further enhanced. In particular, the calculation method, statistical combination of the various types of gravity anomalies, has been revised and further developed. This has led to a significant improvement of the African geoid model. Figure 7 shows the difference between the de-trended AFRgeo2019 and the AGP2003 geoid models. The light yellow pattern in Fig. 7 indicates differences below 1 m in magnitude. Figure 7 shows that the differences between the two geoids amount to several meters in the continental area, especially in East Africa. The large differences over the Atlantic Ocean arise from the fact that the AGP2003 didn’t include ocean data in the solution. Figure 7 shows some edge effects, which are again a direct consequence of using no data outside the African continent in the AGP2003 solution.

Fig. 7
figure 7

Difference between the de-trended AFRgeo2019 and the AGP2003 geoid models. Contour interval: 1 m

Full size image

As the AFRGDB_v1.0, which has been the basis for computing the AFRgeo_v1.0, has been greatly influenced by a wrong data set in Morocco (cf. Abd-Elmotaal et al. 2015, 2019), it has been decided to skip the comparison between AFRgeo_v1.0 and the current geoid model.

7 Conclusions

In this paper, we successfully computed an updated version of the African geoid model. The computed geoid model is based on the window remove-restore technique (Abd-Elmotaal and Kühtreiber 2003), which gives very small and smooth reduced gravity anomalies. This helped to minimize the interpolation errors, especially in the areas of large data gaps. Filling these data gaps with synthesized gravity anomalies using the EIGEN-6C4 geopotential model, complete to degree and order 2190, has stabilized the interpolation process at the data gaps.

The reduced gravity anomalies employed for the AFRgeo2019 geoid model show a very good statistical behaviour (especially on land) because they are centered, smooth and have relatively small range (cf. Fig. 5 and Table 2). The smoothness of the residuals indicates that the interpolation technique proposed by Abd-Elmotaal and Kühtreiber (2019) did not induce aliasing effects, especially in the areas with point data gaps. Hence, they give less interpolation errors, especially in the large gravity data gaps. The reduced gravity data were interpolated using an unequal least-squares interpolation technique, giving the land data the highest precision, the sea data a moderate precision and the underlying grid the lowest precision.

In order to optimally combine the spectral components in the remove-compute-restore technique, the Stokes function in the Stokes integral is replaced by a modified kernel function. In the geoid solution presented, the modification according to Meissl (1971) was used. Alternative modifications have been discussed by Wong and Gore (1969), Jekeli (1980), Wenzel (1982), Heck and Grüninger (1982), Featherstone et al. (1998) or Sjöberg (2003).

Finally, the computed geoid model for Africa has been de-trended by the use of the DIR_R5 GOCE model. In comparison with the previous model AGP2003, the progress made in determining the African height reference surface becomes visible.

Unfortunately, despite of strong efforts, extended precise GNSS positioning data over the African continent have not been made available to the authors. Thus, a rigorous comparison of the presented geoid model with an independent data set can only be made with further international efforts.