Abstract
While investigating odd-cycle free hypergraphs, Győri and Lemons introduced a colored version of the classical theorem of Erdős and Gallai on \(P_k\)-free graphs. They proved that any graph G with a proper vertex coloring and no path of length \(2k+1\) with end vertices of different colors has at most 2kn edges. We show that Erdős and Gallai’s original sharp upper bound of kn holds for their problem as well. We also introduce a version of this problem for trees and present a generalization of the Erdős-Sós conjecture.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Main results
We denote by \(P_\ell \) the path of length \(\ell \) (that is, containing \(\ell \) edges). For a graph G, we denote by E(G) and V(G) the edge and vertex set of G, respectively. We begin by recalling the theorems of Erdős and Gallai about graphs without long paths and cycles.
Theorem 1
(Erdős-Gallai [3]) Let G be an n-vertex graph with no \(P_\ell \), then
and equality holds if and only if \(\ell \) divides n and G is the disjoint union of \(\frac{n}{\ell }\) cliques of size \(\ell \).
Theorem 2
(Erdős-Gallai [3]) Let G be an n-vertex graph with no \(C_m\) for all \(m \ge \ell \), then
and equality holds if and only if \(\ell -2\) divides \(n-1\) and G is a connected graph such that every block of G is a clique of size \(\ell -1\).
In fact, Theorem 1 was deduced as a simple corollary of Theorem 2. In a more recent paper, Győri and Lemons [5] investigated the extremal number of hypergraphs avoiding so-called Berge-cycles. To this end, they introduced a generalization of the theorem of Erdős and Gallai about paths. By a proper vertex coloring of a graph G, we mean a coloring of the vertices of G such that no two adjacent vertices are the same color. Győri and Lemons proved the following.
Theorem 3
(Győri-Lemons [5]) Let k be a positive integer and G be an n-vertex graph with a proper vertex coloring such that G contains no \(P_{2k+1}\) with end vertices of different colors, then
We show that the factor of 2 in Theorem 3 is not needed and, thus, recover the original upper bound from the Erdős-Gallai theorem. We also determine which graphs achieve this upper bound.
Theorem 4
Let \(k\ge 0\) and G be an n-vertex graph with a proper vertex coloring such that G contains no \(P_{2k+1}\) with end vertices of different colors, then
and equality holds if and only if \(2k+1\) divides n and G is the union of \(\frac{n}{2k+1}\) disjoint cliques of size \(2k+1\).
Proof of Theorem 4
By induction on the number of vertices, we may assume that G is connected and has minimum degree \(\delta (G) \ge k\). Indeed, if \(\delta (v)<k\) then
If G is \(C_{\ell }\)-free for all \(\ell \ge 2k+1\), then by Theorem 2 we have
Thus, assume there is a cycle of length at least \(2k+1\), and let C be the smallest such cycle with length \(\ell \). Let the vertices of C be \(v_0,v_1,v_2,\dots ,v_{\ell -1},v_0\), consecutively. Addition and subtraction in subscripts will always be taken modulo \(\ell \). We say that an edge e is outgoing if it has one vertex in V(C) and the other in \(V(G) {\setminus } V(C)\). We say a vertex \(v \in V(C)\) is outgoing if it is contained in an outgoing edge.
We will consider cases based on the value of \(\ell \). Observe that \(\ell =2k+2\) is impossible since \(v_0,v_1,\dots ,v_{2k+1}\) is a path of length \(2k+1\) but \(v_0\) and \(v_{2k+1}\) are adjacent, contradiction.
Case 1 Suppose \(\ell \ge 2k+4\). Since we have chosen \(\ell \) to be the length of the smallest \(C_\ell \) with \(\ell \ge 2k+1\), we have \(v_0\) cannot be adjacent to any of \(v_2,v_3,\dots ,v_{\ell -2k}\) nor any of \(v_{2k},v_{2k+1},\dots ,v_{\ell -2}\), for otherwise we would have a shorter cycle of length at least \(2k+1\). Also note that \(v_0\) is adjacent to \(v_1\) and \(v_{\ell -1}\).
Observe that \(v_0\) cannot have two consecutive neighbors in the \(\ell \)-cycle. Indeed, if \(v_i\) and \(v_{i+1}\) are neighbors of \(v_0\), then we have the following \((2k+1)\)-paths starting at \(v_1\): \(v_1,v_2,\dots ,v_{2k+1},v_{2k+2}\) and \(v_1,v_2,\dots ,v_i,v_0,v_{i+1},v_{i+2},\dots ,v_{2k},v_{2k+1}\). Thus, \(v_{2k+1}\) and \(v_{2k+2}\) would have to be colored the same, but this is impossible since they are neighbors.
If \(v_0\) has a neighbor outside of C, say \(u_0\), then we have two paths of length \(2k+1\): \(u_0,v_0,v_1,\dots ,v_{2k}\) and \(v_{2k},v_{2k-1},\dots ,v_0,v_{\ell -1}\). It follows that \(u_0\) and \(v_{\ell -1}\) have the same color. Similarly, \(u_0\) and \(v_1\) have the same color. Thus, \(v_{\ell -1}\) and \(v_1\) also have the same color, and similarly, for every i such that \(v_i\) is outgoing, we can conclude \(v_{i-1}\) and \(v_{i+1}\) have the same color (Fig. 1).
If \(\ell =2k+4\) and there is an outgoing vertex, say \(v_0\), then \(v_1\) and \(v_{2k+3}\) have the same color (from the previous paragraph), a contradiction since \(v_1\) and \(v_{2k+2}\) also have the same color (they are end vertices of a length \(2k+1\) path along the cycle C). If there is no outgoing vertex in V(C), then C uses all vertices of the graph. Since no vertex of the cycle has two consecutive neighbors, it follows that each degree is bounded by \(2+\lceil \frac{2k-5}{2}\rceil \le k\) and so the number of edges is at most \(\frac{(2k+4)k}{2} = \frac{nk}{2}< nk.\)
If \(\ell \ge 2k+5\), we will show that \(v_0\) has an outgoing edge from the \(\ell \)-cycle C. Suppose not, then since \(v_0\) does not have consecutive neighbors, it follows that \(v_0\) has at most
neighbors, a contradiction. Thus, \(v_0\) and similarly every other \(v_i\) has an outgoing neighbor, and it follows that for every i, the vertices \(v_i\) and \(v_{i+2}\) have the same color. Hence \(v_0\) and \(v_{2k}\) have the same color, contradicting that \(v_0\) and \(v_{2k+1}\) have the same color, since they are end vertices of a \(P_{2k+1}\).
Case 2 Suppose \(\ell = 2k+3\). For all \(0 \le i \le \ell -1\), \(v_{i+2},v_{i+1},\dots ,v_{\ell -1},v_0,\dots ,v_i\) is a path of length \(\ell = 2k+1\), and so \(v_i\) and \(v_{i+2}\) have the same color. Thus, \(v_0\) and \(v_{2k+2}\) have the same color, but they are adjacent, contradiction.
Case 3 Finally, suppose \(\ell = 2k+1\). If no edge is outgoing, then we are done, since by connectivity the total number of edges in the graph is at most \(\left( {\begin{array}{c}2k+1\\ 2\end{array}}\right) = k n\). If indeed the total number of edges is kn, then G is a clique. This is the only case when equality holds. From here on, we will assume there is an outgoing edge.
Observe that if u is not a vertex of C, then u cannot have two consecutive neighbors in C, for otherwise we would have a cycle of length \(2k+2\). Moreover, u cannot be connected to \(v_i\) and \(v_{i+3}\), since there would be paths of length \(2k+1\) from u to \(v_{i+1}\) and \(v_{i+2}\). It follows that u can have at most \(k-1\) neighbors in C and, thus, must have a neighbor outside C.
If there are two consecutive non-outgoing vertices in C, then we may take two such vertices \(v_i\) and \(v_{i+1}\), for some index i, so that the next vertex \(v_{i+2}\) is outgoing. Suppose \(\{v_{i+2},u\}\) is an outgoing edge. By the previous observation, there is an edge \(\{u,w\}\) where \(w \not \in C\). So we have a \(2k+1\) length path from \(v_{i}\) to w. Then \(v_{i+1}\) cannot have two consecutive neighbors from C, since that would also imply that there is also \(2k+1\) length path from w to \(v_{i-1}\). Similarly \(v_i\) cannot have two consecutive neighbors in C, hence \(v_i\) and \(v_{i+1}\) have degree at most k. By removing these two vertices, we remove \(2k-1\) edges, and by the induction hypothesis the resulting graph has at most \(k(n-2)\) edges. So \(e(G)<kn\).
For every i, either \(v_{i+1}\) or \(v_{i+2}\) is an outgoing vertex. Hence the vertex \(v_{i}\) has either the same color as \(v_{i+2}\), if \(v_{i+1}\) is an outgoing vertex, or the same color as \(v_{i+4}\), if \(v_{i+2}\) is an outgoing vertex. Hence by repeatedly applying this argument we obtain that \(v_0\) has the same color as \(v_{2k}\) or \(v_1\), contradiction. \(\square \)
We believe that an analogue of Theorem 3 should hold in the setting of trees. Recall that the extremal number \({{\,\mathrm{ex}\,}}(n,H)\) of a graph H is defined to be the largest number of edges an n-vertex graph may have if it does not contain H as a subgraph. Erdős and Sós made the following famous conjecture about the extremal number of trees.
Conjecture 1
(Erdős-Sós [2]) Let T be a tree with \(k \ge 1\) edges, then \({{\,\mathrm{ex}\,}}(n,T) \le \frac{(k-1)n}{2}\).
A proof of Conjecture 1 for sufficiently large trees has been announced by Ajtai, Komlós, Simonovits and Szemerédi [1].
We introduce a new variation of the extremal function \({{\,\mathrm{ex}\,}}(n,T)\) in the case of trees. Let \({{\,\mathrm{ex}\,}}^c(n,T)\) denote the maximum number of edges possible in an n-vertex graph G with a proper vertex coloring (using any number of colors), such that in every copy of T in G the leaves of T are all the same color.
Theorem 5
Let T be a tree with k edges such that in the (unique) proper vertex 2-coloring of T all leaves are not the same color, then \({{\,\mathrm{ex}\,}}^c(n,T) \le (k-1)n\).
Proof
There is a path of odd length in T with end vertices which are leaves. Let G be an n-vertex graph with more than \((k-1)n\) edges with a proper vertex coloring. We may find a subgraph \(G'\) of G with average degree at least that of G and minimum degree greater than \(k-1\). The proper coloring of G induces a proper coloring of \(G'\) and so applying Theorem 3 for any odd \(\ell \le k\), we may find a copy of \(P_{\ell }\) in \(G'\) with end vertices of distinct colors. We may now build up the rest of the tree in a greedy fashion as every degree in \(G'\) is at least k and T has \(k+1\) vertices. Thus, we have found a copy of T in the graph G with leaves of at least two colors. \(\square \)
Theorem 6
Let T be a tree with k edges such that in the proper vertex 2-coloring of T all leaves are the same color, then \({{\,\mathrm{ex}\,}}^c(n,T) = \left\lfloor {\frac{n^2}{4}}\right\rfloor \), provided n is sufficiently large.
Proof
The fact that all leaves are colored the same by a 2-coloring implies that all paths between pairs of leaves have even length. We add an edge e to T connecting an arbitrary pair of leaves, and let G be the resulting graph. Since G has an odd cycle, its chromatic number is clearly 3, and the deletion of e yields a 2-chromatic graph. It follows from a theorem of Simonovits [7] that if n is sufficiently large, the extremal number of G is precisely \({{\,\mathrm{ex}\,}}(n,G) = \left\lfloor {\frac{n^2}{4}}\right\rfloor \). Thus, in any n-vertex graph with more than \(\left\lfloor {\frac{n^2}{4}}\right\rfloor \) edges we have a copy T with two adjacent leaves, and so in any proper coloring of this graph we have a copy of T with leaves of at least 2 colors. It follows that \({{\,\mathrm{ex}\,}}^c(n,T) \le \left\lfloor {\frac{n^2}{4}}\right\rfloor \), and this bound is realized by the complete bipartite graph \(K_{\left\lfloor {\frac{n}{2}}\right\rfloor ,\left\lceil {\frac{n}{2}}\right\rceil }\). \(\square \)
Remark 1
The paths of even length \(P_{2k}\) are a special case of Theorem 6. Here better bounds on n are known to exist. For example, the result of Füredi [4] on the extremal number of odd cycles implies that \(n \ge 4k\) is sufficient.
We believe that a strengthening of Conjecture 1 should hold for trees whose 2-coloring yields two leaves of different colors.
Conjecture 2
Let T be a tree with \(k \ge 1\) edges such that in the proper vertex 2-coloring of T all leaves are not the same color, then \({{\,\mathrm{ex}\,}}^c(n,T) \le \frac{(k-1)n}{2}\).
One would hope that Conjecture 2 could be deduced directly from Conjecture 1, but unfortunately this does not seem to be the case. We take a first step towards Conjecture 2 by proving it in the case of double stars.
Theorem 7 and its proof
Theorem 7
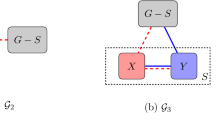
For positive integers a and b, let \(S_{a,b}\) denote the tree on \(a+b+2\) vertices consisting of an edge \(\{u,v\}\) where \(\left|{N(u){\setminus } v}\right|=a\), \(\left|{N(v){\setminus } u}\right|=b\) and \(N(u) \cap N(v) = \varnothing \) (see Fig. 2, left). We have \({{\,\mathrm{ex}\,}}^c(n,S_{a,b}) \le \frac{a+b}{2}n\).
Proof
Let G be a vertex colored graph with \(\left|{E(G)}\right| > \left|{V(G)}\right|\frac{a+b}{2}\). Without loss of generality, suppose \(a\le b\). We may assume by induction that \(\delta (G)>\frac{a+b}{2} \ge a\). Since \({{\,\mathrm{ex}\,}}(m,S_{a,b}) = m\frac{a+b}{2}\) (see, for example [6]), it follows that G contains a copy of \(S_{a,b}\). Suppose this copy is defined by the edge \(\{u,v\}\) together with the disjoint sets \(A\subseteq N(u)\), \(B\subseteq N(v)\) with \(|A|=a, |B|=b\). Now, if there is more than one color in \(A\cup B\), then we are done. So suppose the color of all vertices in \(A \cup B\) is the same. Hence \(A \cup B\) is an independent set.
If u is not adjacent to some \(w \in B\) (see Fig. 2, middle), since \(\left|{N(w)}\right| \ge a +1\), we can pick \(C \subseteq N(w){\setminus }\{u,v\}\) of size a. So the edge \(\{v,w\}\) together with the sets \(B' = (B\cup \{u\})\backslash \{w\}\) and C define an \(S_{a,b}\) where the colors of all vertices in C are different from the colors of \(B'\backslash \{u\}\).
If u is adjacent to all \(w \in B\), then fix \(x\in B\) (see Fig. 2, right). Since \(\left|{N(x)}\right| \ge a +1\), we can pick \(C \subseteq N(x){\setminus }\{u\}\) of size a. Let \(y \in A\) and define \(B' = (B\cup \{y\})\backslash \{x\}\). Observe that \(B'\subseteq N(u)\), and the edge \(\{u,x\}\) together with the sets \(B'\) and C defines an \(S_{a,b}\), where again the color of the vertices in C is different from the color of vertices in \(B'\). \(\square \)
References
Ajtai, Miklós, Komlós, János, Simonovits, Miklós, Szemerédi, Endre: Proof of the Erdős-T. Sós conjecture for large trees (in preparation)
Erdős, Paul: Extremal problems in graph theory. In: Theory of graphs and its applications. Smolenice Publishing House of the Czechoslovak Academy of Science, Prague (1964)
Erdős, Paul, Gallai, Tibor: On maximal paths and circuits of graphs. Acta Mathematica Hungarica 10(3–4), 337–356 (1959)
Füredi, Zoltan, Gunderson, David: Extremal numbers for odd cycles. Comb Probab Comput 24(4), 641–645 (2015)
Győri, Ervin, Lemons, Nathan: 3-uniform hypergraphs avoiding a given odd cycle. Combinatorica 32(2), 187–203 (2012)
McLennan, Andrew: The Erdős-Sós conjecture for trees of diameter four. J Graph Theory 49(4), 291–301 (2005)
Simonovits, Miklós: A method for solving extremal problems in graph theory, stability problems. In Theory of Graphs (Proc. Colloq., Tihany, 1966), pp. 279–319 (1968)
Acknowledgements
Open access funding provided by MTA Alfréd Rényi Institute of Mathematics (MTA RAMKI). The research of all three authors was supported by the National Research, Development and Innovation Office—NKFIH under the Grant K116769.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Salia, N., Tompkins, C. & Zamora, O. An Erdős-Gallai type theorem for vertex colored graphs. Graphs and Combinatorics 35, 689–694 (2019). https://doi.org/10.1007/s00373-019-02026-1
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00373-019-02026-1