Threshold F-policy and N-policy for multi-component machining system with warm standbys

Abstract

This study is concerned with threshold F-policy and N-policy for controlling the arrivals and service in the queueing scenario of a machining system, having active and redundant components. For both F-policy and N-policy models, the queue size distributions are determined by the recursive method. Various performance measures, namely the average number of failed units in the system, probability that the server is busy or idle in the system, etc., are established using the queue size distribution.

Background

In many real-life day-to-day queueing situations as well as industrial systems such as production, communication, transportation, and manufacturing systems, the controlling F-policy and N-policy are being used as cost-effective approaches. Multi-component machines are playing a vital role for solving our daily life problems by reducing the time component. Whenever a machine fails, it causes not only delay in the expected production but also reduction in expected profit. In a multi-component machining system, the F-policy states that failed units are not allowed to enter the system when they reach the capacity of the system. As soon as the queue length of failed units is decreased up to a threshold parameter value F, then the server takes some start-up time and allows the failed units to enter the system for repair. However, the N-policy states that the server will start the service to the failed units only if there are N or more failed units accumulated in the system. The facility of standbys in the machining system is provided for utilizing the proper capacity and desired level of the reliability/availability of the machining system. The smoothness of any machining system can be enhanced by standby support so that the machines can work properly in spite of the failure of some components which are unavailable due to physical/technical constraints. The provision of a ‘serviceman’ along with standby units to replace the operating units is suggested for minimizing the interference of the machining systems.

Machine interference problems with spares are widely studied by many authors in different frameworks using queueing theoretic approaches. The maximum profit with the utilization of any machining system can be obtained by providing proper combination of maintainability and standby support to the system which may improve the system’s reliability under unavoidable techno-economic constraints. It is worthwhile to cite some important contribution in this direction. The analytic solutions of a single-server queueing system with a warm type of standbys were given by Gopalan (1975). The concept of standby support in machine repair problems was incorporated by many researchers, namely Sivazlian and Wang (1989), Gupta and Rao Srinivasa (1996), Wang and Kuo (2000), and many more. Jain (1997) developed a (m, M) machine repair problem model with state-dependent rates and standby support. Jain et al. (2004b) have proposed a bilevel control policy model for machine repair systems. Ke and Wang (2007) obtained the steady-state probabilities of the number of failed machines in the system and other performance measures for the machine repair problem with vacations and two types of spares. A survey report on the machine interference problem has been presented by Haque and Armstrong (2007). Jain et al. (2008) investigated a multi-component repairable system with mixed standbys (warm and cold). Hajeeh and Jabsheh (2009) analyzed a multi-component machining system having two modes of failure. Jain et al. (2010) also published a survey article on various aspects of machine repair problems by emphasizing the practical importance of Markov queueing models. Recently, Yuan and Meng (2011) analyzed the reliability of a warm standby repairable system with priority constraint. The reliability and availability analysis of four series configurations with warm and cold standbys was studied by Hajeeh (2011). More recently, Ke and Wu (2012) have done an investigation on machine repair problem with standbys support.

In queueing modeling, the N-policy concept is mainly incorporated to maintain the techno-economic constraints more effectively. The N-policy is applied by many researchers in queueing problems of a variety of scenarios for providing better cost-effective service to the arrivals. The N-policy utilizes the server’s utility properly with no wastage of available resources (or servers). Firstly, Yadin and Naor (1963) introduced the N-policy concept in queueing modeling. Jain et al. (2004a) considered the N-policy model of a machine repairable system and derived the explicit expressions of the reliability function using Laplace transforms. Zhang and Tian (2004) obtained stationary distributions of queue length and waiting time for the threshold N-policy model. The threshold N-policy model of a degraded multi-component machining system with multiple standbys was studied by Jain and Upadhyaya (2009). Jain and Agrawal (2009) proposed the N-policy model for an unreliable server M^X/M/1 queueing system with server breakdowns. The N-policy model for a machine repair problem was described by Jain and Bhargava (2009). Sharma (2012) developed a cost model for the machine repair system with N-policy and solved the governing equations by the recursive method. Jain et al. (2012b) investigated the performance of a multi-component machining system by developing an N-policy model. They explored the sensitivity and cost analysis for a machining system with different characteristic parameters and provided the numerical results.

Sometimes the server may take setup time before starting the service in the system; this time is defined as the start-up time of the server. Many researchers have used this concept in the field of queueing modeling of machining systems. In the modeling of queueing systems, the threshold F-policy is used for controlling the arrivals in the system. The arrivals are not allowed in the system whenever the number of arrivals reaches the capacity of the system. In such systems, the service is started only when the buffer, i.e., the capacity of the system, is full, and the arrivals are allowed when the queue length decreases to the threshold value F. Any system which contains comparatively small number of customers in the system allows more pleasurable environment which reduces the waiting time, discomforts in the service, and load on the server. Gupta (1995) first introduced the concept of F-policy and gave an interrelationship between N-policy and F-policy models. Wang et al. (2008) considered a G/M/1/K queueing system with F-policy and start-up time by employing the recursive method. Wang and Yang (2009) presented a matrix analytic solution for developing the steady-state solution of a control F-policy M/G/1/K model with exponential start-up time. Yang et al. (2010) considered the F-policy to study the optimization and sensitivity analysis of a queueing system with single vacation. Kuo et al. (2011) demonstrated that the solution algorithm for an F-policy G/M/1/K queue with start-up time can be derived using the N-policy M/G/1/K queue with start-up time. More recently, Jain et al. (2012a) studied the effect of different parameters on various performance measures in the M/M/2/K queuing system with (N, F) policy with multi-optional phase repair and start-up.

In this paper, we analyze the performance measures of F-policy and N-policy models of machine repair problem with warm standby support. In our study, we employ the recursive method to determine the steady-state probabilities of the systems. The model description including assumptions and notations is given in the ‘Model description’ section. The steady-state difference equations governing the models and the recursive method to solve these equations for obtaining the queue size distributions are given in the ‘F-policy model’ section. The performance measures using queue size distribution are derived in the ‘Performance measures’ section. In order to discuss the further extension and to highlight the notable features of the investigation done, concluding remarks are given in the ‘Conclusion’ section.

Model description

In order to study the threshold F-policy and N-policy of a multi-component machining system with warm standbys with a single server, we develop the Markovian model by the birth-death process. To formulate the mathematical model, we construct the governing equations in terms of probabilities using the appropriate rates of inflow and outflow. We develop a (m, M) model for a multi-component system under the assumption that the system fails when there are L = M + S − m + 1 (m = 1, 2,…, M) or more failed units in the system. The following assumptions and notations are used to formulate our model:

• In the F-policy model, the server starts the service when the number of failed units in the system reaches its capacity L. At this time, no failed unit is allowed to queue up in the system until the number of failed units attains the threshold value F.

• In the N-policy model, the server starts the service when there are N or more failed units accumulated in the system. The server leaves the system when it becomes empty, i.e., no failed unit is available in the system.

• It is assumed that the interfailure time and repair time of the failed units and the start-up time of the server are exponentially distributed.

• The server takes some start-up time before providing the service to the failed units. The discipline of rendering the repair is considered according to the first-come first-served discipline.

• When any operating unit fails, it is replaced by an available standby unit. When all the standbys are used, the system may also work till m-operating units function properly.

• When all the standby units are exhausted, the failure rate of the remaining operating units increases due to stress and the system works in degrading mode due to increased load on the system.

• If failure of any unit occurs in case when the system has total L failed units (i.e., the available failed units are equal to the capacity of the system) in the system, it is not permitted to enter the system.

Some notations used for the model formulation are as follows:

• M Total number of operating units in the system

• S Total number of standby units in the system

• α Failure rate of the standby unit

• λ Failure rate of the operating unit

• λ _d Degraded failure rate of remaining operating units (λ _d ≥ λ) when there are less than M but more than m operating units in the system

• μ Repair rate of the server

• β Set-up rate to start allowing failed units for repair in the system

• γ Start-up rate to start the repairing of the failed units in the system

The steady-state probabilities for the system states are defined as follows:

• P_n,j Probability that there are n failed units in the system and the failed units are either allowed (j = 1) or not allowed (j = 0) for repair in the case of the F-policy model

• Q_n,j Probability that there are n failed units in the system and the server is either busy (j = 1) or idle (j = 0) in the case of the N-policy model

The state-dependent failure rate λ _n is given by

$${\lambda }_n=\left\{\begin{array}{ll}\mathit{M\lambda }+\left(S-n\right)\alpha & ;0\le n<S\\ \left(M+S-n\right){\lambda }_d& ;S\le n<L\\ 0& ;\mathrm{otherwise}\end{array}\right..$$

F-policy model

The governing equations

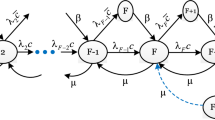
In this section, we construct the steady-state difference equations for the F-policy Markovian model of the machine repair problem. The governing equations are constructed by taking appropriate transition rates (see Figure 1) as follows:

• 1. For j = 0: when failed units (i.e., arrivals) are not allowed in the system.

In this case, to construct the governing equation for state (0, 0), we equate the outflow from state (0, 0) to the inflow from (1, 0). Thus, we obtain

$$\mu P_{1,0}=\beta P_{0,0}.$$

(1)

In a similar manner, by equating the inflow rate from state (n + 1, 0) to state (n, 0) and the outflow rate from state (n, 0) to state 1 ≤ n ≤ L, we get

$$\mu P_{n+1,0}=\left(\mu +\beta \right)P_{n,0};1\le n\le F$$

(2)

$$P_{n+1,0}=P_{n,0};F+1\le n\le L-1$$

(3)

$${\lambda }_{L-1}{P}_{L-1,1}=\mu P_{L,0}.$$

(4)

• 2. For j = 1: when failed units (i.e., arrivals) are allowed for repair in the system.

We construct the equations for state (0, 1) using the inflows from states (1, 1) and (0, 0) to (0, 1) = outflow from state (0, 1). Thus,

$$\mu P_{1,1}+\beta P_{0,0}={\lambda }_0{P}_{0,1}.$$

(5)

Similarly, we consider the inflow from states (n − 1, 1), (n + 1, 1), and (n, 0) to (n, 1) = outflow from state (n, 1), 1 ≤ n ≤ F, and obtain

$$\begin{array}{l}{\lambda }_{n-1}{P}_{n-1,1}+\mu P_{n+1,1}+\beta P_{n,0}\\ =\left({\lambda }_n+\mu \right)P_{n,1};1\le n\le F.\end{array}$$

(6)

Again, using the inflow from states (n − 1, 1) and (n + 1, 1) to (n, 1) = outflow from state (n, 1), where F + 1 ≤ n ≤ L − 1, we get

$$\begin{array}{ll}{\lambda }_{n-1}{P}_{n-1,1}+\mu P_{n+1,1}=& \left({\lambda }_n+\mu \right)P_{n,1};\\ F+1\le n\le L-2.\end{array}$$

(7)

Further balancing the inflow = outflow for state (L − 1, 0), we get

$${\lambda }_{L-2}{P}_{L-2,1}=\left({\lambda }_{L-1}+\mu \right)P_{L-1,1};F\ne L-1.$$

(8)

The normalization condition is given by

$${\displaystyle \sum }_{j=0}^1{\displaystyle \sum }_{n=0}^{L-1}{P}_{n,j}+P_{L,0}=1.$$

(9)

Figure 1

State transition rate diagram for the F -policy model.

Queue size distribution for F-policy

The main task of getting the solution of governing equations is to develop the steady-state probabilities of all the states. The probabilities at steady states can be evaluated by the well-known recursive method for the set of governing difference equations (Equations 1 to 9) of the F-policy model. Now, first we solve Equations 1 to 3 recursively and obtain the steady-state probabilities as

$$P_{n,0}=\delta {\left(1+\delta \right)}^{n-1}{P}_{0,0};1\le n\le F$$

(10)

$$P_{n,0}=\delta {\left(1+\delta \right)}^F{P}_{0,0};F+1\le n\le L$$

(11)

where $\delta =\frac{\beta }{\mu }.$

We find P_{L − 1,1} from Equation 4 using Equation 11:

$$P_{L-1,1}=\frac{\mathit{\mu \delta }{\left(1+\delta \right)}^F}{{\lambda }_{L-1}}{P}_{0,0}.$$

(12)

Now, from Equations 8 and 12, we get

$$P_{L-2,1}=\frac{\left({\lambda }_{L-1}+\mu \right)\mathit{\mu \delta }{\left(1+\delta \right)}^F}{{\lambda }_{L-2}{\lambda }_{L-1}}{P}_{0,0}.$$

(13)

Putting n = L − 2, L − 3,…, F + 1 in Equation 7, we get

$$P_{n,1}=\frac{{\delta }_F}{{{\displaystyle \prod }}_{i=n}^{L-1}{\lambda }_i}{\displaystyle \sum }_{m=0}^{L-n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=n+m+1}^{L-1}\left({\lambda }_i\right)\right\};F\le n\le L-1$$

(14)

where δ _F = μ(1 + δ)^FδP_0,0, and for p > q, we take

$${\displaystyle \prod }_{i=p}^q{\lambda }_i=1;p>q.$$

(15)

In Equation 6, we put n = F, F − 1, F − 2,…, 1 and get

$$P_{F-1,1}=\frac{{\delta }_F}{{{\displaystyle \prod }}_{i=F-1}^{L-1}{\lambda }_i}\left[{\displaystyle \sum }_{m=0}^{L-F}\left\{{\mu }^m{\displaystyle \prod }_{i=m+F}^{L-1}\left({\lambda }_i\right)\right\}\right]-\frac{\delta {\delta }_F}{{\lambda }_{F-1}\left(1+\delta \right)}$$

(15a)

$$\begin{array}{ll}{P}_{F-2,1}=& \frac{{\delta }_F}{{{\displaystyle \prod }}_{i=F-2}^{L-1}{\lambda }_i}\left[{\displaystyle \sum }_{m=0}^{L-\left(F-1\right)}\left\{{\mu }^m{\displaystyle \prod }_{i=m+F-1}^{L-1}\left({\lambda }_i\right)\right\}\right]\\ -\frac{\left({\lambda }_{F-1}+\mu \right)\delta {\delta }_F}{{\lambda }_{F-2}{\lambda }_{F-1}\left(1+\delta \right)}-\frac{\delta {\delta }_F}{{\lambda }_{F-2}{\left(1+\delta \right)}^2}\end{array}$$

(15b)

$$\begin{array}{ll}{P}_{F-3,1}=& \frac{{\delta }_F}{{{\displaystyle \prod }}_{i=F-3}^{L-1}{\lambda }_i}\left[{\displaystyle \sum }_{m=0}^{L-\left(F-2\right)}\left\{{\mu }^m{\displaystyle \prod }_{i=m+F-2}^{L-1}\left({\lambda }_i\right)\right\}\right]\\ -\frac{\left({\lambda }_{F-2}{\lambda }_{F-1}+\mu {\lambda }_{F-1}+{\mu }^2\right)\delta {\delta }_F}{{\lambda }_{F-3}{\lambda }_{F-2}{\lambda }_{F-1}\left(1+\delta \right)}\\ -\frac{\left({\lambda }_{F-2}+\mu \right)\delta {\delta }_F}{{\lambda }_{F-3}{\lambda }_{F-2}{\left(1+\delta \right)}^2}-\frac{\delta {\delta }_F}{{\lambda }_{F-3}{\left(1+\delta \right)}^3}\end{array}$$

(15c)

........ ......... .......... ............ ............ ..........

........ ......... ......... ............ ............ ..........

$$\begin{array}{ll}{P}_{0,1}=& \frac{{\delta }_F}{{{\displaystyle \prod }}_{i=1}^{L-1}{\lambda }_i}\left[{\displaystyle \sum }_{m=0}^{L-2}\left\{{\mu }^m{\displaystyle \prod }_{i=m+2}^{L-1}\left({\lambda }_i\right)\right\}\right]\\ -\frac{\delta {\delta }_F}{\left(1+\delta \right){{\displaystyle \prod }}_{i=1}^{F-1}{\lambda }_i}{\displaystyle \sum }_{m=0}^{F-2}\left\{{\mu }^m{\displaystyle \prod }_{i=m+2}^{L-1}\left({\lambda }_i\right)\right\}\\ -\dots \frac{\delta {\delta }_F}{{\left(1+\delta \right)}^{F-2}{{\displaystyle \prod }}_{i=1}^2{\lambda }_i}{\displaystyle \sum }_{m=0}^1\left\{{\mu }^m{\displaystyle \prod }_{i=m+2}^2\left({\lambda }_i\right)\right\}\\ -\frac{\delta {\delta }_F}{{\lambda }_1{\left(1+\delta \right)}^{F-1}}.\end{array}$$

(15d)

Now, in general, we obtain

$$\begin{array}{ll}{P}_{n,1}=& \frac{{\delta }_F}{{{\displaystyle \prod }}_{i=n}^{L-1}{\lambda }_i}\left[{\displaystyle \sum }_{m=0}^{L-n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=n+m+1}^{L-1}\left({\lambda }_i\right)\right\}\right]\\ -\delta {\delta }_F{\displaystyle \sum }_{k=1}^{F-n}\left[\frac{{{\displaystyle \sum }}_{m=0}^{F-n-k}\left\{{\mu }^m{{\displaystyle \prod }}_{i=n+m+1}^{F-k}\left({\lambda }_i\right)\right\}}{{\left(1+\delta \right)}^k{{\displaystyle \prod }}_{i=n}^{F-k}\left({\lambda }_i\right)}\right]\\ ;0\le n\le F-1.\end{array}$$

(16)

Now, we substitute the values of P_n,j, 1 ≤ n ≤ L and j = 0, 1, from Equations 10, 11, 14, and 16 in the normalizing Equation 9 and obtain the value for P_0,0 as

$$\begin{array}{ll}{P}_{0,0}^{-1}=& {\left(1+\delta \right)}^F\left\{1+\delta \left(L-F\right)\right\}\\ +\mathit{\mu \delta }{\left(1+\delta \right)}^F{\displaystyle \sum }_{n=0}^{L-1}\left[\frac{1}{{{\displaystyle \prod }}_{i=n}^{L-1}{\lambda }_i}{\displaystyle \sum }_{m=0}^{L-n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=n+m+1}^{L-1}\left({\lambda }_i\right)\right\}\right]\\ -\mu {\delta }^2{\left(1+\delta \right)}^F{\displaystyle \sum }_{n=0}^{F-1}\left[{\displaystyle \sum }_{k=1}^{F-n}\left\{\frac{{{\displaystyle \sum }}_{m=0}^{F-n-k}\left({\mu }^m{{\displaystyle \prod }}_{i=n+m+1}^{F-k}{\lambda }_i\right)}{{\left(1+\delta \right)}^k{{\displaystyle \prod }}_{i=n}^{F-k}{\lambda }_i}\right\}\right].\end{array}$$

(17)

N-policy model

The governing equations

Now, we construct the steady-state difference equations for the N-policy model using the appropriate birth-death rates (see Figure 2). For different system states, we equate the outflows to the inflows and get the balance equations in a similar manner as obtained for the F-policy model.

• 1. For j = 0: when the server is idle in the system.

The steady-state equation for state (0, 0), i.e., when no failed unit is present in the system, is obtained using the outflow from state (0, 0) that equals the inflow from state (1, 1) to (0, 0) as

$$\mu Q_{1,1}={\lambda }_0{Q}_{0,0}.$$

(18)

Further, for 1 ≤ n ≤ N − 1, we obtain

$${\lambda }_n{Q}_{n,0}={\lambda }_{n-1}{Q}_{n-1,0};1\le n\le N-1.$$

(19)

Similarly, for other states, we get

$$\left({\lambda }_n+\gamma \right)Q_{n,0}={\lambda }_{n-1}{Q}_{n-1,0};N\le n\le L-1$$

(20)

$$\gamma Q_{L,0}={\lambda }_{L-1}{Q}_{L-1,0}.$$

(21)

• 2. For j = 1: when the server is busy in the system.

Applying the outflow from state (n, 1) that equals the inflow from different states to state (n, 1), we get

$$\left({\lambda }_1+\mu \right)Q_{1,1}=\mu Q_{2,1};N\ne 1$$

(22)

$$\left({\lambda }_n+\mu \right)Q_{n,1}={\lambda }_{n-1}{Q}_{n-1,1}+\mu Q_{n+1,1};2\le n\le N-1$$

(23)

$$\begin{array}{ll}\left({\lambda }_n+\mu \right)Q_{n,1}=& {\lambda }_{n-1}{Q}_{n-1,1}+\mu Q_{n+1,1}\\ +\gamma Q_{n,0};N\le n\le L-1\end{array}$$

(24)

$$\mu Q_{L,1}={\lambda }_{L-1}{Q}_{L-1,1}+\gamma Q_{L,0}.$$

(25)

The normalization condition is given by

$$Q_{0,0}+{\displaystyle \sum }_{j=0}^1{\displaystyle \sum }_{n=1}^L{Q}_{n,j}=1.$$

(26)

Figure 2

State transition rate diagram for the N -policy model.

Queue size distribution for the N-policy model

We use the recursive method to evaluate the steady-state probabilities for the N-policy model from Equations 18 to 26. By solving the steady-state Equation 19 recursively, we obtain

$$Q_{n,0}=\frac{{\lambda }_0}{{\lambda }_n}{Q}_{0,0};1\le n\le N-1.$$

(27)

Now, in Equation 20, we put n = N, N + 1, N + 2,…, L − 1 and get

$$Q_{n,0}=\frac{{\lambda }_0{Q}_{0,0}}{{\lambda }_n}{\displaystyle \prod }_{i=N}^n{\theta }_i;N\le n\le L-1$$

(28)

$$\mathrm{where}{\theta }_i=\frac{{\lambda }_i}{{\lambda }_i+\gamma }.$$

Equation 21 yields

$$Q_{L,0}=\frac{{\lambda }_{L-1}}{\gamma }{Q}_{L-1,0}=\frac{{\theta }_0{P}_{0,0}}{1-{\theta }_0}{\displaystyle \prod }_{i=N}^{L-1}{\theta }_i.$$

(29)

We find Q_1,1 from Equation 18 as

$$Q_{1,1}=\frac{{\lambda }_0}{\mu }{Q}_{0,0}.$$

(30)

From Equation 22, we get

$$Q_{2,1}=\frac{\left({\lambda }_1+\mu \right)}{{\mu }^2}{\lambda }_0{Q}_{0,0}.$$

(31)

In Equation 23, substituting n = 2, 3,…, N − 1 and using Equations 30 and 31, we obtain the steady-state probabilities as

$$Q_{n,1}=\frac{{\lambda }_0{Q}_{0,0}}{{\mu }^n}\left[{\displaystyle \sum }_{m=0}^{n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=m+1}^{n-1}\left({\lambda }_i\right)\right\}\right];1\le n\le N.$$

(32)

Further, we find the values of Q_{N + 1,1}, Q_{N + 2,1}, Q_{N + 3,1},…, Q_L,1 by putting n = N, N + 1, N + 2, N + 3,…, L − 1 in Equation 24 as

$$Q_{N+1,1}=\frac{{\lambda }_0{Q}_{0,0}}{{\mu }^{N+1}}\left[{\displaystyle \sum }_{m=0}^N\left\{{\mu }^m{\displaystyle \prod }_{i=m+1}^N\left({\lambda }_i\right)\right\}\right]-\frac{{\lambda }_0{Q}_{0,0}}{\mu }\left(1-{\theta }_N\right)$$

(33a)

$$\begin{array}{ll}{Q}_{N+2,1}=& \frac{{\lambda }_0{Q}_{0,0}}{{\mu }^{N+2}}\left[{\displaystyle \sum }_{m=0}^{N+1}\left\{{\mu }^m{\displaystyle \prod }_{i=m+1}^{N+1}\left({\lambda }_i\right)\right\}\right]\\ -\frac{{\lambda }_0{Q}_{0,0}}{{\mu }^2}\left\{{\lambda }_{N+1}\left(1-{\theta }_N\right)+\mu \left(1-{\theta }_N{\theta }_{N+1}\right)\right\}\end{array}$$

(33b)

$$\begin{array}{ll}{Q}_{N+3,1}=& \frac{{\lambda }_0{Q}_{0,0}}{{\mu }^{N+3}}\left[{\displaystyle \sum }_{m=0}^{N+2}\left\{{\mu }^m{\displaystyle \prod }_{i=m+1}^{N+2}\left({\lambda }_i\right)\right\}\right]\\ -\frac{{\lambda }_0{Q}_{0,0}}{{\mu }^3}\left\{\begin{array}{c}{\lambda }_{N+2}{\lambda }_{N+1}\left(1-{\theta }_N\right)+\mu {\lambda }_{N+2}\left(1-{\theta }_N{\theta }_{N+1}\right)\\ +{\mu }^2\left(1-{\theta }_N{\theta }_{N+1}{\theta }_{N+2}\right)\end{array}\right\}\end{array}$$

(33c)

$$\begin{array}{ll}{Q}_{N+4,1}=& \frac{{\lambda }_0{Q}_{0,0}}{{\mu }^{N+4}}\left[{\displaystyle \sum }_{m=0}^{N+3}\left\{{\mu }^m{\displaystyle \prod }_{i=m+1}^{N+3}\left({\lambda }_i\right)\right\}\right]\\ -\frac{{\lambda }_0{Q}_{0,0}}{{\mu }^4}\left\{\begin{array}{l}{\lambda }_{N+3}{\lambda }_{N+2}{\lambda }_{N+1}\left(1-{\theta }_N\right)\\ +\mu {\lambda }_{N+3}{\lambda }_{N+2}\left(1-{\theta }_N{\theta }_{N+1}\right)\\ +{\mu }^2{\lambda }_{N+3}\left(1-{\theta }_N{\theta }_{N+1}{\theta }_{N+2}\right)\\ +{\mu }^3\left(1-{\theta }_N{\theta }_{N+1}{\theta }_{N+2}{\theta }_{N+3}\right)\end{array}\right\}\end{array}$$

(33d)

........ ......... .......... ............ ............ ..........

........ ......... ......... ............ ............ ..........

$$\begin{array}{l}{Q}_{L,1}=\frac{{\lambda }_0{Q}_{0,0}}{{\mu }^L}\left[{\displaystyle \sum }_{m=0}^{L-1}\left\{{\mu }^m{\displaystyle \prod }_{i=m+1}^{L-1}\left({\lambda }_i\right)\right\}\right]\\ -\frac{{\lambda }_0{Q}_{0,0}}{{\mu }^{L-N}}\left\{\begin{array}{l}{\lambda }_{L-1}\dots {\lambda }_{N+2}{\lambda }_{N+1}\left(1-{\theta }_N\right)\\ +\mu {\lambda }_{L-1}\dots {\lambda }_{N+2}\left(1-{\theta }_N{\theta }_{N+1}\right)\\ +\dots +{\mu }^{L-N-1}\left(1-{\theta }_N{\theta }_{N+1}{\theta }_{N+2}\dots {\theta }_{L-1}\right)\end{array}\right\}.\end{array}$$

(33e)

In general, we get

$$Q_{n,1}=\frac{{\lambda }_0{Q}_{0,0}}{{\mu }^n}\left[\left[{\displaystyle \sum }_{m=0}^{n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=m+1}^{n-1}\left({\lambda }_i\right)\right\}\right]-{\mu }^N\left[{\displaystyle \sum }_{m=N}^{n-1}\left\{{\mu }^{m-N}\left(1-{\displaystyle \prod }_{i=N}^m\left({\theta }_i\right)\right){\displaystyle \prod }_{i=m+1}^{n-1}\left({\lambda }_i\right)\right\}\right]\right];N+1\le n\le L.$$

(34)

Now, we substitute the values of Q_n,j, 1 ≤ n ≤ L and j = 0, 1, use Q_0,1 = 0 in Equation 26, and find the value of Q_0,0 as follows:

$$\begin{array}{ll}{Q}_{0,0}^{-1}=& {\displaystyle \sum }_{n=0}^{N-1}\left(1+\frac{{\lambda }_0}{{\lambda }_n}\right)+{\displaystyle \sum }_{n=N}^{L-1}\left(\frac{{\lambda }_0}{{\lambda }_n}{\displaystyle \prod }_{i=N}^n{\theta }_i\right)+\frac{{\theta }_0}{1-{\theta }_0}{\displaystyle \prod }_{i=N}^{L-1}{\theta }_i\\ +{\displaystyle \sum }_{n=1}^L\left[\frac{{\lambda }_0}{{\mu }^n}{\displaystyle \sum }_{m=0}^{n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=m+1}^{n-1}\left({\lambda }_i\right)\right\}\right]\\ -{\displaystyle \sum }_{n=N+1}^L\left[\frac{{\lambda }_0}{{\mu }^{n-N}}\left[{\displaystyle \sum }_{m=N}^{n-1}\left\{{\mu }^{m-N}\left(1-{\displaystyle \prod }_{i=N}^m\left({\theta }_i\right)\right){\displaystyle \prod }_{i=m+1}^{n-1}\left({\lambda }_i\right)\right\}\right]\right].\end{array}$$

(35)

The steady-state probabilities evaluated by the recursive method can be used to derive various performance measures for both F- policy and N-policy systems.

Performance measures

We establish some important performance measures for the F-policy and N-policy models by using the steady-state probabilities obtained for different system states. In order to examine the system’s behavior, the quantitative assessment of the performance measures is the main objective and key component of the performance modeling of any queueing system including the machine repair system. Here we are interested to derive system characteristics such as the expected number of failed units, probability that the server is busy or idle in the system, probability of blocking of the system, etc. Using the steady-state probabilities, we derive various performance measures for both models as given below.

F-policy model

In this subsection, we find the expressions for some performance measures in terms of steady-state probabilities such that results can be useful to predict the behavior of the machine repair system operating under the F-policy:

• 1. The expected number of failed units in the system is given by

  $$\begin{array}{l}E\left(N_F\right)={\displaystyle \sum }_{n=1}^{L}n{P}_{n,0}+{\displaystyle \sum }_{n=1}^{L-1}n{P}_{n,1}\\ =\left[\frac{\left\{1-{\left(1+\delta \right)}^F\left(1-\mathit{F\delta }\right)\right\}}{\delta }+\frac{\left(L-F\right)\left(L+F+1\right)}{2}\delta {\left(1+\delta \right)}^F\right.\\ +\mathit{\mu \delta }{\left(1+\delta \right)}^F\left[{\displaystyle \sum }_{n=1}^{L-1}\left[\frac{n}{{{\displaystyle \prod }}_{i=n}^{L-1}{\lambda }_i}{\displaystyle \sum }_{m=0}^{L-n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=n+m+1}^{L-1}\left({\lambda }_i\right)\right\}\right]\right.\\ \left.\left.-\delta {\displaystyle \sum }_{n=1}^{F-1}\left[n{\displaystyle \sum }_{k=1}^{F-n}\left\{\frac{{{\displaystyle \sum }}_{m=0}^{F-n-k}\left({\mu }^m{{\displaystyle \prod }}_{i=n+m+1}^{F-k}{\lambda }_i\right)}{{\left(1+\delta \right)}^k{{\displaystyle \prod }}_{i=n}^{F-k}{\lambda }_i}\right\}\right]\right]\right]P_{0,0}.\end{array}$$

  (36)

• 2. The probability that the server is idle is obtained as

  $$\begin{array}{l}P\left(I_F\right)={\displaystyle \sum }_{j=0}^1{P}_{0,j}=\left[\left[\frac{1}{{{\displaystyle \prod }}_{i=0}^{L-1}{\lambda }_i}{\displaystyle \sum }_{m=0}^{L-1}\left\{{\mu }^m{\displaystyle \prod }_{i=m+1}^{L-1}\left({\lambda }_i\right)\right\}-\delta {\displaystyle \sum }_{k=1}^F\left[\frac{{{\displaystyle \sum }}_{m=0}^{F-k}\left\{{\mu }^m{{\displaystyle \prod }}_{i=m+1}^{F-k}\left({\lambda }_i\right)\right\}}{{\left(1+\delta \right)}^k{{\displaystyle \prod }}_{i=0}^{F-k}\left({\lambda }_i\right)}\right]\right]\mathit{\mu \delta }{\left(1+\delta \right)}^F+1\right]P_{0,0}.\end{array}$$

  (37)

• 3. The probability that server is busy is obtained as

  $$\begin{array}{ll}P\left(B_F\right)& ={\displaystyle \sum }_{n=1}^L{P}_{n,0}+{\displaystyle \sum }_{n=1}^{L-1}{P}_{n,1}\\ =\left[\mathit{\mu \delta }{\left(1+\delta \right)}^F\left[{\displaystyle \sum }_{n=1}^{L-1}\right.\left[\frac{1}{{{\displaystyle \prod }}_{i=n}^{L-1}{\lambda }_i}{\displaystyle \sum }_{m=0}^{L-n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=n+m+1}^{L-1}\left({\lambda }_i\right)\right\}\right]\right.\\ \left.-\delta {\displaystyle \sum }_{n=1}^{F-1}\left[{\displaystyle \sum }_{k=1}^{F-n}\left\{\frac{{{\displaystyle \sum }}_{m=0}^{F-n-k}\left({\mu }^m{{\displaystyle \prod }}_{i=n+m+1}^{F-k}{\lambda }_i\right)}{{\left(1+\delta \right)}^k{{\displaystyle \prod }}_{i=n}^{F-k}{\lambda }_i}\right\}\right]\right]\\ \left.+\left[{\left(1+\delta \right)}^F\left\{1+\delta \left(L-F\right)\right\}-1\right]\right]P_{0,0}.\end{array}$$

  (38)

• 4. The probability that the server takes start-up time before starting the service to failed units is

  $$P\left({\mathrm{ST}}_F\right)={\displaystyle \sum }_{n=0}^F{P}_{n,0}={\left(1+\delta \right)}^F{P}_{0,0}$$

  (39)

• 5. The probability that the system is blocked (i.e., the failed unit is not allowed to join the queue) is

  $$P\left({\mathrm{SB}}_F\right)={\displaystyle \sum }_{n=0}^L{P}_{n,0}={\left(1+\delta \right)}^F\left[1+\delta \left(L-F\right)\right]P_{0,0}.$$

  (40)

• 6. The probability of the buildup state is obtained as

  $$P\left({\mathrm{BS}}_F\right)={\displaystyle \sum }_{n=F+1}^L{P}_{n,0}=\delta {\left(1+\delta \right)}^F\left(L-F\right)P_{0,0}.$$

  (41)

• 7. The expected number of operating units in the system is obtained for two cases as follows:

• (a) Case 1: when S < F

  $$\begin{array}{ll}E\left(O_F\right)=& M-\left[\frac{{\left(1+\delta \right)}^S}{\delta }\left[1-\left\{1-\delta \left(F-S\right)\right\}{\left(1+\delta \right)}^{F-S}\right]\right.\\ -\frac{\delta }{2}{\left(1+\delta \right)}^F\left(L-F-1\right)\left(L+F-2S\right)+\mathit{\mu \delta }{\left(1+\delta \right)}^F\left[{\displaystyle \sum }_{n=S+1}^{L-1}\left[\frac{\left(n-S\right)}{{{\displaystyle \prod }}_{i=n}^{L-1}{\lambda }_i}{\displaystyle \sum }_{m=0}^{L-n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=n+m+1}^{L-1}\left({\lambda }_i\right)\right\}\right]\right.\left.\left.-\delta {\displaystyle \sum }_{n=S+1}^{F-1}\left[\left(n-S\right){\displaystyle \sum }_{k=1}^{F-n}\left\{\frac{{{\displaystyle \sum }}_{m=0}^{F-n-k}\left({\mu }^m{{\displaystyle \prod }}_{i=n+m+1}^{F-k}{\lambda }_i\right)}{{\left(1+\delta \right)}^k{{\displaystyle \prod }}_{i=n}^{F-k}{\lambda }_i}\right\}\right]\right]\right]P_{0,0}\end{array}$$

  (42)

• (a) Case 2: when S ≥ F

  $$\begin{array}{l}E\left(O_F\right)=M\left[\frac{\delta }{2}\left\{{\left(1+\delta \right)}^F\left(L-S\right)\left(L-S+1\right)\right\}\right.\left.+\mathit{\mu \delta }{\left(1+\delta \right)}^F{\displaystyle \sum }_{n=S+1}^{L-1}\left[\frac{\left(n-S\right)}{{{\displaystyle \prod }}_{i=n}^{L-1}{\lambda }_i}{\displaystyle \sum }_{m=0}^{L-n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=n+m+1}^{L-1}\left({\lambda }_i\right)\right\}\right]\right]P_{0,0}\end{array}$$

  (43)

• 8. The expected number of warm standby units in the system is obtained as follows:

• (a) Case 1: when S < F

  $$\begin{array}{ll}E\left(S_F\right)=& \left[\left(1-S\right)+\frac{1}{\delta }\left(1+\delta \right)\left\{{\left(1+\delta \right)}^{S-2}-1\right\}\right.\\ +\mathit{\mu \delta }{\left(1+\delta \right)}^F\left[{\displaystyle \sum }_{n=1}^{S-1}\left[\frac{\left(S-n\right)}{{{\displaystyle \prod }}_{i=n}^{L-1}{\lambda }_i}{\displaystyle \sum }_{m=0}^{L-n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=n+m+1}^{L-1}\left({\lambda }_i\right)\right\}\right]\right.\\ \left.\left.-\delta {\displaystyle \sum }_{n=1}^{S-1}\left[\left(S-n\right){\displaystyle \sum }_{k=1}^{F-n}\left\{\frac{{{\displaystyle \sum }}_{m=0}^{F-n-k}\left({\mu }^m{{\displaystyle \prod }}_{i=n+m+1}^{F-k}{\lambda }_i\right)}{{\left(1+\delta \right)}^k{{\displaystyle \prod }}_{i=n}^{F-k}{\lambda }_i}\right\}\right]\right]\right]P_{0,0}\end{array}$$

  (44)

• (a) Case 2: when S ≥ F

  $$\begin{array}{ll}E\left(S_F\right)=& \left[\left(1-S\right)+\frac{1}{\delta }\left(1+\delta \right)\left\{{\left(1+\delta \right)}^{F-2}-1\right\}\right.\\ +\frac{1}{2}\left(S-F\right){\left(1+\delta \right)}^F\left\{\delta \left(S-F-1\right)+2\right\}\\ +\mathit{\mu \delta }{\left(1+\delta \right)}^F\left[{\displaystyle \sum }_{n=1}^{S-1}\left[\frac{\left(S-n\right)}{{{\displaystyle \sum }}_{i=n}^{L-1}{\lambda }_i}{\displaystyle \sum }_{m=0}^{L-n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=n+m+1}^{L-1}\left({\lambda }_i\right)\right\}\right]\right.\\ \left.\left.-\delta {\displaystyle \sum }_{n=1}^{F-1}\left[\left(S-n\right){\displaystyle \sum }_{k=1}^{F-n}\left\{\frac{{{\displaystyle \sum }}_{m=0}^{F-n-k}\left({\mu }^m{{\displaystyle \prod }}_{i=n+m+1}^{F-k}{\lambda }_i\right)}{{\left(1+\delta \right)}^k{{\displaystyle \prod }}_{i=n}^{F-k}{\lambda }_i}\right\}\right]\right]\right]P_{0,0}\end{array}$$

  (45)

The value of P_0,0 is given by Equation 17.

N-policy model

In the ‘F-policy model’ section, we have determined the steady-state probabilities for different states of the machine interference system under the N-policy. Now, we evaluate some key performance measures as follows:

• 1. The expected number of failed units in the system is given by

  $$E\left(N_N\right)={\displaystyle \sum }_{j=0}^1{\displaystyle \sum }_{n=1}^{L}n{Q}_{n,j}=Q_{0,0}{\displaystyle \sum }_{j=0}^1{\displaystyle \sum }_{n=1}^{L}n{F}_{n,j}$$
  $$\mathrm{where}{Q}_{n,j}=Q_{0,0}{F}_{n,j}\mathrm{and}$$
  $$\begin{array}{ll}{F}_{n,j}=& \left[{\displaystyle \sum }_{n=1}^{N-1}n\left(\frac{{\lambda }_0}{{\lambda }_n}\right)+{\displaystyle \sum }_{n=N}^{L-1}n\left(\frac{{\lambda }_0}{{\lambda }_n}{\displaystyle \prod }_{i=N}^n{\theta }_i\right)+\frac{L{\theta }_0}{1-{\theta }_0}{\displaystyle \prod }_{i=N}^{L-1}{\theta }_i\right]\\ +{\displaystyle \sum }_{n=1}^L\left[\frac{n{\lambda }_0}{{\mu }^n}{\displaystyle \sum }_{m=0}^{n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=m+1}^{n-1}\left({\lambda }_i\right)\right\}\right]\\ -{\displaystyle \sum }_{n=N+1}^L\left[\frac{n{\lambda }_0}{{\mu }^{n-N}}\left[{\displaystyle \sum }_{m=N}^{n-1}\left\{{\mu }^{m-N}\left(1-{\displaystyle \prod }_{i=N}^m\left({\theta }_i\right)\right){\displaystyle \prod }_{i=m+1}^{n-1}\left({\lambda }_i\right)\right\}\right]\right].\end{array}$$

  (46)

• 2. The probability that the server is busy is obtained as

  $$\begin{array}{ll}P\left(B_N\right)=& {\displaystyle \sum }_{n=1}^L{Q}_{n,1}=\left[{\displaystyle \sum }_{n=1}^L\left[\frac{{\lambda }_0}{{\mu }^n}{\displaystyle \sum }_{m=0}^{n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=m+1}^{n-1}\left({\lambda }_i\right)\right\}\right]\right.\\ \left.-{\displaystyle \sum }_{n=N+1}^L\left[\frac{{\lambda }_0}{{\mu }^{n-N}}\left[{\displaystyle \sum }_{m=N}^{n-1}\left\{{\mu }^{m-N}\left(1-{\displaystyle \prod }_{i=N}^m\left({\theta }_i\right)\right){\displaystyle \prod }_{i=m+1}^{n-1}\left({\lambda }_i\right)\right\}\right]\right]\right]Q_{0,0}.\end{array}$$

  (47)

• 3. The probability that the server is idle is obtained as

  $$\begin{array}{l}P\left(I_N\right)={\displaystyle \sum }_{n=0}^L{Q}_{n,0}\\ =\left[{\displaystyle \sum }_{n=0}^{N-1}\left(1+\frac{{\lambda }_0}{{\lambda }_n}\right)+{\displaystyle \sum }_{n=N}^{L-1}\left(\frac{{\lambda }_0}{{\lambda }_n}{\displaystyle \prod }_{i=N}^n{\theta }_i\right)+\frac{{\theta }_0}{1-{\theta }_0}{\displaystyle \prod }_{i=N}^{L-1}{\theta }_i\right]Q_{0,0}.\end{array}$$

  (48)

• 4. The probability that the server takes start-up time before starting the repair of the failed units is

  $$P\left({\mathrm{ST}}_N\right)={\displaystyle \sum }_{n=N}^L{Q}_{n,0}=\left[{\displaystyle \sum }_{n=N}^{L-1}\left(\frac{{\lambda }_0}{{\lambda }_n}{\displaystyle \prod }_{i=N}^n{\theta }_i\right)+\frac{{\theta }_0}{1-{\theta }_0}{\displaystyle \prod }_{i=N}^{L-1}{\theta }_i\right]Q_{0,0}$$

  (49)

• 5. The probability of buildup state is

  $$P\left({\mathrm{BS}}_N\right)={\displaystyle \sum }_{n=1}^{N-1}{Q}_{n,0}={\lambda }_0{Q}_{0,0}{\displaystyle \sum }_{n=1}^{N-1}\left(\frac{1}{{\lambda }_n}\right)$$

  (50)

• 6. The expected number of operating units in the system is obtained for two cases:

• (a) Case 1: when S < N

  $$\begin{array}{ll}P\left(O_N\right)=& \left[{\displaystyle \sum }_{n=S+1}^{N-1}\left(n-S\right)\left(\frac{{\lambda }_0}{{\lambda }_n}\right)+{\displaystyle \sum }_{n=N}^{L-1}\left(n-S\right)\left(\frac{{\lambda }_0}{{\lambda }_n}{\displaystyle \prod }_{i=N}^n{\theta }_i\right)+\frac{\left(L-S\right){\theta }_0}{1-{\theta }_0}{\displaystyle \prod }_{i=N}^{L-1}{\theta }_i\right.+{\displaystyle \sum }_{n=1}^L\left[\frac{\left(n-S\right){\lambda }_0}{{\mu }^n}{\displaystyle \sum }_{m=0}^{n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=m+1}^{n-1}\left({\lambda }_i\right)\right\}\right]\\ \left.-{\displaystyle \sum }_{n=N+1}^L\left[\frac{\left(n-S\right){\lambda }_0}{{\mu }^{n-N}}\left[{\displaystyle \sum }_{m=N}^{n-1}\left\{{\mu }^{m-N}\left(1-{\displaystyle \prod }_{i=N}^m\left({\theta }_i\right)\right){\displaystyle \prod }_{i=m+1}^{n-1}\left({\lambda }_i\right)\right\}\right]\right]\right]Q_{0,0}\end{array}$$

  (51)

• (a) Case 2: when S ≥ N

  $$\begin{array}{ll}P\left(O_N\right)=& \left[{\displaystyle \sum }_{n=S+1}^{L-1}\left(n-S\right)\left(\frac{{\lambda }_0}{{\lambda }_n}{\displaystyle \prod }_{i=N}^n{\theta }_i\right)+\frac{\left(L-S\right){\theta }_0}{1-{\theta }_0}{\displaystyle \prod }_{i=N}^{L-1}{\theta }_i\right.\\ +{\displaystyle \sum }_{n=S+1}^L\left[\frac{\left(n-S\right){\lambda }_0}{{\mu }^n}{\displaystyle \sum }_{m=0}^{n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=m+1}^{n-1}\left({\lambda }_i\right)\right\}\right]\\ \left.-{\displaystyle \sum }_{n=S+1}^L\left[\frac{\left(n-S\right){\lambda }_0}{{\mu }^{n-N}}\left[{\displaystyle \sum }_{m=N}^{n-1}\left\{{\mu }^{m-N}\left(1-{\displaystyle \prod }_{i=N}^m\left({\theta }_i\right)\right){\displaystyle \prod }_{i=m+1}^{n-1}\left({\lambda }_i\right)\right\}\right]\right]\right]Q_{0,0}\end{array}$$

  (52)

• 7. The expected number of warm standby units in the system is determined for two cases as follows:

• (a) Case 1: for S < N

  $$\begin{array}{ll}P\left(S_N\right)=& \left[{\displaystyle \sum }_{n=1}^{S-1}\left(S-n\right)\left(\frac{{\lambda }_0}{{\lambda }_n}\right)\right.\\ \left.+{\displaystyle \sum }_{n=1}^{S-1}\left[\frac{\left(S-n\right){\lambda }_0}{{\mu }^n}{\displaystyle \sum }_{m=0}^{n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=m+1}^{n-1}\left({\lambda }_i\right)\right\}\right]\right]Q_{0,0}\end{array}$$

  (53)

• (a) Case 2: for S ≥ N

  $$\begin{array}{l}P\left(S_N\right)=\left[{\displaystyle \sum }_{n=1}^{N-1}\left(S-n\right)\left(\frac{{\lambda }_0}{{\lambda }_n}\right)+{\displaystyle \sum }_{n=N}^{S-1}\left(S-n\right)\left(\frac{{\lambda }_0}{{\lambda }_n}{\displaystyle \prod }_{i=N}^n{\theta }_i\right)\right.\\ +{\displaystyle \sum }_{n=1}^{S-1}\left[\frac{\left(S-n\right){\lambda }_0}{{\mu }^n}{\displaystyle \sum }_{m=0}^{n-1}\left\{{\mu }^m{\displaystyle \prod }_{i=m+1}^{n-1}\left({\lambda }_i\right)\right\}\right]\\ \left.-{\displaystyle \sum }_{n=N+1}^{S-1}\left[\frac{\left(S-n\right){\lambda }_0}{{\mu }^{n-N}}\left[{\displaystyle \sum }_{m=N}^{n-1}\left\{{\mu }^{m-N}\left(1-{\displaystyle \prod }_{i=N}^m\left({\theta }_i\right)\right){\displaystyle \prod }_{i=m+1}^{n-1}\left({\lambda }_i\right)\right\}\right]\right]\right]Q_{0,0}\end{array}$$

  (54)

The value of Q_0,0 is given by Equation 35.

Conclusion

In this paper, we have explored the concepts of the F-policy and N-policy for multi-component machining systems with warm standbys. The steady-state probability distributions established for both the F-policy and N-policy are further used to establish some performance measures such as the expected number of failed machines in the system, probability that the server is busy or idle in the system, throughput, etc. The explicit expressions of various performance measures are provided which may be further used for the improvement and performance evaluation of many real-time machining systems. The provision of warm types of standbys is a general assumption as in a special case when the failure rate is zero or the same as that of operating units, and it facilitates results for the cold standby case. The study of control policy-based models in the present investigation will be helpful in the quantitative assessment of the system’s reliability and other mean characteristics of many embedded systems such as computer networks, manufacturing systems, transportation systems, etc. In the future, we can further extend our study by considering the mixed type of standbys facility and bulk failure to make it more versatile.