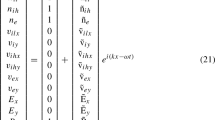Soliton reflection in a magnetized inhomogeneous warm plasma: effect of ionization

Abstract

The reflection of nonlinear solitary waves is studied in a plasma under the effect of an external magnetic field and constant ionization along with finite ion temperature. To investigate the reflection of solitary waves, relevant modified Korteweg–deVries equations for the right and left going waves are derived, and coupled at the point of reflection for obtaining the expression of reflection coefficient. The solitary waves are found to shift after their reflection. Variation of reflection coefficient and shift are studied for different plasma parameters like ion temperature, ionization rate and wave propagation angle or the obliqueness of magnetic field.

Background

A solitary wave is defined as a quantum of energy or quasiparticles that can propagate as a traveling wave in nonlinear systems and is neither preceded nor followed by another such disturbance. A solitary wave is called a soliton if it retains its shape after collision with another solitary wave in the medium. The well-known Korteweg–deVries (KdV) equation describes the physics of various weakly nonlinear dispersive systems and propagation of solitary waves in shallow water [1] and the ion-acoustic waves in plasmas [2]. Most striking feature of the solitons is that they are reflected from the density gradient. In weakly varying medium, these reflected waves are expected to be small. A partial reflection of a solitary wave at the sharp density gradient produced by a negatively biased grid was observed experimentally by Dahiya et al. [3]. Kuehl [4] has investigated theoretically the reflection of ion-acoustic soliton and found that the amplitude of the reflected soliton is much smaller than the amplitude of the incident soliton. Kuehl and Imen [5] have studied the propagation of an ion-acoustic soliton in an inhomogeneous plasma taking into consideration the full set of fluid equations. Nejoh [6] has studied the effect of ion temperature on the soliton propagation characteristics in a collisionless relativistic plasma. Singh and Dahiya [7] have extended this theory for inhomogeneous plasma by obtaining the KdV equation for one-dimensional soliton using reductive perturbation technique (RPT) along with appropriate coordinate transformation. The oblique propagation of solitons in an inhomogeneous plasma has been investigated by Aziz and Stroth [8] in which the effects of electron and ion temperatures along with their concentrations on soliton width and phase velocity were studied. Several experimental studies on solitons and their reflection in different types of plasmas including the ones having negative ions have been conducted by Nakamura group [9–12], Nishida group [13–19] and Lonngren group [20–25]. In addition to the above work, researchers have studied the propagation of solitary waves under the effect of magnetic field [26–30], where the modified characteristics of solitary waves were realized. Reflection of soliton was observed with weak density gradient by Malik et al. [31]. Kumar et al. [32] have studied the soliton reflection in a plasma with trapped electrons and dust grains. On the other hand, the propagation of ion-acoustic waves have been studied in two-electron or -ion temperature plasmas [33–36]. In such plasmas, two groups of the electrons at different temperatures are studied, in which the electron velocity distribution is represented by the superposition of two Maxwellians for the isothermal electrons and by the superposition of two vortex like distributions for the nonisothermal electrons [37]. Linear and nonlinear excitation of ion-acoustic solitary waves in a magnetized plasma containing two temperature electrons and cold ions are studied [38] and the effect of oblique orientation of magnetic field was also observed [39].

This can be seen that the ionization, which takes place in the plasma and modifies the plasma density, has been largely neglected by the researchers. However, we have recently considered this situation and investigated the soliton’s behavior in the plasma [40]. The ionization creates a density gradient in the plasma. Since the solitons are reflected from the density gradient, it becomes quite desirable to examine the soliton reflection in the plasma under the effect of ionization. Since the ions carry finite temperature in the plasmas, the temperature should also be taken into consideration while studying these nonlinear waves and their reflection. Hence, this article is devoted to the problem of soliton reflection in a warm plasma, where ions are magnetized and ionization takes place.

The basic fluid equations are written in the normalized form by considering $n_{\text{p}}$ and $n_{\text{e}}$ as the concentrations of positive ions and the electrons, respectively, $\mathit{\varphi }$ as the electric potential, $Z_{\text{p}}\text{e}$ as the amount of charge associated with a single positive ion, $\overrightarrow{v}$ as the velocity of ion fluid, ${\mathit{\gamma }}_{\text{p}}$ as the corresponding ionization rate, $m_{\text{p}}$ as the ion mass, $T_{\text{e}}$ as the electron temperature in eV, and $\overrightarrow{B}(\equiv B_0\widehat{z})$ as the magnetic field. Hence, the normalized basic fluid equations are given by:

$$\frac{\mathit{\partial }{n}_{\text{p}}}{\mathit{\partial }t}+\overrightarrow{\mathrm{\nabla }}·(n_{\text{p}}\overrightarrow{v})-{\mathit{\gamma }}_{\text{p}}=0,$$

(1)

$$n_{\text{p}}\frac{\mathit{\partial }\overrightarrow{v}}{\mathit{\partial }t}+n_{\text{p}}(\overrightarrow{v}·\overrightarrow{\mathrm{\nabla }})\overrightarrow{v}+n_{\text{p}}{Z}_{\text{p}}\overrightarrow{\mathrm{\nabla }}\mathit{\varphi }-n_{\text{p}}{Z}_{\text{p}}{\left(\frac{{\mathit{\epsilon }}_0}{n_{\text{p}0}{Z}_{\text{p}}^2{m}_{\text{p}}}\right)}^{1/2}{B}_0\left(\overrightarrow{v}\times \widehat{z}\right)+2{\mathit{\sigma }}_{\text{p}}\frac{\mathit{\partial }{n}_{\text{p}}}{\mathit{\partial }x}+{\mathit{\gamma }}_{\text{p}}\overrightarrow{v}=0,$$

(2)

$$n_{\text{e}}-n_{\text{e}0}exp(\mathit{\varphi })=0,$$

(3)

$$Z_{\text{p}}^2\left(\frac{{\mathit{\partial }}^2\mathit{\varphi }}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^2\mathit{\varphi }}{\mathit{\partial }{z}^2}\right)-n_{\text{e}}+Z_{\text{p}}{n}_{\text{p}}=0.$$

(4)

In the above equations, the effect of ionization is considered. Because the ionization is an inelastic collisional phenomenon, the collisions should be taken into consideration to make a deep understanding of this plasma with regard to the excitation of nonlinear solitary waves and their reflection. However, for the sake of simplicity, we have neglected such effects rather the collisional impact enters into calculations through the last term of Eq. (2) in view of the constant rate of ionization under an equilibrium state.

To study the ion-acoustic wave propagation and its evolution as solitary wave in such a plasma, we employ appropriate stretched coordinates and the expansion of physical quantities. In the present case, the wave propagates at an angle θ with the direction of magnetic field and the plasma is inhomogeneous. In view of oblique wave propagation, we take $\widehat{k}·\overrightarrow{r}=(xsin\mathit{\theta }+zcos\mathit{\theta })$ that leads to the following stretched coordinates [41]

$$\mathit{\xi }={\mathit{\epsilon }}^{1/2}\left(\frac{\widehat{k}·\overrightarrow{r}}{{\mathit{\lambda }}_0}-t\right)={\mathit{\epsilon }}^{1/2}\left(\frac{xsin\mathit{\theta }+zcos\mathit{\theta }}{{\mathit{\lambda }}_0}-t\right),\mathit{\tau }={\mathit{\epsilon }}^{3/2}\left(\widehat{k}·\overrightarrow{r}\right)={\mathit{\epsilon }}^{3/2}\left(xsin\mathit{\theta }+zcos\mathit{\theta }\right).$$

Here ${\mathit{\lambda }}_0$ is the phase velocity of the wave and $\widehat{k}$ is the unit wave vector. In the said RPT, the expansion of densities, velocities and potential has to be done in view of the powers of $\mathit{\epsilon }$ in the stretched coordinates such that the effects of nonlinearity and dispersion finally balance each other. Since Lorentz force acts in the perpendicular direction of magnetic field, the variation/perturbation along the transverse directions (x- and y axes) should be different from the one along the direction of magnetic field (z axis). Hence, the expansion of physical quantities is made as follows.

$$f=f_0(x,z)+{\mathit{\epsilon }}^{3/2}{f}_1(x,z,t)+{\mathit{\epsilon }}^2{f}_2(x,z,t)+\cdots ,f\equiv v_x,v_y$$

(5)

$$d=d_0(x,z)+\mathit{\epsilon }{d}_1(x,z,t)+{\mathit{\epsilon }}^2{d}_2(x,z,t)+\cdots ,d\equiv n_{\text{p}},n_{\text{e}},\mathit{\varphi },v_z$$

(6)

$${\mathit{\gamma }}_{\text{p}}={\mathit{\epsilon }}^{3/2}{\mathit{\gamma }}_{\text{p}1}$$

(7)

For plasma to exist, the ionization of gas is a necessary mechanism. The term plasma density usually refers to the electron density, i.e., the number of free electrons per unit volume. The degree of ionization of a plasma is the proportion of atoms that have lost or gained electrons; this is controlled mostly by the temperature. Even a partially ionized gas can have the characteristics of a plasma, in which as little as 1 % of the particles are ionized. In the present case, we assume the ionization to take place at a constant rate. It means γ_p1 represents the rate of the ionization per unit volume. Owing to its constant magnitude, in the forthcoming sections, we take γ_p1 = γ_p for the sake of simplicity.

We obtain equations of zeroth, first and second orders in terms of the smallness parameter $\mathit{\epsilon }$ when we use Eqs. (5)–(7) in the basic fluid equations as in our previous work [40] from which we obtain the phase velocity relation as follows:

$${\mathit{\lambda }}_0=v_{x0}sin\mathit{\theta }+v_{z0}cos\mathit{\theta }\pm \sqrt{Z_{\text{p}}+2{\mathit{\sigma }}_{\text{p}}}cos\mathit{\theta }.$$

(8)

Corresponding to ± sign in Eq. (8), we obtain two types of phase velocity relations. The relation corresponding to plus sign yields the fast mode (phase velocity ${\mathit{\lambda }}_{\text{F}}$), whereas the relation with minus sign corresponds to the slow mode (phase velocity ${\mathit{\lambda }}_{\text{S}}$). For the propagation of these modes, their phase velocities should be positive. If we take ion charge number as unity and ion temperature is eliminated, then Eq. (8) becomes identical to the phase velocity relation we have obtained in our previous work [40] and also the one obtained by Singh and Malik [41] in the absence of negative ions in their plasma model. Since the phase velocity of the fast mode remains always positive, it is observed that this mode always propagates in the plasma. However, for the propagation of slow mode, the following condition on the wave propagation angle θ should be satisfied

$$\mathit{\theta }>{tan}^{-1}\left(\frac{\sqrt{Z_{\text{p}}+2{\mathit{\sigma }}_{\text{p}}}-v_{z0}}{v_{x0}}\right).$$

(9)

The above equation shows that there exists a minimum wave propagation angle (${\mathit{\theta }}_{\text{min}}$) below which the slow mode does not propagate in the plasma. This condition also reduces to the one obtained in Ref. [40] under the limiting condition. However, for the propagation of the fast mode, there is no such condition on the angle θ. This minimum angle ${\mathit{\theta }}_{\text{min}}$ attains larger values for the ions having charge number $Z_{\text{p}}>1$.

Modified KdV (mKdV) equation and its solution

Based on first- and second-order equations, we obtain the following mKdV equation along with the use of phase velocity relation (8)

$$\frac{\mathit{\partial }{v}_{\text{I}}}{\mathit{\partial }\mathit{\tau }}+\mathit{\alpha }{v}_{\text{I}}\frac{\mathit{\partial }{v}_{\text{I}}}{\mathit{\partial }\mathit{\xi }}+\mathit{\beta }\frac{{\mathit{\partial }}^3{v}_{\text{I}}}{\mathit{\partial }{\mathit{\xi }}^3}+\mathit{\gamma }{v}_{\text{I}}=0.$$

(10)

This equation is different from the usual KdV equation by two additional terms arising because of the density gradient and ionization in the plasma. The coefficients α, β, and γ are given by

$$\begin{array}{c}\mathit{\alpha }=\left(\frac{{\mathit{\lambda }}_0-v_{xz}}{Z_{\text{p}}cos\mathit{\theta }}\right)\left(\frac{-Z_{\text{p}}cos\mathit{\theta }\left(R^2{\mathit{\lambda }}_0^2+{\mathit{\sigma }}_{\text{p}}{cos}^2\mathit{\theta }\right)}{{\mathit{\lambda }}_0\left\{{\mathit{\sigma }}_{\text{p}}R{\mathit{\lambda }}_0{R}_{\mathit{\lambda }}-Z_{\text{p}}cos\mathit{\theta }\left(R^2{\mathit{\lambda }}_0^2-{\mathit{\sigma }}_{\text{p}}{cos}^2\mathit{\theta }\right)\right\}}\right),\\ \mathit{\beta }=\left(\frac{cos\mathit{\theta }}{{\mathit{\lambda }}_0^{3}R}+\frac{Z_{\text{p}}{\mathit{\lambda }}_0{R}^{3}sin{}^2\mathit{\theta }{n}_{\text{p}0}}{R_{\mathit{\lambda }}{Z}_{\text{p}}^2{A}^{2}cos\mathit{\theta }}\right)\left(\frac{R{R}_{\mathit{\lambda }}}{2Z_{\text{p}}cos\mathit{\theta }{n}_{\text{p}0}{R}^2{\mathit{\lambda }}_0^2}\right),\\ \mathit{\gamma }=M\frac{\mathit{\partial }{n}_{\text{p}0}}{\mathit{\partial }\mathit{\tau }}+N,\text{where}\\ M=\left(\frac{Z_{\text{p}}{\mathit{\lambda }}_0^3{R}^2}{R_{\mathit{\lambda }}}-\frac{Z_{\text{p}}{\mathit{\lambda }}_0^{2}R\left(\begin{array}{c}{v}_{x0}sin\mathit{\theta }\\ +v_{z0}cos\mathit{\theta }\\ \end{array}\right)\left(1+{cos}^2\mathit{\theta }\right)}{R_{\mathit{\lambda }}}\right)\left[\frac{R{R}_{\mathit{\lambda }}}{2Z_{\text{p}}cos\mathit{\theta }{n}_{\text{p}0}\left(\begin{array}{c}{R}^2{\mathit{\lambda }}_0^2\\ -{\mathit{\sigma }}_{\text{p}}{cos}^2\mathit{\theta }\\ \end{array}\right)-2{\mathit{\sigma }}_{\text{p}}{n}_{\text{p}0}{\mathit{\lambda }}_{0}R{R}_{\mathit{\lambda }}}\right]\\ N=Q_1\left(\frac{-R{R}_{\mathit{\lambda }}}{2Z_{\text{p}}cos\mathit{\theta }{n}_{\text{p}0}\left(R^2{\mathit{\lambda }}_0^2-{\mathit{\sigma }}_{\text{p}}{cos}^2\mathit{\theta }\right)-2{\mathit{\sigma }}_{\text{p}}{n}_{\text{p}0}{\mathit{\lambda }}_{0}R{R}_{\mathit{\lambda }}}\right),\\ Q_1=\frac{-2{\mathit{\sigma }}_{\text{p}}{Z}_{\text{p}}{\mathit{\lambda }}_0{cos}^2\mathit{\theta }}{R_{\mathit{\lambda }}}-\frac{Z_{\text{p}}{\mathit{\lambda }}_{0}cos\mathit{\theta }{\mathit{\gamma }}_{\text{p}}{v}_{zo}}{R_{\mathit{\lambda }}}+\frac{Z_{\text{p}}{\mathit{\lambda }}_0^{2}R{\mathit{\gamma }}_{\text{p}}}{R_{\mathit{\lambda }}}(-Ssin\mathit{\theta }cos\mathit{\theta }-{cos}^2\mathit{\theta }),\\ S=\frac{\left(v_{z0}sin\mathit{\theta }-v_{x0}cos\mathit{\theta }\right)}{\left(v_{xo}sin\mathit{\theta }+v_{z0}cos\mathit{\theta }\right)},R=\frac{sin\mathit{\theta }{v}_{x0}}{{\mathit{\lambda }}_0}+\frac{cos\mathit{\theta }{v}_{z0}}{{\mathit{\lambda }}_0}-1,R_{\mathit{\lambda }}=\frac{{\mathit{\lambda }}_0^2{R}^2-2{\mathit{\sigma }}_{\text{p}}{cos}^2\mathit{\theta }}{{\mathit{\lambda }}_0^{2}R}\\ \end{array}$$

together with $A=B_0{\left(\frac{{\mathit{\epsilon }}_0}{n_{\text{p}0}{Z}_{\text{p}}^2{m}_{\text{p}}}\right)}^{1/2}$ and $v_{xz}=v_{x0}\text{sin}\mathit{\theta }+v_{z0}cos\mathit{\theta }$.

Then, following Singh and Malik [41] and Yan [42], we obtain the soliton solution as

$$\mathit{\varphi }(\mathit{\omega })=\mathit{\varphi }(\mathit{\xi },\mathit{\tau })=\frac{1}{3\mathit{\alpha }b{V}_{\text{L}}}sec{h}^2\{W_{\text{L}}(\mathit{\tau }-V_{\text{L}}\mathit{\xi })\}+\frac{N}{\mathit{\alpha }b{W}_{\text{L}}{V}_{\text{L}}}tanh\{W_{\text{L}}(\mathit{\tau }-V_{\text{L}}\mathit{\xi })\},$$

(11)

where W_L is the inverse of the width given by $W_{\text{L}}=\sqrt{\frac{1}{2\mathit{\beta }{V}_{\text{L}}^3}}$ and V_L represents the velocity shift together with $b(\mathit{\tau })\equiv exp\left(-\int {}^{\mathit{\tau }}M\frac{\mathit{\partial }{n}_{\text{p}o}}{\mathit{\partial }\mathit{\tau }\prime }\text{d}\mathit{\tau }\prime \right)$.

Soliton reflection: soliton shift and reflection condition

As we have considered the incident wave propagation along the direction of $\overrightarrow{k}$, the reflected wave is taken to travel in the $-\overrightarrow{k}$ direction. This yields the following stretched coordinates

$$\mathit{\xi }=-{\mathit{\epsilon }}^{1/2}\left(\frac{\widehat{k}·\overrightarrow{r}}{{\mathit{\lambda }}_0}-t\right)\text{and}\mathit{\tau }=-{\mathit{\epsilon }}^{3/2}\left(\widehat{k}·\overrightarrow{r}\right),$$

(12)

together with ${\mathit{\lambda }}_{0\text{R}}$ as the phase velocity of the wave traveling in the $-\overrightarrow{k}$ direction. Using these stretched coordinates and following the same procedure as adopted for the incident wave, we obtain the following relation for ${\mathit{\lambda }}_{0\text{R}}$

$${\mathit{\lambda }}_{0\text{R}}=-v_{x0}sin\mathit{\theta }-v_{z0}cos\mathit{\theta }\pm \sqrt{Z_{\text{p}}+2{\mathit{\sigma }}_{\text{p}}}cos\mathit{\theta }.$$

(13)

Further, the relevant mKdV equation for the reflected wave in terms of $v_{\text{R}}$($\equiv v_1$) is obtained as

$$\frac{\mathit{\partial }{v}_{\text{R}}}{\mathit{\partial }{\mathit{\tau }}_{\text{R}}}+{\mathit{\alpha }}_{\text{R}}{v}_{\text{R}}\frac{\mathit{\partial }{v}_{\text{R}}}{\mathit{\partial }{\mathit{\xi }}_{\text{R}}}+{\mathit{\beta }}_{\text{R}}\frac{{\mathit{\partial }}^3{v}_{\text{R}}}{\mathit{\partial }{\mathit{\xi }}_{\text{R}}}+{\mathit{\gamma }}_{\text{R}}\frac{\mathit{\partial }{n}_{\text{p}0}}{\mathit{\partial }{\mathit{\tau }}_{\text{R}}}=0$$

(14)

where

$$\begin{array}{c}{\mathit{\alpha }}_{\text{R}}=\left(\frac{{\mathit{\lambda }}_{0\text{R}}-v_{xz}}{Z_{\text{p}}cos\mathit{\theta }}\right)\left(\frac{-Z_{\text{p}}cos\mathit{\theta }\left(R^2{\mathit{\lambda }}_{0\text{R}}^2+{\mathit{\sigma }}_{\text{p}}{cos}^2\mathit{\theta }\right)}{{\mathit{\lambda }}_{0\text{R}}\left\{{\mathit{\sigma }}_{\text{p}}R{\mathit{\lambda }}_{0\text{R}}{R}_{\mathit{\lambda }\text{R}}-Z_{\text{p}}cos\mathit{\theta }\left(R^2{\mathit{\lambda }}_{0\text{R}}^2-{\mathit{\sigma }}_{\text{p}}{cos}^2\mathit{\theta }\right)\right\}}\right)\\ {\mathit{\beta }}_{\text{R}}=\left(\frac{cos\mathit{\theta }}{{\mathit{\lambda }}_{0\text{R}}^{3}R}+\frac{Z_{\text{p}}{\mathit{\lambda }}_{0\text{R}}{R}^{3}sin{}^2\mathit{\theta }{n}_{\text{p}0}}{R_{\mathit{\lambda }\text{R}}{Z}_{\text{p}}^2{A}^{2}cos\mathit{\theta }}\right)\left(\frac{R{R}_{\mathit{\lambda }\text{R}}}{2Z_{\text{p}}cos\mathit{\theta }{n}_{\text{p}0}{R}^2{\mathit{\lambda }}_{0\text{R}}^2}\right)\\ {\mathit{\gamma }}_{\text{R}}=M_{\text{R}}\frac{\mathit{\partial }{n}_{\text{p}0}}{\mathit{\partial }\mathit{\tau }}+N_{\text{R}},\text{where}\\ M_{\text{R}}=\left(\frac{Z_{\text{p}}{\mathit{\lambda }}_{0\text{R}}^3{R}_{\text{R}}^2}{R_{\mathit{\lambda }\text{R}}}+\frac{Z_{\text{p}}{\mathit{\lambda }}_{0\text{R}}^2{R}_{\text{R}}\left(\begin{array}{c}{v}_{x0}sin\mathit{\theta }\\ +v_{z0}cos\mathit{\theta }\\ \end{array}\right)\left(1+{cos}^2\mathit{\theta }\right)}{R_{\mathit{\lambda }\text{R}}}\right)\left[\frac{R_{\text{R}}{R}_{\mathit{\lambda }\text{R}}}{2Z_{\text{p}}cos\mathit{\theta }{n}_{\text{p}0}\left(\begin{array}{c}{R}_{\text{R}}^2{\mathit{\lambda }}_{0\text{R}}^2\\ -{\mathit{\sigma }}_{\text{p}}{cos}^2\mathit{\theta }\\ \end{array}\right)-2{\mathit{\sigma }}_{\text{p}}{n}_{\text{p}0}{\mathit{\lambda }}_{0\text{R}}{R}_{\text{R}}{R}_{\mathit{\lambda }\text{R}}}\right]\\ N_{\text{R}}=Q_{1\text{R}}\left(\frac{-R_{\text{R}}{R}_{\mathit{\lambda }\text{R}}}{2Z_{\text{p}}cos\mathit{\theta }{n}_{\text{p}0}\left(R_{\text{R}}^2{\mathit{\lambda }}_{0\text{R}}^2-{\mathit{\sigma }}_{\text{p}}{cos}^2\mathit{\theta }\right)-2{\mathit{\sigma }}_{\text{p}}{n}_{\text{p}0}{\mathit{\lambda }}_{0\text{R}}{R}_{\text{R}}{R}_{\mathit{\lambda }\text{R}}}\right),\\ Q_{1\text{R}}=\frac{-2{\mathit{\sigma }}_{\text{p}}{Z}_{\text{p}}{\mathit{\lambda }}_{0\text{R}}{cos}^2\mathit{\theta }}{R_{\mathit{\lambda }\text{R}}}+\frac{Z_{\text{p}}{\mathit{\lambda }}_{0\text{R}}cos\mathit{\theta }{\mathit{\gamma }}_{\text{p}}{v}_{zo}}{R_{\mathit{\lambda }\text{R}}}+\frac{Z_{\text{p}}{\mathit{\lambda }}_{0\text{R}}^2{R}_{\text{R}}{\mathit{\gamma }}_{\text{p}}}{R_{\mathit{\lambda }\text{R}}}(-S_{\text{R}}sin\mathit{\theta }cos\mathit{\theta }-{cos}^2\mathit{\theta }),\\ S_{\text{R}}=\frac{\left(v_{z0}sin\mathit{\theta }+v_{x0}cos\mathit{\theta }\right)}{\left(v_{xo}sin\mathit{\theta }+v_{z0}cos\mathit{\theta }\right)},R_{\text{R}}=-\frac{sin\mathit{\theta }{v}_{x0}}{{\mathit{\lambda }}_{0\text{R}}}-\frac{cos\mathit{\theta }{v}_{z0}}{{\mathit{\lambda }}_{0\text{R}}}-1,R_{\mathit{\lambda }\text{R}}=\frac{{\mathit{\lambda }}_0^2{R}_{\text{R}}^2-2{\mathit{\sigma }}_{\text{p}}{cos}^2\mathit{\theta }}{{\mathit{\lambda }}_0^2{R}_{\text{R}}}\end{array}$$

This is worth mentioning here that under the limit ${\mathit{\sigma }}_{\text{p}}\to 0$ the coefficients of mKdV Eqs. (10) and (14) reduce to the ones of Ref. [43]. This substantiates the generality of the calculations.

Now we couple mKdV Eqs. (10) and (14) to study the reflection of the incident soliton [40] by replacing the velocity $v_{\text{I}}$ appearing in Eq. (10) and $v_{\text{R}}$ appearing in Eq. (14) by the total ion fluid velocity $v_{\text{I}}$ + $v_{\text{R}}$. By this, we obtain the following coupled equation:

$$\frac{\mathit{\partial }{\mathit{\nu }}_{\text{R}}}{\mathit{\partial }{\mathit{\tau }}_{\text{R}}}+{\mathit{\alpha }}_{\text{R}}\left({\mathit{\nu }}_I+{\mathit{\nu }}_{\text{R}}\right)\frac{\mathit{\partial }{\mathit{\nu }}_{\text{R}}}{\mathit{\partial }{\mathit{\xi }}_{\text{R}}}+{\mathit{\beta }}_{\text{R}}\frac{{\mathit{\partial }}^3{\mathit{\nu }}_{\text{R}}}{\mathit{\partial }{\mathit{\xi }}_{\text{R}}^3}+{\mathit{\gamma }}_{\text{R}}\left({\mathit{\nu }}_I+v_{\text{R}}\right)=0.$$

(15)

Then, in the resulting equation we use $v_{\text{R}}<<v_{\text{I}}$ in view of [4, 13, 24] and substitute $v_{\text{R}}\left({\mathit{\xi }}_{\text{R}},{\mathit{\tau }}_{\text{R}}\right)=b_{\text{R}}\left({\mathit{\tau }}_{\text{R}}\right)W_{\text{R}}\left({\mathit{\xi }}_{\text{R}},{\mathit{\tau }}_{\text{R}}\right)$ together with $b_{\text{R}}={\text{e}}^{\left(\text{-}{\int }_{}^{{\mathit{\tau }}_{\text{R}}}{\mathit{\gamma }}_{\text{R}}\left(\mathit{\partial }{n}_0/\phantom{\mathit{\partial }{n}_0\mathit{\partial }{\mathit{\tau }}_{\text{R}}\prime }\mathit{\partial }{\mathit{\tau }}_{\text{R}}\prime \right)\text{d}{\mathit{\tau }}_{\text{R}}\prime \right)}$, where ${\mathit{\gamma }}_{\text{R}}=N_{\text{R}}+M_{\text{R}}\frac{\mathit{\partial }{n}_0}{\mathit{\partial }{\mathit{\tau }}_{\text{R}}^{\prime }}$

$$\frac{\mathit{\partial }{W}_{\text{R}}}{\mathit{\partial }{\mathit{\tau }}_{\text{R}}}+\frac{W_{\text{R}}}{b_{\text{R}}}\frac{\mathit{\partial }{b}_{\text{R}}}{\mathit{\partial }{\mathit{\tau }}_{\text{R}}}+{\mathit{\alpha }}_{\text{R}}{v}_{\text{I}}\frac{\mathit{\partial }{W}_{\text{R}}}{\mathit{\partial }{\mathit{\xi }}_{\text{R}}}+{\mathit{\alpha }}_{\text{R}}{W}_{\text{R}}{b}_{\text{R}}\frac{\mathit{\partial }{W}_{\text{R}}}{\mathit{\partial }{\mathit{\xi }}_{\text{R}}}+{\mathit{\beta }}_{\text{R}}\frac{{\mathit{\partial }}^3{W}_{\text{R}}}{\mathit{\partial }{\mathit{\xi }}_{\text{R}}^3}+{\mathit{\gamma }}_{\text{R}}\frac{v_{\text{I}}}{b_{\text{R}}}+{\mathit{\gamma }}_{\text{R}}{W}_{\text{R}}=0$$

(16)

The 2nd and 4th terms of this equation carry the nonlinear effects and the overlapping due to the reflected wave and the 6th term shows the density inhomogeneity effect. A further substitution of $W_{\text{R}}\left({\mathit{\xi }}_{\text{R}},{\mathit{\tau }}_{\text{R}}\right)=h_{\text{R}}\left({\mathit{\tau }}_{\text{R}}\right)+{\tilde{w}}_{\text{R}}\left({\mathit{\xi }}_{\text{R}},{\mathit{\tau }}_{\text{R}}\right)$ together with $\frac{\mathit{\partial }{h}_{\text{R}}}{\mathit{\partial }{\mathit{\tau }}_{\text{R}}}=\frac{v_{\text{I}}}{b_{\text{R}}^2}\frac{\mathit{\partial }{b}_{\text{R}}}{\mathit{\partial }{\mathit{\tau }}_{\text{R}}}$ transforms the coupled Eq. (16) into

$$\frac{\mathit{\partial }{\tilde{w}}_{\text{R}}}{\mathit{\partial }{\mathit{\tau }}_{\text{R}}}+{\mathit{\alpha }}_{\text{R}}{b}_{\text{R}}{\tilde{w}}_{\text{R}}\frac{\mathit{\partial }{\tilde{w}}_{\text{R}}}{\mathit{\partial }{\mathit{\xi }}_{\text{R}}}+{\mathit{\beta }}_{\text{R}}\frac{{\mathit{\partial }}^3{w}_{\text{R}}}{\mathit{\partial }{\mathit{\xi }}_{\text{R}}^3}+2{\mathit{\alpha }}_{\text{R}}{v}_{\text{I}}\frac{\mathit{\partial }{\tilde{w}}_{\text{R}}}{\mathit{\partial }{\mathit{\xi }}_{\text{R}}}=0.$$

(17)

To solve this equation, we use ${\mathit{\eta }}_{\text{R}}=g_{\text{R}}\left({\mathit{\tau }}_{\text{R}}-U_{\text{R}}{\mathit{\xi }}_{\text{R}}\right)$ as a variable transformation. Here $g_{\text{R}}$is the width of the reflected soliton and $U_{\text{R}}$ is the velocity shift of the reflected soliton. With this transformation, Eq. (17) reads

$$\left(2{\mathit{\alpha }}_{\text{R}}{v}_{\text{I}}{U}_{\text{R}}-1\right)\frac{\mathit{\partial }{\tilde{w}}_{\text{R}}}{\mathit{\partial }{\mathit{\eta }}_{\text{R}}}+\left({\mathit{\alpha }}_{\text{R}}{b}_{\text{R}}{U}_{\text{R}}\right){\tilde{w}}_{\text{R}}\frac{\mathit{\partial }{\tilde{w}}_{\text{R}}}{\mathit{\partial }{\mathit{\eta }}_{\text{R}}}+\left(g_{\text{R}}^2{U}_{\text{R}}^3{\mathit{\beta }}_{\text{R}}\right)\frac{{\mathit{\partial }}^3{\tilde{w}}_{\text{R}}}{\mathit{\partial }{\mathit{\eta }}_{\text{R}}^3}=0.$$

(18)

Now we suppose [41, 42] the following solution $w_{\text{R}}({\mathit{\zeta }}_{\text{R}})$ of Eq. (18)

$${\tilde{w}}_{\text{R}}({\mathit{\eta }}_{\text{R}})=N_0+\sum _{j=1}^n{tanh}^{j-1}\left({\mathit{\eta }}_{\text{R}}\right)\left\{M_{j}sech\left({\mathit{\eta }}_{\text{R}}\right)+N_{j}tanh\left({\mathit{\eta }}_{\text{R}}\right)\right\}.$$

The above solution can also be written in terms of the intermediate variable $\mathit{\varsigma }$ as

$${\tilde{w}}_{\text{R}}(\mathit{\varsigma })=\sum _{j=1}^n\left(M_{j}sin\mathit{\varsigma }+N_{j}cos\mathit{\varsigma }\right){cos}^{j-1}\mathit{\varsigma }+N_0;\frac{\text{d}\mathit{\varsigma }}{\text{d}\mathit{\eta }{}_{\text{R}}}=sin\mathit{\varsigma }.$$

(19)

The balance of the leading order of the nonlinear terms to that of the linear terms determines the degree of the polynomial solution as n = 2. So the solution (19) takes the form

$${\tilde{w}}_{\text{R}}(\mathit{\varsigma })=N_0+N_{1}cos\mathit{\varsigma }+M_{1}sin\mathit{\varsigma }+N_2{cos}^2\mathit{\varsigma }+M_{2}cos\mathit{\varsigma }sin\mathit{\varsigma }.$$

(20)

The employment of this solution in Eq. (18) changes the differential equation into a trigonometric polynomial identity of the intermediate variable $\mathit{\varsigma }$ from which we collect all the terms with the same power in sin $\mathit{\varsigma }$ cos^m$\mathit{\varsigma }$, cos^m+1$\mathit{\varsigma }$ (m = 0,1,2,…,), etc., and set their coefficients to zero. For a particular solution where $N_1=M_1=M_2=0$ we obtain a set of equations and after solving them we obtain the values of $N_0$ and $N_2$ as

$$N_0=\frac{-\left(2{\mathit{\alpha }}_{\text{R}}{v}_{\text{I}}{U}_{\text{R}}-1\right)}{{\mathit{\alpha }}_{\text{R}}{b}_{\text{R}}{U}_{\text{R}}}+\frac{2g_{\text{R}}^2{U}_{\text{R}}^3{\mathit{\beta }}_{\text{R}}}{{\mathit{\alpha }}_{\text{R}}{b}_{\text{R}}{U}_{\text{R}}},N_2=\frac{-2g_{\text{R}}^2{U}_{\text{R}}^3{\mathit{\beta }}_{\text{R}}}{{\mathit{\alpha }}_{\text{R}}{b}_{\text{R}}{U}_{\text{R}}}.$$

Using these values in Eq. (20), we arrive at the following soliton solution of Eq. (18)

$$w\left({\mathit{\eta }}_{\text{R}}\right)=\frac{\left(-2{\mathit{\alpha }}_{\text{R}}{v}_{\text{I}}{U}_{\text{R}}+1\right)}{{\mathit{\alpha }}_{\text{R}}{b}_{\text{R}}{U}_{\text{R}}}+\frac{2g_{\text{R}}^2{U}_{\text{R}}^3{\mathit{\beta }}_{\text{R}}}{{\mathit{\alpha }}_{\text{R}}{b}_{\text{R}}{U}_{\text{R}}}sec{h}^2\left({\mathit{\eta }}_{\text{R}}\right).$$

(21)

The coefficient of second term of Eq. (21) represents the reflected soliton amplitude and the first term amounts to the shift that the soliton acquires after its reflection. The shifting of the soliton in the case of finite temperature ions is the same result as obtained in the case of cold plasma [43]. However, depending upon the value of T _i , the magnitude of shift is different in both types of the plasmas. Further, related to the soliton reflection, we note that ${\mathit{\lambda }}_{0\text{R}}$ is positive only when the following condition is met

$$\mathit{\theta }>{tan}^{-1}\left(\frac{\sqrt{Z_{\text{p}}+2{\mathit{\sigma }}_{\text{p}}}-v_{z0}}{v_{x0}}\right).$$

(22)

The above inequality says that the soliton will reflect in the plasma only when the propagation angle is greater than the certain minimum value given by Eq. (22). It means the soliton will not reflect in the plasma if the propagation angle is below that certain minimum value. In addition, we have already seen that the soliton corresponding to the slow wave does not reflect at all, consistent to the case of cold plasma [43].

To examine the strength of the soliton reflection, now we define the reflection coefficient as the ratio of amplitudes of reflected soliton and incident soliton. Thus, the reflection coefficient (say R_F) is given by

$$R_{\text{F}}=\frac{6g_{\text{R}}^2{U}_{\text{R}}^2{\mathit{\beta }}_{\text{R}}\mathit{\alpha }b{V}_{\text{L}}}{{\mathit{\alpha }}_{\text{R}}{b}_{\text{R}}}.$$

(23)

Results and discussion

Figure 1 shows the profiles of incident and reflected solitons, where we find that the amplitude of reflected soliton is lower than the incident soliton. This is consistent to the observations made by other investigators. Based on the sizes of the soliton, we can say that the reflected soliton carries lower energy in comparison with the incident soliton. The difference in the energy leads to the shifting of the soliton, which is evident from Fig. 1. Figure 1 also shows that both the incident and the reflected solitons are compressive solitons in nature. Consistent to Yi et al. [23] and Chauhan et al. [25], the incident soliton does not change its polarity after reflection. However, the solitons have been found to change their polarities in an experiment conducted by Nagasawa and Nishida [15] in an unmagnetized plasma with nonisothermal electrons. In addition, one more interesting thing, which we have found in our case, is that the reflected soliton can shift downward as well as upward depending upon the sign of V_R, which in turn depends on the velocity shift of the reflected soliton. In this regard, we observe that if the velocity shift of the reflected soliton is negative then the reflected soliton will be shifted downward; and the positive shift results into upward shift of the soliton.

Fig. 1

Incident and reflected soliton profiles, when n_p0 = 0.9, ${\mathit{\gamma }}_{\text{p}}$ = 0.01, B₀ = 0.05, T_e = 3 eV and v_x0 = v_z0 = 0.1, V_I = 1.25, V_R = 0.46 for upward shift, V_R = −0.5 for downward shift

In view of the smaller size of the reflected soliton, it is obvious that the reflection coefficient R_F will carry values less than unity. This is also plausible, as we do not consider any exchange of energy of the soliton with the plasma particles. Moreover, all the experiments conducted in plasma models suggest that R_F < 1, i.e. 100 % reflection of the soliton is not possible. This requirement leads to the following condition

$$V_{\text{R}\text{max}}=V_{\text{L}}\sqrt{\frac{{\mathit{\alpha }}_{\text{R}}{b}_{\text{R}}\mathit{\beta }}{3\mathit{\alpha }b{\mathit{\beta }}_{\text{R}}}}.$$

(24)

For better understanding, we have plotted in Fig. 2 this maximum possible value of V_R. From the figure, it is clear that V_Rmax attains lower values for higher rate of ionization.

Fig. 2

Variation of maximum velocity shift for the reflection of soliton, when T_e = 3 eV, v_x0 = v_z0 = 0.06, V_I = 1.26, n_p0 = 0.9, B₀ = 0.05, and $\mathit{\theta }$ = 50^°

Figure 3 shows the variation of the amplitudes of the reflected soliton (marked as Amp_Ref) as well as the incident soliton (marked as Amp_Inc) with respect to the temperature ratio for different values of charge number. We observe that both the incident and reflected solitons have higher amplitude for higher charge number of the ions. We see that the amplitudes of both the solitons are reduced for the larger values of temperature ratio σ_p. The reduction in the amplitude of incident soliton with σ_p is due to the fact that the enhanced σ_p leads to higher values of coefficient α as well as b. This results into smaller values of the soliton amplitudes, contrary to the observation of Malik and Nishida [44]. Since Malik and Nishida [44] did not consider the ionization in the plasma, it can be deduced that due to the ionization the plasma becomes less nonlinear. The same is also true in the case of reflected soliton, where the coefficients α_R and b_R are found to increase with σ_p. Figure 4 shows the variation of the shift and reflection coefficient (marked as RC) with the ion temperature. We notice that weaker is the reflection of the incident soliton, smaller is the magnitude of its shift. The decrease in the reflection coefficient with σ_p is not very sharp, which is because of the fact that the incident soliton does not see as significant effect as the reflected soliton (Fig. 3). For the same reason, the reflection coefficient decreases at a smaller rate with σ_p or ion temperature. We can see from Figs. 3 and 4 that the soliton is reflected strongly at lower values of σ_p, suggesting that the stronger reflection of soliton takes place in a cold plasma. This is because the energy of the incident soliton has lower value (owing to smaller amplitude) for the higher values of σ_p. For this reason, lesser is the amount of energy of the incident soliton and hence, smaller is the amount of energy that is being used in shifting the soliton. Malik et al. [31] had also observed that when the incident soliton is reflected strongly then the amplitude of reflected soliton and the reflection coefficient attain higher values. However, the shift was found to behave oppositely [31]. In contrast to this, in the presence of ionization, the shift and reflection coefficients are found to behave consistently. This is probably the consequence of the ionization. On the other hand, we observe from Fig. 4 that the reflection coefficient and shift attain higher value for the ions of higher charge number.

Fig. 3

Variation of amplitudes of incident and reflected solitons with ion to electron temperature ratio for different charge number, when T_e = 3 eV, v_x0 = v_z0 = 0.06, V_I = 1.26, V_R = 0.38, n_p0 = 0.9, ${\mathit{\gamma }}_{\text{p}}$ = 0.01, B₀ = 0.05, and $\mathit{\theta }$ = 50°

Fig. 4

Variation of shift and reflection coefficient with propagation angle for different charge number, when T_e = 3 eV, v_x0 = v_z0 = 0.06, V_I = 1.26, V_R = 0.38, n_p0 = 0.9, ${\mathit{\gamma }}_{\text{p}}$ = 0.01, B₀ = 0.05, and $\mathit{\theta }$ = 50°. RC represents the reflection coefficient R_F

In contrast to the observation made in the cold plasma [43], the shift also behaves in the same manner as the reflection coefficient (Fig. 5). The enhanced shift in the case of finite temperature plasma can be understood based on the pressure gradient force. If we see the profile of the soliton, we notice that the particles are closely packed in the top region of the compressive soliton. Hence, there develops a pressure gradient force in the direction from top to bottom of the soliton. When reflection takes place, there is a loss of energy, i.e., some particles leave the soliton structure. Because of the developed pressure gradient force, the ions’ flow is more in the case of their finite temperature. For this reason, the soliton is found to shift more in the presence of more ionization, which develops stronger density gradient in the plasma. Although the effect of ionization is not very strong, which may become significant if we take into consideration the effect of collisions between the neutral particles and electrons. For the sake of simplicity we have neglected such collisions, but in our future work, we shall solve the cumbersome problem by taking into consideration these collisions.

Fig. 5

Variation of shift and reflection coefficient with ionization rate, when T_e = 3 eV, v_x0 = v_z0 = 0.06, V_I = 1.26, V_R = 0.46, n_p0 = 0.9, ${\mathit{\sigma }}_{\text{p}}$ = 0.1, B₀ = 0.05, and $\mathit{\theta }$ = 50°

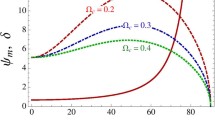
Figure 6 shows that the reflection coefficient is larger for the case of larger wave propagation angle. It means the soliton is strongly reflected, when the wave propagates at a larger angle from the direction of magnetic field. The soliton shift also behaves in the same fashion as the reflection coefficient behaves with θ. Since the shifting of the solitons is a new result based on theoretical attempts, experimentalists need to set-up new experiments concerning soliton reflection in magnetized plasmas in the absence as well as in the presence of the ionization. Actually for larger values of wave propagation angle (same effect as of stronger magnetic field due to larger Lorentz force), the coefficients β and β_R are found to decrease. Since these coefficients correspond to the dispersion properties of plasma and the soliton width is directly proportional to the square root of these coefficients, the soliton width will also reduce for higher values of propagation angle. As per the basic feature of solitons, this is possible when the soliton amplitude enhances to maintain the balance between the effects of dispersion and nonlinearity for soliton formation. Hence, the larger energy soliton is expected to evolve for the case of higher magnetic field, because of which the soliton reflects strongly and it leads to higher values of reflection coefficient (Fig. 6).

Fig. 6

Variation of shift and reflection coefficient with propagation angle, when T_e = 3 eV, v_x0 = v_z0 = 0.06, V_I = 1.26, V_R = 0.38, n_p0 = 0.9, ${\mathit{\sigma }}_{\text{p}}$ = 0.1, B₀ = 0.05, and ${\mathit{\gamma }}_{\text{p}}$ = 0.01

The nonlinear solitary waves/structures, we have studied in the present article, propagate in astrophysical and space related plasmas including the laboratory experiments where the ions are made magnetized with the application of an external magnetic field [30, 45–48]. For example, such a magnetized plasma exists in the Earth’s ionosphere [45], magnetosphere [46] and Van-Allen radiation belts [47] under the effect of Earth’s magnetic field. Finally, this would be worth mentioning that the coexistence of incident and reflected waves may lead to the interaction of two waves (solitons) and hence, a situation of resonance phenomenon may arise if the favorable conditions are met. The phenomenon of resonance of plane wave solitons was for the first time realized by Nishida and Nagasawa [16] and then investigated in detail by Nishida group [16–18].

Conclusion

In conclusion, we say that the modes propagation have been discussed along with their evolution as solitons and the reflection of solitons in an inhomogeneous plasma, including the effect of ionization. Although such plasma supports two types of modes, the slow mode propagates only when the propagation angle attains a value higher than certain minimum value. Out of the two modes, we found only fast mode to get reflected only when certain condition for the propagation angle is satisfied. Interestingly, the solitons are shifted downward as well as upward depending on the velocity shift of the reflected soliton. The polarity of the incident soliton does not change on getting reflected. The effect of ion to electron temperature ratio, ionization rate along with the propagation angle is observed on both the reflected soliton amplitude and the shift.