Far from equilibrium transport on TASEP with pockets

Abstract

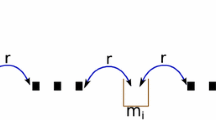
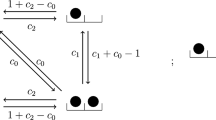
We investigate a geometric adaptation of a totally asymmetric simple exclusion process with open boundary conditions, where each site of a one-dimensional channel is connected to a lateral space (pocket). The number of particles that may be accommodated in each pocket is determined by its capacity q. The continuum mean-field approximation is deployed for the case $q = 1$ where both lattice and pocket strictly follow the hard-core exclusion principle. In contrast, a probability mass function is utilized along with the mean-field theory to investigate the multiple-capacity case, where the pocket violates the hard-core exclusion principle. The effect of both finite and infinite reservoirs has been studied in the model. The explicit expression for particle density has been calculated, and the evolution of the phase diagram in $\alpha -\beta$ parameter space obtained with respect to q and the attachment-detachment rates. In particular, the topology of the phase diagram is found to be unchanged in the neighborhood of $q = 1$. Moreover, the competition between lattice and pocket for finite resources and the unequal Langmuir kinetics captures a phenomenon in the form of a back-and-forth transition. We have also investigated the limiting case $q \rightarrow \infty$. The theoretically obtained phase boundaries and density profiles are validated through extensive Monte Carlo simulations.

Appendices

Appendix A

In this appendix, we provide the explicit calculations and the conditions for the existence of phase boundaries of lattice with multiple-capacity pockets under infinite resources, as discussed in Sect. 4.1.

For $q=1$, we can re-write the expression for pocket density in Eq. (11) as,

$$\begin{aligned} m= \frac{A}{1+A}, \end{aligned}$$

(A1)

where $A=\frac{\Omega _{\text {c}}\rho }{\Omega _{\text {d}}(1-\rho )}$. The transition from HD/LD to HD/HD phase (or vice-versa) occurs along the phase boundary capturing HD/MC phase. The pockets must possess the MC phase for the transition mentioned above to occur, and that happens for $A=1$ only.

Further, for $q\ne 1$, we utilize $m*$ in Eq. (57) to obtain the condition of transition from HD/LD to HD/HD phase which is given as,

$$\begin{aligned} qA^{q+2}-(2+q)(A^{q+1}-A)-q=0. \end{aligned}$$

(A2)

For any choice of q, the above equation holds true only for $A=1$. This proves that all the phase boundaries for the multiple-capacity case are independent of the capacity parameter.

Appendix B: Monte Carlo simulations

In order to support the analytical outcomes based on the mean-field approach, we carry out continuous time Monte Carlo simulations for system size $L=1000$. Here, we use the random sequential update rule for simulations. A single step of the algorithm involves choosing a random site $j \in \{1, 2, ..., L\}$ with equal probability and updating it according to the dynamical rules explicitly mentioned in Sect. 2. This procedure is implemented for $L \times 10^7$ time steps and the first 5% of them are discarded to facilitate the onset of the stationary state. The particle densities from simulations are obtained by averaging its occupation of each site over an interval of 10L. The simulated phase boundaries are computed within an estimated error of less than 1%.