Power-law random banded matrix ensemble as the effective model for many-body localization transition

Abstract

We employ the power-law random banded matrix (PRBM) ensemble with single tuning parameter $\mu$ as the effective model for many-body localization (MBL) transition in random spin systems. We show the PRBM accurately reproduces the eigenvalue statistics on the entire phase diagram through the fittings of high-order spacing ratio distributions $P(r^{(n)})$ as well as number variance $\Sigma ^{2}(l)$, in systems both with and without time-reversal symmetry. For the properties of eigenvectors, it’s shown the entanglement entropy of PRBM displays an evolution from volume-law to area-law behavior which signatures an ergodic–MBL transition, and the critical exponent is found to be $\nu =0.83\pm 0.15$, close to the value obtained in 1D physical model by exact diagonalization, while the computational cost here is much less.

Appendix A: Fitting spin models without \(S_{T}^{z}\) conservation

In this section we use PRBM to fit the eigenvalue statistics of random spin models without $S_{T}^{z}$ conservation; the Hamiltonian is as follows

Fig. 5

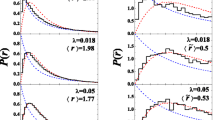
The distributions of $P(r^{(n)})$ in the orthogonal spin model without $S_T^z$ conservation with comparisons to PRBM, the title of each sub-figure indicates the randomness strength h and fitted $\mu$. Bottom right: $\Sigma ^2(l)$ of the physical model and PRBM with $\mu$ fitted through $P(r^{(n)})$, they fit quite well except for the transition region $h\sim 3$. Grey dashed line: $\Sigma ^2(l)$ of PRBM at $\mu =1.26$. Dots and lines stand for physical data and PRBM in all cases

Fig. 6

The distributions of $P(r^{(n)})$ in the unitary spin model without $S_T^z$ conservation at various disorder strengths with comparisons to PRBM with $\beta =2$ and fitted $\mu$. Bottom right: $\Sigma ^2(l)$ of physical model and PRBM. Note here the values of $\mu$ are fitted by $\Sigma ^2(l)$ as listed in the figure legend; they have minor deviations from those fitted through $P(r^{(n)})$, but the relative errors are controlled within 5%. Dots and lines stand for physical data and PRBM in all cases

$$\begin{aligned} H=\sum _{i=1}^{L}{\mathbf {S}}_{i}\cdot {\mathbf {S}}_{i+1}+\sum _{i=1}^{L}\sum _{ \alpha =x,y,z}h^{\alpha }\varepsilon _{i}^{\alpha }S_{i}^{\alpha }\text {.} \end{aligned}$$

(A1)

We will also consider the cases both with and without time-reversal symmetry. For the former, it is the case with $h^{x}=h^{z}=h\ne 0$ and $h^{y}=0$, while for the latter, it is $h^{x}=h^{y}=h^{z}=h\ne 0$. For both models we simulate an $L=13$ system, with Hilbert space dimension $2^{13}=8192$. In all cases, the number of eigenvalue spectrum samples is 400, and we take 400 eigenvalues in the middle to determine $P\left( r^{\left( n\right) }\right)$.

For the orthogonal case, we likewise take several representative randomness strengths to determine spacing ratio distributions $P\left( r^{\left( n\right) }\right)$ and number variance $\Sigma ^{2}\left( l\right)$, and compare them to those of orthogonal PRBM with $\beta =1$, and the results are collected in Fig. 5. This model suffers less from finite-size effect; hence, the fittings are close to perfect. Moreover, the optimal parameter $\mu$ fitted by $P\left( r^{\left( n\right) }\right)$ and $\Sigma ^{2}\left( l\right)$ is very close in most of the phase diagram, except for the transition region $h\sim 3$, as can be viewed from the last sub-figure of Fig. 5.

For the time-reversal breaking case with $h^{x}=h^{y}=h^{z}=h$, the fitting results are displayed in Fig. 6. The finite size effects are slightly larger than the orthogonal case, just like in the models with $S_T^z$ conservation as discussed in the main text. Nevertheless, the deviations between the values of $\mu$ fitted by $P\left( r^{\left( n\right) }\right)$ and $\Sigma ^{2}\left( l\right)$ are still less than 5%.