Lie symmetries, optimal system, group-invariant solutions and dynamical behaviors of solitary wave solutions for a (3+1)-dimensional KdV-type equation

Abstract

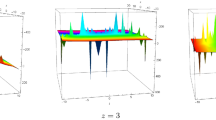
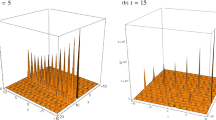
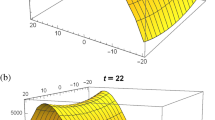
Solitary waves are localized gravity waves that preserve their consistency and henceforth their visibility by the properties of nonlinear hydrodynamics. In this present work, numerous group-invariant solutions of the (3+1)-dimensional KdV-type equation are derived with the virtue of Lie symmetry analysis. Also, we obtain the corresponding infinitesimal generators, Lie point symmetries, geometric vector fields, commutator table and a one-dimensional optimal system of subalgebras. In addition, two-dimensional optimal system of subalgebra is also obtained using one-dimensional optimal system. Several interesting symmetry reductions and corresponding group-invariant solutions of the equation are obtained based on a one-dimensional optimal system of subalgebras. These group-invariant solutions include special functions like the WeierstrassZeta function, W-shaped solitons, M-shaped solitons, bright-dark solitons, solitary waves and rogue waves which we furnish for the first time for this equation. The physical interpretation of the obtained solutions is discussed graphically based on numerical simulation through Mathematica. Furthermore, nonlocal conservation laws are studied via the Ibragimov approach for Lie point symmetries.

Appendix I

$$\begin{aligned} A= \left( \begin{array}{cccccccccc} 1 &{} A_{12} &{} -\epsilon _3 &{} \frac{1}{4} e^{\epsilon _5/2} \epsilon _4 &{} 0 &{} A_{16} &{} A_{17} &{} A_{18} &{} \frac{\epsilon _9}{4} &{} A_{110}\\ 0 &{} e^{\frac{\epsilon _5-\epsilon _1}{4}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} A_{32} &{} e^{\epsilon _1} &{} 0 &{} 0 &{} \frac{1}{20} (-3) e^{\epsilon _1+\epsilon _5} \epsilon _4^2 &{} A_{37} &{} 0 &{} 0 &{} A_{310} \\ 0 &{} A_{42} &{} 0 &{} e^{\frac{\epsilon _5-\epsilon _1}{2}} &{} 0 &{} -e^{\frac{\epsilon _5-\epsilon _1}{2}} \epsilon _7 &{} A_{38} &{} A_{48} &{} 0 &{} A_{410} \\ 0 &{} A_{52} &{} 0 &{} -\frac{1}{2} e^{\epsilon _5/2} \epsilon _2 &{} 1 &{} \frac{1}{2} e^{\epsilon _5/2} \epsilon _2 \epsilon _7-\epsilon _6 &{} -\frac{\epsilon _7}{2} &{} A_{58} &{} \frac{3 \epsilon _9}{4} &{} A_{510} \\ 0 &{} \frac{e^{\epsilon _5} \epsilon _9}{10} &{} 0 &{} 0 &{} 0 &{} e^{\epsilon _5} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \frac{1}{6} e^{\frac{\epsilon _1+\epsilon _5}{2}} \epsilon _8 &{} 0 &{} 0 &{} 0 &{} 0 &{} e^{\frac{\epsilon _1+\epsilon _5}{2}} &{} 0 &{} 0 &{} A_{710} \\ 0 &{} A_{82} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} A_{88} &{} 0 &{} A_{810} \\ 0 &{} A_{92} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{1}{10} (-3) e^{-\frac{\epsilon _1}{4}-\frac{\epsilon _5}{4}} \epsilon _4 &{} A_{98} &{} A_{910} \\ 0 &{} \frac{1}{20} e^{\frac{\epsilon _1+\epsilon _5}{4}} \epsilon _4 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} A_{1010} \\ \end{array} \right) \end{aligned}$$

(170)

where $A_{ij}$ are given below

$$\begin{aligned} A_{12}&=\frac{18 e^{\epsilon _5} \epsilon _3 \epsilon _9 \epsilon _4^2+15 e^{\epsilon _5/2} (\epsilon _{10}-4 \epsilon _3 \epsilon _8-2 \epsilon _7 \epsilon _9) \epsilon _4+300 e^{\epsilon _5/4} \epsilon _2-100 \epsilon _7 \epsilon _8}{1200}, \\ A_{52}&=\frac{1}{120} \left( -30 e^{\epsilon _5/4} \epsilon _2-3 e^{\epsilon _5/2} (\epsilon _{10}-2 \epsilon _7 \epsilon _9) \epsilon _2-2 (5 \epsilon _7 \epsilon _8+6 \epsilon _6 \epsilon _9)\right) , \end{aligned}$$

$$\begin{aligned} \begin{aligned} A_{16}&=\frac{3}{20} e^{\epsilon _5} \epsilon _3 \epsilon _4^2-\frac{1}{4} e^{\epsilon _5/2} \epsilon _4 \epsilon _7, \\ A_{17}&=\frac{1}{10} \left( -3 e^{\epsilon _5/2} \epsilon _3 \epsilon _4-5 \epsilon _7\right) , \\ A_{18}&= \frac{3}{40} \left( 10 \epsilon _8+e^{\epsilon _5/2} \epsilon _4 \epsilon _9\right) , \\ A_{42}&=\frac{1}{20} e^{\frac{\epsilon _5-\epsilon _1}{2}} (\epsilon _{10}-(\epsilon _3+\epsilon _4) \epsilon _8-2 \epsilon _7 \epsilon _9), \\ A_{58}&= \frac{1}{20} \left( 5 \epsilon _8-3 e^{\epsilon _5/2} \epsilon _2 \epsilon _9\right) ,\\ A_{82}&=-\frac{1}{60} e^{-\frac{3 \epsilon _1}{4}-\frac{\epsilon _5}{4}} \left( 3 e^{\epsilon _5/2} \epsilon _3 \epsilon _4+10 \epsilon _7\right) , \\ A_{98}&= e^{-\frac{\epsilon _1}{4}-\frac{3 \epsilon _5}{4}}, \\ A_{110}&=\frac{1}{20} \left( -6 e^{\epsilon _5/2} \epsilon _3 \epsilon _4 \epsilon _9-5 (\epsilon _{10}+4 \epsilon _3 \epsilon _8+2 \epsilon _7 \epsilon _9)\right) ,\\ A_{310}&= e^{\epsilon _1} \epsilon _8+\frac{3}{10} e^{\epsilon _1+\frac{\epsilon _5}{2}} \epsilon _4 \epsilon _9, \\ A_{410}&= \frac{-3}{10} e^{\frac{\epsilon _5-\epsilon _1}{2}} (\epsilon _3+\epsilon _4) \epsilon _9, \\ \end{aligned} \begin{aligned} A_{32}&=\frac{1}{20} e^{\epsilon _1+\frac{\epsilon _5}{2}} \epsilon _4 \epsilon _8-\frac{3}{200} e^{\epsilon _1+\epsilon _5} \epsilon _4^2 \epsilon _9, \\ A_{37}&=\frac{3}{10} e^{\epsilon _1+\frac{\epsilon _5}{2}} \epsilon _4, \\ A_{38}&= \frac{-3}{10} e^{\frac{\epsilon _5-\epsilon _1}{2}} (\epsilon _3+\epsilon _4), \\ A_{48}&= \frac{3}{10} e^{\frac{\epsilon _5-\epsilon _1}{2}} \epsilon _9, \\ A_{88}&= e^{-\frac{3 \epsilon _1}{4}-\frac{\epsilon _5}{4}}, \\ A_{92}&=\frac{1}{20} e^{-\frac{\epsilon _1}{4}-\frac{3 \epsilon _5}{4}} \left( e^{\epsilon _5/2} \epsilon _4 \epsilon _7-2 \epsilon _6\right) , \\ A_{510}&= \frac{1}{4} (\epsilon _{10}-2 \epsilon _7 \epsilon _9), \\ A_{710}&= e^{\frac{\epsilon _1+\epsilon _5}{2}} \epsilon _9,\\ A_{810}&= -e^{-\frac{3 \epsilon _1}{4}-\frac{\epsilon _5}{4}} \epsilon _3,\\ A_{910}&= -e^{-\frac{\epsilon _1}{4}-\frac{3 \epsilon _5}{4}} \epsilon _7, \\ A_{1010}&= e^{\frac{\epsilon _1-\epsilon _5}{4}}. \end{aligned} \end{aligned}$$