Reactivity in prey–predator models at equilibrium under selective harvesting efforts

Abstract

Reactivity is an important feature of every stable state to measure the short-term instability of such stable state in prey–predator models. Asymptotic stability is not a powerful tool to study the dynamics immediately after an equilibrium has disturbed. We are interested in studying the effect of disturbance made by harvesting effort to the stable state of a set of prey–predator models. We consider different scenarios of disturbance made by prey harvesting only, predator harvesting only and selective harvesting on both. We show that disturbance made by prey harvesting causes reactivity of stable state but not in a sustainable way (non-existence of maximum sustainable yield). Further, it is shown that disturbance made by predator harvesting causes reactivity of stable state but in a sustainable way. We study how disturbance made by different harvesting strategies to the asymptotically stable state in the prey–predator system where intraspecific competition rule applied to predator species affects transient dynamics. We find that the transient dynamics properties like reactivity and non-reactivity switch through disturbance made by harvesting but in a sustainable way (maximum sustainable yield exists). Further, we find that asymptotically stable state remains reactive following multiple disturbances made by selective harvesting on both but in a sustainable way (maximum sustainable total yield exists)

Appendix

Appendix A. Proof of Proposition 1.

These parts give the technical proof of the results of the analysis conducted in Sect. 3

The interior equilibrium point $(P_{x1}, P_{y1})$ is given by $P_{x1}=\frac{m_{y}}{\alpha _{y}}$ and $P_{y1}=\frac{r_{x}}{\alpha _{x}}(1-\frac{m_{y}}{\alpha _{y}k_{x}})-\frac{q_{x}e_{x}}{\alpha _{x}}$ provided $e_{x}<\frac{r_{x}}{q_{x}}(1-\frac{m_{y}}{k_{x}\alpha _{y}})$.

The Hermitian matrix is given by at $(P_{x1}, P_{y1})$

$$\begin{aligned} \displaystyle H(J_{1})=\displaystyle \left[ \begin{array}{cc} \displaystyle -\frac{r_{x} P_{x1}}{k_{x}} &{} \frac{-\alpha _{x} P_{x1}+\alpha _{y} P_{y1}}{2} \\ \frac{-\alpha _{x} P_{x1}+\alpha _{y} P_{y1}}{2} &{} 0 \\ \end{array} \right] . \end{aligned}$$

and its characteristic equation is $det(H(J_{1})-\lambda I)=\lambda ^2-(trac(H(J_{1})))\lambda +det(H(J_{1}))=0$ where $trac(H(J_{1}))=-\frac{r_{x} P_{x1}}{k_{x}}$ and $det(H(J_{1}))= \frac{(-\alpha _{x} P_{x1}+\alpha _{y} P_{y1})^2}{4}$.

The eigenvalues are: $\lambda =\frac{\sqrt{ \left( trac(H(J_{1})) \right) ^2-4 Det(H(J_{1}))}+trac(H(J_{1}))}{2}$

The largest part of the eigenvalues of the matrix $H(J_{1})$ is given by

$$\begin{aligned} \lambda _{1}(H(J_{1}))=\frac{\sqrt{ \left( trac(H(J_{1})) \right) ^2-4 Det(H(J_{1}))} \pm trac(H(J_{1}))}{2}\\ \text {or}, \lambda _1(H(J_{1}))=\frac{\sqrt{k_{x}^2 \left( \alpha _{x} P_{x1}-\alpha _{y} P_{y1} \right) ^2+r_{x}^2 P_{x1}^2}-r_{x} P_{x1}}{2k_{x}}. \end{aligned}$$

Therefore, the stable equilibrium point $(P_{x1}, P_{y1})$ is reactive under the disturbance made by prey harvesting if $\lambda _{1}(H(J_{1}))>0$, i.e., either $\alpha _{x} P_{x1}-\alpha _{y} P_{y1}<0$ or, $\alpha _{x} P_{x1}-\alpha _{y} P_{y1}>0$

i.e., either $e_{x}<e_{x1}$ or, $e_{x}>e_{x1}$ where $e_{x1}=\frac{\alpha _{x}}{\alpha _{y}q_{x}}\left[ \frac{\alpha _{y}r_{x}}{\alpha _{x}}(1-\frac{m_{y}}{k_{x}\alpha _{y}})-\frac{\alpha _{x}m_{y}}{\alpha _{y}} \right]$. Clearly, $P_{y1}=0\implies e_{xext}=\frac{r_{x}}{q_{x}}(1-\frac{m_{y}}{k_{x}\alpha _{y}})$

Hence, predator species goes to extinction at $e_{xext}=\frac{r_{x}}{q_{x}}(1-\frac{m_{y}}{k_{x}\alpha _{y}})$ Now $\frac{\hbox {d}\lambda _1(H(J_{1}))}{\hbox {d}e_{x}}<0$ when $e_{x}\in (0, e_{x1})$ and $\frac{\hbox {d}\lambda _1(H(J_{1}))}{\hbox {d}e_{x}}>0$ when $e_{x}\in (e_{x1}, e_{xext})$. The yield $Y_{x}=\frac{q_{x}e_{x}m_{y}}{\alpha _{y}}$ has no maximum in $e_{x}\in (e_{x1}, e_{xext})$.

Therefore, the statements contain in Proposition 1 is proved and given below:

• 1. If $e_{x}\in (0, e_{x1})$, the stable equilibrium point $(P_{x1},P_{y1})$ remains reactive ($\lambda _1(H(J_{1}))>0$) under the disturbance made by prey harvesting and the strength of reactivity decreases with $e_{x}$.

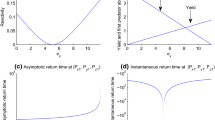
• 2. If $e_{x}\in (e_{x1}, e_{xext})$, the stable equilibrium point $(P_{x1},P_{y1})$ remains also reactive ($\lambda _1(H(J_{1}))>0$) under the disturbance made by prey harvesting and the strength of reactivity increases with $e_{x}$ but MSY rule does not hold good. (see Fig. 1)

Appendix B. Proof of Proposition 2.

The interior equilibrium of model (2) is given by $(P_{x2}, P_{y2})$:

$$\begin{aligned} P_{x2}=\frac{m_{y}+q_{y}e_{y}}{\alpha _{y}} \text { and } P_{y2}=\frac{r_{x}}{\alpha _{x}}(1-\frac{m_{y}+q_{y}e_{y}}{\alpha _{y}k_{x}}) \end{aligned}$$

where $e_{y}<\frac{\alpha _{y}k_{x}-m_{y}}{q_{y}}$.

Following the method which already applied in “Appendix A”, we get the largest eigenvalue of the Hermitian matrix is given by at ($(P_{x2}, P_{y2})$):

$$\begin{aligned} \lambda _{2}(H(J_{2}))=\frac{\sqrt{ \left( trac(H(J_{2})) \right) ^2-4 Det(H(J_{2}))}+trac(H(J_{2}))}{2} \\ \text {or}, \lambda _2(H(J_{2}))=\frac{\sqrt{k_{x}^2 \left( \alpha _{x} P_{x2}-\alpha _{y} P_{y2} \right) ^2+r_{x}^2 P_{x2}^2}-r_{x} P_{x2}}{2k_{x}}. \end{aligned}$$

Therefore, the stable equilibrium point $(P_{x2}, P_{y2})$ is reactive under the disturbance made by prey harvesting if $\lambda _{2}(H(J_{2}))>0$, i.e., either $\alpha _{x} P_{x2}-\alpha _{y} P_{y2}<0$ or, $\alpha _{x} P_{x2}-\alpha _{y} P_{y2}>0$

i.e., either $e_{y}<e_{y1}$ or, $e_{y}>e_{y1}$ where $e_{y1}=\frac{1}{q_{y}}\left( \frac{\alpha _{y}^{2}r_{x}k_{x}}{\alpha _{y}r_{x}+\alpha _{x}^{2}k_{x}}-m_{y} \right)$

Clearly, $P_{y2}=0\implies e_{yext}=\frac{\alpha _{y}k_{x}-m_{y}}{q_{y}}$

Hence, predator species goes to extinction at $e_{yext}=\frac{\alpha _{y}k_{x}-m_{y}}{q_{y}}$

Now $\frac{\hbox {d}\lambda _2(H(J_{2}))}{\hbox {d}e_{y}}<0$ when $e_{y}\in (0, e_{y1})$ and $\frac{\hbox {d}\lambda _2(H(J_{2}))}{\hbox {d}e_{y}}>0$ when $e_{y}\in (e_{y1}, e_{yext})$.

The yield $Y_{y}=\frac{q_{y}e_{y}r_{x}}{\alpha _{x}}(1-\frac{m_{y}+q_{y}e_{y}}{\alpha _{y}k_{x}})$ has maximum at $e_{ymax}=\frac{e_{yext}}{2}$ in $e_{y}\in (e_{y1}, e_{yext})$.

since $\frac{\hbox {d}Y_{y}}{\hbox {d}e_{y}}=0\implies e_{ymax}=\frac{\alpha _{y}k_{x}-m_{y}}{2 q_{y}}$ and $\frac{\hbox {d}^2Y_{y}}{\hbox {d}e_{y}^2}<0$ at $e_{y}=e_{ymax}$

Therefore, the statement contained in Proposition 2 is proved and given below:

• 1. If $e_{y}\in (0, e_{y1})$, the stable equilibrium point $(P_{x2},P_{y2})$ remains reactive ($\lambda _1(H(J_{2}))>0$) under the predator harvesting and the strength of reactivity decreases with $e_{y}$.

• 2. If $e_{y}{\in } (e_{y1}, e_{yext})$, the stable equilibrium point $(P_{x2},P_{y2})$ remains reactive ($\lambda _1(H(J_{2}))>0$) under the disturbance made by predator harvesting and the strength of reactivity increases with $e_{y}$ and MSY rule holds good. (see Fig. 3)

Appendix C. Proof of Proposition 3.

The interior equilibrium of model (3) is given by $(P_{x3}, P_{y3})$:

$$\begin{aligned} P_{x3}=\frac{\left( m_{y}+q_{y}e_{y}\right) }{\alpha _{y}} \text { and } P_{y3}=\frac{\alpha _{y}k_{x}( r_{x}-q_{x}e_{x})-(q_{y}e_{y}+m_{y})r_{x}}{\alpha _{x}\alpha _{y}k_{x}} \end{aligned}$$

where $\alpha _{y}k_{x}q_{x}e_{x}+r_{x}q_{y}e_{y}<r_{x}\left( \alpha _{y}k_{x}-m_{y}\right)$.

Following the method which already applied in “Appendix A”, we get the largest eigenvalue of the Hermitian matrix is given by at $(P_{x3}, P_{y3})$:

$$\begin{aligned} \lambda _{3}(H(J_{3}))=\frac{\sqrt{ \left( trac(H(J_{3})) \right) ^2-4 Det(H(J_{3}))}+trac(H(J_{3}))}{2} \\ \text {or}, \lambda _3(H(J_{3}))=\frac{\sqrt{k_{x}^2 \left( \alpha _{x} P_{x3}-\alpha _{y} P_{y3} \right) ^2+r_{x}^2 P_{x3}^2}-r_{x} P_{x3}}{2k_{x}}. \end{aligned}$$

Therefore, the stable equilibrium point $(P_{x3}, P_{y3})$ is reactive under the disturbance made by selective harvesting on both (prey and predator) if $\lambda _{3}(H(J_{3}))>0$, i.e., either $\alpha _{x} P_{x3}-\alpha _{y} P_{y3}<0$ or, $\alpha _{x} P_{x3}-\alpha _{y} P_{y3}>0$

i.e., either $\left( \alpha _{x}^2k_{x} +\alpha _{y} r_{x}\right) q_{y}e_{y}+\alpha _{y}^2 k_{x} q_{x} e_{x}\le \alpha _{y}r_{x}\left( \alpha _{y}k_{x}-m_{y}\right) -\alpha _{x}^2 k_{x}m_{y}$ or, $\left( \alpha _{x}^2 +\alpha _{y} r_{x}\right) q_{y}e_{y}+\alpha _{y}^2 k_{x} q_{x} e_{x}\ge \alpha _{y}r_{x}\left( \alpha _{y}k_{x}-m_{y}\right) -\alpha _{x}^2 k_{x}m_{y}$.

Clearly, $P_{y3}=0\implies \alpha _{y}k_{x}q_{x}e_{x}+r_{x}q_{y}e_{y}=r_{x}\left( \alpha _{y}k_{x}-m_{y}\right)$

Hence, predator species goes to extinction when $\alpha _{y}k_{x}q_{x}e_{x}+r_{x}q_{y}e_{y}=r_{x}\left( \alpha _{y}k_{x}-m_{y}\right)$

The yield $Y_{xy}=q_{x}e_{x}\left( \frac{m_{y}+q_{y}e_{y}}{\alpha _{y}}\right) +q_{y}e_{y}\left( \frac{\alpha _{y}k_{x}( r_{x}-q_{x}e_{x})-(q_{y}e_{y}+m_{y})r_{x}}{\alpha _{x}\alpha _{y}k_{x}}\right)$ has no maximum.

Let

$$\begin{aligned} H_{xy}= \begin{pmatrix} \frac{\partial ^2Y_{xy}}{\partial e_{x}^{2}} &{} \frac{\partial ^2Y_{xy}}{\partial e_{x} \partial e_{y}} \\ \frac{\partial ^2Y_{xy}}{\partial e_{y} \partial e_{x}} &{} \frac{\partial ^2Y_{xy}}{\partial e_{y}^{2}} \\ \end{pmatrix}. \end{aligned}$$

Clearly, $\frac{\partial ^2Y_{xy}}{\partial e_{x}^{2}}=0$ and implies the Hessian matrix corresponding to $Y_{xy}$ is not negative definite. Consequently, $Y_{xy}$ has no maximum and MSTY does not exist.

Therefore, the statements contained in Proposition 3 are proved and given below:

• 1. If $(e_{x}, e_{y})\in R_{xy}^{-}$ and $R_{xy}^{+}$, the stable equilibrium point $(P_{x3},P_{y3})$ remains reactive ($\lambda _3(H(J_{3}))>0$) under the multiple disturbances made by selective harvesting on both.

• 2. If $(e_{x}, e_{y})\in R_{xy1}\subseteq R_{xy}^{+}$, the reactivity of stable equilibrium point $(P_{x3},P_{y3})$ may be implied extinction of predator species and consequently MSTY rule not holds good. (see Fig. 5)

Appendix A*. Proof of Proposition 1*.

These parts give the technical proof of the results of the analysis conducted in Sect. 3

The interior equilibrium point $(P_{x1*}, P_{y1*})$ is given by

$$\begin{aligned}&P_{x1*}=\frac{k_{x} \left( \alpha _{x} m_{y}+\gamma _{y} r_{x}-\gamma _{y} q_{x} e_{x} \right) }{\alpha _{x} \alpha _{y} k_{x}+\gamma _{y} r_{x}} \text { and } P_{y1*}=\frac{\alpha _{y} k_{x} \left( r_{x}-q_{x}e_{x}\right) -m_{y} r_{x}}{\alpha _{x} \alpha _{y} k_{x}+\gamma _{y} r_{x}}) \text { with }\\&\quad e_{x}<min\left\{ \frac{\alpha _{x}m_{y}+\gamma _{y}r_{x}}{\gamma _{y}q_{x}}, \frac{\alpha _{y}k_{x}r_{x}-m_{y}r_{x}}{\alpha _{y}k_{x}q_{x}} \right\} . \end{aligned}$$

The Hermitian matrix is given by at $(P_{x1*}, P_{y1*})$

$$\begin{aligned} \displaystyle H(J_{1*})=\displaystyle \left[ \begin{array}{cc} \displaystyle -\frac{r_{x} P_{x1*}}{k_{x}} &{} \frac{-\alpha _{x} P_{x1*}+\alpha _{y} P_{y1*}}{2} \\ \frac{-\alpha _{x} P_{x1*}+\alpha _{y} P_{y1*}}{2} &{} -\gamma _{y}P_{y1*} \\ \end{array} \right] . \end{aligned}$$

and its characteristic equation is $det(H(J_{1*})-\lambda I)=\lambda ^2-(trac(H(J_{1*})))\lambda +det(H(J_{1*}))=0$ where $trac(H(J_{1*}))=-\left( \frac{r_{x} P_{x1}}{k_{x}}+\gamma _{y}P_{y1*}\right)$ and $det(H(J_{1*}))=\frac{r_{x}\gamma _{y} P_{x1*}P_{y1*}}{k_{x}} -\frac{(-\alpha _{x} P_{x1}+\alpha _{y} P_{y1})^2}{4}$.

The eigenvalues are: $\lambda =\frac{\sqrt{ \left( trac(H(J_{1*})) \right) ^2-4 Det(H(J_{1*}))} \pm trac(H(J_{1*}))}{2}$

The largest part of the eigenvalues of the matrix $H(J_{1*})$ is given by

$$\begin{aligned} \lambda _{1*}(H(J_{1*}))=\frac{\sqrt{ \left( trac(H(J_{1*})) \right) ^2-4 Det(H(J_{1*}))}+trac(H(J_{1*}))}{2} \end{aligned}$$

Now $\lambda _{1*}(H(J_{1*}))=0\implies k_{x}\left( \alpha _{y} P_{y1*}-\alpha _{x} P_{x1*}\right) ^2=4 r_{x}\gamma _{y}P_{x1*}P_{y1*}$

Clearly, $k_{x}\left( \alpha _{y} P_{y1*}-\alpha _{x} P_{x1*}\right) ^2=4 r_{x}\gamma _{y}P_{x1*}P_{y1*}$ is a quadratic equation of prey harvesting effort $e_{x}$.

Hence, the above equation has two roots of $e_{x}$ say $e_{x1*}$ and $e_{x2*}$ with $0<e_{x1*}<e_{x2*}$. Now $P_{y1*}=0\implies e_{x1ext}=\frac{\left( \alpha _{y}k_{x}-m_{y} \right) r_{x} }{\alpha _{y}k_{x}q_{x}}$

Therefore, predator species goes to extinction at $e_{x}=e_{x1ext}$

Clearly, $\lambda _{1*}(H(J_{1*}))>0$ when $e_{x}\in (0, e_{x1*})$ and $e_{x}\in (e_{x2*}, e_{x1ext})$ and $\lambda _{1*}(H(J_{1*}))<0$ when $e_{x}\in (e_{x1*}, e_{x2*})$

The yield $Y_{x1}=\frac{q_{x}e_{x}k_{x} \left( \alpha _{x} m_{y}+\gamma _{y} r_{x}-\gamma _{y} q_{x} e_{x} \right) }{\alpha _{x} \alpha _{y} k_{x}+\gamma _{y} r_{x}}$ has maximum at $e_{x1max}=\frac{\alpha _{x}m_{y}+\gamma _{y}r_{x}}{2q_{x}\gamma _{y}}$

since $\frac{\hbox {d}Y_{x1}}{\hbox {d}e_{x}}=0\implies e_{x1max}=\frac{\alpha _{x}m_{y}+\gamma _{y}r_{x}}{2q_{x}\gamma _{y}}$ and $\frac{\hbox {d}^2Y_{x1}}{\hbox {d}e_{x}^2}<0$ at $e_{x}=e_{x1max}$

Therefore, the statements contained in Proposition 1* are proved and given below:

• 1. If $e_{x}\in (0, e_{x1*})$, then the stable equilibrium point $(P_{x1*},P_{y1*})$ remains reactive ($\lambda _1*(H(J_{1*}))>0$) under the disturbance made by prey harvesting and the strength of reactivity decreases with $e_{x}$.

• 2. If $e_{x}\in (e_{x1*}, e_{x2*})$, then the stable equilibrium point $(P_{x1*},P_{y1*})$ remains non-reactive ($\lambda _1*(H(J_{1*}))<0$) under the disturbance made by prey harvesting and MSY rule holds good.

• 3. If $e_{x}\in (e_{x2*}, e_{x1ext})$, then the stable equilibrium point $(P_{x1*},P_{y1*})$ remains again reactive ($\lambda _1*(H(J_{1*}))>0$) under the disturbance made by prey harvesting (see Fig. 6).

Appendix B*. Proof of Proposition 2*.

The interior equilibrium of model (6) is given by $(P_{x2*}, P_{y2*})$:

$$\begin{aligned}&P_{x2*}=\frac{\alpha _{x} k_{x} \left( m_{y}+q_{y}e_{y}\right) +\gamma _{y}k_{x}r_{x}}{\alpha _{x} \alpha _{y} k_{x}+\gamma _{y}r_{x}} \text { and } P_{y2*}=\frac{\left( \alpha _{y}k_{x}r_{x}-r_{x}m_{y}-r_{x}q_{y}e_{y}\right) }{\alpha _{x}\alpha _{y}k_{x}+\gamma _{y}r_{x}} \text { with } \\&\quad e_{y}<\frac{\left( \alpha _{y}k_{x}-m_{y}\right) r_{x}}{r_{x}q_{y}} . \end{aligned}$$

Following the method which already applied in “Appendix A*”, we get the largest eigenvalue of the Hermitian matrix is given by at ($(P_{x2*}, P_{y2*})$): The largest part of the eigenvalues of the matrix $H(J_{2*})$ is given by

$$\begin{aligned} \lambda _{2*}(H(J_{2*}))=\frac{\sqrt{ \left( trac(H(J_{2*})) \right) ^2-4 Det(H(J_{2*}))}+trac(H(J_{2*}))}{2} \end{aligned}$$

Now $\lambda _{2*}(H(J_{2*}))=0\implies k_{x}\left( \alpha _{y} P_{y2*}-\alpha _{x} P_{x2*}\right) ^2=4 r_{x}\gamma _{y}P_{x2*}P_{y2*}$

Clearly, $k_{x}\left( \alpha _{y} P_{y2*}-\alpha _{x} P_{x2*}\right) ^2=4 r_{x}\gamma _{y}P_{x2*}P_{y2*}$ is a quadratic equation of prey harvesting effort $e_{y}$.

Hence, the above equation has two roots of $e_{y}$ say $e_{y1*}$ and $e_{y2*}$ with $0<e_{y1*}<e_{y2*}$. Now $P_{y2*}=0\implies e_{y1ext}=\frac{\left( \alpha _{y}k_{x}-m_{y}\right) r_{x}}{r_{x}q_{y}}$

Therefore, predator species goes to extinction at $e_{y}=e_{y1ext}$

Clearly, $\lambda _{2*}(H(J_{2*}))>0$ when $e_{y}\in (0, e_{y1*})$ and $e_{y}\in (e_{y2*}, e_{y1ext})$ and $\lambda _{2*}(H(J_{2*}))<0$ when $e_{y}\in (e_{y1*}, e_{y2*})$

The yield $Y_{y1}=\frac{q_{y}e_{y}\left( \alpha _{y}k_{x}r_{x}-r_{x}m_{y}-r_{x}q_{y}e_{y}\right) }{\alpha _{x}\alpha _{y}k_{x}+\gamma _{y}r_{x}}$ has maximum at $e_{y1max}=\frac{\alpha _{x}m_{y}+\gamma _{y}r_{x}}{2q_{x}\gamma _{y}}$

since $\frac{\hbox {d}Y_{x1}}{\hbox {d}e_{x}}=0\implies e_{x1max}=\frac{\left( \alpha _{y}k_{x}-m_{y}\right) r_{x}}{2r_{x}q_{y}}$ and $\frac{\hbox {d}^2Y_{y1}}{\hbox {d}e_{y}^2}<0$ at $e_{y}=e_{y1max}$

Therefore, the statements contained in Proposition 2* are proved and given below:

• 1. If $e_{y}\in (0, e_{y1*})$, then the stable equilibrium point $(P_{x2*},P_{y2*})$ remains reactive ($\lambda _2*(H(J_{2*}))>0$) under the disturbance made by predator harvesting and the strength of reactivity decreases with $e_{y}$.

• 2. If $e_{y}\in (e_{y1*}, e_{y2*})$, then the stable equilibrium point $(P_{x2*},P_{y2*})$ remains non-reactive ($\lambda _2*(H(J_{2*}))<0$) under the disturbance made by predator harvesting.

• 3. If $e_{y}\in (e_{y2*}, e_{y1ext})$, then the stable equilibrium point $(P_{x2*},P_{y2*})$ remains again reactive ($\lambda _2*(H(J_{2*}))>0$) under the disturbance made by predator harvesting and MSY rule holds good. (see Fig. 8)

Appendix C*. Proof of Proposition 3*.

The interior equilibrium of model (7) is given by $(P_{x3*}, P_{y3*})$:

$$\begin{aligned} (P_{x3*}, P_{y3*})=\left( \frac{\alpha _{x}k_{x}\left( e_{y}q_{y}+m_{y}\right) +\gamma _{y}k_{y} \left( r_{x}-q_{x}e_{x}\right) }{\alpha _{x} \alpha _{y}k_{x}+\gamma _{y}r_{x}}, \frac{\alpha _{y}k_{x}r_{x}-m_{y}r_{x}-\alpha _{y}k_{x}q_{x}e_{x}-r_{x}q_{y}e_{y}}{\alpha _{x}\alpha _{y} k_{x}+\gamma _{y}r_{x}}\right) , \end{aligned}$$

where $\gamma _{y}k_{x}q_{x}e_{x}-\alpha _{x}k_{x}q_{y}e_{y}<\alpha _{x}k_{x}m_{y}+\gamma _{y}k_{x}r_{x}$ and $\alpha _{y} k_{x}q_{x}e_{x}+r_{x}q_{y}e_{y}<\left( \alpha _{y}k_{x}-m_{y}\right) r_{x}$.

Following the method which already applied in “Appendix A*”, we get the largest eigenvalue of the Hermitian matrix given by at $(P_{x3*}, P_{y3*})$:

$$\begin{aligned} \lambda _{3*}(H(J_{3*}))=\frac{\sqrt{ \left( trac(H(J_{3*})) \right) ^2-4 Det(H(J_{3*}))}+trac(H(J_{3*}))}{2}. \end{aligned}$$

Therefore, the stable equilibrium point $(P_{x3*}, P_{y3*})$ is reactive under the disturbance made by selective harvesting on both (prey and predator) if $\lambda _{3*}(H(J_{3*}))>0$, i.e., either $det(H(J_{3*}))<0$ or, $det(H(J_{3*}))>0$

i.e., $k_{x}\left( \alpha _{y} P_{y3*}-\alpha _{x} P_{x3*}\right) ^2=4 r_{x}\gamma _{y}P_{x3*}P_{y3*}$.

Clearly, $P_{y3*}=0\implies \alpha _{y} k_{x}q_{x}e_{x}+r_{x}q_{y}e_{y}=\left( \alpha _{y}k_{x}-m_{y}\right) r_{x}$

Hence, predator species goes to extinction when $\alpha _{y} k_{x}q_{x}e_{x}+r_{x}q_{y}e_{y}=\left( \alpha _{y}k_{x}-m_{y}\right) r_{x}$

The yield $Y_{xy1}=q_{x}e_{x}\frac{\alpha _{x}k_{x}\left( e_{y}q_{y}+m_{y}\right) +\gamma _{y}k_{y} \left( r_{x}-q_{x}e_{x}\right) }{\alpha _{x} \alpha _{y}k_{x}+\gamma _{y}r_{y}} +q_{y}e_{y}\frac{\alpha _{y}k_{x}r_{x}-m_{y}r_{x}-\alpha _{y}k_{x}q_{x}e_{x}-r_{x}q_{y}e_{y}}{\alpha _{x}\alpha _{y} k_{x}+\gamma _{y}r_{x}}$ has maximum, since the Hessian matrix corresponding to $Y_{xy1}$ is negative definite.

Let

$$\begin{aligned} H_{xy1}= \begin{pmatrix} \frac{\partial ^2Y_{xy1}}{\partial e_{x}^{2}} &{} \frac{\partial ^2Y_{xy1}}{\partial e_{x} \partial e_{y}} \\ \frac{\partial ^2Y_{xy1}}{\partial e_{y} \partial e_{x}} &{} \frac{\partial ^2Y_{xy1}}{\partial e_{y}^{2}} \\ \end{pmatrix}. \end{aligned}$$

Clearly, $\frac{\partial ^2Y_{xy}}{\partial e_{x}^{2}}<0$ and $det(H_{xy1})>0$ which implies the Hessian matrix corresponding to $Y_{xy1}$ is negative definite. Consequently, $Y_{xy1}$ has maximum value and MSTY exists (see Fig. 10).

Therefore, the statements contained in Proposition 3* are proved and given below:

• 1. If $(e_{x}, e_{y})\in R_{xy1}$, the stable equilibrium point $(P_{x3*},P_{y3*})$ remains reactive ($\lambda _3*(H(J_{3*}))>0$) under the multiple disturbances made by selective harvesting on both and MSTY rule holds good (see Fig. 10).