U(5) and O(6) shape phase transitions via E(5) inverse square potential solutions

Abstract

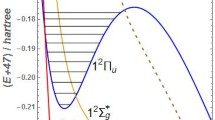
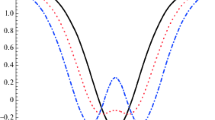
The inverse square potential is used to provide the ‘pictures’ of the transitions symmetry from U(5) to O(6) via the variational procedure of the E(5) solutions. The variation of the single-parameter $\beta _{0}$ of the inverse square potential shifts the E(5) solutions: the energy eigenvalues increase when $\beta _{0}$ increases. In the theoretical prediction of $R_{L/2}$, $\beta _{0}=0$ yields solutions that correspond to the U(5) symmetry of the Bohr Hamiltonian with $R_{4/2}=2.00$. As $\beta _{0}$ increases, the solutions of E(5) materialize with $R_{4/2}=2.189$ at $\beta _{0,max}=3.986$. The solutions leave E(5) and approach O(6) with $R_{4/2}=2.466$ at $\beta _{0}=25$. The solutions of $^{132}Xe$ and $^{134}Xe$ of the E(5) symmetry candidates are fitted and compared with the available experimental values. With the same variational method, the ratios of B(E2) transition rates within the ground state leave O(6) and approach E(5) solution as $\beta _{0}$ increases.

Graphic abstract

Appendix A: Mathematical procedure for calculating B(E2) transition probabilities

The B(E2) transition rates are given as

$$\begin{aligned}&B(E2;\varrho _{i}L_{i}\longrightarrow \varrho _{f}L_{f}) =\dfrac{1}{2L_{i}+1}|\left\langle \varrho _{f}L_{f}||T^{E2}|| \varrho _{i}L_{i}\right\rangle |^{2} \end{aligned}$$

(A1)

$$\begin{aligned}&=\dfrac{2L_{f}+1}{2L_{i}+1} B(E2;\varrho _{f}L_{f}\longrightarrow \varrho _{i}L_{i}) , \end{aligned}$$

(A2)

where L is the angular momentum, $\varrho$ is another quantum number different from L, i denotes initial state, f denotes final state and $T^{E2}$ is the quadrupole operator which has been defined as [29]

$$\begin{aligned} T^{E2}_{\mu }= t\alpha _{\mu }=t\beta \left[ D_{\mu ,0}^{(2)}(\theta _{i})cos\gamma + \dfrac{1}{\sqrt{2}}(D_{\mu ,2}^{(2)}(\theta _{i}) + D_{\mu ,-2}^{(2)}(\theta _{i}))sin \gamma \right] . \end{aligned}$$

(A3)

$\theta _{i}$, $\gamma$ and $\beta$ have been defined in the manuscript. t is a scale factor and $D(\theta _{i})$ represent the Wigner functions of the Euler angle. By following the procedures listed in [29],

$$\begin{aligned} B(E2; L_{n_{\beta },\tau }\longrightarrow (L+2)_{n_{\beta }^{\prime },\tau +1})=\dfrac{(\tau +1)(4\tau +5)}{(2\tau +5)(4\tau +1)}t^{2}I^{2}_{n_{\beta }^{\prime }+1;n_{\beta },\tau } \qquad ; L=2\tau , \end{aligned}$$

(A4)

and

$$\begin{aligned}&B(E2; (L+2)_{n_{\beta }^{\prime },\tau +1}\longrightarrow L_{n_{\beta },\tau })=\dfrac{\tau +1}{2\tau +5}t^{2}I^{2}_{n_{\beta }^{\prime }+1;n_{\beta },\tau } \qquad \qquad \qquad ; L=2\tau . \end{aligned}$$

(A5)

$$\begin{aligned}&I_{n_{\beta }^{\prime }+1;n_{\beta },\tau } = \int _{\beta _{0}=0}^{\beta _{0}=\beta _{\omega }}\beta R_{n_{\beta }^{\prime },\tau +1}(\beta ) R_{n_{\beta },\tau }(\beta )\beta ^{4} d\beta \quad \forall \quad \beta _{\omega }>0, \end{aligned}$$

(A6)

$R_{n_{\beta },\tau }(\beta )$ are the wavefunctions which have been obtained, $n_{\beta }^{\prime }=s^{\prime }-1$ as $n_{\beta } = s-1$ which involve Bessel functions of the wavefunctions. All transitions are normalized to $B(E2 : 2_{0,1}\longrightarrow 0_{0,1} ) = 100$. The lowest B(E2) ratios within the gsb band is

$$\begin{aligned} \dfrac{B(E2; (L+2)_{n_{\beta },\tau +1}\longrightarrow L_{n_{\beta },\tau })}{B(E2; 2_{0,1}\longrightarrow 0_{0,0})} = \dfrac{B(E2; L_{i}\longrightarrow L_{f})}{B(E2, 2_{g}\longrightarrow 0_{g})}= \dfrac{(\tau +1)}{(2\tau +5)}(2n_{\beta }+2\tau +5); \qquad L=2\tau . \end{aligned}$$

(A7)