Wigner functions in quantum mechanics with a minimum length scale arising from generalized uncertainty principle

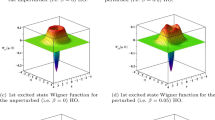
Abstract

In this paper, we generalize the concept of Wigner function in the case of quantum mechanics with a minimum length scale arising due to the application of a generalized uncertainty principle. We present the phase space formulation of such theories following GUP and show that the Weyl transform and the Wigner function satisfy most of their known properties in standard quantum mechanics. We utilize the generalized Wigner function to calculate the phase space average of the Hamiltonian of a quantum harmonic oscillator satisfying deformed Heisenberg algebra. It is also shown that averages of certain quantum mechanical operators in such theories may restrict the value of the deformation parameter specifying the degree of deformation of Heisenberg algebra. All the results presented are for pure states. The results can be generalized for mixed states.

Appendices

Appendix

A Uniqueness of Weyl transform and Wigner function

Our proof of the uniqueness of the definition of Weyl transform in QM following GUP is based on the assumption that the Weyl transform of the identity operator is unity. Keeping this in mind, we now introduce a general function $f(x,p,u,\beta )$ and define the Weyl transform in deformed Heisenberg Algebra as :

$$\begin{aligned} \tilde{A}(x,p) = \int du e^{\frac{ixu}{\hbar }}f(x,p,u,\beta ) \langle p+u/2|\mathbf{A}|p-u/2\rangle \,. \end{aligned}$$

(76)

Our assumption $\tilde{I} = 1$ demands

$$\begin{aligned} \tilde{I} = \int du e^{\frac{ixu}{\hbar }}f(x,p,u,\beta )\langle p+u/2|\mathbf{I}|p-u/2\rangle = 1\,. \end{aligned}$$

(77)

The above integration can easily be done showing that

$$\begin{aligned} f(p,u=0,\beta ) = \frac{1}{(1+\beta p^2)}\,. \end{aligned}$$

(78)

The above form of f does not depend upon x. Henceforth, we assume that in general f only depends on p and u. Now, we want our Weyl transform to satisfy the property

$$\begin{aligned} \frac{1}{h}\int \int \tilde{A}\tilde{B}dxdp= \mathrm{Tr}[\mathbf{A} \mathbf{B}]\,. \end{aligned}$$

(79)

This is very important for our analysis based on the momentum states as it is the key equation to calculate the averages of observable. The left hand side of the above equation can be written as:

$$\begin{aligned} \frac{1}{h}\int \int \tilde{A}\tilde{B}dxdp= & {} \frac{1}{h}\int \int \int \int e^{i\frac{(u_1 + u_2)x}{\hbar }}\langle p+ u_1/{2|\mathbf{A}|p- u_1/2\rangle \langle p+ u_2/2|\mathbf{B}|p- u_2/2\rangle }\\&\times f(\beta , p, u_1)f(\beta , p, u_2)\, du_1 \,du_2 \,dx \,dp\,. \end{aligned}$$

Integrating with respect to x we get a delta function

$$\begin{aligned} \delta (u_1 + u_2) = \frac{1}{2\pi \hbar }\int e^{\frac{i(u_1 + u_2)x}{\hbar }} dx, \end{aligned}$$

(80)

using which we can now write,

$$\begin{aligned} \frac{1}{h}\int \int \tilde{A}\tilde{B}dxdp= & {} \int \int \int \delta (u_1+u_2)\langle p+ u_1/2|\mathbf{A}|p- u_1/2\rangle \langle p+ u_2/2|\mathbf{B}|p- u_2/2\rangle \\&\times f(\beta , p, u_1)f(\beta , p, u_2) \,dp \,du_1\,du_2\\= & {} \int \int \langle p+ u_1/2|\mathbf{A}|p- u_1/2\rangle \langle p- u_1/2 |\mathbf{B}|p\\&+ u_1/2 \rangle f(\beta , p, u_1)f(\beta , p, -u_1) du_1 dp\,. \end{aligned}$$

Defining new variables as $p + \frac{u_{1}}{2} = v$ and $p - \frac{u_{1}}{2} = y$ such that $dp du_1 = dvdy$ the above expression transforms to

$$\begin{aligned} \frac{1}{h}\int \int \tilde{A}\tilde{B}dxdp= \int \int \langle v|\mathbf{A}|y\rangle \langle y|\mathbf{B}|v\rangle f(\beta , p, 2(v-y))f(\beta , p, -2(v-y)) dy\,dv\,.\nonumber \\ \end{aligned}$$

(81)

Now, the right hand side of Eq. (79) is

$$\begin{aligned} \mathrm{Tr}[\mathbf{A \mathbf{B}}] \equiv \int \frac{\langle v|\mathbf{A \mathbf{B}}|v \rangle }{1+\beta v^2} dv=\int \frac{\langle v|\mathbf{A}|y\rangle \langle y|\mathbf{B}|v\rangle }{(1+\beta v^2)(1+\beta y^2)}\,dv\,dy\,. \end{aligned}$$

(82)

We know that if Eq. (81) is equal to the right hand side of Eq. (79), then from the last equation above we must have

$$\begin{aligned} f(\beta , p, 2(v-y))f(\beta , p, -2(v-y))=\frac{1}{(1+\beta v^2)(1+\beta y^2)}\,. \end{aligned}$$

(83)

The above equation yields

$$\begin{aligned} f(\beta ,p,u_1)f(\beta ,p,-u_1) = \frac{1}{\left[ 1+\beta (p+u_1/2)^2\right] \left[ 1+\beta (p-u_1/2)^2\right] }\,. \end{aligned}$$

(84)

This equation provides three different possible forms of the function $f(\beta ,p,u)$ as:

$$\begin{aligned} f(p,u,\beta ) = \frac{1}{\left[ 1+\beta (p+u/2)^2\right] }, \end{aligned}$$

(85)

or

$$\begin{aligned} f(p,u,\beta ) = \frac{1}{\left[ 1+\beta (p-u/2)^2\right] }, \end{aligned}$$

(86)

or

$$\begin{aligned} f(p,u,\beta ) = \frac{1}{\left[ 1+\beta (p+u/2)^2\right] ^{\frac{1}{2}}\left[ 1+\beta (p-u/2)^2\right] ^{\frac{1}{2}}}. \end{aligned}$$

(87)

The Weyl transform of x ($\tilde{x}$) using the above forms of $f(p,u,\beta )$ are given respectively by:

$$\begin{aligned} \tilde{x}= & {} x(1+\beta p^2) - i\hbar \beta p, \end{aligned}$$

(88)

$$\begin{aligned} \tilde{x}= & {} x(1+\beta p^2) + i\hbar \beta p, \end{aligned}$$

(89)

and

$$\begin{aligned} \tilde{x} = x(1+\beta p^2)\,. \end{aligned}$$

(90)

But, Weyl transform of observable (Hermitian operators) is purely real, so we can disregard the form of $f(p,u,\beta )$ which produces complex Weyl transforms. Thus we get the unique form of the Weyl transform to be:

$$\begin{aligned} \tilde{A}(x,p) = \int du e^{\frac{ixu}{\hbar }}\frac{\langle p+u/2|\mathbf{A}|p-u/2\rangle }{\left[ 1+\beta (p+u/2)^2\right] ^{\frac{1}{2}} \left[ 1+\beta (p-u/2)^2\right] ^{\frac{1}{2}}}\,. \end{aligned}$$

(91)

This is exactly the Weyl transform we have used in the paper.

B High momentum behavior of the Wigner function

Wigner function is given by :

$$\begin{aligned} W(x,p) = \frac{1}{h}\int e^{\frac{ix u}{\hbar }} \frac{\phi (p+ u/2)\phi ^*(p- u/2)}{\left[ 1+\beta (p-\frac{u}{2})^{2}\right] ^{\frac{1}{2}}\left[ 1+\beta (p+\frac{u}{2})^{2}\right] ^{\frac{1}{2}}}du. \end{aligned}$$

(92)

Let power of p in the wave function $\phi$ be m. Thus for large p, the Wigner function W(x, p) will go as $p^{2m-2}$. Now, for harmonic oscillator, $\phi$ takes the form :

$$\begin{aligned} \phi _{n}(p) \propto \frac{1}{(1+\beta p^{2})^{\sqrt{q+r_{n}}}}\,F\left( a_{n},-n,c_{n};\frac{1+i\sqrt{\beta }p}{2}\right) , \end{aligned}$$

(93)

where $F\left( a_{n},-n,c_{n};\frac{1+i\sqrt{\beta }p}{2}\right)$ is the Hypergeometric polynomial function or order n. From these facts we can write $m = n-2\sqrt{q+r_n} = n-2j$ where $j \equiv \sqrt{q+r_{n}}=\frac{1}{2}\left( n+\frac{1}{2}\right) +\frac{1}{4}\sqrt{1+16r}$. Therefore $W(x,p) \propto p^{2(n-2j)-2}$ in the high momentum limit.