Ferromagnetism of the semi-simple cubic lattice

Abstract

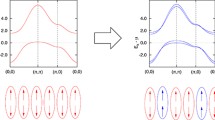
Heisenberg ferromagnet on a lattice with a low coordination number, $Z=3$, has been studied by means of high-temperature series and harmonic spin-wave expansion. The lattice is constructed by removing every second bond from the simple cubic lattice and therefore called ’semi-simple cubic’; it is topologically similar to the Laves graph, alias $K_4$ crystal. The openness of the lattice does not prevent ferromagnetic ordering and the thermal dependence of spontaneous magnetization differs little from that of other common lattices with higher Z. The study extends naturally toward a more general model where the bonds previously removed are now reinstated but endowed with a distinct exchange integral, $J_2$. We concentrate on the more interesting frustrated case, $J_2<0<J_1$, and a first prediction in this direction is that ferromagnetism disappears at $J_2/J_1=2\surd 2-3=-0.172$, giving way to a long-wavelength spiral structure propagating along [111].

Appendices

Spin-wave spectrum, $J_{1}-J_{2}$ model

Consider the lattice depicted in Fig. 1, the interactions along the bold and thin bonds being $J_{1}$ and $J_{2}$, respectively. This is a bcc Bravais lattice with four sites in the primitive cell. The Bravais vectors are as follows:

$$\begin{aligned} {\mathbf {a}}^{\prime }&=\frac{a}{2}\left( \hat{{\mathbf {x}}} +\hat{{\mathbf {y}}}-\hat{\mathbf {z}}\right) ,\\ \mathbf {b^{\prime }}&=\frac{a}{2}\left( -\hat{\mathbf {x}} +\hat{\mathbf {y}}+\hat{\mathbf {z}}\right) ,\\ \mathbf {c}^{\prime }&=\frac{a}{2} \left( \hat{\mathbf {x}}-\hat{\mathbf {y}}+\hat{\mathbf {z}}\right) , \end{aligned}$$

where $\hat{\mathbf {x}}$, $\hat{\mathbf {y}}$, and $\hat{\mathbf {z}}$ are unit vectors parallel to the edges of the cube. The four spins in the primitive cell have the following positions:

$$\begin{aligned} \mathbf {r}_{0}&=\mathbf {0},\quad \mathbf {r}_{1}=\frac{a}{2}\, \hat{\mathbf {x}},\\ \mathbf {r}_{2}&=\frac{a}{2}\, \hat{\mathbf {y}},\quad \mathbf {r}_{3}=\frac{a}{2}\, \hat{\mathbf {z}}. \end{aligned}$$

We write the Heisenberg Hamiltonian in the following form:

$$\begin{aligned} {\hat{H}}=-\sum _{n=1,2}J_{n}\sum _{\mathbf {R}}\sum _{j=0}^3 \sum _{k=1}^3 \hat{\mathbf {S}}_{\mathbf {R}+\mathbf {r}_j}\cdot \hat{\mathbf {S}}_{\mathbf {R}+\mathbf {r}_j+\mathbf {g}_{jkn}}. \end{aligned}$$

(A.1)

Here, $\mathbf {R}$ is a vector running over all sites of the Bravais lattice and $\mathbf {g}_{jkn}$ is a bond vector connecting the spin situated at $\mathbf {R}+\mathbf {r}_j$ with its $k\mathrm{th}$ nearest neighbor of kind n (with whom the interaction is of intensity $J_n$). The exchange energy of one pair of spins equals $-2J_n\hat{\mathbf {S}}_{\mathbf {R}+\mathbf {r}_j}\cdot \hat{\mathbf {S}}_{\mathbf {R}+\mathbf {r}_j+\mathbf {g}_{jkn}}$, for each pair enters twice in the sum.

We introduce spin deviation operators via Holstein–Primakoff bosonization,

$$\begin{aligned} {\hat{S}}_{\mathbf {R}}^{+}\equiv & {} \sqrt{2S}f_{\mathbf {R}}(S)\, b_{\mathbf {R}},\ {\hat{S}}_{\mathbf {R}}^{-}\equiv \sqrt{2S}\, b_{\mathbf {R}}^{\dagger } f_{\mathbf {R}}(S),\nonumber \\ {\hat{S}}_{\mathbf {R}}^{z}\equiv & {} S-{\hat{n}}_{\mathbf {R}},\ {\hat{n}}_{\mathbf {R}}=b_{\mathbf {R}}^{\dagger }b_{\mathbf {R}} \end{aligned}$$

(A.2)

$$\begin{aligned} f_{\mathbf {R}}(S)= & {} \sqrt{1-{\hat{n}}_{\mathbf {R}}/2S} \nonumber \\= & {} 1-\left( {\hat{n}}_{\mathbf {R}}/4S\right) -\textstyle \frac{1}{32}\left( {\hat{n}}_{\mathbf {R}}/S\right) ^{2}+\cdots \end{aligned}$$

(A.3)

The ferromagnetic ground state is the vacuum state for the bosonic operators, $b\left| \mathrm {FM}\right\rangle =0$, $b_{\mathbf {R}}b_{\mathbf {R}}^{\dagger }-b_{\mathbf {R}}^{\dagger }b_{\mathbf {R}}=1$. We set Eqs. (A.2, A.3) into Eq. (A.1) and retain only quadratic terms,

$$\begin{aligned} {\hat{H}} =&E_{0}+{\hat{H}}_{\mathrm {SW}},\nonumber \\ E_{0} \equiv&-12(J_1+J_2)S^{2}N_{R}, \end{aligned}$$

(A.4)

$$\begin{aligned} {\hat{H}}_{\mathrm {SW}} \equiv&e\sum _{\mathbf {R},j} b_{\mathbf {R}+\mathbf {r}_j}^{\dagger } b_{\mathbf {R}+\mathbf {r}_j} \nonumber \\&-\sum _{n}t_{n}\sum _{\mathbf {R},j,k} b_{\mathbf {R}+\mathbf {r}_j}^{\dagger } b_{\mathbf {R}+\mathbf {r}_j+\mathbf {g}_{jkn}},\nonumber \\ e \equiv&3\left( t_{1}+t_{2}\right) ,\quad t_{n}\equiv 2J_{n}S. \end{aligned}$$

(A.5)

Here, $N_{R}$ is the total number of cells in the lattice. Now spin-wave operators are introduced as Fourier transforms of the spin deviation operators,

$$\begin{aligned} b_{j\mathbf {q}}=\frac{1}{\sqrt{N_{R}}}\sum _{\mathbf {R}}e^{i\mathbf {q}\cdot \mathbf {R}}b_{\mathbf {R}+\mathbf {r}_j}. \end{aligned}$$

(A.6)

When expressed in terms of these operators, the Hamiltonian (A.5) becomes

$$\begin{aligned} {\hat{H}}_{\mathrm {SW}}=\sum _{\mathbf {q},i,j} L_{ij} b_{i\mathbf {q}}^{\dagger } b_{j\mathbf {q}}. \end{aligned}$$

(A.7)

Here, $L_{ij}$ is the Liouvillian superoperator matrix, $L_{ij}=\left[ \left[ b_{i\mathbf {q}},{\hat{H}}_{\mathrm {SW}} \right] ,b_{j\mathbf {q}}^{\dagger } \right]$. It has the following explicit form:

$$\begin{aligned} \mathbf {L}=\begin{pmatrix}e &{} -t_{1}-t_{2}e^{-i\mathbf {q} \left( \mathbf {a}^{\prime }+\mathbf {c}^{\prime }\right) } &{} -t_{1}-t_{2}e^{-i\mathbf {q}\left( \mathbf {a}^{\prime }+\mathbf {b}^{\prime }\right) } &{} -t_{1}-t_{2}e^{-i\mathbf {q}\left( \mathbf {b}^{\prime }+\mathbf {c}^{\prime }\right) }\\ -t_{1}-t_{2}e^{i\mathbf {q}\left( \mathbf {a}^{\prime }+\mathbf {c}^{\prime }\right) } &{} e &{} -t_{1}e^{-i\mathbf {qb}^{\prime }}-t_{2}e^{i\mathbf {qc}^{\prime }} &{} -t_{1}e^{i\mathbf {qa}^{\prime }}-t_{2}e^{-i\mathbf {qb}^{\prime }}\\ -t_{1}-t_{2}e^{i\mathbf {q}\left( \mathbf {a}^{\prime }+\mathbf {b}^{\prime }\right) } &{} -t_{1}e^{i\mathbf {qb}^{\prime }}-t_{2}e^{-i\mathbf {qc}^{\prime }} &{} e &{} -t_{1}e^{-i\mathbf {qc}^{\prime }}-t_{2}e^{i\mathbf {qa}^{\prime }}\\ -t_{1}-t_{2}e^{i\mathbf {q}\left( \mathbf {b}^{\prime }+\mathbf {c}^{\prime }\right) } &{} -t_{1}e^{-i\mathbf {qa}^{\prime }}-t_{2}e^{i\mathbf {qb}^{\prime }} &{} -t_{1}e^{i\mathbf {qc}^{\prime }}-t_{2}e^{-i\mathbf {qa}^{\prime }} &{} e \end{pmatrix}. \end{aligned}$$

After some tedious but straightforward manipulations, we obtain the secular equation,

$$\begin{aligned}&\left( e-\varepsilon \right) ^{4} -\left( e-\varepsilon \right) ^{2}\left\{ 6\left( t_{1}^{2}+t_{2}^{2}\right) +4t_{1}t_{2}\left[ \cos \mathbf {q}\left( \mathbf {a}^{\prime } +\mathbf {b}^{\prime }\right) +\cos \mathbf {q}\left( \mathbf {a}^{\prime } +\mathbf {c}^{\prime }\right) \right. \right. \nonumber \\&\qquad \left. \left. +\cos \mathbf {q}\left( \mathbf {b}^{\prime } +\mathbf {c}^{\prime }\right) \right] \right\} \nonumber \\&\qquad -2\left( e-\varepsilon \right) \left( t_{1}+t_{2}\right) ^{3}\left[ \cos \mathbf {q}\left( \mathbf {a}^{\prime } +\mathbf {b}^{\prime }+\mathbf {c}^{\prime }\right) +\cos \mathbf {q}\mathbf {a}^{\prime } +\cos \mathbf {q}\mathbf {b}^{\prime }+\cos \mathbf {q}\mathbf {c}^{\prime }\right] \nonumber \\&\qquad +\left[ t_{1}^{2}+t_{2}^{2}+2t_{1}t_{2}\cos \mathbf {q}\left( \mathbf {a}^{\prime } +\mathbf {b}^{\prime }\right) \right] ^{2}+\left[ t_{1}^{2}+t_{2}^{2} +2t_{1}t_{2}\cos \mathbf {q}\left( \mathbf {a}^{\prime }+\mathbf {c}^{\prime }\right) \right] ^{2}\nonumber \\&\qquad +\left[ t_{1}^{2}+t_{2}^{2}+2t_{1}t_{2}\cos \mathbf {q} \left( \mathbf {c}^{\prime }+\mathbf {b}^{\prime }\right) \right] ^{2} \nonumber \\&\qquad -2\left[ t_{1}^{2}+t_{2}^{2}+2t_{1}t_{2}\cos \mathbf {q} \left( \mathbf {a}^{\prime }+\mathbf {b}^{\prime }\right) \right] \left[ \left( t_{1}^{2}+t_{2}^{2}\right) \cos \mathbf {q} \left( \mathbf {a}^{\prime }+\mathbf {c}^{\prime }\right) +2t_{1}t_{2}\right] \nonumber \\&\qquad -2\left[ t_{1}^{2}+t_{2}^{2}+2t_{1}t_{2}\cos \mathbf {q}\left( \mathbf {a}^{\prime } +\mathbf {c}^{\prime }\right) \right] \left[ \left( t_{1}^{2}+t_{2}^{2}\right) \cos \mathbf {q}\left( \mathbf {b}^{\prime }+\mathbf {c}^{\prime }\right) +2t_{1}t_{2}\right] \nonumber \\&\qquad -2\left[ t_{1}^{2}+t_{2}^{2}+2t_{1}t_{2}\cos \mathbf {q} \left( \mathbf {c}^{\prime }+\mathbf {b}^{\prime }\right) \right] \left[ \left( t_{1}^{2}+t_{2}^{2}\right) \cos \mathbf {q} \left( \mathbf {a}^{\prime }+\mathbf {b}^{\prime }\right) +2t_{1}t_{2}\right] =0 \end{aligned}$$

(A.8)

General expressions for the solutions of this quartic equation are too cumbersome to be useful. Reasonably compact expressions are obtained for special orientations of $\mathbf {q}$. Thus, for $\mathbf {q}\parallel [100]$ one has

$$\begin{aligned} \varepsilon _{0,1} = 4S\left[ J_{1}+J_{2} \mp \sqrt{\left( J_{1}+J_{2}\right) ^{2}\cos ^{2}\frac{qa}{4} -J_{1}J_{2}\sin ^{2}\frac{qa}{2}}\right] \end{aligned}$$

(A.9)

and

$$\begin{aligned} \varepsilon _{3,4} = 4S\left[ 2\left( J_{1}+J_{2}\right) \pm \sqrt{\left( J_{1}+J_{2}\right) ^{2}\sin ^{2}\frac{qa}{4} -J_{1}J_{2}\sin ^{2}\frac{qa}{2}}\right] . \end{aligned}$$

(A.10)

For $\mathbf {q}\parallel [111]$, the solutions are as follows:

$$\begin{aligned} \varepsilon _{0,1}= & {} 2S\left[ \left( J_{1}+J_{2}\right) \left( 3-\cos \frac{qa}{2\surd 3}\right) \right. \nonumber \\&\left. \mp \sqrt{\left( J_{1}+J_{2} \right) ^{2} \left( 3+\cos ^{2}\frac{qa}{2\surd 3}\right) -12J_{1}J_{2}\sin ^{2}\frac{qa}{2\surd 3}} \right] \end{aligned}$$

(A.11)

and

$$\begin{aligned} \varepsilon _{2,3} = 2S\left[ \left( J_{1}+J_{2}\right) \left( 3 +\cos \frac{qa}{2\surd 3}\right) \pm \sqrt{3}\left( J_{1} -J_{2}\right) \sin \frac{qa}{2\surd 3} \right] . \end{aligned}$$

(A.12)

Figure 8 displays the spin-wave spectrum along the symmetry lines in the Brillouin zone of the bcc lattice. The positions of the symmetry points (in the units of $\pi /a$) are as follows: $\varGamma$ (000), H (020), P (111), N (110). The main choice of parameters, $J_2=-0.18\,J_1$, corresponds to a spiral state just after the quantum phase transition. The magnified view in panel (b) contains an extra curve (dashed) for $J_2=-0.17\,J_1$; here the system is still a ferromagnet.

Fig. 8

a Normalized spin-wave energy for $J_2=-0.18\,J_1$. b Magnified view of the bottom-right corner of (a) with an extra curve for $J_2=-0.17\,J_1$

Propagation vector of the spiral

Let us present the acoustic branch of the spin-wave dispersion relation as a power expansion taken to fourth-order terms. The cubic symmetry dictates the following form of this expansion [21]:

$$\begin{aligned} \varepsilon _0 = Dq^2 + C_{100}q^4 + C_\mathrm{anis} \left( q_x^2 q_y^2 + q_y^2 q_z^2 + q_x^2 q_z^2 \right) . \end{aligned}$$

(B.13)

Note that the last term in Eq. (B.13) vanishes for a special orientation of the propagation vector, ${{\varvec{q}}}||[100]$. Therefore, D and $C_{100}$ are found by expanding $\varepsilon _{0}$, Eq. (A.9) with the upper sign:

$$\begin{aligned} D= & {} \frac{J_1^2+6J_1J_2+J_2^2}{J_1+J_2} \, \frac{Sa^2}{8}, \end{aligned}$$

(B.14)

$$\begin{aligned} C_{100}= & {} -\frac{J_1J_2}{J_1+J_2} \, \frac{Sa^4}{32} -\frac{Da^2}{48} +\frac{D^2}{8S(J_1+J_2)}. \end{aligned}$$

(B.15)

For the other high-symmetry orientation, ${{\varvec{q}}}||[111]$, one rewrites Eq. (B.13) as follows:

$$\begin{aligned} \varepsilon _0 = Dq^2 + C_{111}q^4, \end{aligned}$$

(B.16)

where

$$\begin{aligned} C_{111} = C_{100} + \textstyle \frac{1}{3} \, C_\mathrm{anis}. \end{aligned}$$

(B.17)

Now, by expanding $\varepsilon _{0}$, Eq. (A.11) with the upper sign, one finds $C_{111}$ and hence $C_\mathrm{anis}$:

$$\begin{aligned} C_\mathrm{anis} = \frac{J_1J_2}{J_1+J_2} \,\frac{Sa^4}{16} -\frac{Da^2}{48}. \end{aligned}$$

(B.18)

The transition between the ferromagnetic ($q=0$) and the spiral ($q\ne 0$) states is presumably a second-order phase transition in the sense of Landau’s theory, where q (or qa) serves as an order parameter. One can observe in Fig. 8 that as the transition takes place, the global energy minimum remains near $\varGamma$ point ($q=0$).

At the transition point, $D=0$, Eqs. (B.15) and (B.18) become particularly simple, as all but the leading terms vanish. One readily remarks that

$$\begin{aligned} C_\mathrm{anis}< 0~~~~~~\mathrm{and}~~~~~~C_{100}> C_{111} > 0. \end{aligned}$$

(B.19)

It is due to these inequalities that the easy propagation direction is [111] rather than [100], i.e., it is energetically preferable to have ${{\varvec{q}}}||[111]$. So one can adopt Eq. (B.16) as the expression for the energy. In the vicinity of the transition point Landau’s coefficients are given by

$$\begin{aligned} D = \frac{J_2/J_1+3-2\surd 2}{2\surd 2(\surd 2-1)}\, J_1 Sa^2 \end{aligned}$$

(B.20)

and

$$\begin{aligned} C_{111} = \frac{3-2\surd 2}{192(\surd 2-1)} \, J_1 Sa^4. \end{aligned}$$

(B.21)

The order parameter shows a square-root behavior,

$$\begin{aligned} qa = \frac{4}{\sqrt{\surd 2-{4}/{3}}} \sqrt{2\surd 2-3-\frac{J_2}{J_1}} \end{aligned}$$

(B.22)

as characteristic of Landau’s theory of second-order phase transitions.