Skip to main content
SpringerLink
Log in

Nonlinear dynamics analysis of high contact ratio gears system with multiple clearances

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

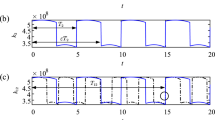
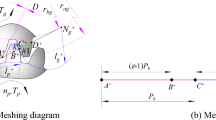
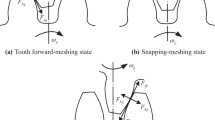
A brief research status on high contact ratio gears (HCRG) is first conducted to obtain a basic understanding. Subsequently, a nonlinear dynamic model of HCRG with multiple clearances is established by the lumped mass method, in which time-varying mesh stiffness (TVMS), static transmission error, gear backlash, and bearing radial clearance are taken into consideration as well. The TVMS of HCRG is calculated based on an improved potential energy model and then fitted into a Fourier series form. After the dimensionless treatment, the system differential equations of motion are solved using Runge–Kutta numerical integration method. With the help of bifurcation diagrams, largest Lyapunov exponent charts, time-domain waveforms, FFT spectra, Poincaré maps, and phase diagrams, the influence of excitation frequency, gear backlash, mesh damping ratio, error fluctuation, and bearing radial clearance on the nonlinear dynamic characteristics of the system is investigated in detail. The results show that with the changes of these analysis parameters, the system exhibits different types of nonlinear behaviors and dynamic evolution mechanism, including period-one, multi-periodic, quasi-periodic, chaotic motions, and jump discontinuity phenomenon. Meanwhile, three typical routes to chaos, namely period-doubling bifurcation to chaos, quasi-period to chaos, and crisis to chaos, are also demonstrated. Additionally, it is found that the bearing radial clearance produces a weaker nonlinear coupling effect when compared to gear backlash. The research results can provide a certain theoretical support for the dynamic design and vibration control of the HCRG.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

References

  1. Cornell RW, Westervelt WW (1978) Dynamic tooth loads and stressing for high contact ratio spur gears. J Mech Des 100(1):69–76

    Google Scholar 

  2. Rosen KM, Frint HK (1982) Design of high contact ratio gears. J Am Helicopter Soc 27(4):65–73

    Google Scholar 

  3. Rameshkumar M, Sivakumar P, Sundaresh S et al (2010) Load sharing analysis of high-contact-ratio spur gears in military tracked vehicle applications. Gear Technol 1:43–50

    Google Scholar 

  4. Staph HE (1976) A parametric analysis of high contact ratio spur gears. ASLE Trans 19(3):201–215

    Google Scholar 

  5. Elkholy AH (1985) Tooth load sharing in high contact ratio spur gears. J Mech Des 107:11–16

    Google Scholar 

  6. Tavakoli MS, Houser DR (1986) Optimum profile modifications for the minimization of static transmission errors of spur gears. J Mech Des 108(1):86–94

    Google Scholar 

  7. Mohanty SC (2003) Tooth load sharing and contact stress analysis of high contact ratio spur gears in mesh. J Inst Eng India 84(2):66–70

    Google Scholar 

  8. Wang JD, Howard I (2005) Finite element analysis of high contact ratio spur gears in mesh. J Tribol 127:469–483

    Google Scholar 

  9. Sánchez MB, Pedrero JI, Pleguezuelos M (2013) Contact stress calculation of high transverse contact ratio spur and helical gear teeth. Mech Mach Theory 64:93–110

    Google Scholar 

  10. Sánchez MB, Pleguezuelos M, Pedrero JI (2014) Tooth-root stress calculation of high transverse contact ratio spur and helical gears. Meccanica 49:347–364

    MATH  Google Scholar 

  11. Sánchez MB, Pleguezuelos M, Pedrero JI (2017) Approximate equations for the meshing stiffness and the load sharing ratio of spur gears including hertzian effects. Mech Mach Theory 109:231–249

    Google Scholar 

  12. Ye SY, Tsai SJ (2016) A computerized method for loaded tooth contact analysis of high-contact-ratio spur gears with or without flank modification considering tip corner contact and shaft misalignment. Mech Mach Theory 97:190–214

    Google Scholar 

  13. Lee CW, Lin HH, Oswald FB et al (1991) Influence of linear profile modification and loading conditions on the dynamic tooth load and stress of high contact ratio gears. J Mech Des 113:473–480

    Google Scholar 

  14. Lin HH, Lee CW, Oswald FB et al (1993) Computer-aided design for high-contact-ratio gears for minimum dynamic load and stress. J Mech Des 115:171–178

    Google Scholar 

  15. Yildirim N, Munro RG (1999) A systematic approach to profile relief design of low and high contact ratio spur gears. Proc Inst Mech Eng Part C 213(6):551–562

    Google Scholar 

  16. Yildirim N, Munro RG (1999) A new type of profile relief for high contact ratio spur gears. Proc Inst Mech Eng Part C 213(6):563–568

    Google Scholar 

  17. Wang JD, Howard I (2007) A further study on high contact ratio spur gears in mesh with double scope tooth profile modification. In: Proceedings of the ASME 2007 international design engineering technical conferences and computers and information in engineering conference, 4–7 September 2007, Las Vegas, Nevada, USA

  18. Velex P, Bruyere J, Gu X (2015) An alternative approach to the definition of profile modifications in high-contact-ratio spur gears. J Mech Des 137(3):1–9

    Google Scholar 

  19. Faggioni M, Samani FS, Bertacchi G (2011) Dynamic optimization of spur gears. Mech Mach Theory 46:544–557

    MATH  Google Scholar 

  20. Özgüven HN, Houser DR (1988) Mathematical-models used in gear dynamics: a review. J Sound Vib 121:383–411

    Google Scholar 

  21. Wang JJ, Li RF, Peng XH (2003) Survey of nonlinear vibration of gear transmission systems. Appl Mech Rev 56(3):309–329

    Google Scholar 

  22. Ozguven HN, Houser DR (1988) Dynamic analysis of high speed gears by using loaded static transmission error. J Sound Vib 125(1):71–83

    Google Scholar 

  23. Ozguven HN (1991) A non-linear mathematical model for dynamic analysis of spur gears including shaft and bearing dynamics. J Sound Vib 145(2):239–260

    Google Scholar 

  24. Kahraman A, Singh R (1990) Non-linear dynamics of a spur gear pair. J Sound Vib 142(1):49–75

    Google Scholar 

  25. Kahraman A, Singh R (1991) Non-linear dynamics of a gear rotor-bearing system with multiple clearances. J Sound Vib 144(3):469–506

    Google Scholar 

  26. Kahraman A, Singh R (1991) Interactions between time-varying mesh stiffness and clearances non-linearities in a geared system. J Sound Vib 146(1):135–156

    Google Scholar 

  27. Blankenship GW, Kahraman A (1995) Steady state forced response of a mechanical oscillator with combined parametric excitation and clearance type nonlinearity. J Sound Vib 185(5):743–765

    MATH  Google Scholar 

  28. Kahraman A, Blankenship GW (1997) Experiments on nonlinear dynamic behavior of an oscillator with clearance and periodically time-varying parameters. J Appl Mech 64:217–226

    Google Scholar 

  29. Theodossiades S, Natsiavas S (2000) Non-linear dynamics of gear-pair systems with periodic stiffness and backlash. J Sound Vib 229(2):287–310

    Google Scholar 

  30. Theodossiades S, Natsiavas S, Goudas I (2000) Dynamic analysis of piecewise linear oscillators with time periodic coefficients. Int J Nonlinear Mech 35(1):53–68

    MathSciNet  MATH  Google Scholar 

  31. Al-shyyab A, Kahraman A (2005) Non-linear dynamic analysis of a multi-mesh gear train using multi-term harmonic balance method: sub-harmonic motions. J Sound Vib 279:417–451

    Google Scholar 

  32. Al-shyyab A, Kahraman A (2005) Non-linear dynamic analysis of a multi-mesh gear train using multi-term harmonic balance method: period-one motions. J Sound Vib 284:151–172

    Google Scholar 

  33. Vaishya M, Singh R (2001) Analysis of periodically varying gear mesh systems with Coulomb friction using Floquet theory. J Sound Vib 243(3):525–545

    Google Scholar 

  34. Vaishya M, Singh R (2001) Sliding friction-induced non-linearity and parametric effects in gear dynamics. J Sound Vib 248(4):671–694

    Google Scholar 

  35. Velex P, Sainsot P (2002) An analytical study of tooth friction excitations in spur and helical gears. Mech Mach Theory 37:641–658

    MATH  Google Scholar 

  36. He S, Gunda R, Singh R (2007) Effect of sliding friction on the dynamics of spur gear pair with realistic time-varying stiffness. J Sound Vib 301:927–949

    Google Scholar 

  37. He S, Cho S, Singh R (2008) Prediction of dynamic friction forces in spur gears using alternate sliding friction formulations. J Sound Vib 309:843–851

    Google Scholar 

  38. Huang K, Xiong YS, Wang T (2017) Research on the dynamic response of high-contact-ratio spur gears influenced by surface roughness under EHL condition. Appl Surf Sci 392:8–18

    Google Scholar 

  39. Ma H, Song R, Pang X et al (2014) Time-varying mesh stiffness calculation of cracked spur gears. Eng Fail Anal 44:179–194

    Google Scholar 

  40. Wan ZG, Cao HR, Zi YY et al (2014) An improved time-varying mesh stiffness algorithm and dynamic modeling of gear-rotor system with tooth root crack. Eng Fail Anal 42:157–177

    Google Scholar 

  41. Saxena A, Parey A, Chouksey M (2016) Time varying mesh stiffness calculation of spur gear pair considering sliding friction and spalling defects. Eng Fail Anal 70:200–211

    Google Scholar 

  42. Karma V, Agarwal AK (2016) Calculation of high contact ratio spur gear mesh stiffness and load sharing ratio using MATLAB & EXCEL spread sheet. Int J Adv Res Sci Eng 5(9):104–119

    Google Scholar 

  43. Raghuwanshi NK, Parey A (2015) Mesh stiffness measurement of cracked spur gear by photoelasticity technique. Measurement 73:439–452

    Google Scholar 

  44. Sainsot P, Velex P, Duverger O (2004) Contribution of gear body to tooth deflections—a new bidimensional analytical formula. J Mech Des 126(4):748–752

    Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (51775156), Natural Science Foundation of Anhui Province of China (1908085QE228) and the Fundamental Research Funds for the Central Universities of China (JZ2018HGTA0206, JZ2018HGBZ0101, PA2019GDZC0101).

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Hefei University of Technology, Hefei, 230009, China

    Kang Huang, Yong Yi & Zhenbang Cheng

  2. Institute of Industry and Equipment Technology, Hefei University of Technology, Hefei, 230009, China

    Yangshou Xiong

  3. Anhui Province Key Lab of Aerospace Structural Parts Forming Technology and Equipment, Hefei, 230009, China

    Yangshou Xiong

  4. HRG Institute (Hefei) of International Innovation, Hefei, 230601, China

    Huan Chen

Authors
  1. Kang Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yong Yi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yangshou Xiong
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Zhenbang Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Huan Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yangshou Xiong.

Additional information

Technical Editor: Pedro Manuel Calas Lopes Pacheco, D.Sc.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, K., Yi, Y., Xiong, Y. et al. Nonlinear dynamics analysis of high contact ratio gears system with multiple clearances. J Braz. Soc. Mech. Sci. Eng. 42, 98 (2020). https://doi.org/10.1007/s40430-020-2190-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-020-2190-0

Keywords

Search

Navigation