Skip to main content
SpringerLink
Log in

Majority Dynamics and the Retention of Information

  • Published:
Israel Journal of Mathematics Aims and scope Submit manuscript

Abstract

We consider a group of agents connected by a social network who participate in majority dynamics: each agent starts with an opinion in {−1, +1} and repeatedly updates it to match the opinion of the majority of its neighbors.

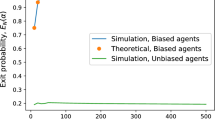
We assume that one of {−1, +1} is the “correct” opinion S, and consider a setting in which the initial opinions are independent conditioned on S, and biased towards it. They hence contain enough information to reconstruct S with high probability. We ask whether it is still possible to reconstruct S from the agents’ opinions after many rounds of updates.

While this is not the case in general, we show that indeed, for a large family of bounded degree graphs, information on S is retained by the process of majority dynamics.

Our proof technique yields novel combinatorial results on majority dynamics on both finite and infinite graphs, with applications to zero temperature Ising models.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. V. Bala and S. Goyal, Learning from neighbours, The Review of Economic Studies, 65 (1998), 595–621.

    Article  MATH  Google Scholar 

  2. E. Berger, Dynamic monopolies of constant size, Journal of Combinatorial Theory, Series B 83 (2001), 191–200.

    Article  MATH  MathSciNet  Google Scholar 

  3. F. Camia, E. De Santis and C. Newman, Clusters and recurrence in the two-dimensional zero-temperature stochastic Ising model, The Annals of Applied Probability 12 (2002), 565–580.

    Article  MATH  MathSciNet  Google Scholar 

  4. E. De Santis and C, Newman, Convergence in energy-lowering (disordered) stochastic spin systems, Journal of Statistical Physics 110 (2003), 431–442.

    Article  MATH  MathSciNet  Google Scholar 

  5. G. Ellison and D. Fudenberg, Rules of thumb for social learning, Journal of Political Economy 101 (1993), 612–643.

    Article  Google Scholar 

  6. L. R. Fontes, R. Schonmann and V. Sidoravicius, Stretched exponential fixation in stochastic Ising models at zero temperature, Communications in Mathematical Physics 228 (2002), 495–518.

    Article  MATH  MathSciNet  Google Scholar 

  7. D. Gale and S. Kariv, Bayesian learning in social networks, Games and Economic Behavior 45 (2003), 329–346.

    Article  MATH  MathSciNet  Google Scholar 

  8. Y, Ginosar and R, Holzman, The majority action on infinite graphs: strings and puppets, Discrete Mathematics 215 (2000), 59–72.

    Article  MATH  MathSciNet  Google Scholar 

  9. E. Goles and J, Olivos, Periodic behaviour of generalized threshold functions, Discrete Mathematics 30 (1980), 187–189.

    Article  MATH  MathSciNet  Google Scholar 

  10. C, D. Howard, Zero-temperature Ising spin dynamics on the homogeneous tree of degree three, Journal of Applied Probability 37 (2000), 736–747.

    Article  MATH  MathSciNet  Google Scholar 

  11. Y. Kanoria and A. Montanari, Majority dynamics on trees and the dynamic cavity method, The Annals of Applied Probability 21 (2011), 1694–1748.

    Article  MATH  MathSciNet  Google Scholar 

  12. D. Kempe, A. Dobra and J, Gehrke, Gossip-based computation of aggregate information, in Proceedings of the 44th Annual Symposium on Foundations of Computer Science, IEEE Computer Society, Washington, DC, 2003, pp. 482–491.

    Google Scholar 

  13. W. McCulloch and W. Pitts, A logical calculus of the ideas immanent in nervous activity, The Bulletin of Mathematical Biophysics 5 (1943), 115–133.

    Article  MATH  MathSciNet  Google Scholar 

  14. G. Moran, On the period-two-property of the majority operator in infinite graphs, Transactions of the American Mathematical Society 347 (1995), 1649–1667.

    Article  MATH  MathSciNet  Google Scholar 

  15. E. Mossel, J. Neeman and O. Tamuz, Majority dynamics and aggregation of information in social networks, Autonomous Agents and Multi-Agent Systems 28 (2014), 408–429.

    Article  Google Scholar 

  16. E. Mossel, A. Sly and O. Tamuz, Strategic learning and the topology of social networks, (2012-08), ArXiv e-prints, 1209.5527.

  17. D. Peleg, Size bounds for dynamic monopolies, Discrete Applied Mathematics 86 (1998), 263–273.

    Article  MATH  MathSciNet  Google Scholar 

  18. D. Shah, Gossip algorithms, Foundations and Trends in Networking, 3 (2009), 1–125.

    Article  Google Scholar 

  19. R. Tessler and O. Louidor, Geometry and Dynamics in Zero Temperature Statistical Mechanics Models, (2010-08), ArXiv e-prints, 1008.5279.

Download references

Author information

Authors and Affiliations

  1. Faculty of Mathematics and Computer Science, The Weizmann Institute of Science, Rehovot, 76100, Israel

    Omer Tamuz

  2. Einstein Institute of Mathematics, The Hebrew University of Jerusalem, Givat Ram, Jerusalem, 91904, Israel

    Ran J. Tessler

Authors
  1. Omer Tamuz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ran J. Tessler
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Omer Tamuz.

Additional information

Omer Tamuz is supported by ISF grant 1300/08, and is a recipient of the Google Europe Fellowship in Social Computing, and this research is supported in part by this Google Fellowship.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tamuz, O., Tessler, R.J. Majority Dynamics and the Retention of Information. Isr. J. Math. 206, 483–507 (2015). https://doi.org/10.1007/s11856-014-1148-2

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11856-014-1148-2

Keywords

Search

Navigation