Optimal Control of Plant Disease Epidemics with Clean Seed Usage

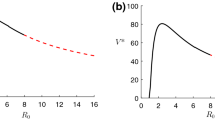
Abstract

The distribution and use of pathogen-free planting material (“clean seeds”) is a promising method to control plant diseases in developing countries. We address the question of minimizing disease prevalence in plants through the optimal usage of clean seeds. We consider the simplest possible S–I model together with a simple economic criterion to be maximized. The static optimization problem shows a diversity of possible outcomes depending on economical and epidemiological parameters. We derive a simple condition showing to what extent subsidizing clean seeds relative to the epidemiological features of the disease may help eradicate or control the disease. Then we consider dynamic optimal control and Pontryagin’s maximum principle to study the optimal usage of clean seeds to control the disease. The dynamical results are comparable to the static ones and are even simpler in some sense. In particular, the condition on the critical subsidy rate that makes clean seed usage economically viable is unchanged from the static optimization case. We discuss how these results may apply to the control of maize lethal necrosis in East-Africa.

Appendices

Appendix A

We define an extremal trajectory ${\hat{\phi }}$ as one where the control $\phi$ maximizes or minimizes the Hamiltonian. It is a function of both the state variable(s) (here S) and the adjoint variable(s) (here $\lambda$). We have the following important result (Lenhart and Workman 2007):

Theorem 1

(First integral of the energy) If both the dynamics and the running cost are time-invariant, the Hamiltonian is constant along an extremal trajectory.

Proof

To avoid any confusion in the notation, we will use Dieudonné’s notation for the partial derivatives of the Hamiltonian $\mathcal {H}(S,\lambda ,\phi )$,

$$\begin{aligned} \mathrm {D_1}\mathcal {H}(S,\lambda ,\phi )= & {} -{\dot{\lambda }}(S,\lambda ,\phi ) ,\\ \mathrm {D_2}\mathcal {H}(S,\lambda ,\phi )= & {} \dot{S}(S,\lambda ,\phi ) . \end{aligned}$$

Let $\widehat{\mathcal {H}}(S,\lambda ) := \mathcal {H}(S,\lambda ,{\hat{\phi }}(S,\lambda )).$ It follows from Danskin’s theorem (see Danskin 1967) that, if the extremalizing ${\hat{\phi }}$ is unique,

$$\begin{aligned} \mathrm {D}_1\widehat{\mathcal {H}}(S,\lambda )= & {} \mathrm {D}_1\mathcal {H}(S,\lambda ,{\hat{\phi }}(S,\lambda )) ,\\ \mathrm {D_2}\widehat{\mathcal {H}}(S,\lambda )= & {} \mathrm {D}_2\mathcal {H}(S,\lambda ,{\hat{\phi }}(S,\lambda )). \end{aligned}$$

Moreover, the only way ${\hat{\phi }}$ could be non-unique would be on a singular arc, where $\mathrm {D}_3\mathcal {H}=0$, so that the conclusion of Danskin’s theorem would still hold. Hence we have

$$\begin{aligned} \frac{\mathrm {d}\widehat{\mathcal {H}}}{\mathrm {d}t}= \mathrm {D}_1\widehat{\mathcal {H}}(S,\lambda )\dot{S}(S,\lambda ,{\hat{\phi }})+\mathrm {D}_2\widehat{\mathcal {H}}(S,\lambda ){\dot{\lambda }}(S,\lambda ,{\hat{\phi }})=-{\dot{\lambda }}\dot{S} + \dot{S}{\dot{\lambda }} = 0 . \end{aligned}$$

$\square$

Appendix B

We used two different solution techniques that gave consistent results. In the main text, we analytically solved the optimal control problem in backward time from every possible value of $S_T$. Conceptually, this yielded a field of optimal orbits in the plane (t, S) as depicted in Fig. 6. However, the blue curves in Fig. 6 were actually computed using an alternative numerical “forward-backward sweep” method to make sure that the results are correct regardless of the method used. The “forward-backward sweep” numerical method yielded the same switching curve as predicted from the mathematical analysis.

In order to numerically compute the optimal control for various values for each parameter, we modified the forward-backward Sweep technique as described in Lenhart and Workman (2007). Our method uses the defined initial conditions of $S(\tau )=S_\tau$ and $\lambda (T)=\lambda _T$ and an initial guess of the control $\phi (t)=\phi _0(t)$ and refines this guess until some convergence criterion has been met. The steps in this method are described as follows:

• 1. Determine an initial guess for the control $\phi _0(t)$.

• 2. For $i \ge 1$, do the following:

  • (a) Solve S(t) by moving forward in time on the region $[\tau ,T]$ and backward in time on the region $[0,\tau ]$ using Runge-Kutta methods (RK4) to approximate the solution to the ODE.

  • (b) Use these values of of S(t) to approximate the solution of the ODE for $\lambda (t)$ by moving backward in time on the region [0, T] and using RK4 with the same timesteps.

  • (c) Calculate an approximation to $\psi (t)$ using S(t) and $\lambda (t)$ and use this to determine an update function $\phi _{fix}(t)$.

  • (d) Update the guess for $\phi$ using values of $\phi _{i-1}(t)$ and $\phi _{fix}(t)$. In our model we use $\phi _i(t)=(1-\alpha )\phi _{i-1}(t)+\alpha \phi _{fix}(t)$ for some $\alpha \in (0,1)$.

  • (e) Continue this process from Step 2 until the following convergence criteria is reached: The relative differences between old and new values, as measured in the infinity norm, are less than a tolerance ($\delta$) for each of the controls, state variables and the adjoints. If convergence is not reached, go to (a) and repeat, unless a maximum number of iterations have been exceeded.

We used this method to compute the optimal trajectories in Fig. 6. In our case, we found that $\alpha =0.1$ was sufficient to generate the optimal control trajectories represented, with $\Delta t = 10^{-3}$ the timestep for RK4 and $\phi _0(t)=0.5$ the initial guess for the control. We used a tolerance of $\delta = 10^{-3}$, for checking the convergence criteria.

Appendix C

To show that there is no singular region of the optimal control in the cases observed, we turn to proof by contradiction.

Assume $\phi ^*$ is singular. Then, by the definition of $\phi ^*$, this means that there exists some interval of time, I, such that $\psi (t)=0$ on this interval I, we have

$$\begin{aligned} \psi (t)=\mu (-c+\lambda (t)(1-S(t))\nu )=0. \end{aligned}$$

Solving for $\lambda$, we get that on I,

$$\begin{aligned} \lambda (t)=\frac{c}{\nu (1-S(t))}, \end{aligned}$$

whenever $S(t) \ne 1$. We can then take the time derivative of this quantity and the state Eq. (5) to get the relationship

$$\begin{aligned} \frac{\mathrm {d}\lambda }{\mathrm {d}t}=\frac{c}{\nu (1-S(t))}(-\beta S(t)+\mu \phi \nu +\mu (1-\nu )). \end{aligned}$$

Equating the above to the relationship derived from the Hamiltonian in Eq. (24) and cancelling out terms, we get the identity

$$\begin{aligned} -\mu p_S +\frac{c}{\nu }\beta =0. \end{aligned}$$

Using the definitions of R and r, we can show that the above identity is equivalent to $R= r\nu$, which is the line dividing the regions in Fig. 7. Since we are only considering the cases $R>r\nu$ and $R<r\nu$, (i.e. $R\ne r\nu$), we conclude that there is no singular region of the optimal control along the switching curve.

Appendix D

In the case of an infinite horizon, we are interested in maximizing

$$\begin{aligned} J(\phi (\cdot ))=\mu \int \limits _0^\infty e^{-\delta t}(p_S S(t)-c\phi (t)) \mathrm {d}t, \end{aligned}$$

(30)

with respect to $\phi \in [0,1]$, subject to the state equation (5) again. In the above $e^{-\delta t}$ is a discount term, with the parameter $\delta > 0$.

To show that the integral in Eq. (30) converges, we use the property that both S(t) and $\phi (t)$ are bounded between 0 and 1:

$$\begin{aligned} \left| \mu \int \limits _0^\infty e^{-\delta t}(p_S S(t)-c\phi (t)) \mathrm {d}t\right|&\le \mu \int \limits _0^\infty \left| e^{-\delta t}(p_S S(t)-c\phi (t))\right| \mathrm {d}t \\&\le \mu \int \limits _0^\infty e^{-\delta t}\max (p_S,c) \mathrm {d}t= \frac{\mu \max (p_S,c)}{\delta } . \end{aligned}$$

The Hamiltonian $\mathcal {H}$ and the switch function $\psi (t)$ are slightly modified with respect to the finite-horizon problem addressed in Sect. 4. This results in the adjoint equation

$$\begin{aligned} \frac{\mathrm{d}\lambda }{\mathrm{d}t} = -\mu p_S e^{-\delta t} + \lambda (t) [(1-S(t))\beta + (\nu \mu \phi (t) - \beta S(t)+\mu (1-\nu ))] , \end{aligned}$$

and switch function

$$\begin{aligned} \psi (t) = \mu \left( - ce^{-\delta t} + \lambda (t) (1-S(t))\nu \right) . \end{aligned}$$

We are interested in a singular control $\phi ^*\in (0,1)$ such that $\psi =0$ along the singular part of the optimal trajectory. This yields

$$\begin{aligned} \lambda (t)=\frac{ce^{-\delta t}}{\nu (1-S(t))} , \end{aligned}$$

and differentiating this in respect to time gives us

$$\begin{aligned} \frac{\mathrm {d}\lambda }{\mathrm {d}t}=ce^{-\delta t}\frac{-\delta + \mu \phi \nu - \beta S + \mu (1-\nu )}{\nu (1-S(t))} . \end{aligned}$$

Setting these two equations for the time derivative of $\lambda$ equal to each other and solving for S(t) results in the following equation for $S^*$

$$\begin{aligned} S^*=1-\frac{\delta }{\nu \mu \left( r-\frac{R}{\nu }\right) }. \end{aligned}$$

A necessary condition for the singular control to exist is $S^*<1$, which occurs whenever $R<r\nu$. This ratio has appeared in previous analysis, and represents the conditions where it is economically beneficial to use clean seeds. From here, we have that $S^*>0$ if and only if

$$\begin{aligned} \delta <\nu \mu \left( r-\frac{R}{\nu }\right) , \end{aligned}$$

meaning the discount rate must be small enough for long term interests to prevail over short term interests.

If $\phi ^* \in (0,1)$ is constant, then the dynamics of the system result in the equilibrium point

$$\begin{aligned} {\bar{S}} = \frac{1}{R}\left( \phi ^*\nu +(1-\nu )\right) . \end{aligned}$$

Equating ${\bar{S}}$ and $S^*$ results in the following expression for $\phi ^*$

$$\begin{aligned} \phi ^*=\frac{1}{\nu }\left( R\left( 1-\frac{\delta }{\nu \mu \left( r-\frac{R}{\nu }\right) }\right) -(1-\nu )\right) = \frac{1}{\nu }\left( RS^*-(1-\nu )\right) . \end{aligned}$$

Letting $K=\nu \mu \left( r-R/\nu \right)$, we get that $0<\phi ^*<1$ only if

$$\begin{aligned} \max \left( K\left( 1-\frac{1}{R}\right) ,0\right)<\delta < K\left( 1-\frac{1-\nu }{R}\right) , \end{aligned}$$

which requires $\mathcal {R}_0=R+\nu >1$ otherwise the upper bound is negative.