Modeling LSD1-Mediated Tumor Stagnation

Abstract

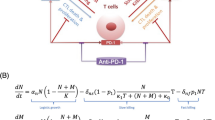
LSD1 (KDMA1) has gained attention in the last decade as a cancer biomarker and drug target. In particular, recent work suggests that LSD1 inhibition alone reduces tumor growth, increases T cell tumor infiltration, and complements PD1/PDL1 checkpoint inhibitor therapy. In order to elucidate the immunogenic effects of LSD1 inhibition, we develop a mathematical model of tumor growth under the influence of the adaptive immune response. In particular, we investigate the anti-tumor cytotoxicity of LSD1-mediated T cell dynamics, in order to better understand the synergistic potential of LSD1 inhibition in combination immunotherapies, including checkpoint inhibitors. To that end, we formulate a non-spatial delay differential equation model and fit to the B16 mouse model data from Sheng et al. (Cell 174(3):549–563, 2018. https://doi.org/10.1016/j.cell.2018.05.052). Our results suggest that the immunogenic effect of LSD1 inhibition accelerates anti-tumor cytotoxicity. However, cytotoxicity does not seem to account for the slower growth observed in LSD1-inhibited tumors, despite evidence suggesting immune-mediation of this effect.

Appendices

Statistical Comparisons in Figures

For the pairwise comparisons in Figs. 4, 6, 8, and 9, we used an unpaired Student’s t test. For each panel, we applied a Benjamini–Hochberg adjustment for multiple testing. In order to validate the choice of a t test, we used the Shapiro–Wilk test for normality. We cannot reject normality for the samples in Figs. 4, 6, and 8 ($P > 0.05$). For Fig. 9, two of the samples were somewhat non-normal. Left to right in Fig. 9, the S–W statistic had values 0.93, 0.85, 0.90, 0.98 corresponding to $P=0.17, 8.8e{-}4, 0.01, 0.81$. We used the same comparison for Fig. 4d as in Sheng et al. (2018).

For the differential gene expression (DGE) analysis for Fig. 7, we used the gene counts from Sheng et al. (2018) (data accessible at NCBI GEO database, accession GSE112230) and the R package edgeR. We normalized the counts using the TMM method and removed minimally expressing genes, leaving us with 12,305 genes remaining. We fit a linear model to compare gene expression between the three experimental tumor conditions: scramble control, LSD1-KO, and LSD1/MDA5 DKO tumors. Our workflow was based upon the tutorial in Core (2019). When adjusting for multiple testing, we used the BH method as before and adjusted for all three pairwise contrasts (between our experimental conditions) for the full set of expressing genes, together.

Description of Statistical Model and MCMC Fitting

Consider the tumor growth data for tumor i as a time series ${\varvec{y}}_i = \left( y_i(t_j) \right) _{j=1}^{n_i}$. We assume a statistical model of the form

$$\begin{aligned} y_i(t)&= f({\varvec{p}}_i, t) + \epsilon _i(t) \end{aligned}$$

(5)

$$\begin{aligned} \epsilon _i(t_1),\ldots ,\epsilon _i(t_n)&\sim _{\text {iid}} N(\mu _i, \sigma _i) \end{aligned}$$

(6)

where $f({\varvec{p}}_i, \cdot )$ is a deterministic model and $\epsilon _i(\cdot )$ is the measurement noise, parameterized by ${\varvec{p}}_i, \mu _i, \sigma _i$ individually for each tumor time series i. The model $f({\varvec{p}}_i, \cdot )$ is the solution to either our main DDE model (1) described in Sect. 2.1, (1), or one of the alternative ODE models in Sect. 2.1 (2, 3, 4). We use ${\varvec{f}}({\varvec{p}}_i)$ to denote $\left( f({\varvec{p}}_i, t_j) \right) _j$, i.e., the estimated time series from our model, corresponding to the data ${\varvec{y}}_i$. For our measurement noise, we ideally would have $\mu _i = 0$ for each tumor. We make this assumption for model fitting, but estimate $\mu _i$ for the purposes of model validation below, in order to strengthen the likelihood of simple alternative models.

Given a model f and parameters ${\varvec{p}}_i, \mu _i, \sigma _i$, the conditional log-likelihood is given by

$$\begin{aligned} \log L ({\varvec{y}}_i \mid f, {\varvec{p}}_i, \mu _i, \sigma _i) =&- n_i \log (\sqrt{2 \pi } \sigma _i)\nonumber \\&-\frac{1}{2} \sum _{j=1}^{n_i} \left( \frac{y_i(t_j) - f({\varvec{p}}_i,t_j) - \mu _i}{\sigma _i} \right) ^2 \end{aligned}$$

(7)

For the purposes of model fitting, we estimated ${\hat{{\varvec{p}}}}_i$ for fixed $\sigma _i$ using a Markov chain Monte Carlo,¹ under the assumption that $\mu _i = 0$. We linearly interpolated our data ${\varvec{y_i}} \mapsto {\tilde{{\varvec{y}}}_i}$ so that we had 5 data points per day, in order to ensure smooth fits. Per standard practice, we employ the $\ell _2$ error as the target function g, for which $e^g \propto L$:

$$\begin{aligned} g ({\tilde{{\varvec{y}}}_i} \mid f, {\hat{{\varvec{p}}}}_i, \mu _i, \sigma _i)&= - || {\tilde{{\varvec{y}}}_i} - {\varvec{f}}({\hat{{\varvec{p}}}}_i) ||_{\ell ^2}^2 \nonumber \\&= - \sum _{j=1}^{n_i} \left( {\tilde{y}}_i(t_j) - f({\hat{{\varvec{p}}}}_i,t_j) \right) ^2 \end{aligned}$$

(8)

To find ${\varvec{f}}({\varvec{p}}_i)$, we need to solve systems (1, 2, 3, 4). The one-dimensional systems 2, 3 have well-known closed-form solutions:

$$\begin{aligned} C(t)&= \mu \exp \left[ e^{-\alpha t} \log \left( \frac{C_0}{\mu } \right) \right] \end{aligned}$$

(9)

$$\begin{aligned} C(t)&= \frac{\mu C_0}{C_0 + (\mu - C_0) e^{-\alpha t} } \end{aligned}$$

(10)

For our main model (1) and the two compartment model (4), we solved our equations numerically using the R package diffeqr, which is a convenient wrapper for the Julia suite DifferentialEquations.jl.

To validate our model, we compared it to each of the alternative choices of f, for each tumor i, using the standard Bayesian Information Criterion (BIC):

$$\begin{aligned} BIC_i = N_p \log (n_i) - 2 \log {{\hat{L}}} \end{aligned}$$

(11)

where $N_p$ is the number of free parameters for our model, i.e., the length of $({\varvec{p}}_i, \sigma _i)$. In particular, these are 7, 4, 4, 6 for models (1), (2), (3), and (4), respectively. Substituting (7) into (11) and using our estimate ${\varvec{p}}_i$, we have

$$\begin{aligned} BIC_i&= N_p \log (n_i) + 2 n_i \log {\sqrt{2 \pi } {\hat{\sigma }}_i} + \frac{1}{{\hat{\sigma }}_i^2} || {\varvec{y_i}} - {\varvec{f}}({\hat{{\varvec{p}}}}_i) ||_{\ell ^2}^2 \end{aligned}$$

(12)

$$\begin{aligned} BIC_i&= N_p \log (n_i) + 2 n_i \log ({\hat{\sigma }}_i) + n_i(1 + \log (2 \pi )) \end{aligned}$$

(13)

$$\begin{aligned} \text { where } {\hat{\sigma }}_i^2&= \frac{|| {\varvec{y_i}} - {\varvec{f}}({\hat{{\varvec{p}}}}_i) ||_{\ell ^2}^2}{n_i} \end{aligned}$$

(14)

Supplementary Tables

See Tables 2 and 3.

Table 2 Estimated model parameter values

Table 3 Logistic growth for immune deficient tumors

Marginal Parameter Densities

See Fig. 12.

Fig. 12

Prior and posterior parameter distribution for main model fitting (LSD1-KO #5). Presented are the prior and posterior distribution of the parameters ${\varvec{p}}_i$ of model (1), taken from the MCMC, where i is one of the LSD1-KO tumors. In order from left to right, the panels here correspond to $\alpha , \mu , \ell , r, \log _{10}(s_{\mathrm {H}}), \log _{10}(s_K)$