Skip to main content
SpringerLink
Log in

Are Two-Patch Models Sufficient? The Evolution of Dispersal and Topology of River Network Modules

  • Original Article
  • Published:
Bulletin of Mathematical Biology Aims and scope Submit manuscript

Abstract

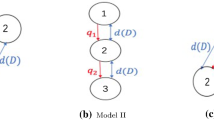
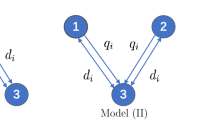
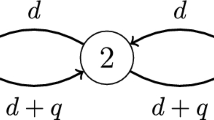
We study the dynamics of two competing species in three-patch models and illustrate how the topology of directed river network modules may affect the evolution of dispersal. Each model assumes that patch 1 is at the upstream end, patch 3 is at the downstream end, but patch 2 could be upstream, or middle stream, or downstream, depending on the specific topology of the modules. We posit that individuals are subject to both unbiased dispersal between patches and passive drift from one patch to another, depending upon the connectivity of patches. When the drift rate is small, we show that for all models, the mutant species can invade when rare if and only if it is the slower disperser. However, when the drift rate is large, most models predict that the faster disperser wins, while some predict that there exists one evolutionarily singular strategy. The intermediate range of drift is much more complex: most models predict the existence of one singular strategy, but it may or may not be evolutionarily stable, again depending upon the topology of modules, while one model even predicts that for some intermediate drift rate, singular strategy does not exist and the faster disperser wins the competition.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Ballyk M, Dung L, Jones DA, Smith HL (1998) Effects of random motility on microbial growth and competition in a flow reactor. SIAM J Appl Math 59:573–596

    MathSciNet  MATH  Google Scholar 

  • Cantrell RS, Cosner C, DeAngelis DL, Padrón V (2007) The ideal free distribution as an evolutionarily stable strategy. J Biol Dyn 1:249–271

    MathSciNet  MATH  Google Scholar 

  • Cantrell RS, Cosner C, Lou Y (2012) Evolutionary stability of ideal free dispersal strategies in patchy environments. J Math Biol 65:943–965

    MathSciNet  MATH  Google Scholar 

  • Cantrell RS, Cosner C, Lam K-Y (2017) On resident-invader dynamics in infinite dimensional dynamical systems. J Differ Equ 263:4565–4616

    MATH  Google Scholar 

  • Cantrell RS, Cosner C, Lou Y, Schreiber S (2017) Evolution of natal dispersal in spatially heterogeneous environments. Math Biosci 283:136–144

    MathSciNet  MATH  Google Scholar 

  • DeAngelis DL, Wolkowicz G, Lou Y, Jiang Y, Novak M, Svanback R, Araujo M, Jo YS, Cleary EA (2011) The effect of travel loss on evolutionarily stable distributions of populations in space. Am Nat 178:15–29

    Google Scholar 

  • Dieckmann U, Law R (1996) The dynamical theory of coevolution: a derivation from stochastic ecological processes. J Math Biol 34:579–612

    MathSciNet  MATH  Google Scholar 

  • Dockery J, Hutson V, Mischaikow K, Pernarowski M (1998) The evolution of slow dispersal rates: a reaction-diffusion model. J Math Biol 37:61–83

    MathSciNet  MATH  Google Scholar 

  • Du Y, Lou B, Peng R, Zhou M (2020) The Fisher-KPP equation over simple graphs: varied persistence states in river networks. J Math Biol 80:1559–1616

    MathSciNet  MATH  Google Scholar 

  • Fagan WF (2002) Connectivity, fragmentation, and extinction risk in dendritic metapopulations. Ecology 83:3243–3249

    Google Scholar 

  • Geritz SAH, Kisdi E, Meszena G, Metz JAJ (1998) Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evol Ecol 12:35–57

    Google Scholar 

  • Golubitsky M, Hao W, Lam K-Y, Lou Y (2017) Dimorphism by singularity theory in a model for river ecology. Bull Math Biol 79:1051–1069

    MathSciNet  MATH  Google Scholar 

  • Grant EHC, Lowe WH, Fagan WF (2007) Living in the branches: population dynamics and ecological processes in dendritic networks. Ecol Lett 10:165–175

    Google Scholar 

  • Hamida Y (2017) The evolution of dispersal for the case of two patches and two-species with travel loss, M.S. Thesis, Ohio State University

  • Hao WR, Lam K-Y, Lou Y Ecological and evolutionary dynamics in advective environments: Critical domain size and boundary conditions, Discrete Contin Dyn Syst Ser B (in press)

  • Hastings A (1983) Can spatial variation alone lead to selection for dispersal? Theor Popul Biol 24:244–251

    MATH  Google Scholar 

  • Huang Q, Jin Y, Lewis MA (2016) R0 analysis of a benthic-drift model for a stream population. SIAM J Appl Dyn Syst 15:287–321

    MathSciNet  MATH  Google Scholar 

  • Jin Y, Lewis MA (2011) Seasonal influences on population spread and persistence in streams II: Critical domain size. SIAM J Appl Math 71:1241–1262

    MathSciNet  MATH  Google Scholar 

  • Jin Y, Lewis MA (2012) Seasonal influences on population spread and persistence in streams: Spreading speeds. J Math Biol 65:403–439

    MathSciNet  MATH  Google Scholar 

  • Jin Y, Hilker F, Steffler P, Lewis MA (2014) Seasonal invasion dynamics in a spatially heterogeneous river with fluctuating flows. Bull Math Biol 76:1522–1565

    MathSciNet  MATH  Google Scholar 

  • Jin Y, Peng R, Shi JP (2019) Population dynamics in river networks. J Nonlinear Sci 29:2501–2545

    MathSciNet  MATH  Google Scholar 

  • Jin Y, Huang Q, Steffler PM, Lewis MA (2019) Population persistence of a benthic-drift model in a depth-averaged river. AIMS Math 4(6):1768–1795

    MathSciNet  Google Scholar 

  • Kirkland S, Li C-K, Schreiber SJ (2006) On the evolution of dispersal in patchy environments. SIAM J Appl Math 66:1366–1382

    MathSciNet  MATH  Google Scholar 

  • Lam K-Y, Lou Y, Lutscher F (2014) Evolution of dispersal in closed advective environments. J Biol Dyn 9(Suppl. 1):188–212

    MathSciNet  MATH  Google Scholar 

  • Lam K-Y, Lou Y, Lutscher F (2016) The emergence of range limits in advective environments. SIAM J Appl Math 76:641–662

    MathSciNet  MATH  Google Scholar 

  • Levin SA, Cohen D, Hastings A (1984) Dispersal strategies in patchy environments. Theor Popul Biol 26:165–191

    MathSciNet  MATH  Google Scholar 

  • Lou Y (2019) Ideal free distribution in two patches. J Nonlinear Model Anal 2:151–167

    Google Scholar 

  • Lou Y, Lutscher F (2014) Evolution of dispersal in open advective environments. J Math Biol 69:1319–1342

    MathSciNet  MATH  Google Scholar 

  • Lou Y, Zhou P (2015) Evolution of dispersal in advective homogeneous environment: the effect of boundary conditions. J Differ Equ 259:141–171

    MathSciNet  MATH  Google Scholar 

  • Lou Y, Xiao D, Zhou P (2016) Qualitative analysis for a Lotka–Volterra competition system in advective homogeneous environment. Discrete Contin Dyn Syst Ser A 36:953–969

    MathSciNet  MATH  Google Scholar 

  • Lou Y, Zhao X-Q, Zhou P (2019) Global dynamics of a Lotka–Volterre competition-diffusion-advection system in heterogeneous environments. J Math Pure Appl 121:47–82

    MATH  Google Scholar 

  • Lutscher F, Pachepsky E, Lewis MA (2005) The effect of dispersal patterns on stream populations. SIAM Rev 47:749–772

    MathSciNet  MATH  Google Scholar 

  • Lutscher F, Lewis MA, McCauley E (2006) Effects of heterogeneity on spread and persistence in rivers. Bull Math Biol 68:2129–2160

    MathSciNet  MATH  Google Scholar 

  • Lutscher F, McCauley E, Lewis MA (2007) Spatial patterns and coexistence mechanisms in systems with unidirectional flow. Theor Popul Biol 71:267–277

    MATH  Google Scholar 

  • Maynard-Smith J, Price GR (1973) The logic of animal conflict. Nature 246:15–18

    MATH  Google Scholar 

  • McPeek MA, Holt RD (1992) The evolution of dispersal in spatially and temporally varying environments. Am Nat 140:1010–1027

    Google Scholar 

  • Noble L (2015) Evolution of Dispersal in Patchy Habitats, Ph.D Thesis, Ohio State University. http://orcid.org/0000-0002-2092-2817

  • Pachepsky E, Lutscher F, Nisbet RM, Lewis MA (2015) Persistence, spread and the drift paradox. Theor Popul Biol 67:61–73

    MATH  Google Scholar 

  • Ramirez JM (2012) Population persistence under advection-diffusion in river networks. J Math Biol 65:919–942

    MathSciNet  MATH  Google Scholar 

  • Samia Y, Lutscher F, Hastings A (2015) Connectivity, passability and heterogeneity interact to determine fish population persistence in river networks. J R Soc Interface 12:20150435

    Google Scholar 

  • Sarhad J, Carlson R, Anderson KE (2014) Population persistence in river networks. J Math Biol 69:401–448

    MathSciNet  MATH  Google Scholar 

  • Speirs DC, Gurney WSC (2001) Population persistence in rivers and estuaries. Ecology 82:1219–1237

    Google Scholar 

  • Vasilyeva O (2017) Competition of multiple species in advective environments. Bull Math Biol 79:1274–1294

    MathSciNet  MATH  Google Scholar 

  • Vasilyeva O, Lutscher F (2011) Population dynamics in rivers: analysis of steady states. Can Appl Math Quart 18:439–469

    MathSciNet  MATH  Google Scholar 

  • Vasilyeva O, Lutscher F (2012) Competition of three species in an advective environment. Nonlinear Anal RWA 13:1730–1748

    MathSciNet  MATH  Google Scholar 

  • Vasilyeva O, Lutscher F (2012) Competition in advective environments. Bull Math Biol 74:2935–2958

    MathSciNet  MATH  Google Scholar 

  • Wang Y, Shi JP (2019) Persistence and extinction of population in reaction-diffusion-advection model with weak Allee effect growth. SIAM J Appl Math 79:1293–1313

    MathSciNet  MATH  Google Scholar 

  • Wang Y, Shi JP (2020) Dynamics of a reaction-diffusion Benthic-drift model with strong Allee effect growth. J Differ Equ 269:7605–7642

    MATH  Google Scholar 

  • Wang Y, Shi JP, Wang JF (2019) Persistence and extinction of population in reaction-diffusion-advection model with strong Allee effect growth. J Math Biol 78:2093–2140

    MathSciNet  MATH  Google Scholar 

  • Xiang J, Fang Y (2019) Evolutionarily stable dispersal strategies in a two-patch advective environment. Discrete Contin Dyn Syst Ser B 24:1875–1887

    MathSciNet  MATH  Google Scholar 

  • Zhang B, Lam K-Y, Ni W-M, Collins KM, Fu Z, Zhai L, Lou Y, DeAngelis DL, Hastings A (2020) Directed movement changes coexistence outcomes in heterogeneous environments, submitted 28pp

  • Zhao X-Q, Zhou P (2016) On a Lotka–Volterra competition model: the effects of advection and spatial variation. Calc Var Partial Diff 55:73

    MathSciNet  MATH  Google Scholar 

  • Zhou P (2016) On a Lotka–Volterra competition system: diffusion vs advection. Calc Var Partial Diff 55:137

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors sincerely thank two anonymous referees for their insightful comments and suggestions. HYJ is partially supported by the NSFC grant No. 11571364. KYL and YL are partially supported by the NSF grant DMS-1853561.

Author information

Authors and Affiliations

  1. Institute for Mathematical Sciences, Renmin University of China, Beijing, 100872, China

    Hongyan Jiang

  2. Department of Mathematics, Ohio State University, Columbus, OH, 43210, USA

    King-Yeung Lam & Yuan Lou

Authors
  1. Hongyan Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. King-Yeung Lam
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yuan Lou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yuan Lou.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jiang, H., Lam, KY. & Lou, Y. Are Two-Patch Models Sufficient? The Evolution of Dispersal and Topology of River Network Modules. Bull Math Biol 82, 131 (2020). https://doi.org/10.1007/s11538-020-00803-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11538-020-00803-1

Keywords

Mathematics Subject Classification

Search

Navigation