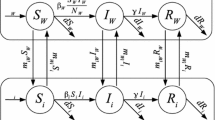
Appendix A
Model equation
$$\begin{aligned} \dfrac{\mathrm{d}S}{\mathrm{d}t}&= b - \beta \dfrac{\kappa E + \tau I_{a}}{N_h}S - \dfrac{\theta \beta _v \phi I_v}{N_h}S - dS + m_2 S_1 - mS, \nonumber \\ \dfrac{\mathrm{d}E}{\mathrm{d}t}&= \beta \dfrac{\kappa E + \tau I_{a}}{N_h}S + \dfrac{\theta \beta _v \phi I_v}{N_h}S - dE - \gamma E + m_2 E_1 - mE, \nonumber \\ \dfrac{\mathrm{d}I_{a}}{\mathrm{d}t}&= \gamma E - dI_{a} - \delta I_{a} + m_2 I_{a1} - mI_{a},\nonumber \\ \dfrac{\mathrm{d}I_{b}}{\mathrm{d}t}&= \delta I_{a} - \alpha I_{b} - dI_{b} + q I_{b1}, \nonumber \\ \dfrac{\mathrm{d}R}{\mathrm{d}t}&= \alpha I_{b} - dR + m_2 R_1 - mR, \nonumber \\ \dfrac{\mathrm{d}S_v}{\mathrm{d}t}&= b_v - \beta _v \lambda _v \dfrac{\kappa _v E + \tau _v I_{a}}{N_h}S_v - d_v S_v, \nonumber \\ \dfrac{\mathrm{d}E_v}{\mathrm{d}t}&= \beta _v \lambda _v \dfrac{\kappa _v E + \tau _v I_{a}}{N_h}S_v - d_v E_v - \psi _v E_v, \nonumber \\ \dfrac{\mathrm{d}I_v}{\mathrm{d}t}&= \psi _v E_v - d_v I_v, \nonumber \\ \dfrac{\mathrm{d}S_1}{\mathrm{d}t}&= b_1 - \beta _1\dfrac{\kappa _1 E_1 + \tau _1 I_{a1}}{N_{h1}}S_1 - \dfrac{\theta _1 \beta _{v1} \phi _{1} I_{v1} S_1}{N_{h1}} - d_1 S_1 - m_2 S_1 + mS , \nonumber \\ \dfrac{\mathrm{d}E_1}{\mathrm{d}t}&= \beta _1\dfrac{\kappa _1 E_1 + \tau _1 I_{a1}}{N_{h1}}S_1 + \dfrac{\theta _1\beta _{v1}\phi _1 I_{v1} S_1}{N_{h1}} - d_1 E_1 - \gamma _1 E_1 - m_2 E_1 + mE , \nonumber \\ \dfrac{\mathrm{d}I_{a1}}{\mathrm{d}t}&= \gamma _1 E_1 - d_1 I_{a1} - \delta _1 I_{a1} - m_2 I_{a1} + mI_{a}, \nonumber \\ \dfrac{\mathrm{d}I_{b1}}{\mathrm{d}t}&= \delta _1 I_{a1} - \alpha _1 I_{b1} - d_1I_{b1} - q I_{b1}, \nonumber \\ \dfrac{\mathrm{d}R_1}{\mathrm{d}t}&= \alpha _1 I_{b1} - d_1 R_1 - m_2 R_1 + mR, \nonumber \\ \dfrac{\mathrm{d}S_{v1}}{\mathrm{d}t}&= b_{v1} - \beta _{v1}\lambda _{v1} \dfrac{\kappa _{v1} E_1 + \tau _{v1} I_{a1}}{N_{h1}}S_{v1} - d_{v1} S_{v1}, \nonumber \\ \dfrac{\mathrm{d}E_{v1}}{\mathrm{d}t}&= \beta _{v1}\lambda _{v1} \dfrac{\kappa _{v1} E_1 + \tau _{v1} I_{a1}}{N_{h1}}S_{v1} - d_{v1}E_{v1} - \psi _{v1} E_{v1}, \nonumber \\ \dfrac{\mathrm{d}I_{v1}}{\mathrm{d}t}&= \psi _{v1} E_{v1} - d_{v1} I_{v1}. \end{aligned}$$
(8)
1.1 Positive Invariance
By Theorem A.4 in Thieme (2003), there exists a unique solution with values in \(\mathbb {R}^{16}_+\) that is defined on some interval [0, a) with \(a \in (0, \infty ).\) If \(a < \infty ,\) then \(\limsup _{t \rightarrow a-} \overline{N}(t) = \infty .\) We add all host equations in the system (3) and then derive the following inequality
$$\begin{aligned} \dfrac{\mathrm{d}\overline{N}}{\mathrm{d}t} \le b^* - d^* \overline{N}, \end{aligned}$$
in which \(b^*=b+b_{1}\) and \(d^*=\min \{d,d_{1}\}\). Assume that there exists a positive number c such that
$$\begin{aligned} b^* \le \dfrac{d^*}{2}\overline{N}\ \text {whenever}\ ||(S^T,J)|| = \overline{N} \ge c. \end{aligned}$$
By Diekmann and Heesterbeek (2000), \(\frac{d\overline{N}(t)}{dt} \le -\frac{d^*}{2}\overline{N}(t)\) whenever \(t \in [0,a)\) and \(\overline{N}(t) \ge c.\) This implies \(\overline{N}(t) \le \max \{c,\overline{N}(0)\}\) for all \(t \in [0,a).\) So \(a = \infty ,\) and \(\limsup _{t \rightarrow \infty } \overline{N}(t) \le c.\) Similarly, summing the total vector equations together, we have
$$\begin{aligned} \dfrac{\mathrm{d}\overline{N}_{v}}{\mathrm{d}t} \le b^*_v -d^*_v \overline{N}_{v}, \end{aligned}$$
in which \(b^*_{v}=b_{v}+b_{v1}\) and \(d^*_{v}=\min \{d_{v},d_{v1}\}\). If there exists a positive number \(c_{v}\) such that
$$\begin{aligned} b^*_{v} \le \dfrac{d^*_{v}}{2}\overline{N}_{v} \quad \text {whenever} \quad ||(S^T_{v},J_{v})|| = \overline{N}_{v} \ge c_{v}, \end{aligned}$$
then the total vector population \(\overline{N}_v(t) \le \max \{c_{v},\overline{N}_v(0)\}\) for all \(t \in [0,a).\) So \(a = \infty ,\) and \(\limsup _{t \rightarrow \infty } \overline{N_v}(t) \le c_{v}.\) We then conclude that system (3) is epidemiologically feasible and mathematically well-posed in \(\mathbb {D} = \mathbb {D}_h \cup \mathbb {D}_v \subset \mathbb {R}^{10}_+ \times \mathbb {R}^6_+\), in which \(\mathbb {D}_h\) is the domain of the total human population and \(\mathbb {D}_v\) is the domain for the total vector population.
1.1.1 The Disease-Free Equilibrium
At the disease-free equilibrium, there is no infection in either the human or the vector population. First, let us assume that there is no movement between the satellite city and the urban city. The system (3) without mobility then has a disease-free equilibrium \(E^0\), given by
$$\begin{aligned} E^0 = \left( \dfrac{b}{d},0,0,0,0,\dfrac{b_v}{d_v},0,0,\dfrac{b_1}{d_1},0,0,0,0, \dfrac{b_{v1}}{d_{v1}},0,0\right) \in \mathbb {R}^{16}_+. \end{aligned}$$
(9)
To obtain the disease-free equilibrium \(E^0_m\) for the system (3) with mobility, we note first that we are led to solving the equilibrium subsystem associated to the susceptible populations, in the form
$$\begin{aligned} \begin{aligned} b + m_2S_1 - (d + m)S&=0, \\ b_1 + mS - (d_1 + m_2)S_1&=0. \end{aligned} \end{aligned}$$
(10)
This subsystem has the solutions
$$\begin{aligned} S^{**} = \dfrac{b(d_1 + m_2) + b_1 m_2}{dd_1 + dm_2 + md_1}, \qquad \qquad S^{**}_1 = \dfrac{b_1 (d + m) + m b}{dd_1 + dm_2 + md_1}. \end{aligned}$$
It then follows that
$$\begin{aligned} E^0_m = \bigg (\dfrac{b(d_1 + m_2) + b_1 m_2}{dd_1 + dm_2 + md_1}, 0, 0, 0, 0, \dfrac{b_v}{d_v}, 0, 0, \dfrac{b_1 (d + m) + m b}{dd_1 + dm_2 + md_1}, 0, 0, 0, 0, \dfrac{b_{v1}}{d_{v1}}, 0, 0\bigg ). \end{aligned}$$
1.2 Computation of the Basic Reproduction Number \(R_0\)
To use the next-generation method, we note that the equations which model the dynamics of the infected compartments E, \(I_a\), \(I_b\), \(E_v\) and \(I_v\) of the urban city and \(E_1\), \(I_{a1}\), \(I_{b1}\), \(E_{v1}\) and \(I_{v1}\) of the satellite city in (3) are
$$\begin{aligned} \dfrac{\mathrm{d}E}{\mathrm{d}t}&= \beta \dfrac{\kappa E + \tau I_{a}}{N_h}S + \dfrac{\theta \beta _v \phi I_v}{N_h}S - dE - \gamma E + m_2 E_1 - mE, \nonumber \\ \dfrac{\mathrm{d}I_{a}}{\mathrm{d}t}&= \gamma E - dI_{a} - \delta I_{a} + m_2 I_{a1} - mI_{a},\nonumber \\ \dfrac{\mathrm{d}I_{b}}{\mathrm{d}t}&= \delta I_{a} - \alpha I_{b} - dI_{b} + q I_{b1}, \nonumber \\ \dfrac{\mathrm{d}E_v}{\mathrm{d}t}&= \beta _v \lambda _v \dfrac{\kappa _v E + \tau _v I_{a}}{N_h}S_v - d_v E_v - \psi _v E_v, \nonumber \\ \dfrac{\mathrm{d}I_v}{\mathrm{d}t}&= \psi _v E_v - d_v I_v, \nonumber \\ \dfrac{\mathrm{d}E_1}{\mathrm{d}t}&= \beta _1\dfrac{\kappa _1 E_1 + \tau _1 I_{a1}}{N_{h1}}S_1 + \dfrac{\theta _1\beta _{v1}\phi _1 I_{v1} S_1}{N_{h1}} - d_1 E_1 - \gamma _1 E_1 - m_2 E_1 + mE , \nonumber \\ \dfrac{\mathrm{d}I_{a1}}{\mathrm{d}t}&= \gamma _1 E_1 - d_1 I_{a1} - \delta _1 I_{a1} - m_2 I_{a1} + mI_{a}, \nonumber \\ \dfrac{\mathrm{d}I_{b1}}{\mathrm{d}t}&= \delta _1 I_{a1} - \alpha _1 I_{b1} - d_1I_{b1} - q I_{b1}, \nonumber \\ \dfrac{\mathrm{d}E_{v1}}{\mathrm{d}t}&= \beta _{v1}\lambda _{v1} \dfrac{\kappa _{v1} E_1 + \tau _{v1} I_{a1}}{N_{h1}}S_{v1} - d_{v1}E_{v1} - \psi _{v1} E_{v1},\nonumber \\ \dfrac{\mathrm{d}I_{v1}}{\mathrm{d}t}&= \psi _{v1} E_{v1} - d_{v1} I_{v1}.\nonumber \\ \end{aligned}$$
(11)
To fix our ideas, let us focus on the urban city, that is, on the first five equations of (11). With the notations of van den Driessche and Watmough (2002), \(\mathcal {F}\) and \(\mathcal {V}\) are given by
$$\begin{aligned} \mathcal {F} = \left[ \begin{array}{*{1}c} \beta \dfrac{\kappa E + \tau I_{a}}{N_h}S + \dfrac{\theta \beta _v \phi I_v}{N_h}S \\ 0 \\ 0 \\ \beta _v \lambda _v \dfrac{\kappa _v E + \tau _v I_{a}}{N_h}S_v \\ 0 \\ \end{array} \right] , \quad \mathcal {V} = \left[ \begin{array}{*{1}c} dE + \gamma E - m_2 E_1 + mE \\ - \gamma E + dI_{a} + \delta I_{a} - m_2 I_{a1} + mI_{a} \\ - \delta I_{a} + \alpha I_{b} + dI_{b} - q I_{b1} \\ d_v E_v + \psi _v E_v \\ - \psi _v E_v + d_v I_v \\ \end{array} \right] . \end{aligned}$$
Assuming that \(m=m_2=0\), the associated Jacobian matrices of \(\mathcal {F}\) and \(\mathcal {V}\) at the disease-free equilibrium are given by
$$\begin{aligned} F= & {} \left[ \begin{array}{*{5}c} \beta \kappa &{}\quad \beta \tau &{}\quad 0 &{}\quad 0 &{}\quad \theta \beta _v \phi \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \dfrac{\beta _v \lambda _v \kappa _v b_vd}{bd_v} &{}\quad \dfrac{\beta _v \lambda _v \tau _v b_vd}{bd_v} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right] ,\\ V= & {} \left[ \begin{array}{*{5}c} (d + \gamma )&{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ -\gamma &{}\quad (d + \delta ) &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad -\delta &{}\quad (\alpha + d) &{} 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad (d_v + \psi _v) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -\psi _v &{}\quad d_v \\ \end{array} \right] . \end{aligned}$$
The basic reproduction number \(R_0\) equals the spectral radius (dominant eigenvalue) of the matrix \(FV^{-1}\), given by:
$$\begin{aligned} R_{0} =\dfrac{R_{hh} + \sqrt{R^2_{hh} + 4R^2_{hv}}}{2}, \end{aligned}$$
where
$$\begin{aligned} R_{hh}&= \dfrac{\beta (\tau \gamma + \kappa (d + \delta ))}{(d + \gamma )(d + \delta )}, \\ R_{hv}&= \sqrt{\dfrac{\theta \beta ^2_v \phi \psi _v \lambda _v b_v d\bigg (\tau _v (d_v + \psi _v) + \kappa _v (d + \delta )\bigg )}{bd^2_v(d + \gamma )(d + \delta )(d_v + \psi _v)}}. \end{aligned}$$
1.2.1 The Basic Reproduction Number for the System with Mobility
If the infection exists in a single community which is connected to another community through population mobility, the phenomenon related to the movements of individuals should be reflected in the disease threshold. When the communities are connected by migration, the community-specific reproduction numbers are given by
$$\begin{aligned} R_{01M} =\dfrac{R_{hh1M} + \sqrt{R^2_{hh1M} + 4R^2_{hv1M}}}{2} \quad \text {and} \quad R_{02M} =\dfrac{R_{hh2M} + \sqrt{R^2_{hh2M} + 4R^2_{hv2M}}}{2}. \end{aligned}$$
To compute \(R_{01M}\) and \(R_{02M}\), we substitute the disease-free equilibrium points with movement for
$$\begin{aligned} S^* = \dfrac{b(d_1 + m_2) + b_1 m_2}{dd_1 + dm_2 + md_1},\quad S^*_1 = \dfrac{b_1(d + m) + mb}{dd_1 + dm_2 + md_1},\quad S^*_v = \dfrac{b_v}{d_v},\quad S^*_{v1} = \dfrac{b_{v1}}{d_{v1}} \end{aligned}$$
into the Jacobian matrix for F before computing for the eigenvalues of the matrix \(FV^{-1}\). We obtain the following results
$$\begin{aligned} R_{hh1M}&= \dfrac{\beta (\tau \gamma + \kappa (d + \delta + m))}{(d + \gamma + m)(d + \delta + m)}, \\ R_{hv1M}&= \sqrt{\dfrac{\theta \beta ^2_v \phi \psi _v \lambda _v b_v (dd_1 + dm_2 + md_1)(\tau _v(d_v + \psi _v) + \kappa _v(d + \delta + m))}{d^2_v(b(d_1 + m_2) + b_1m_2)(d + \gamma + m)(d + \delta + m)(d_v + \psi _{v})}}, \\ R_{hh2M}&=\dfrac{\beta _1 (\tau _1 \gamma _1 + \kappa _1 (d_1 + \delta _1 + m_2))}{(d_1 + \gamma _1)(d_1 + \delta _1 + m_2)}, \\ R_{hv2M}&= \sqrt{\dfrac{\theta _1 \beta ^2_{v1} \phi _1 \psi _{v1} \lambda _{v1} b_{v1} (dd_1 + dm_2 + md_1)(\tau _{v1} (d_{v1} + \psi _{v1}) + \kappa _{v1}(d_1 + \delta _1 + m_2))}{d^2_{v1}(b_1 (d + m) + mb)(d_1 + \gamma _1 + m_2)(d_1 + \delta _1 + m_2)(d_{v1} + \psi _{v1})}}. \end{aligned}$$
An estimation of the basic reproduction number, hereby denoted as \(R_0^m\), can then be given as the maximum of the community-specific reproduction numbers
$$\begin{aligned} R_0^m=\max \{R_{01M},R_{02M}\}. \end{aligned}$$
For a single isolated community, the corresponding persistence condition is \(R_0 > 1\), which holds only if \( R_{hh} + R^2_{hv} > 1\). That is,
$$\begin{aligned}&R_0> 1\\&\implies \dfrac{R_{hh} + \sqrt{R^2_{hh} + 4R^2_{hv}}}{2}> 1, \\&\implies R_{hh} + \sqrt{R^2_{hh} + 4R^2_{hv}}> 2, \\&\implies \sqrt{R^2_{hh} + 4R^2_{hv}}> 2 - R_{hh}, \\&\implies \bigg (\sqrt{R^2_{hh} + 4R^2_{hv}}\bigg )^2> (2 - R_{hh})^2, \\&\implies R^2_{hh} + 4R^2_{hv}> 4 - 4R_{hh} + R^2_{hh}, \\&\implies 4R_{hh} + 4R^2_{hv}> 4, \\&\implies R_{hh} + R^2_{hv} > 1. \end{aligned}$$
1.3 Uniform Strong Disease Persistence and Existence of Endemic Equilibria
Under the assumption of the constant recruitment, it is easy to see that the host is strongly uniformly persistent. Since the recruitment rates b and \(b_1\) are positive constants, \(S^T(t) > (0,0)\) for all \(t > 0\), and there exist two positive constants \(\delta _1^*\) and \(\delta _2^*\) such that
$$\begin{aligned} \lim \inf _{t \rightarrow \infty } S^T(t) \ge (\delta _1^*,\delta _2^*) \end{aligned}$$
for all non-negative solutions in model system (3). In fact, by the first subsystem in the system (3)
$$\begin{aligned} \dfrac{\mathrm{d}S}{\mathrm{d}t}&= b - \bigg (d + \dfrac{\beta (\kappa E + \tau I_{a})}{N_h} + \dfrac{\theta \beta _v \phi I_v}{N_h} \bigg ) S + m_2 S_1 - mS,\\&>b - \big (d + \beta (\kappa + \tau ) + \theta \beta _v \phi \big ) S - mS. \end{aligned}$$
Then, there exists a \(\delta _1^*\in (0,+\infty )\), independent of the solution, such that
$$\begin{aligned} \liminf _{t \rightarrow \infty } S(t) \ge \dfrac{b}{d + \beta (\kappa + \tau ) + \theta \beta _v \phi +m} =: \delta _1^*. \end{aligned}$$
Similarly, there exists a \(\delta _2^*\in (0,+\infty )\) such that
$$\begin{aligned} \liminf _{t \rightarrow \infty } S_1(t) \ge \delta _2^*. \end{aligned}$$
Since \(S^T(t)>> (0,0)\) for \(t > 0\), the subsequent persistence results do not need the solutions of system (3) to satisfy \(S^T(0)>> (0,0)\). Also, if \(R_{0M} > 1\), and all recruitment rates b and \(b_1\) are positive constants, then there exists some \(\epsilon > 0\) such that
$$\begin{aligned} \liminf _{t \rightarrow \infty } ~\ C_i(t) \ge \epsilon ,\ i=1,2,\ C\in \mathbb {C}\ \mathrm {and}\ C=(C_1,C_2) \end{aligned}$$
for all non-negative solutions of system (3) with
$$\begin{aligned} \big (E^T(0), I^T_{a}(0), I^T_{b}(0), E^T_v(0), I^T_v(0)\big ) > 0. \end{aligned}$$
Let
$$\begin{aligned} \mathbb {X} = \left\{ (S^T, E^T, I^T_a, I^T_b, R^T, S^T_v, E^T_v, I^T_v) \in (0,\infty )^{16}| (S^T, S^T_v)\in (0,+\infty )^4 \ \mathrm{and} \right. \\ \left. (E^T, I^T_a, I^T_b, R^T, E^T_v, I^T_v) \in \mathbb {R}^{12}_+ \right\} . \end{aligned}$$
By Theorem A.32 of Thieme (2003), the solution takes its values in \(\mathbb {X}\) for \(t > 0\). Define \(\rho : \mathbb {X} \rightarrow \mathbb {R}_+\) by
$$\begin{aligned} \rho (S^T, E^T, I^T_a, I^T_b, R^T,N_v) = I, \end{aligned}$$
for fixed \(I\in \{I_a,I_{a1},I_b,I_{b1},I_v,I_{v1}\}\), and \(\widetilde{\rho } : \mathbb {X} \rightarrow \mathbb {R}_+\) by
$$\begin{aligned} \widetilde{\rho }(S^T, E^T, I^T_a, I^T_b, R^T,N_v) = \frac{I_a+I_b}{N_h}+\frac{I_{a1}+I_{b1}}{N_{h1}}+\frac{I_v+I_{v1}}{\overline{N_v}}. \end{aligned}$$
In the language Sect. A.5 of Thieme (2003), the semiflow \(\Phi \) induced by the solutions of system (3) is uniformly weakly \(\rho \)-persistent by Theorem 4.3 in Dhirasakdanon et al. (2007). The compactness condition in Sect. A.5 of Thieme (2003) follows from the known results above. Notice that every total orbit \(\omega : \mathbb {R} \rightarrow X\) of \(\Phi \) is associated with a solution of system (3) that is defined for all times and takes value in \(\mathbb {X}\). By the irreducibility of the matrix \(\left( \begin{array}{cc} 0&{}\quad m\\ m_2&{}\quad 0\\ \end{array} \right) \), \(\widetilde{\rho }(\omega (0))>0\) whenever \(\rho (\omega (t))>0\) for all \(t\in \mathbb {R}\). The claim for \(C\in \{I^T_a, I^T_b,I^T_v\}\) now follows from Theorem A.34 in Thieme (2003). For \(C \in \{E^T, R^T,E^T_v\}\), modify \(\widetilde{\rho }(S^T, E^T, I^T_a, I^T_b, R^T, N_v) = C_i\). For \(C=S^T\), the statement has already been shown in the content above. Similarly, for \(C=S^T_v\), the statement should be easily shown. The existence of an (endemic) equilibrium of system (3) in \((0,\infty )^{16}\) follows from Theorem 1.3.7. in Dhirasakdanon et al. (2007).
Optimal Control Strategies
We use Pontryagin’s maximum principle to determine the necessary conditions for optimal control of the epidemic disease. We incorporate three time-dependent control variables into the model (3) to determine the optimal strategy for controlling the disease. The model (3) then becomes
$$\begin{aligned} \dfrac{\mathrm{d}S}{\mathrm{d}t}&= b - \beta \dfrac{\kappa E + \tau I_{a}}{N_h}S - \dfrac{\theta \beta _v \phi I_v}{N_h}S - d S + (1 - u_1(t))m_2 S_1 - (1 - u_2(t))m S, \nonumber \\ \dfrac{\mathrm{d}E}{\mathrm{d}t}&= \beta \dfrac{\kappa E + \tau I_{a}}{N_h}S + \dfrac{\theta \beta _v \phi I_v}{N_h}S - d E - \gamma E + (1 - u_1(t))m_2 E_1\nonumber \\&\quad - (1 - u_2(t))m E,\nonumber \\ \dfrac{\mathrm{d}I_{a}}{\mathrm{d}t}&= \gamma E - d I_{a} - \delta I_{a} + (1 - u_1(t))m_2 I_{a1} - (1 - u_2(t))m I_{a}, \nonumber \\ \dfrac{\mathrm{d}I_{b}}{\mathrm{d}t}&= \delta I_{a} - \alpha I_{b} - dI_{b} + (1 - u_3(t))q I_{b1}, \nonumber \\ \dfrac{\mathrm{d}R}{\mathrm{d}t}&= \alpha I_{b} - d R + (1 - u_1(t))m_2 R_1 - (1 - u_2(t))m R, \nonumber \\ \dfrac{\mathrm{d}S_v}{\mathrm{d}t}&= b_v - \beta _v \lambda _v \dfrac{\kappa _v E + \tau _v I_{a}}{N_h}S_v - d_v S_v, \nonumber \\ \dfrac{\mathrm{d}E_v}{\mathrm{d}t}&= \beta _v \lambda _v \dfrac{\kappa _v E + \tau _v I_{a}}{N_h}S_v - d_v E_v - \psi _v E_v, \nonumber \\ \dfrac{\mathrm{d}I_v}{\mathrm{d}t}&= \psi _v E_v - d_v I_v,\nonumber \\ \dfrac{\mathrm{d}S_1}{\mathrm{d}t}&= b_1 - \beta _1\dfrac{\kappa _1 E_1 + \tau _1 I_{a1}}{N_{h1}}S_1 - \dfrac{\theta _1 \beta _{v1} \phi _{1} I_{v1}}{N_{h1}}S_1 - d_1 S_1 - (1 - u_1(t))m_2 S_1 \nonumber \\&\quad + (1 - u_2(t))m S, \nonumber \\ \dfrac{\mathrm{d}E_1}{\mathrm{d}t}&= \beta _1\dfrac{\kappa _1 E_1 + \tau _1 I_{a1}}{N_{h1}}S_1 + \dfrac{\theta _1 \beta _{v1} \phi _1 I_{v1}}{N_{h1}}S_1 - d_1 E_1 - \gamma _1 E_1 - (1 - u_1(t))m_2 E_1\nonumber \\&\quad + (1 - u_2(t))m E, \nonumber \\ \dfrac{\mathrm{d}I_{a1}}{\mathrm{d}t}&= \gamma _1 E_1 - d_1 I_{a1} - \delta _1 I_{a1} - (1 - u_1(t))m_2 I_{a1} + (1 - u_2(t))m I_{a}, \nonumber \\ \dfrac{\mathrm{d}I_{b1}}{\mathrm{d}t}&= \delta _1 I_{a1} - \alpha _1 I_{b1} - d_1 I_{b1} - (1 - u_2(t))q I_{b1}, \nonumber \\ \dfrac{\mathrm{d}R_1}{dt}&= \alpha _1 I_{b1} - d_1 R_1 - (1 - u_1(t))m_2 R_1 + (1 - u_2(t))m R, \nonumber \\ \dfrac{\mathrm{d}S_{v1}}{\mathrm{d}t}&= b_{v1} - \beta _{v1} \lambda _{v1} \dfrac{\kappa _{v1} E_1 + \tau _{v1} I_{a1}}{N_{h1}}S_{v1} - d_{v1} S_{v1}, \nonumber \\ \dfrac{\mathrm{d}E_{v1}}{\mathrm{d}t}&= \beta _{v1} \lambda _{v1} \dfrac{\kappa _{v1} E_1 + \tau _{v1} I_{a1}}{N_{h1}}S_{v1} - d_{v1}E_{v1} - \psi _{v1} E_{v1}, \nonumber \\ \dfrac{\mathrm{d}I_{v1}}{\mathrm{d}t}&= \psi _{v1} E_{v1} - d_{v1}I_{v1}. \end{aligned}$$
(12)
The control variables, \(u_1(t)\), \(u_2(t)\) and \(u_3(t)\), are bounded, Lebesgue integrable functions. Our control problem involves a situation in which the number of mildly infectious individuals, severe infected individuals and the cost of applying screening control \(u_1(t)\), \(u_2(t)\) and \(u_3(t)\) are minimized subject to the system (12). The objective function is defined as
$$\begin{aligned} J(u_1,u_2,u_3) = \int _{0}^{T} \left[ c_{1}I_{a} + c_{2}I_{b} + c_{3}I_{a1} + c_{4}I_{b1} + c_{5}u^{2}_1 + c_{6}u^{2}_2 + c_{7}u^{2}_3 \right] \mathrm{d}t, \end{aligned}$$
(13)
where \(I_a\), \(I_{a1}\), \(I_{b}\) and \(I_{b1}\) are the total infected human populations, T is the final time and the coefficients \(c_{1}, c_{2}, c_{3}, c_{4}, c_{5}, c_{6}, c_{7}\) are positive weights. Our aim is to minimize the total number of infected humans and minimize the costs of control mechanisms \(u_1(t)\), \(u_2(t)\) and \(u_3(t)\) at the same time. Thus, we search for an optimal control \((u^{*}_1,\ u^{*}_2,\ u^{*}_3)\) such that
$$\begin{aligned} J(u^{*}_1,u^{*}_2,u^{*}_3)=\min _{u_1,\ u_2,\ u_3} \left\{ J(u_1,u_2,u_3)|u_1,u_2,u_3 \in \varOmega \right\} , \end{aligned}$$
(14)
where the control set
$$\begin{aligned} \varOmega = \left\{ (u_1,\ u_2,\ u_3)| u_i: \ [0,T \ ] \rightarrow \ [0,1 \ ]\text { Lebesgue measurable,} \quad i = 1,\ 2,\ 3 \right\} . \end{aligned}$$
The existence of an optimal control is a result of the convexity of the integrand of J with respect to \(u_1\), \(u_2\) and \(u_3\), a priori boundedness of the state variables, and the Lipschitz property of the state system with regard to the state variables. The Pontryagin’s maximum principle (Pontryagin et al. 1962) converts the equation (12) and the equation (13) into a problem of minimizing a Hamiltonian H with respect to \(u_1\), \(u_2\) and \(u_3\).
$$\begin{aligned}&H = c_{1}I_a + c_{2}I_b + c_{3}I_{a1} + c_{4}I_{b1} + c_{5}u^{2}_1 + c_{6}u^{2}_2 + c_{7}u^{2}_3, \nonumber \\&\quad +\, \lambda _{S} \left\{ b - \beta \dfrac{\kappa E + \tau I_{a}}{N_h}S - \dfrac{\theta \beta _v \phi I_v}{N_h}S - d S + (1 - u_1(t))m_2 S_1 - (1 - u_2(t))m S \right\} , \nonumber \\&\quad + \lambda _{E} \left\{ \beta \dfrac{\kappa E + \tau I_{a}}{N_h}S + \dfrac{\theta \beta _v \phi I_v}{N_h}S - d E - \gamma E + (1 - u_1(t))m_2 E_1 - (1 - u_2(t))m E \right\} , \nonumber \\&\quad + \lambda _{I_{a}} \left\{ \gamma E - d I_{a} - \delta I_{a} + (1 - u_1(t))m_2 I_{a1} - (1 - u_2(t))m I_{a}\right\} , \nonumber \\&\quad + \lambda _{I_{b}} \left\{ \delta I_{a} - \alpha I_{b} - dI_{b} + (1 - u_3(t))q I_{b1} \right\} ,\nonumber \\&\quad + \lambda _{R} \left\{ \alpha I_{b} - d R + (1 - u_1(t))m_2 R_1 - (1 - u_2(t))m R \right\} , \nonumber \\&\quad + \lambda _{S_{v}} \left\{ b_v - \beta _v \lambda _v \dfrac{\kappa _v E + \tau _v I_{a}}{N_h}S_v - d_v S_v \right\} , \nonumber \\&\quad + \lambda _{E_{v}} \left\{ \beta _v \lambda _v \dfrac{\kappa _v E + \tau I_{a}}{N_h}S_v - d_v E_v - \psi _v E_v \right\} , \nonumber \\&\quad + \lambda _{I_{v}} \left\{ \psi _v E_v - d_v I_v \right\} ,\nonumber \\&\quad + \lambda _{S_{1}} \left\{ b_1 - \beta _1\dfrac{\kappa _1 E_1 + \tau _1 I_{a1}}{N_{h1}}S_1 - \dfrac{\theta _1 \beta _{v1} \phi _1 I_{v1}}{N_{h1}}S_1- d_1 S_1 \right. \nonumber \\&\quad \left. - (1 - u_1(t))m_2 S_1 + (1 - u_2(t))m S \right\} , \nonumber \\&\quad + \lambda _{E_{1}} \left\{ \beta _1\dfrac{\kappa _1 E_1 + \tau _1 I_{a1}}{N_{h1}}S_1 + \dfrac{\theta _1 \beta _{v1} \phi _1 I_{v1}}{N_{h1}}S_1 - d_1 E_1 - \gamma _1 E_1 \right. \nonumber \\&\quad \left. - (1 - u_1(t))m_2 E_1 + (1 - u_2(t))m E) \right\} , \nonumber \\&\quad + \lambda _{I_{a1}} \left\{ \gamma _1 E_1 - d_1 I_{a1} - \delta _1 I_{a1} - (1 - u_1(t))m_2 I_{a1} + (1 - u_2(t))m I_{a} \right\} ,\nonumber \\&\quad + \lambda _{I_{b1}} \left\{ \delta _1 I_{a1} - \alpha _1 I_{b1} - d_1 I_{b1} - (1 - u_3(t)) q I_{b1}\right\} ,\nonumber \\&\quad + \lambda _{R_1} \left\{ \alpha _1 I_{b1} - d_1 R_1 - (1 - u_1(t))m_2 R_1 + (1 - u_2(t))m R \right\} , \nonumber \\&\quad + \lambda _{S_{v1}} \left\{ b_{v1} - \beta _{v1} \lambda _{v1}\dfrac{\kappa _{v1} E_1 + \tau _{v1} I_{a1}}{N_{h1}}S_{v1} - d_{v1} S_{v1}\right\} , \nonumber \\&\quad + \lambda _{E_{v1}} \left\{ \beta _{v1}\lambda _{v1} \dfrac{\kappa _{v} E_1 + \tau _{v} I_{a1}}{N_{h1}}S_{v1} - d_{v1}E_{v1} - \psi _{v1} E_{v1}\right\} , \nonumber \\&\quad + \lambda _{I_{v1}} \left\{ \psi _{v1} E_{v1} - d_{v1}I_{v1}\right\} , \end{aligned}$$
(15)
where \(\lambda _{S}\), \(\lambda _{E}\), \(\lambda _{I_{a}}\), \(\lambda _{I_{b}}\),\(\lambda _{R}\), \(\lambda _{S_{v}}\), \(\lambda _{E_{v}}\), \(\lambda _{I_{v}}\), \(\lambda _{S_1}\), \(\lambda _{E_1}\), \(\lambda _{I_{a1}}\), \(\lambda _{I_{b1}}\), \(\lambda _{R_1}\), \(\lambda _{S_{v1}}\), \(\lambda _{E_{v1}}\) and \(\lambda _{I_{v1}}\) are the adjoint variables or co-state variables. The system of equations is found by taking the appropriate partial derivatives of the Hamiltonian (15) with respect to the associated state variables.
$$\begin{aligned} -\dfrac{\mathrm{d}\lambda _{S}}{\mathrm{d}t}&= \bigg [\beta \dfrac{\kappa E + \tau I_{a}}{N_h}\left( 1 - \dfrac{S}{N_h}\right) + \dfrac{\theta \beta _v \phi I_{v}}{N_h}\left( 1 - \dfrac{S}{N_h}\right) + d + (1 - u_2(t))m \bigg ]\lambda _{S}\\&\quad - \bigg [\beta \dfrac{\kappa E + \tau I_{a}}{N_h}\left( 1 - \dfrac{S}{N_h}\right) + \dfrac{\theta \beta _{v} \phi I_{v}}{N_h}\left( 1 - \dfrac{S}{N_h}\right) \bigg ]\lambda _{E}, \\&\quad + \bigg [ \beta _v \lambda _v \dfrac{\kappa _v E + \tau _v I_{a}}{N^2_h}S_v \bigg ](\lambda _{S_{v}} - \lambda _{E_{v}}) - (1 - u_2(t))m\lambda _{S_1},\\ -\dfrac{\mathrm{d}\lambda _{E}}{\mathrm{d}t}&= \bigg [\beta \dfrac{\kappa }{N_h}\left( 1 - \dfrac{E}{N_h}\right) \bigg ]\lambda _{S} - \bigg [\beta \dfrac{\kappa }{N_h}\left( 1 - \dfrac{E}{N_h}\right) + d + \gamma + (1 - u_2(t))m\bigg ]\lambda _{E} \\&\quad - \gamma \lambda _{I_{a}} + \bigg [\beta _v \lambda _v \frac{\kappa _v}{N_h}\left( 1 - \frac{E}{N_h}\right) \bigg ] \lambda _{S_{v}} - \bigg [\beta _v \lambda _v \frac{\kappa _v}{N_h}\left( 1 - \frac{E}{N_h}\right) \bigg ] \lambda _{E_{v}}\\&\quad - (1 - u_2(t))m\lambda _{E_1},\\ -\dfrac{\mathrm{d}\lambda _{I_{a}}}{\mathrm{d}t}&= - c_1 + \bigg [\beta \dfrac{\tau }{N_h}\left( 1 - \dfrac{I_{a}}{N_h}\right) \bigg ]\lambda _{S} - \bigg [\beta \dfrac{\tau }{N_h}\left( 1 - \dfrac{I_{a}}{N_h}\right) \bigg ]\lambda _{E}\\&\quad + \ [(d + \delta ) + (1 - u_2(t))m \ ]\lambda _{I_{a}}- \delta \lambda _{I_{b}}+ \bigg [\beta _v \lambda _v \dfrac{\tau _v}{N_h}\left( 1 - \dfrac{I_{a}}{N_h}\right) \bigg ] \lambda _{S_{v}} \\&\quad - \bigg [ \beta _v \lambda _v \dfrac{\tau _v}{N_h}\left( 1 - \dfrac{I_{a}}{N_h}\right) \bigg ] \lambda _{E_v}- (1 - u_2(t))m\lambda _{I_{a1}},\\ -\dfrac{\mathrm{d}\lambda _{I_{b}}}{\mathrm{d}t}&= - c_2 + (\alpha + d)\lambda _{I_{b}} - \alpha \lambda _{R}, \\ -\dfrac{\mathrm{d}\lambda _{R}}{\mathrm{d}t}&= (d + (1 - u_2(t))m)\lambda _{R} - (1 - u_2(t))m\lambda _{R_1},\\ -\dfrac{\mathrm{d}\lambda _{S_{v}}}{\mathrm{d}t}&= \bigg [\beta _v \lambda _v \dfrac{\kappa _v E + \tau _v I_{a}}{N_h} + d_v\bigg ] \lambda _{S_{v}} - \bigg [\beta _v \lambda _v \dfrac{\kappa _v E + \tau _v I_{a}}{N_h}\bigg ]\lambda _{E_{v}}, \\ -\dfrac{\mathrm{d}\lambda _{E_{v}}}{\mathrm{d}t}&= \bigg [d_v + \psi _v \bigg ]\lambda _{E_{v}} - \psi _v \lambda _{I_{v}}, \\ -\dfrac{\mathrm{d}\lambda _{I_{v}}}{\mathrm{d}t}&= (d_v)\lambda _{I_{v}} + \bigg [\dfrac{\theta \beta _v \phi }{N_h}S\bigg ]\lambda _{S} - \bigg [\dfrac{\theta \beta _v \phi }{N_h}S\bigg ]\lambda _{E}, \\ \dfrac{\mathrm{d}\lambda _{S_1}}{\mathrm{d}t}&= \bigg [\beta _1\dfrac{\kappa _1 E_1 + \tau _1 I_{a1}}{N_{h1}}\left( 1 - \dfrac{S_1}{N_{h1}}\right) + \dfrac{\theta _1 \beta _{v1} \phi _1 I_{v1}}{N_{h1}}\left( 1 - \dfrac{S_1}{N_{h1}}\right) \\&\quad + d_1 + (1 - u_1(t))m_2 \bigg ]\lambda _{S_1} \\&\quad - \bigg [ \beta _1\dfrac{\kappa _1 E_1 + \tau _1 I_{a1}}{N_{h1}}\left( 1 - \dfrac{S_1}{N_{h1}}\right) + \dfrac{\theta _1 \beta _{v1} \phi _1 I_{v1}}{N_{h1}}\left( 1 - \dfrac{S_1}{N_{h1}}\right) \bigg ]\lambda _{E_1}\\&\quad + \bigg [\beta _{v1} \lambda _{v1} \dfrac{\kappa _{v1} E_1 + \tau _{v1} I_{a1}}{N^2_{h1}}S_{v1} \bigg ] (\lambda _{S_{v1}} - \lambda _{E_{v1}}) - (1 - u_1(t))m_2\lambda _{S},\\ -\dfrac{\mathrm{d}\lambda _{E_{1}}}{\mathrm{d}t}&= \bigg [\beta _1 \dfrac{\kappa _1}{N_{h1}}\left( 1 - \dfrac{E_1}{N_{h1}}\right) \bigg ]\lambda _{S_1} - \bigg [\beta _1 \dfrac{\kappa _1}{N_{h1}}\left( 1 - \dfrac{E_1}{N_{h1}}\right) \\&\quad + d_1 + \gamma _1 + (1 - u_1(t))m_2\bigg ]\lambda _{E_1}\\&\quad - \gamma _1 \lambda _{I_{a1}} + \bigg [\beta _{v1} \lambda _{v1} \dfrac{\kappa _{v1}}{N_{h1}}\left( 1 - \dfrac{E_1}{N_{h1}}\right) \bigg ] (\lambda _{S_{v1}} - \lambda _{E_{v1}}) - (1 - u_1(t))m_2\lambda _{E},\\ -\dfrac{\mathrm{d}\lambda _{I_{a1}}}{\mathrm{d}t}&= - c_3 + \bigg [\beta _1 \dfrac{\tau _1}{N_{h1}}\left( 1 - \dfrac{I_{a1}}{N_{h1}}\right) \bigg ]\lambda _{S_1} - \bigg [\beta _1 \dfrac{\tau _1}{N_{h1}}(1 - \dfrac{I_{a1}}{N_{h1}}) \bigg ]\lambda _{E_1} \\&\quad + \ [d_1 + \delta _1 + (1 - u_1(t))m_2 \ ]\lambda _{I_{a1}} - \delta _1 \lambda _{I_{b1}} \\&\quad + \bigg [\beta _{v1} \lambda _{v1}\dfrac{\tau _{v1}}{N_{h1}}\left( 1 - \dfrac{I_{a1}}{N_{h1}}\right) \bigg ](\lambda _{S_{v1}} - \lambda _{E_{v1}})- \big [ (1 - u_1(t))m_2 \big ] \lambda _{I_a},\\ -\dfrac{\mathrm{d}\lambda _{I_{b1}}}{\mathrm{d}t}&= - c_4 + \big [ \alpha _1 + d_1 + (1 - u_3(t) q \big ]\lambda _{I_{b1}} - \big [ (1 - u_3(t))q \big ] \lambda _{I_b} - \alpha _1 \lambda _{R_1}, \\ -\dfrac{\mathrm{d}\lambda _{R_1}}{\mathrm{d}t}&= (d_1 + (1 - u_1(t))m_2)\lambda _{R_1} - \big [ (1 - u_1(t))m_2 \big ] \lambda _{R},\\ -\dfrac{\mathrm{d}\lambda _{S_{v1}}}{\mathrm{d}t}&= \bigg [\beta _{v1} \lambda _{v1} \dfrac{\kappa _{v1} E_1 + \tau _{v1} I_{a1}}{N_{h1}} + d_{v1}\bigg ] \lambda _{S_{v1}} - \bigg [ \beta _{v1}\lambda _{v1}\dfrac{\kappa _{v1} E_1 + \tau _{v1} I_{a1}}{N_{h1}}\bigg ]\lambda _{E_{v1}}, \\ -\dfrac{\mathrm{d}\lambda _{E_{v1}}}{\mathrm{d}t}&= \bigg [d_{v1} + \psi _{v1} \bigg ]\lambda _{E_{v1}} - \psi _{v1} \lambda _{I_{v1}}, \\ -\dfrac{\mathrm{d}\lambda _{I_{v1}}}{\mathrm{d}t}&= (d_{v1})\lambda _{I_{v1}} + \bigg [\dfrac{\theta _1 \beta _{v1} \phi _{v1}S_1}{N_{h1}}\bigg ]\lambda _{S_1} - \bigg [\dfrac{\theta _1 \beta _{v1} \phi _{v1}S_1}{N_{h1}}\bigg ]\lambda _{E_1}. \end{aligned}$$
Furthermore, the transversality conditions are
$$\begin{aligned}&\lambda _{S}(T) = \lambda _{E}(T) = \lambda _{I_{a}}(T) = \lambda _{I_{b}}(T) = \lambda _{R}(T) = \lambda _{S_{v}}(T) = \lambda _{E_{v}}(T) = \lambda _{I_{v}}(T) \\&\quad = \lambda _{S_{1}}(T) = \lambda _{E_{1}}(T) = \lambda _{I_{a1}}(T) = \lambda _{I_{b1}}(T) = \lambda _{R_{1}}(T) = \lambda _{S_{v1}}(T) = \lambda _{E_{v1}}(T)\\&\quad = \lambda _{I_{v1}} (T) = 0. \end{aligned}$$
Finally, since in our optimal control problem, there are no terminal value for the state variable, we give transversality conditions at the final time T by
$$\begin{aligned} \lambda _i (T) = 0, i = 1,2,3. \end{aligned}$$
On the interior of the control set, where \(0< u_i < 1\), for \(i = 1,\ 2,\ 3\), we have
$$\begin{aligned} \dfrac{\partial H}{\partial u_{1}}&= 2c_5 u_1 - m_2 S_1\lambda _{S} - m_2 E_1 \lambda _{E} - m_2 I_{a1} \lambda _{I_a} - m_2 R_1 \lambda _R + m_2 S_1 \lambda _{S_1} \\&\quad + m_2 E_1 \lambda _{E_1}+ m_2 I_{a1} \lambda _{I_{a1}} + m_2 R_1 \lambda _{R_1} = 0,\\ \dfrac{\partial H}{\partial u_{2}}&= 2c_6 u_2 + mS\lambda _S + mE\lambda _{E} + mI_a\lambda _{I_{a}} + mR\lambda _R - mS\lambda _{S_{1}} - mE\lambda _{E_1} \\&\quad - mI_a\lambda _{I_{a1}}- mR\lambda _{R_1} = 0,\\ \dfrac{\partial H}{\partial u_{3}}&= 2c_7 u_3 - q I_{b1}\lambda _{I_b} + q I_{b1}\lambda _{I_{b1}} = 0. \end{aligned}$$
We obtain
$$\begin{aligned} u^{**} _{1}&= \dfrac{1}{2c_5}\bigg [ m_2 S_1\lambda _{S} + m_2 E_1 \lambda _{E} + m_2 I_{a1} \lambda _{I_a} + m_2 R_1 \lambda _R - m_2 S_1 \lambda _{S_1} - m_2 E_1 \lambda _{E_1}\\&\quad - m_2 I_{a1} \lambda _{I_{a1}} - m_2 R_1 \lambda _{R_1} \bigg ], \\ u^{**}_{2}&= \dfrac{1}{2c_6} \bigg [- mS\lambda _S - mE\lambda _{E} - mI_a\lambda _{I_{a}} - mR\lambda _R + mS\lambda _{S_{1}} + mE\lambda _{E_1} \\&\quad + mI_a\lambda _{I_{a1}} + mR\lambda _{R_1} \bigg ], \\ u^{**}_3&= \dfrac{1}{2c_7} \bigg [q I_{b1}\lambda _{I_b} - q I_{b1}\lambda _{I_{b1}}\bigg ]. \end{aligned}$$
By the standard control arguments involving the bounds on the control variables, we conclude that
$$\begin{aligned} u^*_{1}= & {} \left\{ \begin{array}{ll} 0 &{}\quad {\text {if}} \ u^{**}_{1} \le 0 \\ u^{**}_{1} &{}\quad {\text {if}} \ 0< u^{**}_{1}< 1,\\ 1 &{}\quad \text {if} \ u^{**}_{1} \ge 1 \end{array} \right. \\ u^*_{2}= & {} \left\{ \begin{array}{ll} 0 &{}\quad {\text {if}} \ u^{**}_{2} \le 0 \\ u^{**}_{2} &{}\quad {\text {if}} \ 0< u^{**}_{2}< 1,\\ 1 &{}\quad {\text {if}} \ u^{**}_{2} \ge 1 \end{array} \right. \\ u^*_{3}= & {} \left\{ \begin{array}{ll} 0 &{}\quad {\text {if}} \ u^{**}_{3} \le 0 \\ u^{**}_{3} &{}\quad {\text {if}} \ 0< u^{**}_{3} < 1\\ 1 &{}\quad {\text {if}} \ u^{**}_{3} \ge 1 \end{array} \right. , \end{aligned}$$
that is,
$$\begin{aligned} u^*_{1}&= \min \left\{ 1,\max \big (0, u^{**} _{1} \big ) \right\} , \\ u^*_{2}&= \min \left\{ 1, \max \big (0, u^{**} _{2} \big ) \right\} , \\ u^*_{3}&= \min \left\{ 1, \max \big (0, u^{**} _{3}\big ) \right\} . \end{aligned}$$
Appendix B
Consider a simplified model with a single category of infectives for each location and no active movements for infectives, in the form.
$$\begin{aligned} \dfrac{\mathrm{d}S}{\mathrm{d}t}&= b - \beta \dfrac{\kappa E + \tau I_{a}}{N_h}S - \dfrac{\theta \beta _v \phi I_v}{N_h}S - dS + m_2 S_1 - mS, \nonumber \\ \dfrac{\mathrm{d}E}{\mathrm{d}t}&= \beta \dfrac{\kappa E + \tau I_{a}}{N_h}S + \dfrac{\theta \beta _v \phi I_v}{N_h}S - dE - \gamma E + m_2 E_1 - mE, \nonumber \\ \dfrac{\mathrm{d}I_{a}}{\mathrm{d}t}&= \gamma E - dI_{a} - \alpha I_{a} + q I_{a1},\nonumber \\ \dfrac{\mathrm{d}R}{\mathrm{d}t}&= \alpha I_{a} - dR + m_2 R_1 - mR, \nonumber \\ \dfrac{\mathrm{d}S_v}{\mathrm{d}t}&= b_v - \beta _v \lambda _v \dfrac{\kappa _v E + \tau _v I_{a}}{N_h}S_v - d_v S_v, \nonumber \\ \dfrac{\mathrm{d}E_v}{\mathrm{d}t}&= \beta _v \lambda _v \dfrac{\kappa _v E + \tau _v I_{a}}{N_h}S_v - d_v E_v - \psi _v E_v, \nonumber \\ \dfrac{\mathrm{d}I_v}{\mathrm{d}t}&= \psi _v E_v - d_v I_v, \nonumber \\ \dfrac{\mathrm{d}S_1}{\mathrm{d}t}&= b_1 - \beta _1\dfrac{\kappa _1 E_1 + \tau _1 I_{a1}}{N_{h1}}S_1 - \dfrac{\theta _1 \beta _{v1} \phi _{1} I_{v1} S_1}{N_{h1}} - d_1 S_1 - m_2 S_1 + mS , \nonumber \\ \dfrac{\mathrm{d}E_1}{\mathrm{d}t}&= \beta _1\dfrac{\kappa _1 E_1 + \tau _1 I_{a1}}{N_{h1}}S_1 + \dfrac{\theta _1\beta _{v1}\phi _1 I_{v1} S_1}{N_{h1}} - d_1 E_1 - \gamma _1 E_1 - m_2 E_1 + mE , \nonumber \\ \dfrac{\mathrm{d}I_{a1}}{\mathrm{d}t}&= \gamma _1 E_1 - d_1 I_{a1} - \alpha _1 I_{a1} - q I_{a1}, \nonumber \\ \dfrac{\mathrm{d}R_1}{\mathrm{d}t}&= \alpha _1 I_{a1} - d_1 R_1 - m_2 R_1 + mR, \nonumber \\ \dfrac{\mathrm{d}S_{v1}}{\mathrm{d}t}&= b_{v1} - \beta _{v1}\lambda _{v1} \dfrac{\kappa _{v1} E_1 + \tau _{v1} I_{a1}}{N_{h1}}S_{v1} - d_{v1} S_{v1}, \nonumber \\ \dfrac{\mathrm{d}E_{v1}}{\mathrm{d}t}&= \beta _{v1}\lambda _{v1} \dfrac{\kappa _{v1} E_1 + \tau _{v1} I_{a1}}{N_{h1}}S_{v1} - d_{v1}E_{v1} - \psi _{v1} E_{v1}, \nonumber \\ \dfrac{\mathrm{d}I_{v1}}{\mathrm{d}t}&= \psi _{v1} E_{v1} - d_{v1} I_{v1}. \end{aligned}$$
(16)
Using the next-generation method, we obtain F and V as follows:
$$\begin{aligned} F= & {} \left[ \begin{array}{*{8}c} \beta \kappa &{} \beta \tau &{} 0 &{} \theta \beta _v \phi &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \dfrac{\beta _v \lambda _v \kappa _v b_vd}{bd_v} &{} \dfrac{\beta _v \lambda _v \tau _v b_vd}{bd_v} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} \beta _1 \kappa _1 &{} \beta _1 \tau _1 &{} 0 &{} \theta _1 \beta _{v1} \phi _1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \dfrac{\beta _{v1} \lambda _{v1} \kappa _{v1} b_{v1} d_1}{b_1 d_{v1}} &{} \dfrac{\beta _{v1} \lambda _{v1} \tau _{v1} b_{v1} d_1}{b_1 d_{v1}} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array} \right] ,\\ V= & {} \left[ \begin{array}{*{8}c} (d + \gamma + m) &{} 0 &{} 0 &{} 0 &{} -m_2 &{} 0 &{} 0 &{} 0 \\ -\gamma &{} (d + \alpha ) &{} 0 &{} 0 &{} 0 &{} -q &{} 0 &{} 0\\ 0 &{} 0 &{} (d_v + \psi _{v}) &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} -\psi _{v} &{} d_v &{} 0 &{} 0 &{} 0 &{} 0\\ -m &{} 0 &{} 0 &{} 0 &{} (d_1 + \gamma _1 + m_2) &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -\gamma &{} (d_1 + \alpha _1 + q) &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} (d_{v1} + \psi _{v1}) &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -\psi _{v1} &{} d_{v1} \end{array} \right] . \end{aligned}$$
The matrix \(FV^{-1}\) is given by
$$\begin{aligned} FV^{-1}= & {} \left[ \begin{array}{*{8}c} a &{}\quad b &{}\quad 0 &{}\quad c &{}\quad d &{}\quad e &{}\quad f &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ g &{}\quad h &{}\quad 0 &{}\quad 0 &{}\quad k &{}\quad l &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ m &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad n &{}\quad p &{}\quad q &{}\quad r \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ s &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad t &{}\quad u &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right] , \end{aligned}$$
where
$$\begin{aligned} a&= {\frac{\beta \,\kappa \, \left( d_{1}+\gamma _{1}+m_{2} \right) }{dd_{1} +dm_{2}+d\gamma _{1}+d_{1}\,\gamma +d_{1}\,m+\gamma \,m_{2}+\gamma \, \gamma _{1}+m\gamma _{1}}} \\&\quad + {\frac{\beta \,\tau \, \left( (d_{1}+m_{2}+q+\alpha _{1} +\gamma _{1}) d_{1}\,\gamma \,+\gamma \,m_{2}\,q+\gamma \,m_{2}\,\alpha _{1}+ \gamma \,q\gamma _{1}+\gamma \,\alpha _{1}\,\gamma _{1}+mq\gamma _{1} \right) }{ \left( \alpha +d \right) \left( dd_{1}+dm_{2}+d\gamma _{1}+ d_{1}\,\gamma +d_{1}\,m+\gamma \,m_{2}+\gamma \,\gamma _{1}+m\gamma _{1} \right) \left( d_{1}+\alpha _{1}+q \right) }}, \\ b&= {\frac{\beta \,\tau }{\alpha +d}}, \\ c&= {\frac{\theta \,\beta _{v}\,\phi \,\psi _{v}}{ \left( d_{v}+\psi _{v} \right) d_{v}}}, \\ d&= {\frac{\theta \,\beta _{v}\,\phi }{d_{v}}}, \\ e&= {\frac{\beta \,\kappa \,m_{2}}{dd_{1}+dm_{2}+d\gamma _{1}+d_{1}\,\gamma + d_{1}\,m+\gamma \,m_{2}+\gamma \,\gamma _{1}+m\gamma _{1}}} \\&\quad + {\frac{\beta \,\tau \, \left( dq\gamma _{1}+d_{1}\,\gamma \,m_{2}+\gamma \,m_{2}\,q+ \gamma \,m_{2}\,\alpha _{1}+\gamma \,q\gamma _{1}+mq\gamma _{1} \right) }{ \left( \alpha +d \right) \left( dd_{1}+dm_{2}+d\gamma _{1}+d_{1}\, \gamma +d_{1}\,m+\gamma \,m_{2}+\gamma \,\gamma _{1}+m\gamma _{1} \right) \left( d_{1}+\alpha _{1}+q \right) }}, \\ f&= {\frac{\beta \,\tau \,q}{ \left( d_{1}+\alpha _{1}+q \right) \left( \alpha +d \right) }}, \\ g&= {\frac{\beta _{v}\,\lambda _{v}\,\kappa _{v}\,b_{v}\,d \left( d_{1}+ \gamma _{1}+m_{2} \right) }{bd_{v}\, \left( dd_{1}+dm_{2}+d\gamma _{1}+d _{1}\,\gamma +d_{1}\,m+\gamma \,m_{2}+\gamma \,\gamma _{1}+m\gamma _{1} \right) }} \\&\quad +\, {\frac{\beta _{v}\,\lambda _{v}\,\tau _{v}\,b_{v}\,d \left( ( d_{1}+m_{2}+q+\alpha _{1}+\gamma _{1})d_{1}\,\gamma \,+\gamma \,m_{2}\,q+\gamma \,m_{2} \,\alpha _{1}+\gamma \,q\gamma _{1}+\gamma \,\alpha _{1}\,\gamma _{1}+mq \gamma _{1} \right) }{bd_{v}\, \left( \alpha +d \right) \left( dd_{1}+d m_{2}+d\gamma _{1}+d_{1}\,\gamma +d_{1}\,m+\gamma \,m_{2}+\gamma \,\gamma _ {1}+m\gamma _{1} \right) \left( d_{1}+\alpha _{1}+q \right) }}, \\ h&= {\frac{\beta _{v}\,\lambda _{v}\,\tau _{v}\,b_{v}\,d}{bd_{v}\, \left( \alpha +d \right) }}, \\ k&= {\frac{\beta _{v}\,\lambda _{v}\,\kappa _{v}\,b_{v}\,dm_{2}}{bd_{v}\, \left( dd_{1}+dm_{2}+d\gamma _{1}+d_{1}\,\gamma +d_{1}\,m+\gamma \,m_{2} +\gamma \,\gamma _{1}+m\gamma _{1} \right) }} \\&\quad +\, {\frac{\beta _{v}\,\lambda _ {v}\,\tau _{v}\,b_{v}\,d \left( dq\gamma _{1}+d_{1}\,\gamma \,m_{2}+ \gamma \,m_{2}\,q+\gamma \,m_{2}\,\alpha _{1}+\gamma \,q\gamma _{1}+mq \gamma _{1} \right) }{bd_{v}\, \left( \alpha +d \right) \left( dd_{1}+d m_{2}+d\gamma _{1}+d_{1}\,\gamma +d_{1}\,m+\gamma \,m_{2}+\gamma \,\gamma _ {1}+m\gamma _{1} \right) \left( d_{1}+\alpha _{1}+q \right) }}, \\ l&= {\frac{\beta _{v}\,\lambda _{v}\,\tau _{v}\,b_{v}\,dq}{bd_{v}\, \left( d _{1}+\alpha _{1}+q \right) \left( \alpha +d \right) }}, \\ m&= {\frac{\beta _{1}\,\kappa _{1}\,m}{dd_{1}+dm_{2}+d\gamma _{1}+d_{1}\, \gamma +d_{1}\,m+\gamma \,m_{2}+\gamma \,\gamma _{1}+m\gamma _{1}}} \\&\quad + {\frac{\beta _{1}\,\tau _{1}\,\gamma _{1}\,m}{ \left( dd_{1}+dm_{2}+d\gamma _{1} +d_{1}\,\gamma +d_{1}\,m+\gamma \,m_{2}+\gamma \,\gamma _{1}+m\gamma _{1} \right) \left( d_{1}+\alpha _{1}+q \right) }}, \\ n&= {\frac{\beta _{1}\,\kappa _{1}\, \left( d+\gamma +m \right) }{dd_{1}+dm_ {2}+d\gamma _{1}+d_{1}\,\gamma +d_{1}\,m+\gamma \,m_{2}+\gamma \,\gamma _{1 }+m\gamma _{1}}} \\&\quad +\,{\frac{\beta _{1}\,\tau _{1}\,\gamma _{1}\, \left( d+ \gamma +m \right) }{ \left( dd_{1}+dm_{2}+d\gamma _{1}+d_{1}\,\gamma +d_{ 1}\,m+\gamma \,m_{2}+\gamma \,\gamma _{1}+m\gamma _{1} \right) \left( d_{ 1}+\alpha _{1}+q \right) }}, \\ p&= {\frac{\beta _{1}\,\tau _{1}}{d_{1}+\alpha _{1}+q}}, \\ q&= {\frac{\theta _{1}\,\beta _{1v}\,\phi _{1}\,\psi _{{ v1} }}{ \left( d_{{ v1}}+\psi _{{ v1}} \right) d_{{ v1}}}}, \\ r&= {\frac{\theta _{1}\,\beta _{1v}\,\phi _{1}}{d_{{ v1}}}}, \\ s&= {\frac{\beta _{{ v1}}\,\lambda _{{ v1}}\,\kappa _{{ v1}}\,b_{{ v1}}\,d_{1}\,m}{b_{1}\,d_{{ v1}}\, \left( dd_{1}+dm_{2}+d\gamma _{1}+d_{1}\,\gamma +d_{1}\,m+\gamma \,m_{2}+\gamma \,\gamma _{1}+m\gamma _{ 1} \right) }} \\&\quad +\, {\frac{\beta _{{ v1}}\,\lambda _{{ v1}}\,\tau _{{ v1}}\,b_{{ v1}}\,d_{1}\,\gamma _{1}\,m}{b_{1}\,d_{{ v1}}\, \left( dd_{1}+dm_{2}+d\gamma _{1}+d_{1}\,\gamma +d_{1}\,m+\gamma \,m_{2} +\gamma \,\gamma _{1}+m\gamma _{1} \right) \left( d_{1}+\alpha _{1}+q \right) }}, \\ t&= {\frac{\beta _{{ v1}}\,\lambda _{{ v1}}\,\kappa _{{ v1}}\,b_{{ v1}}\,d_{1}\, \left( d+\gamma +m \right) }{b_{1}\,d_{{ v1}}\, \left( dd_{1}+dm_{2}+d\gamma _{1}+d_{1}\,\gamma +d_{1}\,m+\gamma \,m_{2} +\gamma \,\gamma _{1}+m\gamma _{1} \right) }} \\&\quad + {\frac{\beta _{{ v1}}\, \lambda _{{ v1}}\,\tau _{{ v1}}\,b_{{ v1}}\,d_{1}\,\gamma _{1}\, \left( d+\gamma +m \right) }{b_{1}\,d_{{ v1}}\, \left( dd_{1}+dm_{2 }+d\gamma _{1}+d_{1}\,\gamma +d_{1}\,m+\gamma \,m_{2}+\gamma \,\gamma _{1}+ m\gamma _{1} \right) \left( d_{1}+\alpha _{1}+q \right) }},\\ u&= {\frac{\beta _{{ v1}}\,\lambda _{{ v1}}\,\tau _{{ v1}}\,b_{{ v1}}\,d_{1}}{b_{1}\,d_{{ v1}}\, \left( d_{1}+\alpha _{1}+q \right) }}. \end{aligned}$$
The basic reproduction number \(R_0^s\) (we use the superscript s to denote the fact that we refer to the simplified model) is the spectral radius (dominant eigenvalue) of the matrix \(FV^{-1}\). We substitute different values of the passive (q) and active (m and \(m_2\)) movement rates to obtain the associated values of \(R_0^s\). The effects of the passive movement on the global basic reproduction number \(R_0^s\) are shown in Fig. 6.