Spatial Model for Oncolytic Virotherapy with Lytic Cycle Delay

Abstract

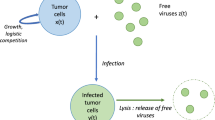
We formulate a mathematical model of functional partial differential equations for oncolytic virotherapy which incorporates virus diffusivity, tumor cell diffusion, and the viral lytic cycle based on a basic oncolytic virus dynamics model. We conduct a detailed analysis for the dynamics of the model and carry out numerical simulations to demonstrate our analytic results. Particularly, we establish the positive invariant domain for the $\omega$ limit set of the system and show that the model has three spatially homogenous equilibriums solutions. We prove that the spatially uniform virus-free steady state is globally asymptotically stable for any viral lytic period delay and diffusion coefficients of tumor cells and viruses when the viral burst size is smaller than a critical value. We obtain the conditions, for example the ratio of virus diffusion coefficient to that of tumor cells is greater than a value and the viral lytic cycle, is greater than a critical value, under which the spatially uniform positive steady state is locally asymptotically stable. We also obtain conditions under which the system undergoes Hopf bifurcations, and stable periodic solutions occur. We point out medical implications of our results which are difficult to obtain from models without combining diffusive properties of viruses and tumor cells with viral lytic cycles.

Appendix: Stability and Direction of the Hopf Bifurcations

Theory of functional reaction–diffusion systems says that a family of spatially homogeneous or inhomogeneous periodic solutions may bifurcate from the positive homogeneous equilibrium state $E^{*}$ of the system (5) when $\tau$ crosses through the critical value $\tau ^{*}$. In Appendix, we investigate the stability and direction of Hopf bifurcations by using the center manifold theorem and the normal formal theory of partial functional differential equation (Faria 2000; Wu 2012). Basically, the system (5) firstly is represented as an abstract ODE system. Secondly, at the center manifold of the ODE system corresponding to $E^{*}$, the normal form or Taylor expansion of the ODE system is computed. Then, the coefficients of the first four terms of the normal form will reveal all the properties of the periodical solutions (Hassard et al. 1981). At the end, we briefly describe the numerical method we use to solve our system.

Let $u_1(\cdot ,t)=u(\cdot ,\tau t)-u^{*},~u_2(\cdot ,t)=w(\cdot ,\tau t)-w^{*},~u_3(\cdot ,t)=v(\cdot ,\tau t)-v^{*}$ and $U(t)=(u_1(\cdot ,t),u_2(\cdot ,t),u_3(\cdot ,t))^T$. Then, the system (5) can be written as an equation in the function space $\mathscr {C}=C([-1,0],X):$

$$\begin{aligned} \frac{\text {d}U(t)}{\text {d}t}=\tau D\Delta U(t)+L(\tau )(U_t)+f(U_t,\tau ), \end{aligned}$$

(19)

where $D=\text {diag}(d_1,d_1,d_2)$, $L(\tau )(\cdot ):\mathscr {C}\rightarrow X$ and $f:\mathscr {C}\times \mathbb {R}\mathscr {c}\rightarrow X$ are given, respectively, by

$$\begin{aligned} L(\tau )(\varphi )= & {} \tau L_1\varphi (0)+\tau L_2\varphi (-1),\\ f(\varphi ,\tau )= & {} \tau (f_1(\varphi ,\tau ),~f_2(\varphi ,\tau ), ~f_3(\varphi ,\tau ))^T, \end{aligned}$$

with

$$\begin{aligned} f_1(\varphi ,\tau )= & {} -r\varphi _1^2(0)-r\varphi _1(0) \varphi _2(0)-a\varphi _1(0)\varphi _3(0),\\ f_2(\varphi ,\tau )= & {} a\varphi _1(-\tau )\varphi _3(-\tau ), \\ f_3(\varphi ,\tau )= & {} -a\varphi _1(0)\varphi _3(0), \end{aligned}$$

for $\varphi =(\varphi _1,\varphi _2,\varphi _3)^\text {T} \in \mathscr {C}$.

Let $\tau =\tau ^{*}+\sigma$, then (19) can be rewritten as

$$\begin{aligned} \frac{\text {d}U(t)}{\text {d}t}=\tau ^{*} D \Delta U(t)+L(\tau ^{*})(U_t)+F(U_t,\sigma ), \end{aligned}$$

(20)

where

$$\begin{aligned} F(\varphi ,\sigma )=\sigma D \Delta \varphi (0)+L(\sigma )(\varphi ) +f(\varphi ,\tau ^{*}+\sigma ),\end{aligned}$$

for $\varphi \in \mathscr {C}$.

From the previous subsection, when $\sigma =0$ (i.e. $\tau =\tau ^{*}$) the system (20) undergoes Hopf bifurcation at the equilibrium (0, 0, 0), it is also clear that $\pm \text {i}\omega ^{*}\tau ^{*}$ are simply purely imaginary eigenvalues of the linearized system of (20) at the origin

$$\begin{aligned} \frac{\text {d}U(t)}{\text {d}t}=(\tau ^{*}+\sigma ) D \Delta U(t)+L(\tau ^{*}+\sigma )(U_t), \end{aligned}$$

(21)

with $\sigma =0$ and all other eigenvalues of (21) at $\sigma =0$ have negative real parts.

The eigenvalues of $\tau D \Delta$ on X are $-\tau d_1\mu _n$ (the number of multiples is two) and $-\tau d_2\mu _n,~n\in \mathbb {N}_0$, with corresponding eigenfunctions $\beta _n^1(x)=(\gamma _n(x),0,0)^T, ~\beta _n^2(x)=(0,\gamma _n(x),0)^T$ and $\beta _n^3(x)=(0,0, \gamma _n(x))^T$, where $\gamma _n(x)=\frac{\phi _n(x)}{(\int _\omega \phi _n(x)\text {d}x)^{\frac{1}{2}}}.$

We have that the solution operator of (21) is a $C_0$ semigroup, and the infinitesimal generator $A_{\sigma }$ is given by

$$\begin{aligned} A_{\sigma }\phi ={\left\{ \begin{array}{ll} \dot{\phi }(\theta ), &{}\theta \in [-r,0), \\ D\Delta \phi (0)+L(\tau ^{*}+\sigma )(\phi ), \qquad &{}\theta =0. \end{array}\right. } \end{aligned}$$

(22)

and the domain $\text {dom}(A_{\sigma })$ of $A_{\sigma }$ is

$$\begin{aligned} \text {dom}(A_{\sigma }):=\{\phi \in \mathscr {C}: \dot{\phi } \in \mathscr {C}, \phi (0)\in \text {dom}(\Delta ), \dot{\phi }(0)=D\Delta \phi (0)+L(\tau ^{*}+\sigma )(\phi )\}. \end{aligned}$$

Hence, Eq. (20) can be rewritten as the abstract ODE in $\mathscr {C}$:

$$\begin{aligned} \dot{U}_t=A_{\sigma }U_t+R(\sigma ,U_t), \end{aligned}$$

(23)

where

$$\begin{aligned} R(\sigma , U_t)(\theta )={\left\{ \begin{array}{ll} 0 , &{}\theta \in [-1, 0),\\ F(\sigma , U_t), \quad &{}\theta =0. \end{array}\right. } \end{aligned}$$

We denote

$$\begin{aligned} \beta _n=\{(1, 0,0)^{\text {T}}\gamma _n, (0, 1,0)^{\text {T}} \gamma _n,(0,0,1)^{\text {T}}\gamma _n\}. \end{aligned}$$

For $\phi =(\phi ^{^{(1)}},\phi ^{^{(2)}})^{T}\in \mathscr {C}$, we denote

$$\begin{aligned} \phi _n=\langle \phi ,\beta _n\rangle =\left( \langle \phi ^{^{(1)}}, \gamma _n\rangle , \langle \phi ^{^{(2)}},\gamma _n\rangle , \langle \phi ^{^{(3)}},\gamma _n\rangle \right) ^\text {T}. \end{aligned}$$

Define $A_{\sigma , n}$ as

$$\begin{aligned} A_{\sigma ,n}(\phi _n(\theta )\gamma _n)={\left\{ \begin{array}{ll} \dot{\phi }_n(\theta )\gamma _n,&{} \theta \in [-1,0), \\ \int _{-r}^{0}\text {d}\eta _n(\sigma ,\theta )\phi _n(\theta ) \gamma _n , \qquad &{}\theta =0. \end{array}\right. } \end{aligned}$$

(24)

Furthermore, we have

$$\begin{aligned} L_{\sigma , n}(\phi _n)=(\tau ^{*}+\sigma )L_1\phi _n(0) +(\tau ^{*}+\sigma )L_2\phi _n(-1), \end{aligned}$$

and

$$\begin{aligned} -\mu _n D\phi _n(0)+L_{\sigma ,n}(\phi _n)=\int _{-1}^{0} \text {d}\eta _n(\sigma ,\theta )\phi _n(\theta ), \end{aligned}$$

where

$$\begin{aligned} \eta _n(\sigma ,\theta )=\left\{ \begin{array}{ll} -(\tau ^{*}+\sigma )L_2, &{} \theta =-1,\\ 0, &{} \theta \in (-1,0),\\ (\tau ^{*}+\sigma )(L_1-\mu _nD), &{} \theta =0. \end{array}\right. \end{aligned}$$

Define $\mathscr {C}^{*}=C([0,1];X)$ and a bilinear form $(\cdot ,\cdot )$ on $\mathscr {C}^{*}\times \mathscr {C}$

$$\begin{aligned} (\psi ,\phi )=\sum _{k,j=0}^\infty (\psi _k,\phi _j)_c \int _\Omega \gamma _k\gamma _j\text {d}x, \end{aligned}$$

where $(\cdot ,\cdot )_c$ is the bilinear form defined on $C^{*}\times C$

$$\begin{aligned} (\psi _n,\phi _n)_c=\overline{\psi }_n^T(0)\phi _n(0) -\int _{-1}^0\int _{\xi =0}^\theta \overline{\psi }_n^T(\xi -\theta ) \text {d}\eta _n(0,\theta )\phi _n(\xi )\text {d}\xi , \end{aligned}$$

and

$$\begin{aligned} \psi =\sum _{n=0}^\infty \psi _n\gamma _n\in \mathscr {C}^{*}, ~\phi =\sum _{n=0}^\infty \phi _n\gamma _n\in \mathscr {C}, \end{aligned}$$

with

$$\begin{aligned} \phi _n\in C=C([-1,0],\mathbb {R}^2),~~\psi _n \in C^{*}=([0,1],\mathbb {R}^2). \end{aligned}$$

Notice that

$$\begin{aligned} \int _\Omega \gamma _k\gamma _j\text {d}x=0~~\text{ for }~~k\ne j, \end{aligned}$$

we have

$$\begin{aligned} (\psi ,\phi )=\sum _{n=0}^\infty (\psi _n,\phi _n)_c, \end{aligned}$$

We define the adjoint operator $A^{*}$ of $A_0$

$$\begin{aligned} A^{*}\psi (s)=\left\{ \begin{array}{ll} -\dot{\psi }(s),~&{} s\in (0,1],\\ \sum _{n=0}^\infty \int _{-1}^0\text {d} \eta _n^T(0,t)\psi _n(-t)\gamma _n,~&{}s=0. \end{array}\right. \end{aligned}$$

Let

$$\begin{aligned} q(\theta )\gamma _{n_0}=q(0)e^{i\omega ^{*}\tau ^{*}\theta }\gamma _{n_0}, ~q^{*}(s)\gamma _{n_0}=q^{*}(0)e^{i\omega ^{*}\tau ^{*} s}\gamma _{n_0} \end{aligned}$$

be the eigenfunctions of $A_0,$ and $A^{*}$ corresponds to $i\omega ^{*}\tau ^{*}$ and $-i\omega ^{*}\tau ^{*}$, respectively. By direct calculations, we chose

$$\begin{aligned} q(0)=(1, C_1,C2)^\text {T},~q^{*}(0)=M(1,C_3, C_4)^\text {T} \end{aligned}$$

where

$$\begin{aligned} C_1= & {} \frac{a^2u^{*}v^{*}-(\text {i}\omega ^{*} +d_1\mu _{n_0}+ru^{*})(\text {i}\omega ^{*} +d_2\mu _{n_0}+au^{*}+c)}{abu^{*}+ru^{*} (\text {i}\omega ^{*}+d_2\mu _{n_0}+au^{*}+c)},\\ C_2= & {} -\frac{(\text {i}\omega ^{*}+d_1\mu _{n_0} +ru^{*})b+rau^{*}v^{*}}{abu^{*}+ru^{*} (\text {i}\omega ^{*}+d_2\mu _{n_0}+au^{*}+c)},\\ C_3= & {} \frac{(-\text {i}\omega ^{*}+d_1\mu _{n_0} +ru^{*})(-\text {i}\omega ^{*}+d_2\mu _{n_0}+au^{*}+c) -a^2u^{*}v^{*}}{av^{*}\text {e}^{-\text {i}\omega ^{*}\tau ^{*}} (-\text {i}\omega ^{*}+d_2\mu _{n_0}+c)},\\ C_4= & {} \frac{(-\text {i}\omega ^{*}+d_1\mu _{n_0} +ru^{*})u^{*}-au^{*}v^{*}}{v^{*} (-\text {i}\omega ^{*}+d_2\mu _{n_0}+c)} \end{aligned}$$

and

$$\begin{aligned} \overline{M}=\frac{1}{1+C_1\overline{C_3} +C_2\overline{C_4}+\tau ^{*}a\overline{C_3} (v^{*}+u^{*}C_2)\text {e}^{-\text {i}\omega \tau ^{*}}}. \end{aligned}$$

Obviously, $(q^{*},q)_{c}=1$. Then, we decompose $\mathscr {C}$ by

$$\begin{aligned} \Lambda =\{\pm i\omega ^{*}\tau ^{*}\}, \end{aligned}$$

$\mathscr {C}=P\oplus Q$, where

$$\begin{aligned} P= & {} \{zq\gamma _{n_0}+\overline{z} \overline{q}\gamma _{n_0}|z\in \mathbb {C}\},\\ Q= & {} \{\phi \in \mathscr {C}|(q^{*}\gamma _{n_0},\phi ) =0~\text {and}~(\overline{q}^{*}\gamma _{n_0},\phi )=0\}. \end{aligned}$$

Thus, system (23) could be rewritten as

$$\begin{aligned} U_t=z(t)q(\cdot )\gamma _{n_0}+\bar{z}(t) \bar{q}(\cdot )\gamma _{n_0}+W(t,\cdot ), \end{aligned}$$

where

$$\begin{aligned} \quad W(t,\cdot )\in Q. \end{aligned}$$

As in Hassard et al. (1981), we have

$$\begin{aligned} z(t)=(q^{*}\gamma _{n_0}, U_t),\qquad W(t,\theta )=U_t(\theta )-2\text {Re}\{z(t)q(\theta )\gamma _{n_0}\}. \end{aligned}$$

(25)

Then, it follows that

$$\begin{aligned} \dot{z}(t)=i\omega _0z(t)+\bar{q}^{*\text {T}}(0) \langle F(0, U_t), \beta _{n_0}\rangle , \end{aligned}$$

(26)

where

$$\begin{aligned} \langle F, \beta _{n} \rangle :=(\langle F_1, \gamma _{n}\rangle , \langle F_2, \gamma _{n} \rangle , \langle F_3, \gamma _{n} \rangle )^\text {T}, \end{aligned}$$

With the center manifold theorem (Lin et al. 1992), there exists a center manifold $\mathcal {C}_0$ and on $\mathcal {C}_0$, we have

$$\begin{aligned} W(t,\theta )=W(z(t),\bar{z}(t),\theta )=W_{20}(\theta )\frac{z^2}{2}+W_{11}(\theta )z\bar{z} +W_{02}(\theta )\frac{\bar{z}^2}{2}+\cdots , \end{aligned}$$

(27)

where z and $\bar{z}$ are local coordinates for center manifold $\mathcal {C}_0$ in the direction of $q\gamma _{n_0}$ and $\bar{q}\gamma _{n_0}$, respectively. For solution $U_t\in \mathcal {C}_0$, we denote

$$\begin{aligned} F(0, U_t)\mid _{\mathcal {C}_0}=\tilde{F}(0, z, \bar{z}), \end{aligned}$$

and

$$\begin{aligned} \tilde{F}(0, z, \bar{z})=\tilde{F}_{zz}''\frac{z^2}{2}+\tilde{F}_{z\bar{z}}''z\bar{z}+\tilde{F}_{\bar{z}\bar{z}}''\frac{\bar{z}^2}{2} +\tilde{F}_{zz\bar{z}}''\frac{z^2\bar{z}}{2}+\cdots . \end{aligned}$$

For convenience, we rewrite (26) as

$$\begin{aligned} \dot{z}(t)=i\omega _0z(t)+g(z,\bar{z}), \end{aligned}$$

and denote

$$\begin{aligned} g(z,\bar{z})=g_{20}\frac{z^2}{2} +g_{11}z\bar{z}+g_{02}\frac{\bar{z}^2}{2} +g_{21}\frac{z^2\bar{z}}{2}+\cdots . \end{aligned}$$

From direct calculation, we get

$$\begin{aligned} g_{20}= & {} 2\overline{M}\tau ^{*}\int _\Omega \gamma _{n_0}^3 \text {d}x(-r-rC_1-aC_2+aC_2\text {e}^{-2\text {i}\omega ^{*} \tau ^{*}}\overline{C_3}-aC_2\overline{C_4}),\\ g_{11}= & {} \overline{M}\tau ^{*}\int _\Omega \gamma _{n_0}^3 \text {d}x[-2r-r(C_1+\overline{C_1})-a(C_2+\overline{C_2})\\&+\,a(C_2+\overline{C_2})\overline{C_3}-a(C_2+\overline{C_2}) \overline{C_4}],\\ g_{02}= & {} 2\overline{M}\tau ^{*}\int _\Omega \gamma _{n_0}^3 \text {d}x(-r-r\overline{C}_1-a\overline{C}_2+a\overline{C}_2 \text {e}^{2\text {i}\omega ^{*}\tau ^{*}}\overline{C_3} -a\overline{C}_2\overline{C_4}) \end{aligned}$$

and

$$\begin{aligned} g_{21}= & {} \overline{M}\tau ^{*}\int _\Omega \Big \{\Big [-r(2w_{20}^{(1)}(0) +4w_{11}^{(1)}(0))\\&-\,r(w_{20}^{(2)}(0)+2w_{11}^{(2)}(0) +\overline{C}_1w_{20}^{(1)}(0)+2C_1w_{11}^{(1)}(0))\\&-\,a(w_{20}^{(3)}(0)+2w_{11}^{(3)}(0)+\overline{C}_2w_{20}^{(1)}(0) +2C_2w_{11}^{(1)}(0))\Big ]\gamma _{n_0}^2\\&+\,a(w_{20}^{(3)}(-1)\text {e}^{\text {i}\omega ^{*}\tau ^{*}} +2w_{11}^{(3)}(-1)\text {e}^{-\text {i}\omega ^{*}\tau ^{*}} +\overline{C}_2w_{20}^{(1)}(-1)\text {e}^{\text {i}\omega ^{*}\tau ^{*}}\\&+\,2C_2w_{11}^{(1)}(-1)\text {e}^{-\text {i}\omega ^{*}\tau ^{*}}) \gamma _{n_0}^2\overline{C_3}-\,a(w_{20}^{(3)}(0)+2w_{11}^{(3)}(0)\\&+\,\overline{C}_2w_{20}^{(1)}(0) +2C_2w_{11}^{(1)}(0))\gamma _{n_0}^2\overline{C_4}\Big \} \text {d}x. \end{aligned}$$

Here, $w_{11}$ and $w_{20}$ are need to be computed. From (25), we have

$$\begin{aligned} \dot{W}&=\dot{U}_t-\dot{z}q\gamma _{n_0} -\dot{\bar{z}}\bar{q}\gamma _{n_0} \nonumber \\&={\left\{ \begin{array}{ll} A W-2\text {Re}\{g(z,\bar{z})q(\theta )\}\gamma _{n_0},&{} \theta \in [-r,0),\nonumber \\ A W-2\text {Re}\{g(z,\bar{z})q(\theta )\}\gamma _{n_0}+\tilde{F},\quad &{}\theta =0, \end{array}\right. }\nonumber \\&\doteq A W + H(z,\bar{z},\theta ), \end{aligned}$$

(28)

where

$$\begin{aligned} H(z,\bar{z},\theta )=H_{20}(\theta )\frac{z^2}{2} +H_{11}(\theta )z\bar{z}+H_{02}(\theta )\frac{\bar{z}^2}{2}+\cdots . \end{aligned}$$

Obviously,

$$\begin{aligned} H_{20}(\theta )&={\left\{ \begin{array}{ll} -g_{20}q(\theta )\gamma _{n_0}-\bar{g}_{02}\bar{q}(\theta ) \gamma _{n_0}, &{}\theta \in [-r,0),\\ -g_{20}q(0)\gamma _{n_0}-\bar{g}_{02}\bar{q}(0)\gamma _{n_0} +\tilde{F}''_{zz}, \quad &{} \theta =0,\\ \end{array}\right. }\\ H_{11}(\theta )&={\left\{ \begin{array}{ll} -g_{11}q(\theta )\gamma _{n_0}-\bar{g}_{11} \bar{q}(\theta )\gamma _{n_0}, &{}\theta \in [-r,0),\\ -g_{11}q(0)\gamma _{n_0}-\bar{g}_{11}\bar{q}(0) \gamma _{n_0}+\tilde{F}''_{z\bar{z}}, \quad &{} \theta =0,\\ \end{array}\right. }\\&\cdots . \end{aligned}$$

Comparing the coefficients of (28) with the derived function of (27), we obtain

$$\begin{aligned} (A_0 -2\text {i}\omega _0 I)W_{20}(\theta )=-H_{20}(\theta ), \quad A_0 W_{11}(\theta )=-H_{11}(\theta ),~\cdots . \end{aligned}$$

(29)

From (22) and (29), for $\theta \in [-1,0)$, we have

$$\begin{aligned} W_{20}(\theta )= & {} -\frac{g_{20}}{\text {i}\omega ^{*} \tau ^{*}}q(\theta )\gamma _{n_0}-\frac{\bar{g}_{02}}{3\text {i}\omega ^{*}\tau ^{*}}\overline{q}(\theta ) \gamma _{n_0}+E_1\text {e}^{2\text {i}\omega ^{*} \tau ^{*}\theta }, \nonumber \\ W_{11}(\theta )= & {} \frac{g_{11}}{\text {i} \omega ^{*}\tau ^{*}}q(0)\text {e}^{\text {i} \omega ^{*}\tau ^{*}\theta }\gamma _{n_0} -\frac{\bar{g}_{11}}{\text {i}\omega ^{*} \tau ^{*}}\overline{q}(0)\text {e}^{-\text {i} \omega ^{*}\tau ^{*}\theta }\gamma _{n_0}+E_2, \end{aligned}$$

(30)

where $E_1$ and $E_2$ are both three-dimensional vectors in X and can be determined by setting $\theta =0$ in H. In fact, set $\theta =0$ and by (29) and (30), we obtain

$$\begin{aligned} (A_0 -2\text {i}\omega ^{*}\tau ^{*}I)E_1\text {e}^{2\text {i} \omega ^{*}\tau ^{*}\theta }\mid _{\theta =0}=-\tilde{F}''_{zz}, \quad A_0 E_2\mid _{\theta =0}=-\tilde{F}''_{z\bar{z}}. \end{aligned}$$

(31)

The terms $\tilde{F}''_{zz}$ and $\tilde{F}''_{z\bar{z}}$ are elements in the space $\mathscr {C}$, and

$$\begin{aligned} \tilde{F}''_{zz}=\sum _{n=1}^{\infty }\langle \tilde{F}''_{zz}, \beta _n \rangle \gamma _n, \quad \tilde{F}''_{z\bar{z}} =\sum _{n=1}^{\infty }\langle \tilde{F}''_{z\bar{z}}, \beta _n \rangle \gamma _n. \end{aligned}$$

We denote

$$\begin{aligned} E_1=\sum _{n=0}^{\infty }E_1^n \gamma _n,~~E_2 =\sum _{n=0}^{\infty }E_2^n \gamma _n, \end{aligned}$$

then from (31) we have

$$\begin{aligned} \begin{array}{ll} (A_0-2\text {i}\omega ^{*}\tau ^{*}I)E_1^n \gamma _n \text {e}^{2\text {i}\omega ^{*}\tau ^{*}\theta }\mid _{\theta =0}=-\langle \tilde{F}''_{zz}, \beta _n \rangle \gamma _n,\\ A_0 E_2^n \gamma _n\mid _{\theta =0}=-\langle \tilde{F}''_{z\bar{z}}, \beta _n \rangle \gamma _n, \\ n=0,1,\cdots . \end{array} \end{aligned}$$

Thus, $E_1^n$ and $E_2^n$ could be calculated by

$$\begin{aligned} \begin{array}{l} E_1^n=\left( 2\text {i}\omega ^{*}\tau ^{*}I-\displaystyle {\int }_{-1}^0\text {e}^{2\text {i}\omega ^{*}\tau ^{*}\theta }\text {d}\eta _n(0,\theta )\right) ^{-1}\langle \tilde{F}''_{zz}, \beta _n \rangle ,\\ E_2^n=-\left( \displaystyle {\int }^0_{-1}\text {d}\eta _n(0,\theta )\right) ^{-1}\langle \tilde{F}''_{z\overline{z}}, \beta _n \rangle , \\ n=0,1,\cdots , \end{array} \end{aligned}$$

where

$$\begin{aligned} \tilde{F}_{20}= & {} 2\tau ^{*}\left( \begin{array}{c} -r-rC_1-aC_2\\ aC_2\text {e}^{-2\text {i}\omega ^{*}\tau ^{*}}\\ -aC_2 \end{array}\right) ,\\ \tilde{F}_{11}= & {} \tau ^{*}\left( \begin{array}{c} -2r-r(C_1+\overline{C}_1)-a(C_2+\overline{C}_2)\\ a(C_2+\overline{C}_2)\\ -a(C_2+\overline{C}_2) \end{array}\right) . \end{aligned}$$

Hence, $g_{21}$ could be represented explicitly.

We denote

$$\begin{aligned} c_1(0)= & {} \frac{i}{2\omega ^{*}\tau ^{*}}\left( g_{20}g_{11} -2|g_{11}|^2-\frac{1}{3}|g_{02}|^2\right) +\frac{1}{2}g_{21},\nonumber \\ \mu= & {} -\frac{\text {Re}(c_1(0))}{\tau ^{*} \text {Re}(\lambda '(\tau ^{*}))},~~~ \beta _2=2\text {Re}(c_1(0)),\nonumber \\ T_2= & {} -\frac{1}{\omega ^{*}\tau ^{*}}(\text {Im}(c_1(0)) +\mu _2(\omega ^{*}+\tau ^{*}\text {Im}(\lambda '(\tau ^{*}))). \end{aligned}$$

(32)

Then, by the general Hopf bifurcation theory (see Hassard et al. 1981), we know that $\mu$ determines the directions of the Hopf bifurcation: If $\mu >0(<0)$, then the direction of the Hopf bifurcation is forward (backward), that is the bifurcating periodic solutions exist when $a>0(<0)$; $\beta _2$ determines the stability of the bifurcating periodic solutions: The bifurcating periodic solutions are orbitally stable(unstable) if $\beta _2<0(>0)$, and $T_2$ determines the period of the bifurcation periodic solutions: The period increases(decreases) if $T_2>0(<0)$.

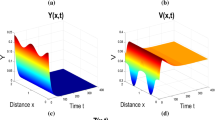
We now describe briefly the numerical method we use to solve the system (5) as follows. For $\Omega =(0,p\pi )\times (0,q\pi )$, let $x_i=ih_x, i=1,2,\cdots , l, h_x=\frac{p\pi }{l},y_j=jh_y, j=1,2,\cdots , m, h_y=\frac{q\pi }{m}, ,t_k=kh_t, h_t=\frac{\tau }{N}$ (N is a positive integer), and $u(i,j,k)=u(x_i,y_j,t_k),v(i,j,k) =v(x_i,y_j,t_k),w(i,j,k)=w(x_i,y_j,t_k)$. We replace $\frac{\partial u(x_i,y_j,t_k)}{\partial t}$ with a first-order difference $\frac{u(i,j,k+1)-u(i,j,k)}{h_t}$ and replace $\frac{\partial ^2 u(x_i,y_j,t_k)}{\partial x^2}+\frac{\partial ^2 u(x_i,y_j,t_k)}{\partial y^2}$ with a second-order difference $\frac{u(i+1,j,k)-2u(i,j,k)+u(i-1,j,k)}{h_x}+\frac{u(i,j+1,k) -2u(i,j,k)+u(i,j-1,k)}{h_y}$. Similarly, we take differences of the partial derivative of v and w. Then, we get a system of difference equations:

$$\begin{aligned} \left\{ \begin{array}{ll} u(i,j,k+1)= &{} u(i,j,k)+h_td_1\left( \frac{u(i+1,j,k)-2u(i,j,k) +u(i-1,j,k)}{h_x}\right. \\ &{}\left. +\,\frac{u(i,j+1,k)-2u(i,j,k)+u(i,j-1,k)}{h_y}\right) \\ &{}+\,h_t(ru(i,j,k)(1-u(i,j,k)-w(i,j,k))-au(i,j,k)v(i,j,k)),\\ w(i,j,k+1)= &{} w(i,j,k)+h_td_1\left( \frac{w(i+1,j,k)-2w(i,j,k)+w(i-1,j,k)}{h_x}\right. \\ &{}+\,\left. \frac{w(i,j+1,k)-2w(i,j,k)+w(i,j-1,k)}{h_y}\right) \\ &{}+\,h_t(au(i,j,k-N)v(i,j,k-N)-w(i,j,k)),\\ v(i,j,k+1)= &{} v(i,j,k)+h_td_2\left( \frac{v(i+1,j,k)-2v(i,j,k) +v(i-1,j,k)}{h_x}\right. \\ &{}\left. +\,\frac{v(i,j+1,k)-2v(i,j,k)+v(i,j-1,k)}{h_y}\right) \\ &{}+\,h_t(bw(i,j,k)-au(i,j,k)v(i,j,k)-cv(i,j,k)). \end{array}\right. \end{aligned}$$

We implement this method in MATLAB and obtain numerical solutions of the system (5).