Comments on “A Mathematical Study to Control Visceral Leishmaniasis: An Application to South Sudan”

Abstract

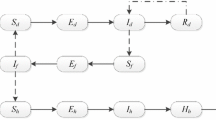
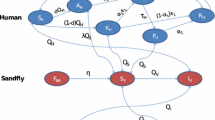
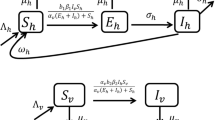
Deterministic (ordinary differential equation) models for the transmission dynamics of vector-borne diseases that incorporate disease-induced death in the host(s) population(s) are generally known to exhibit the phenomenon of backward bifurcation (where a stable disease-free equilibrium of the model coexists with a stable endemic equilibrium when the associated reproduction number of the model is less than unity). Further, it is well known that, in these models, the phenomenon of backward bifurcation does not occur when the disease-induced death rate is negligible (e.g., if the disease-induced death rate is set to zero). In a recent paper on the transmission dynamics of visceral leishmaniasis (a disease vectored by sandflies), titled “A Mathematical Study to Control Visceral Leishmaniasis: An Application to South Sudan,” published in Bulletin of Mathematical Biology, Vol. 79, Pages 1110–1134, 2017, Ghosh et al. (2017) stated that their deterministic model undergoes a backward bifurcation even when the disease-induced mortality in the host population is set to zero. This result is contrary to the well-established theory on the dynamics of vector-borne diseases. In this short note, we illustrate some of the key errors in the Ghosh et al. (2017) study.

Appendices

Appendix A: Proof of Theorem 3.1

Proof

Consider the model (1) in the absence of disease-induced mortality in the host population (i.e., $\delta =0$). Setting $\delta =0$ in the model (1) shows that $N_{H}(t) \rightarrow N^*_{H}$ as ${t\rightarrow \infty }$ (hence, the limiting value of $N_H(t)$, given by $N_H^{*}$, will be used in the analysis for this setting). The proof of Theorem 3.1 is based on using the center manifold theorem (see, for instance, Blayneh et al. (2010), Castillo-Chavez and Song (2004) and Hussaini et al. (2016) for details on how the method is applied). After transforming the system (model equations) onto a center manifold (where the resulting linearized system has a zero eigenvalue and all other eigenvalues having negative real part), it can then be shown that the Jacobian of the linearized system (with $\delta = 0$) has left ($\mathbf v$) and right ($\mathbf w$) eigenvectors, given, respectively, by

$$\begin{aligned} \mathbf v =(v_1,\ldots ,v_{11})^\mathrm{T}\,\,\mathrm{and}\,\,\mathbf w =(w_1,\ldots ,w_{11})^\mathrm{T}, \end{aligned}$$

where

$$\begin{aligned} v_1= & {} 0, v_2 = \epsilon _2 \gamma _H v_4 + Gv_{11}> 0, v_3 = \epsilon _1 \alpha _1 v_4 + Gv_{11}>0,\\ v_4= & {} \dfrac{\tau _H}{K_3}v_5> 0, v_5 = \dfrac{Gv_{11}}{\lambda K_4}> 0, \\ v_6= & {} v_7 = 0, v_8 = \dfrac{b p^A_v v_{11} S^*_V}{\Pi _A}> 0, v_9 = v_{10} = 0, v_{11} = v_{11} > 0, \end{aligned}$$

and,

$$\begin{aligned} w_1= & {} \dfrac{-b p^v_H w_{11}}{\mu _H}< 0, w_2 = \dfrac{\sigma b p^v_H w_{11}}{K_1}> 0, w_3 = \dfrac{(1-\sigma ) b p^v_H w_{11}}{K_2}> 0,\\ w_4= & {} \dfrac{\epsilon _2 \gamma _H w_2 + \alpha _1 \epsilon _1 w_3}{K_3}> 0, \\ w_5= & {} \dfrac{\tau _H w_4}{K_4}> 0, w_6 = \dfrac{(1-\epsilon _2)\gamma _H w_2 + \alpha _1 (1-\epsilon _1) w_3 + \alpha _2 w_5}{K_5}> 0,\\ w_7= & {} -\dfrac{b p^v_A w_{11}}{\mu _A} < 0, \\ w_8= & {} \dfrac{b p^v_A w_{11}}{\mu _A}> 0, w_9 = 0,\, w_{10} = - w_{11}, \, w_{11} = w_{11} > 0, \end{aligned}$$

with $G = \dfrac{b p^H_v \lambda S^*_V}{S^*_H}, K_1=\gamma _H+\mu _H,\,K_2=\alpha _1+\mu _H,\,K_3=\tau _H+\mu _H, \,K_4=\alpha _2+\mu _H,\,K_5=\beta +\mu _H$ and $K_6=\eta +\mu _{NA}$. Hence, it follows from Theorem 4.1 in Castillo-Chavez and Song (2004) that the associated bifurcation coefficients of the model (1) are given, respectively, by (noting from above that $w_1<0$, $w_{10}<0$, $w_2>0$, $w_3>0$, $w_5>0$, $w_8>0$, $v_2>0$ and $v_3>0$):

$$\begin{aligned} a_1 =&\ 2 \, b \biggl \{ w_1p^v_H \Bigl [ v_2\sigma (S^*_A)^2 + v_3(1-\sigma )(S^*_A)^2 \Bigr ]\\&+ w_{10} \Bigl [ w_2p^H_v\lambda (S^*_A)^2 + w_8p^A_vS^*_HS^*_A + w_3p^H_v(S^*_A)^2 \\ {}&+ w_5p^H_v(S^*_A)^2 \Bigr ] - v_8w_8p^v_A S^*_HS^*_A \biggr \} < 0, \\ b_1 =&\ b \left[ v_2\sigma + v_3(1 - \sigma ) \right] > 0. \end{aligned}$$

Thus, it follows from Theorem 4.1 in Castillo-Chavez and Song (2004) that the model (1), with $\delta = 0$, does not undergo a backward bifurcation at ${\mathcal {R}}_{0} = 1$. $\square$

Appendix B: Proof of Theorem 3.2

Proof

Consider the model (1) with $\delta =0$. Let ${\mathcal R}_{01}\le 1$. Furthermore, consider the following linear Lyapunov function:

$$\begin{aligned} {\mathcal {L}}= g_1A_H+g_2K_H+g_3D_H+g_4P_H+g_5I_A+g_6I_V, \end{aligned}$$

(3)

where (noting that $K_i (i=1,2,3,4)>0$ are as defined in Sect. 2),

$$\begin{aligned} g_1= & {} \frac{K_2\mu _F\Pi _Ab p^H_v\eta F^*_{NA}(\tau _H\gamma _H\epsilon _2+\lambda K_3K_4 )}{\mu _F N_H},\,\\ g_2= & {} \frac{K_1\mu _F\Pi _Ab p^H_v\eta F^*_{NA}(\alpha _1\epsilon _1\tau _H+K_3K_4)}{ \mu _FN_H},\\ g_3= & {} \frac{K_1K_2\mu _F\Pi _Ab p^H_v\eta F^*_{NA}\tau _H}{\mu _F N_H},\,g_4=\frac{K_1K_2K_3\mu _F\Pi _Ab p^H_v\eta F^*_{NA}}{ \mu _FN_H},\,\\ g_5= & {} \frac{\mu _F\Pi _AK_1K_2K_3K_4bp^A_v\eta F^*_{NA}}{\mu _F\mu _AN_A},\\ g_6= & {} {\mu _F\Pi _AK_1K_2K_3K_4}, \end{aligned}$$

with Lyapunov derivative (where a dot differentiation with respect to time t)

$$\begin{aligned} \dot{{\mathcal {L}}}&= g_1\dot{A}_H+g_2\dot{K}_H+g_3\dot{D}_H+g_4\dot{P}_H+g_5\dot{I}_A+g_6\dot{I}_V,\\&=\,\frac{K_2\mu _F\Pi _Ab p^H_v\eta F^*_{NA}(\tau _H\gamma _H\epsilon _2+\lambda K_3K_4 )}{ \mu _FN_H}\left( \frac{\sigma b p^v_HI_V S_H}{N_H}-K_1A_H\right) \\&\quad +\frac{K_1\mu _F\Pi _Ab p^H_v\eta F^*_{NA}(\alpha _1\epsilon _1\tau _H+K_3K_4)}{\mu _F N_H}\left[ \frac{(1-\sigma ) b p^v_HI_V S_H}{N_H}-K_2K_H\right] \\&\quad +\frac{K_1K_2\mu _F\Pi _Ab p^H_v\tau _H\eta F^*_{NA}}{\mu _F N_H}\left( \alpha _1\epsilon _1 K_H+\gamma _H\epsilon _2A_H-K_3D_H\right) \\&\quad +\frac{K_1K_2K_3\mu _F\Pi _Ab p^H_v\eta F^*_{NA}}{\mu _F N_H} \left( \tau _HD_H-K_4P_H\right) \\&\quad +\frac{\mu _F\Pi _AK_1K_2K_3K_4bp^A_v\eta F^*_{NA}}{\mu _F\mu _AN_A}\left( \frac{bp^v_AI_VS_A}{N_A}-\mu _AI_A\right) \\&\quad +{\mu _F\Pi _AK_1K_2K_3K_4}\left[ \frac{b p^H_vS_V(K_H+P_H+\lambda A_H)}{N_H}+\frac{bp^A_vS_VI_A}{N_A}-\mu _F I_V\right] ,\\&=\mu _Fg_6\biggl [\frac{\sigma b p^v_H S_HM_2}{N_H}\left( \frac{\tau _H\gamma _H\epsilon _2}{K_1K_3K_4}+\frac{\lambda }{K_1}\right) \\&\quad +\frac{(1-\sigma ) bp^v_H S_H M_2}{N_H}\left( \frac{\alpha _1\tau _H\epsilon _1}{K_2K_3K_4}+ \frac{1}{K_2}\right) +\frac{b^2p^v_Ap^A_vS_AS_V}{\mu _F\mu _AN^2_A}-1\biggr ]I_V,\\&\le \, \mu _F g_6\left[ ({\mathcal {R}}_{01})^2-1\right] I_V \,\,(\mathrm{\, since}\,\, S_H(t)<N_H(t),\,\,S_A(t)<N_A(t)\\&\le \,\frac{\Pi _A}{\mu _A}\,\,\mathrm{and}\,\,S_V(t)<\frac{\eta F^*_{NA}}{\mu _F}\,\,\mathrm{in}\,\,\Omega ). \end{aligned}$$

Hence, $\dot{{\mathcal {L}}}\le 0$ if ${\mathcal {R}}_{01}\le 1$ with $\dot{{\mathcal {L}}}= 0$ if and only if $I_V=0$. It follows, by substituting $I_V(t)=0$ into the model (1), that $(A_H(t),K_H(t),D_H(t),P_H(t),R_H(t),I_A(t),I_V(t))\rightarrow (0,0,0,0,0,0,0),$ as $t\rightarrow \infty$. Furthermore, substituting $(A_H, K_H, D_H, P_H, R_H,I_A, I_V)(t)=(0,0,0,0,0)$ into the full model shows that $S_H(t)\rightarrow \frac{\Pi _H}{\mu _H}$, $S_A(t)\rightarrow \frac{\Pi _A}{\mu _A}$, $F_{NA}(t)\rightarrow F^*_{NA}$ and $S_V(t)\rightarrow \frac{\eta F^*_{NA}}{\mu _F}$, as $t\rightarrow \infty .$ Therefore, ${\mathcal {L}}$ is a Lyapunov function in $\Omega \backslash {\mathcal {E}}_0$, and it follows from LaSalle’s invariance principle (LaSalle and Lefschetz 1976) that every solution to the model (1) (with $\delta =0$), with initial conditions in $\Omega \backslash {\mathcal {E}}_0$, converges to the non-trivial disease-free equilibrium (${\mathcal {E}}_{1}$) as $t\rightarrow \infty$ whenever ${\mathcal R}_{01}<1.$ Hence, for the case of the model (1) with no disease-induced death in the host population (i.e., $\delta =0)$, the non-trivial disease-free equilibrium of the model, ${\mathcal {E}}_1$, is globally asymptotically stable in $\Omega \backslash {\mathcal {E}}_0$ if ${\mathcal {R}}_{01}\le 1$. $\square$

Appendix C: Proof of Theorem 3.3

Proof

Consider the model given by (1). It can be shown (as in Appendix A) that the associated right and left eigenvectors of the linearized system associated with the model (1) are given, respectively, by

$$\begin{aligned} \mathbf w =(w_1,\ldots ,w_{11})^\mathrm{T},\,\,\mathrm{and}\,\,\mathbf v =(v_1,\ldots ,v_{11})^\mathrm{T}, \end{aligned}$$

where (noting that $\epsilon _2< 1$),

$$\begin{aligned} w_1= & {} -{\frac{bp^v_{{{ H}}}w_{{11}}}{\mu _{{H}}}},\,w_2=\frac{\sigma b p^v_Hw_{11}}{K_1},\,w_3=\frac{(1-\sigma ) b p^v_Hw_{11}}{K_7},\,\\ w_4= & {} {\frac{\alpha _{{1}}\epsilon _{{1}}w_{{3}}+\epsilon _{{2}}\gamma _{{H}}w_ {{2}}}{{ K_3}}},\,w_5={\frac{\tau _{{H}}w_{{4}}}{K_{{4}}}},\\ w_6= & {} {\frac{ \left( 1-\epsilon _{{2}} \right) \gamma _{{H}}w_{{2}}+\alpha _{{ 1}} \left( 1-\epsilon _{{1}} \right) w_{{3}}+\alpha _{{2}}w_{{5}}}{{ K_5}}},\,\,w_7=- \,{\frac{{bp_{{A}}}^{v}w_{{11}}}{\mu _{{A}}}} ,\,\,w_8=\,{\frac{{bp_{{A}}}^{v}w_{{11}}}{\mu _{{A}}}},\\ w_9= & {} \frac{r\kappa _F\left( 1-\frac{S^*_V}{C}\right) (w_{10}+w_{11})}{K_6+\frac{r\kappa _F S^*_V}{C}},\,\,\\ w_{10}= & {} \frac{A_1(r\kappa _{{F}}S^*_{{V}}+C{ K_6})}{-Cr\kappa _{{F}}+r\kappa _{{F}}F^*_{{NA}}+r\kappa _{{F}}S^*_{{V}}+C{ K_6}},\,\, w_{11}=w_{11}, \end{aligned}$$

and,

$$\begin{aligned} v_1= & {} 0,\,\,v_2=\epsilon _{{2}}\gamma _{{H}}v_{{4}}+{\frac{bp^H_{{{ v}}}\lambda \,S^*_{{ V}} \left( v_{{11}}-v_{{10}} \right) }{S^*_{{H}}}},\,\,\\ v_3= & {} \epsilon _{{1}}\alpha _{{1}}v_{{4}}+{\frac{bp^H_{{{ v}}}S^*_{{V}} \left( v_{{11}}-v_{{10}} \right) }{S^*_{{H}}}},\,\, v_4={\frac{\tau _{{H}}v_{{5}}}{{ K_3}}},\\ v_5= & {} {\frac{bp^H_{{{ v}}}S^*_{{V}} \left( v_{{11}}-v_{{10}} \right) }{S^*_{ {H}}{} { K_4}}},v_6=v_7=0,\,\,v_8={\frac{bp^A_{{{ v}}}S^*_{{V}} \left( v_{{11}}-v_{{10}} \right) }{S^*_{ {A}}\mu _{{A}}}},\,\,\\ v_9= & {} \frac{\eta v_{10}C}{K_6C+r\kappa _FS^*_V},\, v_{10}=0,\,v_{11}=v_{11}, \end{aligned}$$

with,

$$\begin{aligned} A_1={\frac{w_{{11}} \left( C-F^*_{{NA}} \right) \eta \,r\kappa _{{F}}}{\mu _{{F}} \left( r\kappa _{{F}}S^*_{{V}}+{ K_6}\,C \right) }}-{\frac{bS^*_{{V}} \left( \lambda \,p^H_{{{ v}}}w_{{2}}S^*_{{A}}+p^A_{{{ v}}}w_{{8}}S^*_{ {H}}+p^H_{{{ v}}}w_{{3}}S^*_{{A}}+p^H_{{{ v}}}w_{{5}}S^*_{{A}} \right) }{S^*_{{H}}S^*_{{A}}\mu _{{F}}}}. \end{aligned}$$

It follows from Theorem 4.1 in Castillo-Chavez and Song (2004) that the associated bifurcation coefficients, $a_2$ and $b_2$, are given, respectively, by

$$\begin{aligned} \begin{aligned} a_2=&-p^H_vv_{11}w_1(S^{*}_A)^2S^*_H\left( \lambda w_2+w_3+w_5\right) \\&+(1-\sigma )p^{v*}_Hv_3w_{11}S^*_H(S^{*}_A)^2(w_4+w_5+w_6)\\&-p^A_vv_{11}w_8(S^{*}_H)^2S^{*}_A(w_7+w_8)+p^A_vv_{11}w_8w_{10}(S^{*}_H)^2S^{*}_A-p^v_Av_8w_8w_{11}(S^{*}_H)^2S^{*}_A\\&-(S^{*}_A)^2(w_2+w_3+w_4+w_5+w_6)\\&\left( \lambda p^H_vv_{11}w_2S^{*}_H+(1-\sigma )p^{v*}_Hv_2w_{11}S^{*}_H+2p^H_vv_{11}S^{*}_H[w_3+w_5]\right) \end{aligned} \end{aligned}$$

(4)

and,

$$\begin{aligned} b_2=w_{{11}}b \left[ \sigma \,v_{{2}}+v_{{3}}(1-\sigma ) \right] >0. \end{aligned}$$

(5)

Hence, it follows from (4), the bifurcation coefficient $a_2$ is positive if the following inequality holds:

$$\begin{aligned} H>C+D+p^v_Av_8w_8w_{11}(S^{*}_H)^2S^*_A, \end{aligned}$$

(6)

where

$$\begin{aligned} H= & {} -\,p^H_vv_{11}w_1(S^{*}_A)^2S^*_H\left( \lambda w_2+w_3+w_5\right) \\&+\,(1-\sigma )p^{v*}_Hv_3w_{11}S^*_H(S^{*}_A)^2(w_4+w_5+w_6)+\ p^A_vv_{11}w_8w_{10}(S^{*}_H)^2S^{*}_A, \\ C= & {} p^A_vv_{11}w_8(S^{*}_H)^2S^{*}_A(w_7+w_8),\\ D= & {} (S^{*}_A)^2(w_2+w_3+w_4+w_5+w_6)\\&\left( \lambda p^H_vv_{11}w_2S^{*}_H+(1-\sigma )p^{v*}_Hv_2w_{11}S^{*}_H+2p^H_vv_{11}S^{*}_H[w_3+w_5]\right) . \end{aligned}$$

Since the coefficient $b_2$ is automatically positive, it follows that the model (1) will undergo a backward bifurcation at ${\mathcal {R}}_0=1$ if Inequality (6) holds. $\square$