Improving Parameter Inference from FRAP Data: an Analysis Motivated by Pattern Formation in the Drosophila Wing Disc

Abstract

Fluorescence recovery after photobleaching (FRAP) is used to obtain quantitative information about molecular diffusion and binding kinetics at both cell and tissue levels of organization. FRAP models have been proposed to estimate the diffusion coefficients and binding kinetic parameters of species for a variety of biological systems and experimental settings. However, it is not clear what the connection among the diverse parameter estimates from different models of the same system is, whether the assumptions made in the model are appropriate, and what the qualities of the estimates are. Here we propose a new approach to investigate the discrepancies between parameters estimated from different models. We use a theoretical model to simulate the dynamics of a FRAP experiment and generate the data that are used in various recovery models to estimate the corresponding parameters. By postulating a recovery model identical to the theoretical model, we first establish that the appropriate choice of observation time can significantly improve the quality of estimates, especially when the diffusion and binding kinetics are not well balanced, in a sense made precise later. Secondly, we find that changing the balance between diffusion and binding kinetics by changing the size of the bleaching region, which gives rise to different FRAP curves, provides a priori knowledge of diffusion and binding kinetics, which is important for model formulation. We also show that the use of the spatial information in FRAP provides better parameter estimation. By varying the recovery model from a fixed theoretical model, we show that a simplified recovery model can adequately describe the FRAP process in some circumstances and establish the relationship between parameters in the theoretical model and those in the recovery model. We then analyze an example in which the data are generated with a model of intermediate complexity and the parameters are estimated using models of greater or less complexity, and show how sensitivity analysis can be used to improve FRAP model formulation. Lastly, we show how sophisticated global sensitivity analysis can be used to detect over-fitting when using a model that is too complex.

Appendix 1

1.1 Appendix 1.1: The General Framework

The general form of the system of reaction–diffusion equations that we shall use hereafter has the following form.

$$\begin{aligned} \frac{\partial c}{\partial t}= & {} D_c \nabla ^2 c + \bar{R}(c,\bar{p})~~~~~~~ \text{ in }~~ \Omega \end{aligned}$$

(30)

$$\begin{aligned} \mathbf{n} \cdot D_c \nabla c= & {} \bar{J} ~~~~~~~ \text{ on }~~ \partial \Omega \end{aligned}$$

(31)

$$\begin{aligned} c(r,0)= & {} c_0( r), \end{aligned}$$

(32)

Here the vector $c = (c_1, c_2, \dots , c_m)$ is the vector of chemical concentrations, $D_c$ is assumed to be a constant diagonal matrix, and J is a prescribed flux on$\partial \Omega$. $\Omega$ is a bounded region in $\mathfrak {R}^q, q = 1,2$ with a smooth boundary and outward normal $\mathbf{n}$. The functions $\bar{R}_i$ give the net rate of production of the ith species, and they are herein always linear or quadratic polynomials in the $c_i$’s. The vector $\bar{p}$ is a parameter vector, which can include the kinetic constants and perhaps species that appear in the kinetic mechanism but do not change significantly on the timescale of interest. As described in the preceding example, we can regard these equations as appropriate for a thin fluid layer over a 1D or 2D domain. In applications to the wing disc, the geometry of the hexagonal packing of cells is more complex than the description above and a mathematical description that accounts for the geometric complexity is far more complex. A 2D model of the disc that incorporates this complexity is given in Umulis and Othmer (2015).

This system can be non-dimensionalized as follows. Let L be a measure of the size of the system, $C_i$ be a reference concentration for species i, and $\omega ^{-1}$ be a timescale characteristic of the reactions.⁷ Define the dimensionless quantities $u_i = c_i/C_i$, $\tau = \omega t$, $D_i = D_{ci}/\omega L^2$, and ${\xi } = r/L$, where $r \equiv (x_1, \dots , x_q)$. The dimensionless governing equations are

$$\begin{aligned} \begin{array}{ll} \dfrac{\partial u}{\partial \tau } =D \nabla ^2u + R(u,p) &{} \text{ in }~~ \Omega \\ \mathbf{n} \cdot D \nabla u = J &{} \text{ on }~~ \partial \Omega \\ u ({\xi },0) = u_{0}({\xi }), \end{array} \end{aligned}$$

(33)

where $D = \hbox {diag}\{D_1, D_2, \dots , D_m\}$, $J_i = \bar{J}_i/(\omega C_i)$, R(u, p) is the dimensionless form of $\bar{R}(c,\bar{p})$, and $\Omega$ is scaled. If the species that do not diffuse the corresponding $D_i$ and $J_i$ are zero, and unless stated otherwise, we assume that all boundary fluxes are zero, i.e., we impose homogeneous Neumann boundary conditions.

We show later that in many FRAP experiments, the kinetics can be linearized, and therefore, in the majority of what follows we focus on linear kinetic models, and we write the system (33) as

$$\begin{aligned} \frac{\partial u}{\partial \tau }= & {} D \nabla ^2 u + K u \nonumber \\ \mathbf{n}\cdot \nabla u= & {} 0 , \qquad \text{ on }~~ \partial \Omega \nonumber \\ u(\xi ,0)= & {} u_{0}(\xi ) \end{aligned}$$

(34)

This system has solutions of the form

$$\begin{aligned} u(\xi ,\tau ) = \sum _{n=0}^{\infty } y_{n}(\tau ) \phi _n \end{aligned}$$

(35)

where $\phi _n$ is a solution of the scalar eigenvalue problem

$$\begin{aligned} \begin{array}{l} \nabla ^2 \phi _n = - \alpha _n^2 \phi _n\\ \mathbf{n} \cdot \nabla \phi _n = 0 \end{array} \end{aligned}$$

(36)

and $y_n$ is given by

$$\begin{aligned} y_n(\tau ) = e^{(K-\alpha _n^2 {{D}})\tau }y_{n}(0). \end{aligned}$$

(37)

For a reasonable boundary, the eigenfunctions ${\phi _n}$ form a complete orthonormal set under the standard $L_2$ inner product $[u,v] = \int u(\xi )v(\xi ) d\xi$, and the solution of (34) can be written as (Othmer and Scriven 1969)

$$\begin{aligned} u ({\xi },\tau ) = \sum _{n=0}^{\infty } e^{(K-\alpha _n^2 {{D}})\tau }y_{n}(0) \phi _n({\xi }.) \end{aligned}$$

(38)

The initial condition can be written

$$\begin{aligned} u_0(\xi ) = \sum _{n=0}^{\infty }y_{n}(0) \phi _n({\xi }) \end{aligned}$$

(39)

and therefore, $y_n(0) = \langle u_0(\xi ),\phi _n\rangle$, where here and hereafter $\langle \cdot , \cdot \rangle$ denotes the real or complex, as appropriate, Euclidean inner product, taken component-wise when one argument is a vector and the other a scalar.

Remark 2

If the influx is nonzero, i.e., $J\ne 0$, we let $w=u-u^s$ where $u^s$ is the steady-state solution. Then, w satisfies

$$\begin{aligned} \frac{\partial w}{\partial \tau }=D {\bigtriangledown ^2 w}+Kw \end{aligned}$$

(40)

with zero Neumann boundary conditions. The solution w has the representation given at (38), and u is obtained from this. In particular, when $m=1$, we obtain the solution given at (17).

The difficulty in FRAP analysis of multi-component systems, even when they are linear, stems from the structure of (38). To simplify the analysis, suppose that the family of matrices $\{K-\alpha _n^2 D\}$ is semisimple—which means that they can be diagonalized—for all n. Then, the matrix exponential has the representation

$$\begin{aligned} e^{(K-\alpha _n^2 {{D}})\tau } = \sum _{j=1}^m e^{\lambda _{jn}\tau }P_{jn} \end{aligned}$$

(41)

where the projections $P_{jn}$ are associated with a given $\lambda _{jn}$ (Kato 1966). Since we assume that the $\{K-\alpha _n^2 D\}$ are semisimple, they have the representation

$$\begin{aligned} P_{jn} = \Psi _{jn}*\Psi _{jn}^*\end{aligned}$$

(42)

wherein $\Psi _{jn}$ is an eigenvector of $K-\alpha _n^2 {{D}}$ associated with $\lambda _{jn}$ and $\Psi _{jn}^*$ is the corresponding adjoint eigenvector. The action of any P on a vector u is defined by

$$\begin{aligned} Pu = \langle \Psi _{jn}^*,u\rangle \Psi _{jn}. \end{aligned}$$

The eigenvector $\Psi _{jn}=(\Psi _{1jn},\Psi _{2jn},\dots ,\Psi _{mjn})^T \in \mathfrak {R}^m$ is a solution of the algebraic eigenvalue problem

$$\begin{aligned} (K -\alpha _n^2 D - \lambda _{jn} I)\Psi _{jn} = 0, \qquad j = 1, 2, \dots , m, \quad n=0,1, \dots . \end{aligned}$$

(43)

and the eigenvalues $\lambda _{jn}$ are solutions of the characteristic equation

$$\begin{aligned} det(K -\alpha _n^2 D - \lambda I) =0. \end{aligned}$$

(44)

The problem simplifies significantly when K and D commute, for then the eigenvalues of $K-\alpha _n^2 {{D}}$ are simply $\lambda _{jn}= \lambda _j^K - \alpha _n^2\lambda _j^{D}$.

The characteristic equation is an mth degree polynomial for an m-component system. Thus, while the representation at (41) has the apparently simple form of a sum of exponentials, the eigenvalues $\lambda _{jn}$ and the eigenfunctions $\Psi _{jn}$ are complicated functions of the kinetic rate parameters and the diffusion constants. The case $m=1$ is as done previously, and only if $m =2$ or 3 can one make analytical progress toward understanding how the eigenvalues and eigenfunctions depend on the rate parameters (Othmer and Scriven 1969), and only in these cases can one hope to gain analytical insights into the problem of extracting rate parameters from FRAP data. We turn to these cases in the following sections.

If $R(u,p)=Ku+F({u,\xi },\tau )$, the general solution of (33) can be written as

$$\begin{aligned} u({\xi },\tau )=\int _{\Omega } G({\xi }-{\xi '},\tau )u_{0}({\xi '})\hbox {d}{\xi '}+ \int _{0}^{t}\int _{\Omega }G({\xi },{\xi '},\tau -\tau ')F(u,{\xi },\tau ')\hbox {d}{\xi '}\hbox {d}\tau ' \end{aligned}$$

(45)

where $G(\mathbf{\xi },{\xi '},t)$ is the Green’s function for the linear operator $L=D \nabla ^2+K$. This has the representation

$$\begin{aligned} G({\xi }-{\xi '},\tau -\tau ')= \sum _{n=0}^\infty \sum _{j=1}^m e^{\lambda _{jn}(\tau -\tau ')}P_{jn} \phi _n(\xi )\phi _n(\xi ') \end{aligned}$$

(46)

This form (45) can be used when diffusion during bleaching and waiting periods is incorporated in the analysis.

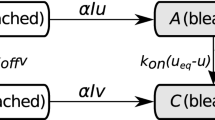
1.2 Appendix 1.2: A Special Case: Diffusion and Binding only

The general framework allows for first-order reactions of any type [of which there are four—cf. Gadgil et al. (2005)], but when the only processes are diffusion of the fluorescent species and binding to one or more independent immobile sites more can be said about the solutions. Suppose there are $m-1$ independent types of binding sites, as shown in Fig. 18. In Appendix 1.4, we re-derive the known fact (Sprague et al. 2004) that for a single binding site, the recovery process can be modeled as a linear process, even though the binding step is nonlinear, and point out that the on- and off-rates in the resulting equations are composites of parameters in the original equations (Sprague et al. 2004). The analysis given there can be applied to the case of $m-1$ independent types of binding sites, although the amount of unbound fluorescent molecules is the solution of a higher-order polynomial when there is more than one type of site. This leads to the linear system

$$\begin{aligned} \frac{\partial u_1}{\partial \tau }= & {} D \nabla ^2 u_1 - \sum _{k=2}^{m}B_k(u_1,u_k,\tau ) \qquad \text{ for } \quad \xi \in (0,1)\nonumber \\ \dfrac{\hbox {d}u_k}{\hbox {d} \tau }= & {} B_k (u_1,u_k,\tau )\equiv k_{k1}u_1 - k_{1k}u_k \qquad k = 2, \dots , m \nonumber \\ u(\xi ,0)= & {} u_{0}(\xi ) \end{aligned}$$

(47)

Thus, the matrices K and D in (34) take the following form.

$$\begin{aligned} K = \begin{bmatrix} -\sum \nolimits _{j=2}^{m}k_{j1}&\quad k_{12}&\quad k_{13}&\quad \dots&\quad k_{1m} \\ k_{21}&\quad -k_{12}&\quad 0&\quad \dots&\quad 0 \\ \vdots&\\ k_{m1}&\quad 0&\quad 0&\quad \dots&\quad -k_{1m} \\ \end{bmatrix} \end{aligned}$$

(48)

and $D= \hbox {diag}(D_1, 0,0, \dots ,0)$. The columns of the matrix K sum to zero, and therefore, K is singular, and if the $k_{ij}$ are all nonzero, it is irreducible and an application of the Perron–Frobenius theorem shows that the zero eigenvalue is simple. The fact that the kinetic steps are mass preserving implies that the left eigenvector of K corresponding to the zero eigenvalue is $(1,1,1, \dots , 1)^T$, and therefore,

$$\begin{aligned} \dfrac{\partial }{\partial \tau } (u_1 + u_2 + \dots + u_m) = D_1\nabla ^2 u_1, \end{aligned}$$

(49)

which reflects the fact that the total local concentration only changes due to diffusion.

Fig. 18

The notation for $m-1$ binding sites

The matrix K can be symmetrized, and therefore, the eigenvalues are all real and non-positive. The kinetic interactions involved in binding are restricted to the reaction simplex defined by the relation $\sum _{i=1}^m u_i(t) = \sum _{i=1}^m u_i(0)$. The foregoing properties of K also imply that there is a unique steady state of the equation

$$\begin{aligned} \dfrac{\hbox {d}u}{\hbox {d} \tau } = K u \end{aligned}$$

on the simplex defined by the initial condition. Equation (49) shows how the simplices vary in space due to diffusion, but two useful extreme cases arise when either diffusion is slow relative to the binding or it is rapid relative to binding. The first case arises when either the on-rate or the off-rate of every binding step is large relative to $\tau _D^{-1} = D_{1}/L^2$. Then, a singular-perturbation analysis shows that to leading order in the small parameter $\epsilon \equiv \tau _R/\tau _D$, the kinetics reach the steady state on the reaction simplex defined by the initial data at every point in space, and these simplices then evolve slowly on the diffusion timescale.

In this limit, the free and bound forms are related by

$$\begin{aligned} u_i = \dfrac{k_{i1}}{k_{1i}}u_1 \equiv K_i u_1, \quad i = 2, \dots , m. \end{aligned}$$

(50)

to within correction terms proportional to $\epsilon$.⁸ As a result, (49) becomes

$$\begin{aligned} \dfrac{\partial }{\partial \tau } \left( 1 +\sum _{i=2}^m K_i\right) u_1 = D_1\nabla ^2 u_1 \end{aligned}$$

(51)

which leads to a diffusion equation for $u_1$ with the effective diffusion coefficient

$$\begin{aligned} D_{1,\mathrm{eff}} = \dfrac{D_1}{1 +\sum _{i=2}^m K_i} \end{aligned}$$

(52)

This reduction of the diffusion coefficient in the presence of rapid binding was apparently first observed by Crank (1975).

When $\tau _D \ll \tau _R$, i.e.,   $D_1/L^2$ is much larger than the largest kinetic rate constant, one can show that to lowest order the spatial distribution of fluorescent molecules relaxes to a uniform state given by

$$\begin{aligned} \overline{u}_1(\xi ,t) \sim \overline{u}_1(0) - \sum _{k=2}^{m}\int _0^t \overline{B_k}(u_1,u_k,\tau ) \hbox {d} \tau \end{aligned}$$

(53)

where the overbar denotes the spatial average and $\overline{B_k}(u_1,u_k,\tau ) \equiv k_i^+\overline{u}_1 - k_i^-\overline{u}_i$. This solution can then be used in the binding equations to obtain an explicit expression for the $\bar{u}_k(\tau ), k = 2, \dots , m$. Thus, the evolution on the slow timescale is simply the readjustment of the fractions of bound fluorescent molecules. Since the diffusion timescale depends on the length scale of the domain, the balance between diffusion and binding can be controlled by altering the size of the bleaching region.

1.3 Appendix 1.3: A Summary of the FRAP Protocol

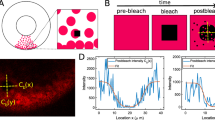
The setup and the sequence of steps in a typical FRAP experiment that uses a confocal laser scanning microscope (CLSM) are as follows, and assuming that diffusion is the only transport process, the steps are modeled as shown below which also explains Fig. 1. We describe them in generality here, and detailed descriptions of the models used for parameter estimation are given later. Both bleaching and scanning steps are done pixel by pixel and line by line.

Step 1: Prebleaching Use a low-intensity laser to scan the fluorescence density in the entire domain $\Omega$ which includes the ROI. The evolution of the concentrations of fluorescent molecules during the prebleaching time $[0,T_0]$ (cf. Fig. 1) is governed by

$$\begin{aligned} \frac{\partial c}{\partial t}=D{\bigtriangledown ^2 c} + R(c) -I_p c \end{aligned}$$

where R(c) represents the reaction processes and $I_p$ is the prebleaching function. The prebleaching process is usually modeled as a first-order process as above, and in a 2D domain, the intensity is given by

$$\begin{aligned} I_p(t,x,y) = I_{p_0} \exp \left( -\dfrac{2[(x-X(t))^2+(y-Y(t))^2]}{r_0^2} \right) , \end{aligned}$$

wherein $x=X(t), y=Y(t)$, and $x,y \in \Omega$ describes the prebleaching path of the laser.

Step 2: Bleaching Use a high-intensity beam to bleach the ROI for an interval of length $T_1$. In this phase,

$$\begin{aligned} \frac{\partial c}{\partial t}=D{\bigtriangledown ^2 c} +R(c)-I c \end{aligned}$$

with initial conditions obtained from the end of the prebleaching period. The differences between prebleaching and bleaching are the laser intensity and pixel dwell time for scanning, as well as the scanning domain.

Step 3: Postbleaching This usually comprises a waiting time $T_2$ between the end of bleaching and the beginning of observation. During the observation time, use a low-intensity beam to image the fluorescence recovery process. During the waiting time,

$$\begin{aligned} \frac{\partial c}{\partial t}=D{\bigtriangledown ^2 c} +R(c) \end{aligned}$$

with initial conditions obtained from the end of Step 2.

During the observation period $T_3$,

$$\begin{aligned} \frac{\partial c}{\partial t}=D{\bigtriangledown ^2 c} +R(c)-I_p c \end{aligned}$$

with initial conditions obtained from the end of the waiting period.

The inconsistencies in FRAP are partly from different assumptions for models. One of the disparate assumptions lies in that of initial conditions for recovery phase, the obtainment of which can be divided into two categories among existing FRAP models. The first one is modeling all the previous processes before recovery phase to get the initial conditions (Kang et al. 2009; Braeckmans et al. 2007, 2003; Mazza et al. 2008). By modeling the prebleaching, bleaching, and recovery phase, the analytical solution representing FRAP data can be derived in some special occasions and with certain assumptions (Braeckmans et al. 2003). It provides us insights into how the bleaching process and others affect the FRAP recovery; however, it requires prior knowledge of some parameters to model activities of the laser beam. Another way which is more popular to estimate parameters is to only model the recovery phase with assumptions about the initial conditions which can be obtained by the first postbleach image of fluorescence. In this category, there are three different kinds of assumptions which all neglect the bleaching effect with imaging process in recovery phase. One natural assumption is the piece-wise constant initial conditions from direct measurement of the size of the photobleaching spot (Sprague et al. 2004). This is validated when the bleaching is homogeneous, and the bleaching time is negligible. Another one is also the piece-wise constant initial conditions, but is deduced from the final recovery concentration and the conservation of fluorescence (Hinow et al. 2006). It is an improvement from the first one, but still is limited to the cases where the boundaries of the bleached region are relatively sharp and the observational photobleaching is negligible. When the boundaries of the bleached region are smoothed by diffusion before observation, the piece-wise constant is not able to capture the characteristics of the initial condition, which may cause large errors in parameter estimation (Mueller et al. 2008). Thus, for the third kind, some Gaussian or Gaussian-edge function fitted by the initial data, which results from the Gaussian assumption of the laser profile, is used for the initial condition (Mueller et al. 2008). It has been shown that using the Gaussian expression of the initial postbleach profile alters the estimates of parameters in comparison with the first or second utilization of initial condition; however, the utilization of Gaussian function needs to be carefully justified. It is not convincing that the utilization of Gaussian function as the initial condition produces better estimations, because in real biological system, the true values of binding/unbinding rates as well as the diffusion coefficient are unknown. In our simulations, we only simulate the data without with homogenous and instantaneous bleaching process, and thus, we estimate parameters by only modeling the recovery with piece-wise constant initial conditions.

1.4 Appendix 1.4: Justification of the Assumption of Linear Kinetics in FRAP Modeling

Suppose that there is one diffusing species that can bind to an immobile receptor, and let $(u_1, v_1)$ and $(u_2, v_2)$ be the free and bound concentrations of fluorescent and bleached molecules, respectively. These satisfy the following equations.

$$\begin{aligned} \frac{\partial u_1}{\partial \tau }= & {} D_1 {\bigtriangledown ^2 u_1} -k^+ u_1 [R]+k^- u_2\nonumber \\ \frac{\partial u_2}{\partial \tau }= & {} k^+ u_1 [R]-k^- u_2 \end{aligned}$$

(54)

$$\begin{aligned} \frac{\partial v_1}{\partial \tau }= & {} D_1 {\bigtriangledown ^2 v_1} -k^+ v_1 [R]+k^- v_2\nonumber \\ \frac{\partial v_2}{\partial \tau }= & {} k^+ v_1 [R]-k^- v_2 \end{aligned}$$

(55)

where [R] is the concentration of free binding sites.

The sums $w_1=u_1+v_1$ and $w_2= u_2 + v_2$ satisfy

$$\begin{aligned} \frac{\partial w_1}{\partial \tau }= & {} D_1 {\bigtriangledown ^2 w_1} -k^+ w_1 \end{aligned}$$

(56)

$$\begin{aligned} \frac{\partial w_2}{\partial \tau }= & {} k^+ w_1 [R]-k^- w_2. \end{aligned}$$

(57)

If adequate time has elapsed before bleaching begins, one can assume that the system is at steady state prior to bleaching, and further assume that bleaching does not perturb the binding reactions, it merely substitutes a bleached for a fluorescent molecule. Then, throughout the bleaching process $w_1 = w_1^s$, the steady-state value of the free concentration, and the total free concentration of binding sites is given by

$$\begin{aligned} R = R_T\dfrac{\hat{K}}{\hat{K}+ w_1^s}, \end{aligned}$$

(58)

where $R_T = R + w_2$ is the total concentration (free and occupied) of binding sites and $\hat{K} = k^{-}/k^{+}$. Similarly, the concentration of bound sites is

$$\begin{aligned} w_2^s = R_T\dfrac{w_1^s}{\hat{K} + w_1^s}. \end{aligned}$$

Let $W = w_1 + w_2$ be the total concentration of all forms of the molecules, which here is assumed constant point-wise in space and time. Then, it follows that $w_1^s$ is the solution of a quadratic equation whose coefficients involve K, W, and $R_T$, and the solution of this quadratic then leads to the free site concentration (58), and (54) can be written as

$$\begin{aligned} \frac{\partial u_1}{\partial \tau }= & {} D_1 {\bigtriangledown ^2 u_1} -k^+ u_1 + k^- u_2\nonumber \\ \frac{\partial u_2}{\partial \tau }= & {} k^+ u_1 - k^- u_2 \end{aligned}$$

(59)

where $k^+=k^+( [R_T] -w_2^s)$ and $k^-=k^-$. This is the linear system widely used in this context. However, the constant $k^+$ is a composite constant that involves three separate constants in an experiment, and two other independent measurements are needed to determine the three independent constants.

To define the initial conditions, let $I_0(\xi ) = u_{10}(\xi ) + u_{20}(\xi )$ be the initial concentration of the fluorescent molecules in space at the onset of the recovery phase of an experiment, which is usually measured directly from the first postbleaching image. If we assume that bleaching in the ROI is instantaneous (i.e., $T_1$ = 0), then the initial condition for equation (59) is

$$\begin{aligned} u_{10}=\frac{I_0(\xi )}{1+ K_d^{-1}} \qquad \text{ and } \qquad u_{20}=\frac{I_0(\xi )}{1+K_d}. \end{aligned}$$

where $K_d \equiv k^-/k^+$ is the dissociation constant. In the simulations described in the text, these are piece-wise constant functions. If bleaching is not instantaneous, then diffusion alters the initial condition, and the initial conditions for the recovery period must be computed using the equations applicable to the interval $[T_0,T_0 + T_1]$ given in Sect. 1.

1.5 Appendix 1.5: Analysis of the Eigenvalues and Eigenvector for a Two-Component System

In the following, we use eigenvalues/eigenvectors to analyze how FRAP data are determined by the parameters in the model.

Let

$$\begin{aligned} Q=K-\alpha _{n}^2 D =\begin{pmatrix} -k^+-\alpha _{n}^2 D_1 \quad k^-\\ k^+\quad -k^-\end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} \gamma = k^+-k^-+ \alpha _{n}^2 D_1 \end{aligned}$$

Then, the eigenvalues of the matrix Q are:

$$\begin{aligned} \lambda _{1n}= & {} -\frac{1}{2} \left( k^++k^-+\alpha _{n}^2 D_1 \right) + \root \of {\gamma ^2+ 4 k^+k^-})\\ \lambda _{2n}= & {} -\frac{1}{2} \left( k^++k^-+\alpha _{n}^2 D_1 \right) - \root \of {\gamma ^2+ 4 k^+k^-})\\ \lambda _{10}= & {} -(k^++k^-), \lambda _{20}=0. \end{aligned}$$

The averaged fluorescent intensity can be written as

$$\begin{aligned} \overline{u_1}+\overline{u_2} \equiv (\overline{u_1}_0+\overline{u_2}_0)+\displaystyle \sum _{n=1}^{\infty } g(n)(\overline{u_1}_n+\overline{u_2}_n) =y_{10}+y_{20}+\displaystyle \sum _{n=1}^{\infty } g(n)(d_{1n}e^{\lambda _{1n}t} + d_{2n}e^{\lambda _{2n}t} ) \end{aligned}$$

(60)

where

$$\begin{aligned} u_{10}= & {} \frac{k^+y_{10}-k^-y_{20}}{k^++k^-} e^{\lambda _{10}t} + \frac{k^-y_{10} + k^-y_{20}}{k^++k^-}\\ u_{20}= & {} \frac{k^-y_{20}-k^+y_{10}}{k^++k^-} e^{\lambda _{10}t} + \frac{k^+y_{10} + k^+y_{20}}{k^++k^-} \end{aligned}$$

(thus, $u_0+u_{20}=y_{10}+y_{20}$)

$$\begin{aligned} g(n)=\frac{1}{n(l_R-l_L)\pi }[\sin (n\pi l_R)-\sin (n\pi l_L)]. \end{aligned}$$

Note that

$$\begin{aligned} \lambda _{1n} \lambda _{2n}= & {} \alpha _n^2 D_1 k^-\\ d_{1n}= & {} \frac{y_{1n}+y_{2n}}{2} - \frac{\alpha _n^2 D_1(y_{2n}-y_{1n})}{2\sqrt{\gamma ^2+4k^+k^-}}-\frac{(k^++k^-)(y_{1n}+y_{2n})}{2\sqrt{ \gamma ^2+4k^+k^-}}\\ d_{2n}= & {} \frac{y_{1n}+y_{2n}}{2} + \frac{\alpha _n^2 D_1 (y_{2n}-y_{1n})}{2\sqrt{\gamma ^2+4k^+k^-}} + \frac{(k^++k^-)(y_{1n}+y_{2n})}{2\sqrt{\gamma ^2+4k^+k^-}} \end{aligned}$$

since

$$\begin{aligned} y_{10}+y_{20}= & {} \frac{1}{N} \displaystyle \sum _{k=1}^{N} I_0(k)\\ y_{1n}+y_{2n}= & {} \frac{1}{N} \displaystyle \sum _{k=1}^{N} I_0(k) \left( \cos \frac{n\pi }{N}(k-1)+\cos \frac{n\pi }{N}k\right) \end{aligned}$$

Note that it is positive and independent of the parameters

$$\begin{aligned} y_{2n}-y_{1n}=\frac{k^+-k^-}{k^++k^-}\frac{1}{N} \displaystyle \sum _{k=1}^{N} I_0(k) \left( \cos \frac{n\pi }{N}(k-1)+\cos \frac{n\pi }{N}k\right) = \frac{k^+-k^-}{k^++k^-} (y_{1n}+y_{2n}) \end{aligned}$$

If we define

$$\begin{aligned} f(n)= g(n) \frac{y_{1n}+y_{2n}}{2} \end{aligned}$$

we have

$$\begin{aligned} \overline{u_1}+\overline{u_2} = \frac{1}{N} \displaystyle \sum _{k=1}^{N} I_0(k) + \displaystyle \sum _{n=1}^{\infty } f(n) ( c_{1n}e^{\lambda _{1n}t} + c_{2n}e^{\lambda _{2n}t} ) \end{aligned}$$

(61)

where

$$\begin{aligned} c_{1n}= & {} 1 - \frac{\alpha _n^2 D_1 \frac{k^+-k^-}{k^++k^-}}{\sqrt{\gamma ^2+4k^+k^-}}-\frac{k^++k^-}{\sqrt{\gamma ^2+4k^+k^-}}\\ c_{2n}= & {} 1 + \frac{\alpha _n^2 D_1 \frac{k^+-k^-}{k^++k^-}}{\sqrt{\gamma ^2+4k^+k^-}} + \frac{k^++k^-}{\sqrt{\gamma ^2+4k^+k^-}} \end{aligned}$$

Note that $c_{1n}, c_{2n}>0$, $\lambda _{1n}, \lambda _{2n} <0$ .

As n increases, $c_{1n}$ increases, $c_{2n}$ decreases, both $\lambda _{1n}$ and $\lambda _{2n}$ decrease (algebraically).

Moreover, as $n\rightarrow \infty$, $\lambda _{1n} \rightarrow -\alpha _{n}^2 D_1$ , $\lambda _{2n} \rightarrow -k^-$, and if $k^+> k^-$,

$$\begin{aligned} c_{1n} \rightarrow 2 \frac{k^-}{k^++k^-},\quad c_{2n} \rightarrow 2 \frac{k^+}{k^++k^-} \end{aligned}$$

if $k^+< k^-$,

$$\begin{aligned} c_{1n} \rightarrow 2 \frac{k^+}{k^++k^-},\quad c_{2n} \rightarrow 2 \frac{k^-}{k^++k^-} \end{aligned}$$

and if $k^+= k^-$,

$$\begin{aligned} c_{1n} \rightarrow 1, c_{2n} \rightarrow 1. \end{aligned}$$

One may first estimate the eigenvalues and corresponding eigenvectors from FRAP data based on equation (61). Then by the relationship between unknown parameters and eigenvalues and eigenvectors, targeted diffusion coefficient and kinetic parameters may be eventually estimated. Moreover, the quantitative analysis of eigenvalues may lead to some more insights into parameter estimation. These aspects can be explored in the future.

1.6 Appendix 1.6: Implementation of Sensitivity Analysis

The indices of variance-based sensitivity measures are usually done by the Monte Carlo method. In practice, instead of generating pseudo-randomly distributed points in the parameter space in traditional Monte Carlo method, the low discrepancy quasi-random number generator is used to improve the efficiency of the estimators. This is known as the quasi-Monte Carlo method. It is implemented as follows [taken from Saltelli et al. (2010)].

• 1. ‘Generate an $N \times 2k$ sample matrix with respect to the probability distributions of the input variables—the parameters. N is the number of sample points. k is the dimension of parameter space, i.e., the number of parameters.

• 2. Use the first k columns of the matrix as matrix A, and the remaining k columns as matrix B, which generates two independent samples of N points in the k-dimensional parameter space.

• 3. Build k further $N \times k$ matrices $A_B^i$ for $i=1,2,\dots ,k$, such that the ith column of $A_B^i$ is equal to the ith column of B, and the remaining columns are from A.

• 4. The A, B, and the k $A_B^i$ matrices specify $N \times (k+2)$ points in the parameter space (one for each row). Run the model at each point, giving a total of $N \times (k+2)$ model evaluations, i.e., the correspondingf(A), f(B) and $f(A_B^i)$ values.

• 5. Calculate the sensitivity indices using the estimators discussed below.’

There are a number of Monte Carlo estimators for both indices. Two that are currently widely used are according to the rule proposed by Saltelli et al. (2010).

$$\begin{aligned}&V_{p_i} (E_{P\sim i}(\mathcal {E}\mid p_i) \approx \frac{1}{N} \sum _{j=1}^N f(B)_j ( f(A_b^i)_j- f(A)_j )\\&\quad E_{X \sim i} (V_{p_i}(\mathcal {E}\mid p_{\sim i}) \approx \frac{1}{2N} \sum _{j=1}^N ( f(A_b^i)_j- f(A)_j )^2 \end{aligned}$$

They are used for the estimation of $S_i$ and $S_{Ti}$, respectively.

1.7 Appendix 1.7: The Complex Model used in Sect. 5.2

$$\begin{aligned} \frac{\partial u_1}{\partial \tau }=D_1 {\bigtriangledown ^2 u_1} -k^+u_1+k^-u_2\nonumber \\ \frac{\partial u_2}{\partial \tau }=k^+u_1-k^-u_2 -k^i u_2 + k^o u_3\nonumber \\ \frac{\partial u_3}{\partial \tau }=-k^i u_2 - k^o u_3 - k^t u_3 - k^{d1} u_3\nonumber \\ \frac{\partial u_4}{\partial \tau }=- k^t u_3 - k^{d2} u_4 \end{aligned}$$

(62)