Modelling Drug Abuse Epidemics in the Presence of Limited Rehabilitation Capacity

Abstract

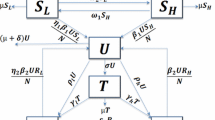
The abuse of drugs is now an epidemic globally whose control has been mainly through rehabilitation. The demand for drug abuse rehabilitation has not been matched with the available capacity resulting in limited placement of addicts into rehabilitation. In this paper, we model limited rehabilitation through the Hill function incorporated into a system of nonlinear ordinary differential equations. Not every member of the community is equally likely to embark on drug use, risk structure is included to help differentiate those more likely (high risk) to abuse drugs and those less likely (low risk) to abuse drugs. It is shown that the model has multiple equilibria, and using the centre manifold theory, the model exhibits the phenomenon of backward bifurcation whose implications to rehabilitation are discussed. Sensitivity analysis and numerical simulations are performed. The results show that saturation in rehabilitation will in the long run lead to the escalation of drug abuse. This means that limited access to rehabilitation has negative implications in the fight against drug abuse where rehabilitation is the main form of control. This suggests that increased access to rehabilitation is likely to lower the drug abuse epidemic.

Appendices

Appendix 1: Coefficients of Polynomial (19)

$$\begin{aligned} \xi _0= & {} \frac{K^2\mu (\mu +\varepsilon _1 +\varepsilon _2)}{(1-\varGamma _1)}\left[ \mu K(1-\varGamma _1)+\alpha q(1-\varGamma _2)\!+\!\alpha (1-q)(1\!-\!\varGamma _3)\right] \left( 1-{\mathcal {R}}_a\right) ,\\ \xi _1= & {} K (\alpha \beta _2 \eta \mu \varPsi _1+\alpha \beta _2 \mu \varPsi _1+\alpha \beta _2 \varPsi _1 \varepsilon _2+2 \alpha \mu ^2+2 \alpha \mu \varepsilon _2-2 \beta _2 \eta \varLambda \mu \varPsi _1 \\&-\,\beta _2^2 \eta \varLambda \varPsi _1^2, \\&-\,\beta _2 \eta \mu \rho _1 \varPsi _1^2-\beta _2 \mu \rho _1 \varPsi _1^2-\rho _2 \varPsi _2 (\beta _2 \varPsi _1 (\eta \mu +\mu +\varepsilon _2)+2 \mu (\mu +\varepsilon _2))\\&-\,2 \beta _2 \varLambda \varPsi _1 \varepsilon _2 \\&-\,\beta _2 \rho _1 \varPsi _1^2 \varepsilon _2-\beta _1^2 \eta K^2 \varLambda +\varepsilon _1 \,(\beta _2 \eta \varPsi _1 (\alpha +K \mu -2 \varLambda -\rho _1 \varPsi _1-\rho _2 \varPsi _2) \\&+\,\mu (2 \alpha +3 K \mu -2 \rho _1 \varPsi _1-2 \rho _2 \varPsi _2))+\beta _2 \eta K \mu ^2 \varPsi _1+\beta _2 K \mu ^2 \varPsi _1\\&+\,\beta _2 K \mu \varPsi _1 \varepsilon _2+3 K \mu ^3 +\,\beta _1 K (-\varPsi _1 (2 \beta _2 \eta \varLambda +(\eta +1) \mu \rho _1)-(\eta +1) \mu \rho _2 \varPsi _2 \\&+\,\eta \varepsilon _1 (\alpha +K \mu -3 \varLambda -\rho _1 \varPsi _1-\rho _2 \varPsi _2) \\&+\,\varepsilon _2 (\alpha +K \mu -3 \varLambda -\rho _1 \varPsi _1-\rho _2 \varPsi _2)+\mu \\&\times \,(\alpha (\eta +1)-3 \eta \varLambda +(\eta +1) K \mu +3 (\eta -1) \varLambda p)) \\&+\,3 K \mu ^2 \varepsilon _2-2 \mu ^2 \rho _1 \varPsi _1+2 \beta _2 \eta \varLambda \mu p \varPsi _1-2 \beta _2 \varLambda \mu p \varPsi _1-2 \mu \rho _1 \varPsi _1 \varepsilon _2), \\ \end{aligned}$$

$$\begin{aligned} \xi _2= & {} \alpha \beta _2 \eta \mu \varPsi _1+\alpha \beta _2^2 \eta \varPsi _1^2+\alpha \beta _2 \mu \varPsi _1+\alpha \beta _2 \varPsi _1 \varepsilon _2+\alpha \mu \varepsilon _2-\beta _2 \eta \varLambda \mu \varPsi _1-\beta _2^2 \eta \varLambda \varPsi _1^2\\&-\,\beta _2 \eta \mu \rho _1 \varPsi _1^2 -\beta _2^2\eta \rho _1 \varPsi _1^3-\beta _2 \mu \rho _1 \varPsi _1^2-\rho _2 \varPsi _2 (\beta _2 \varPsi _1+\mu )(\beta _2 \eta \varPsi _1+\mu +\varepsilon _2)\\&-\beta _2 \varLambda \varPsi _1 \varepsilon _2-\beta _2 \rho _1 \varPsi _1^2 \varepsilon _2+\,\beta _1^2 \eta K^2 (\alpha +K \mu -3 \varLambda -\rho _1 \varPsi _1-\rho _2 \varPsi _2) \\&+\varepsilon _1 (\mu (\alpha +3 K \mu -\rho _1 \varPsi _1-\rho _2 \varPsi _2)+\mu ^2 (\alpha +3 K \mu ) \\&-\,\beta _2 \eta \varPsi _1 (-\alpha -2 K \mu +\varLambda +\rho _1 \varPsi _1+\rho _2 \varPsi _2))+2 \beta _2 \eta K \mu ^2 \varPsi _1+\beta _2^2 \eta \\&\times \, K \mu \varPsi _1^2+2 \beta _2 K \mu ^2 \varPsi _1+\,2 \beta _2 K \mu \varPsi _1 \varepsilon _2+\beta _1 K (-2 \rho _2 \varPsi _2 (\beta _2 \eta \varPsi _1 \\&+\eta \mu +\mu )-2 \varPsi _1 ((\eta +1) \mu \rho _1-\beta _2 \eta (\alpha +K \mu -2 \varLambda -\rho _1 \varPsi _1)) \\&+\,\eta \varepsilon _1 (2 \alpha +3 K \mu -3 \varLambda -2 \rho _1 \varPsi _1-2 \rho _2 \varPsi _2)+\varepsilon _2 \\&\times \, (2 \alpha +3 K \mu -3 \varLambda -2 \rho _1 \varPsi _1-2 \rho _2 \varPsi _2)+\,\beta _2 \eta \varLambda \mu p \varPsi _1 \\&+\,\mu (2 \alpha (\eta +1)-3 \eta \varLambda +3 (\eta +1) K \mu +3 (\eta -1) \varLambda p))+3 K \mu ^2 \varepsilon _2\\&-\,\beta _2 \varLambda \mu p \varPsi _1-\mu \rho _1 \varPsi _1 \varepsilon _2-\mu ^2 \rho _1 \varPsi _1, \\ \xi _3= & {} \mu (\varepsilon _1 (\beta _2 \eta \varPsi _1+\mu )+(\beta _2 \varPsi _1+\mu )(\beta _2 \eta \varPsi _1+\mu +\varepsilon _2))+\beta _1^2 \eta K \\&\times \,(2 \alpha +3 K \mu -3 \varLambda -2 \rho _1 \varPsi _1-2 \rho _2 \varPsi _2) \\&+\,\beta _1 (-\rho _2 \varPsi _2 (2 \beta _2 \eta \varPsi _1+\eta \mu +\mu )-\varPsi _1 \\&\times \,((\eta +1) \mu \rho _1+2 \beta _2 \eta (-\alpha -2 K \mu +\varLambda +\rho _1 \varPsi _1)) \\&+\,\eta \varepsilon _1 (\alpha +3 K \mu -\varLambda -\rho _1 \varPsi _1-\rho _2 \varPsi _2)+\varepsilon _2 \\&\times \,(\alpha +3 K \mu -\varLambda -\rho _1 \varPsi _1-\rho _2 \varPsi _2) \\&+\,\mu (\alpha (\eta +1)-\eta \varLambda +3 (\eta +1) K \mu +(\eta -1) \varLambda p)), \\ \xi _4= & {} \beta _1 (\mu (2 \beta _2 \eta \varPsi _1+\eta \mu +\mu +\eta \varepsilon _1+\varepsilon _2)+\beta _1 \eta \\&\times \,(\alpha +3 K \mu -\varLambda -\rho _1 \varPsi _1-\rho _2 \varPsi _2)), \\ \xi _5= & {} \beta _1^2 \eta \mu . \end{aligned}$$

Appendix 2: Number of Positive Roots of Polynomial (19)

Table 2 Number of positive roots

Table 3 Number of positive roots

Table 4 Number of positive roots

Table 5 Number of positive roots

Appendix 3: Associated Nonzero Partial Derivatives of F at the Drug-Free Equilibrium

$$\begin{aligned} \frac{\partial ^2 f_1}{\partial x_1\partial x_3}= & {} \frac{\partial ^2 f_1}{\partial x_3\partial x_1}=\frac{\beta ^* _1 \mu \left( \mu (p-1)-\varepsilon _1\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) }, \quad \\ \frac{\partial ^2 f_1}{\partial x_1\partial x_4}= & {} \frac{\partial ^2 f_1}{\partial x_4\partial x_1}=\frac{\beta ^* _1 \theta \mu \left( \mu (p-1)-\varepsilon _1\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) },\\ \frac{\partial ^2 f_1}{\partial x_2\partial x_3}= & {} \frac{\partial ^2 f_1}{\partial x_3\partial x_2}=\frac{\beta ^* _1 \mu \left( \mu p+\varepsilon _2\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) },\quad \\ \frac{\partial ^2 f_1}{\partial x_2\partial x_4}= & {} \frac{\partial ^2 f_1}{\partial x_4\partial x_2}=\frac{\beta ^* _1 \theta \mu \left( \mu p+\varepsilon _2\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) }, \\ \frac{\partial ^2 f_1}{\partial x_3\partial x_3}= & {} \frac{2 \beta ^* _1 \mu \left( \mu p+\varepsilon _2\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) },\quad \\\frac{\partial ^2 f_1}{\partial x_3\partial x_4}= & {} \frac{\partial ^2 f_1}{\partial x_4\partial x_3} =\frac{\beta ^* _1 (\theta +1) \mu \left( \mu p+\varepsilon _2\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) }, \\ \frac{\partial ^2 f_1}{\partial x_3\partial x_5}= & {} \frac{\partial ^2 f_1}{\partial x_5\partial x_3}=\frac{\beta ^* _1 \mu \left( \mu p+\varepsilon _2\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) },\quad \\\frac{\partial ^2 f_1}{\partial x_4\partial x_4}= & {} \frac{2 \beta ^* _1 \theta \mu \left( \mu p+\varepsilon _2\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) }, \\ \frac{\partial ^2 f_1}{\partial x_4\partial x_5}= & {} \frac{\partial ^2 f_1}{\partial x_5\partial x_4}=\frac{\beta ^* _1 \theta \mu \left( \mu p+\varepsilon _2\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) },\quad \\ \frac{\partial ^2 f_2}{\partial x_1\partial x_3}= & {} \frac{\partial ^2 f_2}{\partial x_3\partial x_1} =\frac{\beta ^* _1 \eta \mu \left( \mu +\mu (-p)+\varepsilon _1\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) }, \\ \frac{\partial ^2 f_2}{\partial x_1\partial x_4}= & {} \frac{\partial ^2 f_2}{\partial x_4\partial x_1}=\frac{\beta ^* _1 \eta \theta \mu \left( \mu +\mu (-p)+\varepsilon _1\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) },\quad \\ \frac{\partial ^2 f_2}{\partial x_2\partial x_3}= & {} \frac{\partial ^2 f_2}{\partial x_3\partial x_2}=-\frac{\beta ^* _1 \eta \mu \left( \mu p+\varepsilon _2\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) },\\ \frac{\partial ^2 f_2}{\partial x_2\partial x_4}= & {} \frac{\partial ^2 f_2}{\partial x_4\partial x_2}=-\frac{\beta ^* _1 \eta \theta \mu \left( \mu p+\varepsilon _2\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) },\quad \\ \frac{\partial ^2 f_2}{\partial x_3\partial x_3}= & {} \frac{2 \beta ^* _1 \eta \mu \left( \mu +\mu (-p)+\varepsilon _1\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) }, \\ \end{aligned}$$

$$\begin{aligned} \frac{\partial ^2 f_2}{\partial x_3\partial x_4}= & {} \frac{\partial ^2 f_2}{\partial x_4\partial x_3}=-\frac{\beta ^* _1 \eta (\theta +1) \mu \left( \mu (p-1)-\varepsilon _1\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) },\quad \\ \frac{\partial ^2 f_2}{\partial x_3\partial x_5}= & {} \frac{\partial ^2 f_2}{\partial x_5\partial x_3} =\frac{\beta ^* _1 \eta \mu \left( \mu +\mu (-p)+\varepsilon _1\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) } \\ \frac{\partial ^2 f_2}{\partial x_4\partial x_5}= & {} \frac{\partial ^2 f_2}{\partial x_5\partial x_4}=\frac{\beta ^* _1 \eta \theta \mu \left( \mu +\mu (-p)+\varepsilon _1\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) },\quad \\\frac{\partial ^2 f_2}{\partial x_4\partial x_4}= & {} \frac{2 \beta ^* _1 \eta \theta \mu \left( \mu +\mu (-p)+\varepsilon _1\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) }, \\ \frac{\partial ^2 f_3}{\partial x_1\partial x_3}= & {} \frac{\partial ^2 f_3}{\partial x_3\partial x_1}=\frac{\beta ^* _1 (\eta -1) \mu \left( \mu (p-1)-\varepsilon _1\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) },\quad \\ \frac{\partial ^2 f_3}{\partial x_1\partial x_4}= & {} \frac{\partial ^2 f_3}{\partial x_4\partial x_1}=\frac{\beta ^* _1 (\eta -1) \theta \mu \left( \mu (p-1)-\varepsilon _1\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) }, \\ \frac{\partial ^2 f_3}{\partial x_2\partial x_3}= & {} \frac{\partial ^2 f_3}{\partial x_3\partial x_2} =\frac{\beta ^* _1 (\eta -1) \mu \left( \mu p+\varepsilon _2\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) },\quad \\ \frac{\partial ^2 f_3}{\partial x_2\partial x_4}= & {} \frac{\partial ^2 f_3}{\partial x_4\partial x_2} =\frac{\beta ^* _1 (\eta -1) \theta \mu \left( \mu p+\varepsilon _2\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) }, \\ \frac{\partial ^2 f_3}{\partial x_3\partial x_3}= & {} \frac{2 \left( \alpha \varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) +\beta ^* _1 K^2 \mu \left( \mu (\eta (p-1)-p)-\eta \varepsilon _1-\varepsilon _2\right) \right) }{K^2 \varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) }, \\ \frac{\partial ^2 f_3}{\partial x_3\partial x_4}= & {} \frac{\partial ^2 f_3}{\partial x_4\partial x_3} =\frac{\beta ^* _1 (\theta +1) \mu \left( \mu (\eta (p-1)-p)-\eta \varepsilon _1-\varepsilon _2\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) }, \\ \frac{\partial ^2 f_3}{\partial x_3\partial x_5}= & {} \frac{\partial ^2 f_3}{\partial x_5\partial x_3}=\frac{\beta ^* _1 \mu \left( \mu (\eta (p-1)-p)-\eta \varepsilon _1-\varepsilon _2\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) }, \\ \frac{\partial ^2 f_3}{\partial x_4\partial x_4}= & {} \frac{2 \beta ^* _1 \theta \mu \left( \mu (\eta (p-1)-p)-\eta \varepsilon _1-\varepsilon _2\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) }, \\ \frac{\partial ^2 f_3}{\partial x_4\partial x_5}= & {} \frac{\partial ^2 f_3}{\partial x_5\partial x_4}=\frac{\beta ^* _1 \theta \mu \left( \mu (\eta (p-1)-p)-\eta \varepsilon _1-\varepsilon _2\right) }{\varLambda \left( \mu +\varepsilon _1+\varepsilon _2\right) }, \\ \frac{\partial ^2 f_4}{\partial x_3\partial x_3}= & {} -\frac{2 \alpha (1-q)}{K^2},\quad \frac{\partial ^2 f_5}{\partial x_3\partial x_3}=-\frac{2 \alpha q}{K^2}, \\ \frac{\partial ^2 f_1}{\partial x_3\partial \beta ^*_1}= & {} -\frac{\mu p+\varepsilon _2}{\mu +\varepsilon _1+\varepsilon _2},\quad \frac{\partial ^2 f_1}{\partial x_4\partial \beta ^*_1}=-\frac{\theta \left( \mu p+\varepsilon _2\right) }{\mu +\varepsilon _1+\varepsilon _2}, \\ \frac{\partial ^2 f_2}{\partial x_3\partial \beta ^*_1}= & {} \frac{\eta \left( \mu (p-1)-\varepsilon _1\right) }{\mu +\varepsilon _1+\varepsilon _2},\quad \frac{\partial ^2 f_2}{\partial x_4\partial \beta ^*_1}=\frac{\eta \theta \left( \mu (p-1)-\varepsilon _1\right) }{\mu +\varepsilon _1+\varepsilon _2}, \\ \frac{\partial ^2 f_3}{\partial x_3\partial \beta ^*_1}= & {} \frac{\mu (\eta -\eta p+p)+\eta \varepsilon _1+\varepsilon _2}{\mu +\varepsilon _1+\varepsilon _2},\quad \!\frac{\partial ^2 f_3}{\partial x_4\partial \beta ^*_1}\!=\!\frac{\theta \left( \mu (\eta -\eta p+p)+\eta \varepsilon _1+\varepsilon _2\right) }{\mu +\varepsilon _1+\varepsilon _2}. \end{aligned}$$

Appendix 4: Expressions for $\Delta _1$ and $\Delta _2$

$$\begin{aligned} \Delta _1= & {} -K^2\theta \mu \beta ^*_1(1-\eta )(p\mu +\varepsilon _2)v_3u_2u_4-K^2\mu \beta ^*_1(1-\eta )(p\mu +\varepsilon _2)v_3u_2u_3\\&+\,2\alpha \varLambda (\mu +\varepsilon _1+\varepsilon _2)v_3u^2_3 \\ \Delta _2= & {} K^2\mu \beta ^*_1((p+(1-p)\eta )\mu +\eta \varepsilon _1+\varepsilon _2)((1+\theta )u_4+u_5)u_3v_3 \\&-\,\mu \beta ^*_1 K^2(1-\eta )((1-p)\mu +\varepsilon _1)v_3u_1u_3 \\&+\,K^2\theta \mu \beta ^*_1((p+(1-p)\eta )\mu +\eta \varepsilon _1+\varepsilon _2)(2u_4+u_5)u_4v_3\\&+\,2\alpha \varLambda (\mu +\varepsilon _1+\varepsilon _2)((1-q)v_4+qv_5)u^2_3 \\&+\,2\mu K^2\beta ^*_1((p+(1-p)\eta )\mu +\eta \varepsilon _1 \\&+\,\varepsilon _2)u^2_3v_3-\mu \theta \beta ^*_1 K^2(1-\eta )((1-p)\mu +\varepsilon _1)v_3u_1u_4. \end{aligned}$$