Population Growth Combined with Wide Offspring Distributions can Increase Fixation Rate and Reduce Genetic Diversity

Abstract

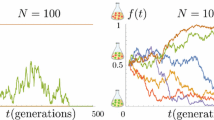
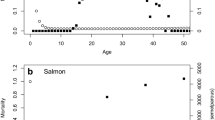
Genetic diversity grows with the population size in most neutral evolution models. Empirical evidence of large populations with limited diversity has been proposed to be due either to genetic bottlenecks or to selection. An alternative explanation is that the limited diversity is a result of rare reproduction events. Indeed, recent estimates of the offspring number distribution highlight the role of large reproduction events. We here show that in a large class of models containing such rare events, genetic diversity decreases as the population size increases, in neutral evolution models. For many realistic offspring number distributions, the contribution of rare events to the dynamics grows with the population size. In the context of genetic diversity, these rare events induce a decrease in the time to the most recent common ancestor and in the genetic heterogeneity as the population grows. This phenomenon may explain the observed rapid fixation of genes in large populations, in the absence of observable selection or bottlenecks.

Appendices

Appendix 1: Asymptotic Analysis of Truncated Power Laws

Let $U_N$ be a r.v. with truncated power law distribution:

$$\begin{aligned} P\left( {U_N =k} \right) =D_N k^{-\alpha } \quad \hbox {for} \quad k=1,2,\ldots ,N, \end{aligned}$$

(10)

where $D_N$ is the normalizing constant. Note that

$$\begin{aligned} E\left[ {U_N^m } \right] =\sum _{k=1}^N {D_N k^{m-\alpha }} , \quad \frac{ 1}{D_N }=\sum _{k=1}^N {k^{-\alpha }} . \end{aligned}$$

(11)

The asymptotic approximations of these sums are well known (we write $f\sim g$ for $\lim \limits _{N\rightarrow \infty } f/g=1)$:

$$\begin{aligned} \sum _{k=1}^N {k^{-\alpha }} \sim \left\{ {{\begin{array}{lll} {N^{1-\alpha }/\left( {1-\alpha } \right) }&{} \quad \hbox {if} &{} -\infty<\alpha<1 \\ {\log N}&{} \quad \hbox {if} &{} \alpha =1 \\ {\zeta \left( \alpha \right) }&{} \quad \hbox {if} &{} 1<\alpha <\infty \\ \end{array} } } \right. , \end{aligned}$$

where $\zeta$ denotes the Riemann zeta function. From this, it immediately follows that

$$\begin{aligned} E\left[ {U_N} \right] =D_N \sum _{k=1}^N {k^{1-\alpha }} \sim \left\{ {{\begin{array}{lll} {\left( {1-\alpha } \right) N/\left( {2-\alpha } \right) }&{} \quad \hbox {if} &{} -\infty<\alpha<1 \\ {N/\log N}&{} \quad \hbox {if} &{} \alpha =1 \\ {N^{2-\alpha }/\left( {\left( {2-\alpha } \right) \zeta \left( \alpha \right) } \right) }&{}\quad \hbox {if} &{} 1<\alpha<2 \\ {\left( {\log N} \right) /\zeta \left( 2 \right) }&{} \quad \hbox {if} &{} \alpha =2 \\ {\zeta \left( {\alpha -1} \right) /\zeta \left( \alpha \right) }&{} \quad \hbox {if} &{} 2<\alpha <\infty \\ \end{array}}} \right. \end{aligned}$$

and

$$\begin{aligned} \hbox {var}\left[ {U_N} \right] \sim \left\{ {{ \begin{array}{lll} {\left( {1-\alpha } \right) N^{2}/\left( {\left( {3-\alpha } \right) \left( {2-\alpha } \right) ^{2}} \right) }&{} \quad \hbox {if} &{} -\infty<\alpha<1 \\ {N^{2}/\left( {2\log N} \right) }&{} \quad \hbox {if} &{} \alpha =1 \\ {N^{3-\alpha }/\left( {\left( {3-\alpha } \right) \zeta \left( \alpha \right) } \right) } &{}\quad \hbox {if} &{} 1<\alpha<3 \\ {\left( {\log N} \right) /\zeta \left( 3 \right) } &{} \quad \hbox {if} &{} \alpha =3 \\ {\zeta \left( {\alpha -2} \right) /\zeta \left( \alpha \right) -\left( {\zeta \left( {\alpha -1} \right) /\zeta \left( \alpha \right) } \right) ^{2}} &{}\quad \hbox {if} &{} 3<\alpha <\infty \\ \end{array} } } \right. . \end{aligned}$$

Thus, we can conclude that in the notation of Theorem 1, the choice of MC as a modified Moran model with $U_N$ distributed as above will lead to MG having a decreasing TMRCA of a sample as time passes if and only if $\alpha <2$.

Appendix 2: Simulation Methods

For the growing population model, we simulate the entire process forward in time. First we generate the times of reproduction events as exponentials with rate equal to N, the current population size. Then we generate the embedded jump chain by drawing at each transition a (uniformly) random member of the population to reproduce, drawing his number of offspring from the law of $U_N +c$ and drawing a random sample of size $N-U_N$ from the previous generation who will survive to the next generation. We iterate this (with different values of N), maintain the entire history of the embedded chain in memory and average out the waiting times to recover a realization of the continuous process.

To calculate the TMRCA of a sample, we simply follow its ancestral line in the generated lineage tree up to the first occurrence of a single ancestor.

To calculate the heterozigosity and mean pairwise difference of the population, we superimposed a mutation model independent of reproduction events, with exponentially distributed mutation events.