Multicellular Mathematical Modelling of Mesendoderm Formation in Amphibians

Abstract

The earliest cell fate decisions in a developing embryo are those associated with establishing the germ layers. The specification of the mesoderm and endoderm is of particular interest as the mesoderm is induced from the endoderm, potentially from an underlying bipotential group of cells, the mesendoderm. Mesendoderm formation has been well studied in an amphibian model frog, Xenopus laevis, and its formation is driven by a gene regulatory network (GRN) induced by maternal factors deposited in the egg. We have recently demonstrated that the axolotl, a urodele amphibian, utilises a different topology in its GRN to specify the mesendoderm. In this paper, we develop spatially structured mathematical models of the GRNs governing mesendoderm formation in a line of cells. We explore several versions of the model of mesendoderm formation in both Xenopus and the axolotl, incorporating the key differences between these two systems. Model simulations are able to reproduce known experimental data, such as Nodal expression domains in Xenopus, and also make predictions about how the positional information derived from maternal factors may be interpreted to drive cell fate decisions. We find that whilst cell–cell signalling plays a minor role in Xenopus, it is crucial for correct patterning domains in axolotl.

Appendices

Appendix 1: Model Formulation

Here we describe the formulation of our mathematical models, which are an extension of those in Middleton et al. (2009, 2013) and Brown et al. (2014). As our models include a large number of equations, we introduce the system part by part.

1.1 Nodal Signalling

We extend the Nodal signalling model developed in Middleton et al. (2013) to include regulation of Nodal by the maternal factors VegT (V) and $\beta$-catenin (C). The maternal factors are modelled as intracellular protein deposits, which are degraded at a constant rate, $\mu _V$ and $\mu _C$, respectively.

$$\begin{aligned} V \mathop {\rightarrow }^{\mu _V}\emptyset , \quad C \mathop {\rightarrow }^{\mu _C}\emptyset , \end{aligned}$$

(13)

We now proceed to describe the rest of the Nodal–Antivin signalling network, first formulated by Middleton et al. (2013). Nodal and Smad families are treated as single components in our models, motivated by a single Nodal gene acting in mesendoderm formation in axolotl (Swiers et al. 2010), together with noting that the multiple Nodal genes present in Xenopus are not present in other vertebrates.

Nodal ligands ($N^o$) bind to free receptors (R) in a reversible reaction to become Nodal-bound receptors ($R^\diamond$) with $k_N$ and $k_{-N}$ being the association and dissociation rates of Nodal to its receptor:

$$\begin{aligned} N^o+R\mathop {\rightleftharpoons }^{k_N}_{k_{-N}}R^\diamond . \end{aligned}$$

(14)

Following the binding of Nodal to its receptor, intracellular Smad2 (S) becomes phosphorylated, forming PSmad2 (P). It is assumed that this occurs via the formation of an intermediate complex ($R^{\diamond \diamond }$). Nodal-bound receptors are rephosphorylated instantaneously after the formation of PSmad2:

$$\begin{aligned} S+R^\diamond \mathop {\rightleftharpoons }^{k_S}_{k_{-S}}R^{\diamond \diamond }\mathop {\rightarrow }\limits ^{k_p}P+R^\diamond \end{aligned}$$

(15)

PSmad2 then regulates downstream targets of the pathway, including Nodal itself, where the activation of downstream targets is modelled using a Hill function and PSmad2 is turned over at a rate $\mu _P$.

We assume that Nodal and Antivin mRNA and extracellular proteins are degraded at rates proportional to their concentrations ($\mu _N$,$\mu _T$,${\mu _N^o}$,${\mu _T^o}$):

$$\begin{aligned} N \mathop {\rightarrow }^{\mu _N}\emptyset ,\quad T \mathop {\rightarrow }^{\mu _T}\emptyset , \quad N^o \mathop {\rightarrow }^{\mu _{N^o}}\emptyset ,\quad T ^o\mathop {\rightarrow }^{\mu _{T^o}}\emptyset . \end{aligned}$$

(16)

Both Nodal and Antivin mRNA are assumed to be translated into protein and immediately secreted from the cell (see “Appendix 2” for further details), at a rate proportional to their concentration, with rate constants $\delta _N$ and $\delta _T$, respectively:

$$\begin{aligned} N \mathop {\rightarrow }^{\delta _N} N^o+N, \quad T \mathop {\rightarrow }^{\delta _T} T^o+T. \end{aligned}$$

(17)

Antivin is a downstream target of Nodal signalling, which acts to antagonise Nodal signalling. This is modelled using two different mechanisms: receptor-mediated repression and heterodimer-mediated repression. In receptor-mediated repression, Antivin ligands ($T^o$) bind to a free receptor to form an Antivin-bound receptor ($R^\ddagger$) which is inactive; the rate of association and dissociation of Antivin to free receptors are $k_T$ and $k_{-T}$:

$$\begin{aligned} R+T^o\mathop {\rightleftharpoons }^{k_T}_{k_{-T}}R^\ddagger \end{aligned}$$

(18)

In heterodimer-mediated repression, an Antivin ligand binds directly to a Nodal ligand to form a Nodal–Antivin heterodimer ($T^\ddagger$) which is inactive, with association and dissociation rates $l_T$ and $l_{-T}$:

$$\begin{aligned} N^o+T^o\mathop {\rightleftharpoons }^{l_T}_{l_{-T}}T^\ddagger \mathop {\rightarrow }\limits ^{\mu _{T^\ddagger }}\emptyset \end{aligned}$$

(19)

Extracellular Nodal, extracellular Antivin and Nodal–Antivin heterodimer can move between neighbouring cells with rates of transmission $\sigma _N$, $\sigma _T$ and $\sigma _{T^\ddagger }$, respectively. All other species do not move between cells.

We note that the intracellular, receptor and extracellular protein concentrations are defined as the number of molecules per intracellular, cell membrane and extracellular volume, respectively. We thus need to introduce the extracellular and membrane volume fractions $\rho =\nu _e/\nu _{j}$ and $\nu =\nu _M/\nu _{j}$ where $\nu _{j}$, $\nu _E$ and $\nu _M$ are the local intracellular, extracellular and membrane volumes, respectively.

Equations are formulated using the law of mass action, and thus, the equations governing Nodal signalling in cell j are given by:

$$\begin{aligned} \frac{dT^o_{j}}{dt}&=\sigma _T \Delta T_{j}^o +\underbrace{\frac{\nu }{\rho }\left( k_{-T}R^\ddagger _{j}-k_TT^o_{j}R_{j}\right) }_{\text {receptor mediated repression}}+\frac{\delta _T}{\rho }T_{j}\underbrace{-l_TN^o_{j}T^o_{j}+l_{-T}T^\ddagger _{j}}_{\text {heterodimer mediated repression}}-\mu _{T^0}T^o_{j}, \end{aligned}$$

(20a)

$$\begin{aligned} \frac{dN^o_{j}}{dt}&=\sigma _N \Delta N_{j}^o+\frac{\nu }{\rho }\left( k_{-N}R^\diamond _{j}-k_NN^o_{j}R_{j}\right) \underbrace{-l_TN^o_{j}T^o_{j}+l_{-T}T^\ddagger _{j}}_{\text {heterodimer mediated repression}}\nonumber \\&\quad \,+\frac{\delta _N}{\rho }N_{j}-\mu _{N^0}N^o_{j}, \end{aligned}$$

(20b)

$$\begin{aligned} \frac{dT^\ddagger _{j}}{dt}&=\sigma _{T^\ddagger } \Delta T^\ddagger _{j}+\underbrace{l_TN^o_{j}T^o_{j}-l_{-T}T^\ddagger _{j}}_{\text {heterodimer mediated repression}}-\mu _{T^\ddagger }T^\ddagger _{j}, \end{aligned}$$

(20c)

$$\begin{aligned} \frac{dT_{j}}{dt}&=\lambda _{P,T}\mathcal {H}\left( \frac{P_{j}}{\theta _{P,T}}\right) -\mu _{T}T_{j},\end{aligned}$$

(20d)

$$\begin{aligned} \frac{dN_{j}}{dt}&=F_Y(V_{j}, C_{j},P_{j})-\mu _{N}N_{j}, \end{aligned}$$

(20e)

$$\begin{aligned} \frac{dP_{j}}{dt}&=k_p\nu R^{\diamond \diamond }_{j}-\mu _PP_{j},\end{aligned}$$

(20f)

$$\begin{aligned} \frac{dR_{j}}{dt}&=k_{-N}R^\diamond _{j}-k_NN^o_{j}R_{j}+\underbrace{k_{-T}R^\ddagger _{j}-k_TT^o_{j}R_{j}}_{\text {receptor mediated repression}}, \end{aligned}$$

(20g)

$$\begin{aligned} \frac{dR^\diamond _{j}}{dt}&=-k_{-N}R^\diamond _{j}+k_NN^o_{j}R_{j} - k_sR^\diamond _{j} S_{j} +\left( k_{-s}+k_p\right) R^{\diamond \diamond }_{j},\end{aligned}$$

(20h)

$$\begin{aligned} \frac{dR^{\diamond \diamond }_{j}}{dt}&=-\left( k_{-s}+k_p\right) R^{\diamond \diamond }_{j}+k_sR^\diamond _{j} S_{j},\end{aligned}$$

(20i)

$$\begin{aligned} \frac{dR^\ddagger _{j}}{dt}&=-k_{-T}R^\ddagger _{j}+k_TT^o_{j}R_{j}, \end{aligned}$$

(20j)

where the term giving the production of Nodal is described in Sect. 3.1 of the main text.

1.2 FGF Signalling

The reactions involved in our formulation of the FGF signalling pathway are given in Sect. 3.2 of the main text, applying the law of mass action to (7)–(9) results in the following system of dimensional ordinary differential equations:

$$\begin{aligned} \frac{dE^o_{j}}{dt}&=\sigma _E \Delta E_{j}^o+\frac{\delta _E}{\rho } E_{j} - \frac{\nu }{\rho }\left( k_E E^o_{j}-k_{-E}F^\diamond _{j}\right) -\mu _{E^o}E^o_{j},\end{aligned}$$

(21a)

$$\begin{aligned} \frac{dE_{j}}{dt}&=\lambda _{B,E}\mathcal {H} \left( \frac{B_{j}}{\theta _{B,E}}\right) -\mu _E E_{j},\end{aligned}$$

(21b)

$$\begin{aligned} \frac{dK^*_{j}}{d\tau }&=\nu k_{K^*} F^{\diamond \diamond }_{j}-\mu _{K^*} K^*_{j},\end{aligned}$$

(21c)

$$\begin{aligned} \frac{dF^\diamond _{j}}{d\tau }&=k_EE^o_{j}F_{j}-k_{-E}F^\diamond _{j}-k_KF^\diamond _{j} K_j+(k_{-K}+k_{K^*})F^{\diamond \diamond }_{j},\end{aligned}$$

(21d)

$$\begin{aligned} \frac{dF^{\diamond \diamond }_{j}}{d\tau }&=k_K F^\diamond _{j} K_j -(k_{-K}+k_{K*})F^{\diamond \diamond }_{j},\end{aligned}$$

(21e)

$$\begin{aligned} \frac{dF_{j}}{d\tau }&=-k_E E^o_{j} F_{j} + k_{-E} F^\diamond _{j} \end{aligned}$$

(21f)

1.3 Xenopus Network Downstream of Nodal

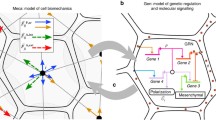
Based on the Xenopus mesendoderm shown in Fig. 1a, the time evolution of Brachyury, Goosecoid, Mix, Siamois and Lim1 in Xenopus is governed by

$$\begin{aligned} \dfrac{dB_j}{dt}&= \left\{ \lambda _{K^*,B}\mathcal {H} \left( \frac{K^*}{\theta _{K^*,B}}\right) +\lambda _{V,B}\mathcal {H}\left( \frac{V_j}{\theta _{V,B}}\right) \right. \nonumber \\&\left. +\lambda _{P,B}\mathcal {H}\left( \frac{P_j}{\theta _{P,B}}\right) \right\} \left\{ 1- \mathcal {H} \left( \frac{G_j}{\theta _{G,B}}+\frac{M_j}{\theta _{M,B}}\right) \right\} - \mu _B B_j, \end{aligned}$$

(22a)

$$\begin{aligned} \dfrac{dG_j}{dt}&= \left\{ \lambda _{LI,G} \mathcal {H}\left( \frac{L_j}{\theta _{L,G}}\right) \mathcal {H}\left( \frac{I_j}{\theta _{I,G}}\right) + \lambda _{M,G} \mathcal {H}\left( \frac{M_j}{ \theta _{M,G}}\right) \right\} \left\{ 1- \mathcal {H}\left( \frac{G_j}{\theta _{G,G}}\right) \right\} \nonumber \\&\quad \, - \mu _{G} G_j, \end{aligned}$$

(22b)

$$\begin{aligned} \dfrac{dM_j}{dt}&= \left\{ \lambda _{V,M}\mathcal {H}\left( \frac{V_j}{\theta _{V,M}}\right) +\lambda _{N,M} \mathcal {H}\left( \frac{P_j}{\theta _{P,M}}\right) \right\} \left\{ 1-\mathcal {H}\left( \frac{B_j}{\theta _{B,M}}\right) \right\} - \mu _{M} M_j,\end{aligned}$$

(22c)

$$\begin{aligned} \dfrac{d I_j}{dt}&= \lambda _{C,I} \mathcal {H}\left( \frac{C_j}{ \theta _{C,I}}\right) - \mu _{j} I_j,\end{aligned}$$

(22d)

$$\begin{aligned} \dfrac{dL_j}{dt}&= \lambda _{P,L}\mathcal {H}\left( \frac{P_j}{\theta _{P,L}}\right) -\mu _{L} L_j. \end{aligned}$$

(22e)

1.4 Axolotl Network Downstream of Nodal

Based on the axolotl mesendoderm GRN shown in Fig. 1b, the time evolution of Brachyury, Goosecoid, Mix and Lim1 in axolotl is governed by

$$\begin{aligned} \dfrac{dB_j}{dt}&= \left\{ \lambda _{K^*,B}\mathcal {H} \left( \frac{K^*}{\theta _{K^*,B}}\right) +\lambda _{P,B}\mathcal {H}\left( \frac{P_j}{\theta _{P,B}}\right) \mathcal {H} \left( \frac{M_j}{\theta _{M,B}}\right) \right\} \left\{ 1- \mathcal {H} \left( \frac{G_j}{\theta _G,B}\right) \right\} \nonumber \\&\quad \,- \mu _B B_j, \end{aligned}$$

(23a)

$$\begin{aligned} \dfrac{dG_j}{dt}&= \left\{ \lambda _{L,G} \mathcal {H}\left( \frac{L_j}{\theta _{L,G}}\right) + \lambda _{M,G} \mathcal {H}\left( \frac{M_j}{ \theta _{M,G}}\right) \right\} \left\{ 1- \mathcal {H}\left( \frac{G_j}{\theta _{G,G}}\right) \right\} - \mu _{G} G_j, \end{aligned}$$

(23b)

$$\begin{aligned} \dfrac{dM_j}{dt}&=\lambda _{N,M} \mathcal {H}\left( \frac{P_j}{\theta _{P,M}}\right) \left\{ 1-\mathcal {H}\left( \frac{B_j}{\theta _{B,M}}\right) \right\} - \mu _{M} M_j, \end{aligned}$$

(23c)

$$\begin{aligned} \dfrac{dL_j}{dt}&= \lambda _{P,L}\mathcal {H}\left( \frac{P_j}{\theta _{P,L}}\right) -\mu _{L} L_j. \end{aligned}$$

(23d)

1.5 Nondimensionalisation

We proceed by nondimensionalising (20)–(23) following the scalings used in Middleton et al. (2013) which/textbfwe summarise here. Dimensionless time ($\tau$) is based on the rate of turnover and secretion of intracellular Antivin, such that $\tau \equiv \mu _N t$. The dimensionless rates of signalling ($\hat{\sigma }_X$), turnover ($\hat{\mu }_Y$) and dissociation of receptors ($\hat{k}_{-Z}$) are defined by $\hat{\sigma }_X \equiv \sigma _X / \mu _N$ for $X\in \left\{ {N,T,T^\ddagger ,E}\right\}$, $\hat{\mu }_Y \equiv \mu _Y/ \mu _N$ for $Y\in \left\{ {N,T,E}\right\}$ and $\hat{k}_{-Z} \equiv k_{-Z}/ \mu _N$ for $Z\in \left\{ {N,T,,T^\ddagger ,E,S,K}\right\}$. Dimensionless rates of secretion of Nodal, Antivin and FGF are given by $\hat{\delta }_N \equiv \delta _N/\mu _N$ and $\hat{\delta }_X \equiv \delta _X / \mu _N$ for $X\in \left\{ {T,E}\right\}$. Dimensionless association rates are $\hat{k}_s \equiv k_sS/\mu _N$, $\hat{k}_K \equiv k_KK/\mu _N$, $\hat{k}_Y \equiv k_YR^\bullet /\mu _N$ for $Y\in \left\{ N,T\right\}$ and $\hat{k}_E \equiv k_EF^\bullet /\mu _N$. The association and dissociation rates of the Nodal–Antivin complex are scaled by $\hat{l}_T \equiv l_T R^\bullet / \left( \mu _N+\delta _N\right)$ and $\hat{l}_{-T} \equiv l_{-T}/ \left( \mu _N+\delta _N\right)$. The nondimensional phosphorylation rate of Smad2 is $\hat{k}_P \equiv k_P/ k_{-S}$, and the nondimensional phosphorylation rate of MAPK is $\hat{k}_{K*}\equiv {k}_{K*} / \left( \mu _N+\delta _N\right)$. Nondimensional rates of production are: $\hat{\lambda }_{P,N}\equiv {\lambda }_{P,N} /\mu _NR^\bullet$, $\hat{\lambda }_{P,T}\equiv {\lambda }_{P,T} /\mu _NR^\bullet$ and $\hat{\lambda }_{C,N}\equiv {\lambda }_{C,N} /\mu _NR^\bullet$. Dimensionless concentrations are based on the total number of receptors, such that for $X\in \left\{ N,N^o,R^\diamond ,R^{\diamond \diamond },R\right\}$ we have $\hat{X}=X/R^\bullet$ and for $Y \in \left\{ E^o,K*,F,F^\diamond ,F^{\diamond \diamond }\right\}$ we have $\hat{Y}=Y/F^\bullet$. The dimensionless concentration of P-Smad2 is $\hat{P} \equiv k_sP / k_{-S}$, and remaining concentrations are given by $\hat{Z}\equiv Z/ \theta _Z$, where the following are written for notational simplicity:$\theta _G \equiv \theta _{G,B},\;\;\;\theta _B \equiv \theta _{B,E},\;\;\;\theta _E \equiv \theta _{E,B},\;\;\;\theta _L \equiv \theta _{L,G},\;\;\;\theta _M \equiv \theta _{M,B}.$ We define the following dimensionless thresholds: $\hat{\theta }_{P,N}\equiv k_s\theta _{P,N} / k_{-S}$, $\hat{\theta }_{P,T}\equiv \theta _{P,T} / R^\bullet$, $\hat{\theta }_{K*,B}\equiv \theta _{K*,B} / F^\bullet$, $\hat{\theta }_{P,B}\equiv k_S\theta _{P,B} / k_{-S}$ and $\hat{\theta }_{P,M}\equiv k_S\theta _{P,M} / k_{-S}$. Remaining dimensionless rates of production, turnover and thresholds are defined by $\hat{\lambda }_{Y,Z}\equiv \lambda _{Y,Z} / \theta _Z\mu _N$, $\hat{\mu }_Z \equiv {\mu }_Z/\mu _N$ and $\hat{\theta }_{X,Z} \equiv \theta _{X,Z} / \theta _{Z}$.

1.5.1 Parameter Sizes

We again follow the work of Middleton (2007) and Middleton et al. (2013) in making the following assumptions about the rate at which certain processes occur, based on the fact that intracellular Nodal is turned over at a faster rate than extracellular Nodal (i.e. $\mu _N\ll \mu _{N^o}$). It is assumed that other processes occur on a similarly fast timescale and we make the following rescalings

(24)

for $X=$(N,S,T,E,K), $Y=$(N,P,S,T,E,K), $Z_1=$($N^o$,$T^o$,$E^o$,$K^*$,P), $Z_2=(N^o,T^o,E^o)$ where $\varepsilon =\mu _N / \mu _{N^o}\ll 1$. After applying the scalings described in this section, we defining the following for notational simplicity: $\bar{\delta }_N = \hat{\delta }_N/\rho$, $\bar{k}_P = \rho \hat{k}_P \hat{k}_s S^{-1}$, $\bar{k}_{-S}=\hat{k}_{_S}(1+\hat{k}_P)-\bar{k}_P,$ $\bar{\nu }=\nu / \rho ,$ $\bar{\delta }_E \equiv \dfrac{\hat{\delta }_E}{\rho }\hat{\theta }_{M^*,B}$.

1.6 Dimensionless Equations

After applying the scalings described above, dropping the hats for notational simplicity, the nondimensional forms of (20) are

$$\begin{aligned} \dfrac{d V_j}{dt}&=-\mu _V V_j,\end{aligned}$$

(25a)

$$\begin{aligned} \dfrac{d C_j}{dt}&=-\mu _C C_j,\end{aligned}$$

(25b)

$$\begin{aligned} \varepsilon \frac{dT^o_{j}}{d\tau }&=\sigma _T\Delta T^o_{j}+\bar{\nu }\left( k_{-T}R^\ddagger _{j}-k_TT^o_{j}R_{j}\right) -l_TN^o_{j}T^o_{j}+l_{-T}T^\ddagger _{j}+\bar{\delta }_T T_{j}-\mu _{T^0}T^o_{j},\end{aligned}$$

(25c)

$$\begin{aligned} \varepsilon \frac{dN^o_{j}}{d\tau }&=\sigma _N\Delta N^o_{j}+\bar{\nu }\left( k_{-N}R^\diamond _{j}-k_NN^o_{j}R_{j}\right) -l_TN^o_{j}T^o_{j}+l_{-T}T^\ddagger _{j}+\bar{\delta }_NN_{j}-\mu _{N^0}N^o_{j},\end{aligned}$$

(25d)

$$\begin{aligned} \varepsilon \frac{dT^\ddagger _{j}}{d\tau }&=\sigma _{T^\ddagger }\Delta T^\ddagger _{j}+l_TN^o_{j}T^o_{j}-l_{-T}T^\ddagger _{j}-\mu _{T^\ddagger }T^\ddagger _{j},\end{aligned}$$

(25e)

$$\begin{aligned} \frac{dT_{j}}{d\tau }&=\lambda _{P,T}\mathcal {H}\left( \frac{P_{j}}{\theta _{P,T}}\right) -\mu _{T}T_{j},\end{aligned}$$

(25f)

$$\begin{aligned} \varepsilon \frac{dP_{j}}{d\tau }&=\bar{k}_p\nu R^{\diamond \diamond }_{j}-\mu _PP_{j},\end{aligned}$$

(25g)

$$\begin{aligned} \frac{dN_{j}}{d\tau }&=\mathcal {F}_Y(V_j,C_j,P_j)-N_{j},\end{aligned}$$

(25h)

$$\begin{aligned} \varepsilon \frac{dR_{j}}{d\tau }&=k_{-N}R^\diamond _{j}-k_NN^o_{j}R_{j}+k_{-T}R^\ddagger _{j}-k_TT^o_{j}R_{j},\end{aligned}$$

(25i)

$$\begin{aligned} \varepsilon \frac{dR^\diamond _{j}}{d\tau }&= -k_{-N}R^\diamond _{j}+k_NN^o_{j}R_{j}- k_sR^\diamond _{j} +\left( \bar{k}_{-s}+\bar{k}_p\right) R^{\diamond \diamond }_{j},\end{aligned}$$

(25j)

$$\begin{aligned} \varepsilon \frac{dR^{\diamond \diamond }_{j}}{d\tau }&=k_sR^\diamond _{j} -\left( \bar{k}_{-s}+\bar{k}_p\right) R^{\diamond \diamond }_{j},\end{aligned}$$

(25k)

$$\begin{aligned} \varepsilon \frac{dR^\ddagger _{j}}{d\tau }&=-k_{-T}R^\ddagger _{j}+k_TT^o_{j}R_{j}, \end{aligned}$$

(25l)

where $\mathcal {F}_Y(V_j,C_j,P_j)$ is given by one of the three following functions

$$\begin{aligned} \mathcal {F}_{X1X2}(V_j,C_j,P_j)&=\lambda _{V,N} \mathcal {H}\left( \frac{V_j}{\theta _{V,N}}\right) +\lambda _{P,N}\left( 1+ \lambda _{C,N} \mathcal {H}\left( \frac{C_j}{\theta _{C,N}}\right) \right) \mathcal {H}\left( \dfrac{P_j}{\theta _{P,N}} \right) ,\end{aligned}$$

(26)

$$\begin{aligned} \mathcal {F}_{X5X6}(V_j,C_j,P_j)&=\lambda _{V,N} \mathcal {H}\left( \frac{V_j}{\theta _{V,N}}\right) \mathcal {H}\left( \frac{C_j}{\theta _{C,N}}\right) \end{aligned}$$

(27)

or

$$\begin{aligned} \mathcal {F}_{A1}&=\lambda _{C,N2} \mathcal {H}\left( \frac{C_j}{\theta _{C,N2}}\right) +\lambda _{P,N}\left( 1+ \lambda _{C,N} \mathcal {H}\left( \frac{C_j}{\theta _{C,N}}\right) \right) \mathcal {H}\left( \dfrac{P_j}{\theta _{P,N}} \right) \end{aligned}$$

(28)

Components of the FGF signalling pathway are governed by the following nondimensional equations

$$\begin{aligned} \varepsilon \frac{dE^o_{j}}{d\tau }&=\sigma _E \Delta E_{j}^o - \bar{\nu }\left( k_E E^o_{j}-k_{-E}F^\diamond _{j}\right) +\bar{\delta }_E E_{j}-\mu _{E^o}E^o_{j},\end{aligned}$$

(29a)

$$\begin{aligned} \frac{dE_j}{d\tau }&=\lambda _{B,E}\mathcal {H}({B_{j}})-\mu _E E_{j},\end{aligned}$$

(29b)

$$\begin{aligned} \varepsilon \frac{dK^*_{j}}{d\tau }&=\nu k_{K^*} F^{\diamond \diamond }_{j}-\mu _{K^*} K^*_{j},\end{aligned}$$

(29c)

$$\begin{aligned} \varepsilon \frac{dF^\diamond _{j}}{d\tau }&=k_EE^o_{j}F_{j}-k_{-E}F^\diamond _{j}-k_KF^\diamond _{j}+(k_{-K}+k_{K^*})F^{\diamond \diamond }_{j},\end{aligned}$$

(29d)

$$\begin{aligned} \varepsilon \frac{dF^{\diamond \diamond }_{j}}{d\tau }&=k_K F^\diamond _{j}-(k_{-K}+k_{K*})F^{\diamond \diamond }_{j},\end{aligned}$$

(29e)

$$\begin{aligned} \varepsilon \frac{dF_{j}}{d\tau }&=-k_E E^o_{j} F_{j} + k_{-E} F^\diamond _{j} \end{aligned}$$

(29f)

The nondimensional equations governing the time evolution of Brachyury, Goosecoid, Mix, Siamois and Lim1 in Xenopus are, respectively

$$\begin{aligned} \dfrac{dB_j}{d\tau }&= \left\{ \lambda _{E,B}\mathcal {H} \left( \frac{K^*}{\theta _{K^*,B}}\right) +\lambda _{V,B}\mathcal {H}\left( {V_j}\right) +\lambda _{P,B}\mathcal {H}\left( \frac{P_j}{\theta _{P,B}}\right) \right\} \left\{ 1- \mathcal {H} \left( {G_j}+{M_j}\right) \right\} \nonumber \\&\quad \,- \mu _B B_j, \end{aligned}$$

(30a)

$$\begin{aligned} \dfrac{dG_j}{d\tau }&= \left\{ \lambda _{LI,G} \mathcal {H}\left( {L_j}\right) \mathcal {H}\left( {I_j}\right) + \lambda _{M,G} \mathcal {H}\left( \frac{M_j}{ \theta _{M,G}}\right) \right\} \left\{ 1- \mathcal {H}\left( \frac{G_j}{\theta _{G,G}}\right) \right\} - \mu _{G} G_j, \end{aligned}$$

(30b)

$$\begin{aligned} \dfrac{dM_j}{d\tau }&= \left\{ \lambda _{V,M}\mathcal {H}\left( \frac{V_j}{\theta _{V,M}}\right) +\lambda _{N,M} \mathcal {H}\left( \frac{P_j}{\theta _{P,M}}\right) \right\} \left\{ 1-\mathcal {H}\left( \frac{B_j}{\theta _{B,M}}\right) \right\} - \mu _{M} M_j,\end{aligned}$$

(30c)

$$\begin{aligned} \dfrac{d I_j}{d\tau }&= \lambda _{C,I} \mathcal {H}\left( \frac{C_j}{ \theta _{C,I}}\right) - \mu _{j} I_j,\end{aligned}$$

(30d)

$$\begin{aligned} \dfrac{dL_j}{d\tau }&= \lambda _{P,L}\mathcal {H}\left( \frac{P_j}{\theta _{P,L}}\right) -\mu _{L} L_j. \end{aligned}$$

(30e)

The nondimensional equations governing the time evolution of Brachyury, Goosecoid, Mix and Lim1 in axolotl are, respectively

$$\begin{aligned} \frac{dB_{j}}{d\tau }&=\left\{ \lambda _{K*,B}\mathcal {H}\left( \frac{K^*_{j}}{\theta _{K*,B}}\right) +\lambda _{P,B}\mathcal {H}\left( \frac{P_{j}}{\theta _{P,B}}\right) \mathcal {H}\left( {M_{j}}\right) \right\} \left\{ 1-\mathcal {H}\left( {G_{j}}\right) \right\} -\mu _BB_{j}, \end{aligned}$$

(31a)

$$\begin{aligned} \frac{dG_{j}}{d\tau }&=\left\{ \lambda _{L,G}\mathcal {H}\left( {L_{j}}\right) +\lambda _{M,G}\mathcal {H}\left( \frac{M_{j}}{\theta _{M,G}}\right) \right\} \left\{ 1-\mathcal {H}\left( \frac{G_{j}}{\theta _{G,G}}\right) \right\} -\mu _GG_{j},\end{aligned}$$

(31b)

$$\begin{aligned} \frac{dM_{j}}{d\tau }&=\lambda _{P,M}\mathcal {H}\left( \frac{P_{j}}{\theta _{P,M}}\right) \left\{ 1-\mathcal {H}\left( \frac{B_{j}}{\theta _{B,M}}\right) \right\} -\mu _MM_{j},\end{aligned}$$

(31c)

$$\begin{aligned} \frac{dL_{j}}{d\tau }&=\lambda _{P,L}\mathcal {H}\left( \frac{P_{j}}{\theta _{P,L}}\right) -\mu _LL_{j}, \end{aligned}$$

(31d)

Appendix 2: Modelling Transcription, Translation and Secretion of Signalling Molecules

Throughout this work, we adopt the following framework for modelling the transcription, secretion and translation of signalling molecules (other aspects, such as the association and dissociation of proteins, are modelled using the law of mass action and are described elsewhere). Let m be the concentration of some mRNA, which is transcribed at some rate $\lambda$ and turned over at rate $\mu _m$. Schematically, we write:

$$\begin{aligned} \emptyset \mathop {\rightarrow }^{\lambda } m \mathop {\rightarrow }^{\mu _m}\emptyset . \end{aligned}$$

(32)

Let the intracellular and extracellular concentrations of protein which the mRNA encodes be given by p and $p^o$. The mRNA is translated into protein at a rate $\delta _{\mathrm{trans}}$ proportional to its concentration. mRNA is not consumed during this process. The protein can either be turned over in the cell, or secreted. Both are assumed to occur at a rate proportional to the concentration of protein in the cell, at rates given by $\mu _{\mathrm{p}}$ and $\delta _{\mathrm{sec}}$, respectively. We further assume that the extracellular protein is turned over at rate $\mu _{p^o}$. Schematically, we write:

$$\begin{aligned} m\mathop {\rightarrow }^{\delta _{\mathrm{trans}}} m+p, \quad p\mathop {\rightarrow }^{\mu _p}\emptyset , \quad p\mathop {\rightarrow }^{\delta _{\mathrm{sec}}}p^{o}\mathop {\rightarrow }^{\mu _{p^o}}\emptyset . \end{aligned}$$

(33)

The equations governing the concentration of mRNA, intracellular protein and extracellular protein are given by:

$$\begin{aligned} \dfrac{dm}{dt}&=\lambda -\mu _m m,\end{aligned}$$

(34a)

$$\begin{aligned} \dfrac{dp}{dt}&=\delta _{\mathrm{trans}} m-(\mu _p+\delta _{\mathrm{sec}} )p,\end{aligned}$$

(34b)

$$\begin{aligned} \dfrac{dp^o}{dt}&=\delta _{\mathrm{sec}} p-\mu _{p^o}p^o. \end{aligned}$$

(34c)

Since this is only intended as an illustrative example, we neglect differences in volume between the extracellular and intracellular compartments (this is discussed further below). To ensure that the number of parameters in the models we develop do not become excessive, we henceforth simplify this process by assuming that the mRNA is immediately translated into protein and then secreted by the cell, so that schematically we instead write:

$$\begin{aligned} m\mathop {\rightarrow }^{\delta _{\mathrm{sec}}} m+p^o, \quad p^{o}\mathop {\rightarrow }^{\mu _{p^o}}\emptyset , \end{aligned}$$

(35)

so that the governing equations can be written as:

$$\begin{aligned} \dfrac{dm}{dt}&=\lambda -\mu _m m,\end{aligned}$$

(36a)

$$\begin{aligned} \dfrac{dp^o}{dt}&=\delta _{\mathrm{sec}} m-\mu _{p^o}p^o. \end{aligned}$$

(36b)

We note that adopting (35) instead of (33) is equivalent (up to a scaling) to assuming that protein translation ($\delta _{\mathrm{trans}}$) and intracellular turnover ($\mu _{p}$) occur on a much faster timescale than other processes under consideration in (34). Thus, under this assumption, the level of intracellular protein p can be taken to be proportional (approximately) to the level of mRNA (i.e. $p=\delta _{\mathrm{trans}} /\mu _p m$), which can be directly substituted into the equation governing extracellular protein concentration in (34):

$$\begin{aligned} \dfrac{{d}m}{{d}t}&=\lambda -\mu _m m,\\ \dfrac{{d}p^o}{{d}t}&=\delta _{\mathrm{sec}} \delta _{\mathrm{trans}} /\mu _p m-\mu _{p^o}p^o, \end{aligned}$$

which is of the same form as 36.