Individual Vaccination as Nash Equilibrium in a SIR Model with Application to the 2009–2010 Influenza A (H1N1) Epidemic in France

Abstract

The vaccination against ongoing epidemics is seldom compulsory but remains one of the most classical means to fight epidemic propagation. However, recent debates concerning the innocuity of vaccines and their risk with respect to the risk of the epidemic itself lead to severe vaccination campaign failures, and new mass behaviors appeared driven by individual self-interest. Prompted by this context, we analyze, in a Susceptible–Infected–Recovered model, whether egocentric individuals can reach an equilibrium with the rest of the society. Using techniques from the “Mean Field Games” theory, we extend previous results and show that an equilibrium exists and characterizes completely the individual best vaccination strategy (with or without discounting). We also compare with a strategy based only on overall societal optimization and exhibit a situation with nonnegative price of anarchy. Finally, we apply the theory to the 2009–2010 Influenza A (H1N1) vaccination campaign in France and hint that a group of individuals stopped vaccinating at levels that indicated a pessimistic perception of the risk of the vaccine.

Appendices

Appendix 1: On the Societal and Individual SIR Model with Vaccination

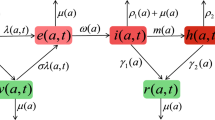
The mathematical description of the SIR model with vaccination has to take into account the possibility of instantaneous vaccination, which means that a non-negligible proportion of the total population can be vaccinated instantaneously at some time t. A first consequence is that $S(0)$ can be strictly less than $S_{0^-}$ (when some vaccination occurs at time 0). Recall that $V(t)$ represents the proportion of people vaccinated by the time t. If, for instance, nobody vaccinates before time $t^*=0.25$ years (3 months) and 30 % of the population vaccinates at time $t^*$, this means that $V(t)$ is discontinuous at this point (see Fig. 11 for an illustration). In particular, it is not derivable and neither will be $S(t)$; as such it is not possible to use in Eq. (1) the derivative $\mathrm{d}S(t)/\mathrm{d}t$. This explains why the equation is only written in the differential form: $\mathrm{d}S(t) = - \beta S(t) I(t) \mathrm{d}t - \mathrm{d}U(t)$. In this writing, all objects have a well-defined mathematical meaning: $\mathrm{d}U(t)$ is a positive measure which, for our example, will be the Dirac mass $0.3 \delta _{t^*}$. We refer to Bressan and Rampazzo (1991), Dal Maso and Rampazzo (1991), Miller (1996), and Silva and Vinter (1997) for the mathematical properties of the solutions to such evolution equations. In the particular situation when U(t) has a jump at 0, we will have $S_{0^-}- S(0)= U(0)- U(0^-)= U(0)$.

Fig. 11

Illustration of instantaneous vaccination of 30 % of the population at time $t^*=0.25$. The function $V(t)= \int _{0^-}^{t^*} \mathrm{d}U(\tau )$ is plotted. It has a discontinuity at time $t^*$ and is equal to $H(\cdot -t^*)$ with $H(\cdot )$ the Heaviside function

In this dynamics, all individuals are the same. Each individual is following a continuous time Markov dynamics jumping between the states susceptible, infected, recovered and vaccinated. Let $M_t$ be the state of one such individual at time t. The time of the jump from the infected to the recovered class is a exponential random variable of mean $1/\gamma$. We write in terms of probabilities:

$$\begin{aligned} {\mathbb {P}}\left( M_{t + \Delta t} = \mathrm{Recovered} \Big | M_{t} = \mathrm{Infected} \right) = \gamma \Delta t + o(\Delta t). \end{aligned}$$

(13)

For a given individual in the susceptible class at time t, the probability to be infected during the time interval $[t,t+\Delta t]$ is $\beta I(t) \Delta t + o(\Delta t)$; therefore,

$$\begin{aligned} {\mathbb {P}}\left( M_{t + \Delta t}=\mathrm{Infected} \Big | M_{t}=\mathrm{Susceptible} \right) = \beta I(t) \Delta t + o(\Delta t). \end{aligned}$$

(14)

On the other hand, denote by $\varphi _I(t)$ the probability of infection (in the absence of vaccination) during the time interval [0, t]. Then

$$\begin{aligned}&{{\mathbb {P}}} \Big ( M_{t + \Delta t}=\mathrm{Infected} \Big | M_{t}=\mathrm{Susceptible} \Big )\nonumber \\&\quad = \frac{ {\mathbb {P}}\left( M_{t + \Delta t}=\mathrm{Infected}, M_{t}=\mathrm{Susceptible} \right) }{ {\mathbb {P}}\left( M_{t}=\mathrm{Susceptible} \right) } \nonumber \\&\quad =\frac{\varphi _I(t + \Delta t)- \varphi _I(t) }{1- \varphi _I(t)} =\frac{1}{1- \varphi _I(t)} \varphi _I'(t) \Delta t + o(\Delta t). \end{aligned}$$

(15)

Passing to the limit $\Delta t \rightarrow 0$ in Eqs. (14) and (15), we obtain:

$$\begin{aligned} \varphi _I'(t) = \beta I(t) (1 - \varphi _I(t)), \varphi _I(0^-) = 0. \end{aligned}$$

(16)

Therefore, $\varphi _I$ is given by formula (2). Note that since $I(t)$ is continuous, $\varphi _I$ is differentiable everywhere.

In particular, for an individual in the susceptible class at time $\tau$ that does not vaccinate any more from that time on, the probability of infection after time $\tau$ is:

$$\begin{aligned} \frac{\varphi _I(\infty )- \varphi _I(\tau )}{1- \varphi _I(\tau )}. \end{aligned}$$

(17)

We can prove, by direct computations, that $\mathrm{d}U=0$ on $[\tau , \infty [$ implies:

$$\begin{aligned} \frac{\varphi _I(\infty )- \varphi _I(\tau )}{1- \varphi _I(\tau )} = \frac{\zeta (S(\tau ),I(\tau ))}{S(\tau )}. \end{aligned}$$

(18)

Remark 2

Since $\varphi _I(\infty ) < 1$ the cost $J_\mathrm{pure}({\varPi }_\infty )$ is not the limit of the costs $J_\mathrm{pure}({\varPi }_t)$ (for $t\rightarrow \infty$). On the contrary $J_\mathrm{pure}^{\mathcal {D}}({\varPi }_\infty ) = \lim _{t\rightarrow \infty } J_\mathrm{pure}^{\mathcal {D}}({\varPi }_t)$.

Appendix 2: Individual Strategies

The simplest individual strategy is to vaccinate or not at some given time (provided he is still susceptible). Such a strategy is called a pure strategy. However, pure strategies do not always have good theoretical properties and in his Nobel award winning work John Forbes Nash proved that on the contrary, any finite game admits equilibrium if mixed strategies are allowed. A mixed strategy is a probability law on the set of all pure strategies. With the notations of Sect. 1.1, the mixed strategy are probability laws on $[0,\infty ]$ with special meaning of values 0 (immediate vaccination) and $\infty$ (no vaccination). The CDF function $\varphi _V(t)$ is such that $\varphi _V(0^-)=0$ (no vaccination before time 0). Note that $\varphi _V$ is not necessary a continuous function (the discussion is very much similar to the one in “Appendix 1”). In particular, when the individual chooses the pure strategy ${\varPi }_{t^*}$, then $\varphi _V$ is the Heaviside function $H(\cdot - t^*)$. See the illustration in Fig. 12.

Fig. 12

Individual cumulative probability of vaccination $\varphi _V(t)$ is an increasing, right continuous with left limits (càdlàg) function with $\varphi _V(0^-)=0$, $\varphi _V(\infty )\le 1$

It may also be necessary to impose some constraints. Suppose that global vaccination (at the society level) can only happen with the maximal rate of $u_\mathrm{max}$ percent of population in a unit time. Then, with the notations in Eq. (1): $U(t+ \Delta t)-U(t) \le u_\mathrm{max} \Delta t$. Suppose now that all individuals want to vaccinate at the same time with the same $\varphi _V$, then the constraint above, coupled with (9), implies that $\varphi _V$ is differentiable in any t with $S(t) > 0$ and denoting $f_V(t)=\frac{u_\mathrm{max}}{S(t)}$:

$$\begin{aligned} {\forall t \ge 0\,\mathrm{with}\,S(t)>0:} \ \frac{\mathrm{d} \varphi _V(t)}{\mathrm{d}t} \le f_V(t) (1- \varphi _V(t)). \end{aligned}$$

(19)

Another interpretation of the constraint is the following: when the number of people that want to vaccinate exceeds, the capacity of the vaccination centers people will have to wait. In this model, all individuals are the same (that is, have the same characteristics therefore same strategies) then the probability for a given individual to obtain vaccination in a time interval $[t,t+\Delta t]$ is $\frac{u_\mathrm{max} \Delta t}{S(t)}$. The probability to be not yet vaccinated at time t but be vaccinated by time $t+\Delta t$ is on the one hand $\frac{\varphi _V(t+\Delta t) - \varphi _V(t)}{1-\varphi _V(t)}$ and on the other hand is $\left( \frac{u_\mathrm{max} \Delta t}{S(t)} \right) + o(\Delta t)$; for $\Delta t \rightarrow 0$ we obtain the constraint

$$\begin{aligned} \frac{\mathrm{d} \varphi _V(t)}{\mathrm{d}t} \le \frac{u_\mathrm{max} (1- \varphi _V(t)) }{S(t)}. \end{aligned}$$

(20)

Appendix 3: Proof of the Properties of the Individual Optimal Strategy: The Undiscounted Case

We set ${\mathcal {D}}=0$.

Theorem 1

(Case $u_\mathrm{max}<\infty$) Let U be a given societal policy in (1), increasing, $U(t)\le 1$, $\forall t\ge 0$ and $f_V(t)=\frac{u_\mathrm{max}}{S(t)}$. Suppose that the set of admissible individual strategies is composed of all increasing functions $\varphi _V$ differentiable in any t with $S(t) > 0$ such that:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\varphi _V(0^-)=0;}\\ {\varphi _V(\infty )\le 1};\\ {\forall t \ge 0\,\mathrm{with}\,S(t)>0:} \frac{\mathrm{d} \varphi _V(t)}{\mathrm{d}t} \le f_V(t) (1- \varphi _V(t)).\\ \end{array}\right. } \end{aligned}$$

(21)

Then, the individual optimal strategy $\varphi _V^*$ that minimizes the cost in Eq. (4) (with the system (1)) is:

• (a) If $r_I\le r_V$: $\varphi _V^*(t)=0$.

• (b) If $r_I> r_V$ and $\varphi _I(\infty ) \le r_V/r_I$ then $\varphi _V^*(t)=0$.

• (c) If $r_I> r_V$ and $\varphi _I(\infty ) > r_V/r_I$ then $\varphi _V^*(t)$ is the solution of

  $$\begin{aligned} {\left\{ \begin{array}{ll} {\varphi _V^*(0^-)=0, \varphi _V^*(\infty )\le 1, \ \varphi _V^*\,\mathrm{increasing}}\\ {\forall t \in [0,\inf _{\tau \ge 0}\{ \tau | S(\tau ) = 0 \}[:} \frac{\mathrm{d} \varphi _V^* (t)}{\mathrm{d}t} = f_V(t) \mathbbm {1}_{[0, \theta _I]} (1- \varphi _V^*(t))\\ \varphi _V^*(\inf _{\tau \ge 0}\{ \tau | S(\tau ) = 0 \}^-) = \varphi _V^*(\theta _I^-) = \varphi _V^*(\infty ). \end{array}\right. } \end{aligned}$$

  (22)

  The parameter $\theta _I$ is the unique solution of the equation:

  $$\begin{aligned} \frac{\varphi _I(\infty )- \varphi _I(\theta _I)}{1- \varphi _I(\theta _I)} = \frac{r_V}{r_I}. \end{aligned}$$

  (23)

Proof

We use individual cost in the form in Eq. (4). It may be noted that:

$$\begin{aligned} r_V- r_I\varphi _I(\infty ) + (r_I- r_V) \varphi _I(t) = r_V(1-\varphi _I(t)) + (r_V- r_I) (\varphi _I(\infty ) - \varphi _I(t)). \end{aligned}$$

(24)

Case (a) If $r_I\le r_V$, since $\varphi _I$ is an increasing function, the quantity in (24) is the sum of positive terms. The minimum attainable value is therefore zero and it obtained when $\mathrm{d} \varphi _V(t) = 0 \ \forall t$. Or $\varphi _V(0^-) = 0$ thus $\varphi _V(t) = 0$ $\forall t \ge 0$.

Cases (b) and (c) If $r_I\ge r_V$ let us compute

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d} t} \left[ r_V- r_I\varphi _I(\infty ) + (r_I- r_V) \varphi _I(t) \right] = (r_I- r_V) \frac{\mathrm{d} \varphi _I(t)}{\mathrm{d}t} \ge 0, \end{aligned}$$

(25)

(recall that $\varphi _I(t)$ is increasing) and moreover $r_V- r_I\varphi _I(\infty ) + (r_I- r_V) \varphi _I(0) = r_V- r_I\varphi _I(\infty )$ is positive as soon as $\varphi _I(\infty ) \le r_V/r_I$. To minimize the cost, vaccination should not occur when the term to integrate against $\mathrm{d}\varphi _V(t)$ is positive therefore there is no vaccination if $\varphi _I(\infty ) \le r_V/r_I$.

If $\varphi _I(\infty ) > r_V/r_I$, vaccination occurs for all t such that $r_V- r_I\varphi _I(\infty ) + (r_I- r_V) \varphi _I(t) \le 0$, or equivalently $\frac{\varphi _I(\infty ) - \varphi _I(t) }{1-\varphi _I(t)} \ge \frac{r_V}{r_I}$.

Moreover,

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \left[ \frac{\varphi _I(\infty ) - \varphi _I(t) }{1-\varphi _I(t)} \right] = - \frac{[1- \varphi _I(\infty )]}{[1-\varphi _I(t)]^2} \frac{\mathrm{d} \varphi _I(t)}{\mathrm{d}t} < 0. \end{aligned}$$

(26)

Then, $t \mapsto \frac{\varphi _I(\infty ) - \varphi _I(t) }{1-\varphi _I(t)}$ is a decreasing, continuous function from $\varphi _I(\infty )$ to zero. To minimize the cost, the vaccination should appear right at the beginning and last until the boundary of the domain ${\varOmega }$ is attained by the dynamics (1) or until time $\theta _I$, the unique solution of $\frac{\varphi _I(\infty ) - \varphi _I(\theta _I) }{1-\varphi _I(\theta _I)} = \frac{r_V}{r_I}$. Therefore, in order to minimize the integral, one has to set $\mathrm{d} \varphi _V= 0$ on $[\theta _I, \infty [$ and vaccinate on $[0, \theta _I[$ with maximal values coming first. Taking into account the constraint (21), we obtain Eq. (22) because $\int _0^{\inf _{\tau \ge 0}\{ \tau | S(\tau )=0 \}} \frac{u_\mathrm {max}}{S(t)}\hbox {d}t = \infty$. $\square$

Remark 3

There is no individual vaccination if $r_V/ r_I> 1- e^{-\beta /\gamma }$.

The next results applies when the individual vaccination can be unbounded, i.e., $\mathrm{d}\varphi _V$ can contain Dirac masses.

Theorem 2

(Case $u_\mathrm{max}=\infty$) The individual strategy $\varphi _V^*$ that minimizes the cost (4) with the system (1) is:

• (a) if $r_I\varphi _I(\infty ) < r_V$ then $\varphi _V^* \equiv 0$,

• (b) if $r_I\varphi _I(\infty ) > r_V$ then $\mathrm{d} \varphi _V^* = \delta _0$,

• (c) if $r_I\varphi _I(\infty ) = r_V$ then $\mathrm{d} \varphi _V^* = \alpha \delta _0$ with $\alpha$ arbitrary in [0, 1].

Proof

Case (a) If $\int _{0^-}^{\infty } r_V- r_I\varphi _I(\infty ) + (r_I- r_V) \varphi _I(t) \mathrm{d}\varphi _V(t)$ is positive, then the minimum is greater than $r_I\varphi _I(\infty )$. This value is attained only if $\int _{0^-}^{\infty } r_V- r_I\varphi _I(\infty ) + (r_I- r_V) \varphi _I(t) \mathrm{d}\varphi _V(t) = 0$ so $\varphi _V(t) = 0$ for all t.

Case (b) The strict monotony of the integrand $r_V- r_I\varphi _I(\infty ) + (r_I- r_V) \varphi _I(t)$ allows to write:

$$\begin{aligned}&\int _{0^-}^{\infty } r_V- r_I\varphi _I(\infty ) + (r_I- r_V) \varphi _I(t) \mathrm{d}\varphi _V(t) \\&\quad \ge \int _{0^-}^{\infty } \left[ r_V- r_I\varphi _I(\infty ) + (r_I- r_V) \varphi _I(t)\right] _{t=0^-} \mathrm{d}\varphi _V(t) \\&\quad = \left[ r_V- r_I\varphi _I(\infty ) \right] \int _{0^-}^{\infty } \mathrm{d}\varphi _V(t) \ge r_V- r_I\varphi _I(\infty ), \end{aligned}$$

where we used $\varphi _V(\infty )\le 1$ and $r_V- r_I\varphi _I(\infty ) \le 0$. This gives a lower bound for the minimum. The bound is attained when both inequalities become equalities that is $\mathrm{d} \varphi _V(t)$ is the Dirac mass in 0.

Case (c) The difference with the previous case is that the last term $r_V- r_I\varphi _I(\infty )$ is 0. Therefore, the last inequality is always satisfied. We obtain the conclusion. $\square$

Appendix 4: Equilibrium Strategy: The Undiscounted Case

We set ${\mathcal {D}}=0$.

Theorem 3

(Case $u_\mathrm{max}<\infty$) Consider admissible individual strategies as in Theorem 1. Then:

• (a) If $r_V\ge r_I$ or $r_V< r_I$ and $I_{0^-}+ r_V/ r_IS_{0^-}+(\gamma /\beta ) \ln (1-r_V/r_I) \le 0$ then the unique equilibrium is $U=0=\varphi _V$.

• (b) Otherwise consider the dynamics $(Y_1^{\infty }, Y_2^{\infty })$ starting from $S_{0^-}, I_{0^-}$ with $\mathrm{d}U= u_\mathrm{max} \mathrm{d}t$ at all times until $S(t) =~0$. Let $\theta ^{u_\mathrm{max}}(S_{0^-}, I_{0^-})$ be the first time when this dynamics touches the ensemble of curves:

  $$\begin{aligned} \left\{ (S,I) \in \overline{{\varOmega }} \left| I+ (r_V/ r_I) S+(\gamma /\beta ) \ln (1-r_V/r_I)= 0 \right. \right\} \cup \left\{ (S,I) \in \overline{{\varOmega }} \Big |S=0\right\} .\nonumber \\ \end{aligned}$$

  (27)

  Then, the unique equilibrium is:

  $$\begin{aligned} \mathrm{d}U(t)= & {} u_\mathrm{max}\mathbbm {1}_{[0, \theta ^{u_\mathrm{max}}(S_{0^-}, I_{0^-})]}(t) \mathrm{d}t, \end{aligned}$$

  (28)
  $$\begin{aligned} {\frac{\mathrm{d}\varphi _V(\mathrm{t})}{\mathrm{\mathrm{d}t}}}= & {} (1-\varphi _V(t)) {\mathrm{f}_\mathrm{V}(t) }\mathbbm {1}_{[0, \theta ^{u_\mathrm{max}}(S_{0^-}, I_{0^-})]}(t). \end{aligned}$$

  (29)

Proof

Case (a) If $r_V> r_I$ then any optimal individual strategy is $\varphi _V=0$ and the compatibility relation (9) imply $U=0$. Therefore, the only possible equilibrium in this case is $U=0=\varphi _V$. It is easy to see that this is effectively an equilibrium.

If $r_V\le r_I$ and $\zeta (S_{0^-}, I_{0^-}) \le (r_V/r_I) S_{0^-}$, from Eqs. (18) and (26) it follows that an individual strategy that vaccinates cannot be optimal, thus $\varphi _V=0$. As before we obtain the unique equilibrium $U=0=\varphi _V$.

Case (b) Since $\zeta (S_{0^-}, I_{0^-}) > r_V/r_IS_{0^-}$ any optimal individual strategy must satisfy (22). Therefore, from the compatibility relation (9) we obtain $\mathrm{d}U(t) = u_\mathrm{max}\mathbbm {1}_{[0, \theta ]}(t)$ for some $\theta \ge 0$. We have to find $\theta$ such that $\theta$ is solution of (23) for $\mathrm{d}U(t) = u_\mathrm{max}\mathbbm {1}_{[0, \theta ]}(t)$. This is a fixed point equation.

Let $(S,I)$ be the solution of the system (1) with $\mathrm{d}U(t) = u_\mathrm{max}\mathbbm {1}_{[0, \theta ]}(t)$. Since $\mathrm{d}U=0$ on $[\theta ,\infty ]$ by Eq. (18), any $\theta$ solution of (23) is also solution of

$$\begin{aligned} \zeta (S(\theta ), I(\theta )) = r_V/r_IS(\theta ). \end{aligned}$$

(30)

But $(S, I)= (Y_1^{\infty }, Y_2^{\infty })$ for $t \le \theta$, thus:

$$\begin{aligned} \frac{\zeta (S(\theta ), I(\theta ))}{S(\theta )} = \frac{\zeta (Y_1^{\infty }(\theta ), Y_2^{\infty }(\theta ))}{Y_1^{\infty }(\theta )}. \end{aligned}$$

(31)

Therefore, any $\theta$ that represents an equilibrium is also solution of the equation:

$$\begin{aligned} \frac{\zeta (Y_1^{\infty }(\theta ), Y_2^{\infty }(\theta ))}{Y_1^{\infty }(\theta )} = \frac{r_V}{r_I}. \end{aligned}$$

(32)

But,

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t} \left[ \frac{\zeta (Y_1^{\infty }(t), Y_2^{\infty }(t))}{Y_1^{\infty }(t)} \right] \\&\quad = \frac{1}{(Y_1^{\infty }(t))^2} \left[ \left( \frac{\partial \zeta }{\partial S} \frac{\mathrm{d} Y_1^{\infty }(t)}{\mathrm{d} t} + \frac{\partial \zeta }{\partial I} \frac{\mathrm{d} Y_2^{\infty }(t)}{\mathrm{d}t} \right) Y_1^{\infty }(t) - \zeta \frac{\mathrm{d} Y_1^{\infty }(t)}{\mathrm{d} t} \right] \\&\quad = \frac{(\zeta - Y_1^{\infty }(t))(\zeta u_\mathrm{max}+ \beta Y_1^{\infty }(t) Y_2^{\infty }(t)(\zeta - Y_1^{\infty }(t) + \gamma /\beta ))}{(\gamma / \beta ) (Y_1^{\infty }(t))^2 (1+\beta /\gamma (\zeta -Y_1^{\infty }(t)))} < 0, \end{aligned}$$

because $\zeta < S$ and $\zeta > S- \gamma / \beta$ (see Laguzet and Turinici 2015 for details and the expressions of the partial derivative of $\zeta$).

Thus, if (32) has a solution, then this solution is unique. Therefore, in any case at most one equilibrium exists. Under the hypothesis $\zeta (S_{0^-}, I_{0^-}) < \frac{r_V}{r_I} S_{0^-}$ Eq. (32) does have a solution so $\theta$ is also solution of Eq. (30), and this is the equilibrium. $\square$

Theorem 4

(Case $u_\mathrm{max}=\infty$) The equilibrium is:

• (a) If $r_V\ge r_I$ or $r_V< r_I$ and $I_{0^-}+ (r_V/ r_I) S_{0^-}+(\gamma /\beta ) \ln (1-r_V/r_I)\le 0$ then the unique equilibrium is $\mathrm{d}U=0$ and $\mathrm{d}\varphi _V= 0$ (no vaccination).

• (b) If $I_{0^-}+ (\gamma /\beta ) \ln (1- r_V/ r_I) > 0$ then the unique equilibrium is $\mathrm{d}U=\delta _0 S_{0^-}$ and $\mathrm{d}\varphi _V= \delta _0$ (total instantaneous vaccination).

• (c) Otherwise the unique equilibrium is $\mathrm{d}U= \alpha ^* \delta _0$ and $\mathrm{d}\varphi _V= (\alpha ^*/S_{0^-}) \delta _0$ (partial instantaneous vaccination) with $\alpha ^* = r_V((I_{0^-}+ r_V/r_IS_{0^-}+ \gamma /\beta )\ln (1-r_V/r_I))/r_I$.

Proof

Previous results indicate that in the unbounded case the individual optimal strategies are of the form $\mathrm{d} \varphi _V=\eta \delta _0$ thus $\mathrm{d}U=\eta S_{0^-}\delta _0$. Moreover, let $\alpha =\eta S_{0^-}$ and recall that $S(0)= S(0^-)- \alpha = S_{0^-}-\alpha$; moreover:

$$\begin{aligned} \frac{\mathrm{d}}{d \alpha } \left[ \frac{\zeta (S_{0^-}-\alpha , I_{0^-})}{S_{0^-}-\alpha } \right]&= \frac{1}{(S_{0^-}-\alpha )^2} \left[ \frac{\partial \xi }{\partial S} (-1) (S_{0^-}-\alpha ) - \xi (-1) \right] \\&= \frac{\zeta (\zeta - S_{0^-}+\alpha )}{\left( S_{0^-}- \alpha \right) ^2 \left( \gamma /\beta + \zeta - S_{0^-}+ \alpha \right) } < 0, \end{aligned}$$

so the function $\alpha \rightarrow \frac{\zeta (S_{0^-}-\alpha , I_{0^-})}{S_{0^-}-\alpha }$ is decreasing. Recall that $\zeta (S_{0^-}- \alpha , I_{0^-}) / (S_{0^-}- \alpha ) = r_V/r_I$ is the same as $I_{0^-}+ r_V/r_I(S_{0^-}- \alpha ) + \gamma / \beta \ln (1-r_V/ r_I) = 0$. Similar arguments as in the proof of the Theorem 3 apply and allow to reach the conclusion. $\square$

Proposition 1

The vaccination region of the (OS) strategy contains the vaccination region of the (EIS) strategy.

Proof

In the (OS) strategy, the vaccination only stops if $\partial _{S} \zeta \le \frac{r_V}{r_I}$ (see Laguzet and Turinici 2015 for details). Or $\partial _{S} \zeta = \frac{\zeta }{S} \frac{1}{1+ \frac{\beta }{\gamma } (\zeta - S)}$ and $\zeta - S\le 0$ so $1+ \frac{\beta }{\gamma } (\zeta - S) \le 1$. Then, $\frac{\zeta }{S} \le \partial _{S} \zeta \le \frac{r_V}{r_I}$ and the conclusion follows. $\square$

Appendix 5: Relation Between Global and Individual Cost

Lemma 1

Let $\varphi _V$ and U satisfy Eq. (9). Then, the individual cost is the average of the global cost, that is:

$$\begin{aligned} \frac{1}{S_{0^-}} J_\mathrm{soc}(S_{0^-}, I_{0^-}, U) = J_\mathrm{indi}(\varphi _V). \end{aligned}$$

(33)

Proof

We can write:

$$\begin{aligned} \int _{0^-}^{\infty } r_I(1- \varphi _V(t)) \mathrm{d} \varphi _I(t) = \int _{0^-}^{\infty } r_I(1-\varphi _V(t))(1-\varphi _I(t)) \left[ - \frac{\mathrm{d} S(t)}{S(t)} - \frac{\mathrm{d} U(t)}{S(t)} \right] \end{aligned}$$

(34)

because from (1) for $S(t) \ne 0$: $\frac{\mathrm{d} \varphi _I(t)}{1 - \varphi _I(t)} = \beta I(t) =- \frac{\mathrm{d} S(t)}{S(t)} - \frac{\mathrm{d} U(t)}{S(t)}$.

Furthermore, (9) implies:

$$\begin{aligned} \int _{0^-}^{\infty } r_V(1-\varphi _I(t)) \mathrm{d} \varphi _V(t) = \int _{0^-}^{\infty } r_V(1-\varphi _V(t))(1-\varphi _I(t)) \left[ \frac{\mathrm{d}U(t)}{S(t)}\right] . \end{aligned}$$

(35)

By summing Eqs. (34) and (35), we get:

$$\begin{aligned} J_\mathrm{indi}(\varphi _V)&= \int _{0^-}^{\infty } (1- \varphi _V(t))(1-\varphi _I(t)) \left[ -r_I\frac{\mathrm{d} S(t)}{S(t)} -r_I\frac{\mathrm{d}U(t)}{S(t)} + r_V\frac{\mathrm{d}U(t)}{S(t)} \right] \nonumber \\&= \int _{0^-}^{\infty } \frac{S(t)}{S_{0^-}} \left[ -r_I\frac{\mathrm{d} S(t)}{S(t)} -r_I\frac{\mathrm{d}U(t)}{S(t)} + r_V\frac{\mathrm{d}U(t)}{S(t)} \right] \nonumber \\&= \frac{1}{S_{0^-}} \int _{0^-}^{\infty } \left[ -r_I\mathrm{d} S(t) -r_I\mathrm{d}U(t) + r_V\mathrm{d}U(t) \right] , \end{aligned}$$

(36)

where we used $(1-\varphi _V(t))(1-\varphi _I(t)) = S(t)/S_{0^-}$. Using Eq. (16) and the definition of $J_\mathrm{soc}(S_{0^-}, I_{0^-}, U)$ in Eq. (10), we obtain the result. $\square$

Corollary 1

The average cost per person with the (OS) strategy is lower than the average cost per person with the (EIS) strategy.

Proof

Denote by $U^G$ the (OG) strategy and $\varphi _V^G$ its individual counterpart. Also denote by $\varphi _V^I$ the individual strategy in the (EIS) equilibrium and $U^I$ its global counterpart. By the definition of the optimality of $U^G$: $J_\mathrm{soc}(S_{0^-},I_{0^-}, U^G) \le J_\mathrm{soc}(S_{0^-},I_{0^-}, U^I)$. From Lemma 1 after simplification by $S_{0^-}$, we obtain: $J_\mathrm{indi}(\varphi _V^G) \le J_\mathrm{indi}(\varphi _{I}^{G})$ which is the conclusion. $\square$

Appendix 6: Some Properties of the Discounted Number of Infected

In this section and in “Appendix 7” we consider ${\mathcal {D}}>0$ and $u_\mathrm{max}=\infty$. Define $I^*= (r_V{\mathcal {D}})/((r_I- r_V) \beta )$ and $\zeta _d( S_{0^-}, I_{0^-}) = \int _{0^-}^{\infty } e^{-{\mathcal {D}}t} \beta S(t) I(t) \mathrm{d}t$ where $(S(t),I(t))$ is a non-vaccinating dynamics starting in $( S_{0^-}, I_{0^-})$. Denote also ${\mathcal {C}}_{r_V/ r_I}= \{ (S,I) \in {\varOmega }| \zeta _d(S,I) = (r_V/r_I) S\}$.

Lemma 2

• 1. The point $(0,I^*)$ is always below the curve ${\mathcal {C}}_{r_V/ r_I}$. In particular, either ${\mathcal {C}}_{r_V/ r_I}$ intersects the line $I=I^*$ in a point $(S^*,I^*) \in {\varOmega }$ or ${\mathcal {C}}_{r_V/ r_I}$ is completely above the line $I=I^*$.

• 2. When ${\mathcal {C}}_{r_V/ r_I}\cap \{(S,I) \in {\varOmega }|I= I^*\} \ne \emptyset$ , the non-vaccination dynamics starting from $(S,I) \in {\mathcal {C}}_{r_V/ r_I}$ is entering the domain $\{ (S,I) \in {\varOmega }| \zeta _d(S,I) \le (r_V/r_I) S\}$ if and only if $I\ge I^*$.

Proof

Item 1: It is enough to prove that $\lim _{\epsilon \rightarrow 0} \zeta _d(\epsilon ,I^*)/ \epsilon \le r_V/ r_I$. Let $(S(t),I(t))$ be the evolution of the system without vaccination starting from the point $(\epsilon ,I^*)$. From $I'(t) = (\beta S(t)-\gamma ) I(t)$, we obtain

$I(t) = I^*e^{\int _{0^-}^t (\beta S(u) - \gamma ) \mathrm{d}u} \in [I^*e^{- \gamma t}, I^*e^{(\beta \epsilon - \gamma ) t}]$ and from $S'(t) = (-\beta I(t)) S(t)$ we obtain $S(t) = \epsilon e^{\int _{0^-}^t - \beta I(u) \mathrm{d}u} \in [ \epsilon e^{\int _{0^-}^t - \beta I^*e^{(\beta \epsilon -\gamma ) u } \mathrm{d}u}$, $\epsilon e^{\int _{0^-}^t - \beta I^*e^{-\gamma u } \mathrm{d}u} ]$. For $\epsilon \rightarrow 0$:

$$\begin{aligned} \lim _{\epsilon \rightarrow 0}\frac{\zeta _d(\epsilon ,I^*)}{\epsilon }= & {} \int _{0^-}^\infty e^{-{\mathcal {D}}t} \beta I^*e^{-\gamma t } e^{-\beta I^*\int _{0^-}^t e^{-\gamma u}\mathrm{d}u}\mathrm{d}t \nonumber \\= & {} \int _{0^-}^\infty - e^{-{\mathcal {D}}t} \left( e^{-\beta I^*\int _{0^-}^t e^{-\gamma u} \mathrm{d}u} \right) ' \nonumber \\= & {} 1 - \int _{0^-}^\infty {\mathcal {D}}e^{-{\mathcal {D}}t -\beta I^*\int _{0^-}^t e^{-\gamma u}\mathrm{d}u} \mathrm{d}t\nonumber \\\le & {} 1 - \int _{0^-}^\infty {\mathcal {D}}e^{-{\mathcal {D}}t -\beta I^*t } \mathrm{d}t = r_V/r_I, \end{aligned}$$

(37)

where, in the last inequality, we used that $\int _{0^-}^t e^{-\gamma u} \mathrm{d}u \le t$.

Item 2: It is enough to show that the tangent in $(S^*,I^*)$ to ${\mathcal {C}}_{r_V/ r_I}$ coincides with the direction $(-\beta S^*I^*, \beta S^*I^*- \gamma I^*)$ (the dynamics of the system without vaccination). It is standard to prove (see Laguzet and Turinici 2015) that $\zeta _d$ satisfies the following equation:

$$\begin{aligned} \partial _S\zeta _d(S,I) (-\beta SI) + \partial _I\zeta _d(S,I) (\beta SI-\gamma I) - {\mathcal {D}}\zeta _d(S,I) +\beta SI= 0. \end{aligned}$$

(38)

On the other hand, the normal to the curve ${\mathcal {C}}_{r_V/ r_I}$ in $(S^*,I^*)$ is $(\partial _S\zeta _d(S^*,I^*)- r_V/r_I,\partial _I\zeta _d(S^*,I^*))$. A simple computation shows that the condition

$$\begin{aligned} (\partial _S\zeta _d(S^*,I^*)- r_V/r_I,\partial _I\zeta _d(S^*,I^*)) \perp (-\beta S^*I^*, \beta S^*I^*- \gamma I^*) \end{aligned}$$

(39)

reduces to (38) when $I=I^*$. $\square$

Appendix 7: Individual and Equilibrium Strategy with a Discount Factor

Let g be the following function:

$$\begin{aligned} g(t) = r_I({\varPhi }_I(t) - {\varPhi }_I(\infty ) ) + r_Ve^{- {\mathcal {D}}t} (1-\varphi _I(t)). \end{aligned}$$

(40)

The individual cost functional can then be written as:

$$\begin{aligned} J_\mathrm{indi}^{{\mathcal {D}}}(\varphi _V) = r_I{\varPhi }_I(\infty ) + \int _{0^-}^{\infty } g(t) \mathrm{d}\varphi _V(t). \end{aligned}$$

(41)

Since $I(t)$ is continuous with continuous derivative the same is true for g and

$$\begin{aligned} g'(t) = e^{-{\mathcal {D}}t} (1-\varphi _I) \Big [ (r_I- r_V) \beta I- r_V{\mathcal {D}}\Big ]. \end{aligned}$$

(42)

Therefore, the function g is increasing when $I< I^*$ and decreasing otherwise. On the other hand, $I$ decreases to zero at $\infty$ and may remain superior to $I^*$ on a bounded time interval. As such, depending on $(S_{0^-},I_{0^-})$ and U, the following possible behaviors can occur:

• g(t) is decreasing from $g(0) >0$ to $g(\infty )=0$

• g(t) is decreasing from g(0) to some value $g(t_1)$, increases from $g(t_1)$ to $g(t_2)$ and then decreases from $g(t_2)$ to $g(\infty )=0$.

The minimum of $J_\mathrm{indi}^{{\mathcal {D}}}(\varphi _V)$ is realized as following:

• (A) If $g(t) >0$ for all t then $\varphi _V=0$ (never vaccinate).

• (B) If $\inf _{t \ge 0} g(t)<0$ then the optimum is realized when $\mathrm{d} \varphi _V$ is a Dirac mass placed at the (unique) time $\tau _*$ such that $g(\tau _*)=\inf _{t \ge 0} g(t)$. In particular $\tau _* < \infty$.

• (C) Otherwise there exists an unique $\tau _*$ such that $g(\tau _*)=0$ and the optimal strategies are $\mathrm{d}\varphi _V= \alpha \delta _{\tau _*}$ ($\delta _{\tau _*}$ being the Dirac mass in $\tau _*$), $\alpha \in [0,1]$ arbitrary.

Remark 4

For the individual strategy described in item (B), it is optimal to delay vaccination to a latter time. Such a strategy is never encountered when ${\mathcal {D}}=0$, where vaccination occurs either at $t=0$ or never.

Finally, as in Eq. (18) we can prove that if $\mathrm{d}U=0$ on $[\tau , \infty [$, for any $t\ge \tau$ the value g(t) is positive / negative / null if and only if $\zeta _d(S(t),I(t))$ is less / larger / equal to $(r_V/r_I) S(t)$.

Consider the following notations:

• (I) When, with the notations of Lemma 2, a point $(S^*,I^*) \in {\mathcal {C}}_{r_V/ r_I}$ exists let $S^{**}$ be the unique solution in $[\gamma /\beta ,1]$ of the equation: $x - (\gamma /\beta ) \ln (x) = I^*+ S^*- (\gamma /\beta ) \ln (S^*)$. Then, the domain ${\varOmega }$ is divided in three subdomains: ${\varOmega }_i= \{ (S,I) \in {\varOmega }| \zeta _d(S,I) > (r_V/r_I) S, I> I^*\}$, ${\varOmega }_d=\{ (S,I) \in {\varOmega }| I< I^*, I+S- (\gamma /\beta ) \ln (S) > I^*+ S^*- (\gamma /\beta ) \ln (S^*) \}$, ${\varOmega }_n = {\varOmega }\setminus \overline{{\varOmega }_i \cup {\varOmega }_d }$.

• (II) When ${\mathcal {C}}_{r_V/ r_I}$ is above the line $I=I^*$, ${\varOmega }_i= \{ (S,I) \in {\varOmega }| \zeta _d(S,I) > (r_V/r_I) S\}$, ${\varOmega }_n= \{ (S,I) \in {\varOmega }| \zeta _d(S,I) < (r_V/r_I) S\}$.

Theorem 5

Let $(S_{0^-},I_{0^-}) \in {\varOmega }$; the unique equilibrium of the individual–societal vaccination is the following:

• (a) If $(S_{0^-}, I_{0^-}) \in {\varOmega }_n$ then $\mathrm{d}U=0$ and $\mathrm{d}\varphi _V= 0$ (no vaccination).

• (b) If $(S_{0^-}, I_{0^-}) \in {\varOmega }_i$ let $\alpha \in [0,1]$ be the maximum value such that $( S_{0^-}- \alpha , I_{0^-}) \in \overline{{\varOmega }_i}$. Then, $\mathrm{d}U= \alpha \delta _0$ and $\mathrm{d}\varphi _V= (\alpha /S_{0^-}) \delta _0$ (partial or total instantaneous vaccination).

• (c) If $(S_{0^-}, I_{0^-}) \in {\varOmega }_d$ let $\tau _*$ be the time at which the system (without vaccination) evolving from $(S_{0^-}, I_{0^-})$ reaches the line $I=I^*$. Then, $\mathrm{d}U=(S(\tau _*^-)-S^*) \delta _{\tau _*}$ and $\mathrm{d}\varphi _V= (S(\tau _*^-)/S^*-1) \delta _{\tau _*}$ (vaccination after waiting the time $\tau _*$).

Proof

We will consider only the more involved situation when a point $(S^*,I^*) \in {\mathcal {C}}_{r_V/ r_I}$ exists.

Recall that the evolution of the system without vaccination satisfies $I+S- (\gamma /\beta ) \ln (S) = cst$. Therefore, the frontier of ${\varOmega }_d$ and ${\varOmega }_n$ is a trajectory of the system without vaccination. Let us consider the global vaccination strategy U given in this Theorem. This strategy does not vaccinate in domain ${\varOmega }_n$, vaccinates (instantaneously) in domain ${\varOmega }_i$ and when the evolution starts in domain ${\varOmega }_d$ it waits to reach the line $I=I^*$; at that time it vaccinates until reaching the point $(S^*,I^*)$. This dynamics is illustrated in Fig. 7. In order to prove that this is effectively an equilibrium, we still have to prove that the best individual policies $\varphi _V$ are coherent with U.

But the properties of the function g(t) show that g(t) is positive in ${\varOmega }_n$: Therefore, for a starting point $(S_{0^-},I_{0^-})\in {\varOmega }_n$, the best individual strategy is to never vaccinate.

When the starting point $(S_{0^-},I_{0^-}) \in {\varOmega }_i$, the instantaneous vaccination makes it arrive at time 0 on the boundary ${\varOmega }_n$ and ${\varOmega }_i$; therefore, $g(0^-)=g(0)=0$. Optimal individual strategies are $\eta \delta _0$ with $\eta \in [0,1]$; among those only one is coherent with U (the one described in item (b)).

Finally, when the starting point $(S_{0^-},I_{0^-}) \in {\varOmega }_d$, the free (non-vaccination) evolution makes it arrive at some point $(S(\tau _*^-), I^*)$. Then, at time $\tau _*$ it reaches the point $(S^*,I^*)$ thus $g(\tau _*)= g(\tau _*^-)=0$. But before $\tau _*$ the coordinate $I$ was inferior to $I^*$; thus, g(t) was decreasing to zero during this time. Then, all $\eta \delta _{\tau _*}$, $\eta \in [0,1]$ will be optimal strategies. Among those, only one value of $\eta$ is compatible with U. Thus, the strategies proposed in this Theorem are equilibrium strategies. Uniqueness is proved as in Theorems 1 and 2. $\square$

Remark 5

For ${\mathcal {D}}> 0$ and $u_\mathrm{max}< \infty$, we were not able to find an analytic expression for the domains ${\varOmega }_i$, ${\varOmega }_n$ and ${\varOmega }_d$. The individuals, being aware of the shortage of vaccines, will wait in line in advance to be vaccinated by the optimal time; it is possible to obtain the corresponding Hamilton–Jacobi–Bellmann equilibrium equation, but the equation has to be solved numerically.