A Model for Interstitial Drainage Through a Sliding Lymphatic Valve

Abstract

This study investigates fluid flow and elastic deformation in tissues that are drained by the primary lymphatic system. A model is formulated based on the Rossi hypothesis that states that the primary lymphatic valves, which are formed by overlapping endothelial cells around the circumferential lining of lymphatic capillaries, open in response to swelling of the surrounding tissue. Tissue deformation and interstitial fluid flow through the tissue are treated using the Biot equations of poroelasticity and, the fluid flux (into the interstitium) across the walls of the blood capillaries, is assumed to be linearly related to the pressure difference across the walls via a constant of proportionality (the vascular permeability). The resulting model is solved in a periodic domain containing one blood capillary and one lymphatic capillary starting from a configuration in which the tissue is undeformed. On imposition of a constant pressure difference between blood and lymphatic capillaries, the solutions are found to settle to a steady state. Given that the magnitude of pressure fluctuations in the lymphatic system is much smaller than this pressure difference between blood and lymph, it is postulated that the resulting steady- state solution gives a good representation of the state of the tissue under physiological conditions. The effects of changes to the Young’s modulus of the tissue, the blood-lymphatic pressure difference, vascular permeability and valve dimensions on the steady state are investigated and discussed in terms of their effects on oedema in the context of age- and pregnancy-related changes to the body.

Appendix: Numerical Solution of the Model Using Comsol

Here we describe how we use the finite element package Comsol Multiphysics (CM) to solve the model formulated in Sect. 2. At its most basic, this comprises of comparing the poroelasticity equations defined in CM to Eqs. (7) and (11) and interpreting the boundary conditions (18)–(31) in a form appropriate for CM and then solving for the solid matrix deformations and the interstitial fluid flow.

1.1 The Poroelastic Equations

CM has a poroelastic module that can be used to find numerical solutions to Biot’s equations. This couples together a Darcy’s Law interface (for the flow) to a solid mechanics interface (for the mechanical deformations), which we describe below.

1.1.1 Darcy’s Law Interface

This is used to determine fluid motion through a porous medium. Darcy’s law states that the fluid flux ($\mathbf Q ^{f}$) is linearly related to the pressure gradient in the medium ($\nabla P$) via the relation

$$\begin{aligned} \mathbf Q ^{f}=-\frac{\kappa }{{\mu }}\nabla P, \end{aligned}$$

(49)

where ${\mu }$ is fluid viscosity and $\kappa$ the permeability of the porous medium (for consistency with Sect. 2 $K=\kappa /\upmu$). This is solved together with the fluid continuity equation, which is provided by the CM Poroelasticity Interface

$$\begin{aligned} \nabla \cdot (\mathbf v ^{f})=- \alpha _{b}\frac{\partial }{\partial t}(\nabla \cdot \mathbf u ), \end{aligned}$$

(50)

where for consistency with Sect. 2, we set the Biot-Willis coefficient $\alpha _b=1$.

1.1.2 Solid Mechanics Interface

Following the small displacement assumption, the normal strain components and the shear strain components, $\epsilon _{ij}$, are given from the deformations, $u_{i}$, via

$$\begin{aligned} \epsilon _{ij}=\frac{1}{2}\left( \frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right) . \end{aligned}$$

(51)

and, since we assume plane strain ${\varvec{u}}=(u_1(x_1,x_2), u_2(x_1,x_2),0)$, it follows that $\epsilon _{13}=\epsilon _{23}=\epsilon _{33}=0$.

For a poroelastic material, the stress tensor ($\sigma _{ij}$) is related to the strain tensor by the standard linear constitutive relation $\sigma _{ij}=D_{ijkl} \epsilon _{kl}-P \alpha _b \delta _{ij}$ where the term $-P \alpha _b \delta _{ij}$ is added to account for the pore pressure (here $D_{ijkl}$ is entered into the solid mechanics interface). For isotropic materials, this can be reduced [see e.g. Holmes (2009)] to the form

$$\begin{aligned} \sigma _{ij}=\lambda e_{kk} \delta _{ij} +2 \mu e_{ij} -P \alpha _b \delta _{ij}, \ \text{ where } \ \lambda =\frac{E \nu }{(1+\nu )(1-2\nu )}, \ \mu = \frac{E}{2 (1+\nu )},\nonumber \\ \end{aligned}$$

(52)

and $E$ is Young’s modulus and $\nu$ is the Poisson’s ratio. Under the assumptions of plane strain $\sigma _{13}=\sigma _{31}=0$ and the force balance equations (that are entered into the structural mechanics module) are

$$\begin{aligned} \frac{\partial \sigma _{11}}{\partial x_{1}}+\frac{\partial \sigma _{12}}{\partial x_{2}}= & {} 0, \end{aligned}$$

(53)

$$\begin{aligned} \frac{\partial \sigma _{21}}{\partial x_{1}}+\frac{\partial \sigma _{22}}{\partial x_{2}}= & {} 0. \end{aligned}$$

(54)

The stresses playing a role in the force balance equation are related to the nonzero strain tensor components via

$$\begin{aligned} \left[ \begin{array}{c} \sigma _{11} \\ \sigma _{22} \\ \sigma _{12} \end{array} \right] = \frac{E}{(1+\nu )(1-2\nu )} \left[ \begin{array}{ccc} 1-\nu &{} \nu &{} 0\\ \nu &{} 1-\nu &{} 0 \\ 0 &{} 0 &{} {1-2\nu } \end{array} \right] \left[ \begin{array}{c} \epsilon _{11} \\ \epsilon _{22} \\ \epsilon _{12} \end{array} \right] -\alpha _b P \left[ \begin{array}{c} 1 \\ 1 \\ 0 \end{array} \right] . \end{aligned}$$

(55)

The governing equations are (49)–(51) and (53)–(55), with $\alpha _b=1$, are identical to those in Sect. 2 (i.e. (7) and (11)).

1.1.3 Boundary Conditions

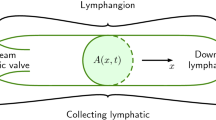
Here we convert our boundary conditions (on the sections of boundary illustrated in Fig. 3) to a form usable by CM.

The Lymphatic Capillary Wall $\partial \Omega _{4}$

The lymphatic capillary wall ($\partial \Omega _{4}$) is split into two parts, which are denoted by $\partial \Omega _{4a}$ and $\partial \Omega _{4b}$, see Fig. 3. Here the boundary $\partial \Omega _{4a}$ corresponds to the open section of the lymphatic valve (through which interstitial fluid flows), while $\partial \Omega _{4b}$ represents the endothelial cell wall (through which there is no flow). We assume that the open section of the lymphatic valve is located half way along the capillary boundary, as illustrated in Fig. 3.

We determine the positions of $\partial \Omega _{4a}$ and $\partial \Omega _{4b}$ by introducing two new variables

$$\begin{aligned} \theta _{s}= & {} \frac{\pi C_{\mathrm{crit}}}{4C(t)}, \end{aligned}$$

(56)

$$\begin{aligned} \theta _{f}= & {} \frac{\pi (2C(t)-C_{\mathrm{crit}})}{4C(t)}. \end{aligned}$$

(57)

Here $\theta _{s}$ and $\theta _{f}$ are the angles from the horizontal to the start of $\partial \Omega _{4a}$ and the end of $\partial \Omega _{4a}$, respectively. Thus, $\partial \Omega _{4a} = \{ \theta | \theta \in [\theta _s,\theta _f] \}$ and $\partial \Omega _{4b} = \{ \theta | \theta \in [0,\theta _s) \} \cup \{ \theta | \theta \in (\theta _f, \pi /2) \}$, where $\theta$ is the angle from the horizontal.

Using these angles in CM allows us to use a single flow boundary condition on $\partial \Omega _4$ and still incorporate the valve mechanics. We determine $C(t)$ by evaluating the boundary integral $C(t)=\int _{\partial \Omega _{4}(t)} \hbox {d}S$. The assumption that the lymphatic valve is closed when $C(t)<C_{\mathrm{crit}}$, and open when $C(t)>C_{\mathrm{crit}}$ implies there is no flow into the lumen if $C(t)<C_{\mathrm{crit}}$ and that fluid flows into the lumen only through $\partial \Omega _{4a}$ when $C(t)>C_{\mathrm{crit}}$. The boundary condition is implemented in CM by the command

$$\begin{aligned} \nabla P \cdot \mathbf n = (\nabla P \cdot \mathbf n + P - P^{l})\times \text{ if }(\theta _{s}<\theta <\theta _{f},1,0). \end{aligned}$$

(58)

This implies that

$$\begin{aligned} P= & {} P^{l} \quad \text{ on } \quad \mathbf x \in \partial \Omega _{4a} \ (i.e.\ \ \ \theta _{s}<\theta <\theta _{f}), \end{aligned}$$

(59)

$$\begin{aligned} \nabla P\cdot \mathbf n= & {} 0 \quad \text{ on } \quad \mathbf x \in \partial \Omega _{4b} \ (i.e.\ \ 0<\theta <\theta _{s} \ \ \text{ and } \ \ \pi /2>\theta >\theta _{f}),~~~~~~~ \end{aligned}$$

(60)

where $P^{l}$ is the fluid pressure of the lymphatic lumen. It is thus equivalent to (18)–(19), the conditions derived in Sect. 2.

The Blood Capillary Wall, Boundary $\partial \Omega _{1}$

The blood capillary wall is permeable to fluid, but provides a resistance to it. We use the boundary condition Pervious Layer in CM to model the flow through this wall. This describes a mass flux through a semi-pervious layer connected to an external fluid source at given pressure ($P^{b}$) and is equivalent to

$$\begin{aligned} \frac{\kappa }{\mu }\nabla P\cdot \mathbf n = L_{p}(P-P^{b}) \quad \text{ on } \quad \mathbf x \in \partial \Omega _{1}, \end{aligned}$$

(61)

and so, where ${\kappa }/{\mu }=K$, is identical to (20).

Remaining Edges of the Periodic Tile, Boundaries $\partial \Omega _{2}$, $\partial \Omega _{3}$, $\partial \Omega _{5}$ and $\partial \Omega _{6}$

The conditions (22), namely

$$\begin{aligned} \nabla P \cdot \mathbf n =0 \quad \text{ on } \quad \mathbf x \in \partial \Omega _{2}\cup \partial \Omega _{3} \cup \partial \Omega _{5}\cup \partial \Omega _{6}, \end{aligned}$$

(62)

are represented by the ‘No Flow’ feature in CM.

Solid Boundary Conditions

Since the periodic tile must remain square as it expands and contracts, its edges have to remain horizontal ($\partial \Omega _{2}$ and $\partial \Omega _{5}$) and vertical ($\partial \Omega _{3}$ and $\partial \Omega _{6}$). Without loss of generality we impose zero normal tissue displacement on boundaries $\partial \Omega _{2}$ and $\partial \Omega _{6}$, but allow them to deform freely in the tangential direction; the latter is equivalent to imposing zero tangential shear stress along the boundaries. These conditions are represented by the Roller condition in CM, that is

$$\begin{aligned} u_{2}=0 \quad \text{ and } \quad \sigma _{21}= & {} 0 \quad \text{ on } \quad \mathbf x \in \partial \Omega _{2}, \end{aligned}$$

(63)

$$\begin{aligned} u_{1}=0 \quad \text{ and } \quad \sigma _{12}= & {} 0 \quad \text{ on } \quad \mathbf x \in \partial \Omega _{6}. \end{aligned}$$

(64)

The edges $\partial \Omega _{3}$ and $\partial \Omega _{5}$ of the periodic tile deform freely in tangential direction (equivalent to tangential shear stress). However, both of these edges are displaced normally by a distance $u_{c}(t)$, which we shall calculate. The Prescribed Displacement feature in CM imposes a condition in which the position of the boundary of the solid matrix is prescribed in one direction and free to deform in the other direction, and in our case is used to impose the conditions

$$\begin{aligned} u_{1}=u_{c}(t) \quad \text{ and } \quad \sigma _{12}= & {} 0 \quad \text{ on } \quad \mathbf x \in \partial \Omega _{3}, \end{aligned}$$

(65)

$$\begin{aligned} u_{2}=u_{c}(t)\quad \text{ and } \quad \sigma _{21}= & {} 0 \quad \text{ on } \quad \mathbf x \in \partial \Omega _{5}, \end{aligned}$$

(66)

where $u_{c}(t)$ is calculated by

$$\begin{aligned} u_{c}(t) = \frac{1}{2L(t)}\left( \int \limits _{\partial \Omega _{1}\cup \partial \Omega _{4}} \ \left[ \int K \nabla P \cdot \mathbf n \ dt \right] \ \hbox {d}S -\int \limits _{\partial \Omega _{1}\cup \partial \Omega _{4}} \mathbf u \cdot \mathbf n \ \hbox {d}S\right) \!. \end{aligned}$$

(67)

Here $L(t)$ is the width of the periodic tile, which is a square, minus the radius of the lymphatic capillary.

The first integral term on the right-hand side of (67) cannot be calculated directly in CM because it is a time-dependent integral and the inbuilt time integrals in CM (timeint and timeavg) are only available during the results evaluation. In order to overcome this difficulty we introduce the new time-dependent variable, $T_{1}(t)$, defined as the solution to

$$\begin{aligned} \frac{d T_{1}}{d t} = \int \limits _{\partial \Omega _{1}\cup \partial \Omega _{4}} K \nabla P \cdot \mathbf n \ \hbox {d}S \quad \text{ and } \quad T_{1}(0)=0, \end{aligned}$$

(68)

so that

$$\begin{aligned} T_1(t)=\int \limits _{\partial \Omega _{1}\cup \partial \Omega _{4}} \ \left[ \int K \nabla P \cdot \mathbf n \ dt \right] \ \hbox {d}S. \end{aligned}$$

It follows from (19) and (20) that

$$\begin{aligned} \frac{d T_{1}}{d t} = \int \limits _{\partial \Omega _{1}} L_p(P-P^b) \ \hbox {d}S +\int \limits _{\partial \Omega _{4a}} K \nabla P \cdot \mathbf n \ \hbox {d}S. \end{aligned}$$

(69)

However, the tangential derivative of $P$ on $\partial \Omega _{4a}$ is zero (i.e. $\nabla P \cdot {\varvec{t}}|_{\partial \Omega _{4a}}=0$), since $P=P^l$ on this section of boundary. It follows that $\nabla P \cdot \mathbf n = |\nabla P|$ (here we expect $\nabla P \cdot {\varvec{n}}>0$ since the pressure acts outward on the boundary). We can thus rewrite (69) as

$$\begin{aligned} \frac{d T_{1}}{d t} = \int \limits _{\partial \Omega _{1}} L_p(P-P^b) \ \hbox {d}S +\int \limits _{\partial \Omega _{4a}} K \left( \left( \frac{\partial P}{\partial x_1} \right) ^2+\left( \frac{\partial P}{\partial x_2} \right) ^2 \right) ^{1/2} \ \hbox {d}S. \end{aligned}$$

(70)

Since both integrals can be integrated straightforwardly using CM the ODE for $T_1(t)$ can be solved by CM. This allows $u_c(t)$ to be determined, since the second integral term on the right-hand side of (67) is readily evaluated using CM.

Blood and Lymphatic Capillary, Boundaries $\partial \Omega _{1}$ and $\partial \Omega _{4}$

Boundary conditions (30)–(31) can be implemented straightforwardly in CM using the Boundary Load feature, which describes a boundary that experiences zero tangential stresses but on which the normal stresses are balanced by an external pressure.