A Modelling Framework for Gene Regulatory Networks Including Transcription and Translation

Abstract

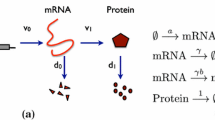
Qualitative models of gene regulatory networks have generally considered transcription factors to regulate directly the expression of other transcription factors, without any intermediate variables. In fact, gene expression always involves transcription, which produces mRNA molecules, followed by translation, which produces protein molecules, which can then act as transcription factors for other genes (in some cases after post-transcriptional modifications). Suppressing these multiple steps implicitly assumes that the qualitative behaviour does not depend on them. Here we explore a class of expanded models that explicitly includes both transcription and translation, keeping track of both mRNA and protein concentrations. We mainly deal with regulation functions that are steep sigmoids or step functions, as is often done in protein-only models. We find that flow cannot be constrained to switching domains, though there can still be asymptotic approach to singular stationary points (fixed points in the vicinity of switching thresholds). This avoids the thorny issue of singular flow, but leads to somewhat more complicated possibilities for flow between threshold crossings. In the infinitely fast limit of either mRNA or protein rates, we find that solutions converge uniformly to solutions of the corresponding protein-only model on arbitrary finite time intervals. This leaves open the possibility that the limit system (with one type of variable infinitely fast) may have different asymptotic behaviour, and indeed, we find an example in which stability of a fixed point in the protein-only model is lost in the expanded model. Our results thus show that including mRNA as a variable may change the behaviour of solutions.

Appendix

A system of the form (1) with autoregulation, i.e. when $\dot{x}_i$ depends on $Z_i,$ may contain so-called switching domains, threshold hyperplanes or intersections of hyperplanes where solutions may remain for a finite or infinite period of time. Several methods have been developed for dealing with the dynamics of the switched system (1) in switching domains (Filippov 1998; Plahte and Kjøglum 2005). Here we propose another method consisting in introducing in a special way a bigger system without autoregulation, which is a singular perturbation to the original system. In the absence of autoregulation, the problem of dealing with switching domains is avoided, and we have a system of the same class as before (i.e., a Glass network), though with twice as many variables. We show that this specifically chosen bigger system has the same dynamics in the singular perturbation limit as the system (1).

To this end, we introduce the following $2n$-dimensional system with $n$ extra artificial variables $y_i$:

$$\begin{aligned} \begin{array}{l} \dot{x}_i=F_i(Z)-G_i(Z)x_i,\qquad i=1,\ldots ,n,\\ \dot{y}_{i}=\frac{1}{\varepsilon }(\Sigma _{i}-\alpha _{i}y_{i}), \\ \end{array} \end{aligned}$$

(39)

where $Z=(Z_{1},\ldots ,Z_{n}),$ $Z_{i}=H(y_{i}, \theta _{y_i},q),$ $\Sigma _{i}=H(x_{i}, \theta _{x_i},q)$. Both steps now involve sigmoid functions, so we call it the sigmoid-sigmoid system (as opposed to the main body of the text, in which the expanded system was a sigmoid-linear system).

This might also be considered as a two-step model for gene regulation in which the first step is expression of a protein (suppressing the transcription and translation steps) and the second is a post-translational modification of the protein by a catalytic (and therefore sigmoidal) reaction.

We show that when the rates $\dot{y}_i$ are infinitely fast ($\varepsilon \rightarrow 0$), the original dynamics of $x_i$ of the type (1) are recovered for a specific choice of sigmoid function $\mathcal {S}$. Note that since $\dot{x}_i$ ($\dot{y}_i$) is independent of $\Sigma _i$ ($Z_i$), all switching hyperplanes $x_i=\theta _{x_i}$ ($y_i=\theta _{y_i}$) are ‘transparent’ (the solution just passes through them).

Let $q>0$ be fixed. Assume that $\varepsilon \rightarrow 0$. The system (39) represents a singular perturbation problem as $\varepsilon \rightarrow 0$ with the fast flow $y_{i}$ and the slow flow $x_i$. The stationary solution $y_{i}^*=\Sigma _{i}/\alpha _{i}$ of the fast flow is obtained from $\Sigma _{i}-\alpha _{i}y_{i}=0$. It is easy to check that the stationary solution $y_{i}^*$ is asymptotically stable for each fixed $x_i$. Thus, all assumptions of the Tikhonov theorem are fulfilled, and the slow flow is therefore governed by

$$\begin{aligned} \dot{x}_i=F_i(Z_{1}^*,\ldots , Z_{n}^*)-G_i(Z_{1}^*,\ldots , Z_{n}^*)x_i, \end{aligned}$$

(40)

where $Z_{i}^*=H(y_{i}^*, \theta _{y_i},q)=H(\Sigma _{i}/\alpha _{i},\theta _{y_i},q)=H(\Sigma _i, \theta _{y_i}\alpha _{i},q)$. If $\theta _{y_i}\alpha _{i}\ge 1,$ then $\Sigma _i<\theta _{y_i}\alpha _{i}$ and $H(\Sigma _i, \theta _{y_i}\alpha _{i},q)\rightarrow 0$ as $q\rightarrow 0$ for any finite $x_i.$ Assume now that the parameters are such that $\theta _{y_i}\alpha _{i}<1$.

If we think of $H(\Sigma _i, \theta _{y_i}\alpha _{i},q)$ as a function of $x_i,$ then from the properties of the Hill function

$$\begin{aligned} H(\Sigma _i, \theta _{y_i}\alpha _{i},q)=\widetilde{H}(x_i, H^{-1}(\theta _{y_i}\alpha _{i},\theta _{x_i},q),q)=\widetilde{H}(x_i, \widehat{\theta }_i,q), \end{aligned}$$

(41)

where $\widetilde{H}(x_i,\widehat{\theta }_i,q)$ is a sigmoid function (not necessarily a Hill function) of $x_i$ with the threshold at $\widehat{\theta }_i=H^{-1}(\theta _{y_i}\alpha _{i},\theta _{x_i},q)=\theta _{x_i}\left( \frac{\theta _{y_i}\alpha _i}{1-\theta _{y_i}\alpha _i}\right) ^q$ and the steepness parameter $q$ (see Fig. 6). Note that since $\theta _{y_i}\alpha _{i}<1,$ the new threshold $\widehat{\theta }_i\rightarrow \theta _{x_i}$ as $q\rightarrow 0$. In a functional form,

$$\begin{aligned} \widetilde{H}(x_i, \widehat{\theta }_i,q)=\frac{\Sigma _i^{1/q}}{\Sigma _i^{1/q}+(\theta _{y_i}\alpha _{i})^{1/q}}= \frac{x_i^{1/q^2}}{x_i^{1/q^2}+\theta _{y_i}^{1/q} \alpha _{i}^{1/q}(x_i^{1/q}+\theta _{x_i}^{1/q})^{1/q}}, \end{aligned}$$

(42)

where $\Sigma _i=H(x_i, \theta _{x_i},q)=\frac{x_i^{1/q}}{x_i^{1/q}+\theta _{x_i}^{1/q}}$.

Fig. 6

The functions $H(x_1,\theta _{y_1},q)$ (solid line) and $\widetilde{H}(x_1, \widehat{\theta }_1,q)$ (dashed line) with $\theta _{y_1}=1,$ $\theta _{x_1}=1,$ $q=0.1,$ $\alpha _1=0.6$ and $\widehat{\theta }_1=H^{-1}(\theta _{y_1}\alpha _{1},\theta _{x_1},q)\approx 1.04$

The system (40) can be rewritten as

$$\begin{aligned} \begin{array}{l} \dot{x}_i=F_i(\widetilde{Z}_1,\ldots ,\widetilde{Z}_n) -G_i(\widetilde{Z}_1,\ldots ,\widetilde{Z}_n)x_i,\qquad i=1,\ldots ,n,\\ \end{array} \end{aligned}$$

(43)

where $\widetilde{Z}_i=\widetilde{H}(x_i, \widehat{\theta }_i,q)$ with $\widehat{\theta }_i=H^{-1}(\theta _{y_i}\alpha _{i},\theta _{x_i},q)\rightarrow \theta _{x_i}$ as $q\rightarrow 0$.

We thus have proven the following result.

Theorem 4

Let $q>0$ be fixed. The solutions $x_i,$ $i=1,\ldots ,n,$ of (39) converge as $\varepsilon \rightarrow 0$ to the solution of the system (43) with the new sigmoid $\widetilde{H}$ given by (41) uniformly on any finite time interval.

We now compare the solutions of the system (43) with solutions of a corresponding system (44) below in which the sigmoids are Hill functions. Note that the $Z_i$ in (44) are functions of $x_i$, whereas the $Z_i$ in (39) are functions of $y_i$.

Theorem 5

Both the solution of the system (43) with a new sigmoid $\widetilde{Z}_i=\widetilde{H}(x_i, \widehat{\theta }_i,q)$ and the solution of the system

$$\begin{aligned} \begin{array}{l} \dot{x}_i=F_i({Z}_1,\ldots ,{Z}_n)-G_i({Z}_1,\ldots ,{Z}_n)x_i,\qquad i=1,\ldots ,n,\\ \end{array} \end{aligned}$$

(44)

with the Hill function $Z_i=H(x_i, \theta _{x_i},q)$ converge as $q\rightarrow 0$ to the same limit solution uniformly on any finite sequence of finite time intervals required for passing regular and switching domains, provided that the sequence of domains for (43) and (44) are the same for sufficiently small $q$.

Proof

Starting at an initial point, we consider one domain at a time, regular or singular, with the corresponding passage time. For a regular domain, the convergence on the corresponding time interval is obvious. For a singular domain, the convergence is proved below using the Tikhonov theorem and the a priori assumption that the limit solution is in a singular domain. Then convergence on each of these finite time periods can be naturally extended to any finite sequence of these finite periods.

Given an ordered set of switching variables $S\subset \{1,\ldots ,n\},$ the ordered set of regular variables $R=\{1,\ldots ,n\}\setminus S,$ and a corresponding Boolean vector $B_R$ of dimension $|R|,$ consider a motion of (43) confined to the switching domain $x_s=\widehat{\theta }_s,$ $s\in S,$ $\widetilde{Z}_r=B_r,$ $r\in R$.

Separating singular and regular parts of the system (43) gives

$$\begin{aligned} \begin{array}{l} \dot{x}_s=F_s(\widetilde{Z})-{G}_s(\widetilde{Z})x_s,\quad s\in S\\ \dot{x}_r=F_r(\widetilde{Z})-{G}_r(\widetilde{Z})x_r, \quad r\in R. \end{array} \end{aligned}$$

(45)

For $i\in S,$ since $\widetilde{Z}_i=H(\Sigma _i, \theta _{y_i}\alpha _{i},q)$ with $\Sigma _i=H(x_i, \theta _{x_i},q),$ by the chain rule,

$$\begin{aligned} \frac{d}{\hbox {d}x_i}\widetilde{Z}_i=\frac{d}{\hbox {d}\Sigma _i}H(\Sigma _i, \theta _{y_i}\alpha _{i},q)\cdot \frac{d}{\hbox {d}x_i}H(x_i, \theta _{x_i},q). \end{aligned}$$

(46)

Differentiating the inverse of the Hill Function,

$$\begin{aligned} y_i=H^{-1}(Z_i,\theta _{y_i},q)=\theta _{y_i}\left( \frac{Z_i}{1-Z_i}\right) ^q, \qquad 0<q\le 1, \qquad \end{aligned}$$

(47)

gives

$$\begin{aligned} \frac{d}{\hbox {d}y_i}H(y_i,\theta _{y_i},q)=\frac{1}{q}\cdot \frac{Z_i(1-Z_i)}{y_i}, \end{aligned}$$

(48)

where $y_i$ is given by (47). Using (48), Eq. (46) yields

$$\begin{aligned} \frac{d}{\hbox {d}x_i}\widetilde{Z}_i=\frac{1}{q}\cdot \frac{\widetilde{Z}_i(1-\widetilde{Z}_i)}{\Sigma _i}\cdot \frac{1}{q}\cdot \frac{{\Sigma }_i(1-{\Sigma }_i)}{x_i} =\frac{1}{q^2}\cdot \frac{\widetilde{Z}_i(1-\widetilde{Z}_i)(1-\Sigma _i)}{x_i}. \end{aligned}$$

(49)

Using the derivative of an inverse function in the left-hand side of the first equation in (45) and inserting (49) gives the equivalent system

$$\begin{aligned} \begin{array}{l} q^2\dot{\widetilde{Z}}_s=\frac{\widetilde{Z}_s(1-\widetilde{Z}_s)(1-\Sigma _s)}{x_s} \Big [F_S(\widetilde{Z})-{G}_s(\widetilde{Z})x_s\Big ], \quad s\in S,\\ \dot{x}_r=F_r(\widetilde{Z})-{G}_r(\widetilde{Z})x_r, \quad r\in R.\\ \end{array} \end{aligned}$$

(50)

Following the singular perturbation theory, the stretching transformation $\tau =\frac{t}{q^2}$ takes the first equation in (50) into

$$\begin{aligned} \begin{array}{l} \widetilde{Z}'_s=\frac{\widetilde{Z}_s(1-\widetilde{Z}_s)(1-\Sigma _s)}{x_s}\Big [F_s (\widetilde{Z}) -{G}_s(\widetilde{Z})x_s\Big ], \quad s\in S, \end{array} \end{aligned}$$

where the prime denotes differentiation with respect to the new ‘fast’ time $\tau$. Letting $q\rightarrow 0$ and assuming a priori that the limit solution belongs to the domain $x_s=\widehat{\theta }_s\rightarrow \theta _{x_s}$ (see lines before (42)), $s\in S,$ $\widetilde{Z}_r=B_r,$ $r\in R,$ i.e. that $\Sigma _s=H_s(x_s,\theta _{x_s},q )\rightarrow H_s(\theta _{x_s},\theta _{x_s},q )=1/2$ gives the boundary layer equation

$$\begin{aligned} \begin{array}{l} \widetilde{Z}^{'}_s=\dfrac{\widetilde{Z}_s(1-\widetilde{Z}_s)}{2\theta _{x_s}}\Big [F_s(\widetilde{Z}) -{G}_s(\widetilde{Z})\theta _{x_s}\Big ] \end{array} \end{aligned}$$

(51)

with $\widetilde{Z}_r=B_r$.

Similarly, see e.g. Plahte and Kjøglum (2005) for details, for the system

$$\begin{aligned} \begin{array}{l} \dot{x}_s=F_s({Z})-{G}_s({Z})x_s,\quad s\in S,\\ \dot{x}_r=F_r({Z})-{G}_r({Z})x_r, \quad r\in R, \end{array} \end{aligned}$$

(52)

with $Z_i=H(x_i, \theta _{x_i},q),$ the boundary layer equation (now in time $\frac{t}{q}$) is

$$\begin{aligned} \begin{array}{l} {Z}^{'}_s=\dfrac{{Z}_s(1-{Z}_s)}{\theta _{x_s}}\Big [F_s({Z}) -{G}_s({Z})\theta _{x_s}\Big ] \end{array} \end{aligned}$$

(53)

with ${Z}_r=B_r$. Clearly, the $\omega$-limit sets of (51) and (53) are the same. The slow dynamics of (45) and (52), which are governed by the asymptotic behaviour of the fast dynamics, are therefore the same. We have proved that the limit dynamics in both cases (the Hill function $H$ and the new sigmoid $\widetilde{H}$) are the same, at least on finite time intervals (because of the application of Tikhonov’s Theorem in both cases). $\square$

Note that the sequence of domains for (43) and (44) is guaranteed to be the same as long as no two variables become switching variables at the same time in the limit $q \rightarrow 0$, which is a set of initial conditions of measure zero.

1.1 Singular Stationary Points in the Sigmoid–Sigmoid System

In this section, we describe some general characteristics of fixed points in switching domains for the sigmoid–sigmoid system. We do not specify the value of $\varepsilon$ here, as we want to keep this analysis as general as possible. We will observe that the dynamics of the expanded system are consistent with the original system for some values of the additional parameters. We also show that the resulting structure of the expanded system makes stability of fixed points in switching domains much harder to achieve.

Consider the expanded system with $\varepsilon >0$ but not necessarily small. Recall that a trajectory of system (39) is on a wall corresponding to variable $x_{j}$ if $x_{j}=\theta _{x_j}$ and all other variables, $x_{i}$ with $i \ne j$ and $\, y_{i} \, \forall i$, are off their thresholds. If there is only 1 threshold for each gene, then each variable of an $n$-dimensional system has $2(n-1)$ walls, where each wall is defined by the other variables being above or below their respective thresholds. In systems without autoregulation, all walls are transparent, meaning that as a single variable, say $x_{j}$, reaches its threshold, $x_{j}=\theta _{x_j}$, it will pass through without its focal point, $\frac{F_{j}(Z)}{G_{j}(Z)}$, changing.

Remark 7

By Assumption 1, the focal point of a trajectory is always in a regular domain when the trajectory itself is in a regular domain. If a trajectory is in a switching domain, it is possible for its focal point to also be in a switching domain.

We analyse a $2M$-dimensional switching domain of (39). We have $M$ $x$-variables switching and $M$ $y$-variables switching.

Using singular perturbation theory, we arrive at the system:

$$\begin{aligned} \begin{array}{l} {{\Sigma }^{'}_1}=\frac{{{\Sigma }}_1(1-{{\Sigma }}_1)}{\theta _{x_1}}\Big (F_1({Z})-{G}_1({Z})\theta _{x_1}\Big )\\ :\\ {{\Sigma }^{'}_m}=\frac{{{\Sigma }}_m(1-{{\Sigma }}_m)}{\theta _{x_m}} \Big (F_m({Z})-{G}_m({Z})\theta _{x_m}\Big )\\ {{Z}^{'}_1}=\frac{{{Z}}_1(1-{{Z}}_1)}{\varepsilon \theta _{y_1}} \Big ({\Sigma _{1}}-\alpha _{1}\theta _{y_1})\Big )\\ :\\ {{Z}^{'}_m}=\frac{{{Z}}_m(1-{{Z}}_m)}{\varepsilon \theta _{y_m}} \Big ({\Sigma _{m}}-\alpha _{m}\theta _{y_m})\Big ).\\ \end{array} \end{aligned}$$

(54)

Theorem 6

Suppose $\mathcal {P}=\left( \Sigma ^{*}_1,\Sigma ^{*}_2,\ldots ,\Sigma ^{*}_m,Z^{*}_1,Z^{*}_2,\ldots ,Z^{*}_m\right)$ with $\Sigma ^{*}_j, Z^{*}_j \in (0,1)$ is a fixed point of (54) and let $J(\mathcal {P})$ denote the Jacobian matrix evaluated at $\mathcal {P}$. If any eigenvalue of $J(\mathcal {P})$ has nonzero real parts, then $\mathcal {P}$ is an unstable fixed point of the system, otherwise $\mathcal {P}$ is neutrally stable in the linearized system.

Proof

The Jacobian matrix evaluated at $\mathcal {P}$ is of the form $J(\mathcal {P})=\begin{bmatrix} 0&A\\ B&0 \end{bmatrix}$ since $\frac{\partial \Sigma ^{\prime }_i}{\partial \Sigma _{j}}=0 \, \forall \, i,j \, \in 1\ldots m$, and $\frac{\partial Z^{\prime }_i}{\partial Z_{j}}=0, \, \forall \, i,j \, \in 1\ldots m$. Block matrices of this type have eigenvalues coming in $\pm$ pairs. This can be demonstrated by showing that if $J(\mathcal {P})V=\lambda V$ with $V=\begin{bmatrix} u\\v\end{bmatrix}$, then $J(\mathcal {P})\begin{bmatrix} -u\\v\end{bmatrix}=-\lambda \begin{bmatrix} -u\\v\end{bmatrix}$. Therefore, for each eigenvalue $\lambda$ of $J(\mathcal {P})$, $-\lambda$ is also an eigenvalue. This implies that the fixed point $\mathcal {P}$ is unstable if $J(\mathcal {P})$ has at least one eigenvalue with nonzero real part, or $J(\mathcal {P}$) has only pure imaginary eigenvalues, making $\mathcal {P}$ neutrally stable in the linearized system.

Example 6

In the original Plahte–Kjøglum system (4), with $\gamma _{1}=0.6, \, \gamma _{2}=0.9$ and $\theta _{1}=\theta _{2}=1$, trajectories either end up at the stable fixed point in the threshold intersection, $x_{1}=\theta _1$ and $x_{2}=\theta _2$, or at the SSP with $x_{1}>\theta _1$ and $x_{2}=\theta _{2}$. The expanded Plahte–Kjøglum system then takes the form

$$\begin{aligned} \begin{array}{l} \dot{x}_1=Z_1+Z_2-2Z_1Z_2-\beta _1x_1\\ \dot{x}_2=1-Z_1Z_2-\beta _2x_2\\ \dot{y}_1=\frac{1}{\varepsilon }\left( \Sigma _1-\alpha _{1}y_{1}\right) \\ \dot{y}_2=\frac{1}{\varepsilon }\left( \Sigma _2-\alpha _{2}y_{2}\right) , \end{array} \end{aligned}$$

(55)

with $\beta _{1}=0.6, \, \beta _{2}=0.9$ and $\theta _{x_1}=\theta _{x_2}=\theta _{y_1}=\theta _{y_2}=1$.

Applying Theorem 6 and an eigenvalue analysis similar to that of Sect. 6, it can be shown that there are parameter values for the expanded system for which the threshold intersection no longer contains stable fixed points, which implies that the dynamics in the expanded system do not match those seen in the original system. This conclusion is independent of the chosen value for $\varepsilon >0$.

The other stable fixed point in the original Plahte–Kjøglum system, (4), is on the wall $\{x_{1}>\theta _{x_{1}},x_{2}=\theta _{x_{2}}\}$. We show that this point is stable in the expanded system (55) as well.

Let $x_{1}>\theta _{x_{1}}$ and $y_{1}>\theta _{y_{1}}$. Then $Z_1=\Sigma _1=1$ and the $x_2,y_2$ equations are independent of $x_1$ and $y_1$:

$$\begin{aligned} \begin{array}{l} \dot{x}_2=1-Z_2-\beta _2x_2,\\ \dot{y}_2=\frac{1}{\varepsilon }(\Sigma _2-\alpha _2y_2). \end{array} \end{aligned}$$

(56)

Applying the singular perturbation theory to (56) in a $\Delta$-vicinity of $(\theta _{x_1},\theta _{y_1})$ gives

$$\begin{aligned} \begin{array}{l} q\dot{\Sigma }_2=\frac{\Sigma _2(1-\Sigma _2)}{x_2}(1-Z_2-\beta _2x_2),\\ q\dot{Z}_2=\frac{Z_2(1-Z_2)}{\varepsilon y_2}(\Sigma _2-\alpha _2y_2). \end{array} \end{aligned}$$

(57)

In the limit $q\rightarrow 0,$ $x_2\rightarrow \theta _{x_{2}}$ and $y_2\rightarrow \theta _{y_{2}}$ and in fast time $\tau =t/q$

$$\begin{aligned} \begin{array}{l} {\Sigma }_2'=\frac{\Sigma _2(1-\Sigma _2)}{\theta _{x_{2}}} (1-Z_2-\beta _2\theta _{x_{2}}),\\ {Z}_2'=\frac{Z_2(1-Z_2)}{\varepsilon \theta _{y_{2}}} (\Sigma _2-\alpha _2\theta _{y_{2}}).\end{array} \end{aligned}$$

(58)

The stationary solution $\Sigma _2^*=\alpha _2\theta _{y_{2}},$ $Z_2^*=1-\beta _2\theta _{x_{2}}$ of (58) is neutrally stable.

Each of the nested closed curves $C^k$ and the corresponding periodic solution $\varphi ^k(\cdot )=(\Sigma _2^k,Z_2^k)$ can be associated with the invariant measure $\mu ^k$ on $[0,1]^{2}$ by

$$\begin{aligned} \mu ^k(A)=\frac{1}{\tau _{C^k}}\lambda (\{\tau \in [0,\tau _{C^k}]: \varphi ^k(\tau )\in A \}) \end{aligned}$$

for any measurable subset $A\subset [0,1]^{2},$ where $\lambda$ is the Lebesgue measure on the real line. Thus, there exist infinitely many invariant measures $\{\mu ^k\}$ of the equation (58). By Artstein’s theory Artstein (2002), Machina et al. (2013b) the variable $x_1$ is governed by the differential inclusion

$$\begin{aligned} \dot{x}_1\in \{ 1-\int \limits _{C^k}^{}Z_2d\mu ^k-\beta _1 x_1\quad | \quad \forall \mu ^k\}. \end{aligned}$$

The latter equation can be rewritten as

$$\begin{aligned} \dot{x}_1\in \{1-\frac{1}{\tau _{C^k}}\int \limits _0^{\tau _{C^k}}Z_2^k(t)\hbox {d}\tau -\beta _1 x_1\quad | \quad \forall k\}. \end{aligned}$$

(59)

Solving (58) for $Z_2$ gives

$$\begin{aligned} \begin{array}{l} {Z}_2=1-\beta _2\theta _{x_{2}}-\frac{\Sigma _2'\theta _{x_{2}}}{\Sigma _2(1-\Sigma _2)}.\\ \end{array} \end{aligned}$$

For any closed orbit $C^k$

$$\begin{aligned} Z_2^{av} = \frac{1}{\tau _{C^k}}\int \limits _0^{\tau _{C^k}}Z_2^k(t)\hbox {d}\tau= & {} \frac{1}{\tau _{C^k}}\int \limits _0^{\tau _{C^k}}(1-\beta _2\theta _{x_{2}}- \frac{\Sigma _2'\theta _{x_{2}}}{\Sigma _2(1-\Sigma _2)})\hbox {d}\tau \\= & {} 1-\beta _2\theta _{x_{2}}-\frac{1}{\tau _{C^k}} \int \limits _0^{\tau _{C^k}}\frac{\theta _{x_{2}}}{\Sigma _2(1-\Sigma _2)} \hbox {d}\Sigma _2 \\= & {} 1-\beta _2\theta _{x_{2}}. \end{aligned}$$

Thus from (59)

$$\begin{aligned} \dot{x}_1=1-Z_2^{av}-\beta _1 x_1, \end{aligned}$$

where $Z_2^{av}=Z_2^*=1-\beta _2\theta _{x_2},$ which is the same slow equation as for the original Plahte–Kjøglum system (Plahte and Kjøglum 2005).