A Global Convergence Result for Processive Multisite Phosphorylation Systems

Abstract

Multisite phosphorylation plays an important role in intracellular signaling. There has been much recent work aimed at understanding the dynamics of such systems when the phosphorylation/dephosphorylation mechanism is distributive, that is, when the binding of a substrate and an enzyme molecule results in the addition or removal of a single phosphate group and repeated binding therefore is required for multisite phosphorylation. In particular, such systems admit bistability. Here, we analyze a different class of multisite systems, in which the binding of a substrate and an enzyme molecule results in the addition or removal of phosphate groups at all phosphorylation sites, that is, we consider systems in which the mechanism is processive, rather than distributive. We show that in contrast to distributive systems, processive systems modeled with mass-action kinetics do not admit bistability and, moreover, exhibit rigid dynamics: each invariant set contains a unique equilibrium, which is a global attractor. Additionally, we obtain a monomial parametrization of the steady states. Our proofs rely on a technique of Johnston for using “translated” networks to study systems with “toric steady states,” recently given sign conditions for the injectivity of polynomial maps, and a result from monotone systems theory due to Angeli and Sontag.

Appendix: Obtaining the Nullspace of \(A^t_\kappa \) from (17)

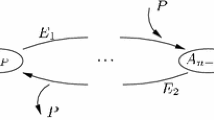
Here, we focus on the nullspace of $A^t_\kappa$ and explain how it can be obtained by studying the directed graph underling network (17), given in Fig. 1 below.

Fig. 1

Directed graph $G$ underlying the translated network (17)

Notation ($G^*$). For a directed graph $G$, we let $G^*$ denote the undirected graph obtained from $G$ by making each directed edge undirected (and allowing multiple edges in the resulting graph).

Definition 8.1

(Directed spanning tree/spanning tree rooted at node $j$). Let $j$ be a node of a directed graph $G$. A subgraph $T$ is a spanning tree (of $G$) rooted at $j$, if it satisfies the following:

• (a) $T$ contains all nodes of $G$,

• (b) the undirected graph $T^*$ is acyclic and connected, and

• (c) for every node $v\ne j$ of $T$, there exists a directed path from $v$ to $j$.

A subgraph is a directed spanning tree of $G$ if it is a spanning tree rooted at $j$, for some node $j$.

Remark 8.2

In a directed graph, a sink is a node that has no outgoing edges. For a spanning tree rooted at $j$, the unique sink is the node $j$. Any acyclic and connected subgraph that contains more than one sink is not a directed spanning tree.

Next, we identify the directed spanning trees of $G$ from Fig. 1. Note that $G$ is cyclic, and due to the unidirectional edges labeled $k_{2n+1}$ and $\ell _1$, $G$ can be traversed in the clockwise direction only.

Remark 8.3

(Acyclic, connected subgraphs of $G$ from Fig. 1). For a subgraph $T$ of $G$ that contains all nodes of $G$, the undirected graph $T^*$ is acyclic and connected if and only if $T$ satisfies the following properties (cf. Fig. 2):

• (i) there is a unique node $p$ such that $T$ contains neither the edge $p \rightarrow p+1$ nor the edge $p \leftarrow p+1$ (where $p+1:=1$ if $p=2n+2$).

• (ii) for all other nodes $q \ne p$, exactly one of the edges $q \rightarrow q+1$, and $q \leftarrow q+1$ is present in $T$.

Fig. 2

(Color figure online) a Subgraph obtained from $G$ by removing edges $p \rightarrow p+1$ and $p \leftarrow p+1$. To obtain a subgraph $T$ for which the undirected graph $T^*$ is acyclic and connected, choose one edge from each pair of reversible edges. By choosing all the blue edges, one obtains two directed paths ending at $j$: one connecting the nodes $p+1$,..., $j-1$ to $j$ and the other connecting $j+1$, ..., $n+1$ to $j$. No choice of edges, however, will connect any of the following nodes to $j$: $n+2$, ..., $2n+2$ and $1$, ..., $p$. Thus, any such subgraph will have at least two sinks. b Spanning tree $T_{j,p}$ (of $G$ from Fig. 1) rooted at $j$; this tree consists of two paths, one from $p$ to $j$ (green, counterclockwise) and one from $p+1$ to $j$ (red, clockwise)

Now, we can determine the directed spanning trees of $G$ (recall Definition 8.1):

Proposition 8.4

(Directed spanning trees of $G$ from Fig. 1). For the directed graph $G$ in Fig. 1, let $j$ and $p$ be integers such that

$$\begin{aligned} 1 \le j \le p \le n+1 \quad \mathrm{or } \quad n+2 \le j \le p \le 2n+2. \end{aligned}$$

(45)

Let $T_{j,p}$ be the subgraph of $G$ that contains all nodes of $G$ and for which the edges are comprised of

• (1) if $j \ne n+1, 2n+2$

  • (A) the clockwise path from node $p+1$ to $j$, and

  • (B) the counterclockwise path from $p$ to $j$ (cf. Fig. 2b).

• (2) if $j=n+1$ or $j=2n+2$, the clockwise path from node $j+1$ to $j$ (where $j+1:=1$ if $j=2n+2$).

Then, $T_{j,p}$ is a directed spanning tree rooted at node $j$ that does not contain the edges $p \rightarrow p+1$ or $p \leftarrow p+1$ (where $p+1:=1$ if $p=2n+2$). Conversely, every spanning tree of $G$ has this form.

Proof

Assume that $T_{j,p}$ is a subgraph as described in the proposition. By Definition 8.1 and Remark 8.3, it remains only to show that there exists a path from every node $v\ne j$ to $j$. Indeed, by points (1) and (4), every node belongs to a path that ends in $j$.

Conversely, let $T$ be a spanning tree of $G$ rooted at $j$. By Remark 8.3, there exists a node $p$ such that $T$ contains neither $p \rightarrow p+1$ nor $p \leftarrow p+1$, so it suffices to check that condition (45) holds and the edges of $T$ satisfy points (1) and (4). We first assume that $p$ violates condition (45). By symmetry between the two cases, we need only to consider the case when $1 \le j \le n+1$ and $p\in \{1, \dots , j-1\} \cup \{n+2, \dots , 2n+2\}$. If $p\in \{1, \dots , j-1\}$, then there is no path in $T$ from $p$ to $j$; similarly, if $p \in \{n+2, \dots , 2n+2\}$, then there is no path from $n+2$ to $j$ (cf. Fig. 2). Thus, $T$ is not a spanning tree rooted at $j$, which is a contradiction. Thus, $T$ must satisfy condition (45), so it remains only to show that it must satisfy points (1) and (4) as well. Indeed, in the first case (that is, if $j \ne n+1, 2n+2$), the paths (A) and (B) are the unique paths in $G$ that do not use $p \rightarrow p+1$ to reach $j$ from $p+1$ and $p$, respectively, and all nodes except $j$ lie on exactly one of these paths, so the two paths comprise the edges of $T$. Similarly, in the remaining case (if $j=n+1$ or $j=2n+2$), the clockwise path from node $j+1$ to $j$ is the unique path in $G$ from $j+1$ to $j$, and all nodes lie along the path (note that $j=p$ in this case). This completes the proof. $\square$

We note the following corollary of Proposition 8.4:

Corollary 8.5

For the directed graph $G$ in Fig. 1, the number of spanning trees rooted at $j$ is

• $n+2-j$, if $j\in \{1, \ldots , n+1\}$

• $2n+3 -j$, if $j\in \{n+2, \ldots , 2n+2\}$.

Consequently, the number of spanning trees rooted at $j$ is at most $n+1$.

Now, we turn to the kernel of $A_\kappa ^t$. In Corollary 5.1, we argued that $\ker (A_\kappa ^t)$ is spanned by a positive vector. This is a consequence of (Thomson and Gunawardena (2009a), Lemma 2), which built on the well-known Matrix-Tree Theorem of algebraic combinatorics (Stanley 1999, §5.6) and also gives an explicit formula for this vector. For this, we need some more notation.

Notation. Following Thomson and Gunawardena (2009a), for a directed spanning tree $T$ of an edge-labeled directed graph $G$, we denote by $L(T)$ the product of all edge labels in the spanning tree $T$:

$$\begin{aligned} L(T) := \prod _{y_i \overset{a}{\rightarrow } y_j \in T} a. \end{aligned}$$

(46)

Note that $L(T) > 0$, as it is a product of rate constants.

Proposition 8.6

Recall the spanning trees $T_{j,p}$ of $G$ from Fig. 1. For the matrix $\tilde{A}_{\kappa }^t$ displayed in (20) for the translated network (17), the nullspace is spanned by the positive vector $\rho \in {\mathbb {R}}_{+}^{2n+2}$ whose coordinates are given below

$$\begin{aligned} \rho _j ={\left\{ \begin{array}{ll} \displaystyle \sum _{p=j}^{n+1} L(T_{j,p}) &{} \mathrm{if~} 1\le j\le n+1 \\ \displaystyle \sum _{i=j-(n+1)}^{n+1} L(T_{j,n+1+i}) &{} \mathrm{if~} n+2 \le j \le 2n+2~. \end{array}\right. } \end{aligned}$$

(47)

The terms $L(T_{j,p})$ are defined in Eq. (48) below.

Proof

Proposition 8.4 and application of (Thomson and Gunawardena (2009a), Lemma 2) to $G$ from Fig. 1.

Next, we will compute the product $L(T_{j,p})$ associated with each spanning tree $T_{j,p}$ of $G$. To this end, we recall the labeling of reactions between adjacent nodes $j$ and $j+1$ for $1\le j \le n-1$:

For a node $j$ with $n+2\le j \le 2n+1$, we write $j$ as $j=n+1 +i$ (so, $1\le i \le n+1$) and recall the labeling of reactions between adjacent nodes $j$ and $j+1$:

Now, we use Proposition 8.4 to compute $L(T_{j,p})$, for a spanning tree $T_{j,p}$ of $G$:

• if $1\le j\le n$, the tree $T_{j,p}$ splits into four paths

  • (a) $p+1 \rightarrow \cdots \rightarrow n+2$, with product of edge labels $k_{2n+1}\, \prod _{i=p+1}^n k_{2i-1} = \prod _{i=p+1}^{n+1} k_{2i-1}$,

  • (b) $n+2\rightarrow \cdots \rightarrow 1$, with product of edge labels $\ell _1 \prod _{i=1}^n, \ell _{2(n+1-i)+1} = \prod _{i=1}^{n+1} \ell _{2(n+1-i)+1}$,

  • (c) $1\rightarrow \cdots \rightarrow j$, with product of edge labels $\prod _{i=1}^{j-1} k_{2i-1}$,

  • (d) $p\rightarrow \cdots \rightarrow j$, with product of edge labels $\prod _{i=j}^{p-1} k_{2i}$.

• if $j=n+1$ (so, $p=n+1$, by Proposition 8.4), the tree $T_{j,p}$ splits into two paths

  • (a) $n+2\rightarrow \cdots \rightarrow 1$, with product of edge labels $\prod _{i=1}^{n+1} \ell _{2(n+1-i)+1}$, as in (b) in the previous case.

  • (b) $1\rightarrow \cdots \rightarrow n+1$, with product of edge labels $\prod _{i=1}^n k_{2i-1}$.

• if $n+2\le j\le 2n+1$, write $j = n+1 + j_0$ and $p= n+1+p_0$, and then split $T_{j,p}$ into four paths (cf. Fig. 2b):

  • (a) $p+1 \rightarrow \cdots \rightarrow 1$, with product of edge labels $\ell _1 \prod _{i=p_0+1}^n \ell _{2(n+1-i)+1} = \prod _{i=p_0+1}^{n+1} \ell _{2(n+1-i)+1}$,

  • (b) $1\rightarrow \cdots \rightarrow n+2$, with product of edge labels $k_{2n+1} \prod _{i=1}^n k_{2i-1} = \prod _{i=1}^{n+1} k_{2i-1}$,

  • (c) $n+2 \rightarrow \cdots \rightarrow j$, with product of edge labels $\prod _{i=1}^{j_0-1} \ell _{2(n+1-i)+1}$,

  • (d) $p\rightarrow \cdots \rightarrow j$, with product of edge labels $\prod _{i=j_0}^{p_0-1} \ell _{2(n+1-i)}$.

• if $j=2n+2$ (so, $p=2n+2$, by Proposition 8.4), the tree $T_{j,p}$ splits into two paths

  • (a) $1\rightarrow \cdots \rightarrow n+2$, with product of edge labels $\prod _{i=1}^{n+1} k_{2i-1}$, as in (b) in the previous case,

  • (b) $n+2\rightarrow \cdots \rightarrow 2n+2$, with product of edge labels $\prod _{i=1}^{n}\ell _{2(n+1-i)+1}$.

Thus, by definition (46), we obtain for $L(T_{j,p})$, where for $i_1<i_0$ we adopt the standard convention $\prod _{i=i_0}^{i_1} \alpha _i := 1$ for the empty product and, as before, $j_0 := j-(n+1)$ and $p_0 := p-(n+1)$:

$$\begin{aligned}&L(T_{j,p}) \nonumber \\&\quad ={\left\{ \begin{array}{ll} \displaystyle \prod _{i=1}^{n+1} \ell _{2(n+1-i)+1} \cdot \prod _{i=1}^{j-1} k_{2i-1} \cdot \prod _{i=j}^{p-1} k_{2i} \cdot \prod _{i=p+1}^{n+1} k_{2i-1} &{} \mathrm{if~} 1\le j\le n \\ \displaystyle \prod _{i=1}^{n+1} \ell _{2(n+1-i)+1} \cdot \prod _{i=1}^n k_{2i-1} &{} \mathrm{if~} j = n+1 \\ \displaystyle \prod _{i=1}^{n+1} k_{2i-1} \cdot \prod _{i=1}^{j_0-1} \ell _{2(n+1-i)+1} \cdot \prod _{i=j_0}^{p_0-1} \ell _{2(n+1-i)} \cdot \prod _{i=p_0+1}^{n+1} \ell _{2(n+1-i)+1} &{} \mathrm{if~} n+2 \le j \le 2n+1 \\ \displaystyle \prod _{i=1}^{n+1} k_{2i-1} \cdot \prod _{i=1}^{n}\ell _{2(n+1-i)+1} &{} \mathrm{if~} j = 2n+2. \end{array}\right. } \end{aligned}$$

(48)