Self-sustained Oscillations in Blood Flow Through a Honeycomb Capillary Network

Abstract

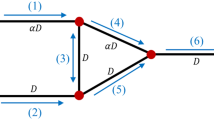
Numerical simulations of unsteady blood flow through a honeycomb network originating at multiple inlets and terminating at multiple outlets are presented and discussed under the assumption that blood behaves as a continuum with variable constitution. Unlike a tree network, the honeycomb network exhibits both diverging and converging bifurcations between branching capillary segments. Numerical results based on a finite difference method demonstrate that as in the case of tree networks considered in previous studies, the cell partitioning law at diverging bifurcations is an important parameter in both steady and unsteady flow. Specifically, a steady flow may spontaneously develop self-sustained oscillations at critical conditions by way of a Hopf bifurcation. Contrary to tree-like networks comprised entirely of diverging bifurcations, the critical parameters for instability in honeycomb networks depend weakly on the system size. The blockage of one or more network segments due to the presence of large cells or the occurrence of capillary constriction may cause flow reversal or trigger a transition to unsteady flow.

Appendix: Governing Equations

The discharge hematocrit, $H_\mathrm{D}$, is the ratio of the volumetric flow rate of the red blood cells, $Q_\mathrm{rbc}$, to that of the whole blood, $Q$: $H_\mathrm{D}\equiv Q_\mathrm{rbc}/{Q}$. The tube hematocrit, $H_\mathrm{T}$, is the volume fraction of the suspended red blood cells inside the tube and differs from the discharge hematocrit, $H_\mathrm{D}$, because the blood cell velocity is higher than the mean plasma velocity in capillary flow. The ratio of the tube hematocrit to the discharge hematocrit is related to the mean cell velocity, $V_\mathrm{rbc}$, by $\chi \equiv H_\mathrm{T}/H_\mathrm{D} = U_m/V_\mathrm{rbc}$, where $U_m$ is the mean blood velocity. Pries et al. (1990) proposed a correlation for the hematocrit ratio,

$$\begin{aligned} \chi = H_\mathrm{D} + (1-H_\mathrm{D}) \, \left( 1 + 1.7 \mathrm{e}^{-0.7 a_\mathrm{c}} - 0.6 \mathrm{e}^{-0.02 a_\mathrm{c}}\right) , \end{aligned}$$

(7)

where the capillary radius, $a_\mathrm{c}$, is measured in $\upmu$m.

Consider the flow of a suspension of red blood cells through a straight, rigid and circular tube of radius $a_\mathrm{c}$ and length $L$. Cell-free zones near the vessel walls are ignored, and the cells are assumed to be distributed uniformly over the cross section. A cell population balance over a differential control volume confined between two parallel plates normal to the $x$ axis leads to a one-dimensional convection equation for the evolution of the discharge hematocrit in each segment (e.g., Davis and Pozrikidis 2011),

$$\begin{aligned} \Big ( \chi + H_\mathrm{D} \frac{\text{ d }\chi }{\text{ d }H_\mathrm{D}} \Big ) \frac{\partial H_\mathrm{D}}{\partial t} + U_m \frac{\partial H_\mathrm{D}}{\partial x} = 0. \end{aligned}$$

(8)

The flow of a suspension of cells through a circular capillary is assumed to follow Poiseuille’s law with an effective fluid viscosity $\mu _\text {eff}$ determined by the volume fraction of the suspended cells and by the radius of the capillary. A pressure difference $\Delta P$ across the segment end nodes produces a flow rate

$$\begin{aligned} Q = -\frac{\text{ d }P}{\text{ d }x}\frac{\pi a_\mathrm{c}^4}{8 \mu _\text {eff}} = \frac{\Delta P}{L} \frac{\pi a_\mathrm{c}^4}{8 \mu _\text {eff}}. \end{aligned}$$

(9)

The effective blood viscosity, $\mu _\text {eff}$, is regarded as a proportionality coefficient relating the flow rate to the pressure gradient and incorporates deviations from a circular cross section in each segment, imperfections, and entrance effects. Integrating Eq. (9) along the length of the capillary provides an expression for the mean velocity of the suspension,

$$\begin{aligned} U_m = \frac{a_\mathrm{c}^2}{8 \bar{\mu }} \, \frac{P_0-P_L}{L}, \end{aligned}$$

(10)

where

$$\begin{aligned} \bar{\mu }\equiv \frac{1}{L} \int _0^L \mu _{\text {eff}} \, \text{ d }x \end{aligned}$$

(11)

is an averaged viscosity.

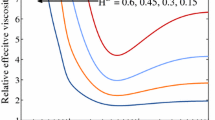
The effective viscosity of blood in a capillary segment depends on the capillary radius and hematocrit. Pries et al. (1994, 1996) proposed a correlation based on in vivo observations,

$$\begin{aligned} \mu _{\mathrm{eff}} = \mu \, \beta \, \left[ \, 1 + \beta \, (\eta _{45} -1) \, \frac{(1-H_\mathrm{D})^C-1}{( 1-0.45)^C-1} \, \right] , \end{aligned}$$

(12)

where $\beta \equiv [a_\mathrm{c}/(a_\mathrm{c}-0.55) ]^2$. The capillary radius, $a_\mathrm{c}$, is measured in $\upmu$m, $\mu = 1.85$ cP is the plasma viscosity, $C = [ \, 0.8+\exp (-0.15 \, a_\mathrm{c}) \,] \, (-1+f^{-1})+f^{-1}$ is a dimensionless exponent, $f=1 + 10 \, (0.20 a_\mathrm{c})^{12}$, and

$$\begin{aligned} \eta _{45} = 6.0 \, \mathrm{e}^{-0.17 a_\mathrm{c}} + 3.2 -2.44\, \mathrm{e}^{-0.06 \, (2 a_\mathrm{c})^{0.645}} \end{aligned}$$

(13)

is the relative blood viscosity at $H_\mathrm{D}=0.45$.

Consider a bifurcation node of a capillary network where one parental capillary segment divides into two descendent segments or two capillary segments converge into one segment. The local configuration involves four pressure nodes representing network junctions that form the end points of the three segments. The dynamics at a bifurcation is governed by mass and population balances. A mass balance requires that $\sum _{i=1}^3 Q_i = 0$, which, using Eq. (9), can be expressed as

$$\begin{aligned} \sum _{i=1}^3 (P_0 - P_i) \frac{{a_\mathrm{c}}_{i}^4}{\bar{\mu }_i L_{i}} = 0, \end{aligned}$$

(14)

where $P_0$ is the pressure at the central node, ${a_\mathrm{c}}_i$ is the radius of capillary $i$, and $Q_i$ is the corresponding flow rate. By convention, $Q_i >0$ when blood is driven away from the bifurcation along the $i$th capillary for $i=1, 2, 3$.

Conservation of the volume of the red blood cells at a bifurcation requires that

$$\begin{aligned} Q_1 H_{\mathrm{D}_1} + Q_2 H_{\mathrm{D}_2} + Q_3 H_{\mathrm{D}_3} = 0, \end{aligned}$$

(15)

where the discharge hematocrit is evaluated at the end of the segment at the bifurcation. In the case of a converging bifurcation where, for example, $Q_1<0,\,Q_2<0$,and $Q_3>0$, the first two streams merge into one and Eq. (15) can be solved for $H_{\mathrm{D}_3}$ in terms of the known $H_{\mathrm{D}_1},\,H_{\mathrm{D}_2}$, and the three flow rates,

$$\begin{aligned} H_{\mathrm{D}_3} = \psi _1 H_{\mathrm{D}_1}+ \psi _2 H_{\mathrm{D}_2}, \end{aligned}$$

(16)

where

$$\begin{aligned} \psi _1 \equiv - Q_1/Q_3, \qquad \psi _2 \equiv - Q_2/Q_3, \end{aligned}$$

(17)

are positive fractional flow rates determined by hydrodynamics.

In the case of a diverging bifurcation where, for example, $Q_1>0,\,Q_2>0$, and $Q_3<0$, the third stream splits into two streams carrying fluid away from the bifurcation, and the red blood cell concentration in each descendent segment depends on the corresponding fractional flow rates. This dependence is incorporated into the model as an effective boundary condition for $H_\mathrm{D}$ at the entrance of the descendent segments at the bifurcation. Introducing the positive cell fractional flow rates

$$\begin{aligned} \phi _1 \equiv - \frac{Q_{\mathrm{rbc}_1}}{Q_{\mathrm{rbc}_3}} = \psi _1 \, \frac{H_{\mathrm{D}_1}}{H_{\mathrm{D}_3}},\qquad \phi _2 \equiv - \frac{Q_{\mathrm{rbc}_2}}{Q_{\mathrm{rbc}_3}} = \psi _2 \, \frac{H_{\mathrm{D}_2}}{H_{\mathrm{D}_3}}, \end{aligned}$$

(18)

the outgoing discharge hematocrits are given by

$$\begin{aligned} H_{\mathrm{D}_1} = \frac{\phi _1}{\psi _1} \, H_{\mathrm{D}_3}, \qquad H_{\mathrm{D}_2} = \frac{\phi _2}{\psi _2} \, H_{\mathrm{D}_3}. \end{aligned}$$

(19)

The cell partitioning law at a bifurcation can be written in terms of the partition function $\phi _1/\phi _2 \equiv \mathcal {F}_1(a_3, H_{\mathrm{D}_3}; \psi _2, a_1/a_2)$ (e.g., Pozrikidis 2009). Consequently,

$$\begin{aligned} \phi _1 = \frac{\mathcal {F}_1}{\mathcal {F}_1+1},\qquad \phi _2 = \frac{1}{\mathcal {F}_1+1}. \end{aligned}$$

(20)

Klitzman and Johnson (1982) proposed a simple partitioning law,

$$\begin{aligned} \mathcal {F}_1 = (\psi _1/\psi _2)^q, \end{aligned}$$

(21)

where $q$ is an unspecified, dimensionless parameter. When $q=1$, all involved hematocrits are equal, $H_{\mathrm{D}_1} = H_{\mathrm{D}_2} = H_{\mathrm{D}_3}$, independent of the individual flow rates. As $q \rightarrow \infty$, all red blood cells are channeled into the descendent branch with the largest flow rate. Pries et al. (1990, 1992) proposed the empirical relation

$$\begin{aligned} \mathcal {F}_1 = \Big ( \frac{a_{2}}{a_{1}} \Big )^{3.48/a_3} \times \Big ( \frac{\psi _1-X_0}{1-\psi _1-X_0} \Big )^q, \end{aligned}$$

(22)

where $q= 1+ 3.49 \, (1-H_{\mathrm{D}_3})/a_3,\,X_0=0.2/a_3$, and the capillary radii, $a_{1}, a_{2}$, and $a_{3}$, are measured in $\upmu$m. When $a_1=a_2$ and $X_0=0$, the functional form of Eq. (21) is recovered. The partitioning law of Fenton et al. (1985b) corresponds to

$$\begin{aligned} \mathcal {F}_1 = {\left\{ \begin{array}{ll} 0 &{}\ \text{ if } \psi _1 < \dfrac{(b_0-1)}{2 b_0}, \\ \dfrac{1+b_0(2 \psi _1 - 1)}{1-b_0(2 \psi _1 -1)} &{}\ \text{ if } \dfrac{(b_0-1)}{2 b_0} \le \psi _1 \le \dfrac{(b_0+1)}{2 b_0}, \\ \infty &{}\ \text{ if } \psi _1 > \dfrac{(b_0+1)}{2 b_0}, \end{array}\right. } \end{aligned}$$

(23)

where $b_0 = 1/[1.4 - \sqrt{D_\mathrm{rbc}/(2a_3)}] \ge 1$ and $D_\mathrm{rbc}$ is the diameter of a red blood cell.