Skip to main content
SpringerLink
Log in

A Mathematical and Numerical Investigation of the Hemodynamical Origins of Oscillations in Microvascular Networks

  • Original Article
  • Published:
Bulletin of Mathematical Biology Aims and scope Submit manuscript

Abstract

Evidence is presented to show that self-sustained oscillations of purely hemodynamical origin are possible in some arcade-type microvascular networks supplied with steady boundary conditions, but that in others the oscillations disappear with sufficient reduction of the time step Δt, showing them to be numerical artefacts. In an attempt to elucidate the mechanisms involved in the onset of fluctuations, we proceed to perform a linear stability analysis for the convective model of Kiani et al. (Microvasc. Res. 45:219–232, 1993; Am. J. Physiol. 266(35):H1822–H1828, 1994), and show that this leads via a system of delay differential equations to a nonlinear eigenvalue problem. This result generalises the characteristic equation obtained by Carr et al. (Ann. Biomed. Eng. 33:764–771, 2005) and Geddes et al. (SIAM J. Appl. Dyn. Syst. 6(4):694–727, 2007) who solved a special case in a two node network. An implicit numerical method is proposed for the computation of blood flows in networks using the convective model.

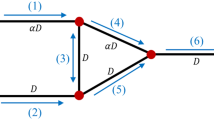
In a moderate size subnetwork of one of the networks chosen by Kiani et al. (Am. J. Physiol. 266(35):H1822–H1828, 1994), the topology, vessel lengths, and diameters of which were based on microvascular networks in the rat mesentery, we compare results generated using the original explicit numerical method of Kiani et al. (Am. J. Physiol. 266(35):H1822–H1828, 1994) with those from our implicit scheme. From the linear stability theory, a critical value D RBC,crit of a red blood cell diameter parameter D RBC in the plasma skimming model of Fenton et al. (Pflügers Arch. 403:396–401, 1985b) is identified for the onset of oscillations about steady state and both the explicit and implicit methods are used to calculate the inflow hematocrit solutions in all vessels of the subnetwork at the critical parameter value, subject to perturbed initial conditions. The results of the implicit method are demonstrated to be in excellent and superior agreement with the predictions of the linear analysis in this case. For values of D RBC slightly larger than D RBC,crit the bifurcating periodic solutions calculated using either the explicit or implicit schemes are characteristic of those of a supercritical Hopf bifurcation and the graphs of D RBC vs. oscillation amplitude would seem to converge as Δt→0.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  • Broyden, C. G. (1965). A class of methods for solving nonlinear simultaneous equations. Math. Comput., 19(92), 577–593.

    Article  MathSciNet  MATH  Google Scholar 

  • Buzsáki, G., & Draguhn, A. (2004). Neuronal oscillations in cortical networks. Science, 304, 1926–1929.

    Article  Google Scholar 

  • Carr, R. T., & Lacoin, M. (2000). Nonlinear dynamics of microvascular flow blood flow. Ann. Biomed. Eng., 28, 641–652.

    Article  Google Scholar 

  • Carr, R. T., Geddes, J. B., & Wu, F. (2005). Oscillations in a simple microvascular network. Ann. Biomed. Eng., 33, 764–771.

    Article  Google Scholar 

  • Cokelet, G. R. (1997). A commentary on the “in vivo viscosity law”. Biorheology, 34(4–5), 363–367. Discussion 369–373.

    Article  Google Scholar 

  • Davis, J. M., & Pozrikidis, C. (2011). Numerical simulation of unsteady blood flow through capillary networks. Bull. Math. Biol., 73, 1857–1880.

    Article  MathSciNet  MATH  Google Scholar 

  • Dawant, B., Levin, M., & Popel, A. S. (1986). Effect of dispersion of vessel diameters and lengths in stochastic networks. I. Modeling of microcirculatory flow. Microvasc. Res., 31, 203–222.

    Article  Google Scholar 

  • Dellimore, J. W., Dunlop, M. J., & Canham, P. B. (1983). Ratio of cells and plasma in blood flowing past branches in small plastic channels. Am. J. Physiol., 244, H635–H643.

    Google Scholar 

  • Eisenstat, S. C., Schultz, M. H., & Sherman, A. H. (1982). Algorithms and data structures for sparse symmetric Gaussian elimination. SIAM J. Sci. Stat. Comput., 2(2), 225–237.

    MathSciNet  Google Scholar 

  • Ellis, C. G., Wrigley, S. M., & Groom, A. C. (1994). Heterogeneity of red blood cell perfusion in capillary networks supplied by a single arteriole in resting skeletal muscle. Circ. Res., 75, 357–368.

    Article  Google Scholar 

  • Fabry, M. E., Kaul, D. K., Carmen, R., Baez, S., Rieder, R., & Nagel, R. L. (1981). Some aspects of the pathophysiology of homozygous Hb CC erythrocytes. J. Clin. Invest., 67(5), 1284–1291.

    Article  Google Scholar 

  • Fagrell, B., Intaglietta, M., & Östergren, J. (1980). Relative hematocrit in human skin capillaries and its relationship to capillary flow velocity. Microvasc. Res., 20, 327–335.

    Article  Google Scholar 

  • Fåhraeus, R. (1929). The suspension stability of the blood. Physiol. Rev., 9, 241–274.

    Google Scholar 

  • Fåhraeus, R., & Lindqvist, T. (1931). The viscosity of blood in narrow capillary tubes. Am. J. Physiol., 96, 562–568.

    Google Scholar 

  • Fenton, B. M., Carr, R. T., & Cokelet, G. R. (1985a). Nonuniform red cell distribution in 20 to 100 μm bifurcations. Microvasc. Res., 29, 103–126.

    Article  Google Scholar 

  • Fenton, B. M., Wilson, D. W., & Cokelet, G. R. (1985b). Analysis of the effects of measured white blood cell entrance times on hemodynamics in a computer model of a microvascular bed. Pflügers Arch., 403, 396–401.

    Article  Google Scholar 

  • Forouzan, O., Yang, X., Sosa, J. M., Burns, J. M., & Shevkoplyas, S. S. (2012). Spontaneous oscillations of capillary blood flow in artificial microvascular networks. Microvasc. Res., 84, 123–132.

    Article  Google Scholar 

  • Fung, Y.-C. (1973). Stochastic flow in capillary blood vessels. Microvasc. Res., 5(1), 34–48.

    Article  MathSciNet  Google Scholar 

  • Furman, M. B., & Olbricht, W. L. (1985). Unsteady cell distributions in capillary networks. Biotechnol. Prog., 1(1), 26–32.

    Article  Google Scholar 

  • Geddes, J. B., Carr, R. T., Karst, N. J., & Wu, F. (2007). The onset of oscillations in microvascular blood flow. SIAM J. Appl. Dyn. Syst., 6(4), 694–727.

    Article  MathSciNet  MATH  Google Scholar 

  • Geddes, J. B., Carr, R. T., Wu, F., Lao, Y., & Maher, M. (2010). Blood flow in microvascular networks: a study in nonlinear biology. Chaos, 20, 045123.

    Article  MathSciNet  Google Scholar 

  • Glass, L. (2001). Synchronization and rhythmic processes in physiology. Nature, 410, 277–284.

    Article  Google Scholar 

  • Griffith, T. M. (1996). Temporal chaos in the microcirculation. Cardiovasc. Res., 31, 342–358.

    Google Scholar 

  • Hestenes, M. R., & Stiefel, E. (1952). Methods of conjugate gradients for solving linear systems. J. Res. Natl. Bur. Stand., 49(6), 410–436.

    Article  MathSciNet  Google Scholar 

  • Hopf, E. (1942). Abzweigung einer periodischen Lösung von einer stationären Lösung eines Differentialsystems. In Berichten der Mathematisch-Physischen Klasse der Sächsischen Akademie der Wissenschaften zu Leipzig (Vol. XCIV, pp. 1–22).

    Google Scholar 

  • Jarlebring, E., & Voss, H. (2005). Rational Krylov for nonlinear eigenproblems, an iterative projection method. Appl. Math.-Czech., 50(6), 543–554.

    Article  MathSciNet  MATH  Google Scholar 

  • Jarlebring, E., Michiels, W., & Meerbergen, K. (2012). A linear eigenvalue algorithm for the nonlinear eigenvalue problem. Numer. Math., 122(1), 169–195. doi:10.1007/s00211-012-0453-0.

    Article  MathSciNet  MATH  Google Scholar 

  • Kiani, M. F., Cokelet, G. R., & Sarelius, I. H. (1993). Effect of diameter variability along a microvessel segment on pressure drop. Microvasc. Res., 45, 219–232.

    Article  Google Scholar 

  • Kiani, M. F., Pries, A. R., Hsu, L. L., Sarelius, I. H., & Cokelet, G. R. (1994). Fluctuations in microvascular blood flow parameters caused by hemodynamic mechanisms. Am. J. Physiol., Heart Circ. Physiol., 266(35), H1822–H1828.

    Google Scholar 

  • Klitzman, B., & Johnson, P. C. (1982). Capillary network geometry and red cell distribution in hamster cremaster muscle. Am. J. Physiol., Heart Circ. Physiol., 242(11), H211–H219.

    Google Scholar 

  • Kublanovskaja, V. N. (1969). The application of Newton’s method to the determination of the eigenvalues of λ-matrices. Dokl. Akad. Nauk SSSR, 188, 1004–1005. Soviet Math. Dokl. 10, 1240–1241.

    MathSciNet  Google Scholar 

  • Kublanovskaya, V. N. (1970). On an approach to the solution of the generalized latent value problem for λ-matrices. SIAM J. Numer. Anal., 7(4), 532–537.

    Article  MathSciNet  MATH  Google Scholar 

  • Levin, M., Dawant, B., & Popel, A. S. (1986). Effect of dispersion of vessel diameters and lengths in stochastic networks. II. Modeling of microvascular hematocrit distribution. Microvasc. Res., 31, 223–234.

    Article  Google Scholar 

  • Lew, H. S. (1972). Role of flow bifurcation in creating an oscillatory flow in capillary blood vessels. J. Biomech., 5(2), 231–238.

    Article  Google Scholar 

  • Liao, X.-H., Qian, Y., Mi, Y.-Y., Xia, Q.-Z., Huang, X.-Q., & Hu, G. (2011). Oscillation sources and wave propagation paths in complex networks consisting of excitable nodes. Front. Phys., 6(1), 124–132.

    Article  Google Scholar 

  • Lorthois, S., & Cassot, F. (2010). Fractal analysis of vascular networks: insights from morphogenesis. J. Theor. Biol., 262, 614–633.

    Article  Google Scholar 

  • Moler, C. B., & Stewart, G. W. (1973). An algorithm for generalized matrix eigenvalue problems. SIAM J. Numer. Anal., 10, 241–256.

    Article  MathSciNet  MATH  Google Scholar 

  • Obrist, D., Weber, B., Buck, A., & Jenny, P. (2010). Red blood cell distribution in simplified capillary networks. Philos. Trans. R. Soc. A, 368, 2897–2918.

    Article  MathSciNet  MATH  Google Scholar 

  • Papenfuss, H.-D., & Gross, J. F. (1981). Microhemodynamics of capillary networks. Biorheology, 18, 673–692.

    Google Scholar 

  • Pop, S. R., Richardson, G., Waters, S. L., & Jensen, O. E. (2007). Shock formation and non-linear dispersion in a microvascular capillary network. Math. Med. Biol., 24(4), 379–400.

    Article  MATH  Google Scholar 

  • Popel, A. S., & Johnson, P. C. (2005). Microcirculation and hemorheology. Annu. Rev. Fluid Mech., 37, 43–69.

    Article  MathSciNet  Google Scholar 

  • Pozrikidis, C. (2009). Numerical simulation of blood flow through microvascular capillary networks. Bull. Math. Biol., 71, 1520–1541.

    Article  MathSciNet  MATH  Google Scholar 

  • Pries, A. R., Secomb, T. W., Gaehtgens, P., & Gross, J. F. (1990). Blood flow in microvascular networks. Experiments and simulation. Circ. Res., 67(4), 826–834.

    Article  Google Scholar 

  • Pries, A. R., Neuhaus, D., & Gaehtgens, P. (1992). Blood viscosity in tube flow: dependence on diameter and hematocrit. Am. J. Physiol., Heart Circ. Physiol., 96(32), H1770–H1778.

    Google Scholar 

  • Pries, A. R., Secomb, T. W., Geßner, T., Sperandio, M. B., Gross, J. F., & Gaehtgens, P. (1994). Resistance to blood flow in microvessels in vivo. Circ. Res., 75, 904–915.

    Article  Google Scholar 

  • Pries, A. R., Secomb, T. W., & Gaehtgens, P. (1996). Biophysical aspects of blood flow in the microvasculature. Cardiovasc. Res., 32, 654–667.

    Google Scholar 

  • Ruhe, A. (1973). Algorithms for the nonlinear eigenvalue problem. SIAM J. Numer. Anal., 10(4), 674–689.

    Article  MathSciNet  MATH  Google Scholar 

  • Ruhe, A. (1996). Computing nonlinear eigenvalues with spectral transformation Arnoldi. ZAMM—Z. Angew. Math. Mech., 76 S2, 17–20.

    Google Scholar 

  • Saad, Y., & Schultz, M. H. (1986). GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput., 7, 856–869.

    Article  MathSciNet  MATH  Google Scholar 

  • Schmid-Schönbein, G. W., Skalak, R., Usami, S., & Chien, S. (1980). Cell distribution in capillary networks. Microvasc. Res., 19, 18–44.

    Article  Google Scholar 

  • Selverston, A. I., & Moulins, M. (1985). Oscillatory neural networks. Annu. Rev. Physiol., 47, 29–48.

    Article  Google Scholar 

  • Sleijpen, G. L. G., Booten, G. L., Fokkema, D. R., & van der Vorst, H. A. (1996). Jacobi Davidson type methods for generalized eigenproblems and polynomial eigenproblems. BIT, 36, 595–633.

    Article  MathSciNet  MATH  Google Scholar 

  • Vogels, T. P., Rajan, K., & Abbott, L. F. (2005). Neural network dynamics. Annu. Rev. Neurosci., 28, 357–376.

    Article  Google Scholar 

  • Voronoi, G. (1908). Nouvelles applications des paramètres continus à la théorie des formes quadratiques. J. Reine Angew. Math., 133, 97–178.

    MATH  Google Scholar 

  • Voss, H. (2003). A Jacobi–Davidson method for nonlinear eigenproblems (Report 66). Arbeitsbereich Mathematik, TU Hamburg-Harburg. Proc. ICCS04, Krakow, Poland, pp. 34–41.

  • Voss, H. (2004). An Arnoldi method for nonlinear eigenvalue problems. BIT, 44(2), 387–401.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

Sylvie Lorthois is thanked for having suggested a study of this problem to the second author a couple of years ago and for proposing Voronoi diagrams as a way of generating large complex arcade-type network topologies. The authors wish to thank Russell T. Carr, Mohammad Kiani, and Axel Pries for supplying them with helpful technical information about the computations performed in some of their articles. This work was partially supported by a Discovery Grant from the Natural Sciences and Engineering Research Council of Canada.

Author information

Authors and Affiliations

  1. Département de mathématiques et de statistique, Université de Montréal, C.P. 6128, succ. centre-ville, Montréal, QC H3C 3J7, Canada

    Yasmine Tawfik & Robert G. Owens

Authors
  1. Yasmine Tawfik
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Robert G. Owens
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Robert G. Owens.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Tawfik, Y., Owens, R.G. A Mathematical and Numerical Investigation of the Hemodynamical Origins of Oscillations in Microvascular Networks. Bull Math Biol 75, 676–707 (2013). https://doi.org/10.1007/s11538-013-9825-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11538-013-9825-6

Keywords

Search

Navigation