Productivity and Equilibrium in Simple Biofilm Models

Abstract

Biofilms are dense, sessile collections of microorganisms with complicated internal structures. However, in many applications internal details are less important, rather basic, averaged information such as overall community productivity are of most interest. This paper studies averaged community functions in the context of one dimensional, single species, single limiting substrate biofilm models. In particular, using a derived formula for flux of substrate into the biofilm as a function of biofilm height and substrate loading, overall community production can be calculated and system equilibria can be characterized. Consequences for equilibria dependence on a number of mechanisms for balancing growth are considered.

Appendices

Appendix A: Proof of Concavity Lemma

Proof

Note that F(0)=0 by definition. Also, since r(S)>0 for S>0, then R(S) is a strictly increasing function of S. Hence, since S(z)>S(0) for z>0, F is real and strictly positive for H>0. Note also, again since r(S)>0 for S>0, that S(0;H) is a strictly decreasing function of H—this is a consequence of a maximum principle for (9), or, alternatively, can be seen via a phase plane analysis—so that $R_{1}-R_{0}(H)=R(S_{\rm ext})-R(S(0;H))$ is a strictly increasing function of H. Thus, F is a strictly increasing function of H and F′(H)>0.

Now choose 0≤H ₁<H ₂. Note

$$ F'(H) = \frac{1}{\sqrt{2D}}\frac{-R'_0(H)}{\sqrt{R_1-R_0(H)}}. $$

Since

$$ \frac{1}{\sqrt{2D}}\frac{1}{\sqrt{R_1-R_0(H_1)}} > \frac{1}{\sqrt{2D}}\frac{1}{\sqrt{R_1-R_0(H_2)}} $$

then F′(H ₁)≥F′(H ₂) will follow if it is the case that $-R'_{0}(H_{1})\geq-R'_{0}(H_{2})\geq0$, i.e., if

$$ R'_0(H_1)\leq R'_0(H_2) \leq0. $$

(13)

Observe that

$$ R'_0(H)=\frac{d}{dH}R\bigl(S(0;H)\bigr)=r \bigl(S(0;H)\bigr)\frac{d}{dH}S(0;H) $$

and, since S(0;H) is a decreasing function of H,

$$ r\bigl(S(0;H_1)\bigr)>r\bigl(S(0;H_2)\bigr)\geq0. $$

Hence, (13) will follow if

$$ \frac{d}{dH}S(0;H_1)<\frac{d}{dH}S(0;H_2)<0. $$

(14)

The remainder of the proof consists of showing for sufficiently small |H ₂−H ₁| that (14) holds and so, tracing back, for sufficiently small |H ₂−H ₁| that F′(H ₁)≥F′(H ₂). As a consequence, F″(H)≤0 for any H>0.

To begin, differentiate (9) with respect to H to obtain

$$ S_{Hzz}(z;H) = \frac{1}{D}r'(S)S_H(z;H) $$

(15)

(where subscripts designate partial derivatives) defined on the domain H>0, z∈[0,H]. Equation (15) is equipped with boundary condition S _Hz (0;H)=0 at z=0 since S _z (0;H)=0 for all H (using smoothness properties of (9) including up to the boundary, derivatives with respect to z and H commute). At the z=H boundary,

using $S(H+\Delta H;H+\Delta H) = S(H;H)=S_{\rm ext}$. Thus, letting ΔH→0 and referring to (5),

$$ S_H(H;H) = -S_z(H;H)=-F(H) $$

is a boundary condition for (15) at z=H.

Claim

If ΔH>0 is sufficiently small, then S _Hz (H;H+ΔH)>S _Hz (H;H).

Proof of claim

Note, using (15) including the z=H boundary condition,

and, using S _z (H;H)=F(H),

$$ S_{zH}(H+\Delta H;H+\Delta H) - S_{zH}(H;H) = F'(H)\Delta H + O\bigl((\Delta H)^2\bigr). $$

(16)

Combining the above computations

$$ S_{Hz}(H;H+\Delta H) = S_{Hz}(H;H) + \biggl(F'(H) + \frac{1}{D}r'(S_{\mathrm{ext}})F(H) \biggr)\Delta H + O \bigl((\Delta H)^2\bigr). $$

Since the quantity in parentheses is positive, the claim follows. □

Returning to the proof of the lemma, let S(z;H _j ), j=1,2 be the solutions of (9) with (dS/dz)| _z=0=0, $S(H_{j})=S_{\rm ext}$. For improved clarity, relabel these solutions as s ⁽¹⁾(z;H ₁) and s ⁽²⁾(z;H ₂) respectively. Consider again (15), except now in the form

$$ \sigma_{Hzz}^{(j)}(z;H_1) = \frac{1}{D}r' \bigl(s^{(j)}\bigr)\sigma_H^{(j)}(z;H_1), \;\;\; j=1,2, $$

on the same domain z∈[0,H ₁] for both j=1 and j=2, with boundary conditions $\sigma_{Hz}^{(j)}(0;H_{1})=0$, j=1,2, at z=0 together with, at z=H ₁, $\sigma_{Hz}^{(1)}(H_{1};H_{1})=S_{Hz}(H_{1};H_{1})$ in the j=1 case or $\sigma_{Hz}^{(2)}(H_{1};H_{1})=S_{Hz}(H_{1};H_{2})$ in the j=2 case. Note that, from above, $\sigma_{H}^{(j)}(H_{1};H_{1})<0$ and, also, for |H ₂−H ₁| sufficiently small, $\sigma_{Hz}^{(1)}(H_{1};H_{1})<\sigma_{Hz}^{(2)}(H_{1};H_{2})<0$. Also, since (d/dH)S(z;H)<0, then s ⁽²⁾(z;H ₂)<s ⁽¹⁾(z;H ₁) for z∈[0,H ₁]. Hence, as by assumption r′(S)>0 and r″(S)≤0, it follows that r′(s ⁽²⁾)≥r′(s ⁽¹⁾)>0 for z∈[0,H ₁]. It then follows that $\sigma^{(1)}_{H}(z;H_{1})<\sigma^{(2)}_{H}(z;H_{2})$ for z∈[0,H ₁]. In particular, $\sigma^{(1)}_{H}(0;H_{1})<\sigma_{H}^{(2)}(0;H_{2})$ for |H ₂−H ₁| sufficiently small, completing the proof. □

Appendix B: Fluid Shear Stress

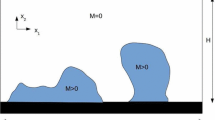
We consider a two-region domain with bulk (Newtonian) fluid in region 1, biofilm in region 2, and with interface z=h(x,t) separating the two regions; see Fig. 7. Material in both regions moves according to an incompressible (biofilm is mostly water) velocity ${\bf u}$ with accompanying pressure field p. Note that biofilm viscosities have been measured to be orders of magnitude larger than the viscosity of water (Shaw et al. 2004) so that μ ⁽¹⁾≫μ ⁽²⁾ where μ ^(j) is the kinematic viscosity of the material in region j. We will hence consider asymptotics in the parameter β=μ ⁽¹⁾/μ ⁽²⁾ through expansions

(17)

in velocity ${\bf u}$ and pressure p. We suppose that ${\bf u}$ satisfies Stokes flow equations in region 2—note that biofilms have been characterized to be viscoelastic fluids, though with elastic relaxation times that are small compared to time scales of interest here, and thus biofilms can be supposed to be low Reynolds number Newtonian fluids for our purposes (Klapper et al. 2002; Shaw et al. 2004). In region 1, ${\bf u}$ may satisfy Stokes or Navier–Stokes flow. At the interface, continuity of ${\bf u}$ as well as of normal stress are required.

Fig. 7

Biofilm (0<z<H, region 2) bulk-fluid (H<z, region 1) domain. Bottom wall (z=0) is stationary

The fields ${\bf u}$, p satisfy the following (Childress 2009):

$$ \frac{1}{\mu^{(1)}}\mathcal{L} {\bf u}^{(1)} = -\frac{1}{\mu^{(1)}} \nabla p^{(1)} + \nabla^2{\bf u}^{(1)},\qquad 0 = -\frac{1}{\mu^{(1)}}\nabla p^{(2)} + \beta\nabla^2{ \bf u}^{(2)} $$

(18)

with $\nabla\cdot{\bf u}^{(1)}=\nabla\cdot{\bf u}^{(2)}=0$ where $\mathcal{L}{\bf u}=0$ (Stokes flow) or $\mathcal{L}{\bf u}=(\partial/\partial t){\bf u}+{\bf u}\cdot\nabla {\bf u}$ (Navier–Stokes flow). At the interface, velocity continuity requires

$$ \mathbf{u}^{(1)}|_{z=H}=\mathbf{u}^{(2)}|_{z=H} $$

and stress continuity requires, also at the interface, $\mu^{(1)}(u_{y}^{(1)}+v_{x}^{(1)})|_{z=H} = \mu^{(2)}(u_{y}^{(2)}+v_{x}^{(2)})|_{z=H}$, $(-p^{(1)}+2\mu^{(1)}v_{y}^{(1)})|_{z=H} = (-p^{(2)}+2\mu^{(2)}v_{y}^{(2)})|_{z=H}$, i.e.,

In the following, we follow the large jump asymptotics method presented in Klapper and Shaw (2007). First plug expansion (17) into the equations as well as interface and boundary conditions to obtain at O(β)

$$ \nabla^2\mathbf{u}_0^{(2)}=0, \qquad \bigl(u_{0,y}^{(2)}+v_{0,x}^{(2)} \bigr)\big|_{z=H}=0,\qquad v_{0,y}^{(2)}\big|_{z=H}=0 $$

as well as the z=0 boundary condition ${\bf u}^{(2)}={\bf0}$ and the incompressibility condition $\nabla\cdot{\bf u}_{0}^{(2)}=0$. Altogether, we find that ${\bf u}_{0}^{(2)}={\bf0}$.

Continuing now with the O(β ⁰) problem, consider first the region 1 problem

$$ \frac{1}{\mu^{(1)}}\mathcal{L} {\bf u}^{(1)}_0 = - \frac{1}{\mu^{(1)}}\nabla p^{(1)}_0 + \nabla^2{\bf u}^{(1)}_0 $$

(19)

with boundary condition ${\bf u}_{0}^{(1)}={\bf u}_{0}^{(2)}={\bf0}$ at z=H. In fact, so as to retain generality by avoiding specifying conditions in the bulk fluid region (e.g., geometry, boundary conditions, Reynolds number), we will simply assume a solution ${\bf u}_{0}^{(1)}$ to (19) to be given. Then velocity field ${\bf u}_{0}^{(1)}$ in hand, move to the O(β ⁰) problem in the biofilm region, namely

$$ \nabla^2{\bf u}_1^{(2)} = \frac{1}{\mu^{(1)}} \nabla p_0^{(2)} $$

(20)

with $\nabla\cdot{\bf u}_{1}^{(2)}=0$, ${\bf u}_{1}^{(2)}|_{z=0}=0$, and, at the biofilm-bulk fluid interface z=H, zeroth order stress continuity conditions

Since ${\bf u}_{0}^{(1)}$, ${\bf u}_{0}^{(2)}$ are known then so are f and g. In the special case, by the way, that ${\bf u}_{0}^{(1)}|_{z=H}$ and $p_{0}^{(1)}|_{z=H}$ are independent of x and t, i.e., f and g are constants, then the (also x and t independent) solution to (20) and accompanying boundary conditions are

$$ u_1^{(2)}(z) = fz,\qquad v_1^{(2)}(z)=0, \qquad p_0^{(2)}=g, $$

where f and g are given by $f=u_{0,z}^{(1)}(H)$ and $g= p_{0}^{(1)}(H)$.

Altogether, if we truncate (17) at the current expansion stage, i.e.,

(21)

then the approximations ${\bf u}_{\rm appr}$, $p_{\rm appr}$ satisfy (18) and all accompanying conditions except that the interface velocity jump $[{\bf u}_{\rm appr}]|_{z=H}=O(\beta^{-1})$ rather than zero. For a next order approximation, note that by following the above procedures to compute the next terms ${\bf u}_{1}^{(1)}$, ${\bf u}_{2}^{(2)}$, $p_{1}^{(1)}$, and $p_{1}^{(2)}$, i.e., solving the O(β ⁻¹) problem, the resulting approximation

then the improved approximations $\hat{{\bf u}}_{\rm appr}$, $\hat {p}_{\rm appr}$ again satisfy (18) and all accompanying conditions except that now the interface velocity jump error is $[\hat{{\bf u}}_{\rm appr}]|_{z=H}=O(\beta^{-2})$.

Hence from (21), at least formally, we see that the normal and tangential stresses at the interface z=H are given by the functions f and g respectively (and are in fact O(β ⁰)) to error of O(β ⁻¹). Then, to O(β ⁻¹), the fluid shear stress at the biofilm interface is the same as would be seen if the biofilm were in fact a stationary wall. In this sense, shear stress at the interface is independent of the internal details of the biofilm, and, excepting channel occlusion effects, independent of biofilm thickness. Note as well, by the way, that the interface velocity is given, to O(β ⁻²) correction, by $\beta^{-1}{\bf u}_{1}^{(2)}|_{z=H}$ and hence the interface will generally not remain flat at z=H if f or g varies with x or t, although any such deformation will occur very slowly for large β.