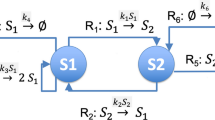
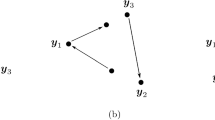
Abstract
Biochemical reaction models show a variety of dynamical behaviors, such as stable steady states, multistability, and oscillations. Biochemical reaction networks with generalized mass action kinetics are represented as directed bipartite graphs with nodes for species and reactions. The bipartite graph of a biochemical reaction network usually contains at least one cycle, i.e., a sequence of nodes and directed edges which starts and ends at the same species node. Cycles can be positive or negative, and it has been shown that oscillations can arise as a result of either a positive cycle or a negative cycle. In earlier work it was shown that oscillations associated with a positive cycle can arise from subnetworks with an odd number of positive cycles. In this article we formulate a similar graph-theoretic condition, which generalizes the negative cycle condition for oscillations. This new graph-theoretic condition for oscillations involves pairs of subnetworks with an even number of positive cycles. An example of a calcium reaction network with generalized mass action kinetics is discussed in detail.
Similar content being viewed by others
References
Alon, U. (2007). Network motifs: theory and experimental approaches. Nat. Rev. Genet., 8, 450–461.
Angeli, D., De Leenheer, P., & Sontag, E. D. (2006). On the structural monotonicity of chemical reaction networks. In 45th IEEE conference on decision and control, pp. 7–12.
Angeli, D., Ferrell, J. E., & Sontag, E. D. (2004). Detection of multistability, bifurcations, and hysteresis in a large class of biological positive-feedback systems. Proc. Natl. Acad. Sci. USA, 101, 1822–1827.
Asner, B. (1970). On the total nonnegativity of the Hurwitz matrix. SIAM J. Appl. Math., 18, 407–418.
Chickarmane, V., Kholodenko, B., & Sauro, H. (2007). Oscillatory dynamics arising from competitive inhibition and multisite phosphorylation. J. Theor. Biol., 244, 68–76.
Clarke, B. (1980). Stability of complex reaction networks. Adv. Chem. Phys., 43, 1–213.
Clarke, B., & Jiang, W. (1993). Method for deriving Hopf and saddle-node bifurcation hypersurfaces and application to a model of the Belousov–Zhabotinskii system. J. Chem. Phys., 99, 4464–4478.
Craciun, G., & Feinberg, M. (2005). Multiple equilibria in complex chemical reaction networks, I: the injectivity property. SIAM J. Appl. Math., 65, 1526–1546.
Craciun, G., & Feinberg, M. (2006). Multiple equilibria in complex chemical reaction networks, II: the species-reactions graph. SIAM J. Appl. Math., 66, 1321–1338.
Craciun, G., Tang, Y., & Feinberg, M. (2006). Understanding bistability in complex enzyme-driven reaction networks. Proc. Natl. Acad. Sci. USA, 103(23), 8697–8702.
Elowitz, M., & Leibler, S. (2000). A synthetic oscillatory network of transcriptional regulators. Nature, 403, 335–338.
Fallat, S. (2001). Bidiagonal factorization of totally nonnegative matrices. Am. Math. Mon., 108, 697–712.
Forger, D., & Peskin, C. (2003). A detailed predictive model of the mammalian circadian clock. Proc. Natl. Acad. Sci. USA, 100, 14806–14811.
Gantmacher, F. R. (1959). Applications of the theory of matrices. New York: Interscience.
Gatermann, K., Eiswirth, M., & Sensse, A. (2005). Toric ideals and graph theory to analyze Hopf bifurcation in mass action systems. J. Symb. Comput., 40, 1361–1382.
Goldbeter, A. (1995). A model for circadian oscillations in the Drosophila period protein (PER). Proc. R. Soc. Lond. B, Biol. Sci., 261, 319–324.
Goldbeter, A. (2007). Biological rhythms as temporal structures. Adv. Chem. Phys., 135, 253–295.
Goodwin, B. C. (1965). Oscillator behavior in enzymatic control processes. Adv. Enzyme Regul., 3, 425–438.
Goryachev, A., & Pokliho, A. (2008). Dynamics of Cdc42 network embodies a Turing-type mechanism of yeast cell polarity. FEBS Lett., 582, 1437–1443.
Griffith, J. (1968). Mathematics of cellular control processes, I: negative feedback to one gene. J. Theor. Biol., 20, 202–208.
Harary, F. (1969). Graph theory. Reading: Addison-Wesley.
Horn, F., & Jackson, R. (1972). General mass action kinetics. Arch. Ration. Mech. Anal., 47, 81–116.
Kitano, H. (2002). Systems biology: a brief review. Science, 295, 1662–1664.
Kitano, H. (2004). Biological robustness. Nat. Rev. Genet., 5, 826–837.
Kruse, K., & Julicher, Fr. (2005). Oscillations in cell biology. Curr. Opin. Cell Biol., 17, 20–26.
Kuznetsov, Y. (2004). Elements of applied bifurcation theory. New York: Springer.
Liu, W. M. (1994). Criterion of Hopf bifurcations without using eigenvalues. J. Math. Anal. Appl., 182, 250–256.
Lancaster, P., & Tismenetsky, M. (1985). The theory of matrices. Orlando: Academic Press.
Locke, J. et al. (2006). Experimental validation of a predicted feedback loop in the multi-oscillator clock of Arabidopsis thaliana. Mol. Syst. Biol., 2, 59.
Milo, R. et al. (2002). Network motifs: Simple building blocks of complex networks. Science, 298, 824–827.
Mincheva, M., & Craciun, G. (2008). Multigraph conditions for multistability, oscillations and pattern formation in biochemical reaction networks. Proc. IEEE, 96, 1281–1291.
Mincheva, M., & Roussel, M. R. (2006). A graph-theoretic method for detecting Turing bifurcations. J. Chem. Phys., 125, 204102.
Mincheva, M., & Roussel, M. R. (2007a). Graph-theoretic methods for the analysis of chemical and biochemical networks, I: multistability and oscillations in ordinary differential equation models. J. Math. Biol., 55, 61–86.
Mincheva, M., & Roussel, M. R. (2007b). Graph-theoretic methods for the analysis of chemical and biochemical networks, II: oscillations in networks with delays. J. Math. Biol., 55, 87–104.
Reidl, J. et al. (2006). Model of calcium oscillations due to negative feedback in olfactory cilia. Biophys. J., 90, 1147–1155.
Rockafellar, R. T. (1970). Convex analysis. Princeton: Princeton University Press.
Schuster, S. (1999). Studies on the stoichiometric structure of enzymatic reaction systems. Theory Biosci. 118, 125–139.
Schuster, S., & Höfer, T. (1991). Determining all extreme semi-positive conservation relations in chemical reaction systems: a test criterion for conservativity. J. Chem. Soc. Faraday Trans., 87, 2561–2566.
Smolen, P., Baxter, D. A., & Byrne, J. H. (2000). Modeling transcriptional control in gene networks. Methods, recent results, and future directions. Bull. Math. Biol., 62, 247–292.
Tsai, T. et al. (2008). Robust, tunable biological oscillators from interlinked positive and negative feedback loops. Science, 321, 126–129.
Tyson, J. J. (1975). Classification of instabilities in chemical reaction systems. J. Chem. Phys., 62, 1010–1015.
Tyson, J. J. (1991). Modeling the cell division cycle: cdc2 and cyclin interactions. Proc. Natl. Acad. Sci. USA, 88, 7328–7332.
Tyson, J. J., & Othmer, H. (1978). The dynamics of feedback control circuits in biochemical pathways. Prog. Theor. Biol., 5, 1–62.
Tyson, J. J., Chen, K. C., & Novak, B. (2003). Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell. Curr. Opin. Cell Biol., 15, 221–231.
Volpert, A., & Hudyaev, S. (1985). Analyses in classes of discontinuous functions and equations of mathematical physics. Dordrecht: Martinus Nijhoff (Chap. 12).
Volpert, A., & Ivanova, A. (1987). Mathematical models in chemical kinetics. In Mathematical modeling (pp. 57–102). Moscow: Nauka (in Russian).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Mincheva, M. Oscillations in Biochemical Reaction Networks Arising from Pairs of Subnetworks. Bull Math Biol 73, 2277–2304 (2011). https://doi.org/10.1007/s11538-010-9620-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11538-010-9620-6