Density-functional-theory formulation of classical and quantum Hooke’s law

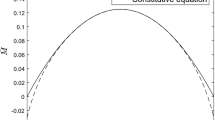
Abstract

A fundamental property of solid materials is their stress state. Stress state of a solid or thin film material has profound effects on its thermodynamic stability and physical and chemical properties. The classical mechanical stress (σ ^M) originates from lattice strain (ɛ), following Hooke’s law: σ ^M=Cɛ, where C is elastic constant matrix. Recently, a new concept of quantum electronic stress (σ ^QE) is introduced to elucidate the extrinsic electronic effects on the stress state of solids and thin films, which follows a quantum analog of classical Hooke’s law: σ ^QE=Ξ(Δn), where Ξ is the deformation potential of electronic states and Δn is the variation of electron density. Here, we present mathematical derivation of both the classical and quantum Hooke’s law from density functional theory. We further discuss the physical origin of quantum electronic stress, arising purely from electronic excitation and perturbation in the absence of lattice strain (ɛ=0), and its relation to the degeneracy pressure of electrons in solid and their interaction with the lattice.